华师七上1.3相反数 课件(共27张PPT)
文档属性
| 名称 | 华师七上1.3相反数 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 08:32:00 | ||
图片预览







文档简介
(共27张PPT)
(华师大版)七年级
上
1.3相反数
有理数
第1章
“—”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
内容总览
目录
教学目标
1.了解相反数的概念;
2.会在数轴上表示两个互为相反数的数,并且发现表示互为相反数的两点在原点的两侧,到原点的距离相等;
3.会对含有多重符号的数进行化简,体会数学符号化和数形结合思想.
新知导入
成语故事《南辕北辙》讲了一个人……
如果点O表示魏国的位置,点A表示楚国的位置,我们假设楚国与魏国的距离为30 km,以魏国为坐标原点,我们规定向南为正方向,而此人从魏国出发向北到了点B也走了30 km,请同学们把这3个点在数轴上表示出来.
现在的位置
魏国
楚国
O
B
A
-30
-20
-10
0
10
20
30
●
●
●
B
新知导入
若我们假设楚国A1与魏国的距离为50km,同样以魏国为坐标原点,规定向南为正方向,而此人从魏国出发向北到了点B1也走了50 km,请同学们也把这2个点在数轴上表示出来.
O
A
●
●
●
B
-30
-10
0
10
20
30
-20
40
50
-40
-50
●
B1
A1
●
思考:观察点A,A1与点B,B1两对点,你发现了什么?
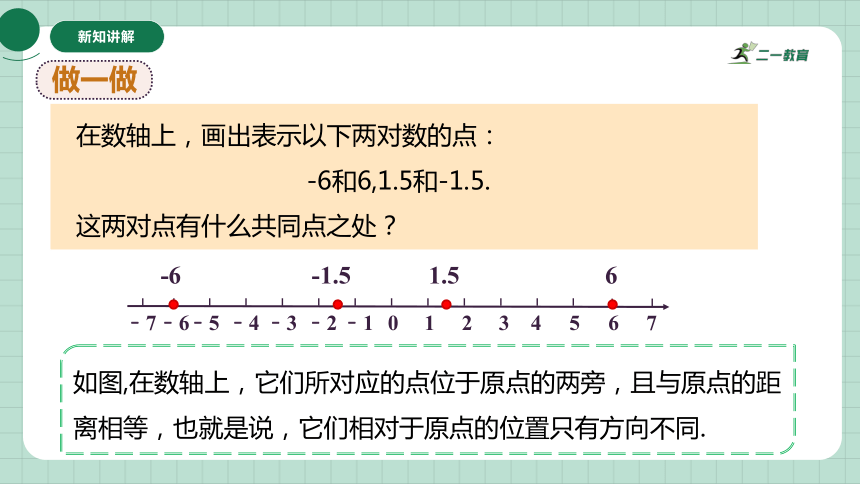
在数轴上,画出表示以下两对数的点:
-6和6,1.5和-1.5.
这两对点有什么共同点之处?
新知讲解
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
-1.5
1.5
-6
6
如图,在数轴上,它们所对应的点位于原点的两旁,且与原点的距离相等,也就是说,它们相对于原点的位置只有方向不同.
做一做
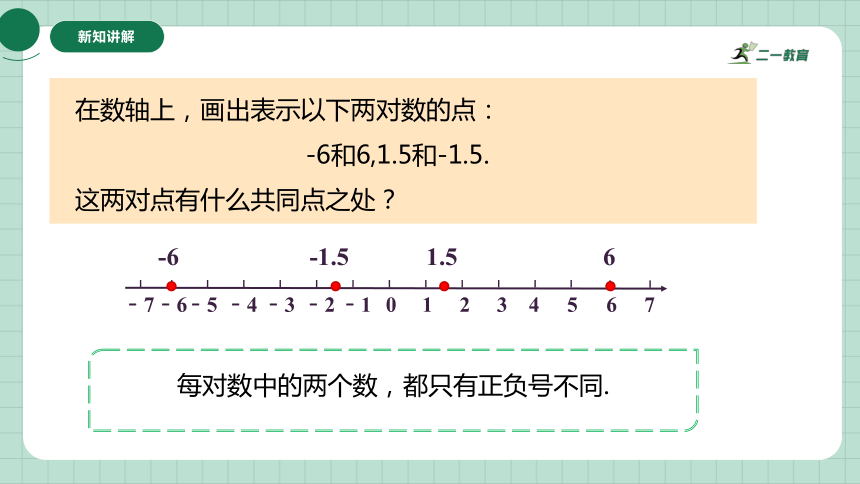
在数轴上,画出表示以下两对数的点:
-6和6,1.5和-1.5.
这两对点有什么共同点之处?
新知讲解
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
-1.5
1.5
-6
6
每对数中的两个数,都只有正负号不同.
新知讲解
一般地,设 a 是一个正数,数轴上与原点的距离是 a 的点有___个,它们分别在正、负半轴上,表示____和_____,这两个数只有______不同.
-a a
符号
-a
a
两
新知讲解
在数轴上,表示互为相反数的两个点分别位于原点的两旁,且与原点的距离相等.
我们规定: 0的相反数是0.
像6和-6、1.5和- 1.5那样,只有正负号不同的两个数称互为相反数,也就是说,其中一个数是另一个数的相反数,
这里,6和-6互为相反数,即6是-6的相反数,-6是6的相反数.
相反数
新知讲解
0
1
2
3
-1
-2
-3
设 a 表示一个数,-a 一定是负数吗?
当 a 是正数时,a 的相反数 -a 是负数;
当 a 是负数时,a 的相反数 -a是正数;
当 a 是 0 时,a 相反数是 0.
新知讲解
例1 分别写出下列各数的相反数:
+5,-7,-3,11.2.
解:+ 5的相反数是-5,- 7的相反数是7,
-3的相反数是-3,11.2的相反数是-11.2.
新知讲解
相反数的求法:
(1) 求一个数的相反数,只需改变这个数前面的符号,即可得到这个数的相反数.
(2) 求一个数的相反数就是在这个数的前面加上“-”号,即a的相反数是-a,其实只是改变这个数的符号.
新知讲解
我们通常在一个数的前面添上 “ -” 号, 表示这个数的相反数 .
例如, - 4、 + 5.5 的相反数分别为:
- (- 4) = 4, - (+ 5.5) = - 5.5.
在一个数的前面添上 “+” 号, 仍表示这个数本身.
例如:+ (- 4) = - 4, + (+ 12) = 12.
数a的相反数
记作-a.
新知讲解
例2 化简:
(1) -(+ 10); (2) + (-0.15);
(3) +(+ 3); (4) -(- 20).
解:(1) -(+10)=-10.
(2) + (-0.15)=-0.15.
(3) + (+3)=+3= 3.
(4) -(-20)=20.
新知讲解
技巧:(一查二定)
式子中含偶数个“-”号时,结果正;
含奇数个“-”号时,结果为负。
凡是“+”都去掉。
符号化简
在任意一个数面前添上“ ”号,就可以得到它的相反数.双重符号化简规则为:同号得 ,异号得 .
-
负
正
新知讲解
练一练
写出下列各数的相反数.
(1)7;
(2)+6.3;
(3)-;
(4)+(-);
(5)-(+3);
(6)-(-2.6)
(1)-7;
(2)-(+6.3) = -6.3;
(3)-(-)= ;
(4)-[+(-)] = ;
(5)-[-(+3)] = ;
(6)-[-(-2.6)] = -2.6
课堂练习
1.下列说法中,正确的是 ( )
A. 正数与负数互为相反数
B. 符号不同的两个数互为相反数
C. 数轴上原点两侧的两个点所表示的数互为相反数
D. 任何一个有理数都有相反数
D
基础题
课堂练习
2.下列各对数中,互为相反数的有( )
①-1与+1;②+(+1)与-1;③-(-2)与+(-2);④-(-)与+(+) ;
⑤+[-(+1)]与-[+(-1)];⑥-(+2)与-(-2).
A.6对 B.5对 C.4对 D.3对
B
基础题
3.一个数在数轴上的对应点与它的相反数在数轴上的对应点的距离是5,那么这个数是( )
A.5或-5 B.2.5或-2.5 C.5或-2.5 D.- 5或2.5
B
课堂练习
4.化简下列各数
(1)-(+15) (2)+(-0.55) (3)+(+8)
(4)-(-19) (5)+[-(-4.1)] (6)-[+(-2)]
解:(1)-(+15)=-15;(2)+(-0.55)=-0.55;
(3)+(+8)=8;(4)-(-19)=19;
(5)+[-(-4.1)]=+(+4.1)=4.1;
(6)-[+(-2)]=-(-2)=2.
基础题
课堂练习
1.若-[-(-x)]=8,则x的相反数是 .
8
提升题
2.已知a是-[-(-5)]的相反数,b比最小的正整数大4,c是相反数等于它本身的数,则a+b+c的值是______.
10
3.已知a是-[-(-5)]的相反数,b比最小的正整数大4,c是相反数为它本身的数,计算3a+4b+5c的值.
课堂练习
解:因为-[-(-5)]=-5,所以a=-(-5)=5.
因为最小的正整数是1,b比最小的正整数大4,
所以b=1+4=5.
因为c是相反数为它本身的数,所以c=0.
所以3a+4b+5c=3×5+4×5+5×0=35.
提升题
化简下列各式,并解答问题:
①-(-2);②+(-);③-[-(-4)];④-[-(+3.5)];
⑤-{-[-(-5)]};⑥-{-[-(+5)]}.
问:(1)当+5前面有2 018个负号时,化简后结果是多少?
(2)当-5前面有2 019个负号时,化简后的结果是多少?你能总结出什么规律?
课堂练习
拓展题
解:①-(-2)=2;②+(-=-;③-[-(-4)]=-4;
④-[-(+3.5)]=3.5;⑤-{-[-(-5)]}=5;
⑥-{-[-(+5)]}=-5.
(1)当+5前面有2 018个负号时,化简后的结果是+5.
(2)当-5前面有2 019个负号时,化简后的结果是+5.
总结规律:一个数的前面有奇数个负号,化简后的结果等于它的相反数,有偶数个负号,化简后的结果等于它本身.
课堂练习
拓展题
课堂总结
1.相反数的定义:
只有正负号不同的两个数称互为相反数.
2.相反数的求法:
(1) 求一个数的相反数,只需改变这个数前面的符号,即可得到这个数的相反数.
(2) 求一个数的相反数就是在这个数的前面加上“-”号,即a的相反数是-a,其实只是改变这个数的符号.
3.在任意一个数面前添上“-”号,就可以得到它的相反数.
双重符号化简规则为:同号得正,异号得负.
板书设计
1.相反数的定义:
2.相反数的求法:
3.多重符号的化简一般有两种方法:
课题:1.3相反数
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
上
1.3相反数
有理数
第1章
“—”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
内容总览
目录
教学目标
1.了解相反数的概念;
2.会在数轴上表示两个互为相反数的数,并且发现表示互为相反数的两点在原点的两侧,到原点的距离相等;
3.会对含有多重符号的数进行化简,体会数学符号化和数形结合思想.
新知导入
成语故事《南辕北辙》讲了一个人……
如果点O表示魏国的位置,点A表示楚国的位置,我们假设楚国与魏国的距离为30 km,以魏国为坐标原点,我们规定向南为正方向,而此人从魏国出发向北到了点B也走了30 km,请同学们把这3个点在数轴上表示出来.
现在的位置
魏国
楚国
O
B
A
-30
-20
-10
0
10
20
30
●
●
●
B
新知导入
若我们假设楚国A1与魏国的距离为50km,同样以魏国为坐标原点,规定向南为正方向,而此人从魏国出发向北到了点B1也走了50 km,请同学们也把这2个点在数轴上表示出来.
O
A
●
●
●
B
-30
-10
0
10
20
30
-20
40
50
-40
-50
●
B1
A1
●
思考:观察点A,A1与点B,B1两对点,你发现了什么?
在数轴上,画出表示以下两对数的点:
-6和6,1.5和-1.5.
这两对点有什么共同点之处?
新知讲解
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
-1.5
1.5
-6
6
如图,在数轴上,它们所对应的点位于原点的两旁,且与原点的距离相等,也就是说,它们相对于原点的位置只有方向不同.
做一做
在数轴上,画出表示以下两对数的点:
-6和6,1.5和-1.5.
这两对点有什么共同点之处?
新知讲解
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
-1.5
1.5
-6
6
每对数中的两个数,都只有正负号不同.
新知讲解
一般地,设 a 是一个正数,数轴上与原点的距离是 a 的点有___个,它们分别在正、负半轴上,表示____和_____,这两个数只有______不同.
-a a
符号
-a
a
两
新知讲解
在数轴上,表示互为相反数的两个点分别位于原点的两旁,且与原点的距离相等.
我们规定: 0的相反数是0.
像6和-6、1.5和- 1.5那样,只有正负号不同的两个数称互为相反数,也就是说,其中一个数是另一个数的相反数,
这里,6和-6互为相反数,即6是-6的相反数,-6是6的相反数.
相反数
新知讲解
0
1
2
3
-1
-2
-3
设 a 表示一个数,-a 一定是负数吗?
当 a 是正数时,a 的相反数 -a 是负数;
当 a 是负数时,a 的相反数 -a是正数;
当 a 是 0 时,a 相反数是 0.
新知讲解
例1 分别写出下列各数的相反数:
+5,-7,-3,11.2.
解:+ 5的相反数是-5,- 7的相反数是7,
-3的相反数是-3,11.2的相反数是-11.2.
新知讲解
相反数的求法:
(1) 求一个数的相反数,只需改变这个数前面的符号,即可得到这个数的相反数.
(2) 求一个数的相反数就是在这个数的前面加上“-”号,即a的相反数是-a,其实只是改变这个数的符号.
新知讲解
我们通常在一个数的前面添上 “ -” 号, 表示这个数的相反数 .
例如, - 4、 + 5.5 的相反数分别为:
- (- 4) = 4, - (+ 5.5) = - 5.5.
在一个数的前面添上 “+” 号, 仍表示这个数本身.
例如:+ (- 4) = - 4, + (+ 12) = 12.
数a的相反数
记作-a.
新知讲解
例2 化简:
(1) -(+ 10); (2) + (-0.15);
(3) +(+ 3); (4) -(- 20).
解:(1) -(+10)=-10.
(2) + (-0.15)=-0.15.
(3) + (+3)=+3= 3.
(4) -(-20)=20.
新知讲解
技巧:(一查二定)
式子中含偶数个“-”号时,结果正;
含奇数个“-”号时,结果为负。
凡是“+”都去掉。
符号化简
在任意一个数面前添上“ ”号,就可以得到它的相反数.双重符号化简规则为:同号得 ,异号得 .
-
负
正
新知讲解
练一练
写出下列各数的相反数.
(1)7;
(2)+6.3;
(3)-;
(4)+(-);
(5)-(+3);
(6)-(-2.6)
(1)-7;
(2)-(+6.3) = -6.3;
(3)-(-)= ;
(4)-[+(-)] = ;
(5)-[-(+3)] = ;
(6)-[-(-2.6)] = -2.6
课堂练习
1.下列说法中,正确的是 ( )
A. 正数与负数互为相反数
B. 符号不同的两个数互为相反数
C. 数轴上原点两侧的两个点所表示的数互为相反数
D. 任何一个有理数都有相反数
D
基础题
课堂练习
2.下列各对数中,互为相反数的有( )
①-1与+1;②+(+1)与-1;③-(-2)与+(-2);④-(-)与+(+) ;
⑤+[-(+1)]与-[+(-1)];⑥-(+2)与-(-2).
A.6对 B.5对 C.4对 D.3对
B
基础题
3.一个数在数轴上的对应点与它的相反数在数轴上的对应点的距离是5,那么这个数是( )
A.5或-5 B.2.5或-2.5 C.5或-2.5 D.- 5或2.5
B
课堂练习
4.化简下列各数
(1)-(+15) (2)+(-0.55) (3)+(+8)
(4)-(-19) (5)+[-(-4.1)] (6)-[+(-2)]
解:(1)-(+15)=-15;(2)+(-0.55)=-0.55;
(3)+(+8)=8;(4)-(-19)=19;
(5)+[-(-4.1)]=+(+4.1)=4.1;
(6)-[+(-2)]=-(-2)=2.
基础题
课堂练习
1.若-[-(-x)]=8,则x的相反数是 .
8
提升题
2.已知a是-[-(-5)]的相反数,b比最小的正整数大4,c是相反数等于它本身的数,则a+b+c的值是______.
10
3.已知a是-[-(-5)]的相反数,b比最小的正整数大4,c是相反数为它本身的数,计算3a+4b+5c的值.
课堂练习
解:因为-[-(-5)]=-5,所以a=-(-5)=5.
因为最小的正整数是1,b比最小的正整数大4,
所以b=1+4=5.
因为c是相反数为它本身的数,所以c=0.
所以3a+4b+5c=3×5+4×5+5×0=35.
提升题
化简下列各式,并解答问题:
①-(-2);②+(-);③-[-(-4)];④-[-(+3.5)];
⑤-{-[-(-5)]};⑥-{-[-(+5)]}.
问:(1)当+5前面有2 018个负号时,化简后结果是多少?
(2)当-5前面有2 019个负号时,化简后的结果是多少?你能总结出什么规律?
课堂练习
拓展题
解:①-(-2)=2;②+(-=-;③-[-(-4)]=-4;
④-[-(+3.5)]=3.5;⑤-{-[-(-5)]}=5;
⑥-{-[-(+5)]}=-5.
(1)当+5前面有2 018个负号时,化简后的结果是+5.
(2)当-5前面有2 019个负号时,化简后的结果是+5.
总结规律:一个数的前面有奇数个负号,化简后的结果等于它的相反数,有偶数个负号,化简后的结果等于它本身.
课堂练习
拓展题
课堂总结
1.相反数的定义:
只有正负号不同的两个数称互为相反数.
2.相反数的求法:
(1) 求一个数的相反数,只需改变这个数前面的符号,即可得到这个数的相反数.
(2) 求一个数的相反数就是在这个数的前面加上“-”号,即a的相反数是-a,其实只是改变这个数的符号.
3.在任意一个数面前添上“-”号,就可以得到它的相反数.
双重符号化简规则为:同号得正,异号得负.
板书设计
1.相反数的定义:
2.相反数的求法:
3.多重符号的化简一般有两种方法:
课题:1.3相反数
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
