专题五 与相似三角形有关的动态变化(含解析)
文档属性
| 名称 | 专题五 与相似三角形有关的动态变化(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 784.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 21:22:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题五 与相似三角形有关的动态变化
类型一 相似三角形中的平移、翻折、旋转
方法技巧:对给定的图形(或其中一部分)进行某种位置变换(平移、翻折或旋转)、然后在新的图形中分析有关图形之间的关系,可根据变换前后对应角相等、对应边相等找到相似三角形的判定条件证明三角形相似
【母题练方法】1.如图,将矩形纸片ABCD(AD>DC)沿着过点D的直线折叠,使点A落在BC边上,落点为F,折痕交AB边于点E.
(1)求证:△EFB∽△FDC;
(2)若AD=10,CD=6,求BE的长;
【子题练变式】2.如图,将线段AB平移得到CD,使A与D对应,B与C对应,连接AD,BC.
(1)求证:∠B=∠ADC;
(2)点G在BC的延长线上,点C与C′关于直线DG对称,直线DC′交BC的延长线于点E.点F在线段CE上,且∠DFE=∠EDF.
①设∠B=α,求∠FDG的度数(用含α的代数式表示);
②证明:.
3.数学兴趣小组探究了以下几何图形.如图①,把一个含有45°角的三角尺放在正方形ABCD中,使45°角的顶点始终与正方形的顶点C重合,绕点C旋转三角尺时,45°角的两边CM,CN始终与正方形的边AD,AB所在直线分别相交于点M,N,连接MN,可得△CMN.
【探究一】如图②,把△CDM绕点C逆时针旋转90°得到△CBH,同时得到点H在直线AB上.求证:∠CNM=∠CNH;
【探究二】在图②中,连接BD,分别交CM,CN于点E,F.求证:△CEF∽△CNM;
【探究三】把三角尺旋转到如图③所示位置,直线BD与三角尺45°角两边CM,CN分别交于点E,F,连接AC交BD于点O,求的值.
类型二 相似中的动点问题
方法技巧:此类题目需在点的运动中寻找相似三角形,通过列方程、分类讨论求解.
【母题练方法】4.如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒,连接MN.若△BMN与△ABC相似,求t的值为 .
【子题练变式】5.如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
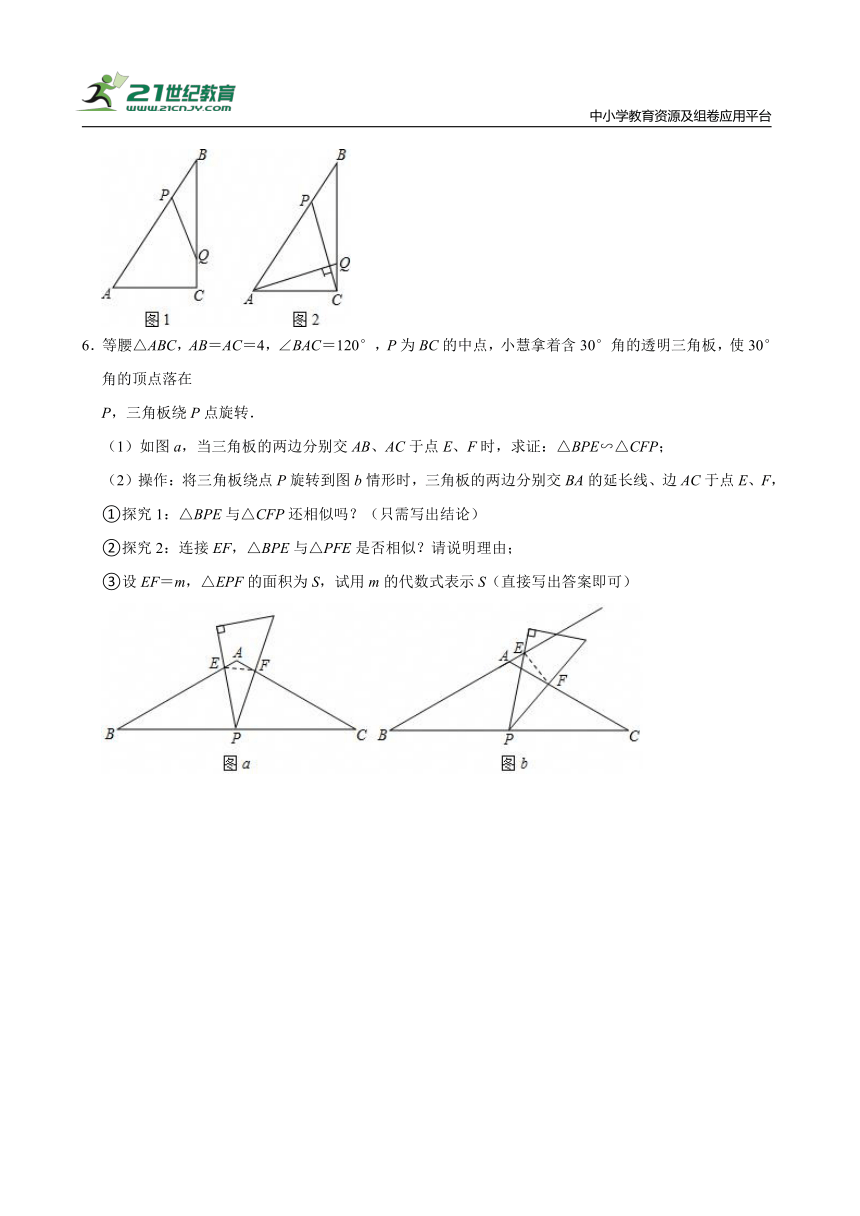
6.等腰△ABC,AB=AC=4,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在
P,三角板绕P点旋转.
(1)如图a,当三角板的两边分别交AB、AC于点E、F时,求证:△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F,
①探究1:△BPE与△CFP还相似吗?(只需写出结论)
②探究2:连接EF,△BPE与△PFE是否相似?请说明理由;
③设EF=m,△EPF的面积为S,试用m的代数式表示S(直接写出答案即可)
专题五 与相似三角形有关的动态变化
类型一 相似三角形中的平移、翻折、旋转
方法技巧:对给定的图形(或其中一部分)进行某种位置变换(平移、翻折或旋转)、然后在新的图形中分析有关图形之间的关系,可根据变换前后对应角相等、对应边相等找到相似三角形的判定条件证明三角形相似
【母题练方法】1.如图,将矩形纸片ABCD(AD>DC)沿着过点D的直线折叠,使点A落在BC边上,落点为F,折痕交AB边于点E.
(1)求证:△EFB∽△FDC;
(2)若AD=10,CD=6,求BE的长;
【思路点拔】(1)由折叠性质得∠DEF=90°,再根据互余性质得出△EFB和△EDC的两个锐角相等,便可由相似三角形的判定得出结论;
(2)由折叠性质得DE,再由勾股定理求得CE,由线段和差求得BE,由勾股定理可求解.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,
根据折叠性质知,∠A=∠DEF=90°,
∴∠BEF+∠BFE=∠BEF+∠DEC=90°,
∴∠BFE=∠DEC,
∴△EFB∽△FDC;
(2)解:由折叠性质知,AD=DF=10,AE=EF,
∵CD=6,
∴CF,
∵AD=BC=10,
∴BF=BC﹣CE=10﹣8=2.
∵EF2=BE2+BF2,
∴BE.
【点评】本题考查了矩形的性质,相似三角形的性质与判定,折叠的性质,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,注意对应相等关系.
【子题练变式】2.如图,将线段AB平移得到CD,使A与D对应,B与C对应,连接AD,BC.
(1)求证:∠B=∠ADC;
(2)点G在BC的延长线上,点C与C′关于直线DG对称,直线DC′交BC的延长线于点E.点F在线段CE上,且∠DFE=∠EDF.
①设∠B=α,求∠FDG的度数(用含α的代数式表示);
②证明:.
【思路点拔】(1)根据平移的性质可得AB∥CD,AB=CD,从而可得四边形ABCD是平行四边形,然后利用平行四边形的性质即可解答;
(2)①利用平行线的性质可得∠B=∠DCF=α,再根据三角形的外角性质可得∠DFE=∠DCF+∠CDF,从而利用角的和差关系可得∠CDE=2∠CDF+∠DCF,然后根据轴对称的性质可得∠CDG=∠C′DG∠CDE=∠CDF∠DCF,从而可得∠CDG﹣∠CDF∠DCF,进而可得∠FDG∠DCFα,即可解答;
②过点G作GH∥CD,交DE于点H,连接GC′,先证明A字模型相似三角形△CDE∽△GHE,从而可得,再根据轴对称的性质可得△CDG≌△C′DG,从而可得CG=C′G,∠DCG=∠DC′G,进而可得∠DC′G=∠HGE,然后证明△HC′G∽△HGE,从而利用相似三角形的性质可得,即可解答.
【解答】(1)证明:由平移得:AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴∠B=∠ADC;
(2)①解:∵AB∥CD,
∴∠B=∠DCF=α,
∵∠DFE是△DCF的一个外角,
∴∠DFE=∠DCF+∠CDF,
∵∠DFE=∠EDF,
∴∠CDE=∠CDF+∠EDF
=∠CDF+∠DFE
=∠CDF+∠DCF+∠CDF
=2∠CDF+∠DCF,
∵点C与C′关于直线DG对称,
∴∠CDG=∠C′DG∠CDE(2∠CDF+∠DCF)=∠CDF∠DCF,
∴∠CDG﹣∠CDF∠DCF,
∴∠FDG∠DCFα,
∴∠FDG的度数为α;
②过点G作GH∥CD,交DE于点H,连接GC′,
∴∠DCG=∠HGE,∠CDH=∠GHE,
∴△CDE∽△GHE,
∴,
∵点C与C′关于直线DG对称,
∴△CDG≌△C′DG,
∴CG=C′G,∠DCG=∠DC′G,
∴∠DC′G=∠HGE,
∵∠GHE=∠GHC′,
∴△HC′G∽△HGE,
∴,
∴,
∴.
【点评】本题考查了相似三角形的判定与性质,平行四边形的判定与性质,轴对称的性质,平移的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
3.数学兴趣小组探究了以下几何图形.如图①,把一个含有45°角的三角尺放在正方形ABCD中,使45°角的顶点始终与正方形的顶点C重合,绕点C旋转三角尺时,45°角的两边CM,CN始终与正方形的边AD,AB所在直线分别相交于点M,N,连接MN,可得△CMN.
【探究一】如图②,把△CDM绕点C逆时针旋转90°得到△CBH,同时得到点H在直线AB上.求证:∠CNM=∠CNH;
【探究二】在图②中,连接BD,分别交CM,CN于点E,F.求证:△CEF∽△CNM;
【探究三】把三角尺旋转到如图③所示位置,直线BD与三角尺45°角两边CM,CN分别交于点E,F,连接AC交BD于点O,求的值.
【思路点拔】在图②中,连接BD,分别交CM,CN于点E,F.求证:△CEF∽△CNM;【探究一】证明△CNM≌△CNH,即可得证;
【探究二】根据正方形的性质证明∠CEF=∠FNB,根据三角形内角和定理得出∠CEF=∠FNB,加上公共角∠ECF=∠NCM,进而可证明;
【探究三】,先证明△ECD∽△NCA,得到∠CED=∠CNA,,将△DMC绕点C逆时针旋转90°得到△BGC,则点G在直线AB上,得出△NCG≌△NCM,根据全等三角形的性质得出∠MNC=∠GNC,进而得到∠CNM=∠CEF,可证明△ECF∽△NCM,根据相似三角形的性质得出,即可得出结论.
【解答】【探究一】证明:∵把△CDM绕点C逆时针旋转90°得到△CBH,同时得到点H在直线AB上,
∴CM=CH,∠MCH=90°,
∴∠NCH=∠MCH﹣∠MCN=90°﹣45°=45°,
∴∠MCN=∠HCN,
在△CNM和△CNH中,
,
∴△CNM≌△CNH(SAS),
∴∠CNM=∠CNH;
【探究二】证明:如图所示,
∵四边形ABCD是正方形,
∴∠DBA=45°,
∵∠MCN=45°,
∴∠FBN=∠FCE=45°,
∵∠EFC=∠BFN,
∴∠CEF=∠FNB,
∵∠CNM=∠CNH,
∴∠CEF=∠CNM,
∵公共角∠ECF=∠NCM,
∴△CEF∽△CNM;
【探究三】解:∵AC,BD是正方形的对角线,
∴∠CDE=180°﹣∠BDC=135°,∠CAN=180°﹣∠BAC=135°,
∴∠CDE=∠CAN,
∵∠MCN=∠DCA=45°,
∴∠MCN﹣∠DCN=∠DCA﹣∠DCN,
即∠ECD=∠NCA,
∴△ECD∽△NCA,
∴∠CED=∠CNA,,
如图所示,将△DMC绕点C逆时针旋转90°得到△BGC,则点G在直线AB上,
∴MC=GC,∠MCG=90°,
∴∠NCG=∠NCM=45°,
∵CN=CN,
∴△NCG≌△NCM(SAS),
∴∠MNC=∠GNC,
∵∠CNA=∠CEF,
∴∠CNM=∠CEF,
∵∠ECF=∠NCM,
∴△ECF∽△NCM,
∴,
即.
【点评】本题是相似形的综合题,主要考查了全等三角形的性质和判定,旋转的性质,正方形的性质,相似三角形的性质和判定,熟练掌握相似三角形的性质和判定是解决问题的关键.
类型二 相似中的动点问题
方法技巧:此类题目需在点的运动中寻找相似三角形,通过列方程、分类讨论求解.
【母题练方法】4.如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒,连接MN.若△BMN与△ABC相似,求t的值为 或 .
【思路点拔】根据题意得出BM,CN,易得BN,BA,分类讨论当△BMN∽△BAC时,利用相似三角形的性质得,解得t;当△BMN∽△BCA时,,解得t,综上所述,△BMN与△ABC相似,得t的值.
【解答】解:由题意知,BM=3t cm,CN=2t cm,
∴BN=(8﹣2t)cm,,
当△BMN∽△BAC时,,
∴,
解得:;
当△BMN∽△BCA时,,
∴,
解得:,
故答案为:或.
【点评】本题主要考查了相似三角形的性质,分类讨论,数形结合是解答此题的关键.
【子题练变式】5.如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
【思路点拔】(1)根据勾股定理求出AB,分△BPQ∽△BAC、△BPQ∽△BCA两种情况,根据相似三角形的性质列出比例式,计算即可;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,BQ=8﹣4t,根据△ACQ∽△CMP,得出AC:CM=CQ:MP,代入计算即可.
【解答】解:(1)①当△BPQ∽△BAC时,
∵,BP=3t,QC=2t,AB=10cm,BC=8cm,
∴,
∴,
②当△BPQ∽△BCA时,
∵,
∴,
∴;
∴或时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=3t,,,,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴,
∴
解得:.
【点评】此题是相似形综合题,主要考查了相似三角形的判定与性质,勾股定理,直角三角形的性质,等腰三角形的性质,由三角形相似得出对应边成比例是解题的关键.
6.等腰△ABC,AB=AC=4,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在
P,三角板绕P点旋转.
(1)如图a,当三角板的两边分别交AB、AC于点E、F时,求证:△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F,
①探究1:△BPE与△CFP还相似吗?(只需写出结论)
②探究2:连接EF,△BPE与△PFE是否相似?请说明理由;
③设EF=m,△EPF的面积为S,试用m的代数式表示S(直接写出答案即可)
【思路点拔】(1)找出△BPE与△CFP的对应角,其中∠BPE+∠CPF=150°,∠CPF+∠CFP=150°,得出∠BPE=∠CFP,从而解决问题;
(2)①小题同前可证,②小题可通过对应边成比例证明,③小题求出△BPE中BE上的高,求出△PEF中EF上的高,得出关系式.
【解答】(1)证明:∵在△ABC中,∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∠EPF=30°,且∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(2)解:①结论:△BPE∽△CFP.
理由:∵在△ABC中,∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∠EPF=30°,且∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP
②结论:△BPE与△PFE相似.
理由:∵△BPE∽△CFP,
∴,而CP=BP,因此,
又因为∠EBP=∠EPF,所以△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).
③由②得△BPE∽△PFE,所以∠BEP=∠PEF.
分别过点P作PM⊥BE,PN⊥EF,垂足分别为M、N,则PM=PN.
连AP,在Rt△ABP中,由∠B=30°,AB=4,可得AP=2.
所以PM,所以PN,
所以SPN×EFm.
【点评】本题属于几何变换综合题,考查了旋转变换,角平分线的性质定理,三角形的面积,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,学会添加常用辅助线,属于中考压轴题.
专题五 与相似三角形有关的动态变化
类型一 相似三角形中的平移、翻折、旋转
方法技巧:对给定的图形(或其中一部分)进行某种位置变换(平移、翻折或旋转)、然后在新的图形中分析有关图形之间的关系,可根据变换前后对应角相等、对应边相等找到相似三角形的判定条件证明三角形相似
【母题练方法】1.如图,将矩形纸片ABCD(AD>DC)沿着过点D的直线折叠,使点A落在BC边上,落点为F,折痕交AB边于点E.
(1)求证:△EFB∽△FDC;
(2)若AD=10,CD=6,求BE的长;
【子题练变式】2.如图,将线段AB平移得到CD,使A与D对应,B与C对应,连接AD,BC.
(1)求证:∠B=∠ADC;
(2)点G在BC的延长线上,点C与C′关于直线DG对称,直线DC′交BC的延长线于点E.点F在线段CE上,且∠DFE=∠EDF.
①设∠B=α,求∠FDG的度数(用含α的代数式表示);
②证明:.
3.数学兴趣小组探究了以下几何图形.如图①,把一个含有45°角的三角尺放在正方形ABCD中,使45°角的顶点始终与正方形的顶点C重合,绕点C旋转三角尺时,45°角的两边CM,CN始终与正方形的边AD,AB所在直线分别相交于点M,N,连接MN,可得△CMN.
【探究一】如图②,把△CDM绕点C逆时针旋转90°得到△CBH,同时得到点H在直线AB上.求证:∠CNM=∠CNH;
【探究二】在图②中,连接BD,分别交CM,CN于点E,F.求证:△CEF∽△CNM;
【探究三】把三角尺旋转到如图③所示位置,直线BD与三角尺45°角两边CM,CN分别交于点E,F,连接AC交BD于点O,求的值.
类型二 相似中的动点问题
方法技巧:此类题目需在点的运动中寻找相似三角形,通过列方程、分类讨论求解.
【母题练方法】4.如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒,连接MN.若△BMN与△ABC相似,求t的值为 .
【子题练变式】5.如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
6.等腰△ABC,AB=AC=4,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在
P,三角板绕P点旋转.
(1)如图a,当三角板的两边分别交AB、AC于点E、F时,求证:△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F,
①探究1:△BPE与△CFP还相似吗?(只需写出结论)
②探究2:连接EF,△BPE与△PFE是否相似?请说明理由;
③设EF=m,△EPF的面积为S,试用m的代数式表示S(直接写出答案即可)
专题五 与相似三角形有关的动态变化
类型一 相似三角形中的平移、翻折、旋转
方法技巧:对给定的图形(或其中一部分)进行某种位置变换(平移、翻折或旋转)、然后在新的图形中分析有关图形之间的关系,可根据变换前后对应角相等、对应边相等找到相似三角形的判定条件证明三角形相似
【母题练方法】1.如图,将矩形纸片ABCD(AD>DC)沿着过点D的直线折叠,使点A落在BC边上,落点为F,折痕交AB边于点E.
(1)求证:△EFB∽△FDC;
(2)若AD=10,CD=6,求BE的长;
【思路点拔】(1)由折叠性质得∠DEF=90°,再根据互余性质得出△EFB和△EDC的两个锐角相等,便可由相似三角形的判定得出结论;
(2)由折叠性质得DE,再由勾股定理求得CE,由线段和差求得BE,由勾股定理可求解.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,
根据折叠性质知,∠A=∠DEF=90°,
∴∠BEF+∠BFE=∠BEF+∠DEC=90°,
∴∠BFE=∠DEC,
∴△EFB∽△FDC;
(2)解:由折叠性质知,AD=DF=10,AE=EF,
∵CD=6,
∴CF,
∵AD=BC=10,
∴BF=BC﹣CE=10﹣8=2.
∵EF2=BE2+BF2,
∴BE.
【点评】本题考查了矩形的性质,相似三角形的性质与判定,折叠的性质,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,注意对应相等关系.
【子题练变式】2.如图,将线段AB平移得到CD,使A与D对应,B与C对应,连接AD,BC.
(1)求证:∠B=∠ADC;
(2)点G在BC的延长线上,点C与C′关于直线DG对称,直线DC′交BC的延长线于点E.点F在线段CE上,且∠DFE=∠EDF.
①设∠B=α,求∠FDG的度数(用含α的代数式表示);
②证明:.
【思路点拔】(1)根据平移的性质可得AB∥CD,AB=CD,从而可得四边形ABCD是平行四边形,然后利用平行四边形的性质即可解答;
(2)①利用平行线的性质可得∠B=∠DCF=α,再根据三角形的外角性质可得∠DFE=∠DCF+∠CDF,从而利用角的和差关系可得∠CDE=2∠CDF+∠DCF,然后根据轴对称的性质可得∠CDG=∠C′DG∠CDE=∠CDF∠DCF,从而可得∠CDG﹣∠CDF∠DCF,进而可得∠FDG∠DCFα,即可解答;
②过点G作GH∥CD,交DE于点H,连接GC′,先证明A字模型相似三角形△CDE∽△GHE,从而可得,再根据轴对称的性质可得△CDG≌△C′DG,从而可得CG=C′G,∠DCG=∠DC′G,进而可得∠DC′G=∠HGE,然后证明△HC′G∽△HGE,从而利用相似三角形的性质可得,即可解答.
【解答】(1)证明:由平移得:AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴∠B=∠ADC;
(2)①解:∵AB∥CD,
∴∠B=∠DCF=α,
∵∠DFE是△DCF的一个外角,
∴∠DFE=∠DCF+∠CDF,
∵∠DFE=∠EDF,
∴∠CDE=∠CDF+∠EDF
=∠CDF+∠DFE
=∠CDF+∠DCF+∠CDF
=2∠CDF+∠DCF,
∵点C与C′关于直线DG对称,
∴∠CDG=∠C′DG∠CDE(2∠CDF+∠DCF)=∠CDF∠DCF,
∴∠CDG﹣∠CDF∠DCF,
∴∠FDG∠DCFα,
∴∠FDG的度数为α;
②过点G作GH∥CD,交DE于点H,连接GC′,
∴∠DCG=∠HGE,∠CDH=∠GHE,
∴△CDE∽△GHE,
∴,
∵点C与C′关于直线DG对称,
∴△CDG≌△C′DG,
∴CG=C′G,∠DCG=∠DC′G,
∴∠DC′G=∠HGE,
∵∠GHE=∠GHC′,
∴△HC′G∽△HGE,
∴,
∴,
∴.
【点评】本题考查了相似三角形的判定与性质,平行四边形的判定与性质,轴对称的性质,平移的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
3.数学兴趣小组探究了以下几何图形.如图①,把一个含有45°角的三角尺放在正方形ABCD中,使45°角的顶点始终与正方形的顶点C重合,绕点C旋转三角尺时,45°角的两边CM,CN始终与正方形的边AD,AB所在直线分别相交于点M,N,连接MN,可得△CMN.
【探究一】如图②,把△CDM绕点C逆时针旋转90°得到△CBH,同时得到点H在直线AB上.求证:∠CNM=∠CNH;
【探究二】在图②中,连接BD,分别交CM,CN于点E,F.求证:△CEF∽△CNM;
【探究三】把三角尺旋转到如图③所示位置,直线BD与三角尺45°角两边CM,CN分别交于点E,F,连接AC交BD于点O,求的值.
【思路点拔】在图②中,连接BD,分别交CM,CN于点E,F.求证:△CEF∽△CNM;【探究一】证明△CNM≌△CNH,即可得证;
【探究二】根据正方形的性质证明∠CEF=∠FNB,根据三角形内角和定理得出∠CEF=∠FNB,加上公共角∠ECF=∠NCM,进而可证明;
【探究三】,先证明△ECD∽△NCA,得到∠CED=∠CNA,,将△DMC绕点C逆时针旋转90°得到△BGC,则点G在直线AB上,得出△NCG≌△NCM,根据全等三角形的性质得出∠MNC=∠GNC,进而得到∠CNM=∠CEF,可证明△ECF∽△NCM,根据相似三角形的性质得出,即可得出结论.
【解答】【探究一】证明:∵把△CDM绕点C逆时针旋转90°得到△CBH,同时得到点H在直线AB上,
∴CM=CH,∠MCH=90°,
∴∠NCH=∠MCH﹣∠MCN=90°﹣45°=45°,
∴∠MCN=∠HCN,
在△CNM和△CNH中,
,
∴△CNM≌△CNH(SAS),
∴∠CNM=∠CNH;
【探究二】证明:如图所示,
∵四边形ABCD是正方形,
∴∠DBA=45°,
∵∠MCN=45°,
∴∠FBN=∠FCE=45°,
∵∠EFC=∠BFN,
∴∠CEF=∠FNB,
∵∠CNM=∠CNH,
∴∠CEF=∠CNM,
∵公共角∠ECF=∠NCM,
∴△CEF∽△CNM;
【探究三】解:∵AC,BD是正方形的对角线,
∴∠CDE=180°﹣∠BDC=135°,∠CAN=180°﹣∠BAC=135°,
∴∠CDE=∠CAN,
∵∠MCN=∠DCA=45°,
∴∠MCN﹣∠DCN=∠DCA﹣∠DCN,
即∠ECD=∠NCA,
∴△ECD∽△NCA,
∴∠CED=∠CNA,,
如图所示,将△DMC绕点C逆时针旋转90°得到△BGC,则点G在直线AB上,
∴MC=GC,∠MCG=90°,
∴∠NCG=∠NCM=45°,
∵CN=CN,
∴△NCG≌△NCM(SAS),
∴∠MNC=∠GNC,
∵∠CNA=∠CEF,
∴∠CNM=∠CEF,
∵∠ECF=∠NCM,
∴△ECF∽△NCM,
∴,
即.
【点评】本题是相似形的综合题,主要考查了全等三角形的性质和判定,旋转的性质,正方形的性质,相似三角形的性质和判定,熟练掌握相似三角形的性质和判定是解决问题的关键.
类型二 相似中的动点问题
方法技巧:此类题目需在点的运动中寻找相似三角形,通过列方程、分类讨论求解.
【母题练方法】4.如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒,连接MN.若△BMN与△ABC相似,求t的值为 或 .
【思路点拔】根据题意得出BM,CN,易得BN,BA,分类讨论当△BMN∽△BAC时,利用相似三角形的性质得,解得t;当△BMN∽△BCA时,,解得t,综上所述,△BMN与△ABC相似,得t的值.
【解答】解:由题意知,BM=3t cm,CN=2t cm,
∴BN=(8﹣2t)cm,,
当△BMN∽△BAC时,,
∴,
解得:;
当△BMN∽△BCA时,,
∴,
解得:,
故答案为:或.
【点评】本题主要考查了相似三角形的性质,分类讨论,数形结合是解答此题的关键.
【子题练变式】5.如图1,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)(如图2)连接AQ,CP,若AQ⊥CP,求t的值.
【思路点拔】(1)根据勾股定理求出AB,分△BPQ∽△BAC、△BPQ∽△BCA两种情况,根据相似三角形的性质列出比例式,计算即可;
(2)过P作PM⊥BC于点M,AQ,CP交于点N,则有PB=5t,PM=3t,BQ=8﹣4t,根据△ACQ∽△CMP,得出AC:CM=CQ:MP,代入计算即可.
【解答】解:(1)①当△BPQ∽△BAC时,
∵,BP=3t,QC=2t,AB=10cm,BC=8cm,
∴,
∴,
②当△BPQ∽△BCA时,
∵,
∴,
∴;
∴或时,△BPQ与△ABC相似;
(2)如图所示,过P作PM⊥BC于点M,AQ,CP交于点N,
则有PB=3t,,,,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM且∠ACQ=∠PMC=90°,
∴△ACQ∽△CMP,
∴,
∴
解得:.
【点评】此题是相似形综合题,主要考查了相似三角形的判定与性质,勾股定理,直角三角形的性质,等腰三角形的性质,由三角形相似得出对应边成比例是解题的关键.
6.等腰△ABC,AB=AC=4,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在
P,三角板绕P点旋转.
(1)如图a,当三角板的两边分别交AB、AC于点E、F时,求证:△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F,
①探究1:△BPE与△CFP还相似吗?(只需写出结论)
②探究2:连接EF,△BPE与△PFE是否相似?请说明理由;
③设EF=m,△EPF的面积为S,试用m的代数式表示S(直接写出答案即可)
【思路点拔】(1)找出△BPE与△CFP的对应角,其中∠BPE+∠CPF=150°,∠CPF+∠CFP=150°,得出∠BPE=∠CFP,从而解决问题;
(2)①小题同前可证,②小题可通过对应边成比例证明,③小题求出△BPE中BE上的高,求出△PEF中EF上的高,得出关系式.
【解答】(1)证明:∵在△ABC中,∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∠EPF=30°,且∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(2)解:①结论:△BPE∽△CFP.
理由:∵在△ABC中,∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
又∠EPF=30°,且∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP
②结论:△BPE与△PFE相似.
理由:∵△BPE∽△CFP,
∴,而CP=BP,因此,
又因为∠EBP=∠EPF,所以△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).
③由②得△BPE∽△PFE,所以∠BEP=∠PEF.
分别过点P作PM⊥BE,PN⊥EF,垂足分别为M、N,则PM=PN.
连AP,在Rt△ABP中,由∠B=30°,AB=4,可得AP=2.
所以PM,所以PN,
所以SPN×EFm.
【点评】本题属于几何变换综合题,考查了旋转变换,角平分线的性质定理,三角形的面积,相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题,学会添加常用辅助线,属于中考压轴题.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
