2026年中考数学题型专项训练 单选题(含解析)
文档属性
| 名称 | 2026年中考数学题型专项训练 单选题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 824.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 21:19:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学题型专项训练 单选题
一.选择题(共20小题)
1.(2025秋 禹城市期末)数形结合A,B,C三个住宅区分别住有某公司职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),如图所示,已知AB=100m,BC=200m,为了方便职工上下班,该公司的接送车打算在此区间内设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.点A B.点B C.点A,B之间 D.点B,C之间
2.(2025秋 沙坪坝区校级月考)对一组代数式:a,b,c(a,b,c≠0)进行如下操作:任意相邻的两个代数式,都用右边的代数式除以左边的代数式,所得之商写在这两个代数式之间,可以产生一个新的代数式列:a,,b,,c,记为代数式列1;将代数式列1按上述方法再做一次操作,可以得到代数式列2;以此类推.通过实际操作,得出以下结论:
①代数式列2为:a,,,a,b,,,b,c;
②代数式列3共18个代数式;
③代数式列3的所有代数式的积是代数式列2的所有代数式积的倍;
④代数式列2023的所有代数式的积为.
上述四个结论正确的有( )个
A.0 B.1 C.2 D.3
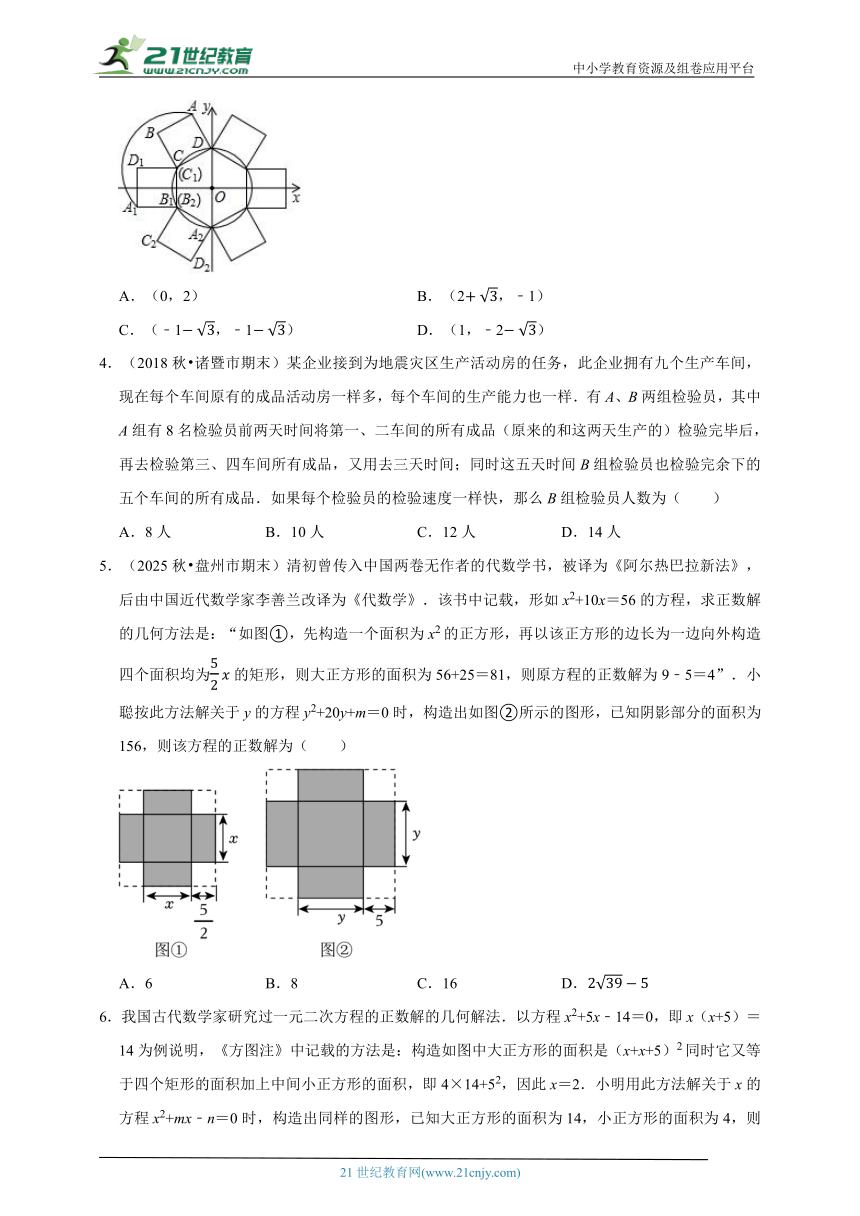
3.(2025秋 天台县模拟)如图,⊙O的半径为2,圆心O在坐标原点,正方形ABCD的边长为2,点A、B在第二象限,点C、D在⊙O上,且点D的坐标为(0,2),现将正方形ABCD绕点C按逆时针方向旋转150°,点B运动到了⊙O上点B1处,点A、D分别运动到了点A1、D1处,即得到正方形A1B1C1D1(点C1与C重合);再将正方形A1B1C1D1绕点B1按逆时针方向旋转150°,点A1运动到了⊙O上点A2处,点D1、C1分别运动到了点D2、C2处,即得到正方形A2B2C2D2(点B2与B1重合),…,按上述方法旋转2020次后,点A2020的坐标为( )
A.(0,2) B.(2,﹣1)
C.(﹣1,﹣1) D.(1,﹣2)
4.(2018秋 诸暨市期末)某企业接到为地震灾区生产活动房的任务,此企业拥有九个生产车间,现在每个车间原有的成品活动房一样多,每个车间的生产能力也一样.有A、B两组检验员,其中A组有8名检验员前两天时间将第一、二车间的所有成品(原来的和这两天生产的)检验完毕后,再去检验第三、四车间所有成品,又用去三天时间;同时这五天时间B组检验员也检验完余下的五个车间的所有成品.如果每个检验员的检验速度一样快,那么B组检验员人数为( )
A.8人 B.10人 C.12人 D.14人
5.(2025秋 盘州市期末)清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如x2+10x=56的方程,求正数解的几何方法是:“如图①,先构造一个面积为x2的正方形,再以该正方形的边长为一边向外构造四个面积均为的矩形,则大正方形的面积为56+25=81,则原方程的正数解为9﹣5=4”.小聪按此方法解关于y的方程y2+20y+m=0时,构造出如图②所示的图形,已知阴影部分的面积为156,则该方程的正数解为( )
A.6 B.8 C.16 D.
6.我国古代数学家研究过一元二次方程的正数解的几何解法.以方程x2+5x﹣14=0,即x(x+5)=14为例说明,《方图注》中记载的方法是:构造如图中大正方形的面积是(x+x+5)2同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,因此x=2.小明用此方法解关于x的方程x2+mx﹣n=0时,构造出同样的图形,已知大正方形的面积为14,小正方形的面积为4,则( )
A.m=2,n=3 B.,n=2
C.,n=2 D.m=2,
7.(2025秋 佳木斯三模)直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现每件小商品售价每降低1元,日销售量增加2件.若日利润保持不变.商家想尽快销售完该款商品.每件售价应定为多少元.( )
A.45 B.50 C.55 D.60
8.(2025秋 罗山县校级月考)生物学家研究发现,很多植物的生长都有下面的规律,即主干长出若干数目的支干后,每个支干又会长出同样数目的小分支.现有符合上述生长规律的某种植物,它的主干、支干和小分支的总数是91,则这种植物每个支干长出小分支的个数是( )
A.9 B.10 C.﹣10 D.9或10
9.(2025秋 岳阳县期中)如图,已知太阳光线AC和DE是平行的,在同一时刻,如果将两根高度相同的木杆竖直插在地面上,那么在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )
A.SAS B.AAS C.SSS D.ASA
10.(2025秋 长春月考)杜甫曾经哀叹“茅屋为秋风所破”,苦于杜甫不曾学过今日几何,不然也不会如此绝望.现在我们来看一茅屋的屋顶剖面,它呈等腰三角形,如果屋檐AB=AC=5米,横梁BC=8米,那么从梁BC上的任意一点D要支一根木头顶住屋顶A处,这根木头需要长度可能是( )
A.2.5米 B.6米 C.4米 D.8米
11.(2025秋 驿城区期末)王林在美术课上将等腰△ABC通过平移设计得到“一棵树”,已知底边AB上的高CD为5cm,沿CD方向向下平移3cm到△A1B1C1的位置,再经过相同的平移到△A2B2C2的位置,下方树干EF长为4cm,则树的高度CF长为( )
A.19cm B.17cm C.16cm D.15cm
12.(2025秋 洛宁县月考)第14届国际数学教育大会(ICME﹣14)会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF:AH=1:3,则sin∠BCF=( )
A. B. C. D.
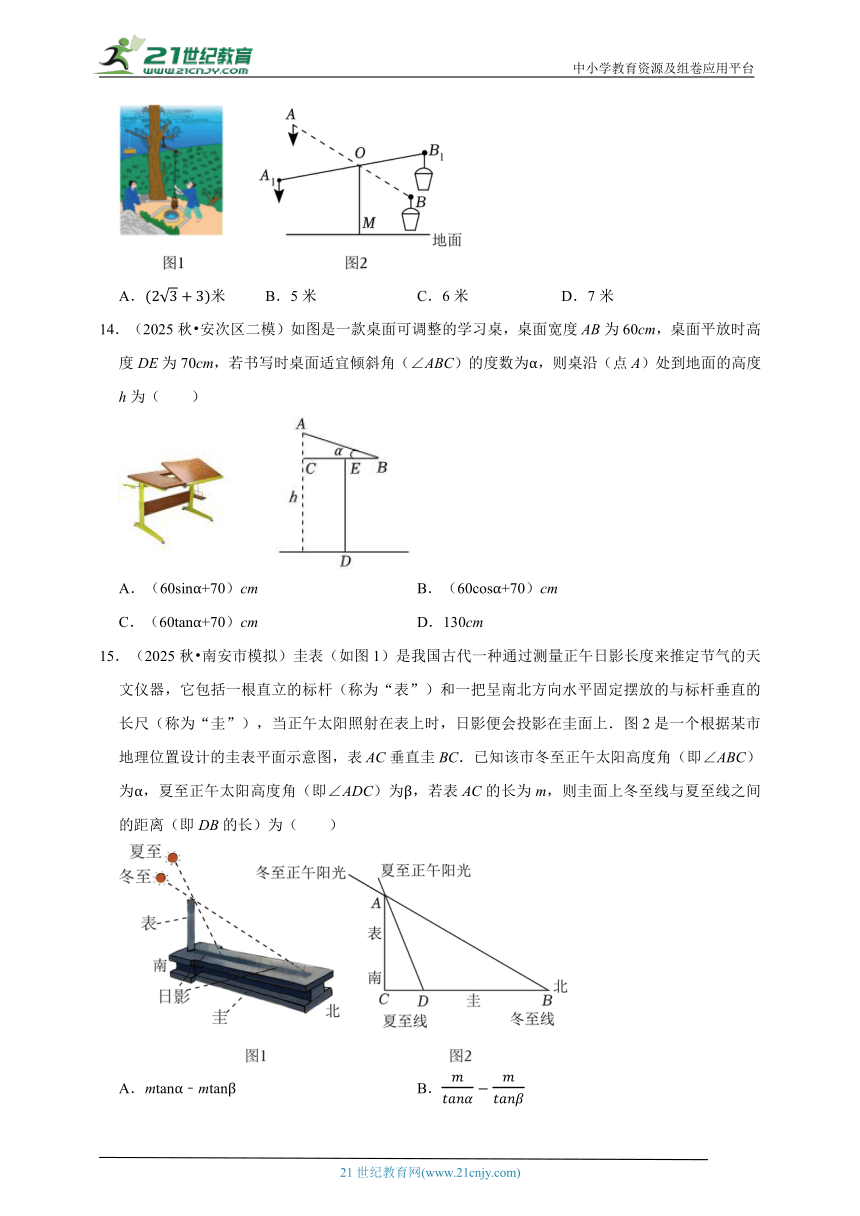
13.(2025秋 龙口市一模)桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子 备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,AB=6米,OA:OB=2:1.当点A位于最高点时,∠AOM=120°.此时,点A到地面的距离为( )
A.米 B.5米 C.6米 D.7米
14.(2025秋 安次区二模)如图是一款桌面可调整的学习桌,桌面宽度AB为60cm,桌面平放时高度DE为70cm,若书写时桌面适宜倾斜角(∠ABC)的度数为α,则桌沿(点A)处到地面的高度h为( )
A.(60sinα+70)cm B.(60cosα+70)cm
C.(60tanα+70)cm D.130cm
15.(2025秋 南安市模拟)圭表(如图1)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标杆(称为“表”)和一把呈南北方向水平固定摆放的与标杆垂直的长尺(称为“圭”),当正午太阳照射在表上时,日影便会投影在圭面上.图2是一个根据某市地理位置设计的圭表平面示意图,表AC垂直圭BC.已知该市冬至正午太阳高度角(即∠ABC)为α,夏至正午太阳高度角(即∠ADC)为β,若表AC的长为m,则圭面上冬至线与夏至线之间的距离(即DB的长)为( )
A.mtanα﹣mtanβ B.
C.msinα﹣mcosβ D.
16.(2025秋 无锡期末)如图1是第七届国际数学教育大会(ICME)会徽,选择其中两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC,sin∠AOB,则tanC的值为( )
A. B. C. D.
17.(2025秋 通榆县一模)“圭表”是中国古代用来确定节气的仪器.某“圭表”示意图如图所示,AC⊥BC,AC=3米,测得某地夏至正午时“表”的影长CD=1米,冬至时的正午太阳高度角∠ABC=α,则夏至到冬至,影长差BD的长为( )
A.(3sinα﹣1)米 B.米
C.(3tanα﹣1)米 D.米
18.(2025秋 深圳三模)小明在科普读物中了解到:每种介质都有自己的折射率,当光从空气射入该介质时,折射率为入射角正弦值与折射角正弦值之比,即折射率(i为入射角,r为折射角).如图,一束光从空气射向横截面为直角三角形的玻璃透镜斜面,经折射后沿垂直AC边的方向射出,已知i=30°,AB=15cm,BC=5cm,则该玻璃透镜的折射率n为( )
A.1.8 B.1.6 C.1.5 D.1.4
19.(2025秋 长春月考)如图所示,学校九年级举行跳绳比赛,图中的四个点分别描述了九年级的四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述1班和3班两个班级情况的点恰好在同一个反比例函数的图象上,则成绩优秀人数最多的是( )
A.1班 B.2班 C.3班 D.4班
20.(2025秋 顺德区期中)《墨经》中有:“景到,在午有端,与景长,说在端”,大约在两千四百年前,墨子和他的学生做的世界上第1个小孔成像的实验.如图所示的实验中,若物距为10cm,像距为18cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是( )cm.
A. B.4 C. D.5
参考答案与试题解析
一.选择题(共20小题)
1.(2025秋 禹城市期末)数形结合A,B,C三个住宅区分别住有某公司职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),如图所示,已知AB=100m,BC=200m,为了方便职工上下班,该公司的接送车打算在此区间内设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.点A B.点B C.点A,B之间 D.点B,C之间
【考点】两点间的距离.
【专题】线段、角、相交线与平行线;应用意识.
【答案】A
【分析】此题为数学知识的应用,由题意设一个停靠点,为使所有的人步行到停靠点的路程之和最小,肯定要尽量缩短两地之间的里程,就用到两点间线段最短定理.
【解答】解:①以点A为停靠点,则所有人的路程的和=15×100+10×300=4500(米),
②以点B为停靠点,则所有人的路程的和=30×100+10×200=5000(米),
③以点C为停靠点,则所有人的路程的和=30×300+15×200=12000(米),
④当在AB之间停靠时,设停靠点到A的距离是m,则(0<m<100),则所有人的路程的和是:30m+15(100﹣m)+10(300﹣m)=4500+5m>4500,
⑤当在BC之间停靠时,设停靠点到B的距离为n,则(0<n<200),则总路程为30(100+n)+15n+10(200﹣n)=5000+35n>4500.
∴该停靠点的位置应设在点A;
故选:A.
【点评】此题为数学知识的应用,考查知识点为两点之间线段最短.
2.(2025秋 沙坪坝区校级月考)对一组代数式:a,b,c(a,b,c≠0)进行如下操作:任意相邻的两个代数式,都用右边的代数式除以左边的代数式,所得之商写在这两个代数式之间,可以产生一个新的代数式列:a,,b,,c,记为代数式列1;将代数式列1按上述方法再做一次操作,可以得到代数式列2;以此类推.通过实际操作,得出以下结论:
①代数式列2为:a,,,a,b,,,b,c;
②代数式列3共18个代数式;
③代数式列3的所有代数式的积是代数式列2的所有代数式积的倍;
④代数式列2023的所有代数式的积为.
上述四个结论正确的有( )个
A.0 B.1 C.2 D.3
【考点】规律型:数字的变化类;列代数式.
【专题】计算题;猜想归纳;运算能力;推理能力;应用意识.
【答案】D
【分析】根据新定义进行计算验证即可解决.
【解答】解:根据题意,由a,b,c(a,b,c≠0),
∴代数列1为:a,,b,,c,
则代数列2为:a,,,a,b,,,b,c,故①对;
代数列3为:a,,,a,,,a,,b,,,b,,,b,,c共17个代数式,故②错误;
∵代数式列2的所有代数式积为:aa×bb×c,
代数式列3的所有代数式的积是:aaabbbc,
∴代数式列3的所有代数式的积是代数式列2的所有代数式积的倍,故③对;
∵代数式列1的所有代数式的积是abc=bc2=bc2×()1﹣1,
代数式列2的所有代数式的积是:bc2×()2﹣1,
代数式列3的所有代数式的积是:bc2×()3﹣1,
......
故代数式列2023的所有代数式的积是:bc2×()2023﹣1,故④对,
故答案选:D.
【点评】本题考查列代数式以及根据新定义解决问题,难度较大切繁琐,细心认真耐心是解决问题的关键.
3.(2025秋 天台县模拟)如图,⊙O的半径为2,圆心O在坐标原点,正方形ABCD的边长为2,点A、B在第二象限,点C、D在⊙O上,且点D的坐标为(0,2),现将正方形ABCD绕点C按逆时针方向旋转150°,点B运动到了⊙O上点B1处,点A、D分别运动到了点A1、D1处,即得到正方形A1B1C1D1(点C1与C重合);再将正方形A1B1C1D1绕点B1按逆时针方向旋转150°,点A1运动到了⊙O上点A2处,点D1、C1分别运动到了点D2、C2处,即得到正方形A2B2C2D2(点B2与B1重合),…,按上述方法旋转2020次后,点A2020的坐标为( )
A.(0,2) B.(2,﹣1)
C.(﹣1,﹣1) D.(1,﹣2)
【考点】坐标与图形变化﹣旋转;规律型:点的坐标.
【专题】动点型;规律型;应用意识.
【答案】B
【分析】如图,由题意发现12次一个循环,由2020÷12=168余数为4,推出A2020的坐标与A4相同,由此即可解决问题.
【解答】解:如图,由题意发现12次一个循环,
∵2020÷12=168余数为4,
∴A2020的坐标与A4相同,
∵A4(2,﹣1),
∴A2020(2,﹣1),
故选:B.
【点评】本题考查坐标与图形的变化﹣旋转,规律型问题,解题的关键是学会探究规律的方法,属于中考选择题中的压轴题.
4.(2018秋 诸暨市期末)某企业接到为地震灾区生产活动房的任务,此企业拥有九个生产车间,现在每个车间原有的成品活动房一样多,每个车间的生产能力也一样.有A、B两组检验员,其中A组有8名检验员前两天时间将第一、二车间的所有成品(原来的和这两天生产的)检验完毕后,再去检验第三、四车间所有成品,又用去三天时间;同时这五天时间B组检验员也检验完余下的五个车间的所有成品.如果每个检验员的检验速度一样快,那么B组检验员人数为( )
A.8人 B.10人 C.12人 D.14人
【考点】一元一次方程的应用.
【专题】应用题;应用意识.
【答案】C
【分析】设A组所检验的每个车间原有成品a件,每个车间1天生产b件,可得A组前两天检验的总件数和后三天检验的总件数为.根据检验员的检验速度相同,可列式等式得到a和b的关系,即可得A组一名检验员每天检验的成品数.再根据B组检验员的人数=五个车间的所有成品÷A组一名检验员每天检验的成品数,列式即可得解.
【解答】解:设每个车间原有成品a件,每个车间每天生产b件产品,根据检验速度相同得:
,
解得a=4b;
则A组每名检验员每天检验的成品数为:2(a+2b)÷(2×8)=12b÷16b.
那么B组检验员的人数为:5(a+5b)÷(b)÷5=45bb÷5=12(人).
故选:C.
【点评】本题考查了一元一次方程的应用,本题是一道叙述比较长的题目,解题时应认真读题,理解各种量之间的关系列出等式.
5.(2025秋 盘州市期末)清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如x2+10x=56的方程,求正数解的几何方法是:“如图①,先构造一个面积为x2的正方形,再以该正方形的边长为一边向外构造四个面积均为的矩形,则大正方形的面积为56+25=81,则原方程的正数解为9﹣5=4”.小聪按此方法解关于y的方程y2+20y+m=0时,构造出如图②所示的图形,已知阴影部分的面积为156,则该方程的正数解为( )
A.6 B.8 C.16 D.
【考点】一元二次方程的应用.
【专题】一元二次方程及应用;运算能力;应用意识.
【答案】A
【分析】先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,利用大正方形的面积=阴影部分的面积+4×小正方形的面积,可得出大正方形的面积,再利用该方程的正数解=大正方形的边长﹣2×小正方形的边长,即可得出结论.
【解答】解:先构造一个面积为y2的正方形,再以该正方形的边长为一边向外构造四个面积均为5y的矩形,
∵阴影部分的面积为156,
∴y2+4×5y=y2+20y=156,
∴大正方形的面积=156+4×52=256,
∴大正方形的边长16,
∴方程y2+20y+m=0的正数解为16﹣2×5=16﹣10=6,
故选:A.
【点评】本题考查了一元二次方程的应用,模仿案例,构造出符合题意的大正方形是解题的关键.
6.我国古代数学家研究过一元二次方程的正数解的几何解法.以方程x2+5x﹣14=0,即x(x+5)=14为例说明,《方图注》中记载的方法是:构造如图中大正方形的面积是(x+x+5)2同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,因此x=2.小明用此方法解关于x的方程x2+mx﹣n=0时,构造出同样的图形,已知大正方形的面积为14,小正方形的面积为4,则( )
A.m=2,n=3 B.,n=2
C.,n=2 D.m=2,
【考点】一元二次方程的应用.
【专题】一元二次方程及应用;运算能力;应用意识.
【答案】D
【分析】画出方程x2+mx﹣n=0的拼图过程,由面积之间的关系得m2=4,4n+4=14,即可得出结论.
【解答】解:如图,
由题意得:m2=4,4n+4=14,
∴m2,n,
故选:D.
【点评】本题考查了一元二次方程的应用,理解一元二次方程的正数解的几何解法是解题的关键.
7.(2025秋 佳木斯三模)直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现每件小商品售价每降低1元,日销售量增加2件.若日利润保持不变.商家想尽快销售完该款商品.每件售价应定为多少元.( )
A.45 B.50 C.55 D.60
【考点】一元二次方程的应用.
【专题】一元二次方程及应用;运算能力;应用意识.
【答案】B
【分析】设每件售价应定为x元,根据按每件60元销售,每天可卖出20件.每降低1元,日销售量增加2件.日利润保持不变.列出一元二次方程,解之取符合题意的值即可.
【解答】解:设每件售价应定为x元,
根据题意得:(x﹣40)[20+2(60﹣x)]=(60﹣40)×20,
解得:x1=50,x2=60(不符合题意,舍去),
即商家想尽快销售完该款商品,每件售价应定为50元.
故选:B.
【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
8.(2025秋 罗山县校级月考)生物学家研究发现,很多植物的生长都有下面的规律,即主干长出若干数目的支干后,每个支干又会长出同样数目的小分支.现有符合上述生长规律的某种植物,它的主干、支干和小分支的总数是91,则这种植物每个支干长出小分支的个数是( )
A.9 B.10 C.﹣10 D.9或10
【考点】一元二次方程的应用.
【专题】一元二次方程及应用;运算能力;应用意识.
【答案】A
【分析】设这种植物每个支干长出的小分支个数是x,根据主干、支干和小分支的总数是91,列出一元二次方程,解之取其正值即可得出答案.
【解答】解:设这种植物每个支干长出的小分支个数是x,
根据题意得:1+x+x2=91,
整理得:x2+x﹣90=0,
解得:x1=9,x2=﹣10(不合题意,舍去),
即这种植物每个支干长出的小分支个数是9,
故选:A.
【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
9.(2025秋 岳阳县期中)如图,已知太阳光线AC和DE是平行的,在同一时刻,如果将两根高度相同的木杆竖直插在地面上,那么在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )
A.SAS B.AAS C.SSS D.ASA
【考点】平行投影;全等图形;全等三角形的判定.
【专题】投影与视图;应用意识.
【答案】B
【分析】先根据题意得出AC∥ED,AH⊥GT,DT⊥GT,AH=DT,进而得∠AGH=∠DKT,∠AHG=∠DTK=90°,据此即可判定△AGH和△DKT全等,从而得出答案.
【解答】解:如图,
,
∵AC∥ED,AH⊥GT,DT⊥GT,AH=DT,
∴∠AGH=∠DKT,∠AHG=∠DTK=90°,
在△AGH和△DKT中,
,
∴△AGH≌△DKT(AAS),
故选:B.
【点评】此题主要考查了全等三角形的判定,平行线的性质,解答此题的关键是理解题意,找出AC∥ED,AH⊥GT,DT⊥GT,AH=DT,进而找出判定三角形全等的判定条件.
10.(2025秋 长春月考)杜甫曾经哀叹“茅屋为秋风所破”,苦于杜甫不曾学过今日几何,不然也不会如此绝望.现在我们来看一茅屋的屋顶剖面,它呈等腰三角形,如果屋檐AB=AC=5米,横梁BC=8米,那么从梁BC上的任意一点D要支一根木头顶住屋顶A处,这根木头需要长度可能是( )
A.2.5米 B.6米 C.4米 D.8米
【考点】勾股定理的应用;等腰三角形的性质.
【专题】等腰三角形与直角三角形;运算能力;推理能力;应用意识.
【答案】C
【分析】过点A作AE⊥BC于点E,由等腰三角形的性质得BE=CE=4米,中由勾股定理求出AE=3米,然后由AE≤AD<AC,即可得出结论.
【解答】解:如图,过点A作AE⊥BC于点E,
∵AB=AC=5米,BC=8米,
∴BE=CEBC8=4(米),
在Rt△ABE中,由勾股定理得:AE3(米),
由题意可知,AE≤AD<AC,
即3米≤AD<5米,
故这根木头需要长度可能是4米,
故选:C.
【点评】本题考查了勾股定理以及等腰三角形的性质等知识,熟练掌握勾股定理和等腰三角形的性质是解题的关键.
11.(2025秋 驿城区期末)王林在美术课上将等腰△ABC通过平移设计得到“一棵树”,已知底边AB上的高CD为5cm,沿CD方向向下平移3cm到△A1B1C1的位置,再经过相同的平移到△A2B2C2的位置,下方树干EF长为4cm,则树的高度CF长为( )
A.19cm B.17cm C.16cm D.15cm
【考点】勾股定理的应用;平移的性质;等腰三角形的性质.
【专题】平移、旋转与对称;应用意识.
【答案】D
【分析】根据平移的性质得到CC1=C1C2=3cm,根据题意计算,得到答案.
【解答】解:由平移的性质可知:CC1=C1C2=3cm,
由题意得:底边AB上的高CD为5cm,沿CD方向向下平移3cm,
∴C2E=5cm,EF=4cm,
∴CF=CC1+C1C2+C2E+EF
=3+3+5+4=15(cm),
故选:D.
【点评】本题考查的是图形的平移,掌握平移的性质是解题的关键.
12.(2025秋 洛宁县月考)第14届国际数学教育大会(ICME﹣14)会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF:AH=1:3,则sin∠BCF=( )
A. B. C. D.
【考点】解直角三角形的应用;全等三角形的判定与性质;勾股定理的应用.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;解直角三角形及其应用;推理能力;应用意识.
【答案】C
【分析】设EF=x,则AH=3x,根据全等三角形,正方形的性质可得AE=4x,再根据勾股定理可得AB=5x,即可求出sin∠ABE的值.
【解答】解:根据题意,设EF=x,则AH=3x,
∵△ABE≌△DAH≌△BCF,四边形EFGH为正方形,
∴AH=BE=3x,EF=HE=x,∠ABE=∠BCF,
∴AE=4x,
∵∠AEB=90°,
在直角三角形ABE中,由勾股定理得:,
∴,
∵∠ABE=∠BCF,
∴sin∠BCF,
故选:C.
【点评】本题考查了解直角三角形的应用,勾股定理的证明,熟练掌握勾股定理是解题的关键.
13.(2025秋 龙口市一模)桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子 备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,AB=6米,OA:OB=2:1.当点A位于最高点时,∠AOM=120°.此时,点A到地面的距离为( )
A.米 B.5米 C.6米 D.7米
【考点】解直角三角形的应用.
【专题】等腰三角形与直角三角形;应用意识.
【答案】B
【分析】过O作EF⊥OM,过A作AG⊥EF于G,求出∠AOE=30°,进而求出AG=AO×sin30°=2,即可求解.
【解答】解:过O作EF⊥OM,过A作AG⊥EF于G,
∵AB=6米,OA:OB=2:1,
∴OA=4米,
∵∠AOM=120°,∠EOM=90°,
∴∠AOE=30°,
在Rt△AOG中,AG=AO sin30°=2(米),
点A位于最高点时到地面的距离为2+3=5(米),
所以点A到地面的距离为5米;
故选:B.
【点评】本题考查解直角三角形的实际应用,解题的关键是根据题目条件,构造直角三角形.
14.(2025秋 安次区二模)如图是一款桌面可调整的学习桌,桌面宽度AB为60cm,桌面平放时高度DE为70cm,若书写时桌面适宜倾斜角(∠ABC)的度数为α,则桌沿(点A)处到地面的高度h为( )
A.(60sinα+70)cm B.(60cosα+70)cm
C.(60tanα+70)cm D.130cm
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】A
【分析】根据题意可得:AC⊥CB,然后在Rt△ACB中,利用锐角三角函数的定义求出AC的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:由题意得:AC⊥CB,
在Rt△ACB中,AB=60cm,∠ABC=α,
∴AC=AB sinα=60sinα(cm),
∵DE=70cm,
∴桌沿(点A)处到地面的高度h=AC+DE=(60sinα+70)cm,
故选:A.
【点评】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
15.(2025秋 南安市模拟)圭表(如图1)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标杆(称为“表”)和一把呈南北方向水平固定摆放的与标杆垂直的长尺(称为“圭”),当正午太阳照射在表上时,日影便会投影在圭面上.图2是一个根据某市地理位置设计的圭表平面示意图,表AC垂直圭BC.已知该市冬至正午太阳高度角(即∠ABC)为α,夏至正午太阳高度角(即∠ADC)为β,若表AC的长为m,则圭面上冬至线与夏至线之间的距离(即DB的长)为( )
A.mtanα﹣mtanβ B.
C.msinα﹣mcosβ D.
【考点】解直角三角形的应用;平行投影.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】先在Rt△ACD中,利用锐角三角函数的定义求出CD的长,然后在Rt△ACB中,利用锐角三角函数的定义求出BC的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:在Rt△ACD中,AC=m,∠ADC=β,
∴CD,
在Rt△ACB中,∠ABC=α,
∴BC,
∴BD=BC﹣CD,
故选:B.
【点评】本题考查了解直角三角形的应用,平行投影,熟练掌握锐角三角函数的定义是解题的关键.
16.(2025秋 无锡期末)如图1是第七届国际数学教育大会(ICME)会徽,选择其中两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC,sin∠AOB,则tanC的值为( )
A. B. C. D.
【考点】解直角三角形的应用.
【专题】计算题;运算能力.
【答案】B
【分析】设AB=3x,则BC=3x,由sin∠AOB,可得BO=7x,因tanC,可得tanC的值.
【解答】解:设AB=3x,则BC=3x,
∵sin∠AOB,
∴BO=7x,
∴tanC,
故选:B.
【点评】本题考查了解直角三角形的应用,关键是掌握正切、正弦的定义.
17.(2025秋 通榆县一模)“圭表”是中国古代用来确定节气的仪器.某“圭表”示意图如图所示,AC⊥BC,AC=3米,测得某地夏至正午时“表”的影长CD=1米,冬至时的正午太阳高度角∠ABC=α,则夏至到冬至,影长差BD的长为( )
A.(3sinα﹣1)米 B.米
C.(3tanα﹣1)米 D.米
【考点】解直角三角形的应用;平行投影.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】根据垂直定义可得∠ACB=90°,然后在Rt△ABC中,利用锐角三角函数的定义求出BC的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:∵AC⊥BC,
∴∠ACB=90°,
在Rt△ABC中,∠ABC=α,AC=3米,
∴BC(米),
∵CD=1米,
∴BD=BC﹣CD=(1)米,
∴影长差BD的长为(1)米,
故选:D.
【点评】本题考查了解直角三角形的应用,平行投影,熟练掌握锐角三角函数的定义是解题的关键.
18.(2025秋 深圳三模)小明在科普读物中了解到:每种介质都有自己的折射率,当光从空气射入该介质时,折射率为入射角正弦值与折射角正弦值之比,即折射率(i为入射角,r为折射角).如图,一束光从空气射向横截面为直角三角形的玻璃透镜斜面,经折射后沿垂直AC边的方向射出,已知i=30°,AB=15cm,BC=5cm,则该玻璃透镜的折射率n为( )
A.1.8 B.1.6 C.1.5 D.1.4
【考点】解直角三角形的应用.
【专题】计算题;解直角三角形及其应用;运算能力.
【答案】C
【分析】先利用互余关系说明∠A=r,再利用直角三角形的边角间关系求出∠A的正弦值,最后利用折射率公式得结论.
【解答】解:∵折射光线沿垂直AC边的方向射出,
∴β+∠A=90°.
∵法线垂直于AB,
∴γ+β=90°.
∴γ=∠A.
∴sinγ=sinA.
n
=1.5.
故选:C.
【点评】本题考查了解直角三角形的应用,掌握直角三角形的边角间关系、计算折射率的公式及“同角的余角相等”等知识点是解决本题的关键.
19.(2025秋 长春月考)如图所示,学校九年级举行跳绳比赛,图中的四个点分别描述了九年级的四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述1班和3班两个班级情况的点恰好在同一个反比例函数的图象上,则成绩优秀人数最多的是( )
A.1班 B.2班 C.3班 D.4班
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】D
【分析】设y(k>0),过4班点,2班点作y轴的平行线交反比例函数于A,B,设1班点为(x1,y1),2班点(x2,y2),3班点为(x3,y3),4班点(x4,y4),点A为(x4,y4'),点B为(x2,y2'),由图象得到y1>y4',y3<y2',依题意得:x1y1,x2y2,x3y3,x4y4分别为1班、2班、3班、4班的优秀人数.于是得到结论.
【解答】解:设y(k>0),
过4班点,2班点作y轴的平行线交反比例函数于A,B,
设1班点为(x1,y1),2班点(x2,y2),3班点为(x3,y3),4班点(x4,y4),点A为(x4,y4'),点B为(x2,y2'),
由图象可知:y1>y4',y3<y2',
依题意得:x1y1,x2y2,x3y3,x4y4分别为1班、2班、3班、4班的优秀人数.
由题意可得:
k=x4y4'=x2y2'=x1y1,
∵y1>y4',y3<y2',
∴x1y1>x4y4'=k,x3y3<x2y2'=k,
∴x4y4>x1y1=x3y3>x2y2,
即:4班优秀人数>1班优秀人数=3班优秀人数>2班优秀人数,
故选:D.
【点评】本题主要考查反比例函数图象与性质的实际应用,读懂题意,熟练掌握反比例函数的图象与性质是解决问题的关键.
20.(2025秋 顺德区期中)《墨经》中有:“景到,在午有端,与景长,说在端”,大约在两千四百年前,墨子和他的学生做的世界上第1个小孔成像的实验.如图所示的实验中,若物距为10cm,像距为18cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是( )cm.
A. B.4 C. D.5
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】A
【分析】“相似三角形对应高线的比等于相似比”,据此即可求解.
【解答】解:已知物距为10cm,像距为18cm,蜡烛火焰倒立的像的高度是6cm,设蜡烛火焰的高度是x cm,
由相似三角形的性质得,
解得,
即蜡烛火焰的高度是,
故选:A.
【点评】本题考查了相似三角形的性质的应用,解答本题的关键要明确:相似三角形对应高线的比等于相似比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学题型专项训练 单选题
一.选择题(共20小题)
1.(2025秋 禹城市期末)数形结合A,B,C三个住宅区分别住有某公司职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),如图所示,已知AB=100m,BC=200m,为了方便职工上下班,该公司的接送车打算在此区间内设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.点A B.点B C.点A,B之间 D.点B,C之间
2.(2025秋 沙坪坝区校级月考)对一组代数式:a,b,c(a,b,c≠0)进行如下操作:任意相邻的两个代数式,都用右边的代数式除以左边的代数式,所得之商写在这两个代数式之间,可以产生一个新的代数式列:a,,b,,c,记为代数式列1;将代数式列1按上述方法再做一次操作,可以得到代数式列2;以此类推.通过实际操作,得出以下结论:
①代数式列2为:a,,,a,b,,,b,c;
②代数式列3共18个代数式;
③代数式列3的所有代数式的积是代数式列2的所有代数式积的倍;
④代数式列2023的所有代数式的积为.
上述四个结论正确的有( )个
A.0 B.1 C.2 D.3
3.(2025秋 天台县模拟)如图,⊙O的半径为2,圆心O在坐标原点,正方形ABCD的边长为2,点A、B在第二象限,点C、D在⊙O上,且点D的坐标为(0,2),现将正方形ABCD绕点C按逆时针方向旋转150°,点B运动到了⊙O上点B1处,点A、D分别运动到了点A1、D1处,即得到正方形A1B1C1D1(点C1与C重合);再将正方形A1B1C1D1绕点B1按逆时针方向旋转150°,点A1运动到了⊙O上点A2处,点D1、C1分别运动到了点D2、C2处,即得到正方形A2B2C2D2(点B2与B1重合),…,按上述方法旋转2020次后,点A2020的坐标为( )
A.(0,2) B.(2,﹣1)
C.(﹣1,﹣1) D.(1,﹣2)
4.(2018秋 诸暨市期末)某企业接到为地震灾区生产活动房的任务,此企业拥有九个生产车间,现在每个车间原有的成品活动房一样多,每个车间的生产能力也一样.有A、B两组检验员,其中A组有8名检验员前两天时间将第一、二车间的所有成品(原来的和这两天生产的)检验完毕后,再去检验第三、四车间所有成品,又用去三天时间;同时这五天时间B组检验员也检验完余下的五个车间的所有成品.如果每个检验员的检验速度一样快,那么B组检验员人数为( )
A.8人 B.10人 C.12人 D.14人
5.(2025秋 盘州市期末)清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如x2+10x=56的方程,求正数解的几何方法是:“如图①,先构造一个面积为x2的正方形,再以该正方形的边长为一边向外构造四个面积均为的矩形,则大正方形的面积为56+25=81,则原方程的正数解为9﹣5=4”.小聪按此方法解关于y的方程y2+20y+m=0时,构造出如图②所示的图形,已知阴影部分的面积为156,则该方程的正数解为( )
A.6 B.8 C.16 D.
6.我国古代数学家研究过一元二次方程的正数解的几何解法.以方程x2+5x﹣14=0,即x(x+5)=14为例说明,《方图注》中记载的方法是:构造如图中大正方形的面积是(x+x+5)2同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,因此x=2.小明用此方法解关于x的方程x2+mx﹣n=0时,构造出同样的图形,已知大正方形的面积为14,小正方形的面积为4,则( )
A.m=2,n=3 B.,n=2
C.,n=2 D.m=2,
7.(2025秋 佳木斯三模)直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现每件小商品售价每降低1元,日销售量增加2件.若日利润保持不变.商家想尽快销售完该款商品.每件售价应定为多少元.( )
A.45 B.50 C.55 D.60
8.(2025秋 罗山县校级月考)生物学家研究发现,很多植物的生长都有下面的规律,即主干长出若干数目的支干后,每个支干又会长出同样数目的小分支.现有符合上述生长规律的某种植物,它的主干、支干和小分支的总数是91,则这种植物每个支干长出小分支的个数是( )
A.9 B.10 C.﹣10 D.9或10
9.(2025秋 岳阳县期中)如图,已知太阳光线AC和DE是平行的,在同一时刻,如果将两根高度相同的木杆竖直插在地面上,那么在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )
A.SAS B.AAS C.SSS D.ASA
10.(2025秋 长春月考)杜甫曾经哀叹“茅屋为秋风所破”,苦于杜甫不曾学过今日几何,不然也不会如此绝望.现在我们来看一茅屋的屋顶剖面,它呈等腰三角形,如果屋檐AB=AC=5米,横梁BC=8米,那么从梁BC上的任意一点D要支一根木头顶住屋顶A处,这根木头需要长度可能是( )
A.2.5米 B.6米 C.4米 D.8米
11.(2025秋 驿城区期末)王林在美术课上将等腰△ABC通过平移设计得到“一棵树”,已知底边AB上的高CD为5cm,沿CD方向向下平移3cm到△A1B1C1的位置,再经过相同的平移到△A2B2C2的位置,下方树干EF长为4cm,则树的高度CF长为( )
A.19cm B.17cm C.16cm D.15cm
12.(2025秋 洛宁县月考)第14届国际数学教育大会(ICME﹣14)会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF:AH=1:3,则sin∠BCF=( )
A. B. C. D.
13.(2025秋 龙口市一模)桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子 备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,AB=6米,OA:OB=2:1.当点A位于最高点时,∠AOM=120°.此时,点A到地面的距离为( )
A.米 B.5米 C.6米 D.7米
14.(2025秋 安次区二模)如图是一款桌面可调整的学习桌,桌面宽度AB为60cm,桌面平放时高度DE为70cm,若书写时桌面适宜倾斜角(∠ABC)的度数为α,则桌沿(点A)处到地面的高度h为( )
A.(60sinα+70)cm B.(60cosα+70)cm
C.(60tanα+70)cm D.130cm
15.(2025秋 南安市模拟)圭表(如图1)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标杆(称为“表”)和一把呈南北方向水平固定摆放的与标杆垂直的长尺(称为“圭”),当正午太阳照射在表上时,日影便会投影在圭面上.图2是一个根据某市地理位置设计的圭表平面示意图,表AC垂直圭BC.已知该市冬至正午太阳高度角(即∠ABC)为α,夏至正午太阳高度角(即∠ADC)为β,若表AC的长为m,则圭面上冬至线与夏至线之间的距离(即DB的长)为( )
A.mtanα﹣mtanβ B.
C.msinα﹣mcosβ D.
16.(2025秋 无锡期末)如图1是第七届国际数学教育大会(ICME)会徽,选择其中两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC,sin∠AOB,则tanC的值为( )
A. B. C. D.
17.(2025秋 通榆县一模)“圭表”是中国古代用来确定节气的仪器.某“圭表”示意图如图所示,AC⊥BC,AC=3米,测得某地夏至正午时“表”的影长CD=1米,冬至时的正午太阳高度角∠ABC=α,则夏至到冬至,影长差BD的长为( )
A.(3sinα﹣1)米 B.米
C.(3tanα﹣1)米 D.米
18.(2025秋 深圳三模)小明在科普读物中了解到:每种介质都有自己的折射率,当光从空气射入该介质时,折射率为入射角正弦值与折射角正弦值之比,即折射率(i为入射角,r为折射角).如图,一束光从空气射向横截面为直角三角形的玻璃透镜斜面,经折射后沿垂直AC边的方向射出,已知i=30°,AB=15cm,BC=5cm,则该玻璃透镜的折射率n为( )
A.1.8 B.1.6 C.1.5 D.1.4
19.(2025秋 长春月考)如图所示,学校九年级举行跳绳比赛,图中的四个点分别描述了九年级的四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述1班和3班两个班级情况的点恰好在同一个反比例函数的图象上,则成绩优秀人数最多的是( )
A.1班 B.2班 C.3班 D.4班
20.(2025秋 顺德区期中)《墨经》中有:“景到,在午有端,与景长,说在端”,大约在两千四百年前,墨子和他的学生做的世界上第1个小孔成像的实验.如图所示的实验中,若物距为10cm,像距为18cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是( )cm.
A. B.4 C. D.5
参考答案与试题解析
一.选择题(共20小题)
1.(2025秋 禹城市期末)数形结合A,B,C三个住宅区分别住有某公司职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),如图所示,已知AB=100m,BC=200m,为了方便职工上下班,该公司的接送车打算在此区间内设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.点A B.点B C.点A,B之间 D.点B,C之间
【考点】两点间的距离.
【专题】线段、角、相交线与平行线;应用意识.
【答案】A
【分析】此题为数学知识的应用,由题意设一个停靠点,为使所有的人步行到停靠点的路程之和最小,肯定要尽量缩短两地之间的里程,就用到两点间线段最短定理.
【解答】解:①以点A为停靠点,则所有人的路程的和=15×100+10×300=4500(米),
②以点B为停靠点,则所有人的路程的和=30×100+10×200=5000(米),
③以点C为停靠点,则所有人的路程的和=30×300+15×200=12000(米),
④当在AB之间停靠时,设停靠点到A的距离是m,则(0<m<100),则所有人的路程的和是:30m+15(100﹣m)+10(300﹣m)=4500+5m>4500,
⑤当在BC之间停靠时,设停靠点到B的距离为n,则(0<n<200),则总路程为30(100+n)+15n+10(200﹣n)=5000+35n>4500.
∴该停靠点的位置应设在点A;
故选:A.
【点评】此题为数学知识的应用,考查知识点为两点之间线段最短.
2.(2025秋 沙坪坝区校级月考)对一组代数式:a,b,c(a,b,c≠0)进行如下操作:任意相邻的两个代数式,都用右边的代数式除以左边的代数式,所得之商写在这两个代数式之间,可以产生一个新的代数式列:a,,b,,c,记为代数式列1;将代数式列1按上述方法再做一次操作,可以得到代数式列2;以此类推.通过实际操作,得出以下结论:
①代数式列2为:a,,,a,b,,,b,c;
②代数式列3共18个代数式;
③代数式列3的所有代数式的积是代数式列2的所有代数式积的倍;
④代数式列2023的所有代数式的积为.
上述四个结论正确的有( )个
A.0 B.1 C.2 D.3
【考点】规律型:数字的变化类;列代数式.
【专题】计算题;猜想归纳;运算能力;推理能力;应用意识.
【答案】D
【分析】根据新定义进行计算验证即可解决.
【解答】解:根据题意,由a,b,c(a,b,c≠0),
∴代数列1为:a,,b,,c,
则代数列2为:a,,,a,b,,,b,c,故①对;
代数列3为:a,,,a,,,a,,b,,,b,,,b,,c共17个代数式,故②错误;
∵代数式列2的所有代数式积为:aa×bb×c,
代数式列3的所有代数式的积是:aaabbbc,
∴代数式列3的所有代数式的积是代数式列2的所有代数式积的倍,故③对;
∵代数式列1的所有代数式的积是abc=bc2=bc2×()1﹣1,
代数式列2的所有代数式的积是:bc2×()2﹣1,
代数式列3的所有代数式的积是:bc2×()3﹣1,
......
故代数式列2023的所有代数式的积是:bc2×()2023﹣1,故④对,
故答案选:D.
【点评】本题考查列代数式以及根据新定义解决问题,难度较大切繁琐,细心认真耐心是解决问题的关键.
3.(2025秋 天台县模拟)如图,⊙O的半径为2,圆心O在坐标原点,正方形ABCD的边长为2,点A、B在第二象限,点C、D在⊙O上,且点D的坐标为(0,2),现将正方形ABCD绕点C按逆时针方向旋转150°,点B运动到了⊙O上点B1处,点A、D分别运动到了点A1、D1处,即得到正方形A1B1C1D1(点C1与C重合);再将正方形A1B1C1D1绕点B1按逆时针方向旋转150°,点A1运动到了⊙O上点A2处,点D1、C1分别运动到了点D2、C2处,即得到正方形A2B2C2D2(点B2与B1重合),…,按上述方法旋转2020次后,点A2020的坐标为( )
A.(0,2) B.(2,﹣1)
C.(﹣1,﹣1) D.(1,﹣2)
【考点】坐标与图形变化﹣旋转;规律型:点的坐标.
【专题】动点型;规律型;应用意识.
【答案】B
【分析】如图,由题意发现12次一个循环,由2020÷12=168余数为4,推出A2020的坐标与A4相同,由此即可解决问题.
【解答】解:如图,由题意发现12次一个循环,
∵2020÷12=168余数为4,
∴A2020的坐标与A4相同,
∵A4(2,﹣1),
∴A2020(2,﹣1),
故选:B.
【点评】本题考查坐标与图形的变化﹣旋转,规律型问题,解题的关键是学会探究规律的方法,属于中考选择题中的压轴题.
4.(2018秋 诸暨市期末)某企业接到为地震灾区生产活动房的任务,此企业拥有九个生产车间,现在每个车间原有的成品活动房一样多,每个车间的生产能力也一样.有A、B两组检验员,其中A组有8名检验员前两天时间将第一、二车间的所有成品(原来的和这两天生产的)检验完毕后,再去检验第三、四车间所有成品,又用去三天时间;同时这五天时间B组检验员也检验完余下的五个车间的所有成品.如果每个检验员的检验速度一样快,那么B组检验员人数为( )
A.8人 B.10人 C.12人 D.14人
【考点】一元一次方程的应用.
【专题】应用题;应用意识.
【答案】C
【分析】设A组所检验的每个车间原有成品a件,每个车间1天生产b件,可得A组前两天检验的总件数和后三天检验的总件数为.根据检验员的检验速度相同,可列式等式得到a和b的关系,即可得A组一名检验员每天检验的成品数.再根据B组检验员的人数=五个车间的所有成品÷A组一名检验员每天检验的成品数,列式即可得解.
【解答】解:设每个车间原有成品a件,每个车间每天生产b件产品,根据检验速度相同得:
,
解得a=4b;
则A组每名检验员每天检验的成品数为:2(a+2b)÷(2×8)=12b÷16b.
那么B组检验员的人数为:5(a+5b)÷(b)÷5=45bb÷5=12(人).
故选:C.
【点评】本题考查了一元一次方程的应用,本题是一道叙述比较长的题目,解题时应认真读题,理解各种量之间的关系列出等式.
5.(2025秋 盘州市期末)清初曾传入中国两卷无作者的代数学书,被译为《阿尔热巴拉新法》,后由中国近代数学家李善兰改译为《代数学》.该书中记载,形如x2+10x=56的方程,求正数解的几何方法是:“如图①,先构造一个面积为x2的正方形,再以该正方形的边长为一边向外构造四个面积均为的矩形,则大正方形的面积为56+25=81,则原方程的正数解为9﹣5=4”.小聪按此方法解关于y的方程y2+20y+m=0时,构造出如图②所示的图形,已知阴影部分的面积为156,则该方程的正数解为( )
A.6 B.8 C.16 D.
【考点】一元二次方程的应用.
【专题】一元二次方程及应用;运算能力;应用意识.
【答案】A
【分析】先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为x的矩形,利用大正方形的面积=阴影部分的面积+4×小正方形的面积,可得出大正方形的面积,再利用该方程的正数解=大正方形的边长﹣2×小正方形的边长,即可得出结论.
【解答】解:先构造一个面积为y2的正方形,再以该正方形的边长为一边向外构造四个面积均为5y的矩形,
∵阴影部分的面积为156,
∴y2+4×5y=y2+20y=156,
∴大正方形的面积=156+4×52=256,
∴大正方形的边长16,
∴方程y2+20y+m=0的正数解为16﹣2×5=16﹣10=6,
故选:A.
【点评】本题考查了一元二次方程的应用,模仿案例,构造出符合题意的大正方形是解题的关键.
6.我国古代数学家研究过一元二次方程的正数解的几何解法.以方程x2+5x﹣14=0,即x(x+5)=14为例说明,《方图注》中记载的方法是:构造如图中大正方形的面积是(x+x+5)2同时它又等于四个矩形的面积加上中间小正方形的面积,即4×14+52,因此x=2.小明用此方法解关于x的方程x2+mx﹣n=0时,构造出同样的图形,已知大正方形的面积为14,小正方形的面积为4,则( )
A.m=2,n=3 B.,n=2
C.,n=2 D.m=2,
【考点】一元二次方程的应用.
【专题】一元二次方程及应用;运算能力;应用意识.
【答案】D
【分析】画出方程x2+mx﹣n=0的拼图过程,由面积之间的关系得m2=4,4n+4=14,即可得出结论.
【解答】解:如图,
由题意得:m2=4,4n+4=14,
∴m2,n,
故选:D.
【点评】本题考查了一元二次方程的应用,理解一元二次方程的正数解的几何解法是解题的关键.
7.(2025秋 佳木斯三模)直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现每件小商品售价每降低1元,日销售量增加2件.若日利润保持不变.商家想尽快销售完该款商品.每件售价应定为多少元.( )
A.45 B.50 C.55 D.60
【考点】一元二次方程的应用.
【专题】一元二次方程及应用;运算能力;应用意识.
【答案】B
【分析】设每件售价应定为x元,根据按每件60元销售,每天可卖出20件.每降低1元,日销售量增加2件.日利润保持不变.列出一元二次方程,解之取符合题意的值即可.
【解答】解:设每件售价应定为x元,
根据题意得:(x﹣40)[20+2(60﹣x)]=(60﹣40)×20,
解得:x1=50,x2=60(不符合题意,舍去),
即商家想尽快销售完该款商品,每件售价应定为50元.
故选:B.
【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
8.(2025秋 罗山县校级月考)生物学家研究发现,很多植物的生长都有下面的规律,即主干长出若干数目的支干后,每个支干又会长出同样数目的小分支.现有符合上述生长规律的某种植物,它的主干、支干和小分支的总数是91,则这种植物每个支干长出小分支的个数是( )
A.9 B.10 C.﹣10 D.9或10
【考点】一元二次方程的应用.
【专题】一元二次方程及应用;运算能力;应用意识.
【答案】A
【分析】设这种植物每个支干长出的小分支个数是x,根据主干、支干和小分支的总数是91,列出一元二次方程,解之取其正值即可得出答案.
【解答】解:设这种植物每个支干长出的小分支个数是x,
根据题意得:1+x+x2=91,
整理得:x2+x﹣90=0,
解得:x1=9,x2=﹣10(不合题意,舍去),
即这种植物每个支干长出的小分支个数是9,
故选:A.
【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
9.(2025秋 岳阳县期中)如图,已知太阳光线AC和DE是平行的,在同一时刻,如果将两根高度相同的木杆竖直插在地面上,那么在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )
A.SAS B.AAS C.SSS D.ASA
【考点】平行投影;全等图形;全等三角形的判定.
【专题】投影与视图;应用意识.
【答案】B
【分析】先根据题意得出AC∥ED,AH⊥GT,DT⊥GT,AH=DT,进而得∠AGH=∠DKT,∠AHG=∠DTK=90°,据此即可判定△AGH和△DKT全等,从而得出答案.
【解答】解:如图,
,
∵AC∥ED,AH⊥GT,DT⊥GT,AH=DT,
∴∠AGH=∠DKT,∠AHG=∠DTK=90°,
在△AGH和△DKT中,
,
∴△AGH≌△DKT(AAS),
故选:B.
【点评】此题主要考查了全等三角形的判定,平行线的性质,解答此题的关键是理解题意,找出AC∥ED,AH⊥GT,DT⊥GT,AH=DT,进而找出判定三角形全等的判定条件.
10.(2025秋 长春月考)杜甫曾经哀叹“茅屋为秋风所破”,苦于杜甫不曾学过今日几何,不然也不会如此绝望.现在我们来看一茅屋的屋顶剖面,它呈等腰三角形,如果屋檐AB=AC=5米,横梁BC=8米,那么从梁BC上的任意一点D要支一根木头顶住屋顶A处,这根木头需要长度可能是( )
A.2.5米 B.6米 C.4米 D.8米
【考点】勾股定理的应用;等腰三角形的性质.
【专题】等腰三角形与直角三角形;运算能力;推理能力;应用意识.
【答案】C
【分析】过点A作AE⊥BC于点E,由等腰三角形的性质得BE=CE=4米,中由勾股定理求出AE=3米,然后由AE≤AD<AC,即可得出结论.
【解答】解:如图,过点A作AE⊥BC于点E,
∵AB=AC=5米,BC=8米,
∴BE=CEBC8=4(米),
在Rt△ABE中,由勾股定理得:AE3(米),
由题意可知,AE≤AD<AC,
即3米≤AD<5米,
故这根木头需要长度可能是4米,
故选:C.
【点评】本题考查了勾股定理以及等腰三角形的性质等知识,熟练掌握勾股定理和等腰三角形的性质是解题的关键.
11.(2025秋 驿城区期末)王林在美术课上将等腰△ABC通过平移设计得到“一棵树”,已知底边AB上的高CD为5cm,沿CD方向向下平移3cm到△A1B1C1的位置,再经过相同的平移到△A2B2C2的位置,下方树干EF长为4cm,则树的高度CF长为( )
A.19cm B.17cm C.16cm D.15cm
【考点】勾股定理的应用;平移的性质;等腰三角形的性质.
【专题】平移、旋转与对称;应用意识.
【答案】D
【分析】根据平移的性质得到CC1=C1C2=3cm,根据题意计算,得到答案.
【解答】解:由平移的性质可知:CC1=C1C2=3cm,
由题意得:底边AB上的高CD为5cm,沿CD方向向下平移3cm,
∴C2E=5cm,EF=4cm,
∴CF=CC1+C1C2+C2E+EF
=3+3+5+4=15(cm),
故选:D.
【点评】本题考查的是图形的平移,掌握平移的性质是解题的关键.
12.(2025秋 洛宁县月考)第14届国际数学教育大会(ICME﹣14)会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF:AH=1:3,则sin∠BCF=( )
A. B. C. D.
【考点】解直角三角形的应用;全等三角形的判定与性质;勾股定理的应用.
【专题】等腰三角形与直角三角形;矩形 菱形 正方形;解直角三角形及其应用;推理能力;应用意识.
【答案】C
【分析】设EF=x,则AH=3x,根据全等三角形,正方形的性质可得AE=4x,再根据勾股定理可得AB=5x,即可求出sin∠ABE的值.
【解答】解:根据题意,设EF=x,则AH=3x,
∵△ABE≌△DAH≌△BCF,四边形EFGH为正方形,
∴AH=BE=3x,EF=HE=x,∠ABE=∠BCF,
∴AE=4x,
∵∠AEB=90°,
在直角三角形ABE中,由勾股定理得:,
∴,
∵∠ABE=∠BCF,
∴sin∠BCF,
故选:C.
【点评】本题考查了解直角三角形的应用,勾股定理的证明,熟练掌握勾股定理是解题的关键.
13.(2025秋 龙口市一模)桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子 备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,AB=6米,OA:OB=2:1.当点A位于最高点时,∠AOM=120°.此时,点A到地面的距离为( )
A.米 B.5米 C.6米 D.7米
【考点】解直角三角形的应用.
【专题】等腰三角形与直角三角形;应用意识.
【答案】B
【分析】过O作EF⊥OM,过A作AG⊥EF于G,求出∠AOE=30°,进而求出AG=AO×sin30°=2,即可求解.
【解答】解:过O作EF⊥OM,过A作AG⊥EF于G,
∵AB=6米,OA:OB=2:1,
∴OA=4米,
∵∠AOM=120°,∠EOM=90°,
∴∠AOE=30°,
在Rt△AOG中,AG=AO sin30°=2(米),
点A位于最高点时到地面的距离为2+3=5(米),
所以点A到地面的距离为5米;
故选:B.
【点评】本题考查解直角三角形的实际应用,解题的关键是根据题目条件,构造直角三角形.
14.(2025秋 安次区二模)如图是一款桌面可调整的学习桌,桌面宽度AB为60cm,桌面平放时高度DE为70cm,若书写时桌面适宜倾斜角(∠ABC)的度数为α,则桌沿(点A)处到地面的高度h为( )
A.(60sinα+70)cm B.(60cosα+70)cm
C.(60tanα+70)cm D.130cm
【考点】解直角三角形的应用.
【专题】解直角三角形及其应用;运算能力.
【答案】A
【分析】根据题意可得:AC⊥CB,然后在Rt△ACB中,利用锐角三角函数的定义求出AC的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:由题意得:AC⊥CB,
在Rt△ACB中,AB=60cm,∠ABC=α,
∴AC=AB sinα=60sinα(cm),
∵DE=70cm,
∴桌沿(点A)处到地面的高度h=AC+DE=(60sinα+70)cm,
故选:A.
【点评】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
15.(2025秋 南安市模拟)圭表(如图1)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标杆(称为“表”)和一把呈南北方向水平固定摆放的与标杆垂直的长尺(称为“圭”),当正午太阳照射在表上时,日影便会投影在圭面上.图2是一个根据某市地理位置设计的圭表平面示意图,表AC垂直圭BC.已知该市冬至正午太阳高度角(即∠ABC)为α,夏至正午太阳高度角(即∠ADC)为β,若表AC的长为m,则圭面上冬至线与夏至线之间的距离(即DB的长)为( )
A.mtanα﹣mtanβ B.
C.msinα﹣mcosβ D.
【考点】解直角三角形的应用;平行投影.
【专题】解直角三角形及其应用;运算能力.
【答案】B
【分析】先在Rt△ACD中,利用锐角三角函数的定义求出CD的长,然后在Rt△ACB中,利用锐角三角函数的定义求出BC的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:在Rt△ACD中,AC=m,∠ADC=β,
∴CD,
在Rt△ACB中,∠ABC=α,
∴BC,
∴BD=BC﹣CD,
故选:B.
【点评】本题考查了解直角三角形的应用,平行投影,熟练掌握锐角三角函数的定义是解题的关键.
16.(2025秋 无锡期末)如图1是第七届国际数学教育大会(ICME)会徽,选择其中两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC,sin∠AOB,则tanC的值为( )
A. B. C. D.
【考点】解直角三角形的应用.
【专题】计算题;运算能力.
【答案】B
【分析】设AB=3x,则BC=3x,由sin∠AOB,可得BO=7x,因tanC,可得tanC的值.
【解答】解:设AB=3x,则BC=3x,
∵sin∠AOB,
∴BO=7x,
∴tanC,
故选:B.
【点评】本题考查了解直角三角形的应用,关键是掌握正切、正弦的定义.
17.(2025秋 通榆县一模)“圭表”是中国古代用来确定节气的仪器.某“圭表”示意图如图所示,AC⊥BC,AC=3米,测得某地夏至正午时“表”的影长CD=1米,冬至时的正午太阳高度角∠ABC=α,则夏至到冬至,影长差BD的长为( )
A.(3sinα﹣1)米 B.米
C.(3tanα﹣1)米 D.米
【考点】解直角三角形的应用;平行投影.
【专题】解直角三角形及其应用;运算能力.
【答案】D
【分析】根据垂直定义可得∠ACB=90°,然后在Rt△ABC中,利用锐角三角函数的定义求出BC的长,从而利用线段的和差关系进行计算,即可解答.
【解答】解:∵AC⊥BC,
∴∠ACB=90°,
在Rt△ABC中,∠ABC=α,AC=3米,
∴BC(米),
∵CD=1米,
∴BD=BC﹣CD=(1)米,
∴影长差BD的长为(1)米,
故选:D.
【点评】本题考查了解直角三角形的应用,平行投影,熟练掌握锐角三角函数的定义是解题的关键.
18.(2025秋 深圳三模)小明在科普读物中了解到:每种介质都有自己的折射率,当光从空气射入该介质时,折射率为入射角正弦值与折射角正弦值之比,即折射率(i为入射角,r为折射角).如图,一束光从空气射向横截面为直角三角形的玻璃透镜斜面,经折射后沿垂直AC边的方向射出,已知i=30°,AB=15cm,BC=5cm,则该玻璃透镜的折射率n为( )
A.1.8 B.1.6 C.1.5 D.1.4
【考点】解直角三角形的应用.
【专题】计算题;解直角三角形及其应用;运算能力.
【答案】C
【分析】先利用互余关系说明∠A=r,再利用直角三角形的边角间关系求出∠A的正弦值,最后利用折射率公式得结论.
【解答】解:∵折射光线沿垂直AC边的方向射出,
∴β+∠A=90°.
∵法线垂直于AB,
∴γ+β=90°.
∴γ=∠A.
∴sinγ=sinA.
n
=1.5.
故选:C.
【点评】本题考查了解直角三角形的应用,掌握直角三角形的边角间关系、计算折射率的公式及“同角的余角相等”等知识点是解决本题的关键.
19.(2025秋 长春月考)如图所示,学校九年级举行跳绳比赛,图中的四个点分别描述了九年级的四个班级竞赛成绩的优秀率y(班级优秀人数占班级参加竞赛人数的百分率)与该班参加竞赛人数x的情况,其中描述1班和3班两个班级情况的点恰好在同一个反比例函数的图象上,则成绩优秀人数最多的是( )
A.1班 B.2班 C.3班 D.4班
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】D
【分析】设y(k>0),过4班点,2班点作y轴的平行线交反比例函数于A,B,设1班点为(x1,y1),2班点(x2,y2),3班点为(x3,y3),4班点(x4,y4),点A为(x4,y4'),点B为(x2,y2'),由图象得到y1>y4',y3<y2',依题意得:x1y1,x2y2,x3y3,x4y4分别为1班、2班、3班、4班的优秀人数.于是得到结论.
【解答】解:设y(k>0),
过4班点,2班点作y轴的平行线交反比例函数于A,B,
设1班点为(x1,y1),2班点(x2,y2),3班点为(x3,y3),4班点(x4,y4),点A为(x4,y4'),点B为(x2,y2'),
由图象可知:y1>y4',y3<y2',
依题意得:x1y1,x2y2,x3y3,x4y4分别为1班、2班、3班、4班的优秀人数.
由题意可得:
k=x4y4'=x2y2'=x1y1,
∵y1>y4',y3<y2',
∴x1y1>x4y4'=k,x3y3<x2y2'=k,
∴x4y4>x1y1=x3y3>x2y2,
即:4班优秀人数>1班优秀人数=3班优秀人数>2班优秀人数,
故选:D.
【点评】本题主要考查反比例函数图象与性质的实际应用,读懂题意,熟练掌握反比例函数的图象与性质是解决问题的关键.
20.(2025秋 顺德区期中)《墨经》中有:“景到,在午有端,与景长,说在端”,大约在两千四百年前,墨子和他的学生做的世界上第1个小孔成像的实验.如图所示的实验中,若物距为10cm,像距为18cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是( )cm.
A. B.4 C. D.5
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】A
【分析】“相似三角形对应高线的比等于相似比”,据此即可求解.
【解答】解:已知物距为10cm,像距为18cm,蜡烛火焰倒立的像的高度是6cm,设蜡烛火焰的高度是x cm,
由相似三角形的性质得,
解得,
即蜡烛火焰的高度是,
故选:A.
【点评】本题考查了相似三角形的性质的应用,解答本题的关键要明确:相似三角形对应高线的比等于相似比.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
