2026年中考数学题型专项训练 解答题(含解析)
文档属性
| 名称 | 2026年中考数学题型专项训练 解答题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 645.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 21:20:53 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学题型专项训练 解答题
一.解答题(共20小题)
1.(2025秋 屯留区月考)学科实践
暑假期间、我市某公园为打造专属夜景景观特别安装了喷水装置,为保持人行绿道干燥,水柱要喷入河中,水柱可近似看作抛物线.图2是截面图,已知人行绿道宽OA=3.5m,AE是河道坝高,坝面AB的坡比为i=1:0.5,在距离喷水口O处2m时,水柱距离人行道的高度达到最大值3m.以点O为原点,直线OA为x轴建立平面直角坐标系.
(1)出于安全考虑,在坝顶A处安装护栏,要求水柱不能喷射到护栏上,求护栏的最大高度.
(2)当水面距离人行道的竖直距离为多少时,水柱恰好落在河水中(水面与AB交点处)?
2.(2025秋 晋源区月考)综合与探究
已知A,B为数轴上的两个点,点A表示的数为a,点B表示的数为b,且8xyb﹣2+(a+2)xy﹣1是关于x,y的三次二项式.
根据上述条件,解答下列问题:
(1)求a,b的值;
(2)若C为数轴上AB之间的点,且BC=5AC,求点C表示的数;
(3)在(2)的条件下,有一动点P从点A开始以每秒2个单位长度的速度沿数轴向左匀速运动,同时另一动点Q从点B开始以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒,是否存在某一时刻t,使得PC=2QC?若存在,直接写出t的值;若不存在,请说明理由.
3.(2025秋 兴县月考)综合与实践
问题情境:元旦晚会舞台布置中需要搭一条抛物线型灯链,最初的设计方案如图1所示,灯链两端连接A,B两点,点C位于点B正下方的地面处,以点A正下方的地面处的点O为原点,OC所在的直线为x轴,OA所在的直线为y轴,建立平面直角坐标系,抛物线解析式的二次项系数为0.03,OC=10米,OA=BC=3米,但实际实施方案后发现最低点过低.
方案修改:莉莉将方案进行修改,如图2,将图1中灯链的最低点固定在距地面2.7米的点N处,点N两侧的灯链形成了两个对称的新抛物线.
(1)求图1中抛物线的解析式.
(2)若图1中抛物线的最低点为M,求点M到OC的距离.
(3)若图2中两个最低点的距离为4米,修改方案后最低点提高了多少米?
4.(2025秋 合肥期末)根据图中情景,解答下列问题:
(1)购买8根跳绳需 元;购买12根跳绳需 元;
(2)购买m根跳绳需多少元?(请你用含有m的式子表示)
(3)小红比小明多买2根,付款时小红反而比小明少7元,你认为这种情况有可能吗?请利用方程知识说明理由.
5.(2025秋 桃城区校级期中)为更好筹备“十四运”的召开,小颖及其小组成员将利用所学知识测量一个广告牌的高度EF.在第一次测量中,小颖来回走动,走到点D时,其影子末端与广告牌影子末端重合于点H,其中DH=1m.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小颖从点D沿着直线FD后退5m到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2m.
如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小颖的身高为1.5m(眼睛到头顶距离忽略不计),平面镜的厚度忽略不计.根据以上信息,求广告牌的高度EF.
6.(2025秋 碑林区校级月考)某校迎来了一百二十年校庆,为了准备校庆,校方决定准备一场别开生面的文艺演出,有歌唱,舞蹈,小舞台剧等节目,为此学校需要采购一批演出服装.现有质量较好且价格合理的A,B两家公司供选择,这两家公司给出的价格都是每套服装100元,经洽谈协商:A公司给出的优惠条件是全部服装单价打8折,但校方需要承担1500元的运费;B公司给出的优惠条件是购买服装不超过100套时不打折,超过100套时,超出部分每套打7折,校方不用承担运费.
(1)分别求出学校购买A,B两公司服装所付的总费用y1(元)和y2(元)与购买服装的数量x(套)之间的函数关系式;
(2)如果该校根据演出人数决定购买180套服装,请通过计算说明学校选择哪家公司的服装花费更少.
7.(2025秋 沈阳月考)数学兴趣小组测量校园内旗杆的高度.如图,小聪在某一时刻测得1m长的竹竿竖直放置时影长1.5m,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长BD=21m,留在墙上的影高CD=2m,求旗杆的高度.
8.(2025秋 沈阳月考)某校将新建图书楼的正门设计为一个抛物线型拱门,并要求所设计的拱门的跨度与拱高之积为48m2,还要兼顾美观、大方、和谐、通畅等因素,设计部门按要求做出了设计方案.现把方案中的拱门图形放入平面直角坐标系中,如图1、2所示,抛物线型拱门的跨度ON=12m,拱高PE=4m.其中,点N在x轴上,PE⊥ON,OE=EN.要在拱门中设置矩形框架,其面积越大越好.
方案一:如图1,矩形框架ABCD的面积记为S1,点A,D在抛物线上,边BC在ON上;
方案二:如图2,矩形框架A'B'C'D'的面积记为S2,点A',D'在抛物线上,边B'C'在ON上.
(1)求抛物线的函数表达式;
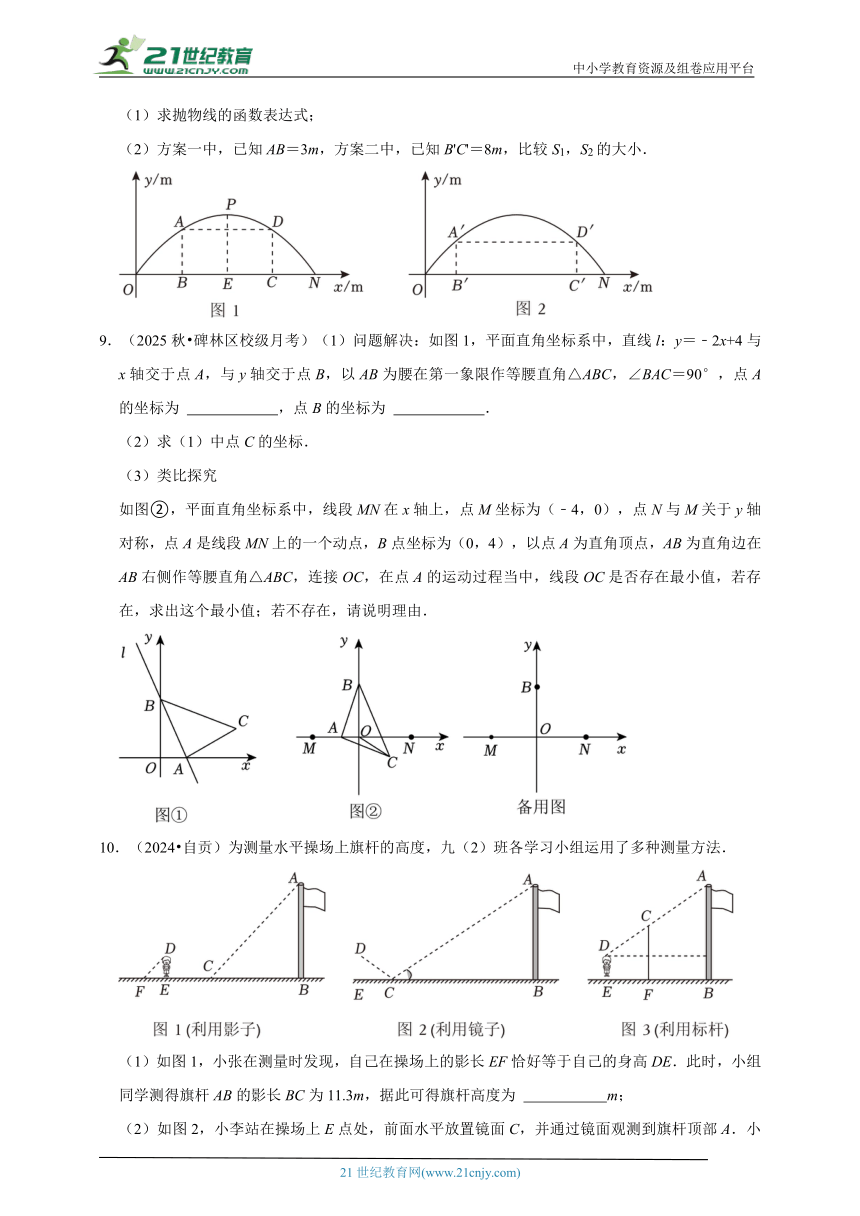
(2)方案一中,已知AB=3m,方案二中,已知B'C'=8m,比较S1,S2的大小.
9.(2025秋 碑林区校级月考)(1)问题解决:如图1,平面直角坐标系中,直线l:y=﹣2x+4与x轴交于点A,与y轴交于点B,以AB为腰在第一象限作等腰直角△ABC,∠BAC=90°,点A的坐标为 ,点B的坐标为 .
(2)求(1)中点C的坐标.
(3)类比探究
如图②,平面直角坐标系中,线段MN在x轴上,点M坐标为(﹣4,0),点N与M关于y轴对称,点A是线段MN上的一个动点,B点坐标为(0,4),以点A为直角顶点,AB为直角边在AB右侧作等腰直角△ABC,连接OC,在点A的运动过程当中,线段OC是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.
10.(2024 自贡)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 m;
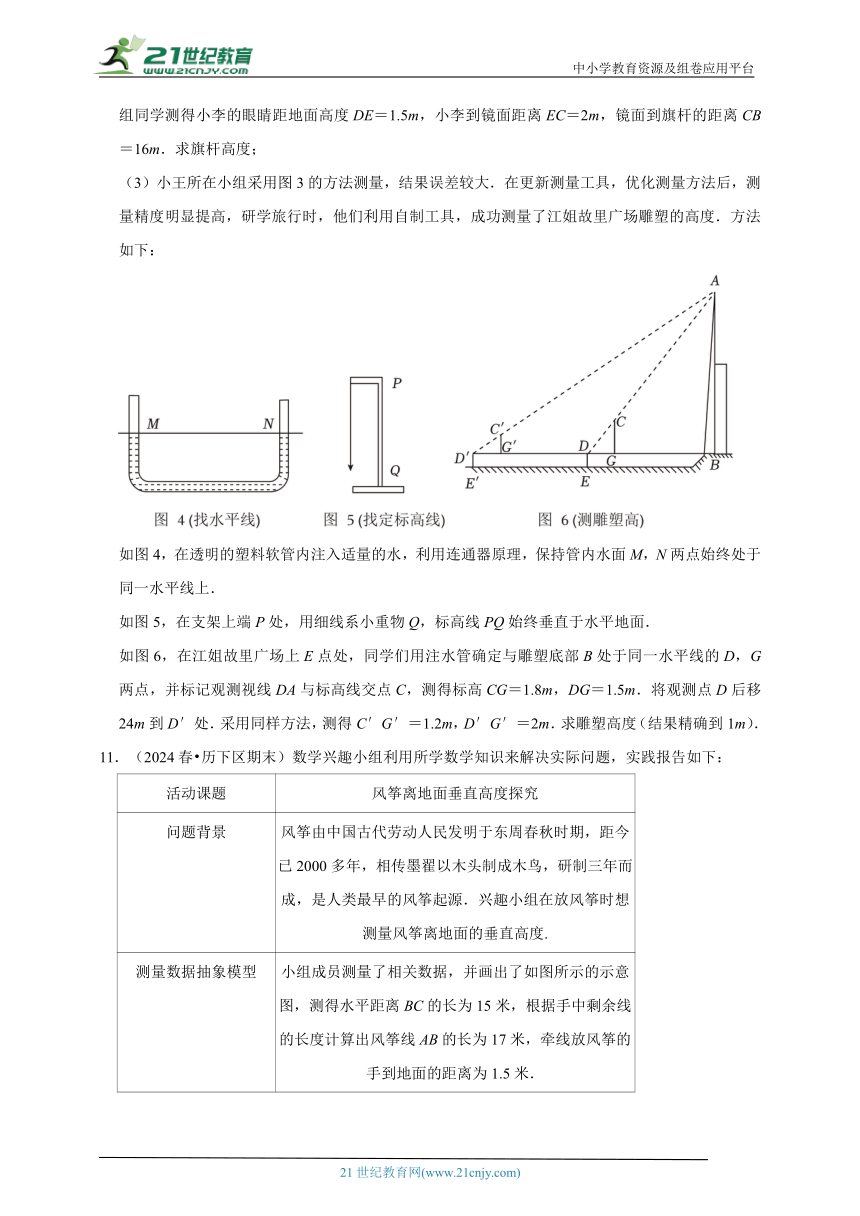
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m.求旗杆高度;
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到D′处.采用同样方法,测得C′G′=1.2m,D′G′=2m.求雕塑高度(结果精确到1m).
11.(2024春 历下区期末)数学兴趣小组利用所学数学知识来解决实际问题,实践报告如下:
活动课题 风筝离地面垂直高度探究
问题背景 风筝由中国古代劳动人民发明于东周春秋时期,距今已2000多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.兴趣小组在放风筝时想测量风筝离地面的垂直高度.
测量数据抽象模型 小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC的长为15米,根据手中剩余线的长度计算出风筝线AB的长为17米,牵线放风筝的手到地面的距离为1.5米.
问题产生 经过讨论,兴趣小组得出以下问题: (1)运用所学勾股定理相关知识,根据测量所得数据,计算出风筝离地面的垂直高度. (2)如果想要风筝沿DA方向再上升12米,且BC长度不变,则他应该再放出多少米线?
问题解决 ……
该报告还没有完成,请你帮助兴趣小组解决以上问题.
12.(2025秋 灯塔市期中)【问题背景】
已知点A,M,N,B在数轴上对应的数分别为﹣1,x﹣1,x+1,11.线段MN沿数轴的正方向以每秒1个单位的速度移动,设移动时间为t秒.例如线段AB的长度为|﹣1﹣11|=12或11﹣(﹣1)=12.
【初步发现】
(1)求线段MN的长度;
【问题解决】
(2)若x=1,回答下列两个问题:
①当点M在点B的左侧,同时点N在点B的右侧时,用含t的代数式表示线段AM+BN的值;
②若点A,B与线段MN同时移动,点A以每秒1个单位长度的速度向数轴的正方向移动,点B以每秒1个单位长度的速度向数轴的负方向移动.在移动过程中,求线段AM+BN的值.(可用含t的代数式表示)
13.(2025秋 隆昌市校级期末)阅读下列材料:利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式,然后由(x+m)2≥0就可求出多项式x2+bx+c的最小值.
例:求多项式x2﹣4x+5的最小值.
解:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1.
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1.
当x=2时,(x﹣2)2+1=1,因此(x﹣2)2+1有最小值,最小值为1,即x2﹣4x+5的最小值为1.
通过阅读,理解材料的解题思路,请解决以下问题:
(1)【理解探究】已知代数式A=x2+8x+7,求A的最小值;
(2)【类比应用】张大爷家有甲、乙两块长方形菜地,已知甲菜地的两边长分别是(5a+1)米、(2a+2)米,乙菜地的两边长分别是(3a+8)米、(3a﹣2)米,试比较这两块菜地的面积S甲和S乙的大小,并说明理由;
(3)【拓展升华】如图,△ABC中,∠C=90°,AC=8cm,BC=16cm,点M,N分别是线段AC和BC上的动点,点M从A点出发以1cm/s的速度向C点运动;同时点N从C点出发以2cm/s的速度向B点运动,当其中一点到达终点时,两点同时停止运动.设运动的时间为t,则当t的值为多少时,△MCN的面积最大,最大值为多少?
14.(2025秋 南浔区期末)七年级数学兴趣小组成员自主开展数学微项目研究,他们决定研究“折线数轴”.
探索“折线数轴”
素材1 如图,将一条数轴在原点O,点B,点C处折一下,得到一条“折线数轴”.图中点A表示﹣9,点B表示12,点C表示24,点D表示36,我们称点A与点D在数轴上的“友好距离”为45个单位长度,并表示为45.
素材2 动点P从点A出发,以2个单位长度/秒的初始速度沿着“折线数轴”向其正方向运动.当运动到点O与点B之间时速度变为初始速度的一半.当运动到点B与点C之间时速度变为初始速度的两倍.经过点C后立刻恢复初始速度.
问题解决
探索1 动点P从点A运动至点B需要多少时间?
探索2 动点P从点A出发,运动t秒至点B和点C之间时,求点P表示的数(用含t的代数式表示);
探索3 动点P从点A出发,运动至点D的过程中某个时刻满足时,求动点P运动的时间.
15.(2025秋 宁波期中)
背景 【长城上可以点无人机送的外卖了】 打开手机外卖软件下单,在长城上也可以点外卖了,最快5分钟收货! 日前,美团无人机在八达岭长城开通了北京首条无人机配送航线,为降落点附近的游客提供了应急救援等商品货物配送服务,这也是北京市内首次开通常态化无人机配送服务. 近年来,中国低空经济发展迅速,成为了经济增长的新动能.
素材1 某商店在无促销活动时,若买5件A商品,8件B商品,共需要2400元;若买8件A商品,5件B商品,共需2280元.
素材2 该商店为了鼓励消费者使用无人机配送服务,开展促销活动: ①若消费者用250元购买无人机配送服务卡,商品一律按标价的七五折出售; ②若消费者不使用无人机配送服务:凡购买店内任何商品,一律按照标价的八折出售.
问题解决
任务1 在该商店在无促销活动时,求A,B商品的销售单价分别是多少元?
任务2 某科技公司计划在促销期间购买A,B两款商品共30件,其中A商品购买a件(0<a<30); ①若使用无人机配送商品,共需要 元; ②若不使用无人机配送商品,共需要 元. (结果均用含a的代数式表示);
任务3 请你帮该科技公司算一算,在任务2的条件下,购买A产品的数量在什么范围内时,使用无人机配送商品更合算?
16.(2025秋 市北区期中)漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.数学活动小组依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现漏刻水位h(cm)是时间t(min)的一次函数,通过观察,每2分钟记录一次箭尺读数,小磊记录实验数据得到如表:
数据记录 第1次 第2次 第3次 第4次 第5次 …
t(min) 0 2 4 6 8 …
h(cm) 2 2.8 3.6 4.0 5.2 …
(1)在小组探究中,小华采用不同的函数关系表达方式(表格、图象、关系式)验证,均发现小磊记录的上表h,t的数据中,有一对数据记录错误.请用学过的相关知识判断,第 次数据是不准确的.
(2)当记录时间为20分钟时,漏刻水位是多少?
(3)求h(cm)与t(min)的函数关系式,并计算当水位为14cm时,对应时间是多少?
17.(2025秋 岳阳县期中)综合与实践:阅读以下材料,唐代文学家韩愈曾赋诗:“天街小雨润如酥,草色遥看近却无”,当代印度诗人泰戈尔也写道:“世界上最遥远的距离,不是瞬间便无处寻觅;而是尚未相遇,便注定无法相聚”,距离是数学、天文学、物理学中的热门话题,唯有对宇宙距离进行测量,人类才能掌握世界的尺度.下面我们结合数轴与绝对值的知识解答下列有关距离的数学问题:
【探究】
①数轴上表示5和1的两点之间的距离是 ;
②数轴上表示﹣1和﹣4的两点之间的距离是 ;
③数轴上表示﹣3和6的两点之间的距离是 ;
【归纳】一般的,数轴上表示数a和数b的两点之间的距离等于 ;
【应用】
①如果表示数a和3的两点之间的距离是5,则可记为:|a﹣3|=5,那么a= ;
②若数轴上表示数a的点位于﹣4与5之间,则|a+4|+|a﹣5|的值为 ;
③结合数轴求出|a+2|+|a﹣1|+|a﹣3|的最小值为 ,此时a为 .
18.(2025秋 扶风县期中)先阅读下面的材料,再解决问题.
【实际问题】如图1,一圆柱的底面半径为5cm,BC是底面直径,高AB为5cm,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
【解决方案】路线1:侧面展开图中的线段AC,如图所示
设路线1的长度为l1,则.
路线2:高线AB+底面直径BC.
设路线2的长度为l2,则.
为比较l1,l2的大小,采用“作差法”:
因为;
所以,所以l1>l2,
所以小明认为路线2较短.
(1)【问题类比】小亮对上述结论有些疑惑,于是他把条件改成“圆柱的底面半径为1cm,高AB为5cm“.请你用上述方法帮小亮比较出l1与l2的大小.
(2)【问题拓展】请你帮他们继续研究:在一般情况下,若圆柱的底面半径为r cm,高为h cm,蚂蚁从A点出发沿圆柱表面爬行到点C,当满足什么条件时,路线2较短?请说明理由.
(3)【问题解决】如图是紧密排列在一起的2个相同的圆柱,高为5cm.当蚂蚁从A点出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.
19.(2025秋 青羊区校级月考)某文体中心提供阅读、观影、球类、游泳、器械等多种文体活动,现有三种收费方式,详情见下表:
收费方式 详细介绍
日卡 日卡一张30元
会员卡 办卡需210元,每活动1小时收费4元
普通卡 进入文体中心要收取10元/日,可免费文体活动2小时,后续收费5元/小时
(注:不足一个小时的按一小时计算)
(1)小明打算这周六去文体中心活动6小时,最少需要花费 元;
(2)小明打算一个月(30天)都去文体中心活动,每天活动的时间为x小时(x为正整数,且x≥2).
①如果小明选择办会员卡一个月需要花费 元;选择办普通卡一个月需要花费 元;(用含x的代数式表示)
②对于会员卡和普通卡两种不同的收费方式,哪种更划算?
20.(2025秋 双城区月考)在中俄贸易博览会前,哈市某展览馆为更好地适应会展需求,对部分展馆地面进行了升级改造,已知该展馆地面为长40米,宽30米的长方形,现计划将其分成两个展览区,其余部分为等宽的通道,设通道的宽度为x米.
(1)求两个展览区的总面积为多少平方米?(请用含x的式子表示)
(2)工程负责人准备用A、B两种彩砖铺设展览区的地面,用防滑材料铺设通道,经市场调查发现,铺设展览区若用A种彩砖每平方米需要90元,若用B种彩砖每平方米需要60元,当x=4时,若铺设展览区的总费用不超过45540元,求最多购买多少平方米A种彩砖?
参考答案与试题解析
一.解答题(共20小题)
1.(2025秋 屯留区月考)学科实践
暑假期间、我市某公园为打造专属夜景景观特别安装了喷水装置,为保持人行绿道干燥,水柱要喷入河中,水柱可近似看作抛物线.图2是截面图,已知人行绿道宽OA=3.5m,AE是河道坝高,坝面AB的坡比为i=1:0.5,在距离喷水口O处2m时,水柱距离人行道的高度达到最大值3m.以点O为原点,直线OA为x轴建立平面直角坐标系.
(1)出于安全考虑,在坝顶A处安装护栏,要求水柱不能喷射到护栏上,求护栏的最大高度.
(2)当水面距离人行道的竖直距离为多少时,水柱恰好落在河水中(水面与AB交点处)?
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】(1)护栏的最大高度为1.3125米;
(2)当水面距离人行道的竖直距离为米时,水柱恰好落在河水中.
【分析】(1)依据题意得二次函数的顶点坐标为(2,3),设该二次函数的解析式为y=a(x﹣2)2+3,再结合经过原点,求出a得到二次函数的解析式为y(x﹣2)2+3,从而可得当x=3.5时,求出y,即可得的答案;
(2)先求出A(3.5,0),B的坐标为(6,﹣5),根据待定系数法求出直线AB的解析式,再与抛物线解析式建立方程组,求解即可得的答案.
【解答】解:(1)由题意得,二次函数的顶点坐标为(2,3),
设该二次函数的解析式为y=a(x﹣2)2+3(a≠0),二次函数经过原点,
∴4a+3=0,
解得,解得a,
∴该二次函数的解析式为y(x﹣2)2+3,
当x=3.5时,y(x﹣2)2+31.3125,
答:护栏的最大高度为1.3125米;
(2)∵河道坝高AE=5米,坝面AB的坡比为i1:0.5,
∴BE=2.5,
则点B与原点O的水平距离为3.5+2.5=6,
∴点B的坐标为(6,﹣5),
又∵点A的坐标为(3.5,0),
设AB的解析式为y1=kx+b(k≠0),
∴,
解得,
∴y1=﹣2x+7(3.5≤x≤6),
∴﹣2x+7(x﹣2)2+3,
解得x1=2(不合题意,舍去),x2,
当x时,y,
答:当水面距离人行道的竖直距离为米时,水柱恰好落在河水中.
【点评】本题主要考查了二次函数的应用,解题时要熟练掌握二次函数的性质是关键.
2.(2025秋 晋源区月考)综合与探究
已知A,B为数轴上的两个点,点A表示的数为a,点B表示的数为b,且8xyb﹣2+(a+2)xy﹣1是关于x,y的三次二项式.
根据上述条件,解答下列问题:
(1)求a,b的值;
(2)若C为数轴上AB之间的点,且BC=5AC,求点C表示的数;
(3)在(2)的条件下,有一动点P从点A开始以每秒2个单位长度的速度沿数轴向左匀速运动,同时另一动点Q从点B开始以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒,是否存在某一时刻t,使得PC=2QC?若存在,直接写出t的值;若不存在,请说明理由.
【考点】一元一次方程的应用;两点间的距离;数轴.
【专题】一次方程(组)及应用;应用意识.
【答案】(1)﹣2,﹣1,4;
(2)3;
(3)t或t.
【分析】(1)由题可得方程1+b﹣2=3,a+2=0,解方程即可得到结论;
(2)根据题意列方程即可得到结论;
(3)由点运动的特点可知P点表示的数为﹣2+2t,Q点表示的数为4﹣4t,分别求出PB,QB,再由已知建立方程|2﹣2t|=2|5﹣4t|,求t的值即可.
【解答】解:(1)∵8xyb﹣2+(a+2)xy﹣1是关于x,y的三次二项式.
∴1+b﹣2=3,a+2=0,
∴b=4,a=﹣2;
(2)∵b=4,a=﹣2,
∴点A表示的数为﹣2,点B表示的数为4,
设点C表示的数为x,
根据题意得,4﹣x=5(x+2),
解得x=﹣1,
∴点C表示的数为﹣1;
(3)存在x值,使得PC=2QC,理由如下:
P点表示的数为﹣2﹣2t,Q点表示的数为4﹣4t,
∴PC=|﹣1+2+2t|=|1+2t|,QC=|4﹣4t+1|=|5﹣4t|,
∵PC=2QC,
∴|1+2t|=2|5﹣4t|,
解得t或t.
【点评】本题考查了一元一次方程的应用,数轴,熟练掌握数轴上点的运动特点是解题的关键.
3.(2025秋 兴县月考)综合与实践
问题情境:元旦晚会舞台布置中需要搭一条抛物线型灯链,最初的设计方案如图1所示,灯链两端连接A,B两点,点C位于点B正下方的地面处,以点A正下方的地面处的点O为原点,OC所在的直线为x轴,OA所在的直线为y轴,建立平面直角坐标系,抛物线解析式的二次项系数为0.03,OC=10米,OA=BC=3米,但实际实施方案后发现最低点过低.
方案修改:莉莉将方案进行修改,如图2,将图1中灯链的最低点固定在距地面2.7米的点N处,点N两侧的灯链形成了两个对称的新抛物线.
(1)求图1中抛物线的解析式.
(2)若图1中抛物线的最低点为M,求点M到OC的距离.
(3)若图2中两个最低点的距离为4米,修改方案后最低点提高了多少米?
【考点】二次函数的应用.
【专题】二次函数的应用;运算能力;应用意识.
【答案】(1)y=0.03x2﹣0.3x+3;
(2)点M到OC的距离为2.25米;
(3)灯链最低点提高了0.21米.
【分析】(1)由题意得A(0,3),B(10,3),进而求出抛物线的对称轴为直线x=5,根据抛物线的对称轴为x求出b即可;
(2)将抛物线的解析式化为顶点式即可得的答案;
(3)根据题意求出左边的新抛物线的解析式的对称轴,根据待定系数法求出新抛物线的解析式即可得的答案.
【解答】解:(1)由题意得A(0,3),B(10,3),
∴抛物线的对称轴为直线x5,
∴设抛物线的解析式为y=0.03x2+bx+3
∵抛物线的对称轴为直线x5,
解得 b=﹣0.3,
∴抛物线的解析式为y=0.03x2﹣0.3x+3;
(2)y=0.03x2﹣0.3x+3=0.03(x﹣5)2+2.25,
答:点M到OC的距离为2.25米;
(3)∵图2中两个新抛物线对称,且最低点之间的水平距离为4米,
∴左边的新抛物线的对称轴为直线 x=5﹣2=3,
设左边的新抛物线的解析式为y=m(x﹣3)2+k,
将点A(0,3),N(5,2.7)代入y=m(x﹣3)2+k,
得,
解得,
2.46﹣2.25=0.21(米).
答:灯链最低点提高了0.21米.
【点评】本题主要考查了二次函数的应用,根据题意求出二次函数的解析式是解决问题的关键.
4.(2025秋 合肥期末)根据图中情景,解答下列问题:
(1)购买8根跳绳需 280 元;购买12根跳绳需 336 元;
(2)购买m根跳绳需多少元?(请你用含有m的式子表示)
(3)小红比小明多买2根,付款时小红反而比小明少7元,你认为这种情况有可能吗?请利用方程知识说明理由.
【考点】一元一次方程的应用;列代数式.
【专题】一次方程(组)及应用;应用意识.
【答案】(1)280,336;
(2)当m≤10时,需要35m元;当m>10时,需要28m元;
(3)这种情况有可能,理由见解答过程.
【分析】(1)根据“跳绳每根35元,超过10根,享受八折优惠”,结合未超过10根,价格=单价×数量,超过10根,价格=单价×数量×折扣,列式计算即可;
(2)分两种情况讨论即可;
(3)若小红比小明多买2根,付款时小红反而比小明少7元成立,唯一的可能性就是小红买的跳绳超过10根打折了,而小明的不足10根没打折,设小明买了x根跳绳,小红买了(x+2)根跳绳,根据题意列出关于x的一元一次方程,解答并作出判断即可.
【解答】解:(1)根据题意得:
35×8=280(元),
即购买8根跳绳需280元;
0.8×35×12=336(元),
即购买12根跳绳需336元,
故答案为:280,336;
(2)当m≤10时,需要钱数为:35m(元);
当m>10时,需要钱数为:35m×0.8=28m(元);
(3)这种情况有可能,理由如下:
若小红比小明多买2根,付款时小红反而比小明少7元成立,
唯一的可能性就是小红买的跳绳超过10根打折了,而小明的不足10根没打折,
设小明买了x根跳绳,小红买了(x+2)根跳绳,
根据题意得:
35x﹣35×0.8(x+2)=7,
解得:x=9,
x+2=11≥10(符合题意),
答:有这种可能性.
【点评】本题考查了一元一次方程的应用,正确找出等量关系,列出一元一次方程是解题的关键.
5.(2025秋 桃城区校级期中)为更好筹备“十四运”的召开,小颖及其小组成员将利用所学知识测量一个广告牌的高度EF.在第一次测量中,小颖来回走动,走到点D时,其影子末端与广告牌影子末端重合于点H,其中DH=1m.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小颖从点D沿着直线FD后退5m到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2m.
如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小颖的身高为1.5m(眼睛到头顶距离忽略不计),平面镜的厚度忽略不计.根据以上信息,求广告牌的高度EF.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】广告牌的高度EF为3m.
【分析】根据镜面反射原理结合相似三角形的判定方法得出△EFH∽△CDH,△EFG∽△ABG,进而利用相似三角形的性质得出EF的长.
【解答】解:设广告牌的高度EF为x m,
依题意知:DB=5m,BG=2m,DH=1m,AB=CD=1.5m.
∴GD=DB﹣BG=3m,
∵CD⊥BF,EF⊥BF,
∴CD∥EF.
∴△EFH∽△CDH.
∴,即.
∴.
∴DFx﹣1.
由平面镜反射规律可得:∠EGF=∠AGB.
∵AB⊥BF,
∴∠ABG=90°=∠EFG.
∴△EFG∽△ABG.
∴,即.
∴.
∴x=3.
故广告牌的高度EF为3m.
【点评】此题主要考查了相似三角形的判定与性质,正确利用已知得出相似三角形是解题关键.
6.(2025秋 碑林区校级月考)某校迎来了一百二十年校庆,为了准备校庆,校方决定准备一场别开生面的文艺演出,有歌唱,舞蹈,小舞台剧等节目,为此学校需要采购一批演出服装.现有质量较好且价格合理的A,B两家公司供选择,这两家公司给出的价格都是每套服装100元,经洽谈协商:A公司给出的优惠条件是全部服装单价打8折,但校方需要承担1500元的运费;B公司给出的优惠条件是购买服装不超过100套时不打折,超过100套时,超出部分每套打7折,校方不用承担运费.
(1)分别求出学校购买A,B两公司服装所付的总费用y1(元)和y2(元)与购买服装的数量x(套)之间的函数关系式;
(2)如果该校根据演出人数决定购买180套服装,请通过计算说明学校选择哪家公司的服装花费更少.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】(1)y1=80x+1500,y2;
(2)B公司.
【分析】(1)分别根据两家公司的优惠条件写出对应函数关系式即可;
(2)将x=180分别代入y1和y2与x之间的函数关系式,求出y1和y2并比较大小即可得出结论.
【解答】解:(1)y1=0.8×100x+1500=80x+1500,
∴y1=80x+1500.
当0≤x≤100时,y2=100x;
当x>100时,y2=100×100+0.7×100(x﹣100)=70x+3000,
∴y2.
(2)当x=180时,y1=80×180+1500=15900,y2=70×180+3000=15600,
∵y1>y2,
∴学校选择B公司的服装花费更少.
【点评】本题考查一次函数的应用,根据题意写出函数关系式是解题的关键.
7.(2025秋 沈阳月考)数学兴趣小组测量校园内旗杆的高度.如图,小聪在某一时刻测得1m长的竹竿竖直放置时影长1.5m,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长BD=21m,留在墙上的影高CD=2m,求旗杆的高度.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】旗杆的高度是16米.
【分析】延长AC,BD相交于点E,BD=21m,CD=2m,由CD∥AB,得出△ABE∽△CDE,得出对应边成比例,代入数据即可得出结果.
【解答】解:如图所示,延长AC,BD相交于点E,
则CD:DE=1:1.5,得DE=1.5CD=3m,
由已知CD∥AB,
∴△ABE∽△CDE,
∴,即,
解得:AB=16.
答:旗杆的高度是16米.
【点评】本题考查平行投影及相似三角形的应用,从实际问题中整理出相似三角形是解题关键.
8.(2025秋 沈阳月考)某校将新建图书楼的正门设计为一个抛物线型拱门,并要求所设计的拱门的跨度与拱高之积为48m2,还要兼顾美观、大方、和谐、通畅等因素,设计部门按要求做出了设计方案.现把方案中的拱门图形放入平面直角坐标系中,如图1、2所示,抛物线型拱门的跨度ON=12m,拱高PE=4m.其中,点N在x轴上,PE⊥ON,OE=EN.要在拱门中设置矩形框架,其面积越大越好.
方案一:如图1,矩形框架ABCD的面积记为S1,点A,D在抛物线上,边BC在ON上;
方案二:如图2,矩形框架A'B'C'D'的面积记为S2,点A',D'在抛物线上,边B'C'在ON上.
(1)求抛物线的函数表达式;
(2)方案一中,已知AB=3m,方案二中,已知B'C'=8m,比较S1,S2的大小.
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】(1)y(x﹣6)2+4;
(2)S1>S2.
【分析】(1)由题意得抛物线顶点坐标为(6,4),设抛物线的函数表达式为y=a(x﹣6)2+4,利用待定系数法解答即可求解;
(2)把y=3代入y(x﹣6)2+4可求出BC,即可求出S1,再根据OB′=NC′=(12﹣8)÷2=2(m)可求出A′B′,进而求出S2,据此即可判断求解;
【解答】解:(1)由题意得,抛物线顶点坐标为(6,4),
设抛物线的函数表达式为y=a(x﹣6)2+4,把(0,0)代入得:
0=a(0﹣6)2+4,
解得,
∴抛物线的函数表达式为y(x﹣6)2+4;
(2)把y=3代入y(x﹣6)2+4得:3(x﹣6)2+4,
解得x1=3,x2=9,
∴BC=9﹣3=6,
∴S1=BC AB=6×3=18(m2);
∵B′C′=8m,
∴OB′=NC′=(12﹣8)÷2=2(m),
把x=2代入t=﹣2x+80得:y(2﹣6)2+4,
∴A′B′,
∴S2=B′C′ A′B′=8(m2),
∵18,
∴S1>S2.
【点评】本题考查了二次函数的应用,利用待定系数法求出二次函数的解析式是解题的关键.
9.(2025秋 碑林区校级月考)(1)问题解决:如图1,平面直角坐标系中,直线l:y=﹣2x+4与x轴交于点A,与y轴交于点B,以AB为腰在第一象限作等腰直角△ABC,∠BAC=90°,点A的坐标为 (2,0) ,点B的坐标为 (0,4) .
(2)求(1)中点C的坐标.
(3)类比探究
如图②,平面直角坐标系中,线段MN在x轴上,点M坐标为(﹣4,0),点N与M关于y轴对称,点A是线段MN上的一个动点,B点坐标为(0,4),以点A为直角顶点,AB为直角边在AB右侧作等腰直角△ABC,连接OC,在点A的运动过程当中,线段OC是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.
【考点】一次函数综合题.
【专题】一次函数及其应用;图形的全等;等腰三角形与直角三角形;应用意识.
【答案】(1)(2,0),(0,4);
(2)点C(6,2);
(3)OC的最小值为2.
【分析】(1)当x=0时,y=4,当y=0时,x=2,即可求解;
(2)由AAS可得△ABO≌△CAH,可得AO=2=CH,OB=4=AH,即可求解;
(3)先证点C在过点N且与MN成45°直线上运动,则OC⊥CN时,CO有最小值,由等腰直角三角形的性质可求解.
【解答】解:(1)∵y=﹣2x+4与x轴交于点A,与y轴交于点B,
∴当x=0时,y=4,
当y=0时,x=2,
∴点A(2,0),点B(0,4),
故答案为:(2,0),(0,4);
(2)如图①,过点C作CH⊥直线OA于H,
∴∠AHC=∠AOB=∠BAC=90°,
∴∠ABO+∠BAO=90°=∠BAO+∠CAH,
∴∠ABO=∠CAH,
又∵AB=AC,
∴△ABO≌△CAH(AAS),
∴AO=CH,OB=AH,
∵点A(2,0),点B(0,4),
∴AO=2=CH,OB=4=AH,
∴OH=6,
∴点C(6,2);
(3)OC有最小值,如图②,过点C作CH⊥MN于H,连接CN,
∵点M坐标为(﹣4,0),点N与M关于y轴对称,
∴点N(4,0),
∴MO=NO=4,
∵B点坐标为(0,4),
∴BO=4=ON=OM,
同理可证△ABO≌△CAH(AAS),
∴AO=CH,OB=AH=6=ON,
∴HN=AO,
∴CH=HN,
∴∠HNC=45°,
∴点C在过点N且与MN成45°直线上运动,
∴OC⊥CN时,CO有最小值,
∵∠HNC=45°,ON=4,
∴OC的最小值为2.
【点评】本题是一次函数综合题,考查了全等三角形的判定和性质,一次函数的性质,等腰直角三角形的性质,添加恰当辅助线构造全等三角形是解题的关键.
10.(2024 自贡)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 11.3 m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m.求旗杆高度;
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到D′处.采用同样方法,测得C′G′=1.2m,D′G′=2m.求雕塑高度(结果精确到1m).
【考点】相似三角形的应用;近似数和有效数字.
【专题】图形的相似;解直角三角形及其应用;应用意识.
【答案】见试题解答内容
【分析】(1)由影长EF恰好等于自己的身高DE,知△DEF是等腰直角三角形,△ABC是等腰直角三角形,故AB=BC=11.3m,
(2)证明△DEC∽△ABC,可得,故AB=12,即旗杆高度为12米;
(3)由△DCG∽△DAB,得,设AB=x m,BD=y m,则,知yx,同理可得,即得,从而,解出x即可得雕塑高度约为31m.
【解答】解:(1)∵影长EF恰好等于自己的身高DE,
∴△DEF是等腰直角三角形,
由平行投影性质可知,△ABC是等腰直角三角形,
∴AB=BC=11.3m,
故答案为:11.3;
(2)如图:
由反射定律可知,∠DCE=∠ACB,
又∠DEC=90°=∠ABC,
∴△DEC∽△ABC,
∴,即,
解得AB=12,
∴旗杆高度为12米;
(3)如图:
∵∠CDG=∠ADB,∠CGD=90°=∠ABD,
∴△DCG∽△DAB,
∴,
设AB=x m,BD=y m,则,
∴yx,
同理可得,
∴,
∴,
解得x=28.8;
经检验,x=28.8是原方程的解,
故AB≈29m,
∴雕塑高度AB约为29m.
【点评】本题考查解直角三角形应用,涉及相似三角形判定与性质,解题的关键是读懂题意,列出方程解决问题.
11.(2024春 历下区期末)数学兴趣小组利用所学数学知识来解决实际问题,实践报告如下:
活动课题 风筝离地面垂直高度探究
问题背景 风筝由中国古代劳动人民发明于东周春秋时期,距今已2000多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.兴趣小组在放风筝时想测量风筝离地面的垂直高度.
测量数据抽象模型 小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC的长为15米,根据手中剩余线的长度计算出风筝线AB的长为17米,牵线放风筝的手到地面的距离为1.5米.
问题产生 经过讨论,兴趣小组得出以下问题: (1)运用所学勾股定理相关知识,根据测量所得数据,计算出风筝离地面的垂直高度. (2)如果想要风筝沿DA方向再上升12米,且BC长度不变,则他应该再放出多少米线?
问题解决 ……
该报告还没有完成,请你帮助兴趣小组解决以上问题.
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】见试题解答内容
【分析】(1)在Rt△ABC中,利用勾股定理求出的AC长,即可得到结论;
(2)在Rt△A′BC中,根据勾股定理求出A′B,即可得到结论.
【解答】解:(1)在Rt△ABC中,∠ACB=90°,BC=15米,AB=17米,
由勾股定理,可得AC8米,
∴AD=AC+CD=8+1.5=9.5(米),
答:风筝离地面的垂直高度为9.5米;
(2)如图,当风筝沿DA方向再上升12米,A'C=20米,
在Rt△A′BC中,∠A'CB=90°,BC=15米,
由勾股定理,可得A′B25米,
则应该再放出25﹣17=8(米),
答:他应该再放出8米长的线.
【点评】本题考查了用勾股定理解决实际问题,解题的关键是熟练掌握直角三角形中的三边关系.
12.(2025秋 灯塔市期中)【问题背景】
已知点A,M,N,B在数轴上对应的数分别为﹣1,x﹣1,x+1,11.线段MN沿数轴的正方向以每秒1个单位的速度移动,设移动时间为t秒.例如线段AB的长度为|﹣1﹣11|=12或11﹣(﹣1)=12.
【初步发现】
(1)求线段MN的长度;
【问题解决】
(2)若x=1,回答下列两个问题:
①当点M在点B的左侧,同时点N在点B的右侧时,用含t的代数式表示线段AM+BN的值;
②若点A,B与线段MN同时移动,点A以每秒1个单位长度的速度向数轴的正方向移动,点B以每秒1个单位长度的速度向数轴的负方向移动.在移动过程中,求线段AM+BN的值.(可用含t的代数式表示)
【考点】列代数式;数轴;绝对值.
【专题】应用题;应用意识.
【答案】(1)2;(2)①2t﹣8;②2t﹣8或10﹣2t,过程见解析.
【分析】(1)根据题干信息可得,线段MN的长度为x+1﹣(x﹣1)=2;
(2)①当x=1时,点A,M,N,B在数轴上对应的数分别为﹣1,t,2+t,11,据此即可求得答案;
②点A,M,N,B在数轴上对应的数分别为﹣1+t,t,2+t,11﹣t,分两种情况:当点N在点B的右侧时和当点N在点B的左侧时,进行求解即可.
【解答】解:(1)依题意可得:线段MN的长度为x+1﹣(x﹣1)=2;
(2)①当x=1时,点A,M,N,B在数轴上对应的数分别为﹣1,t,2+t,11,
∴AM=t﹣(﹣1)=t+1,
BN=2+t﹣11=t﹣9,
∴AM+BN=t+1+t﹣9=2t﹣8;
②点A,M,N,B在数轴上对应的数分别为﹣1+t,t,2+t,11﹣t,
∴AM=t﹣(﹣1+t)=1,
当点N在点B的右侧时,
∴BN=2+t﹣(11﹣t)=2t﹣9,
∴AM+BN=1+2t﹣9=2t﹣8;
当点N在点B的左侧时,
∴BN=11﹣t﹣(2+t)=9﹣2t,
∴AM+BN=1+9﹣2t=10﹣2t,
综上所述,线段AM+BN的值为2t﹣8或10﹣2t.
【点评】本题考查了数轴和两点之间的距离表示,做题的关键是准确的表示出线段的长度.
13.(2025秋 隆昌市校级期末)阅读下列材料:利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式,然后由(x+m)2≥0就可求出多项式x2+bx+c的最小值.
例:求多项式x2﹣4x+5的最小值.
解:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1.
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1.
当x=2时,(x﹣2)2+1=1,因此(x﹣2)2+1有最小值,最小值为1,即x2﹣4x+5的最小值为1.
通过阅读,理解材料的解题思路,请解决以下问题:
(1)【理解探究】已知代数式A=x2+8x+7,求A的最小值;
(2)【类比应用】张大爷家有甲、乙两块长方形菜地,已知甲菜地的两边长分别是(5a+1)米、(2a+2)米,乙菜地的两边长分别是(3a+8)米、(3a﹣2)米,试比较这两块菜地的面积S甲和S乙的大小,并说明理由;
(3)【拓展升华】如图,△ABC中,∠C=90°,AC=8cm,BC=16cm,点M,N分别是线段AC和BC上的动点,点M从A点出发以1cm/s的速度向C点运动;同时点N从C点出发以2cm/s的速度向B点运动,当其中一点到达终点时,两点同时停止运动.设运动的时间为t,则当t的值为多少时,△MCN的面积最大,最大值为多少?
【考点】二次函数的应用;三角形的面积;完全平方公式的几何背景;因式分解﹣运用公式法.
【专题】二次函数的应用;应用意识.
【答案】(1)﹣9;
(2)S甲>S乙;
(3)当t的值为4时,△MCN的面积最大,最大值为16cm2.
【分析】(1)直接利用完全平方公式可得答案;
(2)先求出,再利用完全平方公式即可求解;
(3)根据题意表示出(cm2),再利用完全平方公式即可求解.
【解答】解:(1)x2+8x+7=(x+4)2﹣9,
∵(x+4)2≥0,
∴(x+4)2﹣9≥﹣9,
∴当x=﹣4时,(x+4)2﹣9有最小值,最小值为﹣9,
即A的最小值为﹣9;
(2)∵,,
∴,
∵(a﹣3)2≥0,
∴(a﹣3)2+9≥9>0,
∴S甲>S乙;
(3)由题意得:CM=8﹣t,CN=2t,
∴(cm2),
∵(t﹣4)2≥0,
∴﹣(t﹣4)2≤0,
∴﹣(t﹣4)2+16≤16,
∴当t=4时,﹣(t﹣4)2+16有最大值,最大值为16.
即当t的值为4时,△MCN的面积最大,最大值为16cm2.
【点评】本题考查二次函数的应用,完全平方公式的几何背景,因式分解﹣运用公式法,三角形的面积,熟练掌握二次函数的性质是解答本题的关键.
14.(2025秋 南浔区期末)七年级数学兴趣小组成员自主开展数学微项目研究,他们决定研究“折线数轴”.
探索“折线数轴”
素材1 如图,将一条数轴在原点O,点B,点C处折一下,得到一条“折线数轴”.图中点A表示﹣9,点B表示12,点C表示24,点D表示36,我们称点A与点D在数轴上的“友好距离”为45个单位长度,并表示为45.
素材2 动点P从点A出发,以2个单位长度/秒的初始速度沿着“折线数轴”向其正方向运动.当运动到点O与点B之间时速度变为初始速度的一半.当运动到点B与点C之间时速度变为初始速度的两倍.经过点C后立刻恢复初始速度.
问题解决
探索1 动点P从点A运动至点B需要多少时间?
探索2 动点P从点A出发,运动t秒至点B和点C之间时,求点P表示的数(用含t的代数式表示);
探索3 动点P从点A出发,运动至点D的过程中某个时刻满足时,求动点P运动的时间.
【考点】一元一次方程的应用;数轴;列代数式.
【专题】整式;一次方程(组)及应用;应用意识.
【答案】探索1:秒;
探索2:4t﹣54(t);
探索3:秒或秒.
【分析】探索1:利用时间=路程÷速度,即可求出结论;
探索2:求出点P运动到点C所需时间,当t时,利用点P表示的数=点B表示的数+点P在线段BC段的运动速度×(运动时间),即可用含t的代数式表示出点P表示的数;
探索3:由,及的长,可得出共有2种情况,当点P在点O和点B之间,即t时,点P表示的数为t,进而可得出t,t,结合16,可列出关于t的一元一次方程,解之可求出t的值;当点P在点C的右侧,即t时,点P表示的数为2t﹣15,进而可得出2t﹣27,2t﹣39,结合16,可列出关于t的一元一次方程,解之可求出t的值.
【解答】解:探索1:根据题意得:[0﹣(﹣9)]÷2+(12﹣0)÷(2)
=9÷2+12÷1
12
(秒).
答:动点P从点A运动至点B需要秒;
探索2:(24﹣12)÷(2×2)
12÷4
3
(秒).
根据题意得:当t时,点P表示的数为12+2×2(t)=4t﹣54,
∴当动点P运动至点B和点C之间时,点P表示的数为4t﹣54(t);
探索3:∵24﹣0=24,24﹣12=12,36﹣12=24,
∴16共2两种情况.
当点P在点O和点B之间,即t时,点P表示的数为0+(2)(t)=t,
∴12﹣(t)t,24﹣(t)t,
∴tt=16,
解得:t;
当点P在点C的右侧,即t时,点P表示的数为24+2(t)=2t﹣15,
∴2t﹣15﹣12=2t﹣27,2t﹣15﹣24=2t﹣39,
∴2t﹣27+2t﹣39=16,
解得:t.
答:动点P的运动的时间是秒或秒.
【点评】本题考查了一元一次方程的应用、列代数式以及数轴,解题的关键是:探索1:根据各数量之间的关系,列式计算;探索2:根据各数量之间的关系,用含t的代数式表示出点P表示的数;探索3:找准等量关系,正确列出一元一次方程.
15.(2025秋 宁波期中)
背景 【长城上可以点无人机送的外卖了】 打开手机外卖软件下单,在长城上也可以点外卖了,最快5分钟收货! 日前,美团无人机在八达岭长城开通了北京首条无人机配送航线,为降落点附近的游客提供了应急救援等商品货物配送服务,这也是北京市内首次开通常态化无人机配送服务. 近年来,中国低空经济发展迅速,成为了经济增长的新动能.
素材1 某商店在无促销活动时,若买5件A商品,8件B商品,共需要2400元;若买8件A商品,5件B商品,共需2280元.
素材2 该商店为了鼓励消费者使用无人机配送服务,开展促销活动: ①若消费者用250元购买无人机配送服务卡,商品一律按标价的七五折出售; ②若消费者不使用无人机配送服务:凡购买店内任何商品,一律按照标价的八折出售.
问题解决
任务1 在该商店在无促销活动时,求A,B商品的销售单价分别是多少元?
任务2 某科技公司计划在促销期间购买A,B两款商品共30件,其中A商品购买a件(0<a<30); ①若使用无人机配送商品,共需要 (4750﹣30a) 元; ②若不使用无人机配送商品,共需要 (4800﹣32a) 元. (结果均用含a的代数式表示);
任务3 请你帮该科技公司算一算,在任务2的条件下,购买A产品的数量在什么范围内时,使用无人机配送商品更合算?
【考点】一元一次不等式的应用;列代数式;一元一次方程的应用.
【专题】整式;一次方程(组)及应用;一元一次不等式(组)及应用;应用意识.
【答案】见试题解答内容
【分析】任务1:在该商店在无促销活动时,设A商品的销售单价是x元,B商品的销售单价是y元,根据“某商店在无促销活动时,若买5件A商品,8件B商品,共需要2400元;若买8件A商品,5件B商品,共需2280元”,可列出关于x,y的二元一次方程组,解之即可得出结论;
任务2:根据购买两款商品的总数量及购买A商品的数量,可得出购买(30﹣a)件B商品,再利用总价=单价×数量,结合两种促销方案,即可用含a的代数式表示出使用无人机配送商品及不使用无人机配送商品,所需费用;
任务3:根据使用无人机配送商品更合算,可列出关于a的一元一次不等式,解之可得出a的取值范围,再结合0<a<30,即可得出结论.
【解答】解:任务1:在该商店在无促销活动时,设A商品的销售单价是x元,B商品的销售单价是y元,
根据题意得:,
解得:.
答:在该商店在无促销活动时,A商品的销售单价是160元,B商品的销售单价是200元;
任务2:∵某南山科技公司计划在促销期间购买A,B两款商品共30件,其中A商品购买a件,
∴B商品购买(30﹣a)件.
①若使用无人机配送商品,共需要250+160×0.75a+200×0.75(30﹣a)=(4750﹣30a)元;
②若不使用无人机配送商品,共需要160×0.8a+200×0.8(30﹣a)=(4800﹣32a)元.
故答案为:①(4750﹣30a);②(4800﹣32a);
任务3:根据题意得:4750﹣30a<4800﹣32a,
解得:a<25,
又∵0<a<30,
∴0<a<25.
答:当0<a<25时,使用无人机配送商品更合算.
【点评】本题考查了二元一次方程组的应用、列代数式以及一元一次不等式的应用,解题的关键是:任务1:找准等量关系,正确列出二元一次方程组;任务2:根据各数量之间的关系,用含a的代数式表示出使用无人机配送商品及不使用无人机配送商品所需费用;任务3:根据各数量之间的关系,正确列出一元一次不等式.
16.(2025秋 市北区期中)漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.数学活动小组依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现漏刻水位h(cm)是时间t(min)的一次函数,通过观察,每2分钟记录一次箭尺读数,小磊记录实验数据得到如表:
数据记录 第1次 第2次 第3次 第4次 第5次 …
t(min) 0 2 4 6 8 …
h(cm) 2 2.8 3.6 4.0 5.2 …
(1)在小组探究中,小华采用不同的函数关系表达方式(表格、图象、关系式)验证,均发现小磊记录的上表h,t的数据中,有一对数据记录错误.请用学过的相关知识判断,第 4 次数据是不准确的.
(2)当记录时间为20分钟时,漏刻水位是多少?
(3)求h(cm)与t(min)的函数关系式,并计算当水位为14cm时,对应时间是多少?
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】见试题解答内容
【分析】(1)将表格中的数据在平面直角坐标系中描点并连线,与其它4个点不在同一条直线上的那个点对应的数据不准确;
(2)根据“每分钟漏刻水位升高0.4cm”计算即可;
(3)利用待定系数法求h与t的函数关系式,把h=14代入函数关系式求出对应t的值即可.
【解答】解:(1)将表格中的数据在平面直角坐标系中描点并连线如图所示:
由图可知,坐标为(6,4)的点与其它4个点不在同一条直线上,
∴第4次数据是不准确的.
(2)由表格数据可知,每分钟漏刻水位升高0.4cm,
2+0.4×20=10(cm).
答:当记录时间为20分钟时,漏刻水位是10cm.
(3)设h与t的函数关系式为h=kt+b(k、b为常数,且k≠0).
将坐标(0,2)和(2,2.8)分别代入h=kt+b,
得,
解得,
∴h与t的函数关系式为h=0.4t+2,
当h=14时,得0.4t+2=14,
解得t=30.
答:h与t的函数关系式为h=0.4t+2,当水位为14cm时,对应时间是30min.
【点评】本题考查一次函数的应用,掌握描点作图的方法、待定系数法求函数关系式是解题的关键.
17.(2025秋 岳阳县期中)综合与实践:阅读以下材料,唐代文学家韩愈曾赋诗:“天街小雨润如酥,草色遥看近却无”,当代印度诗人泰戈尔也写道:“世界上最遥远的距离,不是瞬间便无处寻觅;而是尚未相遇,便注定无法相聚”,距离是数学、天文学、物理学中的热门话题,唯有对宇宙距离进行测量,人类才能掌握世界的尺度.下面我们结合数轴与绝对值的知识解答下列有关距离的数学问题:
【探究】
①数轴上表示5和1的两点之间的距离是 4 ;
②数轴上表示﹣1和﹣4的两点之间的距离是 3 ;
③数轴上表示﹣3和6的两点之间的距离是 9 ;
【归纳】一般的,数轴上表示数a和数b的两点之间的距离等于 |a﹣b| ;
【应用】
①如果表示数a和3的两点之间的距离是5,则可记为:|a﹣3|=5,那么a= 8或﹣2 ;
②若数轴上表示数a的点位于﹣4与5之间,则|a+4|+|a﹣5|的值为 9 ;
③结合数轴求出|a+2|+|a﹣1|+|a﹣3|的最小值为 5 ,此时a为 1 .
【考点】一元一次方程的应用;数轴;绝对值.
【专题】实数;一次方程(组)及应用;应用意识.
【答案】【探究】①4;②3;③9,
【归纳】|a﹣b|,
【应用】①8或﹣2;②9;③5,1.
【分析】【探究】运用“数轴上表示数m与数n的两点之间的距离为|m﹣n|”直接计算即可;
【归纳】运用“数轴上表示数m与数n的两点之间的距离为|m﹣n|”直接计算即可;
【应用】①根据绝对值的意义即可得到结论;
②根据阅读材料和探究可知当﹣4≤a≤5时求代数式的值;
③判断出a=1时,三个绝对值的和最小,然后进行计算即可得解.
【解答】解:【探究】
①数轴上表示5和1的两点之间的距离是5﹣1=4;
②数轴上表示﹣1和﹣4的两点之间的距离是﹣1﹣(﹣4)=3;
③数轴上表示﹣3和6的两点之间的距离是6﹣(﹣3)=9,
故答案为:4,3,9;
【归纳】一般的,数轴上表示数a和数b的两点之间的距离等于|a﹣b|,
故答案为:|a﹣b|;
【应用】
①∵|a﹣3|=5,
∴a﹣3=±5,
∴a=8或a=﹣2,
故答案为:8或﹣2;
②∵数轴上表示数a的点位于﹣4与5之间,
∴﹣4<a<5,
∴|a+4|+|a﹣5|=a+4+5﹣a=9,
故答案为:9;
③∵|a+2|+|a﹣1|+|a﹣3|表示数a分别与﹣2、1、3的距离之和,
∴当a=1时|a+2|+|a﹣1|+|a﹣3||可取得最小值为3+0+2=5,
故答案为:5,1.
【点评】本题考查了一元一次方程的应用,数轴、绝对值,解答本题的关键是明确题意,利用数轴的特点解答.
18.(2025秋 扶风县期中)先阅读下面的材料,再解决问题.
【实际问题】如图1,一圆柱的底面半径为5cm,BC是底面直径,高AB为5cm,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
【解决方案】路线1:侧面展开图中的线段AC,如图所示
设路线1的长度为l1,则.
路线2:高线AB+底面直径BC.
设路线2的长度为l2,则.
为比较l1,l2的大小,采用“作差法”:
因为;
所以,所以l1>l2,
所以小明认为路线2较短.
(1)【问题类比】小亮对上述结论有些疑惑,于是他把条件改成“圆柱的底面半径为1cm,高AB为5cm“.请你用上述方法帮小亮比较出l1与l2的大小.
(2)【问题拓展】请你帮他们继续研究:在一般情况下,若圆柱的底面半径为r cm,高为h cm,蚂蚁从A点出发沿圆柱表面爬行到点C,当满足什么条件时,路线2较短?请说明理由.
(3)【问题解决】如图是紧密排列在一起的2个相同的圆柱,高为5cm.当蚂蚁从A点出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.
【考点】平面展开﹣最短路径问题;列代数式.
【专题】等腰三角形与直角三角形;应用意识.
【答案】(1)路线1较短;(2)路线2较短;(3)半径r为.
【分析】(1)将解决方案中的数字替换成所给数字计算即可;
(2)将解决方案中的数字替换成r,h表示出,作差根据题意可得满足的条件;
(3)用含r的式子表示出,根据题意列出等式求出r即可.
【解答】解:(1)因为圆柱的底面半径为1cm,高AB为5cm,
所以路线1:;
路线2:l2=AB+BC=5+2=7,则
因为,
所以,所以l1<l2,
所以路线1较短;
(2)因为圆柱的底面半径为r cm,高为h cm,
所以路线1:,
路线2:,
所以.
因为r恒大于0,所以当(π2﹣4)r﹣4h>0,即时,,
此时路线2较短;
(3)圆柱的高为5cm.
路线1:,
路线2:,
由题意,得25+(2πr)2=(5+4r)2,
解得;
即当圆柱的底面半径r为时,蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等.
【点评】本题考查了勾股定理在蚂蚁爬行最短路径问题中的应用,属于模仿题型,准确理解题中所给解决方案中的思路步骤是解题的关键.
19.(2025秋 青羊区校级月考)某文体中心提供阅读、观影、球类、游泳、器械等多种文体活动,现有三种收费方式,详情见下表:
收费方式 详细介绍
日卡 日卡一张30元
会员卡 办卡需210元,每活动1小时收费4元
普通卡 进入文体中心要收取10元/日,可免费文体活动2小时,后续收费5元/小时
(注:不足一个小时的按一小时计算)
(1)小明打算这周六去文体中心活动6小时,最少需要花费 30 元;
(2)小明打算一个月(30天)都去文体中心活动,每天活动的时间为x小时(x为正整数,且x≥2).
①如果小明选择办会员卡一个月需要花费 (210+120x) 元;选择办普通卡一个月需要花费 150x 元;(用含x的代数式表示)
②对于会员卡和普通卡两种不同的收费方式,哪种更划算?
【考点】一元一次不等式的应用;列代数式;一元一次方程的应用.
【专题】整式;一次方程(组)及应用;一元一次不等式(组)及应用;运算能力;应用意识.
【答案】(1)30;
(2)(210+120x),150x);
(3)当2≤x<7时,选择普通卡更划算;当x=7时,选择普通卡或会员卡都一样;当x>7时,选择会员卡更划算.
【分析】(1)分别求得办日卡、会员卡、普通卡,所需要花费,再比较即可求解;
(2)①根据办会员卡和普通卡的收费方式,列式计算即可求解;
②分3种情况,分别列出一元一次方程或一元一次不等式,解方程或不等式,再求出x=2时,办会员卡和普通卡需要的花费,即可解决问题.
【解答】解:(1)办日卡,需要花费30元;
办会员卡,办卡就需210元,显然不合题意;
办普通卡,需要花费10+5(6﹣2)=30(元);
∴最少需要花费30元,
故答案为:30;
(2)①办会员卡需要花费:210+30×4x=(210+120x)(元),
办普通卡需要花费:30[10+5(x﹣2)]=150x(元),
故答案为:(210+120x),150x);
②当210+120x=150x时,x=7,
当210+120x<150x时,x>7,
当210+120x>150x时,x<7,
当x=2时,办会员卡需要花费210+120x=210+120×2=450(元),
办普通卡需要花费150x=150×2=300(元),
∵450>300,
∴选择普通卡更划算;
综上所述,当2≤x<7时,选择普通卡更划算;当x=7时,选择普通卡或会员卡都一样;当x>7时,选择会员卡更划算.
【点评】本题考查了一元一次不等式的应用、一元一次方程的应用以及列代数式等知识,找出数量关系,正确列出一元一次不等式或一元一次方程是解题的关键.
20.(2025秋 双城区月考)在中俄贸易博览会前,哈市某展览馆为更好地适应会展需求,对部分展馆地面进行了升级改造,已知该展馆地面为长40米,宽30米的长方形,现计划将其分成两个展览区,其余部分为等宽的通道,设通道的宽度为x米.
(1)求两个展览区的总面积为多少平方米?(请用含x的式子表示)
(2)工程负责人准备用A、B两种彩砖铺设展览区的地面,用防滑材料铺设通道,经市场调查发现,铺设展览区若用A种彩砖每平方米需要90元,若用B种彩砖每平方米需要60元,当x=4时,若铺设展览区的总费用不超过45540元,求最多购买多少平方米A种彩砖?
【考点】一元一次不等式的应用;列代数式.
【专题】整式;一元一次不等式(组)及应用;运算能力;应用意识.
【答案】(1)两个展览区的总面积为(6x2﹣180x+1200)平方米;
(2)最多购买366平方米A种彩砖.
【分析】(1)设通道的宽度为x米,则展览区的长为(40﹣2x)米,宽为(30﹣3x)米,再由矩形面积公式计算即可;
(2)求出当x=4时,展览区的总面积为576平方米,设购买m平方米A种彩砖,则购买(576﹣m)平方米B种彩砖,根据铺设展览区的总费用不超过45540元,列出一元一次不等式,解不等式即可.
【解答】解:(1)设通道的宽度为x米,则展览区的长为(40﹣2x)米,宽为(30﹣3x)米,
∴(40﹣2x)(30﹣3x)=1200﹣180x+6x2=(6x2﹣180x+1200)(平方米),
答:两个展览区的总面积为(6x2﹣180x+1200)平方米;
(2)当x=4时,展览区的总面积为6×42﹣180×4+1200=576(平方米),
设购买m平方米A种彩砖,则购买(576﹣m)平方米B种彩砖,
由题意得:90m+60(576﹣m)≤45540,
解得:m≤366,
答:最多购买366平方米A种彩砖.
【点评】本题考查了一元一次不等式的应用以及列代数式等知识,找出数量关系,正确列出一元一次不等式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学题型专项训练 解答题
一.解答题(共20小题)
1.(2025秋 屯留区月考)学科实践
暑假期间、我市某公园为打造专属夜景景观特别安装了喷水装置,为保持人行绿道干燥,水柱要喷入河中,水柱可近似看作抛物线.图2是截面图,已知人行绿道宽OA=3.5m,AE是河道坝高,坝面AB的坡比为i=1:0.5,在距离喷水口O处2m时,水柱距离人行道的高度达到最大值3m.以点O为原点,直线OA为x轴建立平面直角坐标系.
(1)出于安全考虑,在坝顶A处安装护栏,要求水柱不能喷射到护栏上,求护栏的最大高度.
(2)当水面距离人行道的竖直距离为多少时,水柱恰好落在河水中(水面与AB交点处)?
2.(2025秋 晋源区月考)综合与探究
已知A,B为数轴上的两个点,点A表示的数为a,点B表示的数为b,且8xyb﹣2+(a+2)xy﹣1是关于x,y的三次二项式.
根据上述条件,解答下列问题:
(1)求a,b的值;
(2)若C为数轴上AB之间的点,且BC=5AC,求点C表示的数;
(3)在(2)的条件下,有一动点P从点A开始以每秒2个单位长度的速度沿数轴向左匀速运动,同时另一动点Q从点B开始以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒,是否存在某一时刻t,使得PC=2QC?若存在,直接写出t的值;若不存在,请说明理由.
3.(2025秋 兴县月考)综合与实践
问题情境:元旦晚会舞台布置中需要搭一条抛物线型灯链,最初的设计方案如图1所示,灯链两端连接A,B两点,点C位于点B正下方的地面处,以点A正下方的地面处的点O为原点,OC所在的直线为x轴,OA所在的直线为y轴,建立平面直角坐标系,抛物线解析式的二次项系数为0.03,OC=10米,OA=BC=3米,但实际实施方案后发现最低点过低.
方案修改:莉莉将方案进行修改,如图2,将图1中灯链的最低点固定在距地面2.7米的点N处,点N两侧的灯链形成了两个对称的新抛物线.
(1)求图1中抛物线的解析式.
(2)若图1中抛物线的最低点为M,求点M到OC的距离.
(3)若图2中两个最低点的距离为4米,修改方案后最低点提高了多少米?
4.(2025秋 合肥期末)根据图中情景,解答下列问题:
(1)购买8根跳绳需 元;购买12根跳绳需 元;
(2)购买m根跳绳需多少元?(请你用含有m的式子表示)
(3)小红比小明多买2根,付款时小红反而比小明少7元,你认为这种情况有可能吗?请利用方程知识说明理由.
5.(2025秋 桃城区校级期中)为更好筹备“十四运”的召开,小颖及其小组成员将利用所学知识测量一个广告牌的高度EF.在第一次测量中,小颖来回走动,走到点D时,其影子末端与广告牌影子末端重合于点H,其中DH=1m.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小颖从点D沿着直线FD后退5m到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2m.
如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小颖的身高为1.5m(眼睛到头顶距离忽略不计),平面镜的厚度忽略不计.根据以上信息,求广告牌的高度EF.
6.(2025秋 碑林区校级月考)某校迎来了一百二十年校庆,为了准备校庆,校方决定准备一场别开生面的文艺演出,有歌唱,舞蹈,小舞台剧等节目,为此学校需要采购一批演出服装.现有质量较好且价格合理的A,B两家公司供选择,这两家公司给出的价格都是每套服装100元,经洽谈协商:A公司给出的优惠条件是全部服装单价打8折,但校方需要承担1500元的运费;B公司给出的优惠条件是购买服装不超过100套时不打折,超过100套时,超出部分每套打7折,校方不用承担运费.
(1)分别求出学校购买A,B两公司服装所付的总费用y1(元)和y2(元)与购买服装的数量x(套)之间的函数关系式;
(2)如果该校根据演出人数决定购买180套服装,请通过计算说明学校选择哪家公司的服装花费更少.
7.(2025秋 沈阳月考)数学兴趣小组测量校园内旗杆的高度.如图,小聪在某一时刻测得1m长的竹竿竖直放置时影长1.5m,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长BD=21m,留在墙上的影高CD=2m,求旗杆的高度.
8.(2025秋 沈阳月考)某校将新建图书楼的正门设计为一个抛物线型拱门,并要求所设计的拱门的跨度与拱高之积为48m2,还要兼顾美观、大方、和谐、通畅等因素,设计部门按要求做出了设计方案.现把方案中的拱门图形放入平面直角坐标系中,如图1、2所示,抛物线型拱门的跨度ON=12m,拱高PE=4m.其中,点N在x轴上,PE⊥ON,OE=EN.要在拱门中设置矩形框架,其面积越大越好.
方案一:如图1,矩形框架ABCD的面积记为S1,点A,D在抛物线上,边BC在ON上;
方案二:如图2,矩形框架A'B'C'D'的面积记为S2,点A',D'在抛物线上,边B'C'在ON上.
(1)求抛物线的函数表达式;
(2)方案一中,已知AB=3m,方案二中,已知B'C'=8m,比较S1,S2的大小.
9.(2025秋 碑林区校级月考)(1)问题解决:如图1,平面直角坐标系中,直线l:y=﹣2x+4与x轴交于点A,与y轴交于点B,以AB为腰在第一象限作等腰直角△ABC,∠BAC=90°,点A的坐标为 ,点B的坐标为 .
(2)求(1)中点C的坐标.
(3)类比探究
如图②,平面直角坐标系中,线段MN在x轴上,点M坐标为(﹣4,0),点N与M关于y轴对称,点A是线段MN上的一个动点,B点坐标为(0,4),以点A为直角顶点,AB为直角边在AB右侧作等腰直角△ABC,连接OC,在点A的运动过程当中,线段OC是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.
10.(2024 自贡)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m.求旗杆高度;
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到D′处.采用同样方法,测得C′G′=1.2m,D′G′=2m.求雕塑高度(结果精确到1m).
11.(2024春 历下区期末)数学兴趣小组利用所学数学知识来解决实际问题,实践报告如下:
活动课题 风筝离地面垂直高度探究
问题背景 风筝由中国古代劳动人民发明于东周春秋时期,距今已2000多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.兴趣小组在放风筝时想测量风筝离地面的垂直高度.
测量数据抽象模型 小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC的长为15米,根据手中剩余线的长度计算出风筝线AB的长为17米,牵线放风筝的手到地面的距离为1.5米.
问题产生 经过讨论,兴趣小组得出以下问题: (1)运用所学勾股定理相关知识,根据测量所得数据,计算出风筝离地面的垂直高度. (2)如果想要风筝沿DA方向再上升12米,且BC长度不变,则他应该再放出多少米线?
问题解决 ……
该报告还没有完成,请你帮助兴趣小组解决以上问题.
12.(2025秋 灯塔市期中)【问题背景】
已知点A,M,N,B在数轴上对应的数分别为﹣1,x﹣1,x+1,11.线段MN沿数轴的正方向以每秒1个单位的速度移动,设移动时间为t秒.例如线段AB的长度为|﹣1﹣11|=12或11﹣(﹣1)=12.
【初步发现】
(1)求线段MN的长度;
【问题解决】
(2)若x=1,回答下列两个问题:
①当点M在点B的左侧,同时点N在点B的右侧时,用含t的代数式表示线段AM+BN的值;
②若点A,B与线段MN同时移动,点A以每秒1个单位长度的速度向数轴的正方向移动,点B以每秒1个单位长度的速度向数轴的负方向移动.在移动过程中,求线段AM+BN的值.(可用含t的代数式表示)
13.(2025秋 隆昌市校级期末)阅读下列材料:利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式,然后由(x+m)2≥0就可求出多项式x2+bx+c的最小值.
例:求多项式x2﹣4x+5的最小值.
解:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1.
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1.
当x=2时,(x﹣2)2+1=1,因此(x﹣2)2+1有最小值,最小值为1,即x2﹣4x+5的最小值为1.
通过阅读,理解材料的解题思路,请解决以下问题:
(1)【理解探究】已知代数式A=x2+8x+7,求A的最小值;
(2)【类比应用】张大爷家有甲、乙两块长方形菜地,已知甲菜地的两边长分别是(5a+1)米、(2a+2)米,乙菜地的两边长分别是(3a+8)米、(3a﹣2)米,试比较这两块菜地的面积S甲和S乙的大小,并说明理由;
(3)【拓展升华】如图,△ABC中,∠C=90°,AC=8cm,BC=16cm,点M,N分别是线段AC和BC上的动点,点M从A点出发以1cm/s的速度向C点运动;同时点N从C点出发以2cm/s的速度向B点运动,当其中一点到达终点时,两点同时停止运动.设运动的时间为t,则当t的值为多少时,△MCN的面积最大,最大值为多少?
14.(2025秋 南浔区期末)七年级数学兴趣小组成员自主开展数学微项目研究,他们决定研究“折线数轴”.
探索“折线数轴”
素材1 如图,将一条数轴在原点O,点B,点C处折一下,得到一条“折线数轴”.图中点A表示﹣9,点B表示12,点C表示24,点D表示36,我们称点A与点D在数轴上的“友好距离”为45个单位长度,并表示为45.
素材2 动点P从点A出发,以2个单位长度/秒的初始速度沿着“折线数轴”向其正方向运动.当运动到点O与点B之间时速度变为初始速度的一半.当运动到点B与点C之间时速度变为初始速度的两倍.经过点C后立刻恢复初始速度.
问题解决
探索1 动点P从点A运动至点B需要多少时间?
探索2 动点P从点A出发,运动t秒至点B和点C之间时,求点P表示的数(用含t的代数式表示);
探索3 动点P从点A出发,运动至点D的过程中某个时刻满足时,求动点P运动的时间.
15.(2025秋 宁波期中)
背景 【长城上可以点无人机送的外卖了】 打开手机外卖软件下单,在长城上也可以点外卖了,最快5分钟收货! 日前,美团无人机在八达岭长城开通了北京首条无人机配送航线,为降落点附近的游客提供了应急救援等商品货物配送服务,这也是北京市内首次开通常态化无人机配送服务. 近年来,中国低空经济发展迅速,成为了经济增长的新动能.
素材1 某商店在无促销活动时,若买5件A商品,8件B商品,共需要2400元;若买8件A商品,5件B商品,共需2280元.
素材2 该商店为了鼓励消费者使用无人机配送服务,开展促销活动: ①若消费者用250元购买无人机配送服务卡,商品一律按标价的七五折出售; ②若消费者不使用无人机配送服务:凡购买店内任何商品,一律按照标价的八折出售.
问题解决
任务1 在该商店在无促销活动时,求A,B商品的销售单价分别是多少元?
任务2 某科技公司计划在促销期间购买A,B两款商品共30件,其中A商品购买a件(0<a<30); ①若使用无人机配送商品,共需要 元; ②若不使用无人机配送商品,共需要 元. (结果均用含a的代数式表示);
任务3 请你帮该科技公司算一算,在任务2的条件下,购买A产品的数量在什么范围内时,使用无人机配送商品更合算?
16.(2025秋 市北区期中)漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.数学活动小组依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现漏刻水位h(cm)是时间t(min)的一次函数,通过观察,每2分钟记录一次箭尺读数,小磊记录实验数据得到如表:
数据记录 第1次 第2次 第3次 第4次 第5次 …
t(min) 0 2 4 6 8 …
h(cm) 2 2.8 3.6 4.0 5.2 …
(1)在小组探究中,小华采用不同的函数关系表达方式(表格、图象、关系式)验证,均发现小磊记录的上表h,t的数据中,有一对数据记录错误.请用学过的相关知识判断,第 次数据是不准确的.
(2)当记录时间为20分钟时,漏刻水位是多少?
(3)求h(cm)与t(min)的函数关系式,并计算当水位为14cm时,对应时间是多少?
17.(2025秋 岳阳县期中)综合与实践:阅读以下材料,唐代文学家韩愈曾赋诗:“天街小雨润如酥,草色遥看近却无”,当代印度诗人泰戈尔也写道:“世界上最遥远的距离,不是瞬间便无处寻觅;而是尚未相遇,便注定无法相聚”,距离是数学、天文学、物理学中的热门话题,唯有对宇宙距离进行测量,人类才能掌握世界的尺度.下面我们结合数轴与绝对值的知识解答下列有关距离的数学问题:
【探究】
①数轴上表示5和1的两点之间的距离是 ;
②数轴上表示﹣1和﹣4的两点之间的距离是 ;
③数轴上表示﹣3和6的两点之间的距离是 ;
【归纳】一般的,数轴上表示数a和数b的两点之间的距离等于 ;
【应用】
①如果表示数a和3的两点之间的距离是5,则可记为:|a﹣3|=5,那么a= ;
②若数轴上表示数a的点位于﹣4与5之间,则|a+4|+|a﹣5|的值为 ;
③结合数轴求出|a+2|+|a﹣1|+|a﹣3|的最小值为 ,此时a为 .
18.(2025秋 扶风县期中)先阅读下面的材料,再解决问题.
【实际问题】如图1,一圆柱的底面半径为5cm,BC是底面直径,高AB为5cm,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
【解决方案】路线1:侧面展开图中的线段AC,如图所示
设路线1的长度为l1,则.
路线2:高线AB+底面直径BC.
设路线2的长度为l2,则.
为比较l1,l2的大小,采用“作差法”:
因为;
所以,所以l1>l2,
所以小明认为路线2较短.
(1)【问题类比】小亮对上述结论有些疑惑,于是他把条件改成“圆柱的底面半径为1cm,高AB为5cm“.请你用上述方法帮小亮比较出l1与l2的大小.
(2)【问题拓展】请你帮他们继续研究:在一般情况下,若圆柱的底面半径为r cm,高为h cm,蚂蚁从A点出发沿圆柱表面爬行到点C,当满足什么条件时,路线2较短?请说明理由.
(3)【问题解决】如图是紧密排列在一起的2个相同的圆柱,高为5cm.当蚂蚁从A点出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.
19.(2025秋 青羊区校级月考)某文体中心提供阅读、观影、球类、游泳、器械等多种文体活动,现有三种收费方式,详情见下表:
收费方式 详细介绍
日卡 日卡一张30元
会员卡 办卡需210元,每活动1小时收费4元
普通卡 进入文体中心要收取10元/日,可免费文体活动2小时,后续收费5元/小时
(注:不足一个小时的按一小时计算)
(1)小明打算这周六去文体中心活动6小时,最少需要花费 元;
(2)小明打算一个月(30天)都去文体中心活动,每天活动的时间为x小时(x为正整数,且x≥2).
①如果小明选择办会员卡一个月需要花费 元;选择办普通卡一个月需要花费 元;(用含x的代数式表示)
②对于会员卡和普通卡两种不同的收费方式,哪种更划算?
20.(2025秋 双城区月考)在中俄贸易博览会前,哈市某展览馆为更好地适应会展需求,对部分展馆地面进行了升级改造,已知该展馆地面为长40米,宽30米的长方形,现计划将其分成两个展览区,其余部分为等宽的通道,设通道的宽度为x米.
(1)求两个展览区的总面积为多少平方米?(请用含x的式子表示)
(2)工程负责人准备用A、B两种彩砖铺设展览区的地面,用防滑材料铺设通道,经市场调查发现,铺设展览区若用A种彩砖每平方米需要90元,若用B种彩砖每平方米需要60元,当x=4时,若铺设展览区的总费用不超过45540元,求最多购买多少平方米A种彩砖?
参考答案与试题解析
一.解答题(共20小题)
1.(2025秋 屯留区月考)学科实践
暑假期间、我市某公园为打造专属夜景景观特别安装了喷水装置,为保持人行绿道干燥,水柱要喷入河中,水柱可近似看作抛物线.图2是截面图,已知人行绿道宽OA=3.5m,AE是河道坝高,坝面AB的坡比为i=1:0.5,在距离喷水口O处2m时,水柱距离人行道的高度达到最大值3m.以点O为原点,直线OA为x轴建立平面直角坐标系.
(1)出于安全考虑,在坝顶A处安装护栏,要求水柱不能喷射到护栏上,求护栏的最大高度.
(2)当水面距离人行道的竖直距离为多少时,水柱恰好落在河水中(水面与AB交点处)?
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】(1)护栏的最大高度为1.3125米;
(2)当水面距离人行道的竖直距离为米时,水柱恰好落在河水中.
【分析】(1)依据题意得二次函数的顶点坐标为(2,3),设该二次函数的解析式为y=a(x﹣2)2+3,再结合经过原点,求出a得到二次函数的解析式为y(x﹣2)2+3,从而可得当x=3.5时,求出y,即可得的答案;
(2)先求出A(3.5,0),B的坐标为(6,﹣5),根据待定系数法求出直线AB的解析式,再与抛物线解析式建立方程组,求解即可得的答案.
【解答】解:(1)由题意得,二次函数的顶点坐标为(2,3),
设该二次函数的解析式为y=a(x﹣2)2+3(a≠0),二次函数经过原点,
∴4a+3=0,
解得,解得a,
∴该二次函数的解析式为y(x﹣2)2+3,
当x=3.5时,y(x﹣2)2+31.3125,
答:护栏的最大高度为1.3125米;
(2)∵河道坝高AE=5米,坝面AB的坡比为i1:0.5,
∴BE=2.5,
则点B与原点O的水平距离为3.5+2.5=6,
∴点B的坐标为(6,﹣5),
又∵点A的坐标为(3.5,0),
设AB的解析式为y1=kx+b(k≠0),
∴,
解得,
∴y1=﹣2x+7(3.5≤x≤6),
∴﹣2x+7(x﹣2)2+3,
解得x1=2(不合题意,舍去),x2,
当x时,y,
答:当水面距离人行道的竖直距离为米时,水柱恰好落在河水中.
【点评】本题主要考查了二次函数的应用,解题时要熟练掌握二次函数的性质是关键.
2.(2025秋 晋源区月考)综合与探究
已知A,B为数轴上的两个点,点A表示的数为a,点B表示的数为b,且8xyb﹣2+(a+2)xy﹣1是关于x,y的三次二项式.
根据上述条件,解答下列问题:
(1)求a,b的值;
(2)若C为数轴上AB之间的点,且BC=5AC,求点C表示的数;
(3)在(2)的条件下,有一动点P从点A开始以每秒2个单位长度的速度沿数轴向左匀速运动,同时另一动点Q从点B开始以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒,是否存在某一时刻t,使得PC=2QC?若存在,直接写出t的值;若不存在,请说明理由.
【考点】一元一次方程的应用;两点间的距离;数轴.
【专题】一次方程(组)及应用;应用意识.
【答案】(1)﹣2,﹣1,4;
(2)3;
(3)t或t.
【分析】(1)由题可得方程1+b﹣2=3,a+2=0,解方程即可得到结论;
(2)根据题意列方程即可得到结论;
(3)由点运动的特点可知P点表示的数为﹣2+2t,Q点表示的数为4﹣4t,分别求出PB,QB,再由已知建立方程|2﹣2t|=2|5﹣4t|,求t的值即可.
【解答】解:(1)∵8xyb﹣2+(a+2)xy﹣1是关于x,y的三次二项式.
∴1+b﹣2=3,a+2=0,
∴b=4,a=﹣2;
(2)∵b=4,a=﹣2,
∴点A表示的数为﹣2,点B表示的数为4,
设点C表示的数为x,
根据题意得,4﹣x=5(x+2),
解得x=﹣1,
∴点C表示的数为﹣1;
(3)存在x值,使得PC=2QC,理由如下:
P点表示的数为﹣2﹣2t,Q点表示的数为4﹣4t,
∴PC=|﹣1+2+2t|=|1+2t|,QC=|4﹣4t+1|=|5﹣4t|,
∵PC=2QC,
∴|1+2t|=2|5﹣4t|,
解得t或t.
【点评】本题考查了一元一次方程的应用,数轴,熟练掌握数轴上点的运动特点是解题的关键.
3.(2025秋 兴县月考)综合与实践
问题情境:元旦晚会舞台布置中需要搭一条抛物线型灯链,最初的设计方案如图1所示,灯链两端连接A,B两点,点C位于点B正下方的地面处,以点A正下方的地面处的点O为原点,OC所在的直线为x轴,OA所在的直线为y轴,建立平面直角坐标系,抛物线解析式的二次项系数为0.03,OC=10米,OA=BC=3米,但实际实施方案后发现最低点过低.
方案修改:莉莉将方案进行修改,如图2,将图1中灯链的最低点固定在距地面2.7米的点N处,点N两侧的灯链形成了两个对称的新抛物线.
(1)求图1中抛物线的解析式.
(2)若图1中抛物线的最低点为M,求点M到OC的距离.
(3)若图2中两个最低点的距离为4米,修改方案后最低点提高了多少米?
【考点】二次函数的应用.
【专题】二次函数的应用;运算能力;应用意识.
【答案】(1)y=0.03x2﹣0.3x+3;
(2)点M到OC的距离为2.25米;
(3)灯链最低点提高了0.21米.
【分析】(1)由题意得A(0,3),B(10,3),进而求出抛物线的对称轴为直线x=5,根据抛物线的对称轴为x求出b即可;
(2)将抛物线的解析式化为顶点式即可得的答案;
(3)根据题意求出左边的新抛物线的解析式的对称轴,根据待定系数法求出新抛物线的解析式即可得的答案.
【解答】解:(1)由题意得A(0,3),B(10,3),
∴抛物线的对称轴为直线x5,
∴设抛物线的解析式为y=0.03x2+bx+3
∵抛物线的对称轴为直线x5,
解得 b=﹣0.3,
∴抛物线的解析式为y=0.03x2﹣0.3x+3;
(2)y=0.03x2﹣0.3x+3=0.03(x﹣5)2+2.25,
答:点M到OC的距离为2.25米;
(3)∵图2中两个新抛物线对称,且最低点之间的水平距离为4米,
∴左边的新抛物线的对称轴为直线 x=5﹣2=3,
设左边的新抛物线的解析式为y=m(x﹣3)2+k,
将点A(0,3),N(5,2.7)代入y=m(x﹣3)2+k,
得,
解得,
2.46﹣2.25=0.21(米).
答:灯链最低点提高了0.21米.
【点评】本题主要考查了二次函数的应用,根据题意求出二次函数的解析式是解决问题的关键.
4.(2025秋 合肥期末)根据图中情景,解答下列问题:
(1)购买8根跳绳需 280 元;购买12根跳绳需 336 元;
(2)购买m根跳绳需多少元?(请你用含有m的式子表示)
(3)小红比小明多买2根,付款时小红反而比小明少7元,你认为这种情况有可能吗?请利用方程知识说明理由.
【考点】一元一次方程的应用;列代数式.
【专题】一次方程(组)及应用;应用意识.
【答案】(1)280,336;
(2)当m≤10时,需要35m元;当m>10时,需要28m元;
(3)这种情况有可能,理由见解答过程.
【分析】(1)根据“跳绳每根35元,超过10根,享受八折优惠”,结合未超过10根,价格=单价×数量,超过10根,价格=单价×数量×折扣,列式计算即可;
(2)分两种情况讨论即可;
(3)若小红比小明多买2根,付款时小红反而比小明少7元成立,唯一的可能性就是小红买的跳绳超过10根打折了,而小明的不足10根没打折,设小明买了x根跳绳,小红买了(x+2)根跳绳,根据题意列出关于x的一元一次方程,解答并作出判断即可.
【解答】解:(1)根据题意得:
35×8=280(元),
即购买8根跳绳需280元;
0.8×35×12=336(元),
即购买12根跳绳需336元,
故答案为:280,336;
(2)当m≤10时,需要钱数为:35m(元);
当m>10时,需要钱数为:35m×0.8=28m(元);
(3)这种情况有可能,理由如下:
若小红比小明多买2根,付款时小红反而比小明少7元成立,
唯一的可能性就是小红买的跳绳超过10根打折了,而小明的不足10根没打折,
设小明买了x根跳绳,小红买了(x+2)根跳绳,
根据题意得:
35x﹣35×0.8(x+2)=7,
解得:x=9,
x+2=11≥10(符合题意),
答:有这种可能性.
【点评】本题考查了一元一次方程的应用,正确找出等量关系,列出一元一次方程是解题的关键.
5.(2025秋 桃城区校级期中)为更好筹备“十四运”的召开,小颖及其小组成员将利用所学知识测量一个广告牌的高度EF.在第一次测量中,小颖来回走动,走到点D时,其影子末端与广告牌影子末端重合于点H,其中DH=1m.随后,组员在直线DF上平放一平面镜,在镜面上做了一个标记,这个标记在直线DF上的对应位置为点G.镜子不动,小颖从点D沿着直线FD后退5m到B点时,恰好在镜子中看到顶端E的像与标记G重合,此时BG=2m.
如图,已知AB⊥BF,CD⊥BF,EF⊥BF,小颖的身高为1.5m(眼睛到头顶距离忽略不计),平面镜的厚度忽略不计.根据以上信息,求广告牌的高度EF.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】广告牌的高度EF为3m.
【分析】根据镜面反射原理结合相似三角形的判定方法得出△EFH∽△CDH,△EFG∽△ABG,进而利用相似三角形的性质得出EF的长.
【解答】解:设广告牌的高度EF为x m,
依题意知:DB=5m,BG=2m,DH=1m,AB=CD=1.5m.
∴GD=DB﹣BG=3m,
∵CD⊥BF,EF⊥BF,
∴CD∥EF.
∴△EFH∽△CDH.
∴,即.
∴.
∴DFx﹣1.
由平面镜反射规律可得:∠EGF=∠AGB.
∵AB⊥BF,
∴∠ABG=90°=∠EFG.
∴△EFG∽△ABG.
∴,即.
∴.
∴x=3.
故广告牌的高度EF为3m.
【点评】此题主要考查了相似三角形的判定与性质,正确利用已知得出相似三角形是解题关键.
6.(2025秋 碑林区校级月考)某校迎来了一百二十年校庆,为了准备校庆,校方决定准备一场别开生面的文艺演出,有歌唱,舞蹈,小舞台剧等节目,为此学校需要采购一批演出服装.现有质量较好且价格合理的A,B两家公司供选择,这两家公司给出的价格都是每套服装100元,经洽谈协商:A公司给出的优惠条件是全部服装单价打8折,但校方需要承担1500元的运费;B公司给出的优惠条件是购买服装不超过100套时不打折,超过100套时,超出部分每套打7折,校方不用承担运费.
(1)分别求出学校购买A,B两公司服装所付的总费用y1(元)和y2(元)与购买服装的数量x(套)之间的函数关系式;
(2)如果该校根据演出人数决定购买180套服装,请通过计算说明学校选择哪家公司的服装花费更少.
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】(1)y1=80x+1500,y2;
(2)B公司.
【分析】(1)分别根据两家公司的优惠条件写出对应函数关系式即可;
(2)将x=180分别代入y1和y2与x之间的函数关系式,求出y1和y2并比较大小即可得出结论.
【解答】解:(1)y1=0.8×100x+1500=80x+1500,
∴y1=80x+1500.
当0≤x≤100时,y2=100x;
当x>100时,y2=100×100+0.7×100(x﹣100)=70x+3000,
∴y2.
(2)当x=180时,y1=80×180+1500=15900,y2=70×180+3000=15600,
∵y1>y2,
∴学校选择B公司的服装花费更少.
【点评】本题考查一次函数的应用,根据题意写出函数关系式是解题的关键.
7.(2025秋 沈阳月考)数学兴趣小组测量校园内旗杆的高度.如图,小聪在某一时刻测得1m长的竹竿竖直放置时影长1.5m,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长BD=21m,留在墙上的影高CD=2m,求旗杆的高度.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】旗杆的高度是16米.
【分析】延长AC,BD相交于点E,BD=21m,CD=2m,由CD∥AB,得出△ABE∽△CDE,得出对应边成比例,代入数据即可得出结果.
【解答】解:如图所示,延长AC,BD相交于点E,
则CD:DE=1:1.5,得DE=1.5CD=3m,
由已知CD∥AB,
∴△ABE∽△CDE,
∴,即,
解得:AB=16.
答:旗杆的高度是16米.
【点评】本题考查平行投影及相似三角形的应用,从实际问题中整理出相似三角形是解题关键.
8.(2025秋 沈阳月考)某校将新建图书楼的正门设计为一个抛物线型拱门,并要求所设计的拱门的跨度与拱高之积为48m2,还要兼顾美观、大方、和谐、通畅等因素,设计部门按要求做出了设计方案.现把方案中的拱门图形放入平面直角坐标系中,如图1、2所示,抛物线型拱门的跨度ON=12m,拱高PE=4m.其中,点N在x轴上,PE⊥ON,OE=EN.要在拱门中设置矩形框架,其面积越大越好.
方案一:如图1,矩形框架ABCD的面积记为S1,点A,D在抛物线上,边BC在ON上;
方案二:如图2,矩形框架A'B'C'D'的面积记为S2,点A',D'在抛物线上,边B'C'在ON上.
(1)求抛物线的函数表达式;
(2)方案一中,已知AB=3m,方案二中,已知B'C'=8m,比较S1,S2的大小.
【考点】二次函数的应用.
【专题】二次函数的应用;应用意识.
【答案】(1)y(x﹣6)2+4;
(2)S1>S2.
【分析】(1)由题意得抛物线顶点坐标为(6,4),设抛物线的函数表达式为y=a(x﹣6)2+4,利用待定系数法解答即可求解;
(2)把y=3代入y(x﹣6)2+4可求出BC,即可求出S1,再根据OB′=NC′=(12﹣8)÷2=2(m)可求出A′B′,进而求出S2,据此即可判断求解;
【解答】解:(1)由题意得,抛物线顶点坐标为(6,4),
设抛物线的函数表达式为y=a(x﹣6)2+4,把(0,0)代入得:
0=a(0﹣6)2+4,
解得,
∴抛物线的函数表达式为y(x﹣6)2+4;
(2)把y=3代入y(x﹣6)2+4得:3(x﹣6)2+4,
解得x1=3,x2=9,
∴BC=9﹣3=6,
∴S1=BC AB=6×3=18(m2);
∵B′C′=8m,
∴OB′=NC′=(12﹣8)÷2=2(m),
把x=2代入t=﹣2x+80得:y(2﹣6)2+4,
∴A′B′,
∴S2=B′C′ A′B′=8(m2),
∵18,
∴S1>S2.
【点评】本题考查了二次函数的应用,利用待定系数法求出二次函数的解析式是解题的关键.
9.(2025秋 碑林区校级月考)(1)问题解决:如图1,平面直角坐标系中,直线l:y=﹣2x+4与x轴交于点A,与y轴交于点B,以AB为腰在第一象限作等腰直角△ABC,∠BAC=90°,点A的坐标为 (2,0) ,点B的坐标为 (0,4) .
(2)求(1)中点C的坐标.
(3)类比探究
如图②,平面直角坐标系中,线段MN在x轴上,点M坐标为(﹣4,0),点N与M关于y轴对称,点A是线段MN上的一个动点,B点坐标为(0,4),以点A为直角顶点,AB为直角边在AB右侧作等腰直角△ABC,连接OC,在点A的运动过程当中,线段OC是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.
【考点】一次函数综合题.
【专题】一次函数及其应用;图形的全等;等腰三角形与直角三角形;应用意识.
【答案】(1)(2,0),(0,4);
(2)点C(6,2);
(3)OC的最小值为2.
【分析】(1)当x=0时,y=4,当y=0时,x=2,即可求解;
(2)由AAS可得△ABO≌△CAH,可得AO=2=CH,OB=4=AH,即可求解;
(3)先证点C在过点N且与MN成45°直线上运动,则OC⊥CN时,CO有最小值,由等腰直角三角形的性质可求解.
【解答】解:(1)∵y=﹣2x+4与x轴交于点A,与y轴交于点B,
∴当x=0时,y=4,
当y=0时,x=2,
∴点A(2,0),点B(0,4),
故答案为:(2,0),(0,4);
(2)如图①,过点C作CH⊥直线OA于H,
∴∠AHC=∠AOB=∠BAC=90°,
∴∠ABO+∠BAO=90°=∠BAO+∠CAH,
∴∠ABO=∠CAH,
又∵AB=AC,
∴△ABO≌△CAH(AAS),
∴AO=CH,OB=AH,
∵点A(2,0),点B(0,4),
∴AO=2=CH,OB=4=AH,
∴OH=6,
∴点C(6,2);
(3)OC有最小值,如图②,过点C作CH⊥MN于H,连接CN,
∵点M坐标为(﹣4,0),点N与M关于y轴对称,
∴点N(4,0),
∴MO=NO=4,
∵B点坐标为(0,4),
∴BO=4=ON=OM,
同理可证△ABO≌△CAH(AAS),
∴AO=CH,OB=AH=6=ON,
∴HN=AO,
∴CH=HN,
∴∠HNC=45°,
∴点C在过点N且与MN成45°直线上运动,
∴OC⊥CN时,CO有最小值,
∵∠HNC=45°,ON=4,
∴OC的最小值为2.
【点评】本题是一次函数综合题,考查了全等三角形的判定和性质,一次函数的性质,等腰直角三角形的性质,添加恰当辅助线构造全等三角形是解题的关键.
10.(2024 自贡)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
(1)如图1,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3m,据此可得旗杆高度为 11.3 m;
(2)如图2,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5m,小李到镜面距离EC=2m,镜面到旗杆的距离CB=16m.求旗杆高度;
(3)小王所在小组采用图3的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高,研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
如图4,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图5,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图6,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8m,DG=1.5m.将观测点D后移24m到D′处.采用同样方法,测得C′G′=1.2m,D′G′=2m.求雕塑高度(结果精确到1m).
【考点】相似三角形的应用;近似数和有效数字.
【专题】图形的相似;解直角三角形及其应用;应用意识.
【答案】见试题解答内容
【分析】(1)由影长EF恰好等于自己的身高DE,知△DEF是等腰直角三角形,△ABC是等腰直角三角形,故AB=BC=11.3m,
(2)证明△DEC∽△ABC,可得,故AB=12,即旗杆高度为12米;
(3)由△DCG∽△DAB,得,设AB=x m,BD=y m,则,知yx,同理可得,即得,从而,解出x即可得雕塑高度约为31m.
【解答】解:(1)∵影长EF恰好等于自己的身高DE,
∴△DEF是等腰直角三角形,
由平行投影性质可知,△ABC是等腰直角三角形,
∴AB=BC=11.3m,
故答案为:11.3;
(2)如图:
由反射定律可知,∠DCE=∠ACB,
又∠DEC=90°=∠ABC,
∴△DEC∽△ABC,
∴,即,
解得AB=12,
∴旗杆高度为12米;
(3)如图:
∵∠CDG=∠ADB,∠CGD=90°=∠ABD,
∴△DCG∽△DAB,
∴,
设AB=x m,BD=y m,则,
∴yx,
同理可得,
∴,
∴,
解得x=28.8;
经检验,x=28.8是原方程的解,
故AB≈29m,
∴雕塑高度AB约为29m.
【点评】本题考查解直角三角形应用,涉及相似三角形判定与性质,解题的关键是读懂题意,列出方程解决问题.
11.(2024春 历下区期末)数学兴趣小组利用所学数学知识来解决实际问题,实践报告如下:
活动课题 风筝离地面垂直高度探究
问题背景 风筝由中国古代劳动人民发明于东周春秋时期,距今已2000多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.兴趣小组在放风筝时想测量风筝离地面的垂直高度.
测量数据抽象模型 小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC的长为15米,根据手中剩余线的长度计算出风筝线AB的长为17米,牵线放风筝的手到地面的距离为1.5米.
问题产生 经过讨论,兴趣小组得出以下问题: (1)运用所学勾股定理相关知识,根据测量所得数据,计算出风筝离地面的垂直高度. (2)如果想要风筝沿DA方向再上升12米,且BC长度不变,则他应该再放出多少米线?
问题解决 ……
该报告还没有完成,请你帮助兴趣小组解决以上问题.
【考点】勾股定理的应用.
【专题】等腰三角形与直角三角形;运算能力;应用意识.
【答案】见试题解答内容
【分析】(1)在Rt△ABC中,利用勾股定理求出的AC长,即可得到结论;
(2)在Rt△A′BC中,根据勾股定理求出A′B,即可得到结论.
【解答】解:(1)在Rt△ABC中,∠ACB=90°,BC=15米,AB=17米,
由勾股定理,可得AC8米,
∴AD=AC+CD=8+1.5=9.5(米),
答:风筝离地面的垂直高度为9.5米;
(2)如图,当风筝沿DA方向再上升12米,A'C=20米,
在Rt△A′BC中,∠A'CB=90°,BC=15米,
由勾股定理,可得A′B25米,
则应该再放出25﹣17=8(米),
答:他应该再放出8米长的线.
【点评】本题考查了用勾股定理解决实际问题,解题的关键是熟练掌握直角三角形中的三边关系.
12.(2025秋 灯塔市期中)【问题背景】
已知点A,M,N,B在数轴上对应的数分别为﹣1,x﹣1,x+1,11.线段MN沿数轴的正方向以每秒1个单位的速度移动,设移动时间为t秒.例如线段AB的长度为|﹣1﹣11|=12或11﹣(﹣1)=12.
【初步发现】
(1)求线段MN的长度;
【问题解决】
(2)若x=1,回答下列两个问题:
①当点M在点B的左侧,同时点N在点B的右侧时,用含t的代数式表示线段AM+BN的值;
②若点A,B与线段MN同时移动,点A以每秒1个单位长度的速度向数轴的正方向移动,点B以每秒1个单位长度的速度向数轴的负方向移动.在移动过程中,求线段AM+BN的值.(可用含t的代数式表示)
【考点】列代数式;数轴;绝对值.
【专题】应用题;应用意识.
【答案】(1)2;(2)①2t﹣8;②2t﹣8或10﹣2t,过程见解析.
【分析】(1)根据题干信息可得,线段MN的长度为x+1﹣(x﹣1)=2;
(2)①当x=1时,点A,M,N,B在数轴上对应的数分别为﹣1,t,2+t,11,据此即可求得答案;
②点A,M,N,B在数轴上对应的数分别为﹣1+t,t,2+t,11﹣t,分两种情况:当点N在点B的右侧时和当点N在点B的左侧时,进行求解即可.
【解答】解:(1)依题意可得:线段MN的长度为x+1﹣(x﹣1)=2;
(2)①当x=1时,点A,M,N,B在数轴上对应的数分别为﹣1,t,2+t,11,
∴AM=t﹣(﹣1)=t+1,
BN=2+t﹣11=t﹣9,
∴AM+BN=t+1+t﹣9=2t﹣8;
②点A,M,N,B在数轴上对应的数分别为﹣1+t,t,2+t,11﹣t,
∴AM=t﹣(﹣1+t)=1,
当点N在点B的右侧时,
∴BN=2+t﹣(11﹣t)=2t﹣9,
∴AM+BN=1+2t﹣9=2t﹣8;
当点N在点B的左侧时,
∴BN=11﹣t﹣(2+t)=9﹣2t,
∴AM+BN=1+9﹣2t=10﹣2t,
综上所述,线段AM+BN的值为2t﹣8或10﹣2t.
【点评】本题考查了数轴和两点之间的距离表示,做题的关键是准确的表示出线段的长度.
13.(2025秋 隆昌市校级期末)阅读下列材料:利用完全平方公式,将多项式x2+bx+c变形为(x+m)2+n的形式,然后由(x+m)2≥0就可求出多项式x2+bx+c的最小值.
例:求多项式x2﹣4x+5的最小值.
解:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1.
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1.
当x=2时,(x﹣2)2+1=1,因此(x﹣2)2+1有最小值,最小值为1,即x2﹣4x+5的最小值为1.
通过阅读,理解材料的解题思路,请解决以下问题:
(1)【理解探究】已知代数式A=x2+8x+7,求A的最小值;
(2)【类比应用】张大爷家有甲、乙两块长方形菜地,已知甲菜地的两边长分别是(5a+1)米、(2a+2)米,乙菜地的两边长分别是(3a+8)米、(3a﹣2)米,试比较这两块菜地的面积S甲和S乙的大小,并说明理由;
(3)【拓展升华】如图,△ABC中,∠C=90°,AC=8cm,BC=16cm,点M,N分别是线段AC和BC上的动点,点M从A点出发以1cm/s的速度向C点运动;同时点N从C点出发以2cm/s的速度向B点运动,当其中一点到达终点时,两点同时停止运动.设运动的时间为t,则当t的值为多少时,△MCN的面积最大,最大值为多少?
【考点】二次函数的应用;三角形的面积;完全平方公式的几何背景;因式分解﹣运用公式法.
【专题】二次函数的应用;应用意识.
【答案】(1)﹣9;
(2)S甲>S乙;
(3)当t的值为4时,△MCN的面积最大,最大值为16cm2.
【分析】(1)直接利用完全平方公式可得答案;
(2)先求出,再利用完全平方公式即可求解;
(3)根据题意表示出(cm2),再利用完全平方公式即可求解.
【解答】解:(1)x2+8x+7=(x+4)2﹣9,
∵(x+4)2≥0,
∴(x+4)2﹣9≥﹣9,
∴当x=﹣4时,(x+4)2﹣9有最小值,最小值为﹣9,
即A的最小值为﹣9;
(2)∵,,
∴,
∵(a﹣3)2≥0,
∴(a﹣3)2+9≥9>0,
∴S甲>S乙;
(3)由题意得:CM=8﹣t,CN=2t,
∴(cm2),
∵(t﹣4)2≥0,
∴﹣(t﹣4)2≤0,
∴﹣(t﹣4)2+16≤16,
∴当t=4时,﹣(t﹣4)2+16有最大值,最大值为16.
即当t的值为4时,△MCN的面积最大,最大值为16cm2.
【点评】本题考查二次函数的应用,完全平方公式的几何背景,因式分解﹣运用公式法,三角形的面积,熟练掌握二次函数的性质是解答本题的关键.
14.(2025秋 南浔区期末)七年级数学兴趣小组成员自主开展数学微项目研究,他们决定研究“折线数轴”.
探索“折线数轴”
素材1 如图,将一条数轴在原点O,点B,点C处折一下,得到一条“折线数轴”.图中点A表示﹣9,点B表示12,点C表示24,点D表示36,我们称点A与点D在数轴上的“友好距离”为45个单位长度,并表示为45.
素材2 动点P从点A出发,以2个单位长度/秒的初始速度沿着“折线数轴”向其正方向运动.当运动到点O与点B之间时速度变为初始速度的一半.当运动到点B与点C之间时速度变为初始速度的两倍.经过点C后立刻恢复初始速度.
问题解决
探索1 动点P从点A运动至点B需要多少时间?
探索2 动点P从点A出发,运动t秒至点B和点C之间时,求点P表示的数(用含t的代数式表示);
探索3 动点P从点A出发,运动至点D的过程中某个时刻满足时,求动点P运动的时间.
【考点】一元一次方程的应用;数轴;列代数式.
【专题】整式;一次方程(组)及应用;应用意识.
【答案】探索1:秒;
探索2:4t﹣54(t);
探索3:秒或秒.
【分析】探索1:利用时间=路程÷速度,即可求出结论;
探索2:求出点P运动到点C所需时间,当t时,利用点P表示的数=点B表示的数+点P在线段BC段的运动速度×(运动时间),即可用含t的代数式表示出点P表示的数;
探索3:由,及的长,可得出共有2种情况,当点P在点O和点B之间,即t时,点P表示的数为t,进而可得出t,t,结合16,可列出关于t的一元一次方程,解之可求出t的值;当点P在点C的右侧,即t时,点P表示的数为2t﹣15,进而可得出2t﹣27,2t﹣39,结合16,可列出关于t的一元一次方程,解之可求出t的值.
【解答】解:探索1:根据题意得:[0﹣(﹣9)]÷2+(12﹣0)÷(2)
=9÷2+12÷1
12
(秒).
答:动点P从点A运动至点B需要秒;
探索2:(24﹣12)÷(2×2)
12÷4
3
(秒).
根据题意得:当t时,点P表示的数为12+2×2(t)=4t﹣54,
∴当动点P运动至点B和点C之间时,点P表示的数为4t﹣54(t);
探索3:∵24﹣0=24,24﹣12=12,36﹣12=24,
∴16共2两种情况.
当点P在点O和点B之间,即t时,点P表示的数为0+(2)(t)=t,
∴12﹣(t)t,24﹣(t)t,
∴tt=16,
解得:t;
当点P在点C的右侧,即t时,点P表示的数为24+2(t)=2t﹣15,
∴2t﹣15﹣12=2t﹣27,2t﹣15﹣24=2t﹣39,
∴2t﹣27+2t﹣39=16,
解得:t.
答:动点P的运动的时间是秒或秒.
【点评】本题考查了一元一次方程的应用、列代数式以及数轴,解题的关键是:探索1:根据各数量之间的关系,列式计算;探索2:根据各数量之间的关系,用含t的代数式表示出点P表示的数;探索3:找准等量关系,正确列出一元一次方程.
15.(2025秋 宁波期中)
背景 【长城上可以点无人机送的外卖了】 打开手机外卖软件下单,在长城上也可以点外卖了,最快5分钟收货! 日前,美团无人机在八达岭长城开通了北京首条无人机配送航线,为降落点附近的游客提供了应急救援等商品货物配送服务,这也是北京市内首次开通常态化无人机配送服务. 近年来,中国低空经济发展迅速,成为了经济增长的新动能.
素材1 某商店在无促销活动时,若买5件A商品,8件B商品,共需要2400元;若买8件A商品,5件B商品,共需2280元.
素材2 该商店为了鼓励消费者使用无人机配送服务,开展促销活动: ①若消费者用250元购买无人机配送服务卡,商品一律按标价的七五折出售; ②若消费者不使用无人机配送服务:凡购买店内任何商品,一律按照标价的八折出售.
问题解决
任务1 在该商店在无促销活动时,求A,B商品的销售单价分别是多少元?
任务2 某科技公司计划在促销期间购买A,B两款商品共30件,其中A商品购买a件(0<a<30); ①若使用无人机配送商品,共需要 (4750﹣30a) 元; ②若不使用无人机配送商品,共需要 (4800﹣32a) 元. (结果均用含a的代数式表示);
任务3 请你帮该科技公司算一算,在任务2的条件下,购买A产品的数量在什么范围内时,使用无人机配送商品更合算?
【考点】一元一次不等式的应用;列代数式;一元一次方程的应用.
【专题】整式;一次方程(组)及应用;一元一次不等式(组)及应用;应用意识.
【答案】见试题解答内容
【分析】任务1:在该商店在无促销活动时,设A商品的销售单价是x元,B商品的销售单价是y元,根据“某商店在无促销活动时,若买5件A商品,8件B商品,共需要2400元;若买8件A商品,5件B商品,共需2280元”,可列出关于x,y的二元一次方程组,解之即可得出结论;
任务2:根据购买两款商品的总数量及购买A商品的数量,可得出购买(30﹣a)件B商品,再利用总价=单价×数量,结合两种促销方案,即可用含a的代数式表示出使用无人机配送商品及不使用无人机配送商品,所需费用;
任务3:根据使用无人机配送商品更合算,可列出关于a的一元一次不等式,解之可得出a的取值范围,再结合0<a<30,即可得出结论.
【解答】解:任务1:在该商店在无促销活动时,设A商品的销售单价是x元,B商品的销售单价是y元,
根据题意得:,
解得:.
答:在该商店在无促销活动时,A商品的销售单价是160元,B商品的销售单价是200元;
任务2:∵某南山科技公司计划在促销期间购买A,B两款商品共30件,其中A商品购买a件,
∴B商品购买(30﹣a)件.
①若使用无人机配送商品,共需要250+160×0.75a+200×0.75(30﹣a)=(4750﹣30a)元;
②若不使用无人机配送商品,共需要160×0.8a+200×0.8(30﹣a)=(4800﹣32a)元.
故答案为:①(4750﹣30a);②(4800﹣32a);
任务3:根据题意得:4750﹣30a<4800﹣32a,
解得:a<25,
又∵0<a<30,
∴0<a<25.
答:当0<a<25时,使用无人机配送商品更合算.
【点评】本题考查了二元一次方程组的应用、列代数式以及一元一次不等式的应用,解题的关键是:任务1:找准等量关系,正确列出二元一次方程组;任务2:根据各数量之间的关系,用含a的代数式表示出使用无人机配送商品及不使用无人机配送商品所需费用;任务3:根据各数量之间的关系,正确列出一元一次不等式.
16.(2025秋 市北区期中)漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.数学活动小组依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现漏刻水位h(cm)是时间t(min)的一次函数,通过观察,每2分钟记录一次箭尺读数,小磊记录实验数据得到如表:
数据记录 第1次 第2次 第3次 第4次 第5次 …
t(min) 0 2 4 6 8 …
h(cm) 2 2.8 3.6 4.0 5.2 …
(1)在小组探究中,小华采用不同的函数关系表达方式(表格、图象、关系式)验证,均发现小磊记录的上表h,t的数据中,有一对数据记录错误.请用学过的相关知识判断,第 4 次数据是不准确的.
(2)当记录时间为20分钟时,漏刻水位是多少?
(3)求h(cm)与t(min)的函数关系式,并计算当水位为14cm时,对应时间是多少?
【考点】一次函数的应用.
【专题】一次函数及其应用;运算能力;应用意识.
【答案】见试题解答内容
【分析】(1)将表格中的数据在平面直角坐标系中描点并连线,与其它4个点不在同一条直线上的那个点对应的数据不准确;
(2)根据“每分钟漏刻水位升高0.4cm”计算即可;
(3)利用待定系数法求h与t的函数关系式,把h=14代入函数关系式求出对应t的值即可.
【解答】解:(1)将表格中的数据在平面直角坐标系中描点并连线如图所示:
由图可知,坐标为(6,4)的点与其它4个点不在同一条直线上,
∴第4次数据是不准确的.
(2)由表格数据可知,每分钟漏刻水位升高0.4cm,
2+0.4×20=10(cm).
答:当记录时间为20分钟时,漏刻水位是10cm.
(3)设h与t的函数关系式为h=kt+b(k、b为常数,且k≠0).
将坐标(0,2)和(2,2.8)分别代入h=kt+b,
得,
解得,
∴h与t的函数关系式为h=0.4t+2,
当h=14时,得0.4t+2=14,
解得t=30.
答:h与t的函数关系式为h=0.4t+2,当水位为14cm时,对应时间是30min.
【点评】本题考查一次函数的应用,掌握描点作图的方法、待定系数法求函数关系式是解题的关键.
17.(2025秋 岳阳县期中)综合与实践:阅读以下材料,唐代文学家韩愈曾赋诗:“天街小雨润如酥,草色遥看近却无”,当代印度诗人泰戈尔也写道:“世界上最遥远的距离,不是瞬间便无处寻觅;而是尚未相遇,便注定无法相聚”,距离是数学、天文学、物理学中的热门话题,唯有对宇宙距离进行测量,人类才能掌握世界的尺度.下面我们结合数轴与绝对值的知识解答下列有关距离的数学问题:
【探究】
①数轴上表示5和1的两点之间的距离是 4 ;
②数轴上表示﹣1和﹣4的两点之间的距离是 3 ;
③数轴上表示﹣3和6的两点之间的距离是 9 ;
【归纳】一般的,数轴上表示数a和数b的两点之间的距离等于 |a﹣b| ;
【应用】
①如果表示数a和3的两点之间的距离是5,则可记为:|a﹣3|=5,那么a= 8或﹣2 ;
②若数轴上表示数a的点位于﹣4与5之间,则|a+4|+|a﹣5|的值为 9 ;
③结合数轴求出|a+2|+|a﹣1|+|a﹣3|的最小值为 5 ,此时a为 1 .
【考点】一元一次方程的应用;数轴;绝对值.
【专题】实数;一次方程(组)及应用;应用意识.
【答案】【探究】①4;②3;③9,
【归纳】|a﹣b|,
【应用】①8或﹣2;②9;③5,1.
【分析】【探究】运用“数轴上表示数m与数n的两点之间的距离为|m﹣n|”直接计算即可;
【归纳】运用“数轴上表示数m与数n的两点之间的距离为|m﹣n|”直接计算即可;
【应用】①根据绝对值的意义即可得到结论;
②根据阅读材料和探究可知当﹣4≤a≤5时求代数式的值;
③判断出a=1时,三个绝对值的和最小,然后进行计算即可得解.
【解答】解:【探究】
①数轴上表示5和1的两点之间的距离是5﹣1=4;
②数轴上表示﹣1和﹣4的两点之间的距离是﹣1﹣(﹣4)=3;
③数轴上表示﹣3和6的两点之间的距离是6﹣(﹣3)=9,
故答案为:4,3,9;
【归纳】一般的,数轴上表示数a和数b的两点之间的距离等于|a﹣b|,
故答案为:|a﹣b|;
【应用】
①∵|a﹣3|=5,
∴a﹣3=±5,
∴a=8或a=﹣2,
故答案为:8或﹣2;
②∵数轴上表示数a的点位于﹣4与5之间,
∴﹣4<a<5,
∴|a+4|+|a﹣5|=a+4+5﹣a=9,
故答案为:9;
③∵|a+2|+|a﹣1|+|a﹣3|表示数a分别与﹣2、1、3的距离之和,
∴当a=1时|a+2|+|a﹣1|+|a﹣3||可取得最小值为3+0+2=5,
故答案为:5,1.
【点评】本题考查了一元一次方程的应用,数轴、绝对值,解答本题的关键是明确题意,利用数轴的特点解答.
18.(2025秋 扶风县期中)先阅读下面的材料,再解决问题.
【实际问题】如图1,一圆柱的底面半径为5cm,BC是底面直径,高AB为5cm,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线.
【解决方案】路线1:侧面展开图中的线段AC,如图所示
设路线1的长度为l1,则.
路线2:高线AB+底面直径BC.
设路线2的长度为l2,则.
为比较l1,l2的大小,采用“作差法”:
因为;
所以,所以l1>l2,
所以小明认为路线2较短.
(1)【问题类比】小亮对上述结论有些疑惑,于是他把条件改成“圆柱的底面半径为1cm,高AB为5cm“.请你用上述方法帮小亮比较出l1与l2的大小.
(2)【问题拓展】请你帮他们继续研究:在一般情况下,若圆柱的底面半径为r cm,高为h cm,蚂蚁从A点出发沿圆柱表面爬行到点C,当满足什么条件时,路线2较短?请说明理由.
(3)【问题解决】如图是紧密排列在一起的2个相同的圆柱,高为5cm.当蚂蚁从A点出发沿圆柱表面爬行到C点的两条路线长度相等时,求圆柱的底面半径r.
【考点】平面展开﹣最短路径问题;列代数式.
【专题】等腰三角形与直角三角形;应用意识.
【答案】(1)路线1较短;(2)路线2较短;(3)半径r为.
【分析】(1)将解决方案中的数字替换成所给数字计算即可;
(2)将解决方案中的数字替换成r,h表示出,作差根据题意可得满足的条件;
(3)用含r的式子表示出,根据题意列出等式求出r即可.
【解答】解:(1)因为圆柱的底面半径为1cm,高AB为5cm,
所以路线1:;
路线2:l2=AB+BC=5+2=7,则
因为,
所以,所以l1<l2,
所以路线1较短;
(2)因为圆柱的底面半径为r cm,高为h cm,
所以路线1:,
路线2:,
所以.
因为r恒大于0,所以当(π2﹣4)r﹣4h>0,即时,,
此时路线2较短;
(3)圆柱的高为5cm.
路线1:,
路线2:,
由题意,得25+(2πr)2=(5+4r)2,
解得;
即当圆柱的底面半径r为时,蚂蚁从点A出发沿圆柱表面爬行到C点的两条路线长度相等.
【点评】本题考查了勾股定理在蚂蚁爬行最短路径问题中的应用,属于模仿题型,准确理解题中所给解决方案中的思路步骤是解题的关键.
19.(2025秋 青羊区校级月考)某文体中心提供阅读、观影、球类、游泳、器械等多种文体活动,现有三种收费方式,详情见下表:
收费方式 详细介绍
日卡 日卡一张30元
会员卡 办卡需210元,每活动1小时收费4元
普通卡 进入文体中心要收取10元/日,可免费文体活动2小时,后续收费5元/小时
(注:不足一个小时的按一小时计算)
(1)小明打算这周六去文体中心活动6小时,最少需要花费 30 元;
(2)小明打算一个月(30天)都去文体中心活动,每天活动的时间为x小时(x为正整数,且x≥2).
①如果小明选择办会员卡一个月需要花费 (210+120x) 元;选择办普通卡一个月需要花费 150x 元;(用含x的代数式表示)
②对于会员卡和普通卡两种不同的收费方式,哪种更划算?
【考点】一元一次不等式的应用;列代数式;一元一次方程的应用.
【专题】整式;一次方程(组)及应用;一元一次不等式(组)及应用;运算能力;应用意识.
【答案】(1)30;
(2)(210+120x),150x);
(3)当2≤x<7时,选择普通卡更划算;当x=7时,选择普通卡或会员卡都一样;当x>7时,选择会员卡更划算.
【分析】(1)分别求得办日卡、会员卡、普通卡,所需要花费,再比较即可求解;
(2)①根据办会员卡和普通卡的收费方式,列式计算即可求解;
②分3种情况,分别列出一元一次方程或一元一次不等式,解方程或不等式,再求出x=2时,办会员卡和普通卡需要的花费,即可解决问题.
【解答】解:(1)办日卡,需要花费30元;
办会员卡,办卡就需210元,显然不合题意;
办普通卡,需要花费10+5(6﹣2)=30(元);
∴最少需要花费30元,
故答案为:30;
(2)①办会员卡需要花费:210+30×4x=(210+120x)(元),
办普通卡需要花费:30[10+5(x﹣2)]=150x(元),
故答案为:(210+120x),150x);
②当210+120x=150x时,x=7,
当210+120x<150x时,x>7,
当210+120x>150x时,x<7,
当x=2时,办会员卡需要花费210+120x=210+120×2=450(元),
办普通卡需要花费150x=150×2=300(元),
∵450>300,
∴选择普通卡更划算;
综上所述,当2≤x<7时,选择普通卡更划算;当x=7时,选择普通卡或会员卡都一样;当x>7时,选择会员卡更划算.
【点评】本题考查了一元一次不等式的应用、一元一次方程的应用以及列代数式等知识,找出数量关系,正确列出一元一次不等式或一元一次方程是解题的关键.
20.(2025秋 双城区月考)在中俄贸易博览会前,哈市某展览馆为更好地适应会展需求,对部分展馆地面进行了升级改造,已知该展馆地面为长40米,宽30米的长方形,现计划将其分成两个展览区,其余部分为等宽的通道,设通道的宽度为x米.
(1)求两个展览区的总面积为多少平方米?(请用含x的式子表示)
(2)工程负责人准备用A、B两种彩砖铺设展览区的地面,用防滑材料铺设通道,经市场调查发现,铺设展览区若用A种彩砖每平方米需要90元,若用B种彩砖每平方米需要60元,当x=4时,若铺设展览区的总费用不超过45540元,求最多购买多少平方米A种彩砖?
【考点】一元一次不等式的应用;列代数式.
【专题】整式;一元一次不等式(组)及应用;运算能力;应用意识.
【答案】(1)两个展览区的总面积为(6x2﹣180x+1200)平方米;
(2)最多购买366平方米A种彩砖.
【分析】(1)设通道的宽度为x米,则展览区的长为(40﹣2x)米,宽为(30﹣3x)米,再由矩形面积公式计算即可;
(2)求出当x=4时,展览区的总面积为576平方米,设购买m平方米A种彩砖,则购买(576﹣m)平方米B种彩砖,根据铺设展览区的总费用不超过45540元,列出一元一次不等式,解不等式即可.
【解答】解:(1)设通道的宽度为x米,则展览区的长为(40﹣2x)米,宽为(30﹣3x)米,
∴(40﹣2x)(30﹣3x)=1200﹣180x+6x2=(6x2﹣180x+1200)(平方米),
答:两个展览区的总面积为(6x2﹣180x+1200)平方米;
(2)当x=4时,展览区的总面积为6×42﹣180×4+1200=576(平方米),
设购买m平方米A种彩砖,则购买(576﹣m)平方米B种彩砖,
由题意得:90m+60(576﹣m)≤45540,
解得:m≤366,
答:最多购买366平方米A种彩砖.
【点评】本题考查了一元一次不等式的应用以及列代数式等知识,找出数量关系,正确列出一元一次不等式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
