2025年山东省济宁市兖州区小升初数学试卷(含答案)
文档属性
| 名称 | 2025年山东省济宁市兖州区小升初数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 00:00:00 | ||
图片预览




文档简介
2025年山东省济宁市兖州区小升初数学试卷
一、填空。(把要填的内容写在相应题号的横线上)(27个知识点)
1.兖州区的面积约是五百三十五点一平方千米,写作 平方千米,人口约540700人(第七次人口普查),改写成用“万”为单位的数是 人。2025年1月,兖州最低气温是零下10摄氏度,可以写成 ℃。
2.把圆柱的直径扩大到原来的5倍,高不变,侧面积扩大到原来的 倍。
3.为适应“绿色、节能、低碳和环保”的要求,某工厂对生产设备进行了升级。改进设备后,今年的产量是400万吨,比去年的产量提高了二成五,去年的产量是 万吨。
4.8吨7千克= 吨;
2小时40分= 小时;
公顷= 平方米。
5.电话手表里的一个芯片长1.2cm,画在比例尺是10:1的设计图纸上长 cm。
6. :24=0.25= % 折= (填成数)。
7.用数学的眼光看成语“立竿见影”是应用了比例的相关知识,即同一时间,同一地点,杆高和影长成 (填“正”或“反”)比例。如果某一时刻一根竹竿高4米,影长2.6米,那么身高1.4米的明明同学在同一时刻,同一地点的影长是 米。
8.我们学过的数都可以看成是若干个计数单位组成的。如8.05可以看成是805个 组成的;一个数由39个亿、5个百万、3个百组成,这个数是 ;分母是9的最大真分数可以看成是 个 组成的。
9.如图所示是一个空心圆锥和一个空心圆柱组成的容器。在容器内倒入一些细沙,如果将这个容器上面封住并倒立,细沙的高度是 cm。
10.图中每个正方体的棱长是a。
11.一辆客车和一辆货车同时从甲、乙两地相向而行,客车到达中点,货车离中点还有50千米,已知客车和货车的速度比是3:2,甲、乙两地相距 千米。
12.一个盒子里装有红、黄、蓝、黑、绿共5种颜色的玻璃球各12颗,从盒子里至少摸出 颗玻璃球,才能保证一定有两颗同色;至少摸出 颗,才能保证有两种颜色。
13.某校六年级举行了研学实践活动,共用时8小时。其中路上用时与休息时间的比是2:3,参观时间与休息时间的比是4:3,路上用时比参观时间少 %。
二、选择。(10个知识点)
14.(3分)如所示四幅图,每幅图都有一个小图形和一个大图形。下面描述不正确的是( )
A.每幅图中,大图形都是由小图形累加得到。
B.每幅图中,小图形都可以用来测量大图形。
C.大图形里包含几个小图形,测量的结果就是几。
D.每幅图中,大图形都是由9个小图形组成。
15.(3分)我国乒乓球队在各个比赛中屡战屡胜。按照国际乒联的规定,标准的乒乓球质量为2.7g。如果把质量为2.73g的乒乓球记作+0.03g,那么下面三个乒乓球中,最轻的记作( )
A.﹣0.08g B.﹣0.05g C.+0.05g D.+0.08g
16.(3分)乐乐把2000元压岁钱存银行,定期二年,年利率是1.05%。到期时,可得利息多少元?以下列式正确的是( )
A.2000×1.05% B.2000+2000×1.05%
C.2000×1.05%×2 D.2000+2000×1.05%×2
17.(3分)如图所示是正方体的表面展开图,相对面上的两个数互为倒数。a表示的数是( )
A.1 B.6 C. D.
18.(3分)一个圆形花坛的半径为4m,画在比例尺为1:200的图纸上,图上面积为( )cm2。
A.200.96 B.12.56 C.1256 D.2512
19.(3分)一项工程,甲队单独要8天完成,乙队单独要6天完成,甲队的工作效率比乙队慢( )
A. B. C. D.
20.(3分)如图图象表示的是( )之间的关系。
A.正方体的表面积与它的棱长
B.一个人的身高与他的年龄
C.全班人数一定,出勤人数与缺勤人数
D.铅笔的单价一定,铅笔的数量与总价
21.(3分)如图所示表示的是圆柱体积公式推导过程,下面说法错误的是( )
A.运用了“转化”思想。
B.长方体的底面积等于圆柱的侧面积。
C.两者体积相等。
D.长方体的高等于圆柱的高。
22.(3分)体育运动中蕴含着许多数学知识。方方收集相关资料得出以下说法,其中不正确的是( )
A.测立定跳远成绩,应用了垂直的特征。
B.比赛中的比分,应用了“两个数的比表示两个数相除”的知识。
C.抛硬币确定谁先开球,应用了可能性的知识。
D.篮球比赛中,球员的“投篮命中率”,应用了求百分率的知识。
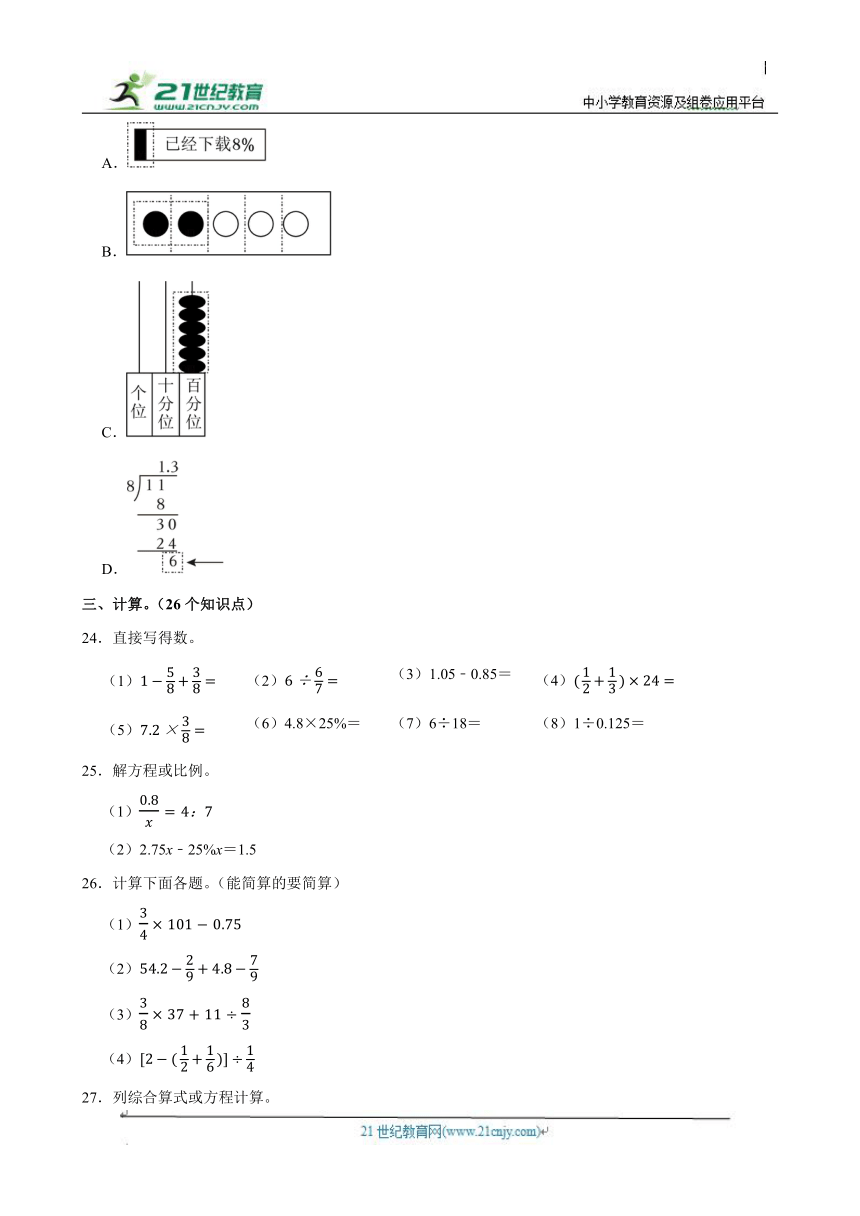
23.(3分)乐乐整理了下面的图和算式,其中画虚线框的部分表示0.6的是( )
A.
B.
C.
D.
三、计算。(26个知识点)
24.直接写得数。
(1) (2) (3)1.05﹣0.85= (4)
(5) (6)4.8×25%= (7)6÷18= (8)1÷0.125=
25.解方程或比例。
(1)
(2)2.75x﹣25%x=1.5
26.计算下面各题。(能简算的要简算)
(1)
(2)
(3)
(4)
27.列综合算式或方程计算。
(1)一个数的是16,这个数的是多少?
(2)80比一个数多25%,这个数是多少?
四、做一做。(按要求做在答题纸相应题号的位置上)(17个知识点)
28.图中每个小方格边长表示1cm,请按要求做题。
(1)图形①的平行四边形沿高分成两部分,把其中的三角形向 平移 cm就转化成了长方形。
(2)画出将图形②的三角形绕点A顺时针旋转90°后的图形。旋转后点B和C对应的位置用数对表示分别是( , )和( , )。
(3)画出图形③关于对称轴对称的另一半,使它成为轴对称图形,它的面积是 cm2。
(4)以图形④的点O为圆心,画出这个圆按2:1放大后的图形。两个圆组成的圆环部分的面积是 cm2。
29.为推动文旅产业数字化转型,某旅游公司在济宁曲阜三孔景区开展游客调研,通过随机抽样的方式,了解游客对不同沉浸式文旅体验项目的偏好,并绘制了如下不完整的条形统计图和扇形统计图。
A.《尼山圣境》沉浸式演艺;
B.《孔庙奇妙夜》数字光影秀;
C.《运河记忆》水幕沉浸式体验;
D.《微山湖上》沉浸式游船演艺;
E.《兴隆迷踪》实景沉浸式剧场;
请根据以上信息,解答下列问题。
(1)本次参与调查的游客共 名。
(2)请将条形统计图补充完整。
(3)在扇形统计图中,E所在的圆心角是 °。
(4)如果该天游客8000人,请你估计对“D.《微山湖上》沉浸式游船演艺”感兴趣的有多少人。(列式计算)
五、解决问题。(写在答题纸相应题号的位置上)(共20个知识点)
30.为响应“体重管理年”,小明制定跑步减肥计划。第一个月他完成计划总里程的,第二个月跑了123千米,此时已跑里程与未跑里程的比是5:1。他制定的跑步计划总里程是多少千米?
31.学校开展“科技知识拓展月”活动,鼓励同学们阅读科技类书籍来丰富知识储备。小林和小芳挑选了同一种科技书进行阅读。两天后,小林已经看了全书的,小芳看了全书的20%,小芳正好看了60页。小林第三天应该从第几页开始看?
32.根据题意选择合适的策略并解答。
①画图;
②列方程;
③列表;
④假设。
毕业典礼快到了,六(2)班同学准备制作装饰花环,22名同学一共制作了76个花环。女生每人制作3个花环,男生每人制作4个花环,制作花环的男生和女生各有多少人?我选择 策略解答。(填序号)解答过程:
33.一个底面半径为10厘米的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到7厘米(如图所示)。这个圆锥形铁块的体积是多少?
2025年山东省济宁市兖州区小升初数学试卷
参考答案与试题解析
一.选择题(共10小题)
题号 14 15 16 17 18 19 20 21 22 23
答案 D A C B B C D B B D
一、填空。(把要填的内容写在相应题号的横线上)(27个知识点)
1.兖州区的面积约是五百三十五点一平方千米,写作 535.1 平方千米,人口约540700人(第七次人口普查),改写成用“万”为单位的数是 54.07万 人。2025年1月,兖州最低气温是零下10摄氏度,可以写成 ﹣10 ℃。
【解答】解:兖州区的面积约是五百三十五点一平方千米,写作:535.1平方千米,人口约540700人(第七次人口普查),改写成用“万”为单位的数是54.07万人。2025年1月,兖州最低气温是零下10摄氏度,可以写成﹣10℃。
故答案为:535.1,54.07万,﹣10。
2.把圆柱的直径扩大到原来的5倍,高不变,侧面积扩大到原来的 5 倍。
【解答】解:因为圆柱的侧面积=底面的周长×高,把圆柱的直径扩大到原来的5倍,底面周长扩大原来的5倍,高不变,侧面积扩大到原来的5倍。
故答案为:5。
3.为适应“绿色、节能、低碳和环保”的要求,某工厂对生产设备进行了升级。改进设备后,今年的产量是400万吨,比去年的产量提高了二成五,去年的产量是 320 万吨。
【解答】解:400÷(1+25%)
=400÷1.25
=320(万吨)
答:去年的产量是320万吨。
故答案为:320。
4.8吨7千克= 8.007 吨;
2小时40分= 2 小时;
公顷= 7500 平方米。
【解答】解:8吨7千克=8.007吨;
2小时40分=2小时;
公顷=7500平方米。
故答案为:8.007;2;7500。
5.电话手表里的一个芯片长1.2cm,画在比例尺是10:1的设计图纸上长 12 cm。
【解答】解:1.2×10=12(cm)
答:画在比例尺是10:1的设计图纸上长12cm。
故答案为:12。
6. 6 :24=0.25= 25 % 二五 折= 二成五 (填成数)。
【解答】解:6:24=0.25=25%二五折=二成五
故答案为:6;25;12;二五;二成五。
7.用数学的眼光看成语“立竿见影”是应用了比例的相关知识,即同一时间,同一地点,杆高和影长成 正 (填“正”或“反”)比例。如果某一时刻一根竹竿高4米,影长2.6米,那么身高1.4米的明明同学在同一时刻,同一地点的影长是 0.91 米。
【解答】解:设同一时刻,同一地点明明同学的影厂是x米。
1.4:x=4:2.6
4x=1.4×2.6
4x=3.64
x=0.91
答:同一时间,同一地点,杆高和影长成正比例;身高1.4米的明明同学在同一时刻,同一地点的影长是0.91米。
故答案为:正,0.91。
8.我们学过的数都可以看成是若干个计数单位组成的。如8.05可以看成是805个 0.01 组成的;一个数由39个亿、5个百万、3个百组成,这个数是 3905000300 ;分母是9的最大真分数可以看成是 8 个 组成的。
【解答】解:我们学过的数都可以看成是若干个计数单位组成的。如8.05可以看成是805个0.01组成的;一个数由39个亿、5个百万、3个百组成,这个数是3905000300;分母是9的最大真分数是,可以看成是8个组成的。
故答案为:0.01;3905000300;8,。
9.如图所示是一个空心圆锥和一个空心圆柱组成的容器。在容器内倒入一些细沙,如果将这个容器上面封住并倒立,细沙的高度是 6 cm。
【解答】解:3+9
=3+3
=6(厘米)
答:细沙的高度是6厘米。
故答案为:6。
10.图中每个正方体的棱长是a。
【解答】解:(2+3×4)a2=14a2
(2+50×4)a2=202a2
11.一辆客车和一辆货车同时从甲、乙两地相向而行,客车到达中点,货车离中点还有50千米,已知客车和货车的速度比是3:2,甲、乙两地相距 300 千米。
【解答】解:50÷(3﹣2)×(3+2)+50
=250+50
=300(千米)
答:甲、乙两地相距300千米。
故答案为:300。
12.一个盒子里装有红、黄、蓝、黑、绿共5种颜色的玻璃球各12颗,从盒子里至少摸出 6 颗玻璃球,才能保证一定有两颗同色;至少摸出 13 颗,才能保证有两种颜色。
【解答】解:最坏情况分析:盒中有5种颜色,若每次摸出的颜色均不同,则最多摸出5颗(每种颜色各1颗)。再摸第6颗时,无论颜色如何,必然与之前摸出的颜色重复。
5+1=6(颗)
假设盒中某一种颜色有12颗,若前12颗均摸出同一种颜色(如红色),此时仍只有一种颜色。再摸第13颗时,由于红色已摸完,必然摸出其它颜色。
12+1=13(颗)
所以,一个盒子里装有红、黄、蓝、黑、绿共5种颜色的玻璃球各12颗,从盒子里至少摸出6颗玻璃球,才能保证一定有两颗同色;至少摸出13颗,才能保证有两种颜色。
故答案为:6;13。
13.某校六年级举行了研学实践活动,共用时8小时。其中路上用时与休息时间的比是2:3,参观时间与休息时间的比是4:3,路上用时比参观时间少 50 %。
【解答】解:(4﹣2)÷4
=2÷4
=50%
答:路上用时比参观时间少50%。
故答案为:50。
二、选择。(10个知识点)
14.(3分)如所示四幅图,每幅图都有一个小图形和一个大图形。下面描述不正确的是( )
A.每幅图中,大图形都是由小图形累加得到。
B.每幅图中,小图形都可以用来测量大图形。
C.大图形里包含几个小图形,测量的结果就是几。
D.每幅图中,大图形都是由9个小图形组成。
【解答】解:如所示四幅图,每幅图都有一个小图形和一个大图形。描述不正确的是每幅图中,大图形都是由9个小图形组成。
故选:D。
15.(3分)我国乒乓球队在各个比赛中屡战屡胜。按照国际乒联的规定,标准的乒乓球质量为2.7g。如果把质量为2.73g的乒乓球记作+0.03g,那么下面三个乒乓球中,最轻的记作( )
A.﹣0.08g B.﹣0.05g C.+0.05g D.+0.08g
【解答】解:﹣0.08<﹣0.05
最轻的记作﹣0.08。
故选:A。
16.(3分)乐乐把2000元压岁钱存银行,定期二年,年利率是1.05%。到期时,可得利息多少元?以下列式正确的是( )
A.2000×1.05% B.2000+2000×1.05%
C.2000×1.05%×2 D.2000+2000×1.05%×2
【解答】解:2000×1.05%×2
故选:C。
17.(3分)如图所示是正方体的表面展开图,相对面上的两个数互为倒数。a表示的数是( )
A.1 B.6 C. D.
【解答】解:由正方体的表面展开图可得,与a相对,则a=1,因此a表示的数是6。
故选:B。
18.(3分)一个圆形花坛的半径为4m,画在比例尺为1:200的图纸上,图上面积为( )cm2。
A.200.96 B.12.56 C.1256 D.2512
【解答】解:4米=400厘米
4002(厘米)
3.14×2×2=12.56(平方厘米)
答:图上面积为12.56cm2。
故选:B。
19.(3分)一项工程,甲队单独要8天完成,乙队单独要6天完成,甲队的工作效率比乙队慢( )
A. B. C. D.
【解答】解:
答:甲队的工作效率比乙队慢。
故选:C。
20.(3分)如图图象表示的是( )之间的关系。
A.正方体的表面积与它的棱长
B.一个人的身高与他的年龄
C.全班人数一定,出勤人数与缺勤人数
D.铅笔的单价一定,铅笔的数量与总价
【解答】解:A.正方体的表面积÷棱长的平方=6(一定),商一定,所以正方体的表面积与它的棱长的平方成正比例,但与它的棱长不成正比例;
B.一个人的身高与他的年龄不成正比例,通常在生长期,人的身高是随着年龄的增长而增长,但是生长期过了后,骨膜会闭合,停止长高;
C.出勤人数+缺勤人数=全班人数(一定),和一定,所以出勤人数与缺勤人数不成比例;
D.总价÷数量=单价(一定),商一定,所以铅笔的数量与总价成正比例。
故选:D。
21.(3分)如图所示表示的是圆柱体积公式推导过程,下面说法错误的是( )
A.运用了“转化”思想。
B.长方体的底面积等于圆柱的侧面积。
C.两者体积相等。
D.长方体的高等于圆柱的高。
【解答】解:把圆柱转化为长方体,利用了转化思想,圆柱的体积与长方体的体积相等;长方体的高就是圆柱的高。
故选:B。
22.(3分)体育运动中蕴含着许多数学知识。方方收集相关资料得出以下说法,其中不正确的是( )
A.测立定跳远成绩,应用了垂直的特征。
B.比赛中的比分,应用了“两个数的比表示两个数相除”的知识。
C.抛硬币确定谁先开球,应用了可能性的知识。
D.篮球比赛中,球员的“投篮命中率”,应用了求百分率的知识。
【解答】解:A.测立定跳远成绩,应用了垂直的特征。本选项说法正确。
B.比赛中的比分,表示比分,不是相除关系,不是比,所以本选项说法错误。
C.抛硬币确定谁先开球,应用了可能性的知识。本选项说法正确。
D.篮球比赛中,球员的“投篮命中率”,应用了求百分率的知识。本选项说法正确。
故选:B。
23.(3分)乐乐整理了下面的图和算式,其中画虚线框的部分表示0.6的是( )
A.
B.
C.
D.
【解答】解:画虚线框的部分表示0.6的是。
故选:D。
三、计算。(26个知识点)
24.直接写得数。
(1) (2) (3)1.05﹣0.85= (4)
(5) (6)4.8×25%= (7)6÷18= (8)1÷0.125=
【解答】解:
(1) (2)7 (3)1.05﹣0.85=0.2 (4)20
(5)2.7 (6)4.8×25%=1.2 (7)6÷18 (8)1÷0.125=8
25.解方程或比例。
(1)
(2)2.75x﹣25%x=1.5
【解答】解:(1)4:7
4x=5.6
x=5.6÷4
x=1.4
(2)2.75x﹣25%x=1.5
2.5x=1.5
x=1.5÷2.5
x=0.6
26.计算下面各题。(能简算的要简算)
(1)
(2)
(3)
(4)
【解答】解:(1)
=75
(2)
=59﹣1
=58
(3)
=18
(4)
27.列综合算式或方程计算。
(1)一个数的是16,这个数的是多少?
(2)80比一个数多25%,这个数是多少?
【解答】解:(1)16
=24
=18
答:这个数的是18。
(2)80÷(1+25%)
=80÷1.25
=64
答:这个数是64。
四、做一做。(按要求做在答题纸相应题号的位置上)(17个知识点)
28.图中每个小方格边长表示1cm,请按要求做题。
(1)图形①的平行四边形沿高分成两部分,把其中的三角形向 右 平移 7 cm就转化成了长方形。
(2)画出将图形②的三角形绕点A顺时针旋转90°后的图形。旋转后点B和C对应的位置用数对表示分别是( 16 , 4 )和( 18 , 7 )。
(3)画出图形③关于对称轴对称的另一半,使它成为轴对称图形,它的面积是 10 cm2。
(4)以图形④的点O为圆心,画出这个圆按2:1放大后的图形。两个圆组成的圆环部分的面积是 9.42 cm2。
【解答】解:(1)图形①的平行四边形沿高分成两部分,把其中的三角形向右平移7cm就转化成了长方形。
(2)(3)(4)如图所示:
。
(2)旋转后点B和C对应的位置用数对表示分别是(16,4)和(18,7)。
(3)(4+6)×2÷2=10(平方厘米)
答:它的面积是10cm2。
(4)2×2×3.14﹣1×1×3.14
=12.56﹣3.14
=9.42(平方厘米)
答:两个圆组成的圆环部分的面积是9.42cm2。
故答案为:右,7;16,4,18,7;10;9.42。
29.为推动文旅产业数字化转型,某旅游公司在济宁曲阜三孔景区开展游客调研,通过随机抽样的方式,了解游客对不同沉浸式文旅体验项目的偏好,并绘制了如下不完整的条形统计图和扇形统计图。
A.《尼山圣境》沉浸式演艺;
B.《孔庙奇妙夜》数字光影秀;
C.《运河记忆》水幕沉浸式体验;
D.《微山湖上》沉浸式游船演艺;
E.《兴隆迷踪》实景沉浸式剧场;
请根据以上信息,解答下列问题。
(1)本次参与调查的游客共 80 名。
(2)请将条形统计图补充完整。
(3)在扇形统计图中,E所在的圆心角是 90 °。
(4)如果该天游客8000人,请你估计对“D.《微山湖上》沉浸式游船演艺”感兴趣的有多少人。(列式计算)
【解答】解:(1)16÷20%=80(名)
答:本次参与调查的游客共80名。
(2)80﹣16﹣13﹣14﹣20=
14÷80×100%=17(名)
条形统计图如下:
(3)20÷80×360°
=0.25×360°
=90°
答:E所在的圆心角是90°。
(4)8000÷80×17
=100×17
=1700(人)
答:如果该天游客8000人,对“D.《微山湖上》沉浸式游船演艺”感兴趣的有1700人。
故答案为:80;90。
五、解决问题。(写在答题纸相应题号的位置上)(共20个知识点)
30.为响应“体重管理年”,小明制定跑步减肥计划。第一个月他完成计划总里程的,第二个月跑了123千米,此时已跑里程与未跑里程的比是5:1。他制定的跑步计划总里程是多少千米?
【解答】解:123÷()
=123÷()
=123
=246(千米)
答:他制定的跑步计划总里程是246千米。
31.学校开展“科技知识拓展月”活动,鼓励同学们阅读科技类书籍来丰富知识储备。小林和小芳挑选了同一种科技书进行阅读。两天后,小林已经看了全书的,小芳看了全书的20%,小芳正好看了60页。小林第三天应该从第几页开始看?
【解答】解:60÷20%1
=3001
=75+1
=76(页)
答:小林第三天应该从第76页开始看。
32.根据题意选择合适的策略并解答。
①画图;
②列方程;
③列表;
④假设。
毕业典礼快到了,六(2)班同学准备制作装饰花环,22名同学一共制作了76个花环。女生每人制作3个花环,男生每人制作4个花环,制作花环的男生和女生各有多少人?我选择 ④ 策略解答。(填序号)解答过程:
【解答】解:选择④策略解答。
女生人数为:
(22×4﹣76)÷(4﹣3)
=12÷1
=12(人)
男生人数为:22﹣12=10(人)
答:男生有10人,女生有12人。
故答案为:④。
33.一个底面半径为10厘米的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到7厘米(如图所示)。这个圆锥形铁块的体积是多少?
【解答】解:3.14×10×10×(7﹣3)
=314×4
=1256(立方厘米)
1256÷(1+3)
=1256÷4
=314(立方厘米)
答:这个圆锥形铁块的体积是314立方厘米。
一、填空。(把要填的内容写在相应题号的横线上)(27个知识点)
1.兖州区的面积约是五百三十五点一平方千米,写作 平方千米,人口约540700人(第七次人口普查),改写成用“万”为单位的数是 人。2025年1月,兖州最低气温是零下10摄氏度,可以写成 ℃。
2.把圆柱的直径扩大到原来的5倍,高不变,侧面积扩大到原来的 倍。
3.为适应“绿色、节能、低碳和环保”的要求,某工厂对生产设备进行了升级。改进设备后,今年的产量是400万吨,比去年的产量提高了二成五,去年的产量是 万吨。
4.8吨7千克= 吨;
2小时40分= 小时;
公顷= 平方米。
5.电话手表里的一个芯片长1.2cm,画在比例尺是10:1的设计图纸上长 cm。
6. :24=0.25= % 折= (填成数)。
7.用数学的眼光看成语“立竿见影”是应用了比例的相关知识,即同一时间,同一地点,杆高和影长成 (填“正”或“反”)比例。如果某一时刻一根竹竿高4米,影长2.6米,那么身高1.4米的明明同学在同一时刻,同一地点的影长是 米。
8.我们学过的数都可以看成是若干个计数单位组成的。如8.05可以看成是805个 组成的;一个数由39个亿、5个百万、3个百组成,这个数是 ;分母是9的最大真分数可以看成是 个 组成的。
9.如图所示是一个空心圆锥和一个空心圆柱组成的容器。在容器内倒入一些细沙,如果将这个容器上面封住并倒立,细沙的高度是 cm。
10.图中每个正方体的棱长是a。
11.一辆客车和一辆货车同时从甲、乙两地相向而行,客车到达中点,货车离中点还有50千米,已知客车和货车的速度比是3:2,甲、乙两地相距 千米。
12.一个盒子里装有红、黄、蓝、黑、绿共5种颜色的玻璃球各12颗,从盒子里至少摸出 颗玻璃球,才能保证一定有两颗同色;至少摸出 颗,才能保证有两种颜色。
13.某校六年级举行了研学实践活动,共用时8小时。其中路上用时与休息时间的比是2:3,参观时间与休息时间的比是4:3,路上用时比参观时间少 %。
二、选择。(10个知识点)
14.(3分)如所示四幅图,每幅图都有一个小图形和一个大图形。下面描述不正确的是( )
A.每幅图中,大图形都是由小图形累加得到。
B.每幅图中,小图形都可以用来测量大图形。
C.大图形里包含几个小图形,测量的结果就是几。
D.每幅图中,大图形都是由9个小图形组成。
15.(3分)我国乒乓球队在各个比赛中屡战屡胜。按照国际乒联的规定,标准的乒乓球质量为2.7g。如果把质量为2.73g的乒乓球记作+0.03g,那么下面三个乒乓球中,最轻的记作( )
A.﹣0.08g B.﹣0.05g C.+0.05g D.+0.08g
16.(3分)乐乐把2000元压岁钱存银行,定期二年,年利率是1.05%。到期时,可得利息多少元?以下列式正确的是( )
A.2000×1.05% B.2000+2000×1.05%
C.2000×1.05%×2 D.2000+2000×1.05%×2
17.(3分)如图所示是正方体的表面展开图,相对面上的两个数互为倒数。a表示的数是( )
A.1 B.6 C. D.
18.(3分)一个圆形花坛的半径为4m,画在比例尺为1:200的图纸上,图上面积为( )cm2。
A.200.96 B.12.56 C.1256 D.2512
19.(3分)一项工程,甲队单独要8天完成,乙队单独要6天完成,甲队的工作效率比乙队慢( )
A. B. C. D.
20.(3分)如图图象表示的是( )之间的关系。
A.正方体的表面积与它的棱长
B.一个人的身高与他的年龄
C.全班人数一定,出勤人数与缺勤人数
D.铅笔的单价一定,铅笔的数量与总价
21.(3分)如图所示表示的是圆柱体积公式推导过程,下面说法错误的是( )
A.运用了“转化”思想。
B.长方体的底面积等于圆柱的侧面积。
C.两者体积相等。
D.长方体的高等于圆柱的高。
22.(3分)体育运动中蕴含着许多数学知识。方方收集相关资料得出以下说法,其中不正确的是( )
A.测立定跳远成绩,应用了垂直的特征。
B.比赛中的比分,应用了“两个数的比表示两个数相除”的知识。
C.抛硬币确定谁先开球,应用了可能性的知识。
D.篮球比赛中,球员的“投篮命中率”,应用了求百分率的知识。
23.(3分)乐乐整理了下面的图和算式,其中画虚线框的部分表示0.6的是( )
A.
B.
C.
D.
三、计算。(26个知识点)
24.直接写得数。
(1) (2) (3)1.05﹣0.85= (4)
(5) (6)4.8×25%= (7)6÷18= (8)1÷0.125=
25.解方程或比例。
(1)
(2)2.75x﹣25%x=1.5
26.计算下面各题。(能简算的要简算)
(1)
(2)
(3)
(4)
27.列综合算式或方程计算。
(1)一个数的是16,这个数的是多少?
(2)80比一个数多25%,这个数是多少?
四、做一做。(按要求做在答题纸相应题号的位置上)(17个知识点)
28.图中每个小方格边长表示1cm,请按要求做题。
(1)图形①的平行四边形沿高分成两部分,把其中的三角形向 平移 cm就转化成了长方形。
(2)画出将图形②的三角形绕点A顺时针旋转90°后的图形。旋转后点B和C对应的位置用数对表示分别是( , )和( , )。
(3)画出图形③关于对称轴对称的另一半,使它成为轴对称图形,它的面积是 cm2。
(4)以图形④的点O为圆心,画出这个圆按2:1放大后的图形。两个圆组成的圆环部分的面积是 cm2。
29.为推动文旅产业数字化转型,某旅游公司在济宁曲阜三孔景区开展游客调研,通过随机抽样的方式,了解游客对不同沉浸式文旅体验项目的偏好,并绘制了如下不完整的条形统计图和扇形统计图。
A.《尼山圣境》沉浸式演艺;
B.《孔庙奇妙夜》数字光影秀;
C.《运河记忆》水幕沉浸式体验;
D.《微山湖上》沉浸式游船演艺;
E.《兴隆迷踪》实景沉浸式剧场;
请根据以上信息,解答下列问题。
(1)本次参与调查的游客共 名。
(2)请将条形统计图补充完整。
(3)在扇形统计图中,E所在的圆心角是 °。
(4)如果该天游客8000人,请你估计对“D.《微山湖上》沉浸式游船演艺”感兴趣的有多少人。(列式计算)
五、解决问题。(写在答题纸相应题号的位置上)(共20个知识点)
30.为响应“体重管理年”,小明制定跑步减肥计划。第一个月他完成计划总里程的,第二个月跑了123千米,此时已跑里程与未跑里程的比是5:1。他制定的跑步计划总里程是多少千米?
31.学校开展“科技知识拓展月”活动,鼓励同学们阅读科技类书籍来丰富知识储备。小林和小芳挑选了同一种科技书进行阅读。两天后,小林已经看了全书的,小芳看了全书的20%,小芳正好看了60页。小林第三天应该从第几页开始看?
32.根据题意选择合适的策略并解答。
①画图;
②列方程;
③列表;
④假设。
毕业典礼快到了,六(2)班同学准备制作装饰花环,22名同学一共制作了76个花环。女生每人制作3个花环,男生每人制作4个花环,制作花环的男生和女生各有多少人?我选择 策略解答。(填序号)解答过程:
33.一个底面半径为10厘米的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到7厘米(如图所示)。这个圆锥形铁块的体积是多少?
2025年山东省济宁市兖州区小升初数学试卷
参考答案与试题解析
一.选择题(共10小题)
题号 14 15 16 17 18 19 20 21 22 23
答案 D A C B B C D B B D
一、填空。(把要填的内容写在相应题号的横线上)(27个知识点)
1.兖州区的面积约是五百三十五点一平方千米,写作 535.1 平方千米,人口约540700人(第七次人口普查),改写成用“万”为单位的数是 54.07万 人。2025年1月,兖州最低气温是零下10摄氏度,可以写成 ﹣10 ℃。
【解答】解:兖州区的面积约是五百三十五点一平方千米,写作:535.1平方千米,人口约540700人(第七次人口普查),改写成用“万”为单位的数是54.07万人。2025年1月,兖州最低气温是零下10摄氏度,可以写成﹣10℃。
故答案为:535.1,54.07万,﹣10。
2.把圆柱的直径扩大到原来的5倍,高不变,侧面积扩大到原来的 5 倍。
【解答】解:因为圆柱的侧面积=底面的周长×高,把圆柱的直径扩大到原来的5倍,底面周长扩大原来的5倍,高不变,侧面积扩大到原来的5倍。
故答案为:5。
3.为适应“绿色、节能、低碳和环保”的要求,某工厂对生产设备进行了升级。改进设备后,今年的产量是400万吨,比去年的产量提高了二成五,去年的产量是 320 万吨。
【解答】解:400÷(1+25%)
=400÷1.25
=320(万吨)
答:去年的产量是320万吨。
故答案为:320。
4.8吨7千克= 8.007 吨;
2小时40分= 2 小时;
公顷= 7500 平方米。
【解答】解:8吨7千克=8.007吨;
2小时40分=2小时;
公顷=7500平方米。
故答案为:8.007;2;7500。
5.电话手表里的一个芯片长1.2cm,画在比例尺是10:1的设计图纸上长 12 cm。
【解答】解:1.2×10=12(cm)
答:画在比例尺是10:1的设计图纸上长12cm。
故答案为:12。
6. 6 :24=0.25= 25 % 二五 折= 二成五 (填成数)。
【解答】解:6:24=0.25=25%二五折=二成五
故答案为:6;25;12;二五;二成五。
7.用数学的眼光看成语“立竿见影”是应用了比例的相关知识,即同一时间,同一地点,杆高和影长成 正 (填“正”或“反”)比例。如果某一时刻一根竹竿高4米,影长2.6米,那么身高1.4米的明明同学在同一时刻,同一地点的影长是 0.91 米。
【解答】解:设同一时刻,同一地点明明同学的影厂是x米。
1.4:x=4:2.6
4x=1.4×2.6
4x=3.64
x=0.91
答:同一时间,同一地点,杆高和影长成正比例;身高1.4米的明明同学在同一时刻,同一地点的影长是0.91米。
故答案为:正,0.91。
8.我们学过的数都可以看成是若干个计数单位组成的。如8.05可以看成是805个 0.01 组成的;一个数由39个亿、5个百万、3个百组成,这个数是 3905000300 ;分母是9的最大真分数可以看成是 8 个 组成的。
【解答】解:我们学过的数都可以看成是若干个计数单位组成的。如8.05可以看成是805个0.01组成的;一个数由39个亿、5个百万、3个百组成,这个数是3905000300;分母是9的最大真分数是,可以看成是8个组成的。
故答案为:0.01;3905000300;8,。
9.如图所示是一个空心圆锥和一个空心圆柱组成的容器。在容器内倒入一些细沙,如果将这个容器上面封住并倒立,细沙的高度是 6 cm。
【解答】解:3+9
=3+3
=6(厘米)
答:细沙的高度是6厘米。
故答案为:6。
10.图中每个正方体的棱长是a。
【解答】解:(2+3×4)a2=14a2
(2+50×4)a2=202a2
11.一辆客车和一辆货车同时从甲、乙两地相向而行,客车到达中点,货车离中点还有50千米,已知客车和货车的速度比是3:2,甲、乙两地相距 300 千米。
【解答】解:50÷(3﹣2)×(3+2)+50
=250+50
=300(千米)
答:甲、乙两地相距300千米。
故答案为:300。
12.一个盒子里装有红、黄、蓝、黑、绿共5种颜色的玻璃球各12颗,从盒子里至少摸出 6 颗玻璃球,才能保证一定有两颗同色;至少摸出 13 颗,才能保证有两种颜色。
【解答】解:最坏情况分析:盒中有5种颜色,若每次摸出的颜色均不同,则最多摸出5颗(每种颜色各1颗)。再摸第6颗时,无论颜色如何,必然与之前摸出的颜色重复。
5+1=6(颗)
假设盒中某一种颜色有12颗,若前12颗均摸出同一种颜色(如红色),此时仍只有一种颜色。再摸第13颗时,由于红色已摸完,必然摸出其它颜色。
12+1=13(颗)
所以,一个盒子里装有红、黄、蓝、黑、绿共5种颜色的玻璃球各12颗,从盒子里至少摸出6颗玻璃球,才能保证一定有两颗同色;至少摸出13颗,才能保证有两种颜色。
故答案为:6;13。
13.某校六年级举行了研学实践活动,共用时8小时。其中路上用时与休息时间的比是2:3,参观时间与休息时间的比是4:3,路上用时比参观时间少 50 %。
【解答】解:(4﹣2)÷4
=2÷4
=50%
答:路上用时比参观时间少50%。
故答案为:50。
二、选择。(10个知识点)
14.(3分)如所示四幅图,每幅图都有一个小图形和一个大图形。下面描述不正确的是( )
A.每幅图中,大图形都是由小图形累加得到。
B.每幅图中,小图形都可以用来测量大图形。
C.大图形里包含几个小图形,测量的结果就是几。
D.每幅图中,大图形都是由9个小图形组成。
【解答】解:如所示四幅图,每幅图都有一个小图形和一个大图形。描述不正确的是每幅图中,大图形都是由9个小图形组成。
故选:D。
15.(3分)我国乒乓球队在各个比赛中屡战屡胜。按照国际乒联的规定,标准的乒乓球质量为2.7g。如果把质量为2.73g的乒乓球记作+0.03g,那么下面三个乒乓球中,最轻的记作( )
A.﹣0.08g B.﹣0.05g C.+0.05g D.+0.08g
【解答】解:﹣0.08<﹣0.05
最轻的记作﹣0.08。
故选:A。
16.(3分)乐乐把2000元压岁钱存银行,定期二年,年利率是1.05%。到期时,可得利息多少元?以下列式正确的是( )
A.2000×1.05% B.2000+2000×1.05%
C.2000×1.05%×2 D.2000+2000×1.05%×2
【解答】解:2000×1.05%×2
故选:C。
17.(3分)如图所示是正方体的表面展开图,相对面上的两个数互为倒数。a表示的数是( )
A.1 B.6 C. D.
【解答】解:由正方体的表面展开图可得,与a相对,则a=1,因此a表示的数是6。
故选:B。
18.(3分)一个圆形花坛的半径为4m,画在比例尺为1:200的图纸上,图上面积为( )cm2。
A.200.96 B.12.56 C.1256 D.2512
【解答】解:4米=400厘米
4002(厘米)
3.14×2×2=12.56(平方厘米)
答:图上面积为12.56cm2。
故选:B。
19.(3分)一项工程,甲队单独要8天完成,乙队单独要6天完成,甲队的工作效率比乙队慢( )
A. B. C. D.
【解答】解:
答:甲队的工作效率比乙队慢。
故选:C。
20.(3分)如图图象表示的是( )之间的关系。
A.正方体的表面积与它的棱长
B.一个人的身高与他的年龄
C.全班人数一定,出勤人数与缺勤人数
D.铅笔的单价一定,铅笔的数量与总价
【解答】解:A.正方体的表面积÷棱长的平方=6(一定),商一定,所以正方体的表面积与它的棱长的平方成正比例,但与它的棱长不成正比例;
B.一个人的身高与他的年龄不成正比例,通常在生长期,人的身高是随着年龄的增长而增长,但是生长期过了后,骨膜会闭合,停止长高;
C.出勤人数+缺勤人数=全班人数(一定),和一定,所以出勤人数与缺勤人数不成比例;
D.总价÷数量=单价(一定),商一定,所以铅笔的数量与总价成正比例。
故选:D。
21.(3分)如图所示表示的是圆柱体积公式推导过程,下面说法错误的是( )
A.运用了“转化”思想。
B.长方体的底面积等于圆柱的侧面积。
C.两者体积相等。
D.长方体的高等于圆柱的高。
【解答】解:把圆柱转化为长方体,利用了转化思想,圆柱的体积与长方体的体积相等;长方体的高就是圆柱的高。
故选:B。
22.(3分)体育运动中蕴含着许多数学知识。方方收集相关资料得出以下说法,其中不正确的是( )
A.测立定跳远成绩,应用了垂直的特征。
B.比赛中的比分,应用了“两个数的比表示两个数相除”的知识。
C.抛硬币确定谁先开球,应用了可能性的知识。
D.篮球比赛中,球员的“投篮命中率”,应用了求百分率的知识。
【解答】解:A.测立定跳远成绩,应用了垂直的特征。本选项说法正确。
B.比赛中的比分,表示比分,不是相除关系,不是比,所以本选项说法错误。
C.抛硬币确定谁先开球,应用了可能性的知识。本选项说法正确。
D.篮球比赛中,球员的“投篮命中率”,应用了求百分率的知识。本选项说法正确。
故选:B。
23.(3分)乐乐整理了下面的图和算式,其中画虚线框的部分表示0.6的是( )
A.
B.
C.
D.
【解答】解:画虚线框的部分表示0.6的是。
故选:D。
三、计算。(26个知识点)
24.直接写得数。
(1) (2) (3)1.05﹣0.85= (4)
(5) (6)4.8×25%= (7)6÷18= (8)1÷0.125=
【解答】解:
(1) (2)7 (3)1.05﹣0.85=0.2 (4)20
(5)2.7 (6)4.8×25%=1.2 (7)6÷18 (8)1÷0.125=8
25.解方程或比例。
(1)
(2)2.75x﹣25%x=1.5
【解答】解:(1)4:7
4x=5.6
x=5.6÷4
x=1.4
(2)2.75x﹣25%x=1.5
2.5x=1.5
x=1.5÷2.5
x=0.6
26.计算下面各题。(能简算的要简算)
(1)
(2)
(3)
(4)
【解答】解:(1)
=75
(2)
=59﹣1
=58
(3)
=18
(4)
27.列综合算式或方程计算。
(1)一个数的是16,这个数的是多少?
(2)80比一个数多25%,这个数是多少?
【解答】解:(1)16
=24
=18
答:这个数的是18。
(2)80÷(1+25%)
=80÷1.25
=64
答:这个数是64。
四、做一做。(按要求做在答题纸相应题号的位置上)(17个知识点)
28.图中每个小方格边长表示1cm,请按要求做题。
(1)图形①的平行四边形沿高分成两部分,把其中的三角形向 右 平移 7 cm就转化成了长方形。
(2)画出将图形②的三角形绕点A顺时针旋转90°后的图形。旋转后点B和C对应的位置用数对表示分别是( 16 , 4 )和( 18 , 7 )。
(3)画出图形③关于对称轴对称的另一半,使它成为轴对称图形,它的面积是 10 cm2。
(4)以图形④的点O为圆心,画出这个圆按2:1放大后的图形。两个圆组成的圆环部分的面积是 9.42 cm2。
【解答】解:(1)图形①的平行四边形沿高分成两部分,把其中的三角形向右平移7cm就转化成了长方形。
(2)(3)(4)如图所示:
。
(2)旋转后点B和C对应的位置用数对表示分别是(16,4)和(18,7)。
(3)(4+6)×2÷2=10(平方厘米)
答:它的面积是10cm2。
(4)2×2×3.14﹣1×1×3.14
=12.56﹣3.14
=9.42(平方厘米)
答:两个圆组成的圆环部分的面积是9.42cm2。
故答案为:右,7;16,4,18,7;10;9.42。
29.为推动文旅产业数字化转型,某旅游公司在济宁曲阜三孔景区开展游客调研,通过随机抽样的方式,了解游客对不同沉浸式文旅体验项目的偏好,并绘制了如下不完整的条形统计图和扇形统计图。
A.《尼山圣境》沉浸式演艺;
B.《孔庙奇妙夜》数字光影秀;
C.《运河记忆》水幕沉浸式体验;
D.《微山湖上》沉浸式游船演艺;
E.《兴隆迷踪》实景沉浸式剧场;
请根据以上信息,解答下列问题。
(1)本次参与调查的游客共 80 名。
(2)请将条形统计图补充完整。
(3)在扇形统计图中,E所在的圆心角是 90 °。
(4)如果该天游客8000人,请你估计对“D.《微山湖上》沉浸式游船演艺”感兴趣的有多少人。(列式计算)
【解答】解:(1)16÷20%=80(名)
答:本次参与调查的游客共80名。
(2)80﹣16﹣13﹣14﹣20=
14÷80×100%=17(名)
条形统计图如下:
(3)20÷80×360°
=0.25×360°
=90°
答:E所在的圆心角是90°。
(4)8000÷80×17
=100×17
=1700(人)
答:如果该天游客8000人,对“D.《微山湖上》沉浸式游船演艺”感兴趣的有1700人。
故答案为:80;90。
五、解决问题。(写在答题纸相应题号的位置上)(共20个知识点)
30.为响应“体重管理年”,小明制定跑步减肥计划。第一个月他完成计划总里程的,第二个月跑了123千米,此时已跑里程与未跑里程的比是5:1。他制定的跑步计划总里程是多少千米?
【解答】解:123÷()
=123÷()
=123
=246(千米)
答:他制定的跑步计划总里程是246千米。
31.学校开展“科技知识拓展月”活动,鼓励同学们阅读科技类书籍来丰富知识储备。小林和小芳挑选了同一种科技书进行阅读。两天后,小林已经看了全书的,小芳看了全书的20%,小芳正好看了60页。小林第三天应该从第几页开始看?
【解答】解:60÷20%1
=3001
=75+1
=76(页)
答:小林第三天应该从第76页开始看。
32.根据题意选择合适的策略并解答。
①画图;
②列方程;
③列表;
④假设。
毕业典礼快到了,六(2)班同学准备制作装饰花环,22名同学一共制作了76个花环。女生每人制作3个花环,男生每人制作4个花环,制作花环的男生和女生各有多少人?我选择 ④ 策略解答。(填序号)解答过程:
【解答】解:选择④策略解答。
女生人数为:
(22×4﹣76)÷(4﹣3)
=12÷1
=12(人)
男生人数为:22﹣12=10(人)
答:男生有10人,女生有12人。
故答案为:④。
33.一个底面半径为10厘米的圆柱形容器,里面装有水。将等底等高的一个圆柱形铁块和一个圆锥形铁块同时放入这个容器中,水面上升到7厘米(如图所示)。这个圆锥形铁块的体积是多少?
【解答】解:3.14×10×10×(7﹣3)
=314×4
=1256(立方厘米)
1256÷(1+3)
=1256÷4
=314(立方厘米)
答:这个圆锥形铁块的体积是314立方厘米。
同课章节目录
