8.3 列联表与独立性检验 教学设计(表格式)
文档属性
| 名称 | 8.3 列联表与独立性检验 教学设计(表格式) | 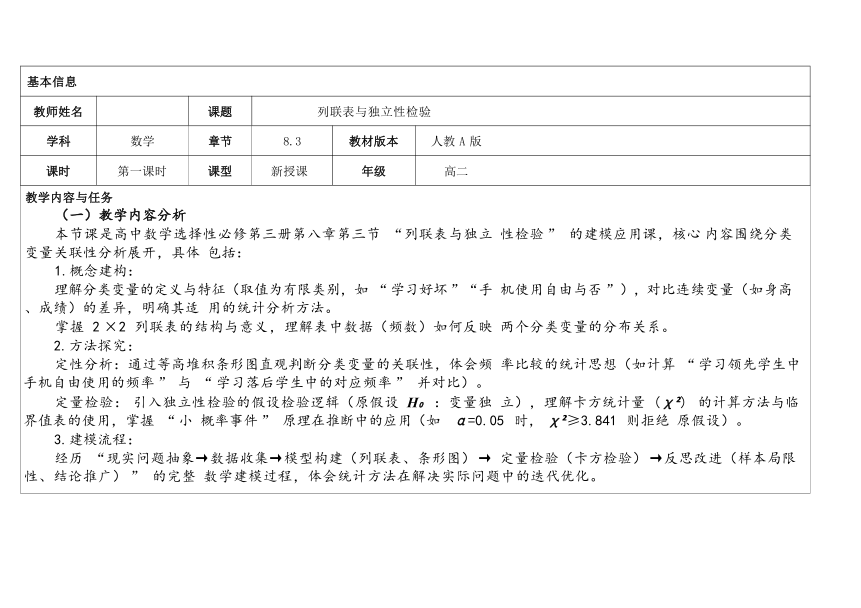 | |
| 格式 | docx | ||
| 文件大小 | 110.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 13:01:53 | ||
图片预览





文档简介
基本信息
教师姓名 课题 列联表与独立性检验
学科 数学 章节 8.3 教材版本 人教 A 版
课时 第一课时 课型 新授课 年级 高二
教学内容与任务 (一)教学内容分析 本节课是高中数学选择性必修第三册第八章第三节 “列联表与独立 性检验 ” 的建模应用课,核心 内容围绕分类变量关联性分析展开,具体 包括: 1.概念建构: 理解分类变量的定义与特征(取值为有限类别,如 “ 学习好坏 ”“手 机使用自由与否 ”),对比连续变量(如身高、成绩)的差异,明确其适 用的统计分析方法。 掌握 2 ×2 列联表的结构与意义,理解表中数据(频数)如何反映 两个分类变量的分布关系。 2.方法探究: 定性分析:通过等高堆积条形图直观判断分类变量的关联性,体会频 率比较的统计思想(如计算 “ 学习领先学生中手机自由使用的频率 ” 与 “ 学习落后学生中的对应频率 ” 并对比)。 定量检验: 引入独立性检验的假设检验逻辑(原假设 H :变量独 立),理解卡方统计量 (χ ) 的计算方法与临界值表的使用,掌握 “ 小 概率事件 ” 原理在推断中的应用(如 α=0.05 时, χ ≥3.841 则拒绝 原假设)。 3.建模流程: 经历 “现实问题抽象→数据收集→模型构建(列联表、条形图) → 定量检验(卡方检验) →反思改进(样本局限性、结论推广) ” 的完整 数学建模过程,体会统计方法在解决实际问题中的迭代优化。
(二)教学重点与难点 1.重点: 2 ×2 列联表的构建与等高堆积条形图的解读,通过频率比较初步判 断变量关联性。 独立性检验的步骤与逻辑(假设提出、卡方计算、临界值对比、结论 推断) ,理解统计结论的概率意义(如 “有 95% 的把握认为变量有关 联 ”)。 2.难点: 从 “样本数据 ” 到 “ 总体推断 ” 的假设检验逻辑(反证法思想: 通过小概率事件推翻原假设)。 卡方统计量的构造原理与卡方分布的直观理解(借助 GGB 动态曲 线演示小概率事件的几何意义)。 (三)教学任务设计 知识与技能任务: 任务 1:结合 “手机使用自 由与学习表现 ” 的情境,识别分类变 量并构建 2×2 列联表,能解释表中数据(a, b, c, d)的实际含义(如 “ 学 习领先且手机自由 ” 的人数为 a)。 任务 2 :使用 SPSS 软件绘制等高堆积条形图,通过观察不同组别 频率差异(如手机自由使用在学习领先组的比例 vs 落后组的比例),初 步判断变量关联性,体会可视化工具在数据分析中的作用。 任务 3:理解独立性检验的四步流程(提出假设→计算 χ →对比临 界值→作出推断),能根据 SPSS 输出的卡方值和临界值表(教材 P131), 写出统计结论(如 “在 α=0.05 的显著性水平下,有理由认为手机使 用 自由与学习表现有关联 ”)。 过程与方法任务: 任务 4(小组合作):分析课堂收集的班级数据是否具有代表性(如 仅为方便样本),讨论样本随机性对结论的影响,提出改进方案(如扩大 样本范围或增加电子产品类型),体会统计推断的严谨性。 情感与素养任务: 任务 6:通过 “ 法官判案 ” 类比假设检验逻辑(无罪假设→证据 推翻) ,感悟统计推断与生活逻辑的联系,培养 “ 用数据说话 ” 的科 学态度。 任务 7:回顾建模过程,归纳 “现实问题→数学抽象→模型检验→ 结论推广 ” 的通用步骤,反思统计方法在解决复杂问题中的价值(如多 变量分析、跨领域应用)。
教学目标 1.通过经历用列联表整理分类变量数据、用 SPSS 绘制等高堆积条形 图的过程,能够识别两个分类变量的关联性,培养数据分析与数学抽象素 养。 2.通过实践卡方检验的假设检验步骤(提出假设、计算卡方值、对比 临界值),能够依据小概率原理作出统计推断,培养逻辑推理与科学探究 能力。 3.通过完成 “手机使用与学习表现 ” 的建模案例及课后 “AI 利用 与性别关联 ” 的迁移任务,能够掌握 “数据收集 — 模型构建 — 检 验改进 ” 的统计建模流程,培养数学建模实践能力与技术工具应用素养。 4.通过智慧课堂实时数据采集、动态图表演示与小组协作探究,能够 体会统计方法的现实价值,强化用数据说话的科学态度与创新思维。
教学策略 依托智慧课堂,实施情境驱动与任务分层策略,融合 SPSS 技术,通 过数据探究、模型构建提升建模实践能力。
教学过程
教学环节 环节目标 教师活动 学生活动 智慧课堂技术应用及分析
一、创设 真 实 情 境,提出 问题 通 过 与 生 活 相 关的情境, 提出问题, 激 发 学 生 学 习 动 力 与思考,这 是 本 节 课 探 讨 活 动 的起点。 结 合 例子,归纳 分 类 变 量 的概念;让 学 生 体 验 数 学 建 模 中 将 实 际 问 题 转 化 为 数 学 问 创设情境:时代发展迅速,我 们的生活无时无刻都需要手机或 与其类似的电子产品。高中生应不 应该手机使用 自 由 ?手机使用对 于我们的学习影响是弊多还是利 多? 询问同学们的观点。 问题 1:部分学习相对领先的 同学有手机使用自由,部分学习相 对落后的同学也有。那“ 学习‘好 坏 ’”与“ 手机使用 自 由与否 ” 有没有关联呢? 教师利用智慧课堂实时反馈 系统的“讨论 ”功能,获得所有同 学的观点,并且引导同学表达观点 和想法。 基于情境提问,确定本节课主 要任务。 基于“任务清单 ”, 小组讨论,沟通交流, 各抒己见表达手机使用 对于学习影响的观点, 发展协同交流的能力; 回忆探究双变量之 间关系的相关性分析和 线性回归模型,思考其 能否应用于此情境问题 的解决; 掌握分类变量的概 念,并将此概念运用到 问题 2 的思考过程中。 实时反馈系统互动: 教师通过 “ 畅言智 慧课堂 ” 的实时投票或 问卷功能,快速收集学生 对 “ 手机使用 自 由与学 习好坏是否有关联 ” 的 观点,即时生成数据统计 图表(如支持 / 反对比 例)。 技术优势:打破传统 举手发言的局限性,实现 全员参与,数据实时可视 化,为后续 “分类变量 ” 概念 的 引 出提供真 实 情 境支撑,符合数学建模中 “ 从现 实问题抽 象数 学 问题 ” 的起点要求。 动态问题引导:
题 的 这 一 步骤。 希 望 培 养 学 生 会 用 数 学 的 眼 光 观 察 现 实 世 界,会用数 学 的 思 维 思 考 现 实 世界。 问题 2:我们之前所学的相关 性分析和回归线性模型可以解决 这个问题吗?为什么? 引导学生思考本章所学的相 关性分析和线性回归模型是否适 用于本问题。 教师引导学生合作探讨,深入 思考发现学过的知识不是很适用, 分析主要原因:现在研究的两个变 量都是只有两种可能,而线性回归 模型更适用于连续型的随机变量; 举例并归纳出“分类变量 ” : 类似于此问题中的“ 学习‘好 坏 ’”,“手机使用是否自由 ”, 还有性别,年级等都是可以使用一 种特殊的随机变量 以 区别不同 的 现象或性质的,这类随机变量称为 分类变量。 本节主要研究的就是取值于 {0,1}的分类变量,如“ 学习相对 领先 ”和“ 学习相对落后 ”就可以 分别用 1,0 表示。 利 用 智 慧 课 堂的 批 注、标注功能,在课件中 动态呈现问题链(如问题 1、 问题 2) ,结合学生 反馈实时调整提问节奏, 引导学生发现 “ 分类变 量 ” 与 “连续变量 ” 的 本质区别。 技术优势:增强课堂 互动的针对性,使学生在 真实数据驱动下主动建 构概念,体现建模思维中 “ 观察 — 抽 象 — 定 义 ” 的关键步骤。
追问:你还能举出哪些分类变 量? 教师引导学生发现问题 1 可以 转化为探究两个分类变量之间的 关联性问题。
设计意图:通过真实情境,培养学生“从生活现象中抽象数学问题 ”的建模能力,使其理解“识别变量类型到 明确建模需求 ”的关键步骤。强化“数学建模始于现实观察 ” 的认知,驱动学生主动提出研究“分类变量关联性 ” 问题。
二、收集 数据,定 性 定 量 分 析 问 题 通 过 问题 3 和问 题 4 的 探 讨,引 出等 高 堆 积 条 形图,让学 生 知 道 可 以 使 用 统 计 软 件 SPSS ( Statistica l Package for the Social 问题 3:基于此问题,并不需 要得出“ 学习‘好坏 ’”与“手机 使用自由 ”之间具体的关系,我们 只想要判断这两个变量之间是否 存在关联性 ,对此你有什 么方法 吗? 引导学生共同探讨,发现可以 采取分别统计出在学习相对领先 学生中手机使用 自 由的学生频率 和学习相对落后学生中手机使用 自由的学生频率,再进行比较的方 式判断,两个变量之间是否存在关 联性。 现场收集数据,通过畅言智慧 学生跟随教师思 路,开拓思维,基于 以 往经验,探索出可使用 已统计样本的频率进行 比较,进而判断双变量 之间是否存在关联性的 思路,培养学生的创新 能力; 基于数据,定量进 行计算频率,定性结合 图表多方面对数据样本 进行分析,激发学习利 用统计软件解决问题的 能力。 数 据 采 集 与即 时 呈 现: 通过 “ 畅言智慧课 堂 ” 发布电子问卷,实 时收集学生的 “ 学习排 名 ” 和 “手机使用自由 ” 数据, 自动生成 2×2 列 联表的频数统计结果(如 a、b、c、d 四格数据)。 技术优势:替代传统 手工统计,瞬间完成数据 汇总 ,让学生聚焦 “ 用 频率比较判断关联性 ” 的核心思路,避免耗时的
Sciences ) 绘 制 等 高 堆 积 条 形 图 并 通 过 等 高 堆 积 条 形 图 直 观 地 看 出 两 变 量 间 的关联性。 引 出 2 × 2 列 联 表,让学生 体 验 数 学 建模的“ 收 集数据 ”, “ 定 性 分 析数据 ”这 些步骤,培 养 学 生 数 据分析,数 学 运 算 的 核心素养。 课堂发放问卷,问卷有两个题目, “ 最近的全科考试总分是否为班 级前 28 名 ”和 “你是否有手机或 与其功能类似的电子产品使用 自 由 (每天使用时长≥50 分钟) ”, 获得实时反馈数据。得到了 2 种数 据,“学习表现 ”的频数分布和“手 机使用自有与否 ”的频数分布 并不是很直观体现关联性,进 而, 引导学生定性,定量得到初步 结论。 问题 4:初中学习 统计图表可 以方便我们观察和比较,上述数据 能否用一个图形比较直观地展示 出来,让我们观察更方便呢?你们 能想到哪些方式或软件吗? 教师引 导 学 生 发现 可以通过 等高堆积条形图实现 。教师使用 SPSS 演示如何用电脑画图。 指出在上述画图过程中,可以 用到 2 × 2 的表格,将该表格进一 步细化,得到一个清晰表示两个分 类变量关系的表格,这种形式的数 据统计表,我们称其为“2 ×2 列联 表 ” (呈现本题中精细的列联表), 人工计算干扰建模逻辑, 体现技术对 “数据收集 与整理 ” 环节的效率提 升。 SPSS 可视化工具 融 合: 教师现场演示 SPSS 绘制等高堆积条形图,学 生 通 过平板 同步观看操 作流程(如数据录入、图 表生成步骤),并实时对 比不同组别的频率差异。 技术优势:将统计软 件操作嵌入课堂,直观展 示 “数据→ 图表→结论 ” 的转化过程,帮助学生建 立 “ 用 图形语言分析分 类变量关联 ” 的建模意 识,突破传统黑板绘图的 静态局限。
介绍列连表中各量的含义。学生再 利用列联表中的数据定量进行频 数的计算比较,得出较为精准的初 步结论。
设计意图:通过“ 电子问卷 →等高堆积图 →列联表 ”的实践操作,培养学生“数据收集 →整理 →初步分析 ”的 建模基本技能,使其掌握“用频率比较和图形直观判断关联性 ”的定量与定性分析方法。列联表的构建强化了“用 表格语言结构化呈现数据 ”的建模表达能力,条形图的动态生成则体现“通过可视化工具简化数据解读 ”的建模策 略,为后续更进一步定量分析奠定模型基础。
三、反思 并 改 进 数 学 模 型,定量 分 析 问 题 通 过 问题 5,让 学 生 回 顾 抽 样 需 要 满 足 样 本 的 随 机 性 和代表性, 感 悟 “ 反 思 ”的重要 性。 呈 现 独 立 性 检 验 的 步 骤 问题 5:虽然通过图表我们可 以直观地判断出两个变量有关联, 但是我们的结论有没有可能出错 呢?为什么呢? 给出提示,这里考察的是频数 和频率。 教师引 导 学 生分析上述 问题 过程中的漏洞,发现收集的样本是 属于方便样本,我们只考察了我们 一个班级的样本,一定程度上不具 有代表性 。此外样本还具有随机 性,结果不一定能反应总体情况。 问题 6: 目前我们样本的选择 学 生 活动:对 于问 题 5,学生提出样本存 在的不足。 带着对问题 6 的探 索, 同时根据教师所提 供的阅读材料进行小组 合作探究,归纳出独立 性检验的步骤和判断准 则。 基 于 问 题 7 的 提 出,小组合作探究进行 逻辑推理和策略构建, 并 在 课 后进 行 实践 尝 数 字 化 资源 支 持 探 究: 课前通过 “ 畅言智 慧课堂 ” 向学生推送卡 方检验的预习材料(如微 课视频、文本案例),课 堂 中 利 用 平板 实时 调取 阅读材料,辅助小组讨论 “独立性检验步骤 ”。 技术优势:构建 “课 前预习 — 课中探究 — 课后拓展 ” 的一体化学 习路径,通过碎片化资源
和用法,让 学 生 初 步 了 解 其 背 后 的 假 设 检验原理, 为 下 一 课 时 中 公 式 推 导 和 理 论 实 践 结 合 运 用 作 铺垫。 让 学 生 体 验 数 学 建 模 中 的“反思改 进 ”,“模 型建立 ”, “ 参 数 求 解 ”,“得 到 问 题 结 论 ” 的 步 骤,培养学 生 反 思 和 创新意识。 通 过 无法进行改变,假设样本具有代表 性, 因为随机性也会犯错,我们这 个结论正确与否无法判断,但是假 如我们犯错,那么犯错的概率是多 大呢? 同时引导学生思考问题 6 的必 要性,逻辑推理认识到如果犯错 概率低,则我们得出的结果大概率 可以认为是正确的,所以有必要得 出犯错的概率大小。 教师活动: 引导学生在真实问 题解决过程中,查阅相关资料,课 本,AI 的搜索结果和独立性检验的 相关知识。 阅读材料课前分享给学生(呈 现在平板上),共同探讨发现可以 用独立性检验解决此问题。 教师分享并且类比法官判案- 疑罪从无原则——先假设被告人 无罪,然后原告进行证据列举,希 望推翻原假设 ,如果所列证据不 足,不能足以证明原假设不成立, 则被告人无罪,教师可以举例进行 详细解释 , 以判断嫌疑人是否为 “ 小偷 ”为例。 试。 降低抽象理论的理解难 度,符合建模课中 “反 思改进模型 ” 所需的知 识铺垫。 SPSS 自动化计算 与 动态模拟: 在 SPSS 中 输 入 列 联表数据,一键生成卡方 值( χ )并对照临界值表, 同时通过 GGB 软件动态 演示卡方分布曲线,直观 解释 “ 小概率事件 ” 的 几何意义(如阴影面积对 应 α=0.05)。 技术优势:将复杂的 公 式 计算转化 为可视化 操作,让学生重点理解假 设检验的逻辑(如 “ 原 假设→ 数据验证→ 推 断 结论 ”),而非机械记忆 公式 ,体现技术对 “ 定 量分析 ” 环节的思维支 撑。 技术优势:满足个性 化学习需求,及时回应学
问题 6,让 学 生 了 解 结 论 的 局 限 性 和 拓 展 如 何 得 到 更 广 泛 的 结 论 的 思考路径。 引导学生将这种推理逻辑运 用 到判断两个变量是否有关联即 两个变量是否独立的方面问题的 解决上,进而介绍独立性检验的具 体操作步骤(理论步骤我们下节课 进行详细探索与证明)。 第一步:提出原假设(零假设) H0:分类变量 X,Y 相互独立(独 立的意思是没有关联性,其严格的 定义下节课给出)。 第二步:根据样本数据整理出的 2×2 列联表,如下表。 (
(
a+b)(c+d)(a+c)(b+d)
构造过程于下节课进行)。
第三步:根据实际需要,定义
小概
率
事件
发
生
的概
率值
上
限
α
(称为小概率值
),
查临界表(教
)计 算 卡 方 值 χ2= n (ad bc)2 的取值。(其 生在建模过程中对 “ 结 论可靠性 ” 的深层思考, 强化 “模型检验与改进 ” 的科学严谨性。
材 131 页),找出对应的χ2的取值 xα(即推断原假设不成立的χ2的取 值下限,称为临界值)。 第四步, 当χ2 ≥ xα 时,即小概 率矛盾事件发生,则有理由推断原 假设 H0 不成立,即认为 X,Y 不相 互独立,并且此推断犯错误的概率 不超过α , 因为P(χ ≥ xα ) = α , 矛盾事件发生的概率不超过α。 当卡方小于等于临界值时,没 有充分理由推断原假设 H0 不成立, 则接受原假设。 进一步解释: χ2的本质是一个 随机变量,当考察样本数量较大, 且原假设 H0 成立的条件下,其近似 服从于自由度为 1 的卡方分布 图 1
由图可知,在原假设 H0 成立的 条件下,χ 大概率取接近于 0 的值, 小概率取得较大的值,所以如果得 出较大χ , 即矛盾的小概率事件发 生,那么我们有把握判断原假设 H0 不成立。 例如,给定小概率事件的概率 定义值α=0.05 ,其几何意义是图中 阴影部分面积,根据临界值表,对 应χ 的取值x0.05 = 3.841,即p(χ 2 ≥ x0.05) = 0.05 。x α 把χ 的取值区间 区分为了(0, xα )和[xα , + ∞)两段, 而χ 落在这两个区间的概率分别为 0.95 和 0.05 。若按χ 的公式算得其 落在[x α , + ∞),则表示小概率事件 发生了,依据假设检验原理,可以 认为原假设 H0 不成立,但是犯错的 可能性,犯错的概率不超过 0.05, 或者说是有不低于 95% 的把握原 假设 H0 不成立;若若按χ 的公式算 得其落在(0, xα )内,则没有充分理 由推断 H0 不成立。这就是独立性检 验的理解。 针对问题 6,利用上述方法, 在 SPSS 中计算χ , 并得出结论。
问题 7:假设我们的样本满足 了代表性和随机性,能否把上述结 论推广到“ 学习‘好坏 ’”与“ 学 生能否自由使用各类电子产品 ”相 关联,若不行,我们该如何改进? 共同探讨改进方案,总结提出 一种参考方案,按照同样的方法, 对于其他电子产品,比如“ 学习表 现‘好坏 ’”与“智能平板自由使 用与否 ”按照同样的方法进行独立 性检验 ,如果都呈现出类似的结 果,就有很大把握得出更广泛的结 论,反之不然。 同学们可以课后进行尝试
设计意图:通过“样本反思 →方法改进 →定量检验 ”的过程,培养学生“模型检验与修正 ”的建模能力,使其 理解统计建模结论具有概率属性,因此需通过严谨的假设检验降低推断误差。技术工具的介入不仅解决计算复杂性, 更让学生聚焦 “建模逻辑而非机械计算 ”,强化“用统计方法验证假设 ”的建模思维,形成 “定性分析 →定量检 验 →模型优化 ”的完整建模链条。
四、回顾 数 学 建 模过程, 总 结 提 升。 加 深 学 生 对 数 学 建 模 过 程的印象, 提 高 学 生 使 用 数 学 建 模 方 法 解 决 问 题 的意识。 问题 8:此实际问题解决过程 是我们数学建模的过程,在相关性 分析和线性回归分析学习中,我们 都经历了数学建模,你能归纳出数 学建模的主要步骤吗? 教师引 导 同 学们基 于 本 节课 案例解决过程总结归纳数学建模 的主要步骤: 首先在实际情境中从数学的 视角发现问题、提出问题、分析问 题、建立模型,确定参数,计算求 解,检验结果,改进模型,最终解 决实际问题。 问题 9:在本节课数学建模过 程中,你有什么感悟与想法? 教师总结:指出相关性分析, 线性回归分析和独立性检验都是 数学模型解决过程中的理论实践 知识; 教学升华,强调学习这些理论 实践知识,不仅是为了考试,更重 要的是以后能运用这些以及其他 统计学方法解决 自 己专业领域的 问题,促进学生的终身学习发展。 对于问题 8,任务 型驱动学习,基于任务 清单,个体回顾反思数 学建模过程,小组讨论, 教师引导共同生成数学 建模解决问题的主要步 骤,并能够迁移应用到 其他数学问题的解决过 程中。 对于问题 9, 回顾 本节课自身预习,学习, 总结阐述自身的想法与 感悟。 思维导图工具结构 化总结: 教师通过智慧课堂 的白板功能,动态生成数 学 建模 步 骤 的思 维 导 图 (情境→ 问题→ 数据→ 模型→检验→结论),学 生同步在平板上标注、补 充个人感悟。 技术优势:将零散的 建模经验系统化,可视化 呈现 “现实问题数学化 ” 的核心路径,便于学生迁 移应用 到 其他 统 计问题 中。 课 堂 实录 回 放 与反 思: 利 用 智 慧 课 堂的 录 播功能,课后向学生推送 课堂重点片段(如 SPSS 操作、卡方分布演示), 支持学生回顾 “模型建 立 ” 和 “ 定量分析 ” 的 关键细节。 技术优势:打破课堂
时间限制,为课后复习和 建模 能 力复盘提供 资 源 支持,强化 “ 总结提升 ” 环节的持续性。
设计意图:通过流程图复盘,帮助学生建立按步骤实施建模的系统化思维,明确各环节的建模目标。课后任务 驱动建模方法迁移应用,培养学生在新情境中独立设计建模方案的能力,实现从课堂建模参与者到自主建模实践者 的能力跃升,最终形成用数学建模解决现实问题的核心素养。
五、课后 作业 理 论 与 实 践 结 合,基于数 学 知 识 的 理解运用, 迁 移 本 节 课 数 学 建 模 的 路 径 拓 展 应 用 解 决 其 他 实际问题。 培 养 学 生 “三会 ”核 心素养,提 引导学生思考探究“A I 工具的 使用情况与性别是否有关联? ” 迁移本节课案例解 决的路径,结合数据收 集软件和统计软件解决 实际问题。 项 目 式 作 业 发 布与 过程追踪: 通过 “ 畅言智慧课 堂 ” 发布课后任务(如 “A I 利用与性别是否有 关联 ”),要求学生自主 设计问卷、用 SPSS 处理 数据并撰写建模报告,教 师可在线跟踪数据收集 进度并实时点评。 技术优势:将课堂所 学的 “ 列联表 — 卡方 检验 ” 建模流程转化为 真实任务,借助平台实现
高 学 生 知 识 迁 移 能 力。 “数据收集 — 分析 — 结论 ” 的全流程数字化 操作 ,培 养 自 主 建模 能 力。
列联表与独立性检验课前阅读材料
一、独立性检验起源:从连续变量到分类变量的分析需求
在统计学中,我们常通过分析两个变量的关系来解决实际问题。此前学习的相关系数(如 Pearson 相关系数)和 线 性回归模型,主要用于研究 连续变量(如身高、考试成绩、家庭收入等,取值为连续数值)之间的关联性。例如,通过 “每 周学习时间 ” 与 “考试分数 ” 的线性回归方程,预测学习时间对成绩的影响。
但现实中大量问题涉及 分类变量(取值为有限个类别的离散变量),例如: “性别 ”(男 / 女)与 “是否喜欢数学 ”(是 / 否)
“手机使用自由 ”(是 / 否)与 “学习表现 ”(领先 / 落后)
对于分类变量,我们需要新的方法来判断它们之间是否存在关联 —— 这就是 独立性检验 的研究目标。
二、独立性检验的大致步骤
独立性检验的逻辑类比于法官判案,遵循疑罪从无原则——先假设被告人无罪,然后原告进行证据列举,希望 推翻原假设,如果所列证据不足,不能足以推翻原假设,则认为被告人无罪。
独立性检验用于判断两个变量是否有关联即两个变量是否独立,具体操作步骤如下:
第一步:提出原假设(零假设)H0:分类变量 X,Y 相互独立(独立的意思是没有关联性,其严格的定义之后给 出)。
第二步 :根据样本数据整理出的 2 ×2 列联表,如下表。
2×2 列联表
计数
手机使用自由与 否 总计
手机 使用不自 由 手机 使用自由
学 习 表 现“好坏” 学习表 现较为落后 a c a+c
学习表 现较为领先 b d b +d
总计 a+b c+d a+b +c+d
计算卡方值的取值。(其构造过程于下节课进行)。
第三步:根据实际需要,定义小概率事件发生的概率值上限α(称为小概率值),查临界表(教材 131 页),找 出对应的χ2的取值 xα(即推断原假设不成立的χ2的取值下限,称为临界值)。
第四步, 当χ2 ≥ xα 时,即小概率矛盾事件发生,则有理由推断原假设 H0 不成立,即认为 X,Y 不相互独立,并 且此推断犯错误的概率不超过α , 因为p(χ ≥ x α ) = α , 矛盾事件发生的概率不超过α。
当卡方小于等于临界值时,没有充分理由推断原假设 H0 不成立,则接受原假设。
进一步解释:χ2的本质是一个随机变量,当考察样本数量较大,且原假设 H0 成立的条件下,其近似服从于自由度 为 1 的卡方分布由图可知,在原假设 H0 成立的条件下,χ2大概率取接近于 0 的值,小概率取得较大的值,所以如果
得出较大χ2 ,即矛盾的小概率事件发生,那么我们有把握判断原假设 H0 不成立。
例如,给定小概率事件的概率定义值α=0.05 ,其几何意义是图中阴影部分面积,根据临界值表,对应χ 的取值 x0.05 = 3.841 ,即p(χ 2 ≥ x0.05) = 0.05 。xα 把χ 的取值区间区分为了(0, xα )和[xα , + ∞)两段,而χ 落在这两个区间的 概率分别为 0.95 和 0.05 。若按χ 的公式算得其落在[x α , + ∞) ,则表示小概率事件发生了,依据假设检验原理,可以 认为原假设 H0 不成立,但是犯错的可能性,犯错的概率不超过 0.05,或者说是有不低于 95%的把握原假设 H0 不成 立;若若按χ 的公式算得其落在(0, x α )内,则没有充分理由推断 H0 不成立。
教师姓名 课题 列联表与独立性检验
学科 数学 章节 8.3 教材版本 人教 A 版
课时 第一课时 课型 新授课 年级 高二
教学内容与任务 (一)教学内容分析 本节课是高中数学选择性必修第三册第八章第三节 “列联表与独立 性检验 ” 的建模应用课,核心 内容围绕分类变量关联性分析展开,具体 包括: 1.概念建构: 理解分类变量的定义与特征(取值为有限类别,如 “ 学习好坏 ”“手 机使用自由与否 ”),对比连续变量(如身高、成绩)的差异,明确其适 用的统计分析方法。 掌握 2 ×2 列联表的结构与意义,理解表中数据(频数)如何反映 两个分类变量的分布关系。 2.方法探究: 定性分析:通过等高堆积条形图直观判断分类变量的关联性,体会频 率比较的统计思想(如计算 “ 学习领先学生中手机自由使用的频率 ” 与 “ 学习落后学生中的对应频率 ” 并对比)。 定量检验: 引入独立性检验的假设检验逻辑(原假设 H :变量独 立),理解卡方统计量 (χ ) 的计算方法与临界值表的使用,掌握 “ 小 概率事件 ” 原理在推断中的应用(如 α=0.05 时, χ ≥3.841 则拒绝 原假设)。 3.建模流程: 经历 “现实问题抽象→数据收集→模型构建(列联表、条形图) → 定量检验(卡方检验) →反思改进(样本局限性、结论推广) ” 的完整 数学建模过程,体会统计方法在解决实际问题中的迭代优化。
(二)教学重点与难点 1.重点: 2 ×2 列联表的构建与等高堆积条形图的解读,通过频率比较初步判 断变量关联性。 独立性检验的步骤与逻辑(假设提出、卡方计算、临界值对比、结论 推断) ,理解统计结论的概率意义(如 “有 95% 的把握认为变量有关 联 ”)。 2.难点: 从 “样本数据 ” 到 “ 总体推断 ” 的假设检验逻辑(反证法思想: 通过小概率事件推翻原假设)。 卡方统计量的构造原理与卡方分布的直观理解(借助 GGB 动态曲 线演示小概率事件的几何意义)。 (三)教学任务设计 知识与技能任务: 任务 1:结合 “手机使用自 由与学习表现 ” 的情境,识别分类变 量并构建 2×2 列联表,能解释表中数据(a, b, c, d)的实际含义(如 “ 学 习领先且手机自由 ” 的人数为 a)。 任务 2 :使用 SPSS 软件绘制等高堆积条形图,通过观察不同组别 频率差异(如手机自由使用在学习领先组的比例 vs 落后组的比例),初 步判断变量关联性,体会可视化工具在数据分析中的作用。 任务 3:理解独立性检验的四步流程(提出假设→计算 χ →对比临 界值→作出推断),能根据 SPSS 输出的卡方值和临界值表(教材 P131), 写出统计结论(如 “在 α=0.05 的显著性水平下,有理由认为手机使 用 自由与学习表现有关联 ”)。 过程与方法任务: 任务 4(小组合作):分析课堂收集的班级数据是否具有代表性(如 仅为方便样本),讨论样本随机性对结论的影响,提出改进方案(如扩大 样本范围或增加电子产品类型),体会统计推断的严谨性。 情感与素养任务: 任务 6:通过 “ 法官判案 ” 类比假设检验逻辑(无罪假设→证据 推翻) ,感悟统计推断与生活逻辑的联系,培养 “ 用数据说话 ” 的科 学态度。 任务 7:回顾建模过程,归纳 “现实问题→数学抽象→模型检验→ 结论推广 ” 的通用步骤,反思统计方法在解决复杂问题中的价值(如多 变量分析、跨领域应用)。
教学目标 1.通过经历用列联表整理分类变量数据、用 SPSS 绘制等高堆积条形 图的过程,能够识别两个分类变量的关联性,培养数据分析与数学抽象素 养。 2.通过实践卡方检验的假设检验步骤(提出假设、计算卡方值、对比 临界值),能够依据小概率原理作出统计推断,培养逻辑推理与科学探究 能力。 3.通过完成 “手机使用与学习表现 ” 的建模案例及课后 “AI 利用 与性别关联 ” 的迁移任务,能够掌握 “数据收集 — 模型构建 — 检 验改进 ” 的统计建模流程,培养数学建模实践能力与技术工具应用素养。 4.通过智慧课堂实时数据采集、动态图表演示与小组协作探究,能够 体会统计方法的现实价值,强化用数据说话的科学态度与创新思维。
教学策略 依托智慧课堂,实施情境驱动与任务分层策略,融合 SPSS 技术,通 过数据探究、模型构建提升建模实践能力。
教学过程
教学环节 环节目标 教师活动 学生活动 智慧课堂技术应用及分析
一、创设 真 实 情 境,提出 问题 通 过 与 生 活 相 关的情境, 提出问题, 激 发 学 生 学 习 动 力 与思考,这 是 本 节 课 探 讨 活 动 的起点。 结 合 例子,归纳 分 类 变 量 的概念;让 学 生 体 验 数 学 建 模 中 将 实 际 问 题 转 化 为 数 学 问 创设情境:时代发展迅速,我 们的生活无时无刻都需要手机或 与其类似的电子产品。高中生应不 应该手机使用 自 由 ?手机使用对 于我们的学习影响是弊多还是利 多? 询问同学们的观点。 问题 1:部分学习相对领先的 同学有手机使用自由,部分学习相 对落后的同学也有。那“ 学习‘好 坏 ’”与“ 手机使用 自 由与否 ” 有没有关联呢? 教师利用智慧课堂实时反馈 系统的“讨论 ”功能,获得所有同 学的观点,并且引导同学表达观点 和想法。 基于情境提问,确定本节课主 要任务。 基于“任务清单 ”, 小组讨论,沟通交流, 各抒己见表达手机使用 对于学习影响的观点, 发展协同交流的能力; 回忆探究双变量之 间关系的相关性分析和 线性回归模型,思考其 能否应用于此情境问题 的解决; 掌握分类变量的概 念,并将此概念运用到 问题 2 的思考过程中。 实时反馈系统互动: 教师通过 “ 畅言智 慧课堂 ” 的实时投票或 问卷功能,快速收集学生 对 “ 手机使用 自 由与学 习好坏是否有关联 ” 的 观点,即时生成数据统计 图表(如支持 / 反对比 例)。 技术优势:打破传统 举手发言的局限性,实现 全员参与,数据实时可视 化,为后续 “分类变量 ” 概念 的 引 出提供真 实 情 境支撑,符合数学建模中 “ 从现 实问题抽 象数 学 问题 ” 的起点要求。 动态问题引导:
题 的 这 一 步骤。 希 望 培 养 学 生 会 用 数 学 的 眼 光 观 察 现 实 世 界,会用数 学 的 思 维 思 考 现 实 世界。 问题 2:我们之前所学的相关 性分析和回归线性模型可以解决 这个问题吗?为什么? 引导学生思考本章所学的相 关性分析和线性回归模型是否适 用于本问题。 教师引导学生合作探讨,深入 思考发现学过的知识不是很适用, 分析主要原因:现在研究的两个变 量都是只有两种可能,而线性回归 模型更适用于连续型的随机变量; 举例并归纳出“分类变量 ” : 类似于此问题中的“ 学习‘好 坏 ’”,“手机使用是否自由 ”, 还有性别,年级等都是可以使用一 种特殊的随机变量 以 区别不同 的 现象或性质的,这类随机变量称为 分类变量。 本节主要研究的就是取值于 {0,1}的分类变量,如“ 学习相对 领先 ”和“ 学习相对落后 ”就可以 分别用 1,0 表示。 利 用 智 慧 课 堂的 批 注、标注功能,在课件中 动态呈现问题链(如问题 1、 问题 2) ,结合学生 反馈实时调整提问节奏, 引导学生发现 “ 分类变 量 ” 与 “连续变量 ” 的 本质区别。 技术优势:增强课堂 互动的针对性,使学生在 真实数据驱动下主动建 构概念,体现建模思维中 “ 观察 — 抽 象 — 定 义 ” 的关键步骤。
追问:你还能举出哪些分类变 量? 教师引导学生发现问题 1 可以 转化为探究两个分类变量之间的 关联性问题。
设计意图:通过真实情境,培养学生“从生活现象中抽象数学问题 ”的建模能力,使其理解“识别变量类型到 明确建模需求 ”的关键步骤。强化“数学建模始于现实观察 ” 的认知,驱动学生主动提出研究“分类变量关联性 ” 问题。
二、收集 数据,定 性 定 量 分 析 问 题 通 过 问题 3 和问 题 4 的 探 讨,引 出等 高 堆 积 条 形图,让学 生 知 道 可 以 使 用 统 计 软 件 SPSS ( Statistica l Package for the Social 问题 3:基于此问题,并不需 要得出“ 学习‘好坏 ’”与“手机 使用自由 ”之间具体的关系,我们 只想要判断这两个变量之间是否 存在关联性 ,对此你有什 么方法 吗? 引导学生共同探讨,发现可以 采取分别统计出在学习相对领先 学生中手机使用 自 由的学生频率 和学习相对落后学生中手机使用 自由的学生频率,再进行比较的方 式判断,两个变量之间是否存在关 联性。 现场收集数据,通过畅言智慧 学生跟随教师思 路,开拓思维,基于 以 往经验,探索出可使用 已统计样本的频率进行 比较,进而判断双变量 之间是否存在关联性的 思路,培养学生的创新 能力; 基于数据,定量进 行计算频率,定性结合 图表多方面对数据样本 进行分析,激发学习利 用统计软件解决问题的 能力。 数 据 采 集 与即 时 呈 现: 通过 “ 畅言智慧课 堂 ” 发布电子问卷,实 时收集学生的 “ 学习排 名 ” 和 “手机使用自由 ” 数据, 自动生成 2×2 列 联表的频数统计结果(如 a、b、c、d 四格数据)。 技术优势:替代传统 手工统计,瞬间完成数据 汇总 ,让学生聚焦 “ 用 频率比较判断关联性 ” 的核心思路,避免耗时的
Sciences ) 绘 制 等 高 堆 积 条 形 图 并 通 过 等 高 堆 积 条 形 图 直 观 地 看 出 两 变 量 间 的关联性。 引 出 2 × 2 列 联 表,让学生 体 验 数 学 建模的“ 收 集数据 ”, “ 定 性 分 析数据 ”这 些步骤,培 养 学 生 数 据分析,数 学 运 算 的 核心素养。 课堂发放问卷,问卷有两个题目, “ 最近的全科考试总分是否为班 级前 28 名 ”和 “你是否有手机或 与其功能类似的电子产品使用 自 由 (每天使用时长≥50 分钟) ”, 获得实时反馈数据。得到了 2 种数 据,“学习表现 ”的频数分布和“手 机使用自有与否 ”的频数分布 并不是很直观体现关联性,进 而, 引导学生定性,定量得到初步 结论。 问题 4:初中学习 统计图表可 以方便我们观察和比较,上述数据 能否用一个图形比较直观地展示 出来,让我们观察更方便呢?你们 能想到哪些方式或软件吗? 教师引 导 学 生 发现 可以通过 等高堆积条形图实现 。教师使用 SPSS 演示如何用电脑画图。 指出在上述画图过程中,可以 用到 2 × 2 的表格,将该表格进一 步细化,得到一个清晰表示两个分 类变量关系的表格,这种形式的数 据统计表,我们称其为“2 ×2 列联 表 ” (呈现本题中精细的列联表), 人工计算干扰建模逻辑, 体现技术对 “数据收集 与整理 ” 环节的效率提 升。 SPSS 可视化工具 融 合: 教师现场演示 SPSS 绘制等高堆积条形图,学 生 通 过平板 同步观看操 作流程(如数据录入、图 表生成步骤),并实时对 比不同组别的频率差异。 技术优势:将统计软 件操作嵌入课堂,直观展 示 “数据→ 图表→结论 ” 的转化过程,帮助学生建 立 “ 用 图形语言分析分 类变量关联 ” 的建模意 识,突破传统黑板绘图的 静态局限。
介绍列连表中各量的含义。学生再 利用列联表中的数据定量进行频 数的计算比较,得出较为精准的初 步结论。
设计意图:通过“ 电子问卷 →等高堆积图 →列联表 ”的实践操作,培养学生“数据收集 →整理 →初步分析 ”的 建模基本技能,使其掌握“用频率比较和图形直观判断关联性 ”的定量与定性分析方法。列联表的构建强化了“用 表格语言结构化呈现数据 ”的建模表达能力,条形图的动态生成则体现“通过可视化工具简化数据解读 ”的建模策 略,为后续更进一步定量分析奠定模型基础。
三、反思 并 改 进 数 学 模 型,定量 分 析 问 题 通 过 问题 5,让 学 生 回 顾 抽 样 需 要 满 足 样 本 的 随 机 性 和代表性, 感 悟 “ 反 思 ”的重要 性。 呈 现 独 立 性 检 验 的 步 骤 问题 5:虽然通过图表我们可 以直观地判断出两个变量有关联, 但是我们的结论有没有可能出错 呢?为什么呢? 给出提示,这里考察的是频数 和频率。 教师引 导 学 生分析上述 问题 过程中的漏洞,发现收集的样本是 属于方便样本,我们只考察了我们 一个班级的样本,一定程度上不具 有代表性 。此外样本还具有随机 性,结果不一定能反应总体情况。 问题 6: 目前我们样本的选择 学 生 活动:对 于问 题 5,学生提出样本存 在的不足。 带着对问题 6 的探 索, 同时根据教师所提 供的阅读材料进行小组 合作探究,归纳出独立 性检验的步骤和判断准 则。 基 于 问 题 7 的 提 出,小组合作探究进行 逻辑推理和策略构建, 并 在 课 后进 行 实践 尝 数 字 化 资源 支 持 探 究: 课前通过 “ 畅言智 慧课堂 ” 向学生推送卡 方检验的预习材料(如微 课视频、文本案例),课 堂 中 利 用 平板 实时 调取 阅读材料,辅助小组讨论 “独立性检验步骤 ”。 技术优势:构建 “课 前预习 — 课中探究 — 课后拓展 ” 的一体化学 习路径,通过碎片化资源
和用法,让 学 生 初 步 了 解 其 背 后 的 假 设 检验原理, 为 下 一 课 时 中 公 式 推 导 和 理 论 实 践 结 合 运 用 作 铺垫。 让 学 生 体 验 数 学 建 模 中 的“反思改 进 ”,“模 型建立 ”, “ 参 数 求 解 ”,“得 到 问 题 结 论 ” 的 步 骤,培养学 生 反 思 和 创新意识。 通 过 无法进行改变,假设样本具有代表 性, 因为随机性也会犯错,我们这 个结论正确与否无法判断,但是假 如我们犯错,那么犯错的概率是多 大呢? 同时引导学生思考问题 6 的必 要性,逻辑推理认识到如果犯错 概率低,则我们得出的结果大概率 可以认为是正确的,所以有必要得 出犯错的概率大小。 教师活动: 引导学生在真实问 题解决过程中,查阅相关资料,课 本,AI 的搜索结果和独立性检验的 相关知识。 阅读材料课前分享给学生(呈 现在平板上),共同探讨发现可以 用独立性检验解决此问题。 教师分享并且类比法官判案- 疑罪从无原则——先假设被告人 无罪,然后原告进行证据列举,希 望推翻原假设 ,如果所列证据不 足,不能足以证明原假设不成立, 则被告人无罪,教师可以举例进行 详细解释 , 以判断嫌疑人是否为 “ 小偷 ”为例。 试。 降低抽象理论的理解难 度,符合建模课中 “反 思改进模型 ” 所需的知 识铺垫。 SPSS 自动化计算 与 动态模拟: 在 SPSS 中 输 入 列 联表数据,一键生成卡方 值( χ )并对照临界值表, 同时通过 GGB 软件动态 演示卡方分布曲线,直观 解释 “ 小概率事件 ” 的 几何意义(如阴影面积对 应 α=0.05)。 技术优势:将复杂的 公 式 计算转化 为可视化 操作,让学生重点理解假 设检验的逻辑(如 “ 原 假设→ 数据验证→ 推 断 结论 ”),而非机械记忆 公式 ,体现技术对 “ 定 量分析 ” 环节的思维支 撑。 技术优势:满足个性 化学习需求,及时回应学
问题 6,让 学 生 了 解 结 论 的 局 限 性 和 拓 展 如 何 得 到 更 广 泛 的 结 论 的 思考路径。 引导学生将这种推理逻辑运 用 到判断两个变量是否有关联即 两个变量是否独立的方面问题的 解决上,进而介绍独立性检验的具 体操作步骤(理论步骤我们下节课 进行详细探索与证明)。 第一步:提出原假设(零假设) H0:分类变量 X,Y 相互独立(独 立的意思是没有关联性,其严格的 定义下节课给出)。 第二步:根据样本数据整理出的 2×2 列联表,如下表。 (
(
a+b)(c+d)(a+c)(b+d)
构造过程于下节课进行)。
第三步:根据实际需要,定义
小概
率
事件
发
生
的概
率值
上
限
α
(称为小概率值
),
查临界表(教
)计 算 卡 方 值 χ2= n (ad bc)2 的取值。(其 生在建模过程中对 “ 结 论可靠性 ” 的深层思考, 强化 “模型检验与改进 ” 的科学严谨性。
材 131 页),找出对应的χ2的取值 xα(即推断原假设不成立的χ2的取 值下限,称为临界值)。 第四步, 当χ2 ≥ xα 时,即小概 率矛盾事件发生,则有理由推断原 假设 H0 不成立,即认为 X,Y 不相 互独立,并且此推断犯错误的概率 不超过α , 因为P(χ ≥ xα ) = α , 矛盾事件发生的概率不超过α。 当卡方小于等于临界值时,没 有充分理由推断原假设 H0 不成立, 则接受原假设。 进一步解释: χ2的本质是一个 随机变量,当考察样本数量较大, 且原假设 H0 成立的条件下,其近似 服从于自由度为 1 的卡方分布 图 1
由图可知,在原假设 H0 成立的 条件下,χ 大概率取接近于 0 的值, 小概率取得较大的值,所以如果得 出较大χ , 即矛盾的小概率事件发 生,那么我们有把握判断原假设 H0 不成立。 例如,给定小概率事件的概率 定义值α=0.05 ,其几何意义是图中 阴影部分面积,根据临界值表,对 应χ 的取值x0.05 = 3.841,即p(χ 2 ≥ x0.05) = 0.05 。x α 把χ 的取值区间 区分为了(0, xα )和[xα , + ∞)两段, 而χ 落在这两个区间的概率分别为 0.95 和 0.05 。若按χ 的公式算得其 落在[x α , + ∞),则表示小概率事件 发生了,依据假设检验原理,可以 认为原假设 H0 不成立,但是犯错的 可能性,犯错的概率不超过 0.05, 或者说是有不低于 95% 的把握原 假设 H0 不成立;若若按χ 的公式算 得其落在(0, xα )内,则没有充分理 由推断 H0 不成立。这就是独立性检 验的理解。 针对问题 6,利用上述方法, 在 SPSS 中计算χ , 并得出结论。
问题 7:假设我们的样本满足 了代表性和随机性,能否把上述结 论推广到“ 学习‘好坏 ’”与“ 学 生能否自由使用各类电子产品 ”相 关联,若不行,我们该如何改进? 共同探讨改进方案,总结提出 一种参考方案,按照同样的方法, 对于其他电子产品,比如“ 学习表 现‘好坏 ’”与“智能平板自由使 用与否 ”按照同样的方法进行独立 性检验 ,如果都呈现出类似的结 果,就有很大把握得出更广泛的结 论,反之不然。 同学们可以课后进行尝试
设计意图:通过“样本反思 →方法改进 →定量检验 ”的过程,培养学生“模型检验与修正 ”的建模能力,使其 理解统计建模结论具有概率属性,因此需通过严谨的假设检验降低推断误差。技术工具的介入不仅解决计算复杂性, 更让学生聚焦 “建模逻辑而非机械计算 ”,强化“用统计方法验证假设 ”的建模思维,形成 “定性分析 →定量检 验 →模型优化 ”的完整建模链条。
四、回顾 数 学 建 模过程, 总 结 提 升。 加 深 学 生 对 数 学 建 模 过 程的印象, 提 高 学 生 使 用 数 学 建 模 方 法 解 决 问 题 的意识。 问题 8:此实际问题解决过程 是我们数学建模的过程,在相关性 分析和线性回归分析学习中,我们 都经历了数学建模,你能归纳出数 学建模的主要步骤吗? 教师引 导 同 学们基 于 本 节课 案例解决过程总结归纳数学建模 的主要步骤: 首先在实际情境中从数学的 视角发现问题、提出问题、分析问 题、建立模型,确定参数,计算求 解,检验结果,改进模型,最终解 决实际问题。 问题 9:在本节课数学建模过 程中,你有什么感悟与想法? 教师总结:指出相关性分析, 线性回归分析和独立性检验都是 数学模型解决过程中的理论实践 知识; 教学升华,强调学习这些理论 实践知识,不仅是为了考试,更重 要的是以后能运用这些以及其他 统计学方法解决 自 己专业领域的 问题,促进学生的终身学习发展。 对于问题 8,任务 型驱动学习,基于任务 清单,个体回顾反思数 学建模过程,小组讨论, 教师引导共同生成数学 建模解决问题的主要步 骤,并能够迁移应用到 其他数学问题的解决过 程中。 对于问题 9, 回顾 本节课自身预习,学习, 总结阐述自身的想法与 感悟。 思维导图工具结构 化总结: 教师通过智慧课堂 的白板功能,动态生成数 学 建模 步 骤 的思 维 导 图 (情境→ 问题→ 数据→ 模型→检验→结论),学 生同步在平板上标注、补 充个人感悟。 技术优势:将零散的 建模经验系统化,可视化 呈现 “现实问题数学化 ” 的核心路径,便于学生迁 移应用 到 其他 统 计问题 中。 课 堂 实录 回 放 与反 思: 利 用 智 慧 课 堂的 录 播功能,课后向学生推送 课堂重点片段(如 SPSS 操作、卡方分布演示), 支持学生回顾 “模型建 立 ” 和 “ 定量分析 ” 的 关键细节。 技术优势:打破课堂
时间限制,为课后复习和 建模 能 力复盘提供 资 源 支持,强化 “ 总结提升 ” 环节的持续性。
设计意图:通过流程图复盘,帮助学生建立按步骤实施建模的系统化思维,明确各环节的建模目标。课后任务 驱动建模方法迁移应用,培养学生在新情境中独立设计建模方案的能力,实现从课堂建模参与者到自主建模实践者 的能力跃升,最终形成用数学建模解决现实问题的核心素养。
五、课后 作业 理 论 与 实 践 结 合,基于数 学 知 识 的 理解运用, 迁 移 本 节 课 数 学 建 模 的 路 径 拓 展 应 用 解 决 其 他 实际问题。 培 养 学 生 “三会 ”核 心素养,提 引导学生思考探究“A I 工具的 使用情况与性别是否有关联? ” 迁移本节课案例解 决的路径,结合数据收 集软件和统计软件解决 实际问题。 项 目 式 作 业 发 布与 过程追踪: 通过 “ 畅言智慧课 堂 ” 发布课后任务(如 “A I 利用与性别是否有 关联 ”),要求学生自主 设计问卷、用 SPSS 处理 数据并撰写建模报告,教 师可在线跟踪数据收集 进度并实时点评。 技术优势:将课堂所 学的 “ 列联表 — 卡方 检验 ” 建模流程转化为 真实任务,借助平台实现
高 学 生 知 识 迁 移 能 力。 “数据收集 — 分析 — 结论 ” 的全流程数字化 操作 ,培 养 自 主 建模 能 力。
列联表与独立性检验课前阅读材料
一、独立性检验起源:从连续变量到分类变量的分析需求
在统计学中,我们常通过分析两个变量的关系来解决实际问题。此前学习的相关系数(如 Pearson 相关系数)和 线 性回归模型,主要用于研究 连续变量(如身高、考试成绩、家庭收入等,取值为连续数值)之间的关联性。例如,通过 “每 周学习时间 ” 与 “考试分数 ” 的线性回归方程,预测学习时间对成绩的影响。
但现实中大量问题涉及 分类变量(取值为有限个类别的离散变量),例如: “性别 ”(男 / 女)与 “是否喜欢数学 ”(是 / 否)
“手机使用自由 ”(是 / 否)与 “学习表现 ”(领先 / 落后)
对于分类变量,我们需要新的方法来判断它们之间是否存在关联 —— 这就是 独立性检验 的研究目标。
二、独立性检验的大致步骤
独立性检验的逻辑类比于法官判案,遵循疑罪从无原则——先假设被告人无罪,然后原告进行证据列举,希望 推翻原假设,如果所列证据不足,不能足以推翻原假设,则认为被告人无罪。
独立性检验用于判断两个变量是否有关联即两个变量是否独立,具体操作步骤如下:
第一步:提出原假设(零假设)H0:分类变量 X,Y 相互独立(独立的意思是没有关联性,其严格的定义之后给 出)。
第二步 :根据样本数据整理出的 2 ×2 列联表,如下表。
2×2 列联表
计数
手机使用自由与 否 总计
手机 使用不自 由 手机 使用自由
学 习 表 现“好坏” 学习表 现较为落后 a c a+c
学习表 现较为领先 b d b +d
总计 a+b c+d a+b +c+d
计算卡方值的取值。(其构造过程于下节课进行)。
第三步:根据实际需要,定义小概率事件发生的概率值上限α(称为小概率值),查临界表(教材 131 页),找 出对应的χ2的取值 xα(即推断原假设不成立的χ2的取值下限,称为临界值)。
第四步, 当χ2 ≥ xα 时,即小概率矛盾事件发生,则有理由推断原假设 H0 不成立,即认为 X,Y 不相互独立,并 且此推断犯错误的概率不超过α , 因为p(χ ≥ x α ) = α , 矛盾事件发生的概率不超过α。
当卡方小于等于临界值时,没有充分理由推断原假设 H0 不成立,则接受原假设。
进一步解释:χ2的本质是一个随机变量,当考察样本数量较大,且原假设 H0 成立的条件下,其近似服从于自由度 为 1 的卡方分布由图可知,在原假设 H0 成立的条件下,χ2大概率取接近于 0 的值,小概率取得较大的值,所以如果
得出较大χ2 ,即矛盾的小概率事件发生,那么我们有把握判断原假设 H0 不成立。
例如,给定小概率事件的概率定义值α=0.05 ,其几何意义是图中阴影部分面积,根据临界值表,对应χ 的取值 x0.05 = 3.841 ,即p(χ 2 ≥ x0.05) = 0.05 。xα 把χ 的取值区间区分为了(0, xα )和[xα , + ∞)两段,而χ 落在这两个区间的 概率分别为 0.95 和 0.05 。若按χ 的公式算得其落在[x α , + ∞) ,则表示小概率事件发生了,依据假设检验原理,可以 认为原假设 H0 不成立,但是犯错的可能性,犯错的概率不超过 0.05,或者说是有不低于 95%的把握原假设 H0 不成 立;若若按χ 的公式算得其落在(0, x α )内,则没有充分理由推断 H0 不成立。
