2026年中考数学核心考点一轮复习 尺规作图(含解析)
文档属性
| 名称 | 2026年中考数学核心考点一轮复习 尺规作图(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 880.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 15:03:57 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考数学一轮复习 尺规作图
一.解答题(共20小题)
1.在学习了矩形与菱形的相关知识后,小明同学进行了更深入的研究,他发现,过矩形的一条对角线的中点作这条对角线的垂线,与矩形两边相交的两点和这条对角线的两个端点构成的四边形是菱形,可利用证明三角形全等得到此结论.根据他的想法与思路,完成以下作图与填空:
(1)如图,在矩形ABCD中,点O是对角线AC的中点.用尺规过点O作AC的垂线,分别交AB,CD于点E,F,连接AF,CE.(不写作法,保留作图痕迹)
(2)已知:矩形ABCD,点E,F分别在AB,CD上,EF经过对角线AC的中点O,且EF⊥AC.求证:四边形AECF是菱形.
证明:∵四边形ABCD是矩形,
∴AB∥CD.
∴① ,∠OCF=∠OAE.
∵点O是AC的中点,
∴② .
∴△CFO≌△AEO(AAS).
∴③ .
又∵OA=OC,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
进一步思考,如果四边形ABCD是平行四边形呢?请你模仿题中表述,写出你猜想的结论:④ .
2.根据背景素材,探索解决问题.
平面直角坐标系中画一个边长为2的正六边形ABCDEF
背景素材 六等分圆原理,也称为圆周六等分问题,是一个古老而经典的几何问题,旨在解决如何使用直尺和圆规将一个圆分成六等份的问题.这个问题由欧几里得在其名著《几何原本》中详细阐述.
已知条件 点C与坐标原点O重合,点D在x轴的正半轴上且坐标为(2,0).
操作步骤 ①分别以点C,D为圆心,CD长为半径作弧,两弧交于点P; ②以点P为圆心,PC长为半径作圆; ③以CD的长为半径,在⊙P上顺次截取; ④顺次连接DE,EF,FA,AB,BC.得到正六边形ABCDEF.
问题解决
任务一 根据以上信息,请你用不带刻度的直尺和圆规,在图中完成这道作图题(保留作图痕迹,不写作法)
任务二 将正六边形ABCDEF绕点D顺时针旋转60°,直接写出此时点E所在位置的坐标: .
3.马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、黑、白彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧.如图1的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图2,已知⊙O和圆上一点M.作法如下:
①以点M为圆心,OM长为半径,作弧交⊙O于A,B两点;
②延长MO交⊙O于点C;
即点A,B,C将⊙O的圆周三等分.
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图2中将⊙O的圆周三等分(保留作图痕迹,不写作法);
(2)根据(1)画出的图形,连接AB,AC,BC,若⊙O的半径为2cm,则△ABC的周长为 cm.
4.【阅读材料】
老师的问题: 已知:如图,AE∥BF. 求作:菱形ABCD,使点C,D分别在BF,AE上. 小明的作法: (1)以A为圆心,AB长为半径画弧,交AE于点D; (2)以B为圆心,AB长为半径画弧,交BF于点C; (3)连接CD. 四边形ABCD就是所求作的菱形.
【解答问题】
请根据材料中的信息,证明四边形ABCD是菱形.
5.【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;
【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
(友情提醒:以上作图均不写作法,但需保留作图痕迹)
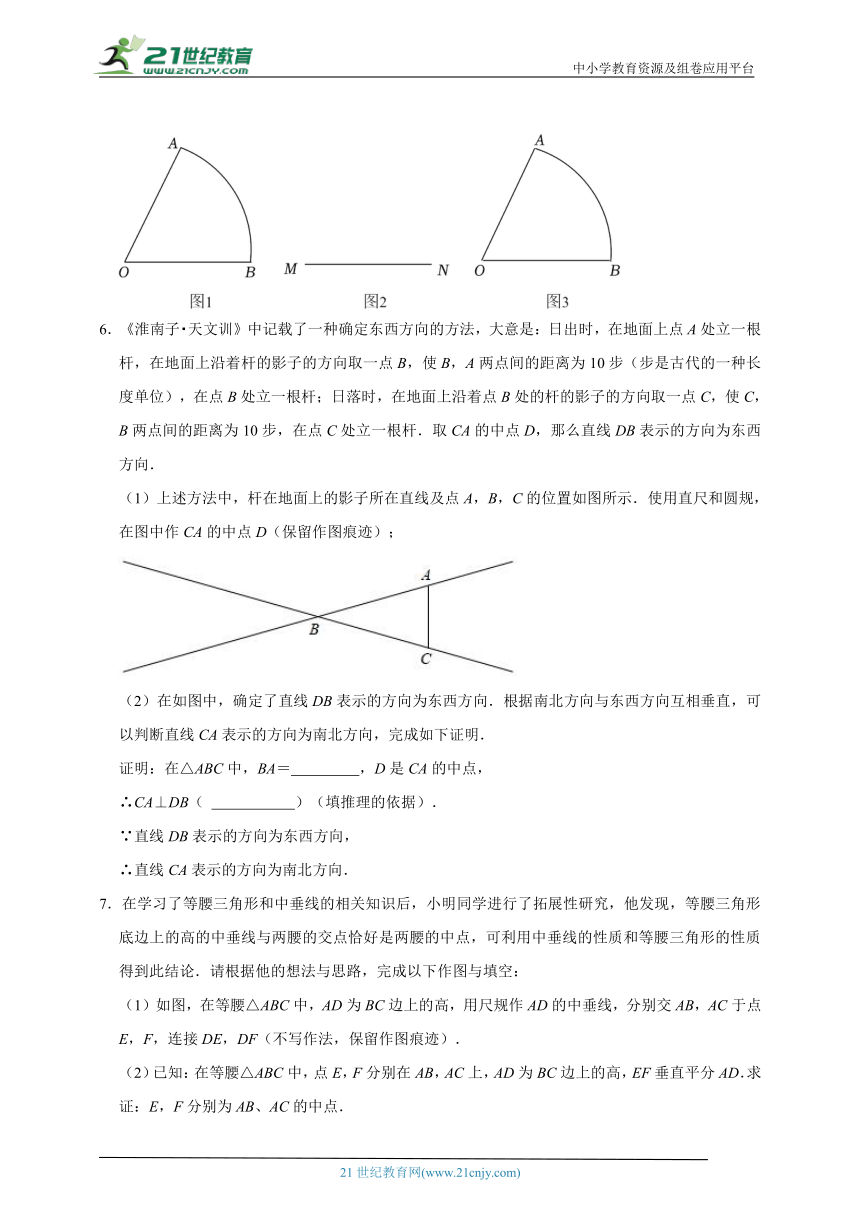
6.《淮南子 天文训》中记载了一种确定东西方向的方法,大意是:日出时,在地面上点A处立一根杆,在地面上沿着杆的影子的方向取一点B,使B,A两点间的距离为10步(步是古代的一种长度单位),在点B处立一根杆;日落时,在地面上沿着点B处的杆的影子的方向取一点C,使C,B两点间的距离为10步,在点C处立一根杆.取CA的中点D,那么直线DB表示的方向为东西方向.
(1)上述方法中,杆在地面上的影子所在直线及点A,B,C的位置如图所示.使用直尺和圆规,在图中作CA的中点D(保留作图痕迹);
(2)在如图中,确定了直线DB表示的方向为东西方向.根据南北方向与东西方向互相垂直,可以判断直线CA表示的方向为南北方向,完成如下证明.
证明:在△ABC中,BA= ,D是CA的中点,
∴CA⊥DB( )(填推理的依据).
∵直线DB表示的方向为东西方向,
∴直线CA表示的方向为南北方向.
7.在学习了等腰三角形和中垂线的相关知识后,小明同学进行了拓展性研究,他发现,等腰三角形底边上的高的中垂线与两腰的交点恰好是两腰的中点,可利用中垂线的性质和等腰三角形的性质得到此结论.请根据他的想法与思路,完成以下作图与填空:
(1)如图,在等腰△ABC中,AD为BC边上的高,用尺规作AD的中垂线,分别交AB,AC于点E,F,连接DE,DF(不写作法,保留作图痕迹).
(2)已知:在等腰△ABC中,点E,F分别在AB,AC上,AD为BC边上的高,EF垂直平分AD.求证:E,F分别为AB、AC的中点.
证明:∵EF垂直平分AD,
∴① ,
∴∠EAD=∠EDA.
∵AD为BC边上的高,
∴∠ADB=90°,
∴∠EDA+∠EDB=90°.
∵在Rt△ABD中,∠EAD+∠B=90°,
∴② ,
∴BE=DE,
∴③ ,
∴点E为AB的中点.
同理可得:点F为AC的中点.
进一步思考,如果△ABC是任意三角形呢?请你模仿题中表述,写出你猜想的结论:④ .
8.在学习圆的相关知识后,小帅同学进行了关于弦切角的相关探索(弦切角定义:顶点在圆上,一边与圆相交,另一边与圆相切的角;如图,直线IJ与⊙O相切于点I,HI是⊙O的一条弦,则∠HIJ就是弦切角),发现弦切角的大小与它所夹弧所对的圆周角度数相关.请根据这个思路完成以下作图和填空.
(1)尺规作图:已知AB是⊙O的直径,延长AB,过点B作⊙O的切线MN;(M在点B左侧,N在点B右侧.保留作图痕迹,不写作法)
(2)如图C、D是圆上两点,在(1)的条件下,∠DBN为弦切角,求证:∠DBN=∠BCD.
证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB= ① .
∵MN是过点B的切线,
∴② .
即∠ABN=90°,
∴∠DBN+∠ABD=90°
∵∠A+∠ABD=90°
∴∠DBN=∠A
又∵∠A和∠C是弧所对的圆周角
∴∠A= ③ .
∴∠DBN=∠C.
由此,我们可以得到弦切角的结论:弦切角 ④ 它所夹弧所对的圆周角.(横线上填:“大于”或“等于”或“小于”)
9.我们知道在含30°的直角三角形中,30°角所对的直角边等于斜边的一半.小红进行了拓展性研究,她发现这个定理反过来说也成立.她通过构造斜边上的中垂线来证明含有30°角,请跟根据她的思路,完善以下作图与填空:
(1)如图,用直尺和圆规作斜边AB的垂直平分线DE,分别与AB、BC交于点D、点E,并连接AE.(只保留作图痕迹)
(2)已知:在△ABC中,∠C=90°,.求证:∠B=30°.
证明:∵DE垂直平分AB,
∴∠ADE=90°,,
∠C=90°,,
∴① ,∠ADE=∠C=90°.
在Rt△ACE和Rt△ADE中,,
∴Rt△ACE≌Rt△ADE(HL),
∴∠CAE=∠DAE.
∵DE垂直平分AB,
∴③ ,
∴∠DAE=∠B.
又∵∠CAB+∠B=180°﹣∠C=90°,
∴∠CAE+∠DAE+∠B=3∠B=90°,
∴∠B=30°.
根据小红的证明过程,进一步发现,30°角与所对直角边的关系,请你完善该逆定理:如果在直角三角形中,一条直角边是斜边的一半,那么④ .
10.水兴县某中学的同学们在学习了《图形的相似》之后,数学柳老师给出了下面的问题:如图,Rt△ABD与Rt△CDB中,斜边AD与BC相交于点M,过点M作MH⊥BD于点H.探究AB、MH、CD之间的数量关系,并证明.
下面是小许同学的探究过程,请根据题意补充完整探究过程.
(1)请在答题卡上完成尺规作图:过点M作MH⊥BD垂足为点H.(保留作图痕迹,不用写作法)
(2)请将①②③④⑤补充完整并填写在答题卡上.
解:∵AB⊥BD,MH⊥BD,
∴MH∥AB.
∴△DMH∽① .
∴.
∵CD⊥BD,MH⊥BD,
∴MH∥CD.
∴△BMH∽② .
∴③ .
∴④ .
(注意:这里要求填写化简之后的数字结果) 小许进一步探究,如果把题设中的三个垂直关系改为:AB∥CD∥MH,请你帮她写出AB、MH、CD这三条线段之间的数量关系⑤ .
11.在学分线性质的过程中,首先要探究角平分线的作图方法,请阅读下列材料,回答问题:
已知:∠AOB,求作:∠AOB的平分线.
作法:(I)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;
(II)分别以点M,N为圆心,大于的长为半径画弧,两弧在∠AOB的内部相交于点C;
(III)画射线OC,则射线OC即为所求.
(1)如图1,射线OC就是∠AOB的角平分线的依据是 ;
A.SAS
B.ASA
C.SSS
D.AAS
(2)课后老师留了一道思考题:
在不限于圆规、直尺的条件下,思考还有没有其他作角平分线的方法?
下面是两位同学给出的两种方法:
①同学1:用三角板按下面方法画角平分线:
如图2,在已知∠AOB的边OA,OB上分别取OC=OD,再分别过点C,D作OA,OB的垂线,两垂线交于点P,画射线OP,则OP平分∠AOB.
请你帮这位同学证明:OP平分∠AOB;
②同学2:用圆规和直尺按下面方法画角平分线:
如图3,以点O为圆心,以任意长为半径画弧与OA,OB分别交于点C,D,再以任意长为半径画弧与OA,OB分别交于点E,F,连接CF,DE交于点P,画射线OP,则OP平分∠AOB.
你认为同学2的这种作角平分线的方法正确吗?若正确,请给出证明过程;若错误,请说明理由.
12.我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.那么,不相等的边(或角)所对的角(或边)之间的大小关系怎样呢?如图,小洲同学通过直观观察发现:在△ABC中,如果AB大于AC,那么AB边所对的∠C大于AC边所对的∠B.为了证明这一发现,小洲同学的解决思路是构造全等三角形将∠C转化为一个三角形的外角,利用三角形的外角大于不相邻的内角使问题得以证明.根据他的思路,完成以下作图与填空:
已知:如图,△ABC中,AB>AC.
求证:∠C>∠B.
(1)尺规作图:作∠A的角平分线AP,交BC于点D,在AB上截取AE=AC,连接DE.(保留作图痕迹)留作图痕迹)
(2)证明:∵AP平分线∠BAC,
∴ .
在△EAD和△CAD中,
∴△EAD≌△CAD(SAS).
∴∠C= .
∵;
,∴∠C>∠B.
进一步思考,在△ABC中,如果已知∠C>∠B呢?请你模仿题中表述,写出你猜想的结论: .
13.【问题背景】在△ABC中,AB,BC,AC三边的边长分别为,,,求这个三角形的面积.小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC,如图1所示.这样不需求△ABC的高,借助网格就能计算三角形的面积.
(1)直接写出△ABC的面积,S△ABC= .
(2)【思维拓展】若△A1B1C1三边的长分别为,,,请利用图2的正方形网格中画出△A1B1C1(每个小正方形的边长为a).
(3)【探索创新】若△A2B2C2的三边长分别为(m>0,n>0,且m≠n),试运用构图法求出△A2B2C2的面积.
14.【问题背景】:数学活动课上,老师将一副三角尺按图1所示位置摆放,分别作出∠AOB,∠BOC的平分线OG,OF,然后提出如下问题:求出∠GOF的度数.
【特例探究】:小明同学决定从特例入手探究老师提出的问题,他将三角尺分别按图2方式摆放,OG,OF仍然分别是∠AOB,∠BOC的角平分线.其中∠AOC=90°,∠BOC=30°.
(1)请你帮助小明计算出∠GOF的度数为 °;
【发现感悟】:小明发现,按图1摆放时,条件不变,虽然不知道∠BOC的度数,但也可以求出∠GOF的度数.
(2)请你帮小明完成这个问题的解答;
(3)积累了以上探究问题的经验,结合图3,若∠AOC=m°,则∠GOF= °;
【类比拓展】:(4)已知∠BOC=m°,若OA是∠BOC外一条射线,,OD,OE分别平分∠AOC,∠AOB,当∠DOE=m°﹣18°时,求出m的值(自己画出示意图求解).
15.(1)操作实践:如图,△ABC中,∠A=90°,∠B=22.5°,请画出一条直线把△ABC分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数.(要求画出一种分割方法即可)
(2)分类探究:已知△ABC中的最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,请直接写出△ABC中最大内角的所有可能值.
16.学习了三角形的中位线定理后,小涵进行了拓展性研究,他发现.连接梯形两腰中点的线段也具有类似的性质.探究过程如下:
(1)用直尺和圆规,作线段CD的垂直平分线,垂足为点F,连接EF,连接AF并延长交线段BC的延长线于点M(只保留作图痕迹):
(2)已知:在四边形ABCD中,AD∥BC,E为AB中点,F为CD中点.
猜想:EF∥AD∥BC,且.
证明:∵F是CD中点,
∴① ,
∵AD∥BC,
∴∠DAF=∠FMC,
在△ADF和△MCF中,
,
∴△ADF≌△MCF,
∴AF=FM,AD=CM,
在△ABM中,E为AB中点,F为AM中点,
∴EF∥BM且③ .
∵BM=BC+CM=BC+AD,
∴EF(AD+BC),EF//AB,EF//CD,
请你根据该探究过程完成下面命题:连接梯形两腰中点的线段平行于两底并④ .
17.学习了角平分线性质后,小明进行了拓展研究,他发现△ABC的外角∠CBE和外角∠BCD的角平分线BF,CF交于点F,他猜想AF平分∠BAC,他的解决思路是利用角平分线性质.过点F分别向BE、BC、CD作垂线,再证明∠BAF和∠CAF这两个角所在的三角形全等得出结论.其中小明已经完成过点F分别向BE、BC作垂线,请根据他的思路完成以下作图与填空.
(1)用直尺和圆规,过点F作FK⊥CD于点K.(保留作图痕迹)
(2)已知:如图,△ABC的外角∠CBE和外角∠BCD的角平分线BF,CF交于点F,FK⊥CD于点K,FH⊥BC于点H,FG⊥BE于点G.求证:∠BAF=∠CAF.
证明:∵BF平分∠CBE,
FH⊥BC于点H,FG⊥BE于点G,
∴FH=① ,
∵CF平分∠BCD,
FK⊥CD于点K,FH⊥BC于点H,
∴FH=FK.
∴② ,
∵FG⊥BE,FK⊥CD,
∴△AGF,△AKF均为直角三角形,
在Rt△AGF和Rt△AKF中:
③∴Rt△AGF≌Rt△AKF(HL).
∴∠BAF=∠CAF.
由此他得出结论:三角形的两(4) 所在直线交点与三角形另一顶点连线平分这个内角.
18.请仔细阅读下面的材料,并完成相应的任务.
作角的平分线
数学兴趣课上,老师让同学们利用尺规作∠AOB的平分线,同学们以小组为单位展开了讨论,勤学小组展示了学习过的作法:如图1,以点O为圆心,任意长为半径作弧,分别交OA,OB于点M,N;再分别以点M,N为圆心,大于的长为半径作弧,两弧相交于点P,作射线OP,则OP即为∠AOB的平分线.
勤学小组的证明过程如下:
连接PM,PN.
…
任务:
(1)请按照上面的材料,写出该证明的剩余部分;
(2)在图2中再设计一种不同的方法作∠AOB的平分线.(要求:尺规作图,保留作图痕迹,不写作法)
19.在学行四边形与正方形的相关知识后,智慧小组进行了更深入的探究.他们发现,如图所示的正方形ABCD,分别取BC,CD的中点N,M,连接AM,DN交于点E,过B作AM的垂线,交AM于点Q,交AD于点P.则四边形BPDN是平行四边形.
(1)用尺规完成以下基本作图:过B作AM的垂线,交AM于点Q,交AD于点P(只保留作图痕迹).
(2)根据(1)中所作图形,智慧小组发现四边形BPDN是平行四边形成立,并给出了证明,请补全证明过程.
证明:∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠C=90°,AD∥BC.
又∵M,N分别为BC,CD的中点,
∴,,
∴① ,
在△ADM与△DCN中,
,
∴△ADM≌△DCN(SAS).
∴② .
又∵∠CDN+∠ADN=90°,
∴∠DAM+∠ADN=90°,
∴∠AED=90°,
又∵BP⊥AE,
∴∠AQP=∠AED=90°,
∴③ .
又∵DP∥BN,
∴四边形BPDN是平行四边形.
进一步思考,智慧小组发现任取BC,CD的上点N,M(M不与C,D重合),DM=CN,连接AM,DN,过B作AM的垂线,交AD于点P,则四边形BPDN是④ .
20.(1)【问题情境】我国古代已经用角尺平分任意角,做法如下:如图①,在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线OC是∠AOB的平分线.请说明此做法的理由;
(2)【拓展实践】某公园的两条小路AB和AC,汇聚形成了一个岔路口A(如图②),现要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到休息椅M和N的距离相等.问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的备用图中作出路灯E的位置.(保留作图痕迹,不写作法)
中考数学一轮复习 尺规作图
参考答案与试题解析
一.解答题(共20小题)
1.在学习了矩形与菱形的相关知识后,小明同学进行了更深入的研究,他发现,过矩形的一条对角线的中点作这条对角线的垂线,与矩形两边相交的两点和这条对角线的两个端点构成的四边形是菱形,可利用证明三角形全等得到此结论.根据他的想法与思路,完成以下作图与填空:
(1)如图,在矩形ABCD中,点O是对角线AC的中点.用尺规过点O作AC的垂线,分别交AB,CD于点E,F,连接AF,CE.(不写作法,保留作图痕迹)
(2)已知:矩形ABCD,点E,F分别在AB,CD上,EF经过对角线AC的中点O,且EF⊥AC.求证:四边形AECF是菱形.
证明:∵四边形ABCD是矩形,
∴AB∥CD.
∴① ∠OFC=∠OEA ,∠OCF=∠OAE.
∵点O是AC的中点,
∴② OC=OA .
∴△CFO≌△AEO(AAS).
∴③ OF=OE .
又∵OA=OC,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
进一步思考,如果四边形ABCD是平行四边形呢?请你模仿题中表述,写出你猜想的结论:④ 四边形AECF是菱形 .
【考点】作图—基本作图;全等三角形的判定与性质;平行四边形的判定与性质;菱形的判定与性质;矩形的性质.
【专题】作图题;几何直观;推理能力.
【答案】(1)见解析;
(2)∠OFC=∠OEA,OC=OA,OF=OE,四边形AECF是菱形.
【分析】(1)根据要求作出图形;
(2)根据对角线互相垂直的平行四边形是菱形证明即可.
【解答】(1)解:图形如图所示:
(2)证明:∵四边形ABCD是矩形,
∴AB∥CD.
∴①∠OFC=∠OEA,∠OCF=∠OAE.
∵点O是AC的中点,
∴②OC=OA.
∴△CFO≌△AEO(AAS).
∴③OF=OE.
又∵OA=OC,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
进一步思考,如果四边形ABCD是平行四边形呢?请你模仿题中表述,写出你猜想的结论:④四边形AECF是菱形.
故答案为:∠OFC=∠OEA,OC=OA,OF=OE,四边形AECF是菱形.
【点评】本题考查作图﹣基本作图,全等三角形的判定和性质,平行四边形的判定和性质,菱形的判定与性质,矩形的性质等知识,解题的关键是正确寻找全等三角形解决问题.
2.根据背景素材,探索解决问题.
平面直角坐标系中画一个边长为2的正六边形ABCDEF
背景素材 六等分圆原理,也称为圆周六等分问题,是一个古老而经典的几何问题,旨在解决如何使用直尺和圆规将一个圆分成六等份的问题.这个问题由欧几里得在其名著《几何原本》中详细阐述.
已知条件 点C与坐标原点O重合,点D在x轴的正半轴上且坐标为(2,0).
操作步骤 ①分别以点C,D为圆心,CD长为半径作弧,两弧交于点P; ②以点P为圆心,PC长为半径作圆; ③以CD的长为半径,在⊙P上顺次截取; ④顺次连接DE,EF,FA,AB,BC.得到正六边形ABCDEF.
问题解决
任务一 根据以上信息,请你用不带刻度的直尺和圆规,在图中完成这道作图题(保留作图痕迹,不写作法)
任务二 将正六边形ABCDEF绕点D顺时针旋转60°,直接写出此时点E所在位置的坐标: (4,0) .
【考点】作图—复杂作图;坐标与图形变化﹣旋转;正多边形和圆.
【专题】作图题;几何直观.
【答案】任务一:见解析;
任务二:(4,0).
【分析】任务一:根据要求作出图形.
任务二:利用旋转变换的性质判断即可.
【解答】解:任务一:图形如图所示:
任务二:将正六边形ABCDEF绕点D顺时针旋转60°,直接写出此时点E所在位置的坐标(4,0).
【点评】本题考查作图﹣复杂作图,正多边形与圆,坐标与图形变化﹣旋转等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
3.马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、黑、白彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧.如图1的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图2,已知⊙O和圆上一点M.作法如下:
①以点M为圆心,OM长为半径,作弧交⊙O于A,B两点;
②延长MO交⊙O于点C;
即点A,B,C将⊙O的圆周三等分.
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图2中将⊙O的圆周三等分(保留作图痕迹,不写作法);
(2)根据(1)画出的图形,连接AB,AC,BC,若⊙O的半径为2cm,则△ABC的周长为 6 cm.
【考点】作图—应用与设计作图;切线的性质;正多边形和圆.
【专题】作图题;几何直观.
【答案】(1)作图见解析;
(2)6.
【分析】(1)根据要求作出图形;
(2)证明△ABC是等边三角形,解直角三角形求出AB即可.
【解答】解:(1)如图,点A,B,C即为所求.
(2)设CM交AB于点E.
∵,
∴AB=CB=AC,∠AOB=120°,
∵,
∴∠AOM=∠BOM=60°,
∵OA=OB,
∴OE⊥AB,AE=EB=AO sin60°=2(cm),
∴AB=2(cm),
∴△ABC的周长为6cm.
故答案为:6.
【点评】本题考查作图﹣应用与设计作图,切线的性质,正多边形与圆等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
4.【阅读材料】
老师的问题: 已知:如图,AE∥BF. 求作:菱形ABCD,使点C,D分别在BF,AE上. 小明的作法: (1)以A为圆心,AB长为半径画弧,交AE于点D; (2)以B为圆心,AB长为半径画弧,交BF于点C; (3)连接CD. 四边形ABCD就是所求作的菱形.
【解答问题】
请根据材料中的信息,证明四边形ABCD是菱形.
【考点】作图—复杂作图;菱形的判定.
【专题】作图题;几何直观;推理能力.
【答案】见试题解答内容
【分析】根据邻边相等的平行四边形是菱形证明即可.
【解答】证明:由作图可知AD=AB=BC,
∵AE∥BF,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
【点评】本题考查作图﹣复杂作图,菱形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
5.【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;
【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
(友情提醒:以上作图均不写作法,但需保留作图痕迹)
【考点】作图—复杂作图;角平分线的性质;等腰直角三角形;扇形面积的计算.
【专题】作图题;几何直观.
【答案】【初步尝试】作图见解析部分;
【问题联想】作图见解析部分;
【问题再解】作图见解析部分.
【分析】【初步尝试】如图1,作∠AOB的角平分线OP即可;
【问题联想】如图2,作线段MN的垂直平分线RT,垂足为R,在射线RT上截取RP=RM,连接MP,NP,三角形MNP即为所求;
【问题再解】方法一:构造等腰直角三角形OBE,作BC⊥OE,以O为圆心,OC为半径画弧交OB于点D,交OA于点F,弧DF即为所求.方法二:作OB的中垂线交OB于点C,然后以C为圆心,CB长为半径画弧交OB中垂线于点D,再以O为圆心,OD长为半径画弧分别交OA、OB于点F、D.则弧DF即为所求.
【解答】解:【初步尝试】如图1,直线OP即为所求;
【问题联想】如图2,三角形MNP即为所求;
【问题再解】如图3中,即为所求.
【点评】本题考查作图﹣复杂作图,等腰直角三角形的性质,扇形的面积等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
6.《淮南子 天文训》中记载了一种确定东西方向的方法,大意是:日出时,在地面上点A处立一根杆,在地面上沿着杆的影子的方向取一点B,使B,A两点间的距离为10步(步是古代的一种长度单位),在点B处立一根杆;日落时,在地面上沿着点B处的杆的影子的方向取一点C,使C,B两点间的距离为10步,在点C处立一根杆.取CA的中点D,那么直线DB表示的方向为东西方向.
(1)上述方法中,杆在地面上的影子所在直线及点A,B,C的位置如图所示.使用直尺和圆规,在图中作CA的中点D(保留作图痕迹);
(2)在如图中,确定了直线DB表示的方向为东西方向.根据南北方向与东西方向互相垂直,可以判断直线CA表示的方向为南北方向,完成如下证明.
证明:在△ABC中,BA= BC ,D是CA的中点,
∴CA⊥DB( 三线合一 )(填推理的依据).
∵直线DB表示的方向为东西方向,
∴直线CA表示的方向为南北方向.
【考点】作图—应用与设计作图;等腰三角形的性质.
【专题】作图题;几何直观.
【答案】(1)作图见解析部分.
(2)证明见解析部分.
【分析】(1)作线段AC的垂直平分线即可.
(2)利用等腰三角形的三线合一的性质解决问题即可.
【解答】解:(1)如图,点D即为所求.
(2)如图,连接BD.
在△ABC中,BA=BC,D是CA的中点,
∴CA⊥DB(三线合一),
∵直线DB表示的方向为东西方向,
∴直线CA表示的方向为南北方向.
故答案为:BC,三线合一.
【点评】本题考查作图﹣应用与设计作图,等腰三角形的性质等知识,解题的关键是理解题意,学会利用等腰三角形的性质解决问题.
7.在学习了等腰三角形和中垂线的相关知识后,小明同学进行了拓展性研究,他发现,等腰三角形底边上的高的中垂线与两腰的交点恰好是两腰的中点,可利用中垂线的性质和等腰三角形的性质得到此结论.请根据他的想法与思路,完成以下作图与填空:
(1)如图,在等腰△ABC中,AD为BC边上的高,用尺规作AD的中垂线,分别交AB,AC于点E,F,连接DE,DF(不写作法,保留作图痕迹).
(2)已知:在等腰△ABC中,点E,F分别在AB,AC上,AD为BC边上的高,EF垂直平分AD.求证:E,F分别为AB、AC的中点.
证明:∵EF垂直平分AD,
∴① AE=DE ,
∴∠EAD=∠EDA.
∵AD为BC边上的高,
∴∠ADB=90°,
∴∠EDA+∠EDB=90°.
∵在Rt△ABD中,∠EAD+∠B=90°,
∴② ∠EDB=∠B ,
∴BE=DE,
∴③ AE=BE ,
∴点E为AB的中点.
同理可得:点F为AC的中点.
进一步思考,如果△ABC是任意三角形呢?请你模仿题中表述,写出你猜想的结论:④ 三角形一边上的高的中垂线与其它两边的交点恰好是这两边的中点 .
【考点】作图—复杂作图;线段垂直平分线的性质;等腰三角形的性质;直角三角形斜边上的中线;三角形中位线定理.
【专题】作图题;几何直观;推理能力.
【答案】(1)见解答;
(2)AE=DE,∠EDB=∠B,AE=BE,三角形一边上的高的中垂线与其它两边的交点恰好是这两边的中点.
【分析】(1)利用基本作图作AD的垂直平分线即可;
(2)先根据线段垂直平分线的性质得到AE=DE,则∠EAD=∠EDA,再根据等角的余角相等得到∠EDB=∠A,所以BE=DE,则AE=BE,从而可判断点E为AB的中点.同理可得点F为AC的中点,
对于任意△ABC,三角形一边上的高的中垂线与其它两边的交点恰好是这两边的中点.
【解答】(1)解:如图,DE、DF为所作;
(2)证明:∵EF垂直平分AD,
∴AE=DE,
∴∠EAD=∠EDA,
∵AD为BC边上的高,
∴∠ADB=90°,
∴∠EDA+∠EDB=90°,
∵在Rt△ABD中,∠EAD+∠B=90°,
∴∠EDB=∠A,
∴BE=DE,
∴AE=BE
∴点E为AB的中点.
同理可得:点F为AC的中点,
如果△ABC是任意三角形,结论:三角形一边上的高的中垂线与其它两边的交点恰好是这两边的中点.
故答案为:AE=DE,∠EDB=∠B,AE=BE,三角形一边上的高的中垂线与其它两边的交点恰好是这两边的中点.
【点评】本题考查了作图﹣复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的性质和等腰三角形的性质.
8.在学习圆的相关知识后,小帅同学进行了关于弦切角的相关探索(弦切角定义:顶点在圆上,一边与圆相交,另一边与圆相切的角;如图,直线IJ与⊙O相切于点I,HI是⊙O的一条弦,则∠HIJ就是弦切角),发现弦切角的大小与它所夹弧所对的圆周角度数相关.请根据这个思路完成以下作图和填空.
(1)尺规作图:已知AB是⊙O的直径,延长AB,过点B作⊙O的切线MN;(M在点B左侧,N在点B右侧.保留作图痕迹,不写作法)
(2)如图C、D是圆上两点,在(1)的条件下,∠DBN为弦切角,求证:∠DBN=∠BCD.
证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB= ① 90° .
∵MN是过点B的切线,
∴② AB⊥MN .
即∠ABN=90°,
∴∠DBN+∠ABD=90°
∵∠A+∠ABD=90°
∴∠DBN=∠A
又∵∠A和∠C是弧所对的圆周角
∴∠A= ③ ∠C .
∴∠DBN=∠C.
由此,我们可以得到弦切角的结论:弦切角 ④ 它所夹的弧所对的圆周角 它所夹弧所对的圆周角.(横线上填:“大于”或“等于”或“小于”)
【考点】作图—复杂作图;垂径定理;圆周角定理;直线与圆的位置关系;切线的判定与性质.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2)90°;AB⊥MN;∠C;它所夹的弧所对的圆周角.
【分析】(1)以B为圆心,任意长度为半径画弧,交AB于点G、H,以G、H为圆心,大于长度为半径画弧,两弧交于点M、N,作直线MN即可;
(2)连接AD,由AB是⊙O的直径,得∠ADB=90°;又MN是过点B的切线,则AB⊥MN,即∠ABN=90°,故有∠DBN=∠A,又∠A=∠C,则∠DBN=∠C,从而得出结论;
【解答】(1)解:①以B为圆心,任意长度为半径画弧,交AB于点G、H;
②以G、H为圆心,大于长度为半径画弧,两弧交于点M、N;
③作直线MN;
∴MN即为所求;
(2)证明:连接AD,如图:
∵AB是⊙O的直径,
∴∠ADB=90°;
∵MN是过点B的切线,
∴AB⊥MN,即∠ABN=90°,
∴90°=∠DBN+∠ABD,
∵90°=∠A+∠ABD,
∴∠A=∠DBN,
又∵∠A和∠C是弧所对的圆周角,
∴∠C=∠A,
∴∠C=∠DBN,
由此,我们可以得到弦切角的结论:弦切角等于它所夹的弧所对的圆周角.
故答案为:90°;AB⊥MN;∠C;它所夹的弧所对的圆周角.
【点评】本题考查了尺规作图——作垂线,圆周角定理,切线的判定与性质,同角的余角相等,熟练掌握知识点的应用是解题的关键.
9.我们知道在含30°的直角三角形中,30°角所对的直角边等于斜边的一半.小红进行了拓展性研究,她发现这个定理反过来说也成立.她通过构造斜边上的中垂线来证明含有30°角,请跟根据她的思路,完善以下作图与填空:
(1)如图,用直尺和圆规作斜边AB的垂直平分线DE,分别与AB、BC交于点D、点E,并连接AE.(只保留作图痕迹)
(2)已知:在△ABC中,∠C=90°,.求证:∠B=30°.
证明:∵DE垂直平分AB,
∴∠ADE=90°,,
∠C=90°,,
∴① AD=AC ,∠ADE=∠C=90°.
在Rt△ACE和Rt△ADE中,,
∴Rt△ACE≌Rt△ADE(HL),
∴∠CAE=∠DAE.
∵DE垂直平分AB,
∴③ AE=BE ,
∴∠DAE=∠B.
又∵∠CAB+∠B=180°﹣∠C=90°,
∴∠CAE+∠DAE+∠B=3∠B=90°,
∴∠B=30°.
根据小红的证明过程,进一步发现,30°角与所对直角边的关系,请你完善该逆定理:如果在直角三角形中,一条直角边是斜边的一半,那么④ 那么这条直角边所对的角也为30° .
【考点】作图—基本作图;全等三角形的判定与性质;角平分线的性质;线段垂直平分线的性质;含30度角的直角三角形;直角三角形斜边上的中线.
【专题】作图题;线段、角、相交线与平行线;图形的全等;等腰三角形与直角三角形;运算能力;推理能力.
【答案】①AD=AC,②AE=AE,③AE=BE,④那么这条直角边所对的角也为30°.
【分析】(1)根据题意画出图形,即可求解;
(2)根据线段垂直平分线的性质的∠ADE=90°,ADAB,求得AD=AC,∠ADE=∠C=90°.根据全等三角形的性质得到∠CAE=∠DAE.根据线段垂直平分线的性质得到AE=BE,求得∠DAE=∠B.于是得到结论.
【解答】(1)解:如图所示,DE为所求线段;
(2)证明:∵DE垂直平分AB,
∴∠ADE=90°,ADAB,
∵∠C=90°,ACAB,
∴AD=AC,∠ADE=∠C=90°.
在Rt△ACE和Rt△ADE中,
,
∴Rt△ACE≌Rt△ADE(HL),
∴∠CAE=∠DAE.
∵DE垂直平分AB,
∴③AE=BE,
∴∠DAE=∠B.
又∵∠CAB+∠B=180°﹣∠C=90°,
∴∠CAE+∠DAE+∠B=3∠B=90°,
∴∠B=30°.
根据小红的证明过程,进一步发现,30°角与所对直角边的关系,请你完善该逆定理:如果在直角三角形中,一条直角边是斜边的一半,那么④那么这条直角边所对的角也为30°.
故答案为:①AD=AC,②AE=AE,③AE=BE,④那么这条直角边所对的角也为30°.
【点评】本题考查了作图﹣基本作图,全等三角形的判定和性质,线段垂直平分线的性质,直角三角形的全等的判断和性质,熟练运用这些性质进行推理是本题的关键.
10.水兴县某中学的同学们在学习了《图形的相似》之后,数学柳老师给出了下面的问题:如图,Rt△ABD与Rt△CDB中,斜边AD与BC相交于点M,过点M作MH⊥BD于点H.探究AB、MH、CD之间的数量关系,并证明.
下面是小许同学的探究过程,请根据题意补充完整探究过程.
(1)请在答题卡上完成尺规作图:过点M作MH⊥BD垂足为点H.(保留作图痕迹,不用写作法)
(2)请将①②③④⑤补充完整并填写在答题卡上.
解:∵AB⊥BD,MH⊥BD,
∴MH∥AB.
∴△DMH∽① △DAB .
∴.
∵CD⊥BD,MH⊥BD,
∴MH∥CD.
∴△BMH∽② △BCD .
∴③ .
∴④ 1 .
(注意:这里要求填写化简之后的数字结果) 小许进一步探究,如果把题设中的三个垂直关系改为:AB∥CD∥MH,请你帮她写出AB、MH、CD这三条线段之间的数量关系⑤ .
【考点】作图—基本作图;相似三角形的判定与性质.
【专题】作图题;图形的相似;几何直观;推理能力.
【答案】(1)画图见解析;
(2)△DAB,△BCD,,1,.
【分析】(1)根据题意,过点M作MH⊥BD垂足为点H;
(2)根据相似三角形的性质与判定,完成填空,即可求解.
【解答】解:(1)如图,MH即为所求;
(2)∵AB⊥BD,MH⊥BD,
∴MH∥AB,
∴△DMH∽△DAB,
∴,
∵CD⊥BD,MH⊥BD,
∴MH∥CD,
∴△BMH∽△BCD,
∴,
∴,
如果把题设中的三个垂直关系改为:AB∥CD∥MH,
∴△DMH∽△DAB,△BMH∽△BCD,
∴,,
∴,
∴.
故答案为:△DAB,△BCD,,1,.
【点评】本题考查了作图﹣基本作图,相似三角形的性质与判定,解决本题的关键是得到△DMH∽△DAB.
11.在学分线性质的过程中,首先要探究角平分线的作图方法,请阅读下列材料,回答问题:
已知:∠AOB,求作:∠AOB的平分线.
作法:(I)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;
(II)分别以点M,N为圆心,大于的长为半径画弧,两弧在∠AOB的内部相交于点C;
(III)画射线OC,则射线OC即为所求.
(1)如图1,射线OC就是∠AOB的角平分线的依据是 C ;
A.SAS
B.ASA
C.SSS
D.AAS
(2)课后老师留了一道思考题:
在不限于圆规、直尺的条件下,思考还有没有其他作角平分线的方法?
下面是两位同学给出的两种方法:
①同学1:用三角板按下面方法画角平分线:
如图2,在已知∠AOB的边OA,OB上分别取OC=OD,再分别过点C,D作OA,OB的垂线,两垂线交于点P,画射线OP,则OP平分∠AOB.
请你帮这位同学证明:OP平分∠AOB;
②同学2:用圆规和直尺按下面方法画角平分线:
如图3,以点O为圆心,以任意长为半径画弧与OA,OB分别交于点C,D,再以任意长为半径画弧与OA,OB分别交于点E,F,连接CF,DE交于点P,画射线OP,则OP平分∠AOB.
你认为同学2的这种作角平分线的方法正确吗?若正确,请给出证明过程;若错误,请说明理由.
【考点】作图—基本作图;全等三角形的判定与性质;角平分线的性质.
【专题】作图题;图形的全等;推理能力.
【答案】(1)C;
(2)①证明见解析,②同学2这种作角平分线的方法正确.证明见解析.
【分析】(1)连接MC,NC,利用SSS证明△OMC≌△ONC即可;
(2)①由作法得OC=OD,则可判断Rt△OPC≌Rt△OPD,从而得到OP平分∠AOB;
②由作法得OC=OD,OE=OF则可判断△OCF≌△ODE,可得到∠CEP=∠OFP,因此可证明△CEP≌△DPF,再根据EP=FP,可得△OEP≌△OFP,从而得到OP平分∠AOB.
【解答】(1)解:连接MC,NC,
由作法得MC=NC,OM=ON,
∵OC=OC,
∴△OMC≌△ONC(SSS),
∴∠AOC=∠BOC;
故选:C;
(2)①证明:由作法得OC=OD,
∵OP=OP,
∴Rt△OPC≌Rt△OPD(HL),
∴∠COP=∠DOP,
∴OP平分∠AOB;
②解:同学2这种作角平分线的方法正确.
理由如下:由作法得OC=OD,OE=OF,可知CE=DF.
在△OCF和△ODE中,
,
∴△OCF≌△ODE(SAS),
∴∠CEP=∠OFP,
在△CEP和△DPF中,
,
∴△CEP≌△DFP(AAS),
∴EP=FP,
在△OEP与△OFP中,
,
∴△OEP≌△OFP(SSS),
∴∠EOP=∠FOP.
即OP平分∠AOB.
【点评】本题考查了作图—基本作图,全等三角形的判定与性质、角平分线的性质,熟练掌握5种基本作图(作已知角的角平分线)是解题的关键.
12.我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.那么,不相等的边(或角)所对的角(或边)之间的大小关系怎样呢?如图,小洲同学通过直观观察发现:在△ABC中,如果AB大于AC,那么AB边所对的∠C大于AC边所对的∠B.为了证明这一发现,小洲同学的解决思路是构造全等三角形将∠C转化为一个三角形的外角,利用三角形的外角大于不相邻的内角使问题得以证明.根据他的思路,完成以下作图与填空:
已知:如图,△ABC中,AB>AC.
求证:∠C>∠B.
(1)尺规作图:作∠A的角平分线AP,交BC于点D,在AB上截取AE=AC,连接DE.(保留作图痕迹)留作图痕迹)
(2)证明:∵AP平分线∠BAC,
∴ ∠BAD=∠CAD .
在△EAD和△CAD中,
∴△EAD≌△CAD(SAS).
∴∠C= ∠AED .
∵;
,∴∠C>∠B.
进一步思考,在△ABC中,如果已知∠C>∠B呢?请你模仿题中表述,写出你猜想的结论: 在同一个三角形中,大边所对角比小边所对角大 .
【考点】作图—复杂作图;三角形的稳定性;全等三角形的判定与性质;角平分线的性质.
【专题】作图题;证明题;图形的全等;几何直观;推理能力.
【答案】(1)见解析;
(2)∠BAD=∠CAD,∠AED,∠B,在同一个三角形中,大边所对角比小边所对角大.
【分析】(1)根据作角平分线的基本作法作图;
(2)根据全等三角形的性质证明.
【解答】(1)解:如图所示即为所求;
(2)证明:∵AP平分线∠BAC,
∴∠BAD=∠CAD,
在△EAD和△CAD中,
,
∴△EAD≌△CAD(SAS),
∴∠C=∠AED,
∵∠AED>∠B,
∴∠C>∠B.
结论:在同一个三角形中,大边所对角比小边所对角大.
故答案为:∠BAD=∠CAD,AD=AD,∠AED,∠B,在同一个三角形中,大边所对角比小边所对角大.
【点评】本题考查了作图﹣复杂作图,掌握全等三角形的判定定理和性质定理是解题的关键.
13.【问题背景】在△ABC中,AB,BC,AC三边的边长分别为,,,求这个三角形的面积.小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC,如图1所示.这样不需求△ABC的高,借助网格就能计算三角形的面积.
(1)直接写出△ABC的面积,S△ABC= .
(2)【思维拓展】若△A1B1C1三边的长分别为,,,请利用图2的正方形网格中画出△A1B1C1(每个小正方形的边长为a).
(3)【探索创新】若△A2B2C2的三边长分别为(m>0,n>0,且m≠n),试运用构图法求出△A2B2C2的面积.
【考点】作图—应用与设计作图;二次根式的应用;勾股定理.
【专题】作图题;几何直观.
【答案】(1);
(2)见解析;
(3)5mn.
【分析】(1)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可;
(2)利用勾股定理,数形结合的射线画出图形;
(3)利用网格构造三角形,利用分割法求出三角形面积.
【解答】解:(1)如图①S△ABC=3×31×22×31×3;
故答案为:;
(2)如图②中,△A1B1C1即为所求;
(3)如图③,△A2B2C2的面积=4n×3m2n×2m4n×m2n×3m=5mn.
【点评】本题考查作图﹣应用与设计作图,二次根式的应用,勾股定理等知识,解题的关键是学会利用数形结合的思想解决问题.
14.【问题背景】:数学活动课上,老师将一副三角尺按图1所示位置摆放,分别作出∠AOB,∠BOC的平分线OG,OF,然后提出如下问题:求出∠GOF的度数.
【特例探究】:小明同学决定从特例入手探究老师提出的问题,他将三角尺分别按图2方式摆放,OG,OF仍然分别是∠AOB,∠BOC的角平分线.其中∠AOC=90°,∠BOC=30°.
(1)请你帮助小明计算出∠GOF的度数为 45 °;
【发现感悟】:小明发现,按图1摆放时,条件不变,虽然不知道∠BOC的度数,但也可以求出∠GOF的度数.
(2)请你帮小明完成这个问题的解答;
(3)积累了以上探究问题的经验,结合图3,若∠AOC=m°,则∠GOF= °;
【类比拓展】:(4)已知∠BOC=m°,若OA是∠BOC外一条射线,,OD,OE分别平分∠AOC,∠AOB,当∠DOE=m°﹣18°时,求出m的值(自己画出示意图求解).
【考点】作图—基本作图;角平分线的定义;余角和补角.
【专题】计算题;分类讨论;运算能力.
【答案】(1)45;
(2)∠GOF=45°;
(3);
(4)m的值为36°或132°.
【分析】(1)∠GOF=∠BOG﹣∠BOF∠AOB∠BOC,∠AOB=120°,∠BOC=30°;
(2)∠GOF=∠BOG﹣∠BOF∠AOB∠BOC,∠AOB=90°+∠BOC;
(3)∠GOF=∠BOG﹣∠BOF∠AOB∠BOC,∠AOB=∠AOC+∠BOC;
(4)分情况讨论.
【解答】解:(1)∵OG,OF分别是∠AOB,∠BOC的角平分线,
∴∠BOG∠AOB,∠BOF∠BOC,
∵∠AOB=∠AOC+∠BOC=120°,∠BOC=30°,
∴∠BOG=60°,∠BOF=15°,
∴∠GOF=∠BOG﹣∠BOF=45°,
故答案为:45;
(2)∠BOF∠BOC,
∠BOG∠AOB(90°+∠BOC)=45°+∠BOF,
∠GOF=∠BOG﹣∠BOF=45°;
(3)∠BOF∠BOC,
∠BOG∠AOB(m°+∠BOC)∠BOF,
∠GOF=∠BOG﹣∠BOF,
故答案为:;
(4),
∠DOE=∠AOE﹣∠AOD∠AOB∠AOCm°m°m°,
∵∠DOE=m°﹣18°,
∴m°﹣18°m°,
解得:m°=36°,
∠DOE=∠AOD+∠AOE∠AOB∠AOCm°+180°m°=180°m°,
∵∠DOE=m°﹣18°,
∴m°﹣18°=180°m°,
解得:m°=132°,
∴m的值为36°或132°.
【点评】本题考查了角平分线,关键是注意分类讨论.
15.(1)操作实践:如图,△ABC中,∠A=90°,∠B=22.5°,请画出一条直线把△ABC分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数.(要求画出一种分割方法即可)
(2)分类探究:已知△ABC中的最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,请直接写出△ABC中最大内角的所有可能值.
【考点】作图—应用与设计作图;三角形内角和定理;等腰三角形的性质.
【专题】作图题;几何直观.
【答案】(1)画图见解析;(2)画图见解析;△ABC的最大内角可能值是117°或108°或90°或84°.
【分析】(1)根据要求作出图形即可;
(2)分四种情形,分别作出图形求解即可.
【解答】解:(1)如图,
(2)设分割线为AD,
图1的最大角=39°+78°=117°,
图2的最大角=24°+(180°﹣2×48°)=108°,
图3的最大角=24°+66°=90°,
图4的最大角=84°,
故△ABC的最大内角可能值是117°或108°或90°或84°.
【点评】本题考查作图﹣应用与设计作图,三角形内角和定理,等腰三角形的性质等知识,解题的关键是学会用分类讨论的思想思考问题.
16.学习了三角形的中位线定理后,小涵进行了拓展性研究,他发现.连接梯形两腰中点的线段也具有类似的性质.探究过程如下:
(1)用直尺和圆规,作线段CD的垂直平分线,垂足为点F,连接EF,连接AF并延长交线段BC的延长线于点M(只保留作图痕迹):
(2)已知:在四边形ABCD中,AD∥BC,E为AB中点,F为CD中点.
猜想:EF∥AD∥BC,且.
证明:∵F是CD中点,
∴① DF=CF ,
∵AD∥BC,
∴∠DAF=∠FMC,
在△ADF和△MCF中,
,
∴△ADF≌△MCF,
∴AF=FM,AD=CM,
在△ABM中,E为AB中点,F为AM中点,
∴EF∥BM且③ EF .
∵BM=BC+CM=BC+AD,
∴EF(AD+BC),EF//AB,EF//CD,
请你根据该探究过程完成下面命题:连接梯形两腰中点的线段平行于两底并④ 等于两底和的一半 .
【考点】作图—基本作图;解直角三角形;全等三角形的判定与性质;线段垂直平分线的性质;三角形中位线定理;梯形中位线定理.
【专题】图形的全等;梯形;尺规作图;推理能力.
【答案】(1)见解析;
(2)①DF=CF; ②∠DFA=∠CFM; ③EFBM;④等于两底和的一半.
【分析】(1)根据要求作出图形;
(2)把四边形问题转化为三角形问题解决.
【解答】解:(1)图形如图所示:
(2)猜想:EF∥AD∥BC,且EF.
证明:∵F是CD中点,
∴①DF=CF,
∵AD∥BC,
∴∠DAF=∠FMC,
在△ADF和△MCF中,
,
∴△ADF≌△MCF(AAS),
∴AF=FM,AD=CM,
在△ABM中,E是AB中点,F是AM中点,
∴EF∥BM且③EF,
∵BM=BC+CM=BC+AD,
∴,EF∥AB,EF∥CD.
请你根据该探究过程完成下面命题:
连接梯形两腰中点的线段平行于两底并且④等于两底和的一半.
故答案为:①DF=CF; ②∠DFA=∠CFM;③EF;④等于两底和的一半.
【点评】本题考查作图﹣基本作图,全等三角形的判定和性质,线段的垂直平分线的性质,三角形中位线定理等知识,解题的关键是正确寻找全等三角形解决问题.
17.学习了角平分线性质后,小明进行了拓展研究,他发现△ABC的外角∠CBE和外角∠BCD的角平分线BF,CF交于点F,他猜想AF平分∠BAC,他的解决思路是利用角平分线性质.过点F分别向BE、BC、CD作垂线,再证明∠BAF和∠CAF这两个角所在的三角形全等得出结论.其中小明已经完成过点F分别向BE、BC作垂线,请根据他的思路完成以下作图与填空.
(1)用直尺和圆规,过点F作FK⊥CD于点K.(保留作图痕迹)
(2)已知:如图,△ABC的外角∠CBE和外角∠BCD的角平分线BF,CF交于点F,FK⊥CD于点K,FH⊥BC于点H,FG⊥BE于点G.求证:∠BAF=∠CAF.
证明:∵BF平分∠CBE,
FH⊥BC于点H,FG⊥BE于点G,
∴FH=① FG ,
∵CF平分∠BCD,
FK⊥CD于点K,FH⊥BC于点H,
∴FH=FK.
∴② FK=FG ,
∵FG⊥BE,FK⊥CD,
∴△AGF,△AKF均为直角三角形,
在Rt△AGF和Rt△AKF中:
③∴Rt△AGF≌Rt△AKF(HL).
∴∠BAF=∠CAF.
由此他得出结论:三角形的两(4) 外角角平分线 所在直线交点与三角形另一顶点连线平分这个内角.
【考点】作图—基本作图;全等三角形的判定与性质;角平分线的性质.
【专题】作图题;几何直观.
【答案】(1)图形见解析;
(2)①FG;②FK=FG;③AF=AF;④外角角平分线.
【分析】(1)根据垂线的基本尺规作图,规范作图即可K.
(2)根据角的平分线的性质定理,FG=FK,再证明Rt△AGF≌Rt△AKF(HL)即可得到结论.
【解答】(1)解:作图如图所示:
则FK即为所求.
(2)证明:∵BF平分∠CBE,FG⊥BE于点G,FH⊥BC于点H,
∴FH=FG,
∵CF平分∠BCD,FH⊥BC于点H,FK⊥CD于点K,
∴FH=FK,
∴FG=FK,
∵FK⊥CD,FG⊥BE,
∴△AGF,△AKF均为直角三角形,
在Rt△AGF和Rt△AKF中:
,
∴Rt△AGF≌Rt△AKF(HL),
∴∠CAF=∠BAF.
由此他得出结论:三角形的两外角角平分线所在直线交点与三角形另一顶点连线平分这个内角.
故答案为:①FG;②FK=FG;③AF=AF;④外角角平分线.
【点评】本题考查了垂线的基本作图,角的平分线的性质定理,直角三角形的全等判定和性质,熟练掌握作图和性质是解题的关键.
18.请仔细阅读下面的材料,并完成相应的任务.
作角的平分线
数学兴趣课上,老师让同学们利用尺规作∠AOB的平分线,同学们以小组为单位展开了讨论,勤学小组展示了学习过的作法:如图1,以点O为圆心,任意长为半径作弧,分别交OA,OB于点M,N;再分别以点M,N为圆心,大于的长为半径作弧,两弧相交于点P,作射线OP,则OP即为∠AOB的平分线.
勤学小组的证明过程如下:
连接PM,PN.
…
任务:
(1)请按照上面的材料,写出该证明的剩余部分;
(2)在图2中再设计一种不同的方法作∠AOB的平分线.(要求:尺规作图,保留作图痕迹,不写作法)
【考点】作图—复杂作图;角平分线的性质.
【专题】作图题;证明题;几何直观;推理能力.
【答案】(1)见解析;
(2)见解析.
【分析】(1)根据作图得OM=ON和MP=NP,可证得△OMP≌△ONP,则有∠MOP=∠NOP;
(2)在OA,OB上分别截取OC=OD,OM=ON,然后连接CN,MD交于点P,作射线OP即可解决问题.
【解答】解:(1)由作图可知:OM=ON,MP=NP,
在△OMP和△ONP,
,
∴△OMP≌△ONP(SSS),
∴∠MOP=∠NOP;
(2)作图如下:(方法不唯一).
【点评】本题主要考查作图﹣复杂作图,画角平分线和全等三角形的判定,解决本题的关键是掌握基本作图方法.
19.在学行四边形与正方形的相关知识后,智慧小组进行了更深入的探究.他们发现,如图所示的正方形ABCD,分别取BC,CD的中点N,M,连接AM,DN交于点E,过B作AM的垂线,交AM于点Q,交AD于点P.则四边形BPDN是平行四边形.
(1)用尺规完成以下基本作图:过B作AM的垂线,交AM于点Q,交AD于点P(只保留作图痕迹).
(2)根据(1)中所作图形,智慧小组发现四边形BPDN是平行四边形成立,并给出了证明,请补全证明过程.
证明:∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠C=90°,AD∥BC.
又∵M,N分别为BC,CD的中点,
∴,,
∴① DM=CN ,
在△ADM与△DCN中,
,
∴△ADM≌△DCN(SAS).
∴② ∠CDN=∠DAM .
又∵∠CDN+∠ADN=90°,
∴∠DAM+∠ADN=90°,
∴∠AED=90°,
又∵BP⊥AE,
∴∠AQP=∠AED=90°,
∴③ BP∥DN .
又∵DP∥BN,
∴四边形BPDN是平行四边形.
进一步思考,智慧小组发现任取BC,CD的上点N,M(M不与C,D重合),DM=CN,连接AM,DN,过B作AM的垂线,交AD于点P,则四边形BPDN是④ 平行四边形 .
【考点】作图—基本作图;全等三角形的判定与性质;平行四边形的判定;正方形的性质.
【专题】图形的全等;多边形与平行四边形;矩形 菱形 正方形;尺规作图;几何直观.
【答案】(1)见解答.
(2)①DM=CN;②∠CDN=∠DAM;③BP∥DN;④平行四边形.
【分析】(1)根据垂线的作图方法作图即可.
(2)结合全等三角形的判定与性质、正方形的性质、平行四边形的判定填空即可.
【解答】(1)解:如图,BQ即为所求.
(2)证明:∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠C=90°,AD∥BC.
又∵M,N分别为BC,CD的中点,
∴,,
∴DM=CN,
在△ADM与△DCN中,
,
∴△ADM≌△DCN(SAS).
∴∠CDN=∠DAM.
又∵∠CDN+∠ADN=90°,
∴∠DAM+∠ADN=90°,
∴∠AED=90°,
又∵BP⊥AE,
∴∠AQP=∠AED=90°,
∴BP∥DN.
又∵DP∥BN,
∴四边形BPDN是平行四边形.
进一步思考,智慧小组发现任取BC,CD的上点N,M(M不与C,D重合),DM=CN,连接AM,DN,过B作AM的垂线,交AD于点P,则四边形BPDN是平行四边形.
故答案为:①DM=CN;②∠CDN=∠DAM;③BP∥DN;④平行四边形.
【点评】本题考查作图—基本作图、全等三角形的判定与性质、正方形的性质、平行四边形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
20.(1)【问题情境】我国古代已经用角尺平分任意角,做法如下:如图①,在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线OC是∠AOB的平分线.请说明此做法的理由;
(2)【拓展实践】某公园的两条小路AB和AC,汇聚形成了一个岔路口A(如图②),现要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到休息椅M和N的距离相等.问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的备用图中作出路灯E的位置.(保留作图痕迹,不写作法)
【考点】作图—应用与设计作图;线段垂直平分线的性质.
【专题】几何图形;应用意识.
【答案】(1)见解析;
(2)见解析.
【分析】(1)证△OMC≌△ONC,得∠AOC=BOC,即可得出结论;
(2)根据角平分线定义及垂直平分线的性质作图即可.
【解答】解:(1)理由:由题意得CM=CN,OM=ON,OC=OC,
∴△OMC≌△ONC,
∴∠AOC=BOC,
∴OC是∠AOB的平分线;
(2)如图,点E即为所求.
【点评】本题考查了全等三角形的判定与性质、等边三角形的性质、角平分线定义以及尺规作图等知识,熟练掌握角平分线定义和等边三角形的性质,证明三角形全等是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学一轮复习 尺规作图
一.解答题(共20小题)
1.在学习了矩形与菱形的相关知识后,小明同学进行了更深入的研究,他发现,过矩形的一条对角线的中点作这条对角线的垂线,与矩形两边相交的两点和这条对角线的两个端点构成的四边形是菱形,可利用证明三角形全等得到此结论.根据他的想法与思路,完成以下作图与填空:
(1)如图,在矩形ABCD中,点O是对角线AC的中点.用尺规过点O作AC的垂线,分别交AB,CD于点E,F,连接AF,CE.(不写作法,保留作图痕迹)
(2)已知:矩形ABCD,点E,F分别在AB,CD上,EF经过对角线AC的中点O,且EF⊥AC.求证:四边形AECF是菱形.
证明:∵四边形ABCD是矩形,
∴AB∥CD.
∴① ,∠OCF=∠OAE.
∵点O是AC的中点,
∴② .
∴△CFO≌△AEO(AAS).
∴③ .
又∵OA=OC,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
进一步思考,如果四边形ABCD是平行四边形呢?请你模仿题中表述,写出你猜想的结论:④ .
2.根据背景素材,探索解决问题.
平面直角坐标系中画一个边长为2的正六边形ABCDEF
背景素材 六等分圆原理,也称为圆周六等分问题,是一个古老而经典的几何问题,旨在解决如何使用直尺和圆规将一个圆分成六等份的问题.这个问题由欧几里得在其名著《几何原本》中详细阐述.
已知条件 点C与坐标原点O重合,点D在x轴的正半轴上且坐标为(2,0).
操作步骤 ①分别以点C,D为圆心,CD长为半径作弧,两弧交于点P; ②以点P为圆心,PC长为半径作圆; ③以CD的长为半径,在⊙P上顺次截取; ④顺次连接DE,EF,FA,AB,BC.得到正六边形ABCDEF.
问题解决
任务一 根据以上信息,请你用不带刻度的直尺和圆规,在图中完成这道作图题(保留作图痕迹,不写作法)
任务二 将正六边形ABCDEF绕点D顺时针旋转60°,直接写出此时点E所在位置的坐标: .
3.马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、黑、白彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧.如图1的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图2,已知⊙O和圆上一点M.作法如下:
①以点M为圆心,OM长为半径,作弧交⊙O于A,B两点;
②延长MO交⊙O于点C;
即点A,B,C将⊙O的圆周三等分.
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图2中将⊙O的圆周三等分(保留作图痕迹,不写作法);
(2)根据(1)画出的图形,连接AB,AC,BC,若⊙O的半径为2cm,则△ABC的周长为 cm.
4.【阅读材料】
老师的问题: 已知:如图,AE∥BF. 求作:菱形ABCD,使点C,D分别在BF,AE上. 小明的作法: (1)以A为圆心,AB长为半径画弧,交AE于点D; (2)以B为圆心,AB长为半径画弧,交BF于点C; (3)连接CD. 四边形ABCD就是所求作的菱形.
【解答问题】
请根据材料中的信息,证明四边形ABCD是菱形.
5.【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;
【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
(友情提醒:以上作图均不写作法,但需保留作图痕迹)
6.《淮南子 天文训》中记载了一种确定东西方向的方法,大意是:日出时,在地面上点A处立一根杆,在地面上沿着杆的影子的方向取一点B,使B,A两点间的距离为10步(步是古代的一种长度单位),在点B处立一根杆;日落时,在地面上沿着点B处的杆的影子的方向取一点C,使C,B两点间的距离为10步,在点C处立一根杆.取CA的中点D,那么直线DB表示的方向为东西方向.
(1)上述方法中,杆在地面上的影子所在直线及点A,B,C的位置如图所示.使用直尺和圆规,在图中作CA的中点D(保留作图痕迹);
(2)在如图中,确定了直线DB表示的方向为东西方向.根据南北方向与东西方向互相垂直,可以判断直线CA表示的方向为南北方向,完成如下证明.
证明:在△ABC中,BA= ,D是CA的中点,
∴CA⊥DB( )(填推理的依据).
∵直线DB表示的方向为东西方向,
∴直线CA表示的方向为南北方向.
7.在学习了等腰三角形和中垂线的相关知识后,小明同学进行了拓展性研究,他发现,等腰三角形底边上的高的中垂线与两腰的交点恰好是两腰的中点,可利用中垂线的性质和等腰三角形的性质得到此结论.请根据他的想法与思路,完成以下作图与填空:
(1)如图,在等腰△ABC中,AD为BC边上的高,用尺规作AD的中垂线,分别交AB,AC于点E,F,连接DE,DF(不写作法,保留作图痕迹).
(2)已知:在等腰△ABC中,点E,F分别在AB,AC上,AD为BC边上的高,EF垂直平分AD.求证:E,F分别为AB、AC的中点.
证明:∵EF垂直平分AD,
∴① ,
∴∠EAD=∠EDA.
∵AD为BC边上的高,
∴∠ADB=90°,
∴∠EDA+∠EDB=90°.
∵在Rt△ABD中,∠EAD+∠B=90°,
∴② ,
∴BE=DE,
∴③ ,
∴点E为AB的中点.
同理可得:点F为AC的中点.
进一步思考,如果△ABC是任意三角形呢?请你模仿题中表述,写出你猜想的结论:④ .
8.在学习圆的相关知识后,小帅同学进行了关于弦切角的相关探索(弦切角定义:顶点在圆上,一边与圆相交,另一边与圆相切的角;如图,直线IJ与⊙O相切于点I,HI是⊙O的一条弦,则∠HIJ就是弦切角),发现弦切角的大小与它所夹弧所对的圆周角度数相关.请根据这个思路完成以下作图和填空.
(1)尺规作图:已知AB是⊙O的直径,延长AB,过点B作⊙O的切线MN;(M在点B左侧,N在点B右侧.保留作图痕迹,不写作法)
(2)如图C、D是圆上两点,在(1)的条件下,∠DBN为弦切角,求证:∠DBN=∠BCD.
证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB= ① .
∵MN是过点B的切线,
∴② .
即∠ABN=90°,
∴∠DBN+∠ABD=90°
∵∠A+∠ABD=90°
∴∠DBN=∠A
又∵∠A和∠C是弧所对的圆周角
∴∠A= ③ .
∴∠DBN=∠C.
由此,我们可以得到弦切角的结论:弦切角 ④ 它所夹弧所对的圆周角.(横线上填:“大于”或“等于”或“小于”)
9.我们知道在含30°的直角三角形中,30°角所对的直角边等于斜边的一半.小红进行了拓展性研究,她发现这个定理反过来说也成立.她通过构造斜边上的中垂线来证明含有30°角,请跟根据她的思路,完善以下作图与填空:
(1)如图,用直尺和圆规作斜边AB的垂直平分线DE,分别与AB、BC交于点D、点E,并连接AE.(只保留作图痕迹)
(2)已知:在△ABC中,∠C=90°,.求证:∠B=30°.
证明:∵DE垂直平分AB,
∴∠ADE=90°,,
∠C=90°,,
∴① ,∠ADE=∠C=90°.
在Rt△ACE和Rt△ADE中,,
∴Rt△ACE≌Rt△ADE(HL),
∴∠CAE=∠DAE.
∵DE垂直平分AB,
∴③ ,
∴∠DAE=∠B.
又∵∠CAB+∠B=180°﹣∠C=90°,
∴∠CAE+∠DAE+∠B=3∠B=90°,
∴∠B=30°.
根据小红的证明过程,进一步发现,30°角与所对直角边的关系,请你完善该逆定理:如果在直角三角形中,一条直角边是斜边的一半,那么④ .
10.水兴县某中学的同学们在学习了《图形的相似》之后,数学柳老师给出了下面的问题:如图,Rt△ABD与Rt△CDB中,斜边AD与BC相交于点M,过点M作MH⊥BD于点H.探究AB、MH、CD之间的数量关系,并证明.
下面是小许同学的探究过程,请根据题意补充完整探究过程.
(1)请在答题卡上完成尺规作图:过点M作MH⊥BD垂足为点H.(保留作图痕迹,不用写作法)
(2)请将①②③④⑤补充完整并填写在答题卡上.
解:∵AB⊥BD,MH⊥BD,
∴MH∥AB.
∴△DMH∽① .
∴.
∵CD⊥BD,MH⊥BD,
∴MH∥CD.
∴△BMH∽② .
∴③ .
∴④ .
(注意:这里要求填写化简之后的数字结果) 小许进一步探究,如果把题设中的三个垂直关系改为:AB∥CD∥MH,请你帮她写出AB、MH、CD这三条线段之间的数量关系⑤ .
11.在学分线性质的过程中,首先要探究角平分线的作图方法,请阅读下列材料,回答问题:
已知:∠AOB,求作:∠AOB的平分线.
作法:(I)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;
(II)分别以点M,N为圆心,大于的长为半径画弧,两弧在∠AOB的内部相交于点C;
(III)画射线OC,则射线OC即为所求.
(1)如图1,射线OC就是∠AOB的角平分线的依据是 ;
A.SAS
B.ASA
C.SSS
D.AAS
(2)课后老师留了一道思考题:
在不限于圆规、直尺的条件下,思考还有没有其他作角平分线的方法?
下面是两位同学给出的两种方法:
①同学1:用三角板按下面方法画角平分线:
如图2,在已知∠AOB的边OA,OB上分别取OC=OD,再分别过点C,D作OA,OB的垂线,两垂线交于点P,画射线OP,则OP平分∠AOB.
请你帮这位同学证明:OP平分∠AOB;
②同学2:用圆规和直尺按下面方法画角平分线:
如图3,以点O为圆心,以任意长为半径画弧与OA,OB分别交于点C,D,再以任意长为半径画弧与OA,OB分别交于点E,F,连接CF,DE交于点P,画射线OP,则OP平分∠AOB.
你认为同学2的这种作角平分线的方法正确吗?若正确,请给出证明过程;若错误,请说明理由.
12.我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.那么,不相等的边(或角)所对的角(或边)之间的大小关系怎样呢?如图,小洲同学通过直观观察发现:在△ABC中,如果AB大于AC,那么AB边所对的∠C大于AC边所对的∠B.为了证明这一发现,小洲同学的解决思路是构造全等三角形将∠C转化为一个三角形的外角,利用三角形的外角大于不相邻的内角使问题得以证明.根据他的思路,完成以下作图与填空:
已知:如图,△ABC中,AB>AC.
求证:∠C>∠B.
(1)尺规作图:作∠A的角平分线AP,交BC于点D,在AB上截取AE=AC,连接DE.(保留作图痕迹)留作图痕迹)
(2)证明:∵AP平分线∠BAC,
∴ .
在△EAD和△CAD中,
∴△EAD≌△CAD(SAS).
∴∠C= .
∵;
,∴∠C>∠B.
进一步思考,在△ABC中,如果已知∠C>∠B呢?请你模仿题中表述,写出你猜想的结论: .
13.【问题背景】在△ABC中,AB,BC,AC三边的边长分别为,,,求这个三角形的面积.小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC,如图1所示.这样不需求△ABC的高,借助网格就能计算三角形的面积.
(1)直接写出△ABC的面积,S△ABC= .
(2)【思维拓展】若△A1B1C1三边的长分别为,,,请利用图2的正方形网格中画出△A1B1C1(每个小正方形的边长为a).
(3)【探索创新】若△A2B2C2的三边长分别为(m>0,n>0,且m≠n),试运用构图法求出△A2B2C2的面积.
14.【问题背景】:数学活动课上,老师将一副三角尺按图1所示位置摆放,分别作出∠AOB,∠BOC的平分线OG,OF,然后提出如下问题:求出∠GOF的度数.
【特例探究】:小明同学决定从特例入手探究老师提出的问题,他将三角尺分别按图2方式摆放,OG,OF仍然分别是∠AOB,∠BOC的角平分线.其中∠AOC=90°,∠BOC=30°.
(1)请你帮助小明计算出∠GOF的度数为 °;
【发现感悟】:小明发现,按图1摆放时,条件不变,虽然不知道∠BOC的度数,但也可以求出∠GOF的度数.
(2)请你帮小明完成这个问题的解答;
(3)积累了以上探究问题的经验,结合图3,若∠AOC=m°,则∠GOF= °;
【类比拓展】:(4)已知∠BOC=m°,若OA是∠BOC外一条射线,,OD,OE分别平分∠AOC,∠AOB,当∠DOE=m°﹣18°时,求出m的值(自己画出示意图求解).
15.(1)操作实践:如图,△ABC中,∠A=90°,∠B=22.5°,请画出一条直线把△ABC分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数.(要求画出一种分割方法即可)
(2)分类探究:已知△ABC中的最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,请直接写出△ABC中最大内角的所有可能值.
16.学习了三角形的中位线定理后,小涵进行了拓展性研究,他发现.连接梯形两腰中点的线段也具有类似的性质.探究过程如下:
(1)用直尺和圆规,作线段CD的垂直平分线,垂足为点F,连接EF,连接AF并延长交线段BC的延长线于点M(只保留作图痕迹):
(2)已知:在四边形ABCD中,AD∥BC,E为AB中点,F为CD中点.
猜想:EF∥AD∥BC,且.
证明:∵F是CD中点,
∴① ,
∵AD∥BC,
∴∠DAF=∠FMC,
在△ADF和△MCF中,
,
∴△ADF≌△MCF,
∴AF=FM,AD=CM,
在△ABM中,E为AB中点,F为AM中点,
∴EF∥BM且③ .
∵BM=BC+CM=BC+AD,
∴EF(AD+BC),EF//AB,EF//CD,
请你根据该探究过程完成下面命题:连接梯形两腰中点的线段平行于两底并④ .
17.学习了角平分线性质后,小明进行了拓展研究,他发现△ABC的外角∠CBE和外角∠BCD的角平分线BF,CF交于点F,他猜想AF平分∠BAC,他的解决思路是利用角平分线性质.过点F分别向BE、BC、CD作垂线,再证明∠BAF和∠CAF这两个角所在的三角形全等得出结论.其中小明已经完成过点F分别向BE、BC作垂线,请根据他的思路完成以下作图与填空.
(1)用直尺和圆规,过点F作FK⊥CD于点K.(保留作图痕迹)
(2)已知:如图,△ABC的外角∠CBE和外角∠BCD的角平分线BF,CF交于点F,FK⊥CD于点K,FH⊥BC于点H,FG⊥BE于点G.求证:∠BAF=∠CAF.
证明:∵BF平分∠CBE,
FH⊥BC于点H,FG⊥BE于点G,
∴FH=① ,
∵CF平分∠BCD,
FK⊥CD于点K,FH⊥BC于点H,
∴FH=FK.
∴② ,
∵FG⊥BE,FK⊥CD,
∴△AGF,△AKF均为直角三角形,
在Rt△AGF和Rt△AKF中:
③∴Rt△AGF≌Rt△AKF(HL).
∴∠BAF=∠CAF.
由此他得出结论:三角形的两(4) 所在直线交点与三角形另一顶点连线平分这个内角.
18.请仔细阅读下面的材料,并完成相应的任务.
作角的平分线
数学兴趣课上,老师让同学们利用尺规作∠AOB的平分线,同学们以小组为单位展开了讨论,勤学小组展示了学习过的作法:如图1,以点O为圆心,任意长为半径作弧,分别交OA,OB于点M,N;再分别以点M,N为圆心,大于的长为半径作弧,两弧相交于点P,作射线OP,则OP即为∠AOB的平分线.
勤学小组的证明过程如下:
连接PM,PN.
…
任务:
(1)请按照上面的材料,写出该证明的剩余部分;
(2)在图2中再设计一种不同的方法作∠AOB的平分线.(要求:尺规作图,保留作图痕迹,不写作法)
19.在学行四边形与正方形的相关知识后,智慧小组进行了更深入的探究.他们发现,如图所示的正方形ABCD,分别取BC,CD的中点N,M,连接AM,DN交于点E,过B作AM的垂线,交AM于点Q,交AD于点P.则四边形BPDN是平行四边形.
(1)用尺规完成以下基本作图:过B作AM的垂线,交AM于点Q,交AD于点P(只保留作图痕迹).
(2)根据(1)中所作图形,智慧小组发现四边形BPDN是平行四边形成立,并给出了证明,请补全证明过程.
证明:∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠C=90°,AD∥BC.
又∵M,N分别为BC,CD的中点,
∴,,
∴① ,
在△ADM与△DCN中,
,
∴△ADM≌△DCN(SAS).
∴② .
又∵∠CDN+∠ADN=90°,
∴∠DAM+∠ADN=90°,
∴∠AED=90°,
又∵BP⊥AE,
∴∠AQP=∠AED=90°,
∴③ .
又∵DP∥BN,
∴四边形BPDN是平行四边形.
进一步思考,智慧小组发现任取BC,CD的上点N,M(M不与C,D重合),DM=CN,连接AM,DN,过B作AM的垂线,交AD于点P,则四边形BPDN是④ .
20.(1)【问题情境】我国古代已经用角尺平分任意角,做法如下:如图①,在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线OC是∠AOB的平分线.请说明此做法的理由;
(2)【拓展实践】某公园的两条小路AB和AC,汇聚形成了一个岔路口A(如图②),现要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到休息椅M和N的距离相等.问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的备用图中作出路灯E的位置.(保留作图痕迹,不写作法)
中考数学一轮复习 尺规作图
参考答案与试题解析
一.解答题(共20小题)
1.在学习了矩形与菱形的相关知识后,小明同学进行了更深入的研究,他发现,过矩形的一条对角线的中点作这条对角线的垂线,与矩形两边相交的两点和这条对角线的两个端点构成的四边形是菱形,可利用证明三角形全等得到此结论.根据他的想法与思路,完成以下作图与填空:
(1)如图,在矩形ABCD中,点O是对角线AC的中点.用尺规过点O作AC的垂线,分别交AB,CD于点E,F,连接AF,CE.(不写作法,保留作图痕迹)
(2)已知:矩形ABCD,点E,F分别在AB,CD上,EF经过对角线AC的中点O,且EF⊥AC.求证:四边形AECF是菱形.
证明:∵四边形ABCD是矩形,
∴AB∥CD.
∴① ∠OFC=∠OEA ,∠OCF=∠OAE.
∵点O是AC的中点,
∴② OC=OA .
∴△CFO≌△AEO(AAS).
∴③ OF=OE .
又∵OA=OC,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
进一步思考,如果四边形ABCD是平行四边形呢?请你模仿题中表述,写出你猜想的结论:④ 四边形AECF是菱形 .
【考点】作图—基本作图;全等三角形的判定与性质;平行四边形的判定与性质;菱形的判定与性质;矩形的性质.
【专题】作图题;几何直观;推理能力.
【答案】(1)见解析;
(2)∠OFC=∠OEA,OC=OA,OF=OE,四边形AECF是菱形.
【分析】(1)根据要求作出图形;
(2)根据对角线互相垂直的平行四边形是菱形证明即可.
【解答】(1)解:图形如图所示:
(2)证明:∵四边形ABCD是矩形,
∴AB∥CD.
∴①∠OFC=∠OEA,∠OCF=∠OAE.
∵点O是AC的中点,
∴②OC=OA.
∴△CFO≌△AEO(AAS).
∴③OF=OE.
又∵OA=OC,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
进一步思考,如果四边形ABCD是平行四边形呢?请你模仿题中表述,写出你猜想的结论:④四边形AECF是菱形.
故答案为:∠OFC=∠OEA,OC=OA,OF=OE,四边形AECF是菱形.
【点评】本题考查作图﹣基本作图,全等三角形的判定和性质,平行四边形的判定和性质,菱形的判定与性质,矩形的性质等知识,解题的关键是正确寻找全等三角形解决问题.
2.根据背景素材,探索解决问题.
平面直角坐标系中画一个边长为2的正六边形ABCDEF
背景素材 六等分圆原理,也称为圆周六等分问题,是一个古老而经典的几何问题,旨在解决如何使用直尺和圆规将一个圆分成六等份的问题.这个问题由欧几里得在其名著《几何原本》中详细阐述.
已知条件 点C与坐标原点O重合,点D在x轴的正半轴上且坐标为(2,0).
操作步骤 ①分别以点C,D为圆心,CD长为半径作弧,两弧交于点P; ②以点P为圆心,PC长为半径作圆; ③以CD的长为半径,在⊙P上顺次截取; ④顺次连接DE,EF,FA,AB,BC.得到正六边形ABCDEF.
问题解决
任务一 根据以上信息,请你用不带刻度的直尺和圆规,在图中完成这道作图题(保留作图痕迹,不写作法)
任务二 将正六边形ABCDEF绕点D顺时针旋转60°,直接写出此时点E所在位置的坐标: (4,0) .
【考点】作图—复杂作图;坐标与图形变化﹣旋转;正多边形和圆.
【专题】作图题;几何直观.
【答案】任务一:见解析;
任务二:(4,0).
【分析】任务一:根据要求作出图形.
任务二:利用旋转变换的性质判断即可.
【解答】解:任务一:图形如图所示:
任务二:将正六边形ABCDEF绕点D顺时针旋转60°,直接写出此时点E所在位置的坐标(4,0).
【点评】本题考查作图﹣复杂作图,正多边形与圆,坐标与图形变化﹣旋转等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
3.马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、黑、白彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧.如图1的彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.如图2,已知⊙O和圆上一点M.作法如下:
①以点M为圆心,OM长为半径,作弧交⊙O于A,B两点;
②延长MO交⊙O于点C;
即点A,B,C将⊙O的圆周三等分.
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图2中将⊙O的圆周三等分(保留作图痕迹,不写作法);
(2)根据(1)画出的图形,连接AB,AC,BC,若⊙O的半径为2cm,则△ABC的周长为 6 cm.
【考点】作图—应用与设计作图;切线的性质;正多边形和圆.
【专题】作图题;几何直观.
【答案】(1)作图见解析;
(2)6.
【分析】(1)根据要求作出图形;
(2)证明△ABC是等边三角形,解直角三角形求出AB即可.
【解答】解:(1)如图,点A,B,C即为所求.
(2)设CM交AB于点E.
∵,
∴AB=CB=AC,∠AOB=120°,
∵,
∴∠AOM=∠BOM=60°,
∵OA=OB,
∴OE⊥AB,AE=EB=AO sin60°=2(cm),
∴AB=2(cm),
∴△ABC的周长为6cm.
故答案为:6.
【点评】本题考查作图﹣应用与设计作图,切线的性质,正多边形与圆等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
4.【阅读材料】
老师的问题: 已知:如图,AE∥BF. 求作:菱形ABCD,使点C,D分别在BF,AE上. 小明的作法: (1)以A为圆心,AB长为半径画弧,交AE于点D; (2)以B为圆心,AB长为半径画弧,交BF于点C; (3)连接CD. 四边形ABCD就是所求作的菱形.
【解答问题】
请根据材料中的信息,证明四边形ABCD是菱形.
【考点】作图—复杂作图;菱形的判定.
【专题】作图题;几何直观;推理能力.
【答案】见试题解答内容
【分析】根据邻边相等的平行四边形是菱形证明即可.
【解答】证明:由作图可知AD=AB=BC,
∵AE∥BF,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
【点评】本题考查作图﹣复杂作图,菱形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
5.【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?
【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;
【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;
【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.
(友情提醒:以上作图均不写作法,但需保留作图痕迹)
【考点】作图—复杂作图;角平分线的性质;等腰直角三角形;扇形面积的计算.
【专题】作图题;几何直观.
【答案】【初步尝试】作图见解析部分;
【问题联想】作图见解析部分;
【问题再解】作图见解析部分.
【分析】【初步尝试】如图1,作∠AOB的角平分线OP即可;
【问题联想】如图2,作线段MN的垂直平分线RT,垂足为R,在射线RT上截取RP=RM,连接MP,NP,三角形MNP即为所求;
【问题再解】方法一:构造等腰直角三角形OBE,作BC⊥OE,以O为圆心,OC为半径画弧交OB于点D,交OA于点F,弧DF即为所求.方法二:作OB的中垂线交OB于点C,然后以C为圆心,CB长为半径画弧交OB中垂线于点D,再以O为圆心,OD长为半径画弧分别交OA、OB于点F、D.则弧DF即为所求.
【解答】解:【初步尝试】如图1,直线OP即为所求;
【问题联想】如图2,三角形MNP即为所求;
【问题再解】如图3中,即为所求.
【点评】本题考查作图﹣复杂作图,等腰直角三角形的性质,扇形的面积等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
6.《淮南子 天文训》中记载了一种确定东西方向的方法,大意是:日出时,在地面上点A处立一根杆,在地面上沿着杆的影子的方向取一点B,使B,A两点间的距离为10步(步是古代的一种长度单位),在点B处立一根杆;日落时,在地面上沿着点B处的杆的影子的方向取一点C,使C,B两点间的距离为10步,在点C处立一根杆.取CA的中点D,那么直线DB表示的方向为东西方向.
(1)上述方法中,杆在地面上的影子所在直线及点A,B,C的位置如图所示.使用直尺和圆规,在图中作CA的中点D(保留作图痕迹);
(2)在如图中,确定了直线DB表示的方向为东西方向.根据南北方向与东西方向互相垂直,可以判断直线CA表示的方向为南北方向,完成如下证明.
证明:在△ABC中,BA= BC ,D是CA的中点,
∴CA⊥DB( 三线合一 )(填推理的依据).
∵直线DB表示的方向为东西方向,
∴直线CA表示的方向为南北方向.
【考点】作图—应用与设计作图;等腰三角形的性质.
【专题】作图题;几何直观.
【答案】(1)作图见解析部分.
(2)证明见解析部分.
【分析】(1)作线段AC的垂直平分线即可.
(2)利用等腰三角形的三线合一的性质解决问题即可.
【解答】解:(1)如图,点D即为所求.
(2)如图,连接BD.
在△ABC中,BA=BC,D是CA的中点,
∴CA⊥DB(三线合一),
∵直线DB表示的方向为东西方向,
∴直线CA表示的方向为南北方向.
故答案为:BC,三线合一.
【点评】本题考查作图﹣应用与设计作图,等腰三角形的性质等知识,解题的关键是理解题意,学会利用等腰三角形的性质解决问题.
7.在学习了等腰三角形和中垂线的相关知识后,小明同学进行了拓展性研究,他发现,等腰三角形底边上的高的中垂线与两腰的交点恰好是两腰的中点,可利用中垂线的性质和等腰三角形的性质得到此结论.请根据他的想法与思路,完成以下作图与填空:
(1)如图,在等腰△ABC中,AD为BC边上的高,用尺规作AD的中垂线,分别交AB,AC于点E,F,连接DE,DF(不写作法,保留作图痕迹).
(2)已知:在等腰△ABC中,点E,F分别在AB,AC上,AD为BC边上的高,EF垂直平分AD.求证:E,F分别为AB、AC的中点.
证明:∵EF垂直平分AD,
∴① AE=DE ,
∴∠EAD=∠EDA.
∵AD为BC边上的高,
∴∠ADB=90°,
∴∠EDA+∠EDB=90°.
∵在Rt△ABD中,∠EAD+∠B=90°,
∴② ∠EDB=∠B ,
∴BE=DE,
∴③ AE=BE ,
∴点E为AB的中点.
同理可得:点F为AC的中点.
进一步思考,如果△ABC是任意三角形呢?请你模仿题中表述,写出你猜想的结论:④ 三角形一边上的高的中垂线与其它两边的交点恰好是这两边的中点 .
【考点】作图—复杂作图;线段垂直平分线的性质;等腰三角形的性质;直角三角形斜边上的中线;三角形中位线定理.
【专题】作图题;几何直观;推理能力.
【答案】(1)见解答;
(2)AE=DE,∠EDB=∠B,AE=BE,三角形一边上的高的中垂线与其它两边的交点恰好是这两边的中点.
【分析】(1)利用基本作图作AD的垂直平分线即可;
(2)先根据线段垂直平分线的性质得到AE=DE,则∠EAD=∠EDA,再根据等角的余角相等得到∠EDB=∠A,所以BE=DE,则AE=BE,从而可判断点E为AB的中点.同理可得点F为AC的中点,
对于任意△ABC,三角形一边上的高的中垂线与其它两边的交点恰好是这两边的中点.
【解答】(1)解:如图,DE、DF为所作;
(2)证明:∵EF垂直平分AD,
∴AE=DE,
∴∠EAD=∠EDA,
∵AD为BC边上的高,
∴∠ADB=90°,
∴∠EDA+∠EDB=90°,
∵在Rt△ABD中,∠EAD+∠B=90°,
∴∠EDB=∠A,
∴BE=DE,
∴AE=BE
∴点E为AB的中点.
同理可得:点F为AC的中点,
如果△ABC是任意三角形,结论:三角形一边上的高的中垂线与其它两边的交点恰好是这两边的中点.
故答案为:AE=DE,∠EDB=∠B,AE=BE,三角形一边上的高的中垂线与其它两边的交点恰好是这两边的中点.
【点评】本题考查了作图﹣复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段垂直平分线的性质和等腰三角形的性质.
8.在学习圆的相关知识后,小帅同学进行了关于弦切角的相关探索(弦切角定义:顶点在圆上,一边与圆相交,另一边与圆相切的角;如图,直线IJ与⊙O相切于点I,HI是⊙O的一条弦,则∠HIJ就是弦切角),发现弦切角的大小与它所夹弧所对的圆周角度数相关.请根据这个思路完成以下作图和填空.
(1)尺规作图:已知AB是⊙O的直径,延长AB,过点B作⊙O的切线MN;(M在点B左侧,N在点B右侧.保留作图痕迹,不写作法)
(2)如图C、D是圆上两点,在(1)的条件下,∠DBN为弦切角,求证:∠DBN=∠BCD.
证明:连接AD.
∵AB是⊙O的直径,
∴∠ADB= ① 90° .
∵MN是过点B的切线,
∴② AB⊥MN .
即∠ABN=90°,
∴∠DBN+∠ABD=90°
∵∠A+∠ABD=90°
∴∠DBN=∠A
又∵∠A和∠C是弧所对的圆周角
∴∠A= ③ ∠C .
∴∠DBN=∠C.
由此,我们可以得到弦切角的结论:弦切角 ④ 它所夹的弧所对的圆周角 它所夹弧所对的圆周角.(横线上填:“大于”或“等于”或“小于”)
【考点】作图—复杂作图;垂径定理;圆周角定理;直线与圆的位置关系;切线的判定与性质.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2)90°;AB⊥MN;∠C;它所夹的弧所对的圆周角.
【分析】(1)以B为圆心,任意长度为半径画弧,交AB于点G、H,以G、H为圆心,大于长度为半径画弧,两弧交于点M、N,作直线MN即可;
(2)连接AD,由AB是⊙O的直径,得∠ADB=90°;又MN是过点B的切线,则AB⊥MN,即∠ABN=90°,故有∠DBN=∠A,又∠A=∠C,则∠DBN=∠C,从而得出结论;
【解答】(1)解:①以B为圆心,任意长度为半径画弧,交AB于点G、H;
②以G、H为圆心,大于长度为半径画弧,两弧交于点M、N;
③作直线MN;
∴MN即为所求;
(2)证明:连接AD,如图:
∵AB是⊙O的直径,
∴∠ADB=90°;
∵MN是过点B的切线,
∴AB⊥MN,即∠ABN=90°,
∴90°=∠DBN+∠ABD,
∵90°=∠A+∠ABD,
∴∠A=∠DBN,
又∵∠A和∠C是弧所对的圆周角,
∴∠C=∠A,
∴∠C=∠DBN,
由此,我们可以得到弦切角的结论:弦切角等于它所夹的弧所对的圆周角.
故答案为:90°;AB⊥MN;∠C;它所夹的弧所对的圆周角.
【点评】本题考查了尺规作图——作垂线,圆周角定理,切线的判定与性质,同角的余角相等,熟练掌握知识点的应用是解题的关键.
9.我们知道在含30°的直角三角形中,30°角所对的直角边等于斜边的一半.小红进行了拓展性研究,她发现这个定理反过来说也成立.她通过构造斜边上的中垂线来证明含有30°角,请跟根据她的思路,完善以下作图与填空:
(1)如图,用直尺和圆规作斜边AB的垂直平分线DE,分别与AB、BC交于点D、点E,并连接AE.(只保留作图痕迹)
(2)已知:在△ABC中,∠C=90°,.求证:∠B=30°.
证明:∵DE垂直平分AB,
∴∠ADE=90°,,
∠C=90°,,
∴① AD=AC ,∠ADE=∠C=90°.
在Rt△ACE和Rt△ADE中,,
∴Rt△ACE≌Rt△ADE(HL),
∴∠CAE=∠DAE.
∵DE垂直平分AB,
∴③ AE=BE ,
∴∠DAE=∠B.
又∵∠CAB+∠B=180°﹣∠C=90°,
∴∠CAE+∠DAE+∠B=3∠B=90°,
∴∠B=30°.
根据小红的证明过程,进一步发现,30°角与所对直角边的关系,请你完善该逆定理:如果在直角三角形中,一条直角边是斜边的一半,那么④ 那么这条直角边所对的角也为30° .
【考点】作图—基本作图;全等三角形的判定与性质;角平分线的性质;线段垂直平分线的性质;含30度角的直角三角形;直角三角形斜边上的中线.
【专题】作图题;线段、角、相交线与平行线;图形的全等;等腰三角形与直角三角形;运算能力;推理能力.
【答案】①AD=AC,②AE=AE,③AE=BE,④那么这条直角边所对的角也为30°.
【分析】(1)根据题意画出图形,即可求解;
(2)根据线段垂直平分线的性质的∠ADE=90°,ADAB,求得AD=AC,∠ADE=∠C=90°.根据全等三角形的性质得到∠CAE=∠DAE.根据线段垂直平分线的性质得到AE=BE,求得∠DAE=∠B.于是得到结论.
【解答】(1)解:如图所示,DE为所求线段;
(2)证明:∵DE垂直平分AB,
∴∠ADE=90°,ADAB,
∵∠C=90°,ACAB,
∴AD=AC,∠ADE=∠C=90°.
在Rt△ACE和Rt△ADE中,
,
∴Rt△ACE≌Rt△ADE(HL),
∴∠CAE=∠DAE.
∵DE垂直平分AB,
∴③AE=BE,
∴∠DAE=∠B.
又∵∠CAB+∠B=180°﹣∠C=90°,
∴∠CAE+∠DAE+∠B=3∠B=90°,
∴∠B=30°.
根据小红的证明过程,进一步发现,30°角与所对直角边的关系,请你完善该逆定理:如果在直角三角形中,一条直角边是斜边的一半,那么④那么这条直角边所对的角也为30°.
故答案为:①AD=AC,②AE=AE,③AE=BE,④那么这条直角边所对的角也为30°.
【点评】本题考查了作图﹣基本作图,全等三角形的判定和性质,线段垂直平分线的性质,直角三角形的全等的判断和性质,熟练运用这些性质进行推理是本题的关键.
10.水兴县某中学的同学们在学习了《图形的相似》之后,数学柳老师给出了下面的问题:如图,Rt△ABD与Rt△CDB中,斜边AD与BC相交于点M,过点M作MH⊥BD于点H.探究AB、MH、CD之间的数量关系,并证明.
下面是小许同学的探究过程,请根据题意补充完整探究过程.
(1)请在答题卡上完成尺规作图:过点M作MH⊥BD垂足为点H.(保留作图痕迹,不用写作法)
(2)请将①②③④⑤补充完整并填写在答题卡上.
解:∵AB⊥BD,MH⊥BD,
∴MH∥AB.
∴△DMH∽① △DAB .
∴.
∵CD⊥BD,MH⊥BD,
∴MH∥CD.
∴△BMH∽② △BCD .
∴③ .
∴④ 1 .
(注意:这里要求填写化简之后的数字结果) 小许进一步探究,如果把题设中的三个垂直关系改为:AB∥CD∥MH,请你帮她写出AB、MH、CD这三条线段之间的数量关系⑤ .
【考点】作图—基本作图;相似三角形的判定与性质.
【专题】作图题;图形的相似;几何直观;推理能力.
【答案】(1)画图见解析;
(2)△DAB,△BCD,,1,.
【分析】(1)根据题意,过点M作MH⊥BD垂足为点H;
(2)根据相似三角形的性质与判定,完成填空,即可求解.
【解答】解:(1)如图,MH即为所求;
(2)∵AB⊥BD,MH⊥BD,
∴MH∥AB,
∴△DMH∽△DAB,
∴,
∵CD⊥BD,MH⊥BD,
∴MH∥CD,
∴△BMH∽△BCD,
∴,
∴,
如果把题设中的三个垂直关系改为:AB∥CD∥MH,
∴△DMH∽△DAB,△BMH∽△BCD,
∴,,
∴,
∴.
故答案为:△DAB,△BCD,,1,.
【点评】本题考查了作图﹣基本作图,相似三角形的性质与判定,解决本题的关键是得到△DMH∽△DAB.
11.在学分线性质的过程中,首先要探究角平分线的作图方法,请阅读下列材料,回答问题:
已知:∠AOB,求作:∠AOB的平分线.
作法:(I)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N;
(II)分别以点M,N为圆心,大于的长为半径画弧,两弧在∠AOB的内部相交于点C;
(III)画射线OC,则射线OC即为所求.
(1)如图1,射线OC就是∠AOB的角平分线的依据是 C ;
A.SAS
B.ASA
C.SSS
D.AAS
(2)课后老师留了一道思考题:
在不限于圆规、直尺的条件下,思考还有没有其他作角平分线的方法?
下面是两位同学给出的两种方法:
①同学1:用三角板按下面方法画角平分线:
如图2,在已知∠AOB的边OA,OB上分别取OC=OD,再分别过点C,D作OA,OB的垂线,两垂线交于点P,画射线OP,则OP平分∠AOB.
请你帮这位同学证明:OP平分∠AOB;
②同学2:用圆规和直尺按下面方法画角平分线:
如图3,以点O为圆心,以任意长为半径画弧与OA,OB分别交于点C,D,再以任意长为半径画弧与OA,OB分别交于点E,F,连接CF,DE交于点P,画射线OP,则OP平分∠AOB.
你认为同学2的这种作角平分线的方法正确吗?若正确,请给出证明过程;若错误,请说明理由.
【考点】作图—基本作图;全等三角形的判定与性质;角平分线的性质.
【专题】作图题;图形的全等;推理能力.
【答案】(1)C;
(2)①证明见解析,②同学2这种作角平分线的方法正确.证明见解析.
【分析】(1)连接MC,NC,利用SSS证明△OMC≌△ONC即可;
(2)①由作法得OC=OD,则可判断Rt△OPC≌Rt△OPD,从而得到OP平分∠AOB;
②由作法得OC=OD,OE=OF则可判断△OCF≌△ODE,可得到∠CEP=∠OFP,因此可证明△CEP≌△DPF,再根据EP=FP,可得△OEP≌△OFP,从而得到OP平分∠AOB.
【解答】(1)解:连接MC,NC,
由作法得MC=NC,OM=ON,
∵OC=OC,
∴△OMC≌△ONC(SSS),
∴∠AOC=∠BOC;
故选:C;
(2)①证明:由作法得OC=OD,
∵OP=OP,
∴Rt△OPC≌Rt△OPD(HL),
∴∠COP=∠DOP,
∴OP平分∠AOB;
②解:同学2这种作角平分线的方法正确.
理由如下:由作法得OC=OD,OE=OF,可知CE=DF.
在△OCF和△ODE中,
,
∴△OCF≌△ODE(SAS),
∴∠CEP=∠OFP,
在△CEP和△DPF中,
,
∴△CEP≌△DFP(AAS),
∴EP=FP,
在△OEP与△OFP中,
,
∴△OEP≌△OFP(SSS),
∴∠EOP=∠FOP.
即OP平分∠AOB.
【点评】本题考查了作图—基本作图,全等三角形的判定与性质、角平分线的性质,熟练掌握5种基本作图(作已知角的角平分线)是解题的关键.
12.我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.那么,不相等的边(或角)所对的角(或边)之间的大小关系怎样呢?如图,小洲同学通过直观观察发现:在△ABC中,如果AB大于AC,那么AB边所对的∠C大于AC边所对的∠B.为了证明这一发现,小洲同学的解决思路是构造全等三角形将∠C转化为一个三角形的外角,利用三角形的外角大于不相邻的内角使问题得以证明.根据他的思路,完成以下作图与填空:
已知:如图,△ABC中,AB>AC.
求证:∠C>∠B.
(1)尺规作图:作∠A的角平分线AP,交BC于点D,在AB上截取AE=AC,连接DE.(保留作图痕迹)留作图痕迹)
(2)证明:∵AP平分线∠BAC,
∴ ∠BAD=∠CAD .
在△EAD和△CAD中,
∴△EAD≌△CAD(SAS).
∴∠C= ∠AED .
∵;
,∴∠C>∠B.
进一步思考,在△ABC中,如果已知∠C>∠B呢?请你模仿题中表述,写出你猜想的结论: 在同一个三角形中,大边所对角比小边所对角大 .
【考点】作图—复杂作图;三角形的稳定性;全等三角形的判定与性质;角平分线的性质.
【专题】作图题;证明题;图形的全等;几何直观;推理能力.
【答案】(1)见解析;
(2)∠BAD=∠CAD,∠AED,∠B,在同一个三角形中,大边所对角比小边所对角大.
【分析】(1)根据作角平分线的基本作法作图;
(2)根据全等三角形的性质证明.
【解答】(1)解:如图所示即为所求;
(2)证明:∵AP平分线∠BAC,
∴∠BAD=∠CAD,
在△EAD和△CAD中,
,
∴△EAD≌△CAD(SAS),
∴∠C=∠AED,
∵∠AED>∠B,
∴∠C>∠B.
结论:在同一个三角形中,大边所对角比小边所对角大.
故答案为:∠BAD=∠CAD,AD=AD,∠AED,∠B,在同一个三角形中,大边所对角比小边所对角大.
【点评】本题考查了作图﹣复杂作图,掌握全等三角形的判定定理和性质定理是解题的关键.
13.【问题背景】在△ABC中,AB,BC,AC三边的边长分别为,,,求这个三角形的面积.小明同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC,如图1所示.这样不需求△ABC的高,借助网格就能计算三角形的面积.
(1)直接写出△ABC的面积,S△ABC= .
(2)【思维拓展】若△A1B1C1三边的长分别为,,,请利用图2的正方形网格中画出△A1B1C1(每个小正方形的边长为a).
(3)【探索创新】若△A2B2C2的三边长分别为(m>0,n>0,且m≠n),试运用构图法求出△A2B2C2的面积.
【考点】作图—应用与设计作图;二次根式的应用;勾股定理.
【专题】作图题;几何直观.
【答案】(1);
(2)见解析;
(3)5mn.
【分析】(1)把三角形的面积看成矩形的面积减去周围的三个三角形面积即可;
(2)利用勾股定理,数形结合的射线画出图形;
(3)利用网格构造三角形,利用分割法求出三角形面积.
【解答】解:(1)如图①S△ABC=3×31×22×31×3;
故答案为:;
(2)如图②中,△A1B1C1即为所求;
(3)如图③,△A2B2C2的面积=4n×3m2n×2m4n×m2n×3m=5mn.
【点评】本题考查作图﹣应用与设计作图,二次根式的应用,勾股定理等知识,解题的关键是学会利用数形结合的思想解决问题.
14.【问题背景】:数学活动课上,老师将一副三角尺按图1所示位置摆放,分别作出∠AOB,∠BOC的平分线OG,OF,然后提出如下问题:求出∠GOF的度数.
【特例探究】:小明同学决定从特例入手探究老师提出的问题,他将三角尺分别按图2方式摆放,OG,OF仍然分别是∠AOB,∠BOC的角平分线.其中∠AOC=90°,∠BOC=30°.
(1)请你帮助小明计算出∠GOF的度数为 45 °;
【发现感悟】:小明发现,按图1摆放时,条件不变,虽然不知道∠BOC的度数,但也可以求出∠GOF的度数.
(2)请你帮小明完成这个问题的解答;
(3)积累了以上探究问题的经验,结合图3,若∠AOC=m°,则∠GOF= °;
【类比拓展】:(4)已知∠BOC=m°,若OA是∠BOC外一条射线,,OD,OE分别平分∠AOC,∠AOB,当∠DOE=m°﹣18°时,求出m的值(自己画出示意图求解).
【考点】作图—基本作图;角平分线的定义;余角和补角.
【专题】计算题;分类讨论;运算能力.
【答案】(1)45;
(2)∠GOF=45°;
(3);
(4)m的值为36°或132°.
【分析】(1)∠GOF=∠BOG﹣∠BOF∠AOB∠BOC,∠AOB=120°,∠BOC=30°;
(2)∠GOF=∠BOG﹣∠BOF∠AOB∠BOC,∠AOB=90°+∠BOC;
(3)∠GOF=∠BOG﹣∠BOF∠AOB∠BOC,∠AOB=∠AOC+∠BOC;
(4)分情况讨论.
【解答】解:(1)∵OG,OF分别是∠AOB,∠BOC的角平分线,
∴∠BOG∠AOB,∠BOF∠BOC,
∵∠AOB=∠AOC+∠BOC=120°,∠BOC=30°,
∴∠BOG=60°,∠BOF=15°,
∴∠GOF=∠BOG﹣∠BOF=45°,
故答案为:45;
(2)∠BOF∠BOC,
∠BOG∠AOB(90°+∠BOC)=45°+∠BOF,
∠GOF=∠BOG﹣∠BOF=45°;
(3)∠BOF∠BOC,
∠BOG∠AOB(m°+∠BOC)∠BOF,
∠GOF=∠BOG﹣∠BOF,
故答案为:;
(4),
∠DOE=∠AOE﹣∠AOD∠AOB∠AOCm°m°m°,
∵∠DOE=m°﹣18°,
∴m°﹣18°m°,
解得:m°=36°,
∠DOE=∠AOD+∠AOE∠AOB∠AOCm°+180°m°=180°m°,
∵∠DOE=m°﹣18°,
∴m°﹣18°=180°m°,
解得:m°=132°,
∴m的值为36°或132°.
【点评】本题考查了角平分线,关键是注意分类讨论.
15.(1)操作实践:如图,△ABC中,∠A=90°,∠B=22.5°,请画出一条直线把△ABC分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数.(要求画出一种分割方法即可)
(2)分类探究:已知△ABC中的最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,请直接写出△ABC中最大内角的所有可能值.
【考点】作图—应用与设计作图;三角形内角和定理;等腰三角形的性质.
【专题】作图题;几何直观.
【答案】(1)画图见解析;(2)画图见解析;△ABC的最大内角可能值是117°或108°或90°或84°.
【分析】(1)根据要求作出图形即可;
(2)分四种情形,分别作出图形求解即可.
【解答】解:(1)如图,
(2)设分割线为AD,
图1的最大角=39°+78°=117°,
图2的最大角=24°+(180°﹣2×48°)=108°,
图3的最大角=24°+66°=90°,
图4的最大角=84°,
故△ABC的最大内角可能值是117°或108°或90°或84°.
【点评】本题考查作图﹣应用与设计作图,三角形内角和定理,等腰三角形的性质等知识,解题的关键是学会用分类讨论的思想思考问题.
16.学习了三角形的中位线定理后,小涵进行了拓展性研究,他发现.连接梯形两腰中点的线段也具有类似的性质.探究过程如下:
(1)用直尺和圆规,作线段CD的垂直平分线,垂足为点F,连接EF,连接AF并延长交线段BC的延长线于点M(只保留作图痕迹):
(2)已知:在四边形ABCD中,AD∥BC,E为AB中点,F为CD中点.
猜想:EF∥AD∥BC,且.
证明:∵F是CD中点,
∴① DF=CF ,
∵AD∥BC,
∴∠DAF=∠FMC,
在△ADF和△MCF中,
,
∴△ADF≌△MCF,
∴AF=FM,AD=CM,
在△ABM中,E为AB中点,F为AM中点,
∴EF∥BM且③ EF .
∵BM=BC+CM=BC+AD,
∴EF(AD+BC),EF//AB,EF//CD,
请你根据该探究过程完成下面命题:连接梯形两腰中点的线段平行于两底并④ 等于两底和的一半 .
【考点】作图—基本作图;解直角三角形;全等三角形的判定与性质;线段垂直平分线的性质;三角形中位线定理;梯形中位线定理.
【专题】图形的全等;梯形;尺规作图;推理能力.
【答案】(1)见解析;
(2)①DF=CF; ②∠DFA=∠CFM; ③EFBM;④等于两底和的一半.
【分析】(1)根据要求作出图形;
(2)把四边形问题转化为三角形问题解决.
【解答】解:(1)图形如图所示:
(2)猜想:EF∥AD∥BC,且EF.
证明:∵F是CD中点,
∴①DF=CF,
∵AD∥BC,
∴∠DAF=∠FMC,
在△ADF和△MCF中,
,
∴△ADF≌△MCF(AAS),
∴AF=FM,AD=CM,
在△ABM中,E是AB中点,F是AM中点,
∴EF∥BM且③EF,
∵BM=BC+CM=BC+AD,
∴,EF∥AB,EF∥CD.
请你根据该探究过程完成下面命题:
连接梯形两腰中点的线段平行于两底并且④等于两底和的一半.
故答案为:①DF=CF; ②∠DFA=∠CFM;③EF;④等于两底和的一半.
【点评】本题考查作图﹣基本作图,全等三角形的判定和性质,线段的垂直平分线的性质,三角形中位线定理等知识,解题的关键是正确寻找全等三角形解决问题.
17.学习了角平分线性质后,小明进行了拓展研究,他发现△ABC的外角∠CBE和外角∠BCD的角平分线BF,CF交于点F,他猜想AF平分∠BAC,他的解决思路是利用角平分线性质.过点F分别向BE、BC、CD作垂线,再证明∠BAF和∠CAF这两个角所在的三角形全等得出结论.其中小明已经完成过点F分别向BE、BC作垂线,请根据他的思路完成以下作图与填空.
(1)用直尺和圆规,过点F作FK⊥CD于点K.(保留作图痕迹)
(2)已知:如图,△ABC的外角∠CBE和外角∠BCD的角平分线BF,CF交于点F,FK⊥CD于点K,FH⊥BC于点H,FG⊥BE于点G.求证:∠BAF=∠CAF.
证明:∵BF平分∠CBE,
FH⊥BC于点H,FG⊥BE于点G,
∴FH=① FG ,
∵CF平分∠BCD,
FK⊥CD于点K,FH⊥BC于点H,
∴FH=FK.
∴② FK=FG ,
∵FG⊥BE,FK⊥CD,
∴△AGF,△AKF均为直角三角形,
在Rt△AGF和Rt△AKF中:
③∴Rt△AGF≌Rt△AKF(HL).
∴∠BAF=∠CAF.
由此他得出结论:三角形的两(4) 外角角平分线 所在直线交点与三角形另一顶点连线平分这个内角.
【考点】作图—基本作图;全等三角形的判定与性质;角平分线的性质.
【专题】作图题;几何直观.
【答案】(1)图形见解析;
(2)①FG;②FK=FG;③AF=AF;④外角角平分线.
【分析】(1)根据垂线的基本尺规作图,规范作图即可K.
(2)根据角的平分线的性质定理,FG=FK,再证明Rt△AGF≌Rt△AKF(HL)即可得到结论.
【解答】(1)解:作图如图所示:
则FK即为所求.
(2)证明:∵BF平分∠CBE,FG⊥BE于点G,FH⊥BC于点H,
∴FH=FG,
∵CF平分∠BCD,FH⊥BC于点H,FK⊥CD于点K,
∴FH=FK,
∴FG=FK,
∵FK⊥CD,FG⊥BE,
∴△AGF,△AKF均为直角三角形,
在Rt△AGF和Rt△AKF中:
,
∴Rt△AGF≌Rt△AKF(HL),
∴∠CAF=∠BAF.
由此他得出结论:三角形的两外角角平分线所在直线交点与三角形另一顶点连线平分这个内角.
故答案为:①FG;②FK=FG;③AF=AF;④外角角平分线.
【点评】本题考查了垂线的基本作图,角的平分线的性质定理,直角三角形的全等判定和性质,熟练掌握作图和性质是解题的关键.
18.请仔细阅读下面的材料,并完成相应的任务.
作角的平分线
数学兴趣课上,老师让同学们利用尺规作∠AOB的平分线,同学们以小组为单位展开了讨论,勤学小组展示了学习过的作法:如图1,以点O为圆心,任意长为半径作弧,分别交OA,OB于点M,N;再分别以点M,N为圆心,大于的长为半径作弧,两弧相交于点P,作射线OP,则OP即为∠AOB的平分线.
勤学小组的证明过程如下:
连接PM,PN.
…
任务:
(1)请按照上面的材料,写出该证明的剩余部分;
(2)在图2中再设计一种不同的方法作∠AOB的平分线.(要求:尺规作图,保留作图痕迹,不写作法)
【考点】作图—复杂作图;角平分线的性质.
【专题】作图题;证明题;几何直观;推理能力.
【答案】(1)见解析;
(2)见解析.
【分析】(1)根据作图得OM=ON和MP=NP,可证得△OMP≌△ONP,则有∠MOP=∠NOP;
(2)在OA,OB上分别截取OC=OD,OM=ON,然后连接CN,MD交于点P,作射线OP即可解决问题.
【解答】解:(1)由作图可知:OM=ON,MP=NP,
在△OMP和△ONP,
,
∴△OMP≌△ONP(SSS),
∴∠MOP=∠NOP;
(2)作图如下:(方法不唯一).
【点评】本题主要考查作图﹣复杂作图,画角平分线和全等三角形的判定,解决本题的关键是掌握基本作图方法.
19.在学行四边形与正方形的相关知识后,智慧小组进行了更深入的探究.他们发现,如图所示的正方形ABCD,分别取BC,CD的中点N,M,连接AM,DN交于点E,过B作AM的垂线,交AM于点Q,交AD于点P.则四边形BPDN是平行四边形.
(1)用尺规完成以下基本作图:过B作AM的垂线,交AM于点Q,交AD于点P(只保留作图痕迹).
(2)根据(1)中所作图形,智慧小组发现四边形BPDN是平行四边形成立,并给出了证明,请补全证明过程.
证明:∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠C=90°,AD∥BC.
又∵M,N分别为BC,CD的中点,
∴,,
∴① DM=CN ,
在△ADM与△DCN中,
,
∴△ADM≌△DCN(SAS).
∴② ∠CDN=∠DAM .
又∵∠CDN+∠ADN=90°,
∴∠DAM+∠ADN=90°,
∴∠AED=90°,
又∵BP⊥AE,
∴∠AQP=∠AED=90°,
∴③ BP∥DN .
又∵DP∥BN,
∴四边形BPDN是平行四边形.
进一步思考,智慧小组发现任取BC,CD的上点N,M(M不与C,D重合),DM=CN,连接AM,DN,过B作AM的垂线,交AD于点P,则四边形BPDN是④ 平行四边形 .
【考点】作图—基本作图;全等三角形的判定与性质;平行四边形的判定;正方形的性质.
【专题】图形的全等;多边形与平行四边形;矩形 菱形 正方形;尺规作图;几何直观.
【答案】(1)见解答.
(2)①DM=CN;②∠CDN=∠DAM;③BP∥DN;④平行四边形.
【分析】(1)根据垂线的作图方法作图即可.
(2)结合全等三角形的判定与性质、正方形的性质、平行四边形的判定填空即可.
【解答】(1)解:如图,BQ即为所求.
(2)证明:∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠C=90°,AD∥BC.
又∵M,N分别为BC,CD的中点,
∴,,
∴DM=CN,
在△ADM与△DCN中,
,
∴△ADM≌△DCN(SAS).
∴∠CDN=∠DAM.
又∵∠CDN+∠ADN=90°,
∴∠DAM+∠ADN=90°,
∴∠AED=90°,
又∵BP⊥AE,
∴∠AQP=∠AED=90°,
∴BP∥DN.
又∵DP∥BN,
∴四边形BPDN是平行四边形.
进一步思考,智慧小组发现任取BC,CD的上点N,M(M不与C,D重合),DM=CN,连接AM,DN,过B作AM的垂线,交AD于点P,则四边形BPDN是平行四边形.
故答案为:①DM=CN;②∠CDN=∠DAM;③BP∥DN;④平行四边形.
【点评】本题考查作图—基本作图、全等三角形的判定与性质、正方形的性质、平行四边形的判定,解题的关键是理解题意,灵活运用所学知识解决问题.
20.(1)【问题情境】我国古代已经用角尺平分任意角,做法如下:如图①,在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线OC是∠AOB的平分线.请说明此做法的理由;
(2)【拓展实践】某公园的两条小路AB和AC,汇聚形成了一个岔路口A(如图②),现要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到休息椅M和N的距离相等.问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的备用图中作出路灯E的位置.(保留作图痕迹,不写作法)
【考点】作图—应用与设计作图;线段垂直平分线的性质.
【专题】几何图形;应用意识.
【答案】(1)见解析;
(2)见解析.
【分析】(1)证△OMC≌△ONC,得∠AOC=BOC,即可得出结论;
(2)根据角平分线定义及垂直平分线的性质作图即可.
【解答】解:(1)理由:由题意得CM=CN,OM=ON,OC=OC,
∴△OMC≌△ONC,
∴∠AOC=BOC,
∴OC是∠AOB的平分线;
(2)如图,点E即为所求.
【点评】本题考查了全等三角形的判定与性质、等边三角形的性质、角平分线定义以及尺规作图等知识,熟练掌握角平分线定义和等边三角形的性质,证明三角形全等是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
