2026年中考数学核心考点一轮复习 三角形(含解析)
文档属性
| 名称 | 2026年中考数学核心考点一轮复习 三角形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 15:07:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学一轮复习 三角形
一.解答题(共20小题)
1.【探究】
(1)已知△ABC和△ADE都是等边三角形.
①如图1,当点D在BC上时,连接CE.请探究CA,CE和CD之间的数量关系,并说明理由;
②如图2,当点D在线段BC的延长线上时,连接CE.请再次探究CA,CE和CD之间的数量关系,并说明理由.【运用】
(2)如图3,等边三角形ABC中,AB=6,点E在AC上,.点D是直线BC上的动点,连接DE,以DE为边在DE的右侧作等边三角形DEF,连接CF.当△CEF为直角三角形时,请直接写出BD的长.
2.在△ABC中,BC=a,AC=b,AB=c,CD是AB边的中线.
【初步探究】(1)如图1,当∠ACB=90°时,请用含a,b的式子表示CD2,CD2= ;
(2)如图2,当AC=BC=a时,请用含a,c的式子表示CD2,CD2= ;
【提出问题】在一般三角形中,如何用a,b,c表示CD2.
【分析问题】在(2)中根据等腰三角形的性质,可在直角三角形中利用勾股定理直接计算出CD2.类似的方法,在一般的三角形中,也可以通过构造直角三角形,利用勾股定理,间接计算出CD2.
【解决问题】如图3,在△ABC中,BC=a,AC=b,AB=c,CD是AB边的中线.求证:.
证明:作△ABC的高CE,
∴∠AEC=∠BEC=90°,
在Rt△AEC和Rt△BEC中,
CA2=CE2+AE2=CE2+(AD﹣ED)2=…
CB2=CE2+BE2=CE2+(BD+ED)2=…
…
(3)请补充完成以上证明过程.
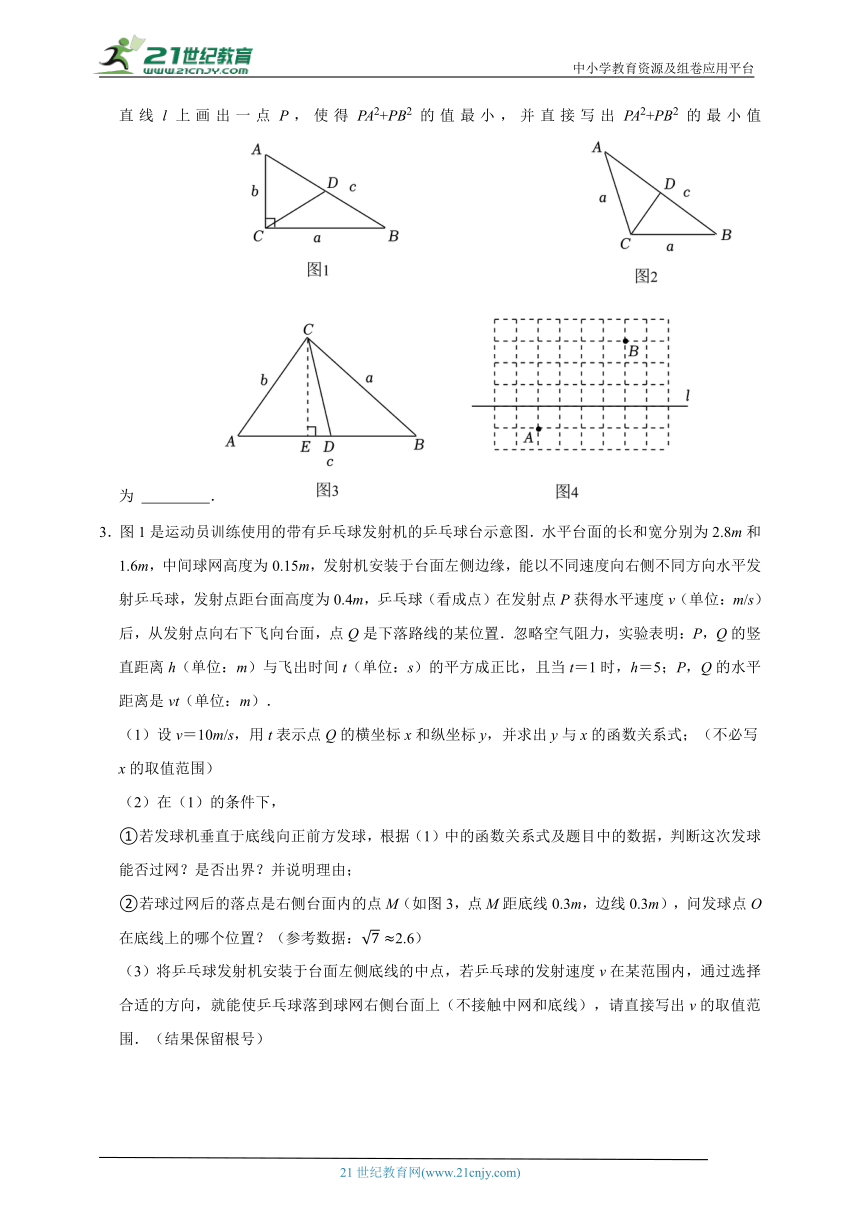
【知识应用】如图4,在边长为1的正方形网格中,A、B两点是网格的交点,利用无刻度直尺在直线l上画出一点P,使得PA2+PB2的值最小,并直接写出PA2+PB2的最小值为 .
3.图1是运动员训练使用的带有乒乓球发射机的乒乓球台示意图.水平台面的长和宽分别为2.8m和1.6m,中间球网高度为0.15m,发射机安装于台面左侧边缘,能以不同速度向右侧不同方向水平发射乒乓球,发射点距台面高度为0.4m,乒乓球(看成点)在发射点P获得水平速度v(单位:m/s)后,从发射点向右下飞向台面,点Q是下落路线的某位置.忽略空气阻力,实验表明:P,Q的竖直距离h(单位:m)与飞出时间t(单位:s)的平方成正比,且当t=1时,h=5;P,Q的水平距离是vt(单位:m).
(1)设v=10m/s,用t表示点Q的横坐标x和纵坐标y,并求出y与x的函数关系式;(不必写x的取值范围)
(2)在(1)的条件下,
①若发球机垂直于底线向正前方发球,根据(1)中的函数关系式及题目中的数据,判断这次发球能否过网?是否出界?并说明理由;
②若球过网后的落点是右侧台面内的点M(如图3,点M距底线0.3m,边线0.3m),问发球点O在底线上的哪个位置?(参考数据:2.6)
(3)将乒乓球发射机安装于台面左侧底线的中点,若乒乓球的发射速度v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上(不接触中网和底线),请直接写出v的取值范围.(结果保留根号)
4.某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.
【特例探究】
(1)如图1,当∠PAB=45°,AB=6时,AC= ,BC= ;
如图2,当sin∠PAB,AB=4时,AC= ,BC= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,在△ABC中,AB=4,BC=2,D、E、F分别是边AB、AC、BC的中点,连接DE并延长至G,使得GE=DE,连接BG,当BG⊥AC于点M时,求GF的长.
5.问题提出
(1)如图1,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 处.
问题探究
(2)如图2,在△ABC中,内角∠ABC的平分线BE和外角∠ACF的平分线CE,相交于点E,连接AE,若∠BEC=40°,请求出∠EAC的度数.
问题解决
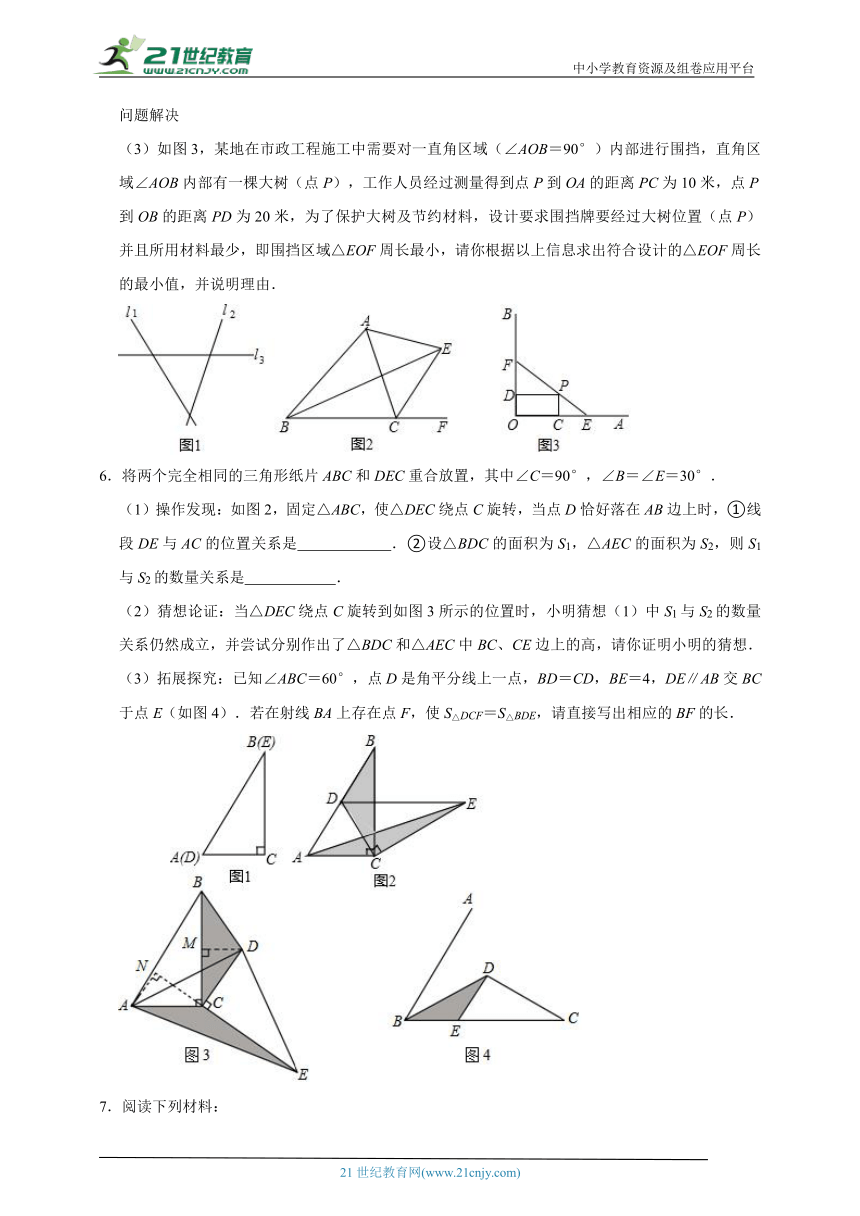
(3)如图3,某地在市政工程施工中需要对一直角区域(∠AOB=90°)内部进行围挡,直角区域∠AOB内部有一棵大树(点P),工作人员经过测量得到点P到OA的距离PC为10米,点P到OB的距离PD为20米,为了保护大树及节约材料,设计要求围挡牌要经过大树位置(点P)并且所用材料最少,即围挡区域△EOF周长最小,请你根据以上信息求出符合设计的△EOF周长的最小值,并说明理由.
6.将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,①线段DE与AC的位置关系是 .②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 .
(2)猜想论证:当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究:已知∠ABC=60°,点D是角平分线上一点,BD=CD,BE=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
7.阅读下列材料:
数学课上,老师出示了这样一个问题
如图1,△ABC中,∠B=45°,点D、B分别在AB、BC,且CA=CD,AE⊥CD,垂足为F,探究线段AD、BD、AE之间的数量关系,并证明,
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现∠BCD与∠BAE存在某种数量关系”
小亮:“通过借助勾股定理或构造三角形证明三角形全等,进而可以得到线段AD、BD、AE之间的数量关系”.
老师:保留原条件,再作AG平分∠CAF交CD于G(如图2).如果给出值,那么可求的值.
(1)写出∠BCD与∠BAE之间的某种数量关系;
(2)探究线段AD、BD、AE之间的数量关系,并证明;
(3)若m,求值(用含m的代数式表示).
8.小超在观看足球比赛时,发现了这样一个问题:两名运动员从不同的位置出发,沿着不同的方向,以不同的速度直线奔跑,什么时候他们离对方最近呢?
小超通过一定的测量,并选择了合适的比例尺,把上述问题抽象成如下数学问题:
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D以1cm/s的速度从点C向点B运动,点E以2cm/s的速度从点A向点B运动,当点E到达点B时,两点同时停止运动,若点D,E同时出发,多长时间后DE取得最小值?
小超猜想当DE⊥AB时,DE最小,探究后发现用几何的知识解决这个问题有一定的困难,于是根据函数的学习经验,设C,D两点间的距离为x cm,D,E两点间的距离为y cm,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小超的探究过程,请补充完整:
(1)由题意可知线段AE和CD的数量关系是 ;
(2)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值:
x/cm 0 1 2 3 4 5
y/cm 6.0 4.8 3.8 2.7 3.0
(说明:补全表格时相关数值保留一位小数)
(3)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题,小超的猜想 ;(填“正确”或“不正确”)当两点同时出发了 s时,DE取得最小值,为 cm.
9.感知:如图①,在△ABC中,分别以AB、AC为边在△ABC外部作等边△ABD、等边△ACE,连接CD、BE,则BE=DC(不需证明);
探究:如图②,在△ABC中,分别以AB、AC为边在△ABC外部作等腰△ABD、等腰△ACE,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD、BE,求证:BE=DC;
应用:如图③,在△ABC中,AB>AC,分别以AB、AC为边在△ABC内部作等腰△ABD、等腰△ACE,点E恰好在BC边上,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD,CE=3cm,CD=2cm,△ABC的面积为10cm2,求△ACD的面积.
10.在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,连接BE,CF.
【发现问题】如图①,若∠BAC=30°,延长BE交CF于点D,则BE与CF的数量关系是 ,∠BDC的度数为 .
【类比探究】如图②,若∠BAC=120°,延长BE,FC相交于点D,请猜想BE与CF的数量关系及∠BDC的度数,并说明理由.
【拓展延伸】如图③,若∠BAC=90°,且点B,E,F在同一条直线上,过点A作AM⊥BF,垂足为点M,请猜想BF,CF,AM之间的数量关系,并说明理由.
11.综合与实践:
【问题背景】人教版教材九年级上册P63第10题“探索研究”:等边△ABD和等边△ACE,将△ACE绕点A旋转到某一位置,要求观察图形,提出问题并加以解决.
【探究发现】
(1)如图1,小明连结BE、CD,并发现∠ADC与∠ABE的数量关系,请你探究后写出证明过程.
(2)如图2,得知小明的结论后,小华又连结DE,已知AC⊥BE,AE=5,BE=12,请你求出DE的长;
【拓展探究】
(3)如图3,小颖画出了等腰直角△ABC和等腰直角△ADE,其中∠BAC=∠DAE=90°,AB=AC,AD=AE,点C在DE上,请你直接写出CD、CE和BC之间的数量关系.
12.问题探究
(1)如图①,在四边形ABCD中,∠BAC=90°,,CD=4,E为AD中点,连接BE,求BE的最大值;
问题解决
(2)如图②,某小区计划在一片足够大的空地上修建四边形的花园ABCD,其中BC=40米,AD=CD,AD⊥CD,AB∥CD,由于受地理位置的影响,∠ABC<90°.根据要求,现计划给该花园修建条笔直的绿色长廊,且绿色长廊的入口O定为BC的中点,出口定为点D,为了尽可能地提高观赏体验,要求绿色长廊OD最长,试求绿色长廊OD最长为多少米?
13.全等三角形是我们初中数学的重要知识点之一,它为我们学习后面几何知识做好铺垫,掌握全等三角形的证明是做一系列复杂几何证明的基础.
【问题初探】
(1)构造全等三角形的方法有很多,有一种常见的方法是作高线,将需要证明的边或角放在两个直角三角形中进而通过全等证明关系.比如,我们可以通过作高线证明三角形中一个重要的结论“在同一个三角形中,如果两个角相等,那么这两个角所对的边也相等”.如图1,在△ABC中,已知∠B=∠C,可证AB=AC,小聪同学的作法是作BC边上的高线AD.现在请你完成小聪同学的证明过程;
【类比分析】
(2)通过上述例子,我们发现通过作高线构造直角三角形证明全等确实是一种有效的方法,由此推出了三角形中的重要结论.现在请你借助上述的方法或结论继续探索,如图2,在△ABC中,已知∠ABC=∠ACB,点E为边AC上一点,点F为边AB延长线上一点,连结EF与边BC交于点D,若点D恰为线段EF中点,试探究线段CE与线段BF的数量关系,并说明理由;
【学以致用】
(3)如图3,在△ABC中,∠CAB=90°,AD,AE分别为△ABC的角平分线和中线,过点E作EF⊥AD与线段AD的延长线交于点G,与边AB的延长线交于点F,已知△ABC的面积是30,线段AF的长为8,求△AED的面积.
14.【阅读理解】
定义:在同一平面内,点A,B分别在射线PM,PN上,过点A垂直PM的直线与过点B垂直PN的直线交于点Q,则我们把∠AQB称为∠APB的“边垂角”(四边形内角和等于360°).
(1)如图1和2,若∠AQB是∠APB的“边垂角”,则∠AQB与∠APB的数量关系是 .
【迁移运用】
(2)如图3,CD,BE分别是△ABC的两条高,两条高交于点F,根据定义,我们知道∠DBE是∠DCE的“边垂角”或∠DCE是∠DBE的“边垂角”,∠DAE的“边垂角”是 .
【拓展延伸】
(3)如图4,若∠ACD是∠ABD的“边垂角”,且AB=AC.BD交AC于点E,点C关于直线BD的对称点为点F,连接AF,EF,且∠CAF=45°,延长BA和CF相交于点G.
①请说明:△AGC≌△AEB;
②请说明:BE=CF+CE.
15.定义:如果1条线段将一个三角形分割成2个等腰三角形,我们把这条线段叫做这个三角形的“双等腰线”.如果2条线段将一个三角形分成3个等腰三角形,我们把这2条线段叫做这个三角形的“三等腰线”.如图1,BE是△ABD的“双等腰线”,AD、BE是△ABC的“三等腰线”.
(1)请在图2三个图中,分别画出△ABC的“双等腰线”,并做必要的标注或说明.
(2)如果一个等腰三角形有“双等腰线”,那么它的底角度数是 .
(3)如图3,△ABC中,∠C∠B,∠B<45°.画出△ABC所有可能的“三等腰线”,使得对∠B取值范围内的任意值都成立,并做必要的标注或说明.(每种可能用一个图单独表示,如果图不够用可以自己补充)
16.定义:三角形一边中线的中点和该边的两个顶点组成的三角形称为中原三角形.如图①,AD是△ABC的中线,F是AD的中点,则△FBC是中原三角形.
(1)求中原三角形与原三角形的面积之比(直接写出答案).
(2)如图②,AD是△ABC的中线,E是边AC上的点,AC=3AE,BE与AD相交于点F,连接CF.求证:△FBC是中原三角形.
(3)如图③,在(2)的条件下,延长CF交AB于点M,连接ME,求△FEM与△ABC的面积之比.
17.如图1,等边△ABC的边长为4,点D是直线AB上异于A,B的一动点,连接CD,以CD为边长,在CD右侧作等边△CDE,连接BE.
【初步感知】
(1)求证:△CAD≌△CBE;
【类比探究】
(2)当点D在直线AB上运动时,①AD与BE的数量关系是 ;
②△BDE的周长是否存在最小值?若存在,求此时AD的长;若不存在,说明理由;
【拓展应用】
(3)当点D在直线AB上运动时,△BDE能否形成直角三角形?若能,请直接写出此时AD的长;若不能,说明理由.
18.【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS
B.SAS
C.AAS
D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=5,EC=3,求线段BF的长.
【灵活运用】
如图③,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
19.【问题情境】
如图1,在Rt△ABC中,∠BCA=90°,∠B=30°,AC=4,AB的垂直平分线交AB于点D,交BC于点E,作射线AE.
(1)则CE的长为 ;
【变式思考】
(2)在“问题情境”的基础上,如图2,点P是射线AE上的动点,过点P分别作PF⊥AB所在直线于点F,作PH⊥BC所在直线于点H.
①求△PHE与△PFA面积之和的最小值;
②连接FH,求FH的最小值是多少?
【拓展探究】
(3)在“问题情境”的基础上,如图3,△ABC内有点Q,且∠AQC=60°,AB、BC上分别有一点M、N,连接QM、QN、MN,直接写出△QMN周长的最小值.
20.【基础巩固】(1)如图1,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE,连接AD,BE;求证:△ACD≌△BCE;
【尝试应用】(2)如图2,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,连接AD,BE,A、D、E三点在一条直线上,BC与DE交于点F;
①求∠BEA的大小;
②若DF=3EF且BE=2,求△BCE的面积;
【拓展提高】(3)如图3,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,点G为DE的中点,AE交BC于点H,连接GH,若GH⊥AB,且S△ABH为18,求CH的长.
中考数学一轮复习 三角形
参考答案与试题解析
一.解答题(共20小题)
1.【探究】
(1)已知△ABC和△ADE都是等边三角形.
①如图1,当点D在BC上时,连接CE.请探究CA,CE和CD之间的数量关系,并说明理由;
②如图2,当点D在线段BC的延长线上时,连接CE.请再次探究CA,CE和CD之间的数量关系,并说明理由.【运用】
(2)如图3,等边三角形ABC中,AB=6,点E在AC上,.点D是直线BC上的动点,连接DE,以DE为边在DE的右侧作等边三角形DEF,连接CF.当△CEF为直角三角形时,请直接写出BD的长.
【考点】三角形综合题.
【专题】压轴题;存在型;模型思想;应用意识.
【答案】(1)①CE+CD=CA,理由详见解析;②CA+CD=CE,理由详见解析;(2)6或6+2.
【分析】(1)①根据条件易证△ABD≌△ACE(SAS),再进行线段转化易得答案;②与第①小问思路一样,证出△ABD≌△ACE(SAS)即可;
(2)由△CEF为直角三角形可知,需要分类讨论确定哪个角是直角三角形,再根据点D的位置关系去讨论即可,因为点D是动点,所以按照前面两问带给我们的思路,去构造类似的全等三角形,进而讨论求解即可.
【解答】解:(1)①CE+CD=CA.理由如下,
∵△ABC和△ADE是等边三角形,
∴AB=AC=BC,AD=AE=DE,∠BAC=∠DAE=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴CE=BD
∵BD+CD=BC,
∴CE+CD=CA.
②CA+CD=CE.理由如下,
∵△ABC和△ADE是等边三角形,
∴AB=AC=BC,AD=AE=DE,∠BAC=∠DAE=60°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴CE=BD,
∵CB+CD=BD,
∴CA+CD=CE.
(2)过E作EH∥AB,则△EHC为等边三角形.
①当点D在H左侧时,如图1,
∵ED=EF,∠DEH=∠FEC,EH=EC,
∴△EDH≌△EFC(SAS),
∴∠ECF=∠EHD=120°,
此时△CEF不可能为直角三角形.
②当点D在H右侧,且在线段CH上时,如图2,
同理可得∴△EDH≌△EFC(SAS),
∴∠FCE=∠EHD=60°,∠FEC=∠DEH<∠HEC=60°,
此时只有∠CFE有可能为90°,
当∠CFE=90°时,∠EDH=90°,
∴ED⊥CH,
∵CH=CE=2,
∴CDCH,
又∵AB=6,
∴BD=6.
③当点D在H右侧,且HC延长线上时,如图3,
此时只有∠CEF=90°,
∵∠DEF=60°,
∴∠CED=30°,
∵∠ECH=60°,
∴∠EDC=CED=30°,
∴CD=CE=2,
∴BD=6+2.
综上:BD的长为6或6+2.
【点评】本题主要考查三角形综合题,熟练掌握全等三角形的性质和判定是解题的关键.
2.在△ABC中,BC=a,AC=b,AB=c,CD是AB边的中线.
【初步探究】(1)如图1,当∠ACB=90°时,请用含a,b的式子表示CD2,CD2= (a2+b2) ;
(2)如图2,当AC=BC=a时,请用含a,c的式子表示CD2,CD2= a2c2 ;
【提出问题】在一般三角形中,如何用a,b,c表示CD2.
【分析问题】在(2)中根据等腰三角形的性质,可在直角三角形中利用勾股定理直接计算出CD2.类似的方法,在一般的三角形中,也可以通过构造直角三角形,利用勾股定理,间接计算出CD2.
【解决问题】如图3,在△ABC中,BC=a,AC=b,AB=c,CD是AB边的中线.求证:.
证明:作△ABC的高CE,
∴∠AEC=∠BEC=90°,
在Rt△AEC和Rt△BEC中,
CA2=CE2+AE2=CE2+(AD﹣ED)2=…
CB2=CE2+BE2=CE2+(BD+ED)2=…
…
(3)请补充完成以上证明过程.
【知识应用】如图4,在边长为1的正方形网格中,A、B两点是网格的交点,利用无刻度直尺在直线l上画出一点P,使得PA2+PB2的值最小,并直接写出PA2+PB2的最小值为 18 .
【考点】三角形综合题.
【专题】几何综合题;压轴题;运算能力;应用意识.
【答案】(1)(a2+b2);
(2)a2c2;
(3)证明见解答;
(4)PA2+PB2的最小值为18,作图见解答.
【分析】【初步探究】(1)利用直角三角形斜边上的中线等于斜边的一半和勾股定理即可求得答案;
(2)利用等腰三角形“三线合一”的性质及勾股定理即可求得答案;
【解决问题】(3)运用勾股定理即可将证明过程补充完整;
【知识应用】作点A关于直线l的对称点A′,连接A′B,AA′,PA,PB,AA′与直线l交于点E,过点B作BF⊥直线l于F,设PE=x,则PF=4﹣x,运用勾股定理可得:PA2+PB2=2x2﹣8x+26=2(x﹣2)2+18,根据非负数的性质即可得出答案.
【解答】【初步探究】(1)解:∵CD是Rt△ABC斜边AB上的中线,
∴CDAB,
∴CD2AB2,
在Rt△ABC中,AB2=AC2+BC2=a2+b2,
∴CD2AB2(a2+b2),
故答案为:(a2+b2);
(2)解:∵AC=BC=a,CD是AB边的中线,
∴CD⊥AB,BDc,
在Rt△BCD中,CD2=BC2﹣BD2=a2c2,
故答案为:a2c2;
【解决问题】(3)证明:作△ABC的高CE,
∴∠AEC=∠BEC=90°,
在Rt△AEC和Rt△BEC中,
CA2=CE2+AE2=CE2+(AD﹣ED)2=CE2+AD2﹣2AD×ED+ED2①,
CB2=CE2+BE2=CE2+(BD+ED)2=CE2+BD2+2BD×ED+ED2②,
∵CD为AB边中线,
∴AD=BDAB,
∵CE是△ABC 的高,
∴∠CED=90°,
∴CE2+ED2=CD2,
∴①+②得:,
∴CD2(CA2+CB2)AB2,
即CD2(a2+b2)c2.
【知识应用】如图4,过点B作BO⊥直线l于O,以直线l为x轴,直线OB为y轴建立平面直角坐标系,
设点P(x,0)是x轴的动点,点Q是AB的中点,连接PA,PB,PQ,
则A(﹣4,﹣1),B(0,3),Q(﹣2,1),
则PA2=(x+4)2+12=x2+8x+17,
PB2=x2+32=x2+9,
PQ2=12+(x+2)2=x2+4x+5,
AB2=42+42=32,
由(2)知,PQ2(PA2+PB2)AB2,
∴x2+4x+5(PA2+PB2)32,
∴PA2+PB2=2(x2+4x+5)+16=2(x+2)2+18,
∴当x=﹣2时,PA2+PB2有最小值18,
此时点P的坐标为(﹣2,0),
如图所示,点P即为所求作的点.
,
【点评】本题是三角形综合题,考查了勾股定理的应用,直角三角形的性质,非负数的性质、因式分解的应用,解答本题的关键是明确题意,利用因式分解的方法和非负数的性质解答.
3.图1是运动员训练使用的带有乒乓球发射机的乒乓球台示意图.水平台面的长和宽分别为2.8m和1.6m,中间球网高度为0.15m,发射机安装于台面左侧边缘,能以不同速度向右侧不同方向水平发射乒乓球,发射点距台面高度为0.4m,乒乓球(看成点)在发射点P获得水平速度v(单位:m/s)后,从发射点向右下飞向台面,点Q是下落路线的某位置.忽略空气阻力,实验表明:P,Q的竖直距离h(单位:m)与飞出时间t(单位:s)的平方成正比,且当t=1时,h=5;P,Q的水平距离是vt(单位:m).
(1)设v=10m/s,用t表示点Q的横坐标x和纵坐标y,并求出y与x的函数关系式;(不必写x的取值范围)
(2)在(1)的条件下,
①若发球机垂直于底线向正前方发球,根据(1)中的函数关系式及题目中的数据,判断这次发球能否过网?是否出界?并说明理由;
②若球过网后的落点是右侧台面内的点M(如图3,点M距底线0.3m,边线0.3m),问发球点O在底线上的哪个位置?(参考数据:2.6)
(3)将乒乓球发射机安装于台面左侧底线的中点,若乒乓球的发射速度v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上(不接触中网和底线),请直接写出v的取值范围.(结果保留根号)
【考点】三角形综合题.
【专题】代数几何综合题;压轴题;运算能力;应用意识.
【答案】(1)yx2+0.4;
(2)①这次发球能过网,会出界.理由见解答;
②发球点O在距右侧边线1.6m处,即左上角;
(3)v.
【分析】(1)运用待定系数法即可求得答案;
(2)①当x=1.4时,y1.42+0.4=0.302>0.15,可判断这次发球能过网;当y=0时,解方程x2+0.4=0,即可判断这次发球会出界;
②如图,过点M作MN⊥OA于N,则AN=0.3m,MN=2.8﹣0.3=2.5m,利用勾股定理即可求得答案;
(3)当垂直底线发球,恰巧过网,此时v值最小,可求得v的最小值为,当斜发球恰巧与右下底线与边线边缘相碰,即球落在右下角点B处时,此时v值最大,可求得v的最大值为,即可得出答案.
【解答】解:(1)设h=kt2,把t=1,h=5代入得:k=5,
∴h=5t2,
当v=10m/s时,点Q的横坐标为10t,纵坐标为0.4﹣h=0.4﹣5t2,
∴x=10t,y=0.4﹣5t2,
∴yx2+0.4;
(2)①这次发球能过网,会出界.理由如下:
∵yx2+0.4,
当x=1.4时,y1.42+0.4=0.302>0.15,
∴这次发球能过网;
当y=0时,x2+0.4=0,
解得:x1=2,x2=﹣2(舍去),
∵22.8,
∴这次发球会出界;
②如图,过点M作MN⊥OA于N,则AN=0.3m,MN=2.8﹣0.3=2.5m,
由①知:OM=2,
在Rt△OMN中,ON1.3(m),
∴OA=ON+AN=1.3+0.3=1.6(m),
答:发球点O在距右侧边线1.6m处,即左上角;
(3)当垂直底线发球,恰巧过网,此时v值最小,
∵中间球网高度为0.15m,
∴y=0.15m,
∴h=0.4﹣0.15=0.25m,
∴h=5t2=0.25,
解得:t1,t2(不符合题意,舍去),
∵底线到中网的距离为1.4m,
∴v,
当斜发球恰巧与右下底线与边线边缘相碰,即球落在右下角点B处时,此时v值最大,如图,连接OB,设右上角为点A,
则OA=0.8m,AB=2.8m,
在Rt△OAB中,OB,
∵这时的h=0.4m,
∴h=5t2=0.4,
解得:t1,t2(不符合题意,舍去),
∴v,
∴v.
【点评】本题考查了待定系数法求二次函数解析式,利用二次函数解决实际问题,勾股定理等,构造直角三角形运用勾股定理是解题关键.
4.某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.
【特例探究】
(1)如图1,当∠PAB=45°,AB=6时,AC= 6 ,BC= 6 ;
如图2,当sin∠PAB,AB=4时,AC= 2 ,BC= 2 ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,在△ABC中,AB=4,BC=2,D、E、F分别是边AB、AC、BC的中点,连接DE并延长至G,使得GE=DE,连接BG,当BG⊥AC于点M时,求GF的长.
【考点】三角形综合题.
【专题】压轴题;应用意识.
【答案】见试题解答内容
【分析】(1)如图1,由等腰直角三角形的性质得到AP=BP=6,根据三角形中位线的性质和平行线分线段成比例定理可得PE=PF=3,利用勾股定理可得AC和BC的长;如图2,根据特殊三角函数值可得∠BAP=30°,计算PB和AP的长,同理由中线的性质和勾股定理可得结论;
(2)设 PF=m,PE=n 则AP=2m,PB=2n,根据勾股定理分别列等式,可得结论;
(3)如图4,作辅助线,证明四边形EFCG是平行四边形,得Q是FG的中点,根据中垂三角形的定义可知:△FCG是中垂三角形,利用(2)中三边的关系可得GF的长.
【解答】(1)解:如图1,∵AF⊥BE,
∴∠APB=∠APE=∠BPF=90°,
∵∠PAB=45°,AB=6,
∴AP=PB=6,
如图1,连接EF,
∵AF,BE是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥AB.且 EFAB,
∴,
∴PE=PF=3,
由勾股定理得:AE=BF3,
∴AC=BC=2AE=6,
如图2,∵sin∠PAB,AB=4,AF⊥BE,
∴∠PAB=30°,
∴BPAB=2,AP=2,
∵AF、BE是△ABC的中线,
∴PEPB=1,PFAP,
由勾股定理得:AE,
BF,
∴AC=2AE=2,BC=2BF=2,
故答案为:6,6,2,2;
(2)解:猜想:AB2、BC2、AC2三者之间的关系是:AC2+BC2=5AB2,
证明:如图3,设 PF=m,PE=n 则AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=AB2①,
在Rt△APE中,(2m)2+n2=()2 ②,
在Rt△BPF中,m2+(2n)2=()2 ③,
由①得:m2+n2,由②+③得:5( m2+n2),
∴AC2+BC2=5AB2;
(3)解:如图4,连接CG,EF,过点F作FN∥BG交CG于点N,FG与AC交于点Q,
∵FN∥BG,BG⊥AC,
∴FN⊥AC,
∵F是BC的中点,
∴N是CG的中点,
∵D、E分别是AB、AC的中点,
∴DE=FC,DE∥FC,
∵ED=EG,
∴EG=FC,EG∥FC,
∴四边形EFCG是平行四边形,
∴Q是FG的中点,
∴△FCG是中垂三角形,
∵AB=4,BC=2,
∴CG=EF=BD=2,FC,
由(2)中结论可知:5FC2=CG2+FG2,
即5×5=(2)2+FG2,
∴GF.
【点评】本题考查三角形综合题、中垂三角形的定义和应用、勾股定理、三角形的中位线定理、平行四边形的性质和判定等知识,解题的关键是学会添加常用辅助线,构造中垂三角形解决问题,属于中考压轴题.
5.问题提出
(1)如图1,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 4 处.
问题探究
(2)如图2,在△ABC中,内角∠ABC的平分线BE和外角∠ACF的平分线CE,相交于点E,连接AE,若∠BEC=40°,请求出∠EAC的度数.
问题解决
(3)如图3,某地在市政工程施工中需要对一直角区域(∠AOB=90°)内部进行围挡,直角区域∠AOB内部有一棵大树(点P),工作人员经过测量得到点P到OA的距离PC为10米,点P到OB的距离PD为20米,为了保护大树及节约材料,设计要求围挡牌要经过大树位置(点P)并且所用材料最少,即围挡区域△EOF周长最小,请你根据以上信息求出符合设计的△EOF周长的最小值,并说明理由.
【考点】三角形综合题.
【专题】压轴题;应用意识.
【答案】见试题解答内容
【分析】(1)作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,然后根据角平分线的性质进行判断;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义列式并整理得到∠BAC=2∠BEC,过点E作EF⊥BA交延长线于F,作EG⊥AC于G,作EH⊥BD于H,根据角平分线上的点到角的两边的距离相等可得EF=FH,EG=EH,然后求出EF=EG,再根据到角的两边距离相等的点在角的平分线上判断出AE是∠CAF的平分线,再根据角平分线的定义解答即可;
(3)根据前两问的启发,设∠AOB、∠AEF、∠BFE的角平分线交于点Q,作QN⊥OB于N,QM⊥OA于M,QH⊥EF于H,连接QP,可得四边形OMQN是正方形,设正方形边长为y,则所求的△OEF的周长为2y,再根据“斜边大于等于直角边”,即PQ≥QH,列出不等式,解不等式可得y的最小值.
【解答】解:作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.
故答案为:4;
(2)解:∵∠ABC与∠ACD的角平分线相交于点E,
∴∠CBE∠ABC,∠ECD∠ACD,
由三角形的外角性质得,∠ACD=∠ABC+∠BAC,
∠ECD=∠BEC+∠CBE,
∴∠ACD=∠BEC∠ABC,
∴(∠ABC+∠BAC)=∠BEC∠ABC,
整理得,∠BAC=2∠BEC,
∵∠BEC=40°,
∴∠BAC=2×40°=80°,
过点E作EH⊥BA交延长线于H,作EG⊥AC于G,作EF⊥BC于F,
∵BE平分∠ABC,
∴EF=EH,
∵CE平分∠ACD,
∴EG=EF,
∴EH=EG,
∴AE是∠CAF的平分线,
∴∠CAE(180°﹣∠BAC)(180°﹣80°)=50°;
(3)如图,设∠AOB、∠AEF、∠BFE的角平分线交于点Q,
作QN⊥OB于N,QM⊥OA于M,QH⊥EF于H.连接QP.
则QN=QH=QM=y,FH=FN,EH=EM,
∴△OEF的周长:OE+OF+EF=OF+FN+OE+EM=ON+OM=QN+QM=2QN=2y,
∵PDOC是矩形,且PD=20,PC=10,
∴ND=y﹣10,CM=y﹣20,
∴QP2=(y﹣10)2+(y﹣20)2
∵PQ≥QH,
∴(y﹣10)2+(y﹣20)2≥y2
∴y2﹣60y+500≥0,
∴(y﹣30)2≥400,
∴y≥50或y≤10(舍),
∴2y≥100,当且仅当P、H重合时取等号.
即△OEF的周长的最小值为100.
【点评】本题为三角形综合题,主要考查了三角形角平分线的性质及其应用.第三问是本题的难点,将△OEF的周长转化为用正方形边长表示同时利用“斜边大于等直角边”原理列出不等式是解答的关键.
6.将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,①线段DE与AC的位置关系是 DE∥AC .②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 S1=S2 .
(2)猜想论证:当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究:已知∠ABC=60°,点D是角平分线上一点,BD=CD,BE=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
【考点】三角形综合题.
【专题】几何综合题;压轴题;应用意识.
【答案】见试题解答内容
【分析】(1)①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行解答;
②根据等边三角形的性质可得AC=AD,再根据直角三角形30°角所对的直角边等于斜边的一半求出ACAB,然后求出AC=BD,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
(2)根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角边”证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明;
(3)过点D作DF1∥BE,求出四边形BEDF1是菱形,根据菱形的对边相等可得BE=DF1,然后根据等底等高的三角形的面积相等可知点F1为所求的点,过点D作DF2⊥BD,求出∠F1DF2=60°,从而得到△DF1F2是等边三角形,然后求出DF1=DF2,再求出∠CDF1=∠CDF2,利用“边角边”证明△CDF1和△CDF2全等,根据全等三角形的面积相等可得点F2也是所求的点,根据菱形和等边三角形的性质可得结论.
【解答】解:(1)①∵△DEC绕点C旋转,点D恰好落在AB边上,
∴AC=CD,
∵∠BAC=90°﹣∠B=90°﹣30°=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,
∴DE∥AC;
②∵∠B=30°,∠C=90°,
∴CD=ACAB,
∴BD=AD=AC,
根据等边三角形的性质,△ACD的边AC、AD上的高相等,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
故答案为:①DE∥AC;②S1=S2;
(2)如图3,∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,
∴∠ACN=∠DCM,
∵在△ACN和△DCM中,
∵,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
(3)如图,过点D作DF1∥BE,连接CF1,易求四边形BEDF1是菱形,
所以BE=DF1=BF1=4,且BE、DF1上的高相等,
此时S△BDE;
过点D作DF2⊥BD,
∵∠ABC=60°,F1D∥BE,
∴∠F2F1D=∠ABC=60°,
∵BF1=DF1,∠F1BD∠ABC=30°,∠F2DB=90°,
∴∠F1DF2=60°,
∴△DF1F2是等边三角形,
∴DF1=DF2,
∵BD=CD,∠ABC=60°,点D是角平分线上一点,
∴∠DBC=∠DCB60°=30°,
∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°,
∠CDF2=360°﹣150°﹣60°=150°,
∴∠CDF1=∠CDF2,
∵在△CDF1和△CDF2中,
,
∴△CDF1≌△CDF2(SAS),
∵S△DCF=S△BDE,
∴点F2也是所求的点,
∵BE=4,
∴BF1=BE=DF1=F1F2=4,
∴BF2=8,
综上,BF的长为4或8.
【点评】本题考查了全等三角形的判定与性质,三角形的面积,等边三角形的判定与性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟练掌握等底等高的三角形的面积相等,以及全等三角形的面积相等是解题的关键,(3)要注意符合条件的点F有两个.
7.阅读下列材料:
数学课上,老师出示了这样一个问题
如图1,△ABC中,∠B=45°,点D、B分别在AB、BC,且CA=CD,AE⊥CD,垂足为F,探究线段AD、BD、AE之间的数量关系,并证明,
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现∠BCD与∠BAE存在某种数量关系”
小亮:“通过借助勾股定理或构造三角形证明三角形全等,进而可以得到线段AD、BD、AE之间的数量关系”.
老师:保留原条件,再作AG平分∠CAF交CD于G(如图2).如果给出值,那么可求的值.
(1)写出∠BCD与∠BAE之间的某种数量关系;
(2)探究线段AD、BD、AE之间的数量关系,并证明;
(3)若m,求值(用含m的代数式表示).
【考点】三角形综合题.
【专题】几何综合题;压轴题;推理能力;应用意识.
【答案】(1)∠BAE+∠BCD=45°;
(2)AD2+AD BD+BD2=AE2;证明见解答;
(3).
【分析】(1)根据三角形外角性质可得∠ADC=∠B+∠BCD=45°+∠BCD,再由CA=CD,AE⊥CD,可得∠CAF=90°﹣∠ACF=2∠BCD,再根据∠BAE+∠ADC=90°,即可求得答案;
(2)如图1,过点C作CG⊥AD于G,可得△BCG是等腰直角三角形,由勾股定理可得AG2+CG2=AC2,即可求得答案;
(3)如图2,延长AG交BC于N,设EN=CN=a,EF=b,则CE=2a,AF=m EF=mb,AE=AF+EF=(m+1)b,由△AEN∽△CEF,可求得,再由△AGF∽△CGN,即可求得答案.
【解答】解:(1)∠BAE+∠BCD=45°.理由如下:
∵∠B=45°,
∴∠ADC=∠B+∠BCD=45°+∠BCD,
∵CA=CD,
∴∠CAD=∠ADC=45°+∠BCD,∠ACF=180°﹣2∠ADC=90°﹣2∠BCD,
∵AE⊥CD,
∴∠AFC=∠AFD=90°,
∴∠CAF=90°﹣∠ACF=2∠BCD,
∵∠BAE+∠ADC=90°,
∴∠BAE+45°+∠BCD=90°,
∴∠BAE+∠BCD=45°;
(2)AD2+AD BD+BD2=AE2.
证明:如图1,过点C作CG⊥AD于G,
由(1)知,∠ACF=90°﹣2∠BCD,∠BAE+∠BCD=45°,
∴∠ACE=∠ACF+∠BCD=90°﹣2∠BCD+∠BCD=90°﹣∠BCD,
又∵∠AEC=∠B+∠BAE=45°+45°﹣∠BCD=90°﹣∠BCD,
∠ACE=∠AEC,
∴AC=AE,
∵CA=CD,CG⊥AD,
∴AG=DGAD,∠AGC=∠BGC=90°,
∵∠B=45°,
∴△BCG是等腰直角三角形,
∴BG=CG=DG+BDAD+BD,
在Rt△ACG中,AG2+CG2=AC2,
∴(AD)2+(AD+BD)2=AE2,
∴AD2+AD BD+BD2=AE2;
(3)如图2,延长AG交BC于N,
由(2)得:AC=AE,
又∵AG平分∠CAF,
∴AN⊥CE,CN=ENCE,
设EN=CN=a,EF=b,
则CE=2a,AF=m EF=mb,AE=AF+EF=(m+1)b,
∵∠ANE=∠CFE=90°,∠AEN=∠CEF,
∴△AEN∽△CEF,
∴,即,
∴,
∵∠AFG=∠CNG=90°,∠AGF=∠CGN,
∴△AGF∽△CGN,
∴,即.
【点评】此题是三角形的综合题,主要考查了等腰三角形的判定和性质,等腰直角三角形判定和性质,相似三角形的判定和性质,三角形内角和定理等知识,利用参数表示线段的长,添加辅助线构造相似三角形是解本题的关键,属于中考数学压轴题,难度较大.
8.小超在观看足球比赛时,发现了这样一个问题:两名运动员从不同的位置出发,沿着不同的方向,以不同的速度直线奔跑,什么时候他们离对方最近呢?
小超通过一定的测量,并选择了合适的比例尺,把上述问题抽象成如下数学问题:
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D以1cm/s的速度从点C向点B运动,点E以2cm/s的速度从点A向点B运动,当点E到达点B时,两点同时停止运动,若点D,E同时出发,多长时间后DE取得最小值?
小超猜想当DE⊥AB时,DE最小,探究后发现用几何的知识解决这个问题有一定的困难,于是根据函数的学习经验,设C,D两点间的距离为x cm,D,E两点间的距离为y cm,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小超的探究过程,请补充完整:
(1)由题意可知线段AE和CD的数量关系是 AE=2CD ;
(2)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值:
x/cm 0 1 2 3 4 5
y/cm 6.0 4.8 3.8 3.0 2.7 3.0
(说明:补全表格时相关数值保留一位小数)
(3)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题,小超的猜想 不正确 ;(填“正确”或“不正确”)当两点同时出发了 4 s时,DE取得最小值,为 2.7 cm.
【考点】三角形综合题.
【专题】压轴题;应用意识.
【答案】见试题解答内容
【分析】(1)根据时间和速度可得AE和CD的长,可得结论;
(2)作辅助线,根据勾股定理计算DE的长,根据二次函数的最值可得结论;
(3)画图象即可;
(4)作辅助线,根据勾股定理计算DE的长,根据二次函数的最值可得结论.
【解答】解:(1)由题意得:AE=2x,CD=x,
∴AE=2CD;
故答案为:AE=2CD;
(2)如图所示,过D作DG⊥AB于G,
由(1)知:CD=x,则BD=8﹣x,
sin∠B,
∴,DG,BG,
∴EG=AE+BG﹣10=2x10,
∴y,
当x=3时,y3;
故答案为:3.0;
(3)如图所示:
(4)由(2)知:y,
∵0≤x≤5,
∴当x=4时,y有最小值是2.7,
故答案为:不正确,4,2.7.
【点评】本题属于三角形和函数的综合题,考查了勾股定理,函数图象,直角三角形的性质等知识,解题的关键是理解题意,学会利用勾股定理解决问题,学会利用图象法解决问题,属于中考压轴题.
9.感知:如图①,在△ABC中,分别以AB、AC为边在△ABC外部作等边△ABD、等边△ACE,连接CD、BE,则BE=DC(不需证明);
探究:如图②,在△ABC中,分别以AB、AC为边在△ABC外部作等腰△ABD、等腰△ACE,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD、BE,求证:BE=DC;
应用:如图③,在△ABC中,AB>AC,分别以AB、AC为边在△ABC内部作等腰△ABD、等腰△ACE,点E恰好在BC边上,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD,CE=3cm,CD=2cm,△ABC的面积为10cm2,求△ACD的面积.
【考点】三角形综合题.
【专题】压轴题;应用意识.
【答案】见试题解答内容
【分析】探究:证明△ADC≌△ABE(SAS),可得BE=DC;
应用:先证明△ADC≌△ABE,可得BE=DC=2,利用面积求得AF=4,根据△ABE的面积与△ACD的面积相等可得结论.
【解答】探究:
证明:∵∠BAD=∠EAC,
∴∠DAC=∠BAE,
在△ACD和△AEB中,
∵,
∴△ACD≌△AEB(SAS),
∴CD=BE;
应用:
∵∠BAD=∠EAC,
∴∠DAC=∠BAE,
在△ACD和△AEB中,
∵,
∴△ACD≌△AEB(SAS),
∴CD=BE=2;
∴BC=BE+CE=2+3=5,
过A作AF⊥BC于F,如图③,
∵△ABC的面积为10cm2,
∴BC AF=10,
5×AF=10,
AF=4,
∴S△ACD=S△ABE2×4=4cm2.
【点评】本题是三角形综合题目,考查了全等三角形的判定与性质、等边三角形的判定与性质等知识,证明三角形全等是解决问题的关键.
10.在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,连接BE,CF.
【发现问题】如图①,若∠BAC=30°,延长BE交CF于点D,则BE与CF的数量关系是 BE=CF ,∠BDC的度数为 30° .
【类比探究】如图②,若∠BAC=120°,延长BE,FC相交于点D,请猜想BE与CF的数量关系及∠BDC的度数,并说明理由.
【拓展延伸】如图③,若∠BAC=90°,且点B,E,F在同一条直线上,过点A作AM⊥BF,垂足为点M,请猜想BF,CF,AM之间的数量关系,并说明理由.
【考点】三角形综合题.
【专题】几何综合题;压轴题;图形的全等;推理能力.
【答案】(1)BE=CF,30°;
(2)BE=CF,∠BDC=60°,证明见解答;
(3)BF=CF+2AM,证明见解答.
【分析】(1)根据等腰三角形的性质,利用SAS证明△ABE≌△ACF即可得出结论;
(2)根据等腰三角形的性质,利用SAS证明△ABE≌△ACF即可得出结论;
(3)利用SAS证明△ABE≌△ACF,可得BE=CF,再由等腰直角三角形的性质可得AM=EM=FM,即EF=2AM,根据BF=BE+EF,等量代换可得BF=CF+2AM.
【解答】解:(1)BE=CF,∠BDC=30°,
理由如下:如图1所示,设AC与BD交于点O,
∵∠BAC=∠EAF=30°,
∴∠BAC+∠CAE=∠EAF+∠CAE,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,∠ABE=∠ACF,
∵∠AOE=∠ABE+∠BAC,∠AOE=∠ACF+∠BDC,
∴∠BDC=∠BAC=30°.
故答案为:BE=CF,30°;
(2)BE=CF,∠BDC=60°,
理由如下:如图2,
∵∠BAC=∠EAF=120°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,∠AEB=∠AFC,
∵∠EAF=120°,AE=AF,
∴∠AEF=∠AFE=30°,
∴∠BDC=∠BEF﹣∠EFD=∠AEB+30°﹣(∠AFC﹣30°)=60°;
(3)【拓展延伸】BF=CF+2AM,
理由如下:如图3,
∵∠BAC=∠EAF=90°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,
∵AE=AF,∠EAF=90°,AM⊥EF,
∴AM=EM=FM,即EF=2AM,
∵BF=BE+EF,
∴BF=CF+2AM.
【点评】本题是三角形综合题,主要考查了全等三角形的判定与性质,等腰三角形和等腰直角三角形的性质,三角形的面积等知识,熟练掌握全等三角形的判定是解题的关键.
11.综合与实践:
【问题背景】人教版教材九年级上册P63第10题“探索研究”:等边△ABD和等边△ACE,将△ACE绕点A旋转到某一位置,要求观察图形,提出问题并加以解决.
【探究发现】
(1)如图1,小明连结BE、CD,并发现∠ADC与∠ABE的数量关系,请你探究后写出证明过程.
(2)如图2,得知小明的结论后,小华又连结DE,已知AC⊥BE,AE=5,BE=12,请你求出DE的长;
【拓展探究】
(3)如图3,小颖画出了等腰直角△ABC和等腰直角△ADE,其中∠BAC=∠DAE=90°,AB=AC,AD=AE,点C在DE上,请你直接写出CD、CE和BC之间的数量关系.
【考点】三角形综合题.
【专题】压轴题;推理能力.
【答案】(1)∠ADC=∠ABE,理由见解析;
(2)13;
(3)CD2+CE2=BC2,理由详见解析.
【分析】(1)通过SAS判定△ACD≌△ABE,根据全等三角形的性质可得结论;
(2)由△ACD≌△ABE得CD=BE=12,再证明∠DCE=90°,由勾股定理可求出DE的长;
(3)与(1)相同,证明全等后,利用勾股定理证明三边关系即可.
【解答】(1)证明:∠ADC=∠ABE,理由如下,
∵△ADB与△ACE均为等边三角形,
∴∠DAB=∠ABD=∠ADB=60°,∠EAC=∠ACE=∠AEC=60°,AD=AB=BD,AE=AC=CE,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE;
(2)解:∵△ACE是等边三角形,BE⊥AC,
∴∠AEB=30°,
由(1)知,△DAC≌△BAE,
∴DC=BE=12,∠ACD=∠AEB=30°,
又∵∠ACE=60°,
∴∠DCE=∠DCA+ACE=30°+60°=90°,
∵CE=AE=5,
∴;
(3)解:CD2+CE2=BC2,理由如下,
如图,连接BE,
∵∠DAE=90°,AD=AE,
∴∠ADE=∠AED=45°,
∴∠BAC=∠EAD=90°,
∴∠BAE=∠CAD,
在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴BE=CD,∠AEB=∠ADC=45°,
∴∠BEC=∠AEB+∠AED=90°,
∴BE2+CE2=BC2,
∴CD2+CE2=BC2.
【点评】本题主要考查旋转的性质以及勾股定理,解题关键是找准边与角的关系证明全等,然后利用勾股定理求解.
12.问题探究
(1)如图①,在四边形ABCD中,∠BAC=90°,,CD=4,E为AD中点,连接BE,求BE的最大值;
问题解决
(2)如图②,某小区计划在一片足够大的空地上修建四边形的花园ABCD,其中BC=40米,AD=CD,AD⊥CD,AB∥CD,由于受地理位置的影响,∠ABC<90°.根据要求,现计划给该花园修建条笔直的绿色长廊,且绿色长廊的入口O定为BC的中点,出口定为点D,为了尽可能地提高观赏体验,要求绿色长廊OD最长,试求绿色长廊OD最长为多少米?
【考点】三角形综合题.
【专题】压轴题;推理能力;模型思想.
【答案】(1)22;
(2)绿色长廊OD最长为(2020)米.
【分析】(1)取AC的中点F,连接EF、BF,在△BEF中,BF+EF>BE,可得当B、E、F三点共线的时候BE最大,此时BE=BF+EF,根据中位线可得出EF的长度,在Rt△ABF中根据勾股定理可得BF的长度,即可得出BE的最大值;
(2)过C作CM⊥AB于M点,在AD上截取DN使DN=BM,连接BN,取CN中点P,连接DP、OP,可证得四边形ADCM为正方形,再证明△CMB≌△CDN,易证△BCN为等腰直角三角形,从而得出BN的长度,根据中位线定理可得出OP的长度;利用直角三角形斜边中线等于斜边的一半求出DP=20,再根据OP+PD>OD可得,当O、P、D三点共线时OD最大,即可得出答案.
【解答】解:(1)如图,取AC的中点F,连接EF、BF,
∵E、F分别是AD和AC的中点,
∴EF为△ADC的中位线,
∴EFCD=2,
在Rt△ABF中,AB=4,AFAC=2,
∴BF2,
在△BEF中,BF+EF>BE,
∴当B、E、F三点共线的时候BE最大,
即此时BE=BF+EF=22;
(2)过C作CM⊥AB于M点,在AD上截取DN使DN=BM,连接BN,取CN中点P,连接DP.OP,如图,
∵CM⊥AB,AB∥CD,
∴∠CMA=∠MCD=∠ADC=90°,
∴四边形ADCM为矩形,
∵AD=CD,
∴矩形ADCM为正方形,
∴CD=CM,
在△CMB与△CDN中,
,
∴△CMB≌△CDN(SAS),
∴CN=CB,∠BCM=∠NCD,
∴∠BCN=∠MCD=90°,
在Rt△BCN中,BC=CN=40,
∴BN40,
在Rt△CDN中,点P为CN中点,
∴DP20,
在Rt△BCN中,点P、O分别为CN、CB中点,
∴OP为△BCN的中位线,
∴OPBN=20,
在△OPD中,OP+PD>OD,
∴当O、P.D三点共线的时OD最大,
即此时OD=OP+PD=2020,
答:绿色长廊OD最长为(2020)米.
【点评】本题是四边形综合题,考查中位线定理的综合应用,结合三角形的全等以及三角形三边长关系,在做此类题目时注意类比每一问之间的关系,一般下一问都会用到上一问的结论和做题思路.
13.全等三角形是我们初中数学的重要知识点之一,它为我们学习后面几何知识做好铺垫,掌握全等三角形的证明是做一系列复杂几何证明的基础.
【问题初探】
(1)构造全等三角形的方法有很多,有一种常见的方法是作高线,将需要证明的边或角放在两个直角三角形中进而通过全等证明关系.比如,我们可以通过作高线证明三角形中一个重要的结论“在同一个三角形中,如果两个角相等,那么这两个角所对的边也相等”.如图1,在△ABC中,已知∠B=∠C,可证AB=AC,小聪同学的作法是作BC边上的高线AD.现在请你完成小聪同学的证明过程;
【类比分析】
(2)通过上述例子,我们发现通过作高线构造直角三角形证明全等确实是一种有效的方法,由此推出了三角形中的重要结论.现在请你借助上述的方法或结论继续探索,如图2,在△ABC中,已知∠ABC=∠ACB,点E为边AC上一点,点F为边AB延长线上一点,连结EF与边BC交于点D,若点D恰为线段EF中点,试探究线段CE与线段BF的数量关系,并说明理由;
【学以致用】
(3)如图3,在△ABC中,∠CAB=90°,AD,AE分别为△ABC的角平分线和中线,过点E作EF⊥AD与线段AD的延长线交于点G,与边AB的延长线交于点F,已知△ABC的面积是30,线段AF的长为8,求△AED的面积.
【考点】三角形综合题.
【专题】压轴题;几何直观.
【答案】(1)见解析;
(2)CE=BF,理由见解析;
(3).
【分析】(1)根据等腰三角形等边对等角得到∠B=∠C,再利用全等三角形即可得证;
(2)作平行线利用中点证△BFD≌△GED,得到BF=EG,最后通过等线段转化即可得证;
(3)参考上述方式构造全等,利用等线段的转化找△AED的面积和△ABC面积得关系.
【解答】(1)证明:过A作AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∵AD=AD,∠B=∠C,
∴△ADB≌△ADC(AAS),
∴AB=AC;
(2)解:CE=BF,
理由:过E作EG∥AB交BC于G,
∴∠F=∠DEG,∠FBD=∠EGD,
∵点D恰为线段EF中点,
∴DF=DE,
∴△BFD≌△GED(AAS),
∴BF=EG,
∵∠ABC=∠ACB,
∴∠EGC=∠ECG,
∴EG=CE,
∴CE=BF;
(3)如图延长FE交AC于点H,过B作BM∥AC,
∵AD是角平分线,
∴∠FAG=∠HAG,
∵AD⊥EF,
∴∠AGD=∠AGF,
∵AG=AG,
∴△AGF≌△AGH(SAS),
AF=AH,∠AHG=∠AFG,
由(2)中证明方法可知△CHE≌△BME(AAS),
∴CH=BM,∠CHE=∠BME,
∴∠AHG=∠BMF=∠AFG,
∴BM=BF,
∵AF=8,
∴设BF=x,则BM=CH=x,AB=8﹣x,
∴AC=AH+CH=8+x,
∴S△ABCAB AC=30,
即(8﹣x)(8+x)=60,
解得x=2,
∵AE是△ABC的中线,
∴AE=BEBC,
∴∠EAB=∠ABE,
∴∠EAD+45°=∠BEF+45°,
∴∠EAD=∠BEP,
∵∠AGE=∠BPE=90°,
∴△AEG≌△EBP(AAS),
∴EG=BP,
∵∠F=45°,
∴BP=PF=PM=EG,
∴ED:EB=EG:EP=1:4,
∴S△AEDS△AEBS△ABC.
∴△AED的面积为.
【点评】本题主要考查了全等三角形的判定和性质、三角形面积公式、平行线的性质等内容,熟练掌握相关知识是解题的关键.
14.【阅读理解】
定义:在同一平面内,点A,B分别在射线PM,PN上,过点A垂直PM的直线与过点B垂直PN的直线交于点Q,则我们把∠AQB称为∠APB的“边垂角”(四边形内角和等于360°).
(1)如图1和2,若∠AQB是∠APB的“边垂角”,则∠AQB与∠APB的数量关系是 ∠AQB+∠APB=180°或∠AQB=∠APB. .
【迁移运用】
(2)如图3,CD,BE分别是△ABC的两条高,两条高交于点F,根据定义,我们知道∠DBE是∠DCE的“边垂角”或∠DCE是∠DBE的“边垂角”,∠DAE的“边垂角”是 ∠DFE .
【拓展延伸】
(3)如图4,若∠ACD是∠ABD的“边垂角”,且AB=AC.BD交AC于点E,点C关于直线BD的对称点为点F,连接AF,EF,且∠CAF=45°,延长BA和CF相交于点G.
①请说明:△AGC≌△AEB;
②请说明:BE=CF+CE.
【考点】三角形综合题.
【专题】压轴题;新定义;几何直观.
【答案】(1)∠AQB+∠APB=180°或∠AQB=∠APB;(2)∠DFE;(3)证明过程详见解析.
【分析】(1)根据图形可得两种情况,分别利用三角形内角和和四边形内角和推导即可;
(2)由“边垂角”定义可得,∠DAE的“边垂角”为∠DFE;
(3)①由“边垂角”可证∠ABE=∠ACF,再根据题干已知条件即可得证;②由①全等推出AG=AE,BE=CG,然后证△AGF≌△AEF,得到GF=EF,最后通过线段的和差即可得证.
【解答】(1)解:若∠AQB是∠APB的“边垂角”,分两种情况:
①如图1:
∵∠AQB是∠APB的“边垂角”,
∴AQ⊥PA,BQ⊥PB,
∴∠PAQ=90°,∠PBQ=90°,
∵∠PAQ+∠AQB+∠APB+∠PBQ=360°,
∴∠AQB+∠APB=180°;
②如图2:
∵∠AQB是∠APB的“边垂角”,
∴AQ⊥PA,BQ⊥PB,
∴∠AQB+∠1=90°,∠APB+∠2=90°,
∵∠1=∠2,
∴∠AQB=∠APB;
综上,∠AQB+∠APB=180°或∠AQB=∠APB.
故答案为:∠AQB+∠APB=180°或∠AQB=∠APB.
(2)解:由“边垂角”定义可得,∠DAE的“边垂角”为∠DFE,
故答案为:∠DFE.
(3)证明:①∵∠ACD是∠ABD的“边垂角”,
∴∠ABE+∠AEB=90°,∠ACD+∠DEC=90°,
∵∠AEB=∠DEC,
∴∠ABE=∠ACF,
∴∠BAE=∠CAG=90°,
∵AB=AC,
∴△AGC≌△AEB(ASA);
②证明:∵△AGC≌△AEB(ASA),
∴AG=AE,BE=CG,
∵∠FAC=45°,
∴∠GAF=90°﹣∠FAC=45°,
∴∠GAF=∠FAE=45°,
∵AF=AF,
∴△AGF≌△AEF(SAS),
∴GF=EF.
∵点C关于直线BE对称点为点F,
∴EF=EC,
∴BE=CG=CF+FG=CF+EF=CF+CE,
∴BE=CF+CE.
【点评】本题主要考查了三角形内角和、直角三角形的性质、全等三角形的判定和性质等内容,熟练掌握相关知识点和添加合适的辅助线是解题的关键.
15.定义:如果1条线段将一个三角形分割成2个等腰三角形,我们把这条线段叫做这个三角形的“双等腰线”.如果2条线段将一个三角形分成3个等腰三角形,我们把这2条线段叫做这个三角形的“三等腰线”.如图1,BE是△ABD的“双等腰线”,AD、BE是△ABC的“三等腰线”.
(1)请在图2三个图中,分别画出△ABC的“双等腰线”,并做必要的标注或说明.
(2)如果一个等腰三角形有“双等腰线”,那么它的底角度数是 72°或36°或45°或()° .
(3)如图3,△ABC中,∠C∠B,∠B<45°.画出△ABC所有可能的“三等腰线”,使得对∠B取值范围内的任意值都成立,并做必要的标注或说明.(每种可能用一个图单独表示,如果图不够用可以自己补充)
【考点】三角形综合题.
【专题】几何综合题;新定义;几何直观;应用意识.
【答案】见试题解答内容
【分析】(1)根据等腰三角形的性质和三角形内角和解答即可;
(2)设底角度数为x,分三种情况利用等腰三角形的性质和三角形内角和解答即可;
(3)根据两种情况、利用等腰三角形的性质和三角形内角和解答即可.
【解答】解:(1)如图2,取AB的中点D,则AD=CD=BD,
∴△ADC和△BCD是等腰三角形;
如图3,取CD=BC,则∠CDB=∠B=70°,
∵∠A=35°,
∴∠ACD=70°﹣35°=35°,
∴∠ACD=∠A,
∴AD=CD=BC,
∴△ADC和△BCD是等腰三角形;
如图4,作AB的垂直平分线DE,交AC于D,交AB于E,连接BD,
∴AD=BD,
∴∠A=∠ABD=27°,
∴∠CDB=54°,
∵∠ABC=81°,
∴∠CBD=81°﹣27°=54°=∠BDC,
∴CD=BC,
∴△ADB和△BCD是等腰三角形;
(2)①设△ABC是以AB、AC为腰的锐角三角形,BD为“双等腰线”,如图5,
当AD=BD,BD=BC时,
设∠A=x°,则∠ABD=x°,
∴∠BDC=∠C=2x°,
∴∠ABC=∠C=2x°,
∵∠A+∠ABC+∠C=180°,
∴x°+2x°+2x°=180°,
∴x=36°,2x=72°,
∴∠C=72°,
②设△ABC是以AB、AC为腰的钝角三角形,AD为“双等腰线”,如图6,
当AB=BD,AD=CD时,
设∠B=y°,则∠C=y°,
∵AD=CD,
∴∠DAC=∠C=y°,
∴∠ADB=2y°,
∵AB=BD,
∴∠BAD=∠ADB=2y°,
∵∠B+∠BAD+∠ADB=180°,
∴y°+2y°+2y°=180°,
∴y=36°,
∴∠B=∠C=36°,
③设△ABC是以AB、AC为腰的直角三角形,AD为“双等腰线”,如图7,
当AB=BD,AD=CD时,AD为BC的垂直平分线,
设∠B=z°,则∠C=z°,∠BAD=z°,
∴∠B+∠BAD=90°,
∴z°+z°=90°,
∴z=45°,
∴∠B=∠C=45°,
④设顶角为x,
可得,x+3x+3x=180°
解得:x=()°,
∴∠C=3x=()°,
故答案为:72°或36°或45°或()°;
(3)∵要画出使得对∠B取值范围内的任意值都成立的“三等腰线”,
∴不能使∠B等于具体的数值,
∴值需要使分割后的三个等腰三角形的底角成比例即可,
第一种画法:如图8,
∵∠C∠B,
设∠B=2x°,∠C=3x°,
当AD、DE将△ABC分成BD=DE,DE=AE,AD=AC的三个等腰三角形时,
则有∠BED=∠B=2x°,∠ADC=∠C=3x°,
∵∠EDC=∠B+∠BED=4x°,
∴∠EDA=∠EDC﹣∠ADC=x°,
∴∠EAD=x°,
∴“三等腰线”使得三个等腰三角形的底角比为∠B:∠C:∠EDA=2:3:1,
即可使得对∠B取值范围内的任意值都成立,
第二种画法:
∵∠C∠B,
设∠B=2x°,∠C=3x°,
当AD、DE将△ABC分成BE=DE,AD=AE,AD=CD的三个等腰三角形时,
则∠EDB=∠B=2x°,∠DAC=∠C=3x°,
∵∠AED=∠B+∠BDE=4x°,
∴∠EDA=4x°,
因此,“三等腰线”使得三个等腰三角形的底角比为∠B:∠C:∠AED=2:3:4,即可使得对∠B取值范围内的任意值都成立,
综上所述,如图所示的两种“三等腰线”可以使得对∠B取值范围内的任意值都成立.
【点评】本题主要考查三角形综合题和作图﹣应用与设计作图,解题的关键是掌握等腰三角形的判定和性质.
16.定义:三角形一边中线的中点和该边的两个顶点组成的三角形称为中原三角形.如图①,AD是△ABC的中线,F是AD的中点,则△FBC是中原三角形.
(1)求中原三角形与原三角形的面积之比(直接写出答案).
(2)如图②,AD是△ABC的中线,E是边AC上的点,AC=3AE,BE与AD相交于点F,连接CF.求证:△FBC是中原三角形.
(3)如图③,在(2)的条件下,延长CF交AB于点M,连接ME,求△FEM与△ABC的面积之比.
【考点】三角形综合题.
【专题】新定义;三角形;图形的相似;几何直观;推理能力;应用意识.
【答案】(1)中原三角形与原三角形的面积之比为1:2;
(2)证明见解答过程;
(3)△FEM与△ABC的面积之比为1:18.
【分析】(1)由F是AD的中点,可得S△DFCS△DAC,S△DFBS△DAB,即有S△FBCS△ABC,故中原三角形与原三角形的面积之比为1:2;
(2)作CE的中点G,连接DG,由AD是△ABC的中线,可得DG是△BCE的中位线,CE=2EG,即得BE∥DG,即EF∥DG,根据AC=3AE,CE=2EG,可得AE=EG,即得AF=DF,从而△FBC是中原三角形;
(3)过D作DH∥CM交AB于H,由DH∥CM,D是BC中点,F是AD中点,可得AM=MH=BH,即知,可得△AME∽△ABC,有∠AME=∠ABC,,从而ME∥BC,△MEF∽△CBF,即有()2,S△FBC=9S△FEM,又S△FBCS△ABC,即得△FEM与△ABC的面积之比为1:18.
【解答】(1)解:∵F是AD的中点,
∴S△DFCS△DAC,S△DFBS△DAB,
∴S△DFC+S△DFBS△DACS△DAB,
∴S△FBCS△ABC,
∴中原三角形与原三角形的面积之比为1:2;
(2)证明:作CE的中点G,连接DG,如图:
∵AD是△ABC的中线,
∴D是BC中点,
∵G是CE中点,
∴DG是△BCE的中位线,CE=2EG,
∴BE∥DG,即EF∥DG,
∵AC=3AE,
∴CE=2AE,
∴AE=EG,
又EF∥DG,
∴AF=DF,即F是AD中点,
∴△FBC是中原三角形;
(3)解:过D作DH∥CM交AB于H,如图:
∵DH∥CM,D是BC中点,
∴BH=MH,
∵DH∥MF,F是AD中点,
∴AM=MH,
∴AM=MH=BH,
∴,
∵AC=3AE,
∴,
又∠MAE=∠BAC,
∴△AME∽△ABC,
∴∠AME=∠ABC,,
∴ME∥BC,
∴△MEF∽△CBF,
∴()2=()2,
∴S△FBC=9S△FEM,
由(1)知:S△FBCS△ABC,
∴9S△FEMS△ABC,
∴S△FEMS△ABC,
∴△FEM与△ABC的面积之比为1:18.
【点评】本题考查三角形综合应用,涉及新定义、三角形中位线定理及推论、三角形面积等,解题的关键是作辅助线,构造三角形中位线.
17.如图1,等边△ABC的边长为4,点D是直线AB上异于A,B的一动点,连接CD,以CD为边长,在CD右侧作等边△CDE,连接BE.
【初步感知】
(1)求证:△CAD≌△CBE;
【类比探究】
(2)当点D在直线AB上运动时,①AD与BE的数量关系是 AD=BE ;
②△BDE的周长是否存在最小值?若存在,求此时AD的长;若不存在,说明理由;
【拓展应用】
(3)当点D在直线AB上运动时,△BDE能否形成直角三角形?若能,请直接写出此时AD的长;若不能,说明理由.
【考点】三角形综合题.
【专题】压轴题;几何直观.
【答案】(1)证明过程见解析;(2)①AD=BE;②2;(3)8或4.
【分析】(1)证△ACD≌△BCE(SAS)即可得证;
(2)①同第一问,证证△ACD≌△BCE(SAS)即可得证;
②由(1)得△ACD≌△BCE(SAS),则BE=AD,因为BD+BE+DE=AB+DE,所以要使△BDE的周长最小,只要DE最小,当CD⊥AB时,CD的长最小,此时DE最小,由“三线合一”即可求出AD的长;
(3)分两种情况:当∠BDE=90°时和当∠BED=90°时,分别作出图形,作CH⊥AB于点H,利用(1)的结果及勾股定理解答即可.
【解答】(1)证明:∵△ABC、△CDE都是等边三角形,
∴.CA=CB=AB,∠A=∠ACB=∠ABC=60°,∠DCE=∠DCE=DEC=60°,CD=CE=DE,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)①如图,当点D在线段AB上、点D在BA延长线上、点D在AB延长线上时,
证明方法同第一问:
∵△ABC、△CDE都是等边三角形,
∴.CA=CB=AB,∠A=∠ACB=∠ABC=60°,∠DCE=∠DCE=DEC=60°,CD=CE=DE,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE.
故答案为:AD=BE.
②△BDE的周长存在最小值,由(1)得△ACD≌△BCE(SAS),
∴BE=AD,
∴BD+BE+DE=AB+DE,
要使△BDE的周长最小,则DE最小,
∵CD=DE,
∴当CD⊥AB时,CD的长最小,如图2,
∵CA=CB=4,CD⊥AB,
∴;
(3)当点D在直线AB上运动时,△BDE能形成直角三角形,分两种情况,
①当∠BDE=90°时,作CH⊥AB于点H,如图3,
∵AB=AC=BC=4,
∴,
∴,
∵∠BDE=90°,∠CDE=60°,
∴∠ADC=30°,
∴CD=2CH=4,
∴,
∴AD=AH+HD=8;
②当∠BED=90°时,作CH⊥AB于点H,如图4,
同理得AH=2,,
设AD=x,
由(1)得△ACD≌△BCE(SAS),
∴BE=AD=x,
∵CD=DE,
由勾股定理得,DH2+CH2=DB2﹣BE2,
即,
解得,x=4,
∴AD=4,
综上,当点D在直线AB上运动时,△BDE能形成直角三角形,AD的值为8或4.
【点评】本题是三角形的综合,主要考查等边三角形的性质、全等三角形的判定与性质、直角三角形的性质、最短路线问题、勾股定理等知识,灵活运用全等三角形的判定与性质、勾股定理是解答本题的关键.
18.【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 B .
A.SSS
B.SAS
C.AAS
D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 2<AD<8 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=5,EC=3,求线段BF的长.
【灵活运用】
如图③,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
【考点】三角形综合题.
【专题】压轴题;几何直观;运算能力;推理能力.
【答案】(1)B;
(2)2<AD<8;
(3)8;
(4).
【分析】【问题情境】(1)根据全等三角形的判定定理解答;
(2)根据三角形的三边关系计算;
【初步运用】延长AD到M,使AD=DM,连接BM,证明△ADC≌△MDB,根据全等三角形的性质解答;
【灵活运用】延长ED到点G,使DG=ED,连接GF,GC,证明△DBE≌△DCG,得到BE=CG,根据勾股定理解答.
【解答】【问题情境】
解:(1)在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
故选:B;
(2)由(1)得:△ADC≌△EDB,
∴AC=BE=6,
在△ABE中,AB﹣BE<AE<AB+BE,
即10﹣6<2AD<10+6,
∴2<AD<8,
故答案为:2<AD<8;
【初步运用】
解:延长AD到M,使AD=DM,连接BM,如图②所示:
∵AE=EF.EF=5,
∴AC=AE+EC=5+3=8,
∵AD是△ABC中线,
∴CD=BD,
在△ADC和△MDB中,
,
∴△ADC≌△MDB(SAS),
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC=8;
【灵活运用】
解:线段BE、CF、EF之间的等量关系为:BE2+CF2=EF2.理由如下:
延长ED到点G,使DG=ED,连接GF,GC,如图③所示:
∵ED⊥DF,
∴EF=GF,
∵D是BC的中点,
∴BD=CD,
在△BDE和△CDG中,
,
∴△DBE≌△DCG(SAS),
∴BE=CG,
∵∠A=90°,
∴∠B+∠ACB=90°,
∵△DBE≌△DCG,EF=GF,
∴BE=CG,∠B=∠GCD,
∴∠GCD+∠ACB=90°,
即∠GCF=90°,
∴Rt△CFG中,由勾股定理得:CF2+GC2=GF2,
∴BE2+CF2=EF2.
【点评】本题是三角形综合题目,考查的是全等三角形的判定和性质、三角形三边关系以及勾股定理的应用等知识;熟练掌握三角形的三边关系和勾股定理,证明三角形全等是解题的关键.
19.【问题情境】
如图1,在Rt△ABC中,∠BCA=90°,∠B=30°,AC=4,AB的垂直平分线交AB于点D,交BC于点E,作射线AE.
(1)则CE的长为 ;
【变式思考】
(2)在“问题情境”的基础上,如图2,点P是射线AE上的动点,过点P分别作PF⊥AB所在直线于点F,作PH⊥BC所在直线于点H.
①求△PHE与△PFA面积之和的最小值;
②连接FH,求FH的最小值是多少?
【拓展探究】
(3)在“问题情境”的基础上,如图3,△ABC内有点Q,且∠AQC=60°,AB、BC上分别有一点M、N,连接QM、QN、MN,直接写出△QMN周长的最小值.
【考点】三角形综合题.
【专题】压轴题;推理能力.
【答案】(1);
(2)①;②2;
(3).
【分析】(1)利用垂直平分线的性质可证∠AEC=60°,再根据tan∠AEC,可得答案;
(2)①过点P作PG⊥AC于点G.首先证明Rt△EAC≌Rt△EAD(HL).设PG=x,则AG,CG=PH,HE,表示出△PHE与△PFA面积之和,利用二次函数的性质可得答案;
②连接BP,取BP的中点O,连接OH,OF,过点B作BM⊥AE于点M.可知△HOF为等边三角形.且HFBP.只要求出BP的最小值即可;
(3)以AC为底边作等腰三角形AOC,使∠AOC=120°,连接OB,作点Q关于BC、AB的对称点Q'、Q'',连接Q'Q'',由轴对称的性质得,△QMN周长为Q'Q'',BQ'=BQ''=BQ,∠Q'BQ''=60°,利用勾股定理求出BO和OA的长,从而解决问题.
【解答】解:(1)∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EAB=∠B=30°,
∴∠AEC=60°,
∴tan∠AEC,
∴CE,
故答案为:;
(2)①过点P作PG⊥AC于点G.
∵DE垂直平分AB,
∴AE=BE.
∴∠EAB=∠B=30°.
∴∠EAC=∠EAB=30°.
∴PF=PG,CE=DE,
∵AE=AE,
∴Rt△EAC≌Rt△EAD(HL).
设PG=x,则AG,CG=PH,HE,
∴△PHE与△PFA面积之和为
.
∴最小值为;
②连接BP,取BP的中点O,连接OH,OF,过点B作BM⊥AE于点M.
∵PF⊥AB,PH⊥BC,点O为PB中点,
∴OP=OF=OB=OH.
∴点P、F、B、H四点在以O为圆心,PB为直径的同一个圆上,
又∵∠EBF=30°,
∴∠HOF=60°.
∴△HOF为等边三角形.
∴HFBP.
∵AC=4,
∴AB=8.
∴BP的最小值为BM=4.
∴FH的最小值为2;
(3)以AC为底边作等腰三角形AOC,使∠AOC=120°,连接OB,作点Q关于BC、AB的对称点Q'、Q'',连接Q'Q'',
由轴对称的性质得,△QMN周长为Q'Q'',BQ'=BQ''=BQ,∠Q'BQ''=60°,
∴△BQ'Q''是等边三角形,
∵∠AQC=60°,
∴点Q在以O为圆心,OA为半径的圆上运动,
当点O、Q、B共线时,QB最小,
延长CO交AB于H,
∵∠ACH=30°,∠CAB=60°,
∴∠AHC=90°,
∴AH=2,CO,BH=AB﹣AH=8﹣2=6,
∴OHOA,
由勾股定理得,OB,
∴BQ的最小值为,
∴△QMN周长的最小值为.
【点评】本题是三角形综合题,主要考查了含30°角的直角三角形的性质,全等三角形的判定与性质,二次函数的性质,勾股定理,轴对称﹣最短路线问题,等边三角形的判定与性质等知识,将△QMN周长转化为Q'Q''的长是解题的关键.
20.【基础巩固】(1)如图1,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE,连接AD,BE;求证:△ACD≌△BCE;
【尝试应用】(2)如图2,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,连接AD,BE,A、D、E三点在一条直线上,BC与DE交于点F;
①求∠BEA的大小;
②若DF=3EF且BE=2,求△BCE的面积;
【拓展提高】(3)如图3,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,点G为DE的中点,AE交BC于点H,连接GH,若GH⊥AB,且S△ABH为18,求CH的长.
【考点】三角形综合题.
【专题】几何综合题;压轴题;图形的全等;等腰三角形与直角三角形;推理能力.
【答案】(1)证明见解答;
(2)①∠BEA=90°;
②S△BCE=2;
(3)CH=6.
【分析】(1)利用SAS证明△ACD≌△BCE;
(2)①由△ABC和△DEC均为等腰直角三角形,可得∠CDE=∠CED=45°,进而得出∠ADC=180°﹣45°=135°,即可求得答案;
②过点D作DG⊥AC于G,DJ⊥BC于J,过点E作EH⊥BC于H,可证得△CDG≌△CEH(AAS),设CJ=DG=EH=x,可得DJ=CG=CH=3x,FHx,FJx,CFx,再利用勾股定理建立方程求得EH,BC=2,再运用S△BCEBC EH即可求得答案;
(3)连接BE,CG,先证得△BEG≌△HCG(SAS),得出BE=CH,∠GBE=∠GHC,进而可得BE∥AC,推出S△CBE=S△ABE,即S△BEH+S△CEH=S△BEH+S△ABH,得出S△CEH=S△ABH=18,即可求得答案.
【解答】(1)证明:∵∠ACB=∠DCE,
即∠ACD+∠BCD=∠BCD+∠BCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS);
(2)解:①∵AC=BC,CD=CE,∠ACB=∠DCE=90°,
∴△ABC和△DEC均为等腰直角三角形,
∴∠CDE=∠CED=45°,
∴∠ADC=180°﹣45°=135°,
同(1)可得△ACD≌△BCE,
∴∠ADC=∠BEC=135°,
∴∠BEA=∠BEC﹣∠CED=135°﹣45°=90°;
②如图,过点D作DG⊥AC于G,DJ⊥BC于J,过点E作EH⊥BC于H,
则∠CGD=∠CJD=∠DJF=∠EHF=90°,四边形CJDG是矩形,
∴DJ=CG,CJ=DG,
∵∠DCG+∠BCD=∠ECH+∠BCD=90°,
∴∠DCG=∠ECH,
在△CDG和△CEH中,
,
∴△CDG≌△CEH(AAS),
∴DG=EH,CG=CH,
∴CJ=DG=EH,
设CJ=DG=EH=x,
∵EH∥DJ,
∴△EFH∽△DFJ,
∴,
∵DF=3EF,
∴,
∴DJ=CG=CH=3x,FJ=3FH,
∴FH+FJ=CH﹣CJ=3x﹣x=2x,
∴FHx,FJx,
∴CF=CJ+FJ=xxx,
∵EH∥AC,
∴△EFH∽△AFC,
∴,
∴AC5x=BC,
在Rt△CDG中,CDx,
∵△ABC和△DEC均为等腰直角三角形,
∴ABAC=5x,DECD=2x,
∵△ACD≌△BCE,
∴AD=BE,
∵BE=2,
∴AD=2,
∴AE=AD+DE=2+2x,
在Rt△ABE中,AE2+BE2=AB2,
(2+2x)2+22=(5x)2,
解得:x1,x2(舍去),
∴EH,BC=2,
∴S△BCEBC EH22;
(3)如图,连接BE,CG,
∵AC=BC,CD=CE,∠ACB=∠DCE=90°,
∴△ABC和△DEC均为等腰直角三角形,
∴∠ABC=45°,
∵点G为DE的中点,
∴∠CGE=90°,CG=EG=DG,
∵GH⊥AB,
∴∠BGH=90°,
∴△BGH是等腰直角三角形,
∴BG=HG,∠BHG=∠ABC=45°,
∵∠BGE+∠EGH=∠HGC+∠EGH,
∴∠BGE=∠HGC,
在△BEG和△HCG中,
,
∴△BEG≌△HCG(SAS),
∴BE=CH,∠GBE=∠GHC,
∵∠GHC=180°﹣∠BHG=135°,
∴∠GBE=135°,
∴∠CBE=∠GBE﹣∠ABC=135°﹣45°=90°,
∴BE∥AC,
∴S△CBE=S△ABE,
即S△BEH+S△CEH=S△BEH+S△ABH,
∴S△CEH=S△ABH,
∵S△ABH=18,
∴S△CEH=18,
∴CH BE=18,
∵BE=CH,
∴CH2=36,
∴CH=6.
【点评】本题是三角形综合题,考查了等腰直角三角形性质,直角三角形性质,全等三角形的判定和性质,勾股定理等,属于中考压轴题,综合性强,难度大,对学生要求很高;解题关键是熟练掌握等腰直角三角形性质等相关知识,合理添加辅助线构造全等三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学一轮复习 三角形
一.解答题(共20小题)
1.【探究】
(1)已知△ABC和△ADE都是等边三角形.
①如图1,当点D在BC上时,连接CE.请探究CA,CE和CD之间的数量关系,并说明理由;
②如图2,当点D在线段BC的延长线上时,连接CE.请再次探究CA,CE和CD之间的数量关系,并说明理由.【运用】
(2)如图3,等边三角形ABC中,AB=6,点E在AC上,.点D是直线BC上的动点,连接DE,以DE为边在DE的右侧作等边三角形DEF,连接CF.当△CEF为直角三角形时,请直接写出BD的长.
2.在△ABC中,BC=a,AC=b,AB=c,CD是AB边的中线.
【初步探究】(1)如图1,当∠ACB=90°时,请用含a,b的式子表示CD2,CD2= ;
(2)如图2,当AC=BC=a时,请用含a,c的式子表示CD2,CD2= ;
【提出问题】在一般三角形中,如何用a,b,c表示CD2.
【分析问题】在(2)中根据等腰三角形的性质,可在直角三角形中利用勾股定理直接计算出CD2.类似的方法,在一般的三角形中,也可以通过构造直角三角形,利用勾股定理,间接计算出CD2.
【解决问题】如图3,在△ABC中,BC=a,AC=b,AB=c,CD是AB边的中线.求证:.
证明:作△ABC的高CE,
∴∠AEC=∠BEC=90°,
在Rt△AEC和Rt△BEC中,
CA2=CE2+AE2=CE2+(AD﹣ED)2=…
CB2=CE2+BE2=CE2+(BD+ED)2=…
…
(3)请补充完成以上证明过程.
【知识应用】如图4,在边长为1的正方形网格中,A、B两点是网格的交点,利用无刻度直尺在直线l上画出一点P,使得PA2+PB2的值最小,并直接写出PA2+PB2的最小值为 .
3.图1是运动员训练使用的带有乒乓球发射机的乒乓球台示意图.水平台面的长和宽分别为2.8m和1.6m,中间球网高度为0.15m,发射机安装于台面左侧边缘,能以不同速度向右侧不同方向水平发射乒乓球,发射点距台面高度为0.4m,乒乓球(看成点)在发射点P获得水平速度v(单位:m/s)后,从发射点向右下飞向台面,点Q是下落路线的某位置.忽略空气阻力,实验表明:P,Q的竖直距离h(单位:m)与飞出时间t(单位:s)的平方成正比,且当t=1时,h=5;P,Q的水平距离是vt(单位:m).
(1)设v=10m/s,用t表示点Q的横坐标x和纵坐标y,并求出y与x的函数关系式;(不必写x的取值范围)
(2)在(1)的条件下,
①若发球机垂直于底线向正前方发球,根据(1)中的函数关系式及题目中的数据,判断这次发球能否过网?是否出界?并说明理由;
②若球过网后的落点是右侧台面内的点M(如图3,点M距底线0.3m,边线0.3m),问发球点O在底线上的哪个位置?(参考数据:2.6)
(3)将乒乓球发射机安装于台面左侧底线的中点,若乒乓球的发射速度v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上(不接触中网和底线),请直接写出v的取值范围.(结果保留根号)
4.某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.
【特例探究】
(1)如图1,当∠PAB=45°,AB=6时,AC= ,BC= ;
如图2,当sin∠PAB,AB=4时,AC= ,BC= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,在△ABC中,AB=4,BC=2,D、E、F分别是边AB、AC、BC的中点,连接DE并延长至G,使得GE=DE,连接BG,当BG⊥AC于点M时,求GF的长.
5.问题提出
(1)如图1,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 处.
问题探究
(2)如图2,在△ABC中,内角∠ABC的平分线BE和外角∠ACF的平分线CE,相交于点E,连接AE,若∠BEC=40°,请求出∠EAC的度数.
问题解决
(3)如图3,某地在市政工程施工中需要对一直角区域(∠AOB=90°)内部进行围挡,直角区域∠AOB内部有一棵大树(点P),工作人员经过测量得到点P到OA的距离PC为10米,点P到OB的距离PD为20米,为了保护大树及节约材料,设计要求围挡牌要经过大树位置(点P)并且所用材料最少,即围挡区域△EOF周长最小,请你根据以上信息求出符合设计的△EOF周长的最小值,并说明理由.
6.将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,①线段DE与AC的位置关系是 .②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 .
(2)猜想论证:当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究:已知∠ABC=60°,点D是角平分线上一点,BD=CD,BE=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
7.阅读下列材料:
数学课上,老师出示了这样一个问题
如图1,△ABC中,∠B=45°,点D、B分别在AB、BC,且CA=CD,AE⊥CD,垂足为F,探究线段AD、BD、AE之间的数量关系,并证明,
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现∠BCD与∠BAE存在某种数量关系”
小亮:“通过借助勾股定理或构造三角形证明三角形全等,进而可以得到线段AD、BD、AE之间的数量关系”.
老师:保留原条件,再作AG平分∠CAF交CD于G(如图2).如果给出值,那么可求的值.
(1)写出∠BCD与∠BAE之间的某种数量关系;
(2)探究线段AD、BD、AE之间的数量关系,并证明;
(3)若m,求值(用含m的代数式表示).
8.小超在观看足球比赛时,发现了这样一个问题:两名运动员从不同的位置出发,沿着不同的方向,以不同的速度直线奔跑,什么时候他们离对方最近呢?
小超通过一定的测量,并选择了合适的比例尺,把上述问题抽象成如下数学问题:
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D以1cm/s的速度从点C向点B运动,点E以2cm/s的速度从点A向点B运动,当点E到达点B时,两点同时停止运动,若点D,E同时出发,多长时间后DE取得最小值?
小超猜想当DE⊥AB时,DE最小,探究后发现用几何的知识解决这个问题有一定的困难,于是根据函数的学习经验,设C,D两点间的距离为x cm,D,E两点间的距离为y cm,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小超的探究过程,请补充完整:
(1)由题意可知线段AE和CD的数量关系是 ;
(2)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值:
x/cm 0 1 2 3 4 5
y/cm 6.0 4.8 3.8 2.7 3.0
(说明:补全表格时相关数值保留一位小数)
(3)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题,小超的猜想 ;(填“正确”或“不正确”)当两点同时出发了 s时,DE取得最小值,为 cm.
9.感知:如图①,在△ABC中,分别以AB、AC为边在△ABC外部作等边△ABD、等边△ACE,连接CD、BE,则BE=DC(不需证明);
探究:如图②,在△ABC中,分别以AB、AC为边在△ABC外部作等腰△ABD、等腰△ACE,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD、BE,求证:BE=DC;
应用:如图③,在△ABC中,AB>AC,分别以AB、AC为边在△ABC内部作等腰△ABD、等腰△ACE,点E恰好在BC边上,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD,CE=3cm,CD=2cm,△ABC的面积为10cm2,求△ACD的面积.
10.在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,连接BE,CF.
【发现问题】如图①,若∠BAC=30°,延长BE交CF于点D,则BE与CF的数量关系是 ,∠BDC的度数为 .
【类比探究】如图②,若∠BAC=120°,延长BE,FC相交于点D,请猜想BE与CF的数量关系及∠BDC的度数,并说明理由.
【拓展延伸】如图③,若∠BAC=90°,且点B,E,F在同一条直线上,过点A作AM⊥BF,垂足为点M,请猜想BF,CF,AM之间的数量关系,并说明理由.
11.综合与实践:
【问题背景】人教版教材九年级上册P63第10题“探索研究”:等边△ABD和等边△ACE,将△ACE绕点A旋转到某一位置,要求观察图形,提出问题并加以解决.
【探究发现】
(1)如图1,小明连结BE、CD,并发现∠ADC与∠ABE的数量关系,请你探究后写出证明过程.
(2)如图2,得知小明的结论后,小华又连结DE,已知AC⊥BE,AE=5,BE=12,请你求出DE的长;
【拓展探究】
(3)如图3,小颖画出了等腰直角△ABC和等腰直角△ADE,其中∠BAC=∠DAE=90°,AB=AC,AD=AE,点C在DE上,请你直接写出CD、CE和BC之间的数量关系.
12.问题探究
(1)如图①,在四边形ABCD中,∠BAC=90°,,CD=4,E为AD中点,连接BE,求BE的最大值;
问题解决
(2)如图②,某小区计划在一片足够大的空地上修建四边形的花园ABCD,其中BC=40米,AD=CD,AD⊥CD,AB∥CD,由于受地理位置的影响,∠ABC<90°.根据要求,现计划给该花园修建条笔直的绿色长廊,且绿色长廊的入口O定为BC的中点,出口定为点D,为了尽可能地提高观赏体验,要求绿色长廊OD最长,试求绿色长廊OD最长为多少米?
13.全等三角形是我们初中数学的重要知识点之一,它为我们学习后面几何知识做好铺垫,掌握全等三角形的证明是做一系列复杂几何证明的基础.
【问题初探】
(1)构造全等三角形的方法有很多,有一种常见的方法是作高线,将需要证明的边或角放在两个直角三角形中进而通过全等证明关系.比如,我们可以通过作高线证明三角形中一个重要的结论“在同一个三角形中,如果两个角相等,那么这两个角所对的边也相等”.如图1,在△ABC中,已知∠B=∠C,可证AB=AC,小聪同学的作法是作BC边上的高线AD.现在请你完成小聪同学的证明过程;
【类比分析】
(2)通过上述例子,我们发现通过作高线构造直角三角形证明全等确实是一种有效的方法,由此推出了三角形中的重要结论.现在请你借助上述的方法或结论继续探索,如图2,在△ABC中,已知∠ABC=∠ACB,点E为边AC上一点,点F为边AB延长线上一点,连结EF与边BC交于点D,若点D恰为线段EF中点,试探究线段CE与线段BF的数量关系,并说明理由;
【学以致用】
(3)如图3,在△ABC中,∠CAB=90°,AD,AE分别为△ABC的角平分线和中线,过点E作EF⊥AD与线段AD的延长线交于点G,与边AB的延长线交于点F,已知△ABC的面积是30,线段AF的长为8,求△AED的面积.
14.【阅读理解】
定义:在同一平面内,点A,B分别在射线PM,PN上,过点A垂直PM的直线与过点B垂直PN的直线交于点Q,则我们把∠AQB称为∠APB的“边垂角”(四边形内角和等于360°).
(1)如图1和2,若∠AQB是∠APB的“边垂角”,则∠AQB与∠APB的数量关系是 .
【迁移运用】
(2)如图3,CD,BE分别是△ABC的两条高,两条高交于点F,根据定义,我们知道∠DBE是∠DCE的“边垂角”或∠DCE是∠DBE的“边垂角”,∠DAE的“边垂角”是 .
【拓展延伸】
(3)如图4,若∠ACD是∠ABD的“边垂角”,且AB=AC.BD交AC于点E,点C关于直线BD的对称点为点F,连接AF,EF,且∠CAF=45°,延长BA和CF相交于点G.
①请说明:△AGC≌△AEB;
②请说明:BE=CF+CE.
15.定义:如果1条线段将一个三角形分割成2个等腰三角形,我们把这条线段叫做这个三角形的“双等腰线”.如果2条线段将一个三角形分成3个等腰三角形,我们把这2条线段叫做这个三角形的“三等腰线”.如图1,BE是△ABD的“双等腰线”,AD、BE是△ABC的“三等腰线”.
(1)请在图2三个图中,分别画出△ABC的“双等腰线”,并做必要的标注或说明.
(2)如果一个等腰三角形有“双等腰线”,那么它的底角度数是 .
(3)如图3,△ABC中,∠C∠B,∠B<45°.画出△ABC所有可能的“三等腰线”,使得对∠B取值范围内的任意值都成立,并做必要的标注或说明.(每种可能用一个图单独表示,如果图不够用可以自己补充)
16.定义:三角形一边中线的中点和该边的两个顶点组成的三角形称为中原三角形.如图①,AD是△ABC的中线,F是AD的中点,则△FBC是中原三角形.
(1)求中原三角形与原三角形的面积之比(直接写出答案).
(2)如图②,AD是△ABC的中线,E是边AC上的点,AC=3AE,BE与AD相交于点F,连接CF.求证:△FBC是中原三角形.
(3)如图③,在(2)的条件下,延长CF交AB于点M,连接ME,求△FEM与△ABC的面积之比.
17.如图1,等边△ABC的边长为4,点D是直线AB上异于A,B的一动点,连接CD,以CD为边长,在CD右侧作等边△CDE,连接BE.
【初步感知】
(1)求证:△CAD≌△CBE;
【类比探究】
(2)当点D在直线AB上运动时,①AD与BE的数量关系是 ;
②△BDE的周长是否存在最小值?若存在,求此时AD的长;若不存在,说明理由;
【拓展应用】
(3)当点D在直线AB上运动时,△BDE能否形成直角三角形?若能,请直接写出此时AD的长;若不能,说明理由.
18.【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS
B.SAS
C.AAS
D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=5,EC=3,求线段BF的长.
【灵活运用】
如图③,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
19.【问题情境】
如图1,在Rt△ABC中,∠BCA=90°,∠B=30°,AC=4,AB的垂直平分线交AB于点D,交BC于点E,作射线AE.
(1)则CE的长为 ;
【变式思考】
(2)在“问题情境”的基础上,如图2,点P是射线AE上的动点,过点P分别作PF⊥AB所在直线于点F,作PH⊥BC所在直线于点H.
①求△PHE与△PFA面积之和的最小值;
②连接FH,求FH的最小值是多少?
【拓展探究】
(3)在“问题情境”的基础上,如图3,△ABC内有点Q,且∠AQC=60°,AB、BC上分别有一点M、N,连接QM、QN、MN,直接写出△QMN周长的最小值.
20.【基础巩固】(1)如图1,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE,连接AD,BE;求证:△ACD≌△BCE;
【尝试应用】(2)如图2,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,连接AD,BE,A、D、E三点在一条直线上,BC与DE交于点F;
①求∠BEA的大小;
②若DF=3EF且BE=2,求△BCE的面积;
【拓展提高】(3)如图3,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,点G为DE的中点,AE交BC于点H,连接GH,若GH⊥AB,且S△ABH为18,求CH的长.
中考数学一轮复习 三角形
参考答案与试题解析
一.解答题(共20小题)
1.【探究】
(1)已知△ABC和△ADE都是等边三角形.
①如图1,当点D在BC上时,连接CE.请探究CA,CE和CD之间的数量关系,并说明理由;
②如图2,当点D在线段BC的延长线上时,连接CE.请再次探究CA,CE和CD之间的数量关系,并说明理由.【运用】
(2)如图3,等边三角形ABC中,AB=6,点E在AC上,.点D是直线BC上的动点,连接DE,以DE为边在DE的右侧作等边三角形DEF,连接CF.当△CEF为直角三角形时,请直接写出BD的长.
【考点】三角形综合题.
【专题】压轴题;存在型;模型思想;应用意识.
【答案】(1)①CE+CD=CA,理由详见解析;②CA+CD=CE,理由详见解析;(2)6或6+2.
【分析】(1)①根据条件易证△ABD≌△ACE(SAS),再进行线段转化易得答案;②与第①小问思路一样,证出△ABD≌△ACE(SAS)即可;
(2)由△CEF为直角三角形可知,需要分类讨论确定哪个角是直角三角形,再根据点D的位置关系去讨论即可,因为点D是动点,所以按照前面两问带给我们的思路,去构造类似的全等三角形,进而讨论求解即可.
【解答】解:(1)①CE+CD=CA.理由如下,
∵△ABC和△ADE是等边三角形,
∴AB=AC=BC,AD=AE=DE,∠BAC=∠DAE=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴CE=BD
∵BD+CD=BC,
∴CE+CD=CA.
②CA+CD=CE.理由如下,
∵△ABC和△ADE是等边三角形,
∴AB=AC=BC,AD=AE=DE,∠BAC=∠DAE=60°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴CE=BD,
∵CB+CD=BD,
∴CA+CD=CE.
(2)过E作EH∥AB,则△EHC为等边三角形.
①当点D在H左侧时,如图1,
∵ED=EF,∠DEH=∠FEC,EH=EC,
∴△EDH≌△EFC(SAS),
∴∠ECF=∠EHD=120°,
此时△CEF不可能为直角三角形.
②当点D在H右侧,且在线段CH上时,如图2,
同理可得∴△EDH≌△EFC(SAS),
∴∠FCE=∠EHD=60°,∠FEC=∠DEH<∠HEC=60°,
此时只有∠CFE有可能为90°,
当∠CFE=90°时,∠EDH=90°,
∴ED⊥CH,
∵CH=CE=2,
∴CDCH,
又∵AB=6,
∴BD=6.
③当点D在H右侧,且HC延长线上时,如图3,
此时只有∠CEF=90°,
∵∠DEF=60°,
∴∠CED=30°,
∵∠ECH=60°,
∴∠EDC=CED=30°,
∴CD=CE=2,
∴BD=6+2.
综上:BD的长为6或6+2.
【点评】本题主要考查三角形综合题,熟练掌握全等三角形的性质和判定是解题的关键.
2.在△ABC中,BC=a,AC=b,AB=c,CD是AB边的中线.
【初步探究】(1)如图1,当∠ACB=90°时,请用含a,b的式子表示CD2,CD2= (a2+b2) ;
(2)如图2,当AC=BC=a时,请用含a,c的式子表示CD2,CD2= a2c2 ;
【提出问题】在一般三角形中,如何用a,b,c表示CD2.
【分析问题】在(2)中根据等腰三角形的性质,可在直角三角形中利用勾股定理直接计算出CD2.类似的方法,在一般的三角形中,也可以通过构造直角三角形,利用勾股定理,间接计算出CD2.
【解决问题】如图3,在△ABC中,BC=a,AC=b,AB=c,CD是AB边的中线.求证:.
证明:作△ABC的高CE,
∴∠AEC=∠BEC=90°,
在Rt△AEC和Rt△BEC中,
CA2=CE2+AE2=CE2+(AD﹣ED)2=…
CB2=CE2+BE2=CE2+(BD+ED)2=…
…
(3)请补充完成以上证明过程.
【知识应用】如图4,在边长为1的正方形网格中,A、B两点是网格的交点,利用无刻度直尺在直线l上画出一点P,使得PA2+PB2的值最小,并直接写出PA2+PB2的最小值为 18 .
【考点】三角形综合题.
【专题】几何综合题;压轴题;运算能力;应用意识.
【答案】(1)(a2+b2);
(2)a2c2;
(3)证明见解答;
(4)PA2+PB2的最小值为18,作图见解答.
【分析】【初步探究】(1)利用直角三角形斜边上的中线等于斜边的一半和勾股定理即可求得答案;
(2)利用等腰三角形“三线合一”的性质及勾股定理即可求得答案;
【解决问题】(3)运用勾股定理即可将证明过程补充完整;
【知识应用】作点A关于直线l的对称点A′,连接A′B,AA′,PA,PB,AA′与直线l交于点E,过点B作BF⊥直线l于F,设PE=x,则PF=4﹣x,运用勾股定理可得:PA2+PB2=2x2﹣8x+26=2(x﹣2)2+18,根据非负数的性质即可得出答案.
【解答】【初步探究】(1)解:∵CD是Rt△ABC斜边AB上的中线,
∴CDAB,
∴CD2AB2,
在Rt△ABC中,AB2=AC2+BC2=a2+b2,
∴CD2AB2(a2+b2),
故答案为:(a2+b2);
(2)解:∵AC=BC=a,CD是AB边的中线,
∴CD⊥AB,BDc,
在Rt△BCD中,CD2=BC2﹣BD2=a2c2,
故答案为:a2c2;
【解决问题】(3)证明:作△ABC的高CE,
∴∠AEC=∠BEC=90°,
在Rt△AEC和Rt△BEC中,
CA2=CE2+AE2=CE2+(AD﹣ED)2=CE2+AD2﹣2AD×ED+ED2①,
CB2=CE2+BE2=CE2+(BD+ED)2=CE2+BD2+2BD×ED+ED2②,
∵CD为AB边中线,
∴AD=BDAB,
∵CE是△ABC 的高,
∴∠CED=90°,
∴CE2+ED2=CD2,
∴①+②得:,
∴CD2(CA2+CB2)AB2,
即CD2(a2+b2)c2.
【知识应用】如图4,过点B作BO⊥直线l于O,以直线l为x轴,直线OB为y轴建立平面直角坐标系,
设点P(x,0)是x轴的动点,点Q是AB的中点,连接PA,PB,PQ,
则A(﹣4,﹣1),B(0,3),Q(﹣2,1),
则PA2=(x+4)2+12=x2+8x+17,
PB2=x2+32=x2+9,
PQ2=12+(x+2)2=x2+4x+5,
AB2=42+42=32,
由(2)知,PQ2(PA2+PB2)AB2,
∴x2+4x+5(PA2+PB2)32,
∴PA2+PB2=2(x2+4x+5)+16=2(x+2)2+18,
∴当x=﹣2时,PA2+PB2有最小值18,
此时点P的坐标为(﹣2,0),
如图所示,点P即为所求作的点.
,
【点评】本题是三角形综合题,考查了勾股定理的应用,直角三角形的性质,非负数的性质、因式分解的应用,解答本题的关键是明确题意,利用因式分解的方法和非负数的性质解答.
3.图1是运动员训练使用的带有乒乓球发射机的乒乓球台示意图.水平台面的长和宽分别为2.8m和1.6m,中间球网高度为0.15m,发射机安装于台面左侧边缘,能以不同速度向右侧不同方向水平发射乒乓球,发射点距台面高度为0.4m,乒乓球(看成点)在发射点P获得水平速度v(单位:m/s)后,从发射点向右下飞向台面,点Q是下落路线的某位置.忽略空气阻力,实验表明:P,Q的竖直距离h(单位:m)与飞出时间t(单位:s)的平方成正比,且当t=1时,h=5;P,Q的水平距离是vt(单位:m).
(1)设v=10m/s,用t表示点Q的横坐标x和纵坐标y,并求出y与x的函数关系式;(不必写x的取值范围)
(2)在(1)的条件下,
①若发球机垂直于底线向正前方发球,根据(1)中的函数关系式及题目中的数据,判断这次发球能否过网?是否出界?并说明理由;
②若球过网后的落点是右侧台面内的点M(如图3,点M距底线0.3m,边线0.3m),问发球点O在底线上的哪个位置?(参考数据:2.6)
(3)将乒乓球发射机安装于台面左侧底线的中点,若乒乓球的发射速度v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上(不接触中网和底线),请直接写出v的取值范围.(结果保留根号)
【考点】三角形综合题.
【专题】代数几何综合题;压轴题;运算能力;应用意识.
【答案】(1)yx2+0.4;
(2)①这次发球能过网,会出界.理由见解答;
②发球点O在距右侧边线1.6m处,即左上角;
(3)v.
【分析】(1)运用待定系数法即可求得答案;
(2)①当x=1.4时,y1.42+0.4=0.302>0.15,可判断这次发球能过网;当y=0时,解方程x2+0.4=0,即可判断这次发球会出界;
②如图,过点M作MN⊥OA于N,则AN=0.3m,MN=2.8﹣0.3=2.5m,利用勾股定理即可求得答案;
(3)当垂直底线发球,恰巧过网,此时v值最小,可求得v的最小值为,当斜发球恰巧与右下底线与边线边缘相碰,即球落在右下角点B处时,此时v值最大,可求得v的最大值为,即可得出答案.
【解答】解:(1)设h=kt2,把t=1,h=5代入得:k=5,
∴h=5t2,
当v=10m/s时,点Q的横坐标为10t,纵坐标为0.4﹣h=0.4﹣5t2,
∴x=10t,y=0.4﹣5t2,
∴yx2+0.4;
(2)①这次发球能过网,会出界.理由如下:
∵yx2+0.4,
当x=1.4时,y1.42+0.4=0.302>0.15,
∴这次发球能过网;
当y=0时,x2+0.4=0,
解得:x1=2,x2=﹣2(舍去),
∵22.8,
∴这次发球会出界;
②如图,过点M作MN⊥OA于N,则AN=0.3m,MN=2.8﹣0.3=2.5m,
由①知:OM=2,
在Rt△OMN中,ON1.3(m),
∴OA=ON+AN=1.3+0.3=1.6(m),
答:发球点O在距右侧边线1.6m处,即左上角;
(3)当垂直底线发球,恰巧过网,此时v值最小,
∵中间球网高度为0.15m,
∴y=0.15m,
∴h=0.4﹣0.15=0.25m,
∴h=5t2=0.25,
解得:t1,t2(不符合题意,舍去),
∵底线到中网的距离为1.4m,
∴v,
当斜发球恰巧与右下底线与边线边缘相碰,即球落在右下角点B处时,此时v值最大,如图,连接OB,设右上角为点A,
则OA=0.8m,AB=2.8m,
在Rt△OAB中,OB,
∵这时的h=0.4m,
∴h=5t2=0.4,
解得:t1,t2(不符合题意,舍去),
∴v,
∴v.
【点评】本题考查了待定系数法求二次函数解析式,利用二次函数解决实际问题,勾股定理等,构造直角三角形运用勾股定理是解题关键.
4.某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形均称为“中垂三角形”.
【特例探究】
(1)如图1,当∠PAB=45°,AB=6时,AC= 6 ,BC= 6 ;
如图2,当sin∠PAB,AB=4时,AC= 2 ,BC= 2 ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想AB2、BC2、AC2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,在△ABC中,AB=4,BC=2,D、E、F分别是边AB、AC、BC的中点,连接DE并延长至G,使得GE=DE,连接BG,当BG⊥AC于点M时,求GF的长.
【考点】三角形综合题.
【专题】压轴题;应用意识.
【答案】见试题解答内容
【分析】(1)如图1,由等腰直角三角形的性质得到AP=BP=6,根据三角形中位线的性质和平行线分线段成比例定理可得PE=PF=3,利用勾股定理可得AC和BC的长;如图2,根据特殊三角函数值可得∠BAP=30°,计算PB和AP的长,同理由中线的性质和勾股定理可得结论;
(2)设 PF=m,PE=n 则AP=2m,PB=2n,根据勾股定理分别列等式,可得结论;
(3)如图4,作辅助线,证明四边形EFCG是平行四边形,得Q是FG的中点,根据中垂三角形的定义可知:△FCG是中垂三角形,利用(2)中三边的关系可得GF的长.
【解答】(1)解:如图1,∵AF⊥BE,
∴∠APB=∠APE=∠BPF=90°,
∵∠PAB=45°,AB=6,
∴AP=PB=6,
如图1,连接EF,
∵AF,BE是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥AB.且 EFAB,
∴,
∴PE=PF=3,
由勾股定理得:AE=BF3,
∴AC=BC=2AE=6,
如图2,∵sin∠PAB,AB=4,AF⊥BE,
∴∠PAB=30°,
∴BPAB=2,AP=2,
∵AF、BE是△ABC的中线,
∴PEPB=1,PFAP,
由勾股定理得:AE,
BF,
∴AC=2AE=2,BC=2BF=2,
故答案为:6,6,2,2;
(2)解:猜想:AB2、BC2、AC2三者之间的关系是:AC2+BC2=5AB2,
证明:如图3,设 PF=m,PE=n 则AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=AB2①,
在Rt△APE中,(2m)2+n2=()2 ②,
在Rt△BPF中,m2+(2n)2=()2 ③,
由①得:m2+n2,由②+③得:5( m2+n2),
∴AC2+BC2=5AB2;
(3)解:如图4,连接CG,EF,过点F作FN∥BG交CG于点N,FG与AC交于点Q,
∵FN∥BG,BG⊥AC,
∴FN⊥AC,
∵F是BC的中点,
∴N是CG的中点,
∵D、E分别是AB、AC的中点,
∴DE=FC,DE∥FC,
∵ED=EG,
∴EG=FC,EG∥FC,
∴四边形EFCG是平行四边形,
∴Q是FG的中点,
∴△FCG是中垂三角形,
∵AB=4,BC=2,
∴CG=EF=BD=2,FC,
由(2)中结论可知:5FC2=CG2+FG2,
即5×5=(2)2+FG2,
∴GF.
【点评】本题考查三角形综合题、中垂三角形的定义和应用、勾股定理、三角形的中位线定理、平行四边形的性质和判定等知识,解题的关键是学会添加常用辅助线,构造中垂三角形解决问题,属于中考压轴题.
5.问题提出
(1)如图1,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 4 处.
问题探究
(2)如图2,在△ABC中,内角∠ABC的平分线BE和外角∠ACF的平分线CE,相交于点E,连接AE,若∠BEC=40°,请求出∠EAC的度数.
问题解决
(3)如图3,某地在市政工程施工中需要对一直角区域(∠AOB=90°)内部进行围挡,直角区域∠AOB内部有一棵大树(点P),工作人员经过测量得到点P到OA的距离PC为10米,点P到OB的距离PD为20米,为了保护大树及节约材料,设计要求围挡牌要经过大树位置(点P)并且所用材料最少,即围挡区域△EOF周长最小,请你根据以上信息求出符合设计的△EOF周长的最小值,并说明理由.
【考点】三角形综合题.
【专题】压轴题;应用意识.
【答案】见试题解答内容
【分析】(1)作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,然后根据角平分线的性质进行判断;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义列式并整理得到∠BAC=2∠BEC,过点E作EF⊥BA交延长线于F,作EG⊥AC于G,作EH⊥BD于H,根据角平分线上的点到角的两边的距离相等可得EF=FH,EG=EH,然后求出EF=EG,再根据到角的两边距离相等的点在角的平分线上判断出AE是∠CAF的平分线,再根据角平分线的定义解答即可;
(3)根据前两问的启发,设∠AOB、∠AEF、∠BFE的角平分线交于点Q,作QN⊥OB于N,QM⊥OA于M,QH⊥EF于H,连接QP,可得四边形OMQN是正方形,设正方形边长为y,则所求的△OEF的周长为2y,再根据“斜边大于等于直角边”,即PQ≥QH,列出不等式,解不等式可得y的最小值.
【解答】解:作直线l1、l2、l3所围成的三角形的外角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.
故答案为:4;
(2)解:∵∠ABC与∠ACD的角平分线相交于点E,
∴∠CBE∠ABC,∠ECD∠ACD,
由三角形的外角性质得,∠ACD=∠ABC+∠BAC,
∠ECD=∠BEC+∠CBE,
∴∠ACD=∠BEC∠ABC,
∴(∠ABC+∠BAC)=∠BEC∠ABC,
整理得,∠BAC=2∠BEC,
∵∠BEC=40°,
∴∠BAC=2×40°=80°,
过点E作EH⊥BA交延长线于H,作EG⊥AC于G,作EF⊥BC于F,
∵BE平分∠ABC,
∴EF=EH,
∵CE平分∠ACD,
∴EG=EF,
∴EH=EG,
∴AE是∠CAF的平分线,
∴∠CAE(180°﹣∠BAC)(180°﹣80°)=50°;
(3)如图,设∠AOB、∠AEF、∠BFE的角平分线交于点Q,
作QN⊥OB于N,QM⊥OA于M,QH⊥EF于H.连接QP.
则QN=QH=QM=y,FH=FN,EH=EM,
∴△OEF的周长:OE+OF+EF=OF+FN+OE+EM=ON+OM=QN+QM=2QN=2y,
∵PDOC是矩形,且PD=20,PC=10,
∴ND=y﹣10,CM=y﹣20,
∴QP2=(y﹣10)2+(y﹣20)2
∵PQ≥QH,
∴(y﹣10)2+(y﹣20)2≥y2
∴y2﹣60y+500≥0,
∴(y﹣30)2≥400,
∴y≥50或y≤10(舍),
∴2y≥100,当且仅当P、H重合时取等号.
即△OEF的周长的最小值为100.
【点评】本题为三角形综合题,主要考查了三角形角平分线的性质及其应用.第三问是本题的难点,将△OEF的周长转化为用正方形边长表示同时利用“斜边大于等直角边”原理列出不等式是解答的关键.
6.将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,①线段DE与AC的位置关系是 DE∥AC .②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是 S1=S2 .
(2)猜想论证:当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究:已知∠ABC=60°,点D是角平分线上一点,BD=CD,BE=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF=S△BDE,请直接写出相应的BF的长.
【考点】三角形综合题.
【专题】几何综合题;压轴题;应用意识.
【答案】见试题解答内容
【分析】(1)①根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行解答;
②根据等边三角形的性质可得AC=AD,再根据直角三角形30°角所对的直角边等于斜边的一半求出ACAB,然后求出AC=BD,再根据等边三角形的性质求出点C到AB的距离等于点D到AC的距离,然后根据等底等高的三角形的面积相等解答;
(2)根据旋转的性质可得BC=CE,AC=CD,再求出∠ACN=∠DCM,然后利用“角角边”证明△ACN和△DCM全等,根据全等三角形对应边相等可得AN=DM,然后利用等底等高的三角形的面积相等证明;
(3)过点D作DF1∥BE,求出四边形BEDF1是菱形,根据菱形的对边相等可得BE=DF1,然后根据等底等高的三角形的面积相等可知点F1为所求的点,过点D作DF2⊥BD,求出∠F1DF2=60°,从而得到△DF1F2是等边三角形,然后求出DF1=DF2,再求出∠CDF1=∠CDF2,利用“边角边”证明△CDF1和△CDF2全等,根据全等三角形的面积相等可得点F2也是所求的点,根据菱形和等边三角形的性质可得结论.
【解答】解:(1)①∵△DEC绕点C旋转,点D恰好落在AB边上,
∴AC=CD,
∵∠BAC=90°﹣∠B=90°﹣30°=60°,
∴△ACD是等边三角形,
∴∠ACD=60°,
又∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE,
∴DE∥AC;
②∵∠B=30°,∠C=90°,
∴CD=ACAB,
∴BD=AD=AC,
根据等边三角形的性质,△ACD的边AC、AD上的高相等,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
故答案为:①DE∥AC;②S1=S2;
(2)如图3,∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,
∴∠ACN=∠DCM,
∵在△ACN和△DCM中,
∵,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),
即S1=S2;
(3)如图,过点D作DF1∥BE,连接CF1,易求四边形BEDF1是菱形,
所以BE=DF1=BF1=4,且BE、DF1上的高相等,
此时S△BDE;
过点D作DF2⊥BD,
∵∠ABC=60°,F1D∥BE,
∴∠F2F1D=∠ABC=60°,
∵BF1=DF1,∠F1BD∠ABC=30°,∠F2DB=90°,
∴∠F1DF2=60°,
∴△DF1F2是等边三角形,
∴DF1=DF2,
∵BD=CD,∠ABC=60°,点D是角平分线上一点,
∴∠DBC=∠DCB60°=30°,
∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°,
∠CDF2=360°﹣150°﹣60°=150°,
∴∠CDF1=∠CDF2,
∵在△CDF1和△CDF2中,
,
∴△CDF1≌△CDF2(SAS),
∵S△DCF=S△BDE,
∴点F2也是所求的点,
∵BE=4,
∴BF1=BE=DF1=F1F2=4,
∴BF2=8,
综上,BF的长为4或8.
【点评】本题考查了全等三角形的判定与性质,三角形的面积,等边三角形的判定与性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟练掌握等底等高的三角形的面积相等,以及全等三角形的面积相等是解题的关键,(3)要注意符合条件的点F有两个.
7.阅读下列材料:
数学课上,老师出示了这样一个问题
如图1,△ABC中,∠B=45°,点D、B分别在AB、BC,且CA=CD,AE⊥CD,垂足为F,探究线段AD、BD、AE之间的数量关系,并证明,
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现∠BCD与∠BAE存在某种数量关系”
小亮:“通过借助勾股定理或构造三角形证明三角形全等,进而可以得到线段AD、BD、AE之间的数量关系”.
老师:保留原条件,再作AG平分∠CAF交CD于G(如图2).如果给出值,那么可求的值.
(1)写出∠BCD与∠BAE之间的某种数量关系;
(2)探究线段AD、BD、AE之间的数量关系,并证明;
(3)若m,求值(用含m的代数式表示).
【考点】三角形综合题.
【专题】几何综合题;压轴题;推理能力;应用意识.
【答案】(1)∠BAE+∠BCD=45°;
(2)AD2+AD BD+BD2=AE2;证明见解答;
(3).
【分析】(1)根据三角形外角性质可得∠ADC=∠B+∠BCD=45°+∠BCD,再由CA=CD,AE⊥CD,可得∠CAF=90°﹣∠ACF=2∠BCD,再根据∠BAE+∠ADC=90°,即可求得答案;
(2)如图1,过点C作CG⊥AD于G,可得△BCG是等腰直角三角形,由勾股定理可得AG2+CG2=AC2,即可求得答案;
(3)如图2,延长AG交BC于N,设EN=CN=a,EF=b,则CE=2a,AF=m EF=mb,AE=AF+EF=(m+1)b,由△AEN∽△CEF,可求得,再由△AGF∽△CGN,即可求得答案.
【解答】解:(1)∠BAE+∠BCD=45°.理由如下:
∵∠B=45°,
∴∠ADC=∠B+∠BCD=45°+∠BCD,
∵CA=CD,
∴∠CAD=∠ADC=45°+∠BCD,∠ACF=180°﹣2∠ADC=90°﹣2∠BCD,
∵AE⊥CD,
∴∠AFC=∠AFD=90°,
∴∠CAF=90°﹣∠ACF=2∠BCD,
∵∠BAE+∠ADC=90°,
∴∠BAE+45°+∠BCD=90°,
∴∠BAE+∠BCD=45°;
(2)AD2+AD BD+BD2=AE2.
证明:如图1,过点C作CG⊥AD于G,
由(1)知,∠ACF=90°﹣2∠BCD,∠BAE+∠BCD=45°,
∴∠ACE=∠ACF+∠BCD=90°﹣2∠BCD+∠BCD=90°﹣∠BCD,
又∵∠AEC=∠B+∠BAE=45°+45°﹣∠BCD=90°﹣∠BCD,
∠ACE=∠AEC,
∴AC=AE,
∵CA=CD,CG⊥AD,
∴AG=DGAD,∠AGC=∠BGC=90°,
∵∠B=45°,
∴△BCG是等腰直角三角形,
∴BG=CG=DG+BDAD+BD,
在Rt△ACG中,AG2+CG2=AC2,
∴(AD)2+(AD+BD)2=AE2,
∴AD2+AD BD+BD2=AE2;
(3)如图2,延长AG交BC于N,
由(2)得:AC=AE,
又∵AG平分∠CAF,
∴AN⊥CE,CN=ENCE,
设EN=CN=a,EF=b,
则CE=2a,AF=m EF=mb,AE=AF+EF=(m+1)b,
∵∠ANE=∠CFE=90°,∠AEN=∠CEF,
∴△AEN∽△CEF,
∴,即,
∴,
∵∠AFG=∠CNG=90°,∠AGF=∠CGN,
∴△AGF∽△CGN,
∴,即.
【点评】此题是三角形的综合题,主要考查了等腰三角形的判定和性质,等腰直角三角形判定和性质,相似三角形的判定和性质,三角形内角和定理等知识,利用参数表示线段的长,添加辅助线构造相似三角形是解本题的关键,属于中考数学压轴题,难度较大.
8.小超在观看足球比赛时,发现了这样一个问题:两名运动员从不同的位置出发,沿着不同的方向,以不同的速度直线奔跑,什么时候他们离对方最近呢?
小超通过一定的测量,并选择了合适的比例尺,把上述问题抽象成如下数学问题:
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点D以1cm/s的速度从点C向点B运动,点E以2cm/s的速度从点A向点B运动,当点E到达点B时,两点同时停止运动,若点D,E同时出发,多长时间后DE取得最小值?
小超猜想当DE⊥AB时,DE最小,探究后发现用几何的知识解决这个问题有一定的困难,于是根据函数的学习经验,设C,D两点间的距离为x cm,D,E两点间的距离为y cm,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小超的探究过程,请补充完整:
(1)由题意可知线段AE和CD的数量关系是 AE=2CD ;
(2)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值:
x/cm 0 1 2 3 4 5
y/cm 6.0 4.8 3.8 3.0 2.7 3.0
(说明:补全表格时相关数值保留一位小数)
(3)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题,小超的猜想 不正确 ;(填“正确”或“不正确”)当两点同时出发了 4 s时,DE取得最小值,为 2.7 cm.
【考点】三角形综合题.
【专题】压轴题;应用意识.
【答案】见试题解答内容
【分析】(1)根据时间和速度可得AE和CD的长,可得结论;
(2)作辅助线,根据勾股定理计算DE的长,根据二次函数的最值可得结论;
(3)画图象即可;
(4)作辅助线,根据勾股定理计算DE的长,根据二次函数的最值可得结论.
【解答】解:(1)由题意得:AE=2x,CD=x,
∴AE=2CD;
故答案为:AE=2CD;
(2)如图所示,过D作DG⊥AB于G,
由(1)知:CD=x,则BD=8﹣x,
sin∠B,
∴,DG,BG,
∴EG=AE+BG﹣10=2x10,
∴y,
当x=3时,y3;
故答案为:3.0;
(3)如图所示:
(4)由(2)知:y,
∵0≤x≤5,
∴当x=4时,y有最小值是2.7,
故答案为:不正确,4,2.7.
【点评】本题属于三角形和函数的综合题,考查了勾股定理,函数图象,直角三角形的性质等知识,解题的关键是理解题意,学会利用勾股定理解决问题,学会利用图象法解决问题,属于中考压轴题.
9.感知:如图①,在△ABC中,分别以AB、AC为边在△ABC外部作等边△ABD、等边△ACE,连接CD、BE,则BE=DC(不需证明);
探究:如图②,在△ABC中,分别以AB、AC为边在△ABC外部作等腰△ABD、等腰△ACE,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD、BE,求证:BE=DC;
应用:如图③,在△ABC中,AB>AC,分别以AB、AC为边在△ABC内部作等腰△ABD、等腰△ACE,点E恰好在BC边上,使AB=AD,AC=AE,且∠BAD=∠CAE,连接CD,CE=3cm,CD=2cm,△ABC的面积为10cm2,求△ACD的面积.
【考点】三角形综合题.
【专题】压轴题;应用意识.
【答案】见试题解答内容
【分析】探究:证明△ADC≌△ABE(SAS),可得BE=DC;
应用:先证明△ADC≌△ABE,可得BE=DC=2,利用面积求得AF=4,根据△ABE的面积与△ACD的面积相等可得结论.
【解答】探究:
证明:∵∠BAD=∠EAC,
∴∠DAC=∠BAE,
在△ACD和△AEB中,
∵,
∴△ACD≌△AEB(SAS),
∴CD=BE;
应用:
∵∠BAD=∠EAC,
∴∠DAC=∠BAE,
在△ACD和△AEB中,
∵,
∴△ACD≌△AEB(SAS),
∴CD=BE=2;
∴BC=BE+CE=2+3=5,
过A作AF⊥BC于F,如图③,
∵△ABC的面积为10cm2,
∴BC AF=10,
5×AF=10,
AF=4,
∴S△ACD=S△ABE2×4=4cm2.
【点评】本题是三角形综合题目,考查了全等三角形的判定与性质、等边三角形的判定与性质等知识,证明三角形全等是解决问题的关键.
10.在△ABC和△AEF中,AB=AC,AE=AF,∠BAC=∠EAF,连接BE,CF.
【发现问题】如图①,若∠BAC=30°,延长BE交CF于点D,则BE与CF的数量关系是 BE=CF ,∠BDC的度数为 30° .
【类比探究】如图②,若∠BAC=120°,延长BE,FC相交于点D,请猜想BE与CF的数量关系及∠BDC的度数,并说明理由.
【拓展延伸】如图③,若∠BAC=90°,且点B,E,F在同一条直线上,过点A作AM⊥BF,垂足为点M,请猜想BF,CF,AM之间的数量关系,并说明理由.
【考点】三角形综合题.
【专题】几何综合题;压轴题;图形的全等;推理能力.
【答案】(1)BE=CF,30°;
(2)BE=CF,∠BDC=60°,证明见解答;
(3)BF=CF+2AM,证明见解答.
【分析】(1)根据等腰三角形的性质,利用SAS证明△ABE≌△ACF即可得出结论;
(2)根据等腰三角形的性质,利用SAS证明△ABE≌△ACF即可得出结论;
(3)利用SAS证明△ABE≌△ACF,可得BE=CF,再由等腰直角三角形的性质可得AM=EM=FM,即EF=2AM,根据BF=BE+EF,等量代换可得BF=CF+2AM.
【解答】解:(1)BE=CF,∠BDC=30°,
理由如下:如图1所示,设AC与BD交于点O,
∵∠BAC=∠EAF=30°,
∴∠BAC+∠CAE=∠EAF+∠CAE,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,∠ABE=∠ACF,
∵∠AOE=∠ABE+∠BAC,∠AOE=∠ACF+∠BDC,
∴∠BDC=∠BAC=30°.
故答案为:BE=CF,30°;
(2)BE=CF,∠BDC=60°,
理由如下:如图2,
∵∠BAC=∠EAF=120°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,∠AEB=∠AFC,
∵∠EAF=120°,AE=AF,
∴∠AEF=∠AFE=30°,
∴∠BDC=∠BEF﹣∠EFD=∠AEB+30°﹣(∠AFC﹣30°)=60°;
(3)【拓展延伸】BF=CF+2AM,
理由如下:如图3,
∵∠BAC=∠EAF=90°,
∴∠BAC﹣∠EAC=∠EAF﹣∠EAC,
即∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(SAS),
∴BE=CF,
∵AE=AF,∠EAF=90°,AM⊥EF,
∴AM=EM=FM,即EF=2AM,
∵BF=BE+EF,
∴BF=CF+2AM.
【点评】本题是三角形综合题,主要考查了全等三角形的判定与性质,等腰三角形和等腰直角三角形的性质,三角形的面积等知识,熟练掌握全等三角形的判定是解题的关键.
11.综合与实践:
【问题背景】人教版教材九年级上册P63第10题“探索研究”:等边△ABD和等边△ACE,将△ACE绕点A旋转到某一位置,要求观察图形,提出问题并加以解决.
【探究发现】
(1)如图1,小明连结BE、CD,并发现∠ADC与∠ABE的数量关系,请你探究后写出证明过程.
(2)如图2,得知小明的结论后,小华又连结DE,已知AC⊥BE,AE=5,BE=12,请你求出DE的长;
【拓展探究】
(3)如图3,小颖画出了等腰直角△ABC和等腰直角△ADE,其中∠BAC=∠DAE=90°,AB=AC,AD=AE,点C在DE上,请你直接写出CD、CE和BC之间的数量关系.
【考点】三角形综合题.
【专题】压轴题;推理能力.
【答案】(1)∠ADC=∠ABE,理由见解析;
(2)13;
(3)CD2+CE2=BC2,理由详见解析.
【分析】(1)通过SAS判定△ACD≌△ABE,根据全等三角形的性质可得结论;
(2)由△ACD≌△ABE得CD=BE=12,再证明∠DCE=90°,由勾股定理可求出DE的长;
(3)与(1)相同,证明全等后,利用勾股定理证明三边关系即可.
【解答】(1)证明:∠ADC=∠ABE,理由如下,
∵△ADB与△ACE均为等边三角形,
∴∠DAB=∠ABD=∠ADB=60°,∠EAC=∠ACE=∠AEC=60°,AD=AB=BD,AE=AC=CE,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE;
(2)解:∵△ACE是等边三角形,BE⊥AC,
∴∠AEB=30°,
由(1)知,△DAC≌△BAE,
∴DC=BE=12,∠ACD=∠AEB=30°,
又∵∠ACE=60°,
∴∠DCE=∠DCA+ACE=30°+60°=90°,
∵CE=AE=5,
∴;
(3)解:CD2+CE2=BC2,理由如下,
如图,连接BE,
∵∠DAE=90°,AD=AE,
∴∠ADE=∠AED=45°,
∴∠BAC=∠EAD=90°,
∴∠BAE=∠CAD,
在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴BE=CD,∠AEB=∠ADC=45°,
∴∠BEC=∠AEB+∠AED=90°,
∴BE2+CE2=BC2,
∴CD2+CE2=BC2.
【点评】本题主要考查旋转的性质以及勾股定理,解题关键是找准边与角的关系证明全等,然后利用勾股定理求解.
12.问题探究
(1)如图①,在四边形ABCD中,∠BAC=90°,,CD=4,E为AD中点,连接BE,求BE的最大值;
问题解决
(2)如图②,某小区计划在一片足够大的空地上修建四边形的花园ABCD,其中BC=40米,AD=CD,AD⊥CD,AB∥CD,由于受地理位置的影响,∠ABC<90°.根据要求,现计划给该花园修建条笔直的绿色长廊,且绿色长廊的入口O定为BC的中点,出口定为点D,为了尽可能地提高观赏体验,要求绿色长廊OD最长,试求绿色长廊OD最长为多少米?
【考点】三角形综合题.
【专题】压轴题;推理能力;模型思想.
【答案】(1)22;
(2)绿色长廊OD最长为(2020)米.
【分析】(1)取AC的中点F,连接EF、BF,在△BEF中,BF+EF>BE,可得当B、E、F三点共线的时候BE最大,此时BE=BF+EF,根据中位线可得出EF的长度,在Rt△ABF中根据勾股定理可得BF的长度,即可得出BE的最大值;
(2)过C作CM⊥AB于M点,在AD上截取DN使DN=BM,连接BN,取CN中点P,连接DP、OP,可证得四边形ADCM为正方形,再证明△CMB≌△CDN,易证△BCN为等腰直角三角形,从而得出BN的长度,根据中位线定理可得出OP的长度;利用直角三角形斜边中线等于斜边的一半求出DP=20,再根据OP+PD>OD可得,当O、P、D三点共线时OD最大,即可得出答案.
【解答】解:(1)如图,取AC的中点F,连接EF、BF,
∵E、F分别是AD和AC的中点,
∴EF为△ADC的中位线,
∴EFCD=2,
在Rt△ABF中,AB=4,AFAC=2,
∴BF2,
在△BEF中,BF+EF>BE,
∴当B、E、F三点共线的时候BE最大,
即此时BE=BF+EF=22;
(2)过C作CM⊥AB于M点,在AD上截取DN使DN=BM,连接BN,取CN中点P,连接DP.OP,如图,
∵CM⊥AB,AB∥CD,
∴∠CMA=∠MCD=∠ADC=90°,
∴四边形ADCM为矩形,
∵AD=CD,
∴矩形ADCM为正方形,
∴CD=CM,
在△CMB与△CDN中,
,
∴△CMB≌△CDN(SAS),
∴CN=CB,∠BCM=∠NCD,
∴∠BCN=∠MCD=90°,
在Rt△BCN中,BC=CN=40,
∴BN40,
在Rt△CDN中,点P为CN中点,
∴DP20,
在Rt△BCN中,点P、O分别为CN、CB中点,
∴OP为△BCN的中位线,
∴OPBN=20,
在△OPD中,OP+PD>OD,
∴当O、P.D三点共线的时OD最大,
即此时OD=OP+PD=2020,
答:绿色长廊OD最长为(2020)米.
【点评】本题是四边形综合题,考查中位线定理的综合应用,结合三角形的全等以及三角形三边长关系,在做此类题目时注意类比每一问之间的关系,一般下一问都会用到上一问的结论和做题思路.
13.全等三角形是我们初中数学的重要知识点之一,它为我们学习后面几何知识做好铺垫,掌握全等三角形的证明是做一系列复杂几何证明的基础.
【问题初探】
(1)构造全等三角形的方法有很多,有一种常见的方法是作高线,将需要证明的边或角放在两个直角三角形中进而通过全等证明关系.比如,我们可以通过作高线证明三角形中一个重要的结论“在同一个三角形中,如果两个角相等,那么这两个角所对的边也相等”.如图1,在△ABC中,已知∠B=∠C,可证AB=AC,小聪同学的作法是作BC边上的高线AD.现在请你完成小聪同学的证明过程;
【类比分析】
(2)通过上述例子,我们发现通过作高线构造直角三角形证明全等确实是一种有效的方法,由此推出了三角形中的重要结论.现在请你借助上述的方法或结论继续探索,如图2,在△ABC中,已知∠ABC=∠ACB,点E为边AC上一点,点F为边AB延长线上一点,连结EF与边BC交于点D,若点D恰为线段EF中点,试探究线段CE与线段BF的数量关系,并说明理由;
【学以致用】
(3)如图3,在△ABC中,∠CAB=90°,AD,AE分别为△ABC的角平分线和中线,过点E作EF⊥AD与线段AD的延长线交于点G,与边AB的延长线交于点F,已知△ABC的面积是30,线段AF的长为8,求△AED的面积.
【考点】三角形综合题.
【专题】压轴题;几何直观.
【答案】(1)见解析;
(2)CE=BF,理由见解析;
(3).
【分析】(1)根据等腰三角形等边对等角得到∠B=∠C,再利用全等三角形即可得证;
(2)作平行线利用中点证△BFD≌△GED,得到BF=EG,最后通过等线段转化即可得证;
(3)参考上述方式构造全等,利用等线段的转化找△AED的面积和△ABC面积得关系.
【解答】(1)证明:过A作AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∵AD=AD,∠B=∠C,
∴△ADB≌△ADC(AAS),
∴AB=AC;
(2)解:CE=BF,
理由:过E作EG∥AB交BC于G,
∴∠F=∠DEG,∠FBD=∠EGD,
∵点D恰为线段EF中点,
∴DF=DE,
∴△BFD≌△GED(AAS),
∴BF=EG,
∵∠ABC=∠ACB,
∴∠EGC=∠ECG,
∴EG=CE,
∴CE=BF;
(3)如图延长FE交AC于点H,过B作BM∥AC,
∵AD是角平分线,
∴∠FAG=∠HAG,
∵AD⊥EF,
∴∠AGD=∠AGF,
∵AG=AG,
∴△AGF≌△AGH(SAS),
AF=AH,∠AHG=∠AFG,
由(2)中证明方法可知△CHE≌△BME(AAS),
∴CH=BM,∠CHE=∠BME,
∴∠AHG=∠BMF=∠AFG,
∴BM=BF,
∵AF=8,
∴设BF=x,则BM=CH=x,AB=8﹣x,
∴AC=AH+CH=8+x,
∴S△ABCAB AC=30,
即(8﹣x)(8+x)=60,
解得x=2,
∵AE是△ABC的中线,
∴AE=BEBC,
∴∠EAB=∠ABE,
∴∠EAD+45°=∠BEF+45°,
∴∠EAD=∠BEP,
∵∠AGE=∠BPE=90°,
∴△AEG≌△EBP(AAS),
∴EG=BP,
∵∠F=45°,
∴BP=PF=PM=EG,
∴ED:EB=EG:EP=1:4,
∴S△AEDS△AEBS△ABC.
∴△AED的面积为.
【点评】本题主要考查了全等三角形的判定和性质、三角形面积公式、平行线的性质等内容,熟练掌握相关知识是解题的关键.
14.【阅读理解】
定义:在同一平面内,点A,B分别在射线PM,PN上,过点A垂直PM的直线与过点B垂直PN的直线交于点Q,则我们把∠AQB称为∠APB的“边垂角”(四边形内角和等于360°).
(1)如图1和2,若∠AQB是∠APB的“边垂角”,则∠AQB与∠APB的数量关系是 ∠AQB+∠APB=180°或∠AQB=∠APB. .
【迁移运用】
(2)如图3,CD,BE分别是△ABC的两条高,两条高交于点F,根据定义,我们知道∠DBE是∠DCE的“边垂角”或∠DCE是∠DBE的“边垂角”,∠DAE的“边垂角”是 ∠DFE .
【拓展延伸】
(3)如图4,若∠ACD是∠ABD的“边垂角”,且AB=AC.BD交AC于点E,点C关于直线BD的对称点为点F,连接AF,EF,且∠CAF=45°,延长BA和CF相交于点G.
①请说明:△AGC≌△AEB;
②请说明:BE=CF+CE.
【考点】三角形综合题.
【专题】压轴题;新定义;几何直观.
【答案】(1)∠AQB+∠APB=180°或∠AQB=∠APB;(2)∠DFE;(3)证明过程详见解析.
【分析】(1)根据图形可得两种情况,分别利用三角形内角和和四边形内角和推导即可;
(2)由“边垂角”定义可得,∠DAE的“边垂角”为∠DFE;
(3)①由“边垂角”可证∠ABE=∠ACF,再根据题干已知条件即可得证;②由①全等推出AG=AE,BE=CG,然后证△AGF≌△AEF,得到GF=EF,最后通过线段的和差即可得证.
【解答】(1)解:若∠AQB是∠APB的“边垂角”,分两种情况:
①如图1:
∵∠AQB是∠APB的“边垂角”,
∴AQ⊥PA,BQ⊥PB,
∴∠PAQ=90°,∠PBQ=90°,
∵∠PAQ+∠AQB+∠APB+∠PBQ=360°,
∴∠AQB+∠APB=180°;
②如图2:
∵∠AQB是∠APB的“边垂角”,
∴AQ⊥PA,BQ⊥PB,
∴∠AQB+∠1=90°,∠APB+∠2=90°,
∵∠1=∠2,
∴∠AQB=∠APB;
综上,∠AQB+∠APB=180°或∠AQB=∠APB.
故答案为:∠AQB+∠APB=180°或∠AQB=∠APB.
(2)解:由“边垂角”定义可得,∠DAE的“边垂角”为∠DFE,
故答案为:∠DFE.
(3)证明:①∵∠ACD是∠ABD的“边垂角”,
∴∠ABE+∠AEB=90°,∠ACD+∠DEC=90°,
∵∠AEB=∠DEC,
∴∠ABE=∠ACF,
∴∠BAE=∠CAG=90°,
∵AB=AC,
∴△AGC≌△AEB(ASA);
②证明:∵△AGC≌△AEB(ASA),
∴AG=AE,BE=CG,
∵∠FAC=45°,
∴∠GAF=90°﹣∠FAC=45°,
∴∠GAF=∠FAE=45°,
∵AF=AF,
∴△AGF≌△AEF(SAS),
∴GF=EF.
∵点C关于直线BE对称点为点F,
∴EF=EC,
∴BE=CG=CF+FG=CF+EF=CF+CE,
∴BE=CF+CE.
【点评】本题主要考查了三角形内角和、直角三角形的性质、全等三角形的判定和性质等内容,熟练掌握相关知识点和添加合适的辅助线是解题的关键.
15.定义:如果1条线段将一个三角形分割成2个等腰三角形,我们把这条线段叫做这个三角形的“双等腰线”.如果2条线段将一个三角形分成3个等腰三角形,我们把这2条线段叫做这个三角形的“三等腰线”.如图1,BE是△ABD的“双等腰线”,AD、BE是△ABC的“三等腰线”.
(1)请在图2三个图中,分别画出△ABC的“双等腰线”,并做必要的标注或说明.
(2)如果一个等腰三角形有“双等腰线”,那么它的底角度数是 72°或36°或45°或()° .
(3)如图3,△ABC中,∠C∠B,∠B<45°.画出△ABC所有可能的“三等腰线”,使得对∠B取值范围内的任意值都成立,并做必要的标注或说明.(每种可能用一个图单独表示,如果图不够用可以自己补充)
【考点】三角形综合题.
【专题】几何综合题;新定义;几何直观;应用意识.
【答案】见试题解答内容
【分析】(1)根据等腰三角形的性质和三角形内角和解答即可;
(2)设底角度数为x,分三种情况利用等腰三角形的性质和三角形内角和解答即可;
(3)根据两种情况、利用等腰三角形的性质和三角形内角和解答即可.
【解答】解:(1)如图2,取AB的中点D,则AD=CD=BD,
∴△ADC和△BCD是等腰三角形;
如图3,取CD=BC,则∠CDB=∠B=70°,
∵∠A=35°,
∴∠ACD=70°﹣35°=35°,
∴∠ACD=∠A,
∴AD=CD=BC,
∴△ADC和△BCD是等腰三角形;
如图4,作AB的垂直平分线DE,交AC于D,交AB于E,连接BD,
∴AD=BD,
∴∠A=∠ABD=27°,
∴∠CDB=54°,
∵∠ABC=81°,
∴∠CBD=81°﹣27°=54°=∠BDC,
∴CD=BC,
∴△ADB和△BCD是等腰三角形;
(2)①设△ABC是以AB、AC为腰的锐角三角形,BD为“双等腰线”,如图5,
当AD=BD,BD=BC时,
设∠A=x°,则∠ABD=x°,
∴∠BDC=∠C=2x°,
∴∠ABC=∠C=2x°,
∵∠A+∠ABC+∠C=180°,
∴x°+2x°+2x°=180°,
∴x=36°,2x=72°,
∴∠C=72°,
②设△ABC是以AB、AC为腰的钝角三角形,AD为“双等腰线”,如图6,
当AB=BD,AD=CD时,
设∠B=y°,则∠C=y°,
∵AD=CD,
∴∠DAC=∠C=y°,
∴∠ADB=2y°,
∵AB=BD,
∴∠BAD=∠ADB=2y°,
∵∠B+∠BAD+∠ADB=180°,
∴y°+2y°+2y°=180°,
∴y=36°,
∴∠B=∠C=36°,
③设△ABC是以AB、AC为腰的直角三角形,AD为“双等腰线”,如图7,
当AB=BD,AD=CD时,AD为BC的垂直平分线,
设∠B=z°,则∠C=z°,∠BAD=z°,
∴∠B+∠BAD=90°,
∴z°+z°=90°,
∴z=45°,
∴∠B=∠C=45°,
④设顶角为x,
可得,x+3x+3x=180°
解得:x=()°,
∴∠C=3x=()°,
故答案为:72°或36°或45°或()°;
(3)∵要画出使得对∠B取值范围内的任意值都成立的“三等腰线”,
∴不能使∠B等于具体的数值,
∴值需要使分割后的三个等腰三角形的底角成比例即可,
第一种画法:如图8,
∵∠C∠B,
设∠B=2x°,∠C=3x°,
当AD、DE将△ABC分成BD=DE,DE=AE,AD=AC的三个等腰三角形时,
则有∠BED=∠B=2x°,∠ADC=∠C=3x°,
∵∠EDC=∠B+∠BED=4x°,
∴∠EDA=∠EDC﹣∠ADC=x°,
∴∠EAD=x°,
∴“三等腰线”使得三个等腰三角形的底角比为∠B:∠C:∠EDA=2:3:1,
即可使得对∠B取值范围内的任意值都成立,
第二种画法:
∵∠C∠B,
设∠B=2x°,∠C=3x°,
当AD、DE将△ABC分成BE=DE,AD=AE,AD=CD的三个等腰三角形时,
则∠EDB=∠B=2x°,∠DAC=∠C=3x°,
∵∠AED=∠B+∠BDE=4x°,
∴∠EDA=4x°,
因此,“三等腰线”使得三个等腰三角形的底角比为∠B:∠C:∠AED=2:3:4,即可使得对∠B取值范围内的任意值都成立,
综上所述,如图所示的两种“三等腰线”可以使得对∠B取值范围内的任意值都成立.
【点评】本题主要考查三角形综合题和作图﹣应用与设计作图,解题的关键是掌握等腰三角形的判定和性质.
16.定义:三角形一边中线的中点和该边的两个顶点组成的三角形称为中原三角形.如图①,AD是△ABC的中线,F是AD的中点,则△FBC是中原三角形.
(1)求中原三角形与原三角形的面积之比(直接写出答案).
(2)如图②,AD是△ABC的中线,E是边AC上的点,AC=3AE,BE与AD相交于点F,连接CF.求证:△FBC是中原三角形.
(3)如图③,在(2)的条件下,延长CF交AB于点M,连接ME,求△FEM与△ABC的面积之比.
【考点】三角形综合题.
【专题】新定义;三角形;图形的相似;几何直观;推理能力;应用意识.
【答案】(1)中原三角形与原三角形的面积之比为1:2;
(2)证明见解答过程;
(3)△FEM与△ABC的面积之比为1:18.
【分析】(1)由F是AD的中点,可得S△DFCS△DAC,S△DFBS△DAB,即有S△FBCS△ABC,故中原三角形与原三角形的面积之比为1:2;
(2)作CE的中点G,连接DG,由AD是△ABC的中线,可得DG是△BCE的中位线,CE=2EG,即得BE∥DG,即EF∥DG,根据AC=3AE,CE=2EG,可得AE=EG,即得AF=DF,从而△FBC是中原三角形;
(3)过D作DH∥CM交AB于H,由DH∥CM,D是BC中点,F是AD中点,可得AM=MH=BH,即知,可得△AME∽△ABC,有∠AME=∠ABC,,从而ME∥BC,△MEF∽△CBF,即有()2,S△FBC=9S△FEM,又S△FBCS△ABC,即得△FEM与△ABC的面积之比为1:18.
【解答】(1)解:∵F是AD的中点,
∴S△DFCS△DAC,S△DFBS△DAB,
∴S△DFC+S△DFBS△DACS△DAB,
∴S△FBCS△ABC,
∴中原三角形与原三角形的面积之比为1:2;
(2)证明:作CE的中点G,连接DG,如图:
∵AD是△ABC的中线,
∴D是BC中点,
∵G是CE中点,
∴DG是△BCE的中位线,CE=2EG,
∴BE∥DG,即EF∥DG,
∵AC=3AE,
∴CE=2AE,
∴AE=EG,
又EF∥DG,
∴AF=DF,即F是AD中点,
∴△FBC是中原三角形;
(3)解:过D作DH∥CM交AB于H,如图:
∵DH∥CM,D是BC中点,
∴BH=MH,
∵DH∥MF,F是AD中点,
∴AM=MH,
∴AM=MH=BH,
∴,
∵AC=3AE,
∴,
又∠MAE=∠BAC,
∴△AME∽△ABC,
∴∠AME=∠ABC,,
∴ME∥BC,
∴△MEF∽△CBF,
∴()2=()2,
∴S△FBC=9S△FEM,
由(1)知:S△FBCS△ABC,
∴9S△FEMS△ABC,
∴S△FEMS△ABC,
∴△FEM与△ABC的面积之比为1:18.
【点评】本题考查三角形综合应用,涉及新定义、三角形中位线定理及推论、三角形面积等,解题的关键是作辅助线,构造三角形中位线.
17.如图1,等边△ABC的边长为4,点D是直线AB上异于A,B的一动点,连接CD,以CD为边长,在CD右侧作等边△CDE,连接BE.
【初步感知】
(1)求证:△CAD≌△CBE;
【类比探究】
(2)当点D在直线AB上运动时,①AD与BE的数量关系是 AD=BE ;
②△BDE的周长是否存在最小值?若存在,求此时AD的长;若不存在,说明理由;
【拓展应用】
(3)当点D在直线AB上运动时,△BDE能否形成直角三角形?若能,请直接写出此时AD的长;若不能,说明理由.
【考点】三角形综合题.
【专题】压轴题;几何直观.
【答案】(1)证明过程见解析;(2)①AD=BE;②2;(3)8或4.
【分析】(1)证△ACD≌△BCE(SAS)即可得证;
(2)①同第一问,证证△ACD≌△BCE(SAS)即可得证;
②由(1)得△ACD≌△BCE(SAS),则BE=AD,因为BD+BE+DE=AB+DE,所以要使△BDE的周长最小,只要DE最小,当CD⊥AB时,CD的长最小,此时DE最小,由“三线合一”即可求出AD的长;
(3)分两种情况:当∠BDE=90°时和当∠BED=90°时,分别作出图形,作CH⊥AB于点H,利用(1)的结果及勾股定理解答即可.
【解答】(1)证明:∵△ABC、△CDE都是等边三角形,
∴.CA=CB=AB,∠A=∠ACB=∠ABC=60°,∠DCE=∠DCE=DEC=60°,CD=CE=DE,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)①如图,当点D在线段AB上、点D在BA延长线上、点D在AB延长线上时,
证明方法同第一问:
∵△ABC、△CDE都是等边三角形,
∴.CA=CB=AB,∠A=∠ACB=∠ABC=60°,∠DCE=∠DCE=DEC=60°,CD=CE=DE,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE.
故答案为:AD=BE.
②△BDE的周长存在最小值,由(1)得△ACD≌△BCE(SAS),
∴BE=AD,
∴BD+BE+DE=AB+DE,
要使△BDE的周长最小,则DE最小,
∵CD=DE,
∴当CD⊥AB时,CD的长最小,如图2,
∵CA=CB=4,CD⊥AB,
∴;
(3)当点D在直线AB上运动时,△BDE能形成直角三角形,分两种情况,
①当∠BDE=90°时,作CH⊥AB于点H,如图3,
∵AB=AC=BC=4,
∴,
∴,
∵∠BDE=90°,∠CDE=60°,
∴∠ADC=30°,
∴CD=2CH=4,
∴,
∴AD=AH+HD=8;
②当∠BED=90°时,作CH⊥AB于点H,如图4,
同理得AH=2,,
设AD=x,
由(1)得△ACD≌△BCE(SAS),
∴BE=AD=x,
∵CD=DE,
由勾股定理得,DH2+CH2=DB2﹣BE2,
即,
解得,x=4,
∴AD=4,
综上,当点D在直线AB上运动时,△BDE能形成直角三角形,AD的值为8或4.
【点评】本题是三角形的综合,主要考查等边三角形的性质、全等三角形的判定与性质、直角三角形的性质、最短路线问题、勾股定理等知识,灵活运用全等三角形的判定与性质、勾股定理是解答本题的关键.
18.【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 B .
A.SSS
B.SAS
C.AAS
D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 2<AD<8 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=5,EC=3,求线段BF的长.
【灵活运用】
如图③,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
【考点】三角形综合题.
【专题】压轴题;几何直观;运算能力;推理能力.
【答案】(1)B;
(2)2<AD<8;
(3)8;
(4).
【分析】【问题情境】(1)根据全等三角形的判定定理解答;
(2)根据三角形的三边关系计算;
【初步运用】延长AD到M,使AD=DM,连接BM,证明△ADC≌△MDB,根据全等三角形的性质解答;
【灵活运用】延长ED到点G,使DG=ED,连接GF,GC,证明△DBE≌△DCG,得到BE=CG,根据勾股定理解答.
【解答】【问题情境】
解:(1)在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
故选:B;
(2)由(1)得:△ADC≌△EDB,
∴AC=BE=6,
在△ABE中,AB﹣BE<AE<AB+BE,
即10﹣6<2AD<10+6,
∴2<AD<8,
故答案为:2<AD<8;
【初步运用】
解:延长AD到M,使AD=DM,连接BM,如图②所示:
∵AE=EF.EF=5,
∴AC=AE+EC=5+3=8,
∵AD是△ABC中线,
∴CD=BD,
在△ADC和△MDB中,
,
∴△ADC≌△MDB(SAS),
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC=8;
【灵活运用】
解:线段BE、CF、EF之间的等量关系为:BE2+CF2=EF2.理由如下:
延长ED到点G,使DG=ED,连接GF,GC,如图③所示:
∵ED⊥DF,
∴EF=GF,
∵D是BC的中点,
∴BD=CD,
在△BDE和△CDG中,
,
∴△DBE≌△DCG(SAS),
∴BE=CG,
∵∠A=90°,
∴∠B+∠ACB=90°,
∵△DBE≌△DCG,EF=GF,
∴BE=CG,∠B=∠GCD,
∴∠GCD+∠ACB=90°,
即∠GCF=90°,
∴Rt△CFG中,由勾股定理得:CF2+GC2=GF2,
∴BE2+CF2=EF2.
【点评】本题是三角形综合题目,考查的是全等三角形的判定和性质、三角形三边关系以及勾股定理的应用等知识;熟练掌握三角形的三边关系和勾股定理,证明三角形全等是解题的关键.
19.【问题情境】
如图1,在Rt△ABC中,∠BCA=90°,∠B=30°,AC=4,AB的垂直平分线交AB于点D,交BC于点E,作射线AE.
(1)则CE的长为 ;
【变式思考】
(2)在“问题情境”的基础上,如图2,点P是射线AE上的动点,过点P分别作PF⊥AB所在直线于点F,作PH⊥BC所在直线于点H.
①求△PHE与△PFA面积之和的最小值;
②连接FH,求FH的最小值是多少?
【拓展探究】
(3)在“问题情境”的基础上,如图3,△ABC内有点Q,且∠AQC=60°,AB、BC上分别有一点M、N,连接QM、QN、MN,直接写出△QMN周长的最小值.
【考点】三角形综合题.
【专题】压轴题;推理能力.
【答案】(1);
(2)①;②2;
(3).
【分析】(1)利用垂直平分线的性质可证∠AEC=60°,再根据tan∠AEC,可得答案;
(2)①过点P作PG⊥AC于点G.首先证明Rt△EAC≌Rt△EAD(HL).设PG=x,则AG,CG=PH,HE,表示出△PHE与△PFA面积之和,利用二次函数的性质可得答案;
②连接BP,取BP的中点O,连接OH,OF,过点B作BM⊥AE于点M.可知△HOF为等边三角形.且HFBP.只要求出BP的最小值即可;
(3)以AC为底边作等腰三角形AOC,使∠AOC=120°,连接OB,作点Q关于BC、AB的对称点Q'、Q'',连接Q'Q'',由轴对称的性质得,△QMN周长为Q'Q'',BQ'=BQ''=BQ,∠Q'BQ''=60°,利用勾股定理求出BO和OA的长,从而解决问题.
【解答】解:(1)∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EAB=∠B=30°,
∴∠AEC=60°,
∴tan∠AEC,
∴CE,
故答案为:;
(2)①过点P作PG⊥AC于点G.
∵DE垂直平分AB,
∴AE=BE.
∴∠EAB=∠B=30°.
∴∠EAC=∠EAB=30°.
∴PF=PG,CE=DE,
∵AE=AE,
∴Rt△EAC≌Rt△EAD(HL).
设PG=x,则AG,CG=PH,HE,
∴△PHE与△PFA面积之和为
.
∴最小值为;
②连接BP,取BP的中点O,连接OH,OF,过点B作BM⊥AE于点M.
∵PF⊥AB,PH⊥BC,点O为PB中点,
∴OP=OF=OB=OH.
∴点P、F、B、H四点在以O为圆心,PB为直径的同一个圆上,
又∵∠EBF=30°,
∴∠HOF=60°.
∴△HOF为等边三角形.
∴HFBP.
∵AC=4,
∴AB=8.
∴BP的最小值为BM=4.
∴FH的最小值为2;
(3)以AC为底边作等腰三角形AOC,使∠AOC=120°,连接OB,作点Q关于BC、AB的对称点Q'、Q'',连接Q'Q'',
由轴对称的性质得,△QMN周长为Q'Q'',BQ'=BQ''=BQ,∠Q'BQ''=60°,
∴△BQ'Q''是等边三角形,
∵∠AQC=60°,
∴点Q在以O为圆心,OA为半径的圆上运动,
当点O、Q、B共线时,QB最小,
延长CO交AB于H,
∵∠ACH=30°,∠CAB=60°,
∴∠AHC=90°,
∴AH=2,CO,BH=AB﹣AH=8﹣2=6,
∴OHOA,
由勾股定理得,OB,
∴BQ的最小值为,
∴△QMN周长的最小值为.
【点评】本题是三角形综合题,主要考查了含30°角的直角三角形的性质,全等三角形的判定与性质,二次函数的性质,勾股定理,轴对称﹣最短路线问题,等边三角形的判定与性质等知识,将△QMN周长转化为Q'Q''的长是解题的关键.
20.【基础巩固】(1)如图1,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE,连接AD,BE;求证:△ACD≌△BCE;
【尝试应用】(2)如图2,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,连接AD,BE,A、D、E三点在一条直线上,BC与DE交于点F;
①求∠BEA的大小;
②若DF=3EF且BE=2,求△BCE的面积;
【拓展提高】(3)如图3,在△ABC与△CDE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,点G为DE的中点,AE交BC于点H,连接GH,若GH⊥AB,且S△ABH为18,求CH的长.
【考点】三角形综合题.
【专题】几何综合题;压轴题;图形的全等;等腰三角形与直角三角形;推理能力.
【答案】(1)证明见解答;
(2)①∠BEA=90°;
②S△BCE=2;
(3)CH=6.
【分析】(1)利用SAS证明△ACD≌△BCE;
(2)①由△ABC和△DEC均为等腰直角三角形,可得∠CDE=∠CED=45°,进而得出∠ADC=180°﹣45°=135°,即可求得答案;
②过点D作DG⊥AC于G,DJ⊥BC于J,过点E作EH⊥BC于H,可证得△CDG≌△CEH(AAS),设CJ=DG=EH=x,可得DJ=CG=CH=3x,FHx,FJx,CFx,再利用勾股定理建立方程求得EH,BC=2,再运用S△BCEBC EH即可求得答案;
(3)连接BE,CG,先证得△BEG≌△HCG(SAS),得出BE=CH,∠GBE=∠GHC,进而可得BE∥AC,推出S△CBE=S△ABE,即S△BEH+S△CEH=S△BEH+S△ABH,得出S△CEH=S△ABH=18,即可求得答案.
【解答】(1)证明:∵∠ACB=∠DCE,
即∠ACD+∠BCD=∠BCD+∠BCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS);
(2)解:①∵AC=BC,CD=CE,∠ACB=∠DCE=90°,
∴△ABC和△DEC均为等腰直角三角形,
∴∠CDE=∠CED=45°,
∴∠ADC=180°﹣45°=135°,
同(1)可得△ACD≌△BCE,
∴∠ADC=∠BEC=135°,
∴∠BEA=∠BEC﹣∠CED=135°﹣45°=90°;
②如图,过点D作DG⊥AC于G,DJ⊥BC于J,过点E作EH⊥BC于H,
则∠CGD=∠CJD=∠DJF=∠EHF=90°,四边形CJDG是矩形,
∴DJ=CG,CJ=DG,
∵∠DCG+∠BCD=∠ECH+∠BCD=90°,
∴∠DCG=∠ECH,
在△CDG和△CEH中,
,
∴△CDG≌△CEH(AAS),
∴DG=EH,CG=CH,
∴CJ=DG=EH,
设CJ=DG=EH=x,
∵EH∥DJ,
∴△EFH∽△DFJ,
∴,
∵DF=3EF,
∴,
∴DJ=CG=CH=3x,FJ=3FH,
∴FH+FJ=CH﹣CJ=3x﹣x=2x,
∴FHx,FJx,
∴CF=CJ+FJ=xxx,
∵EH∥AC,
∴△EFH∽△AFC,
∴,
∴AC5x=BC,
在Rt△CDG中,CDx,
∵△ABC和△DEC均为等腰直角三角形,
∴ABAC=5x,DECD=2x,
∵△ACD≌△BCE,
∴AD=BE,
∵BE=2,
∴AD=2,
∴AE=AD+DE=2+2x,
在Rt△ABE中,AE2+BE2=AB2,
(2+2x)2+22=(5x)2,
解得:x1,x2(舍去),
∴EH,BC=2,
∴S△BCEBC EH22;
(3)如图,连接BE,CG,
∵AC=BC,CD=CE,∠ACB=∠DCE=90°,
∴△ABC和△DEC均为等腰直角三角形,
∴∠ABC=45°,
∵点G为DE的中点,
∴∠CGE=90°,CG=EG=DG,
∵GH⊥AB,
∴∠BGH=90°,
∴△BGH是等腰直角三角形,
∴BG=HG,∠BHG=∠ABC=45°,
∵∠BGE+∠EGH=∠HGC+∠EGH,
∴∠BGE=∠HGC,
在△BEG和△HCG中,
,
∴△BEG≌△HCG(SAS),
∴BE=CH,∠GBE=∠GHC,
∵∠GHC=180°﹣∠BHG=135°,
∴∠GBE=135°,
∴∠CBE=∠GBE﹣∠ABC=135°﹣45°=90°,
∴BE∥AC,
∴S△CBE=S△ABE,
即S△BEH+S△CEH=S△BEH+S△ABH,
∴S△CEH=S△ABH,
∵S△ABH=18,
∴S△CEH=18,
∴CH BE=18,
∵BE=CH,
∴CH2=36,
∴CH=6.
【点评】本题是三角形综合题,考查了等腰直角三角形性质,直角三角形性质,全等三角形的判定和性质,勾股定理等,属于中考压轴题,综合性强,难度大,对学生要求很高;解题关键是熟练掌握等腰直角三角形性质等相关知识,合理添加辅助线构造全等三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
