2026年中考数学核心考点一轮复习 四边形(含解析)
文档属性
| 名称 | 2026年中考数学核心考点一轮复习 四边形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 15:09:47 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中考数学一轮复习 四边形
一.解答题(共20小题)
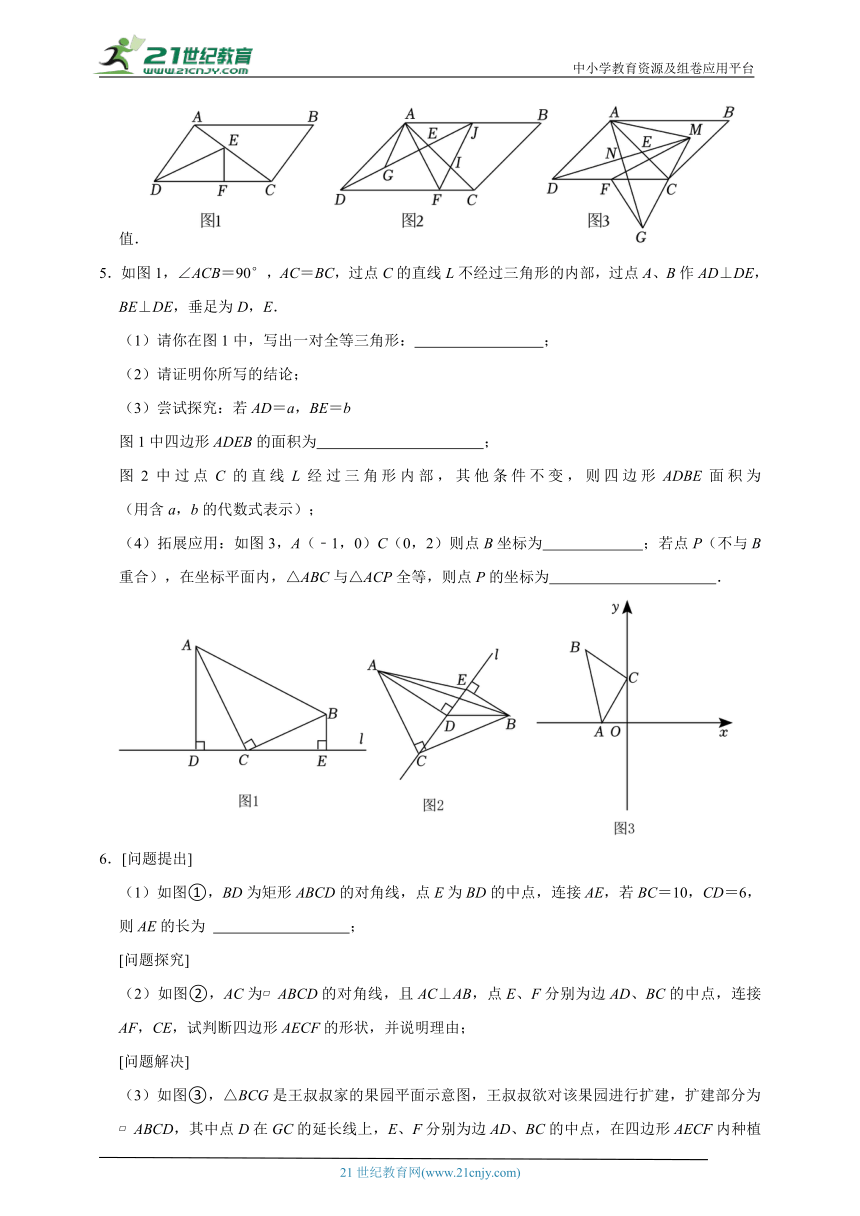
1.【问题情境】如图1,小明把三角板EFG(∠GFE=30°)放置到矩形ABCD中,使得顶点E、F、G分别落在AD、CD、AB上,你发现线段ED与AG有什么数量关系?直接写出结论: (不用证明).
【变式探究】如图2,小明把三角板EFG(∠GFE=30°)放置到矩形ABCD中,使得顶点E、F、G分别在AD、BC、AB边上,若GA=4,AE=6,求BG的长.
【拓展应用】如图3,小明把三角形EFG放置到平行四边形ABCD中,使得顶点E、F、G分别在AD、BC、AB边上,若,,∠FEG=∠BAD,求出的值.
2.综合与实践——平行四边形旋转中的数学问题
问题情境:
已知 ABCD与 A'B'C'D'中,AB=A'B'=6,BC=B'C'=8,∠ABC=∠A'B'C'=60°,同学们利用这样的两张平行四边形纸片开展操作实验,从中发现了许多有趣的数学问题,请你和他们一起进行探究.
拼图思考:
(1)希望小组的同学将 ABCD与 A'B'C'D'按图1的方式摆放,其中,点B与点B'重合,点A'落在BC边上,点C'落在BA边的延长线上,他们提出了如下问题,请你解答:
①连接BE,求证:BE平分∠ABA';
②点D,D′之间的距离为: ;
操作探究:
(2)创新小组的同学在图1的基础上进行了如下操作:保持 ABCD不动,将 A'B'C'D'绕点B沿顺时针方向旋转,连接DD′.
①当线段C'D'与DC交于点P时,连接CC';如图2,求证:点P在DD'的垂直平分线上;
②在 A'B'C'D'旋转的过程中,当点C′恰好落在线段DC的延长线上时,请在图3中补全图形,并直接写出此时点D,D'之间的距离.
3.【问题探究】
(1)如图1,在正方形ABCD中,对角线AC与BD相交于点O,在线段AO上任取一点P(端点除外),连接PD,PB.
①求证:PD=PB;
②将线段DP绕点P逆时针旋转,使点D落在BA的延长线上的点Q处,当点P在线段AO上的位置发生变化时,∠DPQ的大小是否发生变化?请说明理由;
③在探究AQ与OP的数量关系时,小颖作了如图2的辅助线:作PM⊥AB于点M,作PN⊥AD于点N,作PE⊥AO交AB于点E,作EF⊥OB于点F,请你直接写出AQ与OP的数量关系.
【迁移探究】
(2)如图3,将(1)中正方形ABCD换成菱形ABCD,且∠ABC=60°,其他条件不变,试探究AQ与CP的数量关系,并说明理由.
4.在 ABCD中,点E是对角线AC上一点.
(1)如图1,∠DAC=90°,将△ADE沿DE翻折,使得A点的对应点F落在CD上,若AD=3,AC=4,求EF的长;
(2)如图2,∠ADC=45°,AD=AC,点G是DE的中点,AF⊥DE交CD于F点,I是AC上一点,连接FI,延长FI交DE的延长线于点J.若∠J=2∠DAG,AG=EJ,求证:AF+FI=2IJ;
(3)如图3,∠ADC=45°,AD=AC,延长DE至M点使AM=AD,∠DAM的角平分线交DE于点N,交MC延长线于点G,取CD中点F,连接GF,FM.当E在直线AC上运动时,直接写出的最大值.
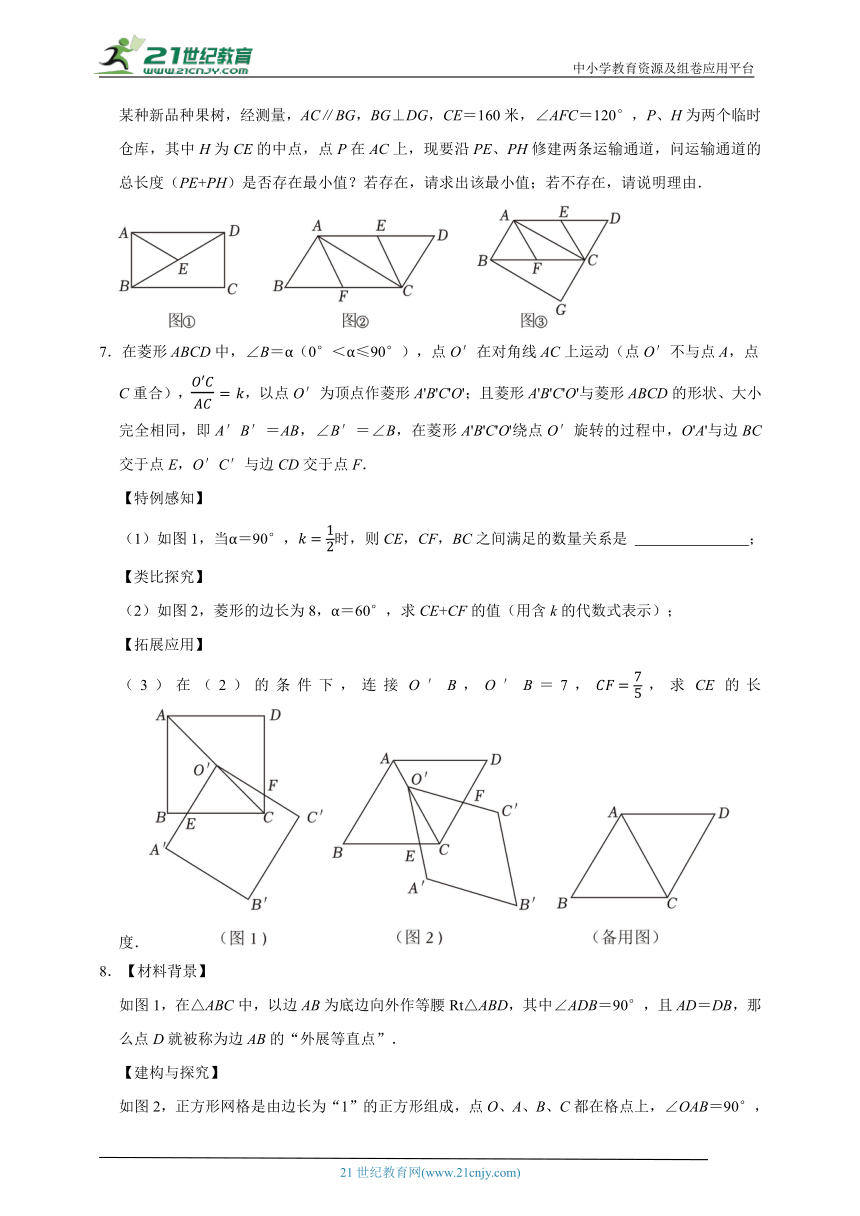
5.如图1,∠ACB=90°,AC=BC,过点C的直线L不经过三角形的内部,过点A、B作AD⊥DE,BE⊥DE,垂足为D,E.
(1)请你在图1中,写出一对全等三角形: ;
(2)请证明你所写的结论;
(3)尝试探究:若AD=a,BE=b
图1中四边形ADEB的面积为 ;
图2中过点C的直线L经过三角形内部,其他条件不变,则四边形ADBE面积为 (用含a,b的代数式表示);
(4)拓展应用:如图3,A(﹣1,0)C(0,2)则点B坐标为 ;若点P(不与B重合),在坐标平面内,△ABC与△ACP全等,则点P的坐标为 .
6.[问题提出]
(1)如图①,BD为矩形ABCD的对角线,点E为BD的中点,连接AE,若BC=10,CD=6,则AE的长为 ;
[问题探究]
(2)如图②,AC为 ABCD的对角线,且AC⊥AB,点E、F分别为边AD、BC的中点,连接AF,CE,试判断四边形AECF的形状,并说明理由;
[问题解决]
(3)如图③,△BCG是王叔叔家的果园平面示意图,王叔叔欲对该果园进行扩建,扩建部分为 ABCD,其中点D在GC的延长线上,E、F分别为边AD、BC的中点,在四边形AECF内种植某种新品种果树,经测量,AC∥BG,BG⊥DG,CE=160米,∠AFC=120°,P、H为两个临时仓库,其中H为CE的中点,点P在AC上,现要沿PE、PH修建两条运输通道,问运输通道的总长度(PE+PH)是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.
7.在菱形ABCD中,∠B=α(0°<α≤90°),点O′在对角线AC上运动(点O′不与点A,点C重合),,以点O′为顶点作菱形A'B'C'O';且菱形A'B'C'O'与菱形ABCD的形状、大小完全相同,即A′B′=AB,∠B′=∠B,在菱形A'B'C'O'绕点O′旋转的过程中,O'A'与边BC交于点E,O′C′与边CD交于点F.
【特例感知】
(1)如图1,当α=90°,时,则CE,CF,BC之间满足的数量关系是 ;
【类比探究】
(2)如图2,菱形的边长为8,α=60°,求CE+CF的值(用含k的代数式表示);
【拓展应用】
(3)在(2)的条件下,连接O′B,O′B=7,,求CE的长度.
8.【材料背景】
如图1,在△ABC中,以边AB为底边向外作等腰Rt△ABD,其中∠ADB=90°,且AD=DB,那么点D就被称为边AB的“外展等直点”.
【建构与探究】
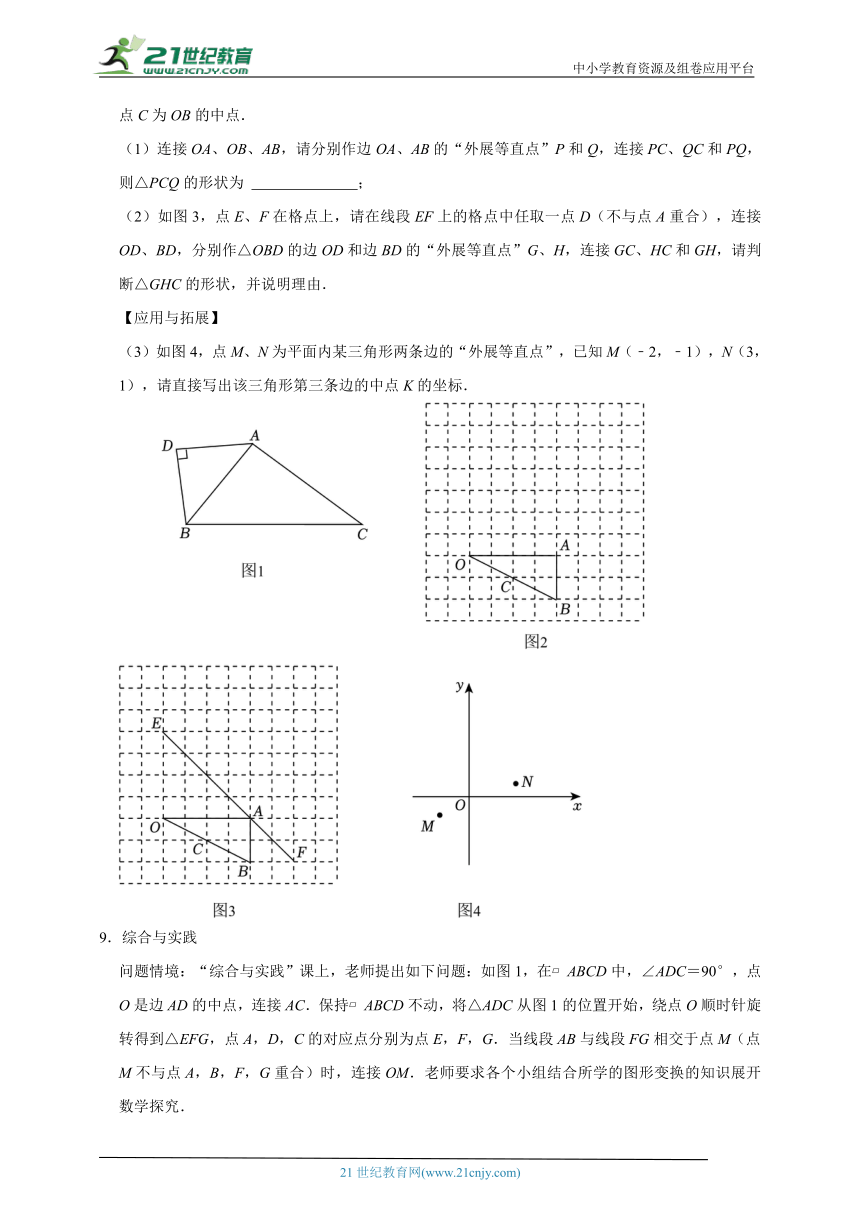
如图2,正方形网格是由边长为“1”的正方形组成,点O、A、B、C都在格点上,∠OAB=90°,点C为OB的中点.
(1)连接OA、OB、AB,请分别作边OA、AB的“外展等直点”P和Q,连接PC、QC和PQ,则△PCQ的形状为 ;
(2)如图3,点E、F在格点上,请在线段EF上的格点中任取一点D(不与点A重合),连接OD、BD,分别作△OBD的边OD和边BD的“外展等直点”G、H,连接GC、HC和GH,请判断△GHC的形状,并说明理由.
【应用与拓展】
(3)如图4,点M、N为平面内某三角形两条边的“外展等直点”,已知M(﹣2,﹣1),N(3,1),请直接写出该三角形第三条边的中点K的坐标.
9.综合与实践
问题情境:“综合与实践”课上,老师提出如下问题:如图1,在 ABCD中,∠ADC=90°,点O是边AD的中点,连接AC.保持 ABCD不动,将△ADC从图1的位置开始,绕点O顺时针旋转得到△EFG,点A,D,C的对应点分别为点E,F,G.当线段AB与线段FG相交于点M(点M不与点A,B,F,G重合)时,连接OM.老师要求各个小组结合所学的图形变换的知识展开数学探究.
初步思考:(1)如图2,连接FD,“勤学”小组在旋转的过程中发现FD∥OM,请你证明这一结论;
操作探究:(2)如图3,连接BG,“善思”小组在旋转的过程中发现OM垂直平分BG,请你证明这一结论;
拓展延伸:(3)已知,CD=2,在旋转的过程中,当以点F,C,D为顶点的三角形是等腰三角形时,请直接写出此时线段AM的长度.
10.在数学探究课上,王宇同学通过作辅助图形的方法,计算动点条件下线段和的最小值,其过程如下:
(1)【观察发现】
如图1,在等边△ABC中,AC=2,CDBC,E,F分别是AB和AC上的动点,且总有BE=AF,阅读下面作辅助图形的方法及推理过程并填空,理解确定DE+DF最小值的方法.
∵在等边△ABC中,AC=2,CDBC,
∴点D为BC边上的中点,∠B=∠ACB.
∴AD⊥BC.
过点A作AG⊥AD,使AG=BD,连接GF.
∴AG∥BC.∴∠GAC=∠ACB=∠B.
又∵AF=BE,∴△AGF≌△BDE(SAS).
∴GF=DE.
连接DG,DF,当D,F,G三点共线时,GF+DF的最小值等于线段DG的长.
连接GC,可证四边形ADCG是矩形,
∴DG=AC.
∴DE+DF的最小值为 .
(2)【类比应用】
如图2,已知正方形ABCD的边长为6,O为对角线的交点,M,N分别是AB,AD上的动点,且总有BM=DN,连接OM,CN,求OM+CN的最小值.
(3)【拓展延伸】
如图3,矩形ABCD中,AB,AD=2,E是AD的中点,F,G分别是BC和DC上的动点,且总有BF=2DG,则EF+2AG的最小值为 .
11.综合与实践课上,老师和同学们开展了一场以“最小值”为主题的探究活动.
【提出问题】老师提出了一个问题:如图1,在矩形ABCD中,AB=3,BC=6,P为AD边上的一动点,以PC为边向右作等边△PCE,连接BE,求BE的最小值;
【探究发现】小明发现:如图4所示,以BC为边向下构造一个等边△BCM,便可得到△PCM≌△ECB,进而将 BE的最小值转化为PM的最小值.
(1)按照小明的想法,请求出BE的最小值;
【拓展应用】
(2)小刚受此启发,举一反三,提出新问题:如图2,若将图1当中构造的等边三角形,改为以PC为边向右构造正方形PCFG,则运动过程中,BG的最小值是 .
(3)小红同学深入研究了小刚的问题,并又提出了新的问题:如图3,若将图2当中构造的正方形改为以PC为边向右构造菱形PCHI,使.∠CPI=120°,也可求得BI的最小值请你直接写出BI最小值为 .
12.综合实践
如图1,点E为正方形ABCD内一点,∠AEB=90°,点E′为正方形ABCD外一点,且BE'⊥CE',BE=BE',延长AE交CE'于点F,连接DE.
(1)试判断四边形BE'FE的形状,并说明理由;
(2)如图2,若DA=DE,请猜想线段CF与E′F的数量关系,并加以证明;
(3)如图1,若AB=15,BE=9,请求出DE的长.
13.在一次数学活动课上,老师带领同学们探究图形的变换问题.老师先提出这样一个问题:
有一张矩形纸片ABCD,其中AB=4,,你能用这张矩形纸片折出一个等边三角形吗?
【操作】小明同学是这样操作的:如图①,先将矩形ABCD沿MN对折;展开后,再将点C沿BE折叠,使点C落在MN上的点F处;再展开,连接BF,CF,则△BCF为等边三角形.
【验证】(1)求证:△BCF为等边三角形;
【应用】(2)连接AF,DF,如图②,求AF的长;
【拓展】(3)将图②中的△BCF绕着点F顺时针旋转α(0°<α<90°)得到△B′C′F(点B,C的对应点分别为B′,C′),连接AB′,DC′,当△AFB'为等腰三角形时,直接写出线段DC′的长.
14.[回顾课本]苏教版八年级下册数学教材“9.5三角形的中位线”一课中给出了“三角形的中位线定理”的证明思路,请根据分析完成证明过程.
已知:如图1,DE是△ABC的中位线,求证:DE∥BC,.
分析:因为点E是AC的中点,可以考虑把△ADE绕点E按顺时针方向旋转180°,得到△CFE,这样就需要证明四边形BCFD是平行四边形……
[探究发现]
如图2,等边△ABC的边长为2,点D、E分别为AB、AC边中点,点F为BC边上任意一点(不与B、C重合),沿DE、DF剪开分成①、②、③三块后,将②、③分别绕点D顺时针、点E逆时针旋转180°恰好能与①拼成 DIHG,求 DIHG周长的最小值.
[拓展作图]
如图3,已知四边形ABCD,现要求只剪两次将其剪成四块,使得剪成的四块能通过适当的摆放拼成一个平行四边形,请在图3中画出两条剪痕,并对剪痕作适当的说明.
15.函数是刻画现实世界的有效模型,函数和现实情境之间的转换可以帮助我们简化问题的处理.
(1)下列情境中,可以用反比例函数刻画的是 ;
A.甲、乙两地相距200km,行驶时间和行驶速度之间的关系;
B.单价为3元的练习本,购买数量和总价的关系;
C.面积为8的矩形,长和宽的关系.
(2)求函数的最小值时,直接求解困难较大,我们可以给函数赋予这样的数学情境:如图1,线段BC=3,AB=1,CD=2,AB⊥BC,CD⊥BC,则AP+PD可表示为 ,(用含有x的代数式表示)请你结合图形,继续完成求解过程.
(3)如图2,四边形ABCD为矩形,AB=6,BC=9,P为矩形ABCD内(不包含边界)一点,过P分别向AB、BC作垂线,垂足为M,N,若四边形MBNP的面积为6,则称点P为“美丽点”,在矩形BEFG中,BE=9,BG=4,过F点的直线l交直线BC于点Q,若直线l上存在“美丽点”,求FQ的取值范围.
16.【探索发现】
(1)如图1,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等,边A1O与边AB相交于点E,边C1O与边CB相交于点F,连接EF.在实验与探究中,小新发现无论正方形A1B1C1O绕点O怎样转动,AE,CF,EF之间一直存在某种数量关系,小新发现通过证明△AOE≌△BOF即可推导出来.
①请你猜想AE,CF,EF之间的数量关系是 .
②小新对图1的进一步研究中发现,延长EO与DC交于一点G,通过证明△AOE≌△COG也可推导出AE,CF,EF之间的数量关系,请你证明△AOE≌△COG.
【类比迁移】
(2)如图2,矩形ABCD的中心O是矩形A1B1C1O的一个顶点,A1O与边AB相交于点E,C1O与边CB相交于点F,连接EF,矩形A1B1C1O可绕着点O旋转,判断AE,CF,EF之间的数量关系并进行证明;
【拓展应用】
(3)如图3,在Rt△ACB中,∠C=90°,AC=5cm,BC=12cm,点D是边AB的中点,∠EDF=90°,它的两条边DE和DF分别与直线AC,BC相交于点E,F,∠EDF可绕着点D旋转,当AE=4cm时,请直接写出线段CF的长度.
17.综合与实践
问题情境:第二十四届国际数学家大会合徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图1,在综合实践课上,同学们绘制了“弦图”并进行探究,获得了以下结论:该图是由四个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH拼成的大正方形ABCD,且∠ABF>∠BAF.
特殊化探究:连接BH.设BF=a,AF=b.
“运河小组”从线段长度的特殊化提出问题:
(1)若AB=5,FG=1,求△ABF的面积.
“武林小组”从a与b关系的特殊化提出问题:
(2)若b=2a,求证:∠BAE=∠BHE.
深入探究:老师进一步提出问题:
(3)如图2,连接BE,延长FA到点I,使AI=AB,作矩形BFIJ.设矩形BFIJ的面积为S1,正方形ABCD的面积为S2,若BE平分∠ABF,求证:S1=S2.
请你解答这三个问题.
18.数学活动课上,某小组将一个含45°的三角尺AEF和一个正方形纸板ABCD如图1摆放,若AE=1,AB=2.将三角尺AEF绕点A逆时针方向旋转α(0°≤α≤90°)角,观察图形的变化,完成探究活动.
【初步探究】
如图2,连接BE,DF并延长,延长线相交于点G,BG交AD于点M.
问题1 BE和DF的数量关系是 ,位置关系是 .
【深入探究】
应用问题1的结论解决下面的问题.
问题2 如图3,连接BD,点O是BD的中点,连接OA,OG.求证OA=OD=OG.
【尝试应用】
问题3 如图4,请直接写出当旋转角α从0°变化到60°时,点G经过路线的长度.
19.【教材呈现】如图是华师版九年级上册数学教材第78页的部分内容.
例1:求证:三角形的一条中位线与第三边上的中线互相平分. 已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC. 求证:AE、DF互相平分. 证明:连接DE、EF.
请根据教材提示,结合图①,写出完整的解题过程.
【拓展】如图②,设图①中的AE与DF的交点为G,连接CD,分别交AE、EF于点H、K.
(1) .
(2)若四边形FGHK的面积为3,则四边形ADEF的面积为 .
20.【模型定义】
它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.他们得知这种模型称为“手拉手模型”.如果把小等腰三角形的腰长看作是小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手.
【模型探究】
(1)如图1,若△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,易证△CDA≌△CEB,则∠AEB的度数为 ;
【模型应用】
(2)如图2,P为等边△ABC内一点,PA:PB:PC=3:4:5,且PA=3,以BP为边构造等边△BPQ,这样就有两个等边三角形共顶点B,然后连接CQ,∠APB的度数是 ;S四边形BPCQ= ;
(3)如图3,点P是等腰直角△ACB中内一点,∠ACB=90°,且CP=1,,AP=2,以CP为直角边构造等腰直角△DCP,点C为直角顶点,则∠CPB的度数是 ;AC的长为 ;
【深化模型】
(4)如图4,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°;⑥CO平分∠BCD,恒成立的结论有 .
【拓展提高】
(5)如图5,在△ABC中,∠ACB=90°,∠BAC=30°,AB=6,若点P是△ABC内一点,则PA+PB+PC的最小值为 .
(6)如图6,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
中考数学一轮复习 四边形
参考答案与试题解析
一.解答题(共20小题)
1.【问题情境】如图1,小明把三角板EFG(∠GFE=30°)放置到矩形ABCD中,使得顶点E、F、G分别落在AD、CD、AB上,你发现线段ED与AG有什么数量关系?直接写出结论: DEAG (不用证明).
【变式探究】如图2,小明把三角板EFG(∠GFE=30°)放置到矩形ABCD中,使得顶点E、F、G分别在AD、BC、AB边上,若GA=4,AE=6,求BG的长.
【拓展应用】如图3,小明把三角形EFG放置到平行四边形ABCD中,使得顶点E、F、G分别在AD、BC、AB边上,若,,∠FEG=∠BAD,求出的值.
【考点】四边形综合题.
【专题】几何综合题;压轴题;矩形 菱形 正方形;图形的相似;推理能力.
【答案】【问题情境】DEAG;
【变式探究】BG=64;
【拓展应用】的值为.
【分析】【问题情境】由四边形ABCD是矩形,可得∠A=∠B=90°,推出△AEG∽△DFE,可得DEAG;
【变式探究】过点F作FH⊥AD于H,则∠EHF=90°,可得△AEG∽△HFE,得出,,进而求得:EH=4,FH=6,再由四边形ABFH是矩形,可得AB=FH=6,即可求得答案;
【拓展应用】延长AD至M,连接FM交CD于P,使∠AMF=∠BAD,可得△AEG∽△MFE,推出,再根据平行四边形性质和等腰三角形性质即可求得答案.
【解答】解:【问题情境】结论:EDAG,理由如下:
如图1,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴∠AGE+∠AEG=90°,
∵∠FEG=90°,∠GFE=30°,
∴∠DEF+∠AEG=90°,tan30°,
∴∠AGE=∠DEF,
∴△AEG∽△DFE,
∴,
∴DEAG,
故答案为:DEAG;
【变式探究】如图2,过点F作FH⊥AD于H,
则∠EHF=90°,
∴∠FEH+∠EFH=90°,
∵∠FEG=90°,
∴∠FEH+∠AEG=90°,
∴∠AEG=∠EFH,
∵∠A=∠EHF=90°,
∴△AEG∽△HFE,
∴,,
∴EH=4,FH=6,
∵∠A=∠B=∠AHF=90°,
∴四边形ABFH是矩形,
∴AB=FH=6,
∴BG=AB﹣AG=64;
【拓展应用】如图3,延长AD至M,连接FM交CD于P,使∠AMF=∠BAD,
∵∠FEG=∠BAD,
∴∠FEG=∠BAD=∠AMF,
∴∠AEG+∠AGE=∠FEM+∠AEG,
∴∠AGE=∠FEM,
∴△AEG∽△MFE,
∴,
∵,,
∴ABAD,AEAD,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD∥BC,∠BAD=∠C,
∴∠CDM=∠BAD=∠AMF=∠C=∠CFP,
∴PD=PM,PC=PF,
∴PC+PD=PF+PM,
即CD=FM=AB,
∴.
【点评】本题是三角形的综合题,熟练掌握三角形全等的判定及性质,轴对称求最短距离的方法是解题的关键.
2.综合与实践——平行四边形旋转中的数学问题
问题情境:
已知 ABCD与 A'B'C'D'中,AB=A'B'=6,BC=B'C'=8,∠ABC=∠A'B'C'=60°,同学们利用这样的两张平行四边形纸片开展操作实验,从中发现了许多有趣的数学问题,请你和他们一起进行探究.
拼图思考:
(1)希望小组的同学将 ABCD与 A'B'C'D'按图1的方式摆放,其中,点B与点B'重合,点A'落在BC边上,点C'落在BA边的延长线上,他们提出了如下问题,请你解答:
①连接BE,求证:BE平分∠ABA';
②点D,D′之间的距离为: 2 ;
操作探究:
(2)创新小组的同学在图1的基础上进行了如下操作:保持 ABCD不动,将 A'B'C'D'绕点B沿顺时针方向旋转,连接DD′.
①当线段C'D'与DC交于点P时,连接CC';如图2,求证:点P在DD'的垂直平分线上;
②在 A'B'C'D'旋转的过程中,当点C′恰好落在线段DC的延长线上时,请在图3中补全图形,并直接写出此时点D,D'之间的距离.
【考点】四边形综合题.
【专题】压轴题;推理能力.
【答案】(1)①证明见解析;②2;
(2)①证明见解析;②20.
【分析】(1)①借助△BAE与△BAE全等求证;②连接DD,判断△DDE′求解即可;
(2)①连接BD,BD,判断△BDD为等腰三角形,利用三线合一求证;②画出满足条件的图形,利用等边三角形求解.
【解答】(1)①证明:∵四边形ABCD、A'B'C'D'是平行四边形,
∴AD∥BC,A'D'∥B'C',
∴四边形A'EAB是平行四边形,∠AEB=∠EBC,
∴AE=B'A',
∵BA=B'A',
∴BA=AE,
∴四边形A'EAB是菱形,
∴BE平分∠ABA'.
②解:连接DD,如图,
由①知四边形ABAE是菱形,
∴AE=AE=CD=6,
∴AD﹣AE=AD﹣AE,
∴ED=ED'=8﹣6=2,
∵∠DED=∠ABA=60°,
∴△EDD为等边三角形,
∴DD'=ED=2.
故答案为:2.
(2)①证明:∵BC=BC',
∴∠BCC'=∠BC'C,
在 ABCD和 A'B'C'D'中,
∵∠ABC=∠AB'C=60°,AB=A'B',
∴∠BCD=∠B'C'D'=120°,CD=C'D',
∴∠PCC'=∠PC'C
∴PC=PC',
∴PD=PD',
∴点P在DD'的垂直平分线上.
②解:如图,
ABCD与 ABCD中,AB=AB=6,BC=B'C'=8,∠ABC=ABC'=60°,
∴CD=C'D'=6,BC=BC'=8,∠CBC'=180°﹣60°﹣60°=60°,
∴△BCC'是等边三角形,
∴CC'=8,
∴DD'=6+6+8=20.
【点评】本题主要考查平行四边形的性质,图形的旋转,全等三角形的判定与性质,等腰三角的性质定,等边三角形的判定与性质.关键是借助三角形全等和等腰三角形的三线合一进行解题.
3.【问题探究】
(1)如图1,在正方形ABCD中,对角线AC与BD相交于点O,在线段AO上任取一点P(端点除外),连接PD,PB.
①求证:PD=PB;
②将线段DP绕点P逆时针旋转,使点D落在BA的延长线上的点Q处,当点P在线段AO上的位置发生变化时,∠DPQ的大小是否发生变化?请说明理由;
③在探究AQ与OP的数量关系时,小颖作了如图2的辅助线:作PM⊥AB于点M,作PN⊥AD于点N,作PE⊥AO交AB于点E,作EF⊥OB于点F,请你直接写出AQ与OP的数量关系.
【迁移探究】
(2)如图3,将(1)中正方形ABCD换成菱形ABCD,且∠ABC=60°,其他条件不变,试探究AQ与CP的数量关系,并说明理由.
【考点】四边形综合题.
【专题】几何综合题;压轴题;推理能力.
【答案】(1)①证明见解答;②∠DPQ的大小不发生变化,∠DPQ=90°;③AQOP;
(2)AQ=CP.
【分析】(1)①根据正方形的性质可得CD=CB,∠DCA=∠BCA=45°,利用SAS证明△DCP≌△BCP即可证得结论;
②过点P作PM⊥AB于M,作PN⊥AD于N,可证得四边形AMPN是正方形,再利用HL证明Rt△DPN≌Rt△QPM,可得∠DPN=∠QPM,再利用角的关系即可证得结论;
③先得出△BEF是等腰直角三角形,BEEF,再证得四边形EFOP是矩形,得出EF=OP,即可求得答案;
(2)过点P作PM⊥AB于M,PE∥BC交AB于E,过点E作EG∥AC交BC于G,结合菱形的性质可得:四边形PEGC是平行四边形,再得出△ABC、△PAE和△BGE都是等边三角形,即可得出答案.
【解答】(1)①证明:∵四边形ABCD是正方形,
∴CD=CB,∠DCA=∠BCA=45°,
∵CP=CP,
∴△DCP≌△BCP(SAS),
∴PD=PB;
②解:∠DPQ的大小不发生变化,∠DPQ=90°;
理由如下:
过点P作PM⊥AB于M,作PN⊥AD于N,如图1,
∵四边形ABCD是正方形,
∴∠DAC=∠BAC=45°,
又∵PM⊥AB,PN⊥AD,
∴PM=PN,
∴四边形AMPN是正方形,
∴∠MPN=90°,
∵PD=PQ,PM=PN,
∴Rt△DPN≌Rt△QPM(HL),
∴∠DPN=∠QPM,
∵∠QPN+∠QPM=90°,
∴∠QPN+∠DPN=90°,
即∠DPQ=90°;
③解:AQOP,理由如下:如图2,
由①②知:PB=PD=PQ,AM=PM,
∵PM⊥AB,
∴BM=QM,
∵∠BAC=45°,
∴∠PEA=45°=∠PAE,
∵PM⊥AE,
∴AM=EM=PM,
∴BM﹣EM=QM﹣AM,
即BE=AQ,
∵∠BFE=90°,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴BEEF,
∵∠POF=∠OPE=∠OFE=90°,
∴四边形EFOP是矩形,
∴EF=OP,
∴AQOP;
(2)解:AQ=CP.理由如下:
∵四边形ABCD是菱形,
∴AC垂直平分BD,
∴PD=PB,
由旋转知:PD=PQ,
∴PQ=PB,
过点P作PM⊥AB于M,PE∥BC交AB于E,过点E作EG∥AC交BC于G,如图3,
则四边形PEGC是平行四边形,
∴PC=EG,
∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAC=60°,
∴△ABC是等边三角形,
同理可得:△PAE和△BGE都是等边三角形,
∴BE=EG=PC,
∵PM⊥AB,
∴MQ=MB,MA=ME,
∴MQ﹣MA=MB﹣ME,
即AQ=BE,
∴AQ=CP.
【点评】本题是正方形和菱形综合题,考查了正方形和菱形的性质,平行四边形的判定和性质,矩形的判定和性质,等边三角形的判定和性质,等腰直角三角形的判定和性质,全等三角形的判定和性质,添加辅助线构造全等三角形和直角三角形是解题关键.
4.在 ABCD中,点E是对角线AC上一点.
(1)如图1,∠DAC=90°,将△ADE沿DE翻折,使得A点的对应点F落在CD上,若AD=3,AC=4,求EF的长;
(2)如图2,∠ADC=45°,AD=AC,点G是DE的中点,AF⊥DE交CD于F点,I是AC上一点,连接FI,延长FI交DE的延长线于点J.若∠J=2∠DAG,AG=EJ,求证:AF+FI=2IJ;
(3)如图3,∠ADC=45°,AD=AC,延长DE至M点使AM=AD,∠DAM的角平分线交DE于点N,交MC延长线于点G,取CD中点F,连接GF,FM.当E在直线AC上运动时,直接写出的最大值.
【考点】四边形综合题.
【专题】压轴题;推理能力.
【答案】(1);
(2)证明过程详见解析;
(3).
【分析】(1)先由勾股定理求得CD=5,再由折叠性质得DF=AD=3,EF=AE,设EF=AE=x,在Rt△EFC中,利用勾股定理列方程求得x值即可;
(2)先根据等腰三角形的性质得到∠ADC=∠ACD=45°,∠DAC=90°,再根据直角三角形斜边中线性质得到,进而得到∠ADG=∠DAG,设∠ADG=∠DAG=α,利用三角形的外角性质结合已知得到∠AGE=∠J=2α,GE=EJ,证明△AEG≌△IEJ(ASA),AG∥FJ得到DE=2AG=2IJ,在DE截取DH=AF,连接AH,证明△ADH≌△CAF(SAS)得到AH=CF,∠DAH=∠ACF=45°,再证明△AHE≌△CFI(AAS)得到HE=FI,进而可得结论;
(3)连接AF,DG,根据等腰三角形的性质得到AG垂直平分DM,则DG=GM,∠DAC=90°,设∠CAM=2β,再根据等腰三角形的等边对等角进行角度运算得∠CMD=45°,进而推导出∠DGC=90°,设AD=AC=2a,则AM=2a,利用直角三角形斜边中线性质得到,利用三角形的三边关系得到,当点F、A、M共线时取等号,进而求得FM的最大值即可求解.
【解答】(1)解:∵AD=3,AC=4,∠DAC=90°,
∴,
由折叠性质得DF=AD=3,EF=AE,
设EF=AE=x,
在Rt△EFC中,CE=AC﹣AE=4﹣x,CF=CD﹣DF=2,
由勾股定理得x2+22=(4﹣x)2,
解得,
∴.
(2)证明:∵∠ADC=45°,AD=AC,
∴∠ADC=∠ACD=45°,则∠DAC=180°﹣45°﹣45°=90°,
∵点G是DE的中点,
∴,
∴∠ADG=∠DAG,设∠ADG=∠DAG=α,
∴∠AGE=∠ADG+∠DAG=2∠DAG=2α,
又∵∠J=2∠DAG,AG=EJ,
∴∠AGE=∠J=2α,GE=EJ,
又∵∠AEG=∠IEJ,
∴△AEG≌△IEJ(ASA),AG∥FJ,
∴AG=IJ,则DE=2AG=2IJ,
∵AF⊥DE,∠DAC=90°,
∴∠FAC+∠AED=∠ADE+∠AED=90°,
∴∠ADE=∠FAC=α,
在DE截取DH=AF,连接AH,
在△ADH和△CAF中,
,
∴△ADH≌△CAF(SAS),
∴AH=CF,∠DAH=∠ACF=45°,
∵∠HAE=∠DAC﹣∠DAH=90°﹣45°=45°,
∴∠HAE=∠FCI=45°,
∵AG∥FJ,∠GAE=90°﹣∠DAG=90°﹣α,
∴∠CIF=∠GAE=90°﹣α,
∵∠AEH=90°﹣∠ADG=90°﹣α,
∴∠AEH=∠CIF,
在△AHE和△CFI中,
,
∴△AHE≌△CFI(AAS),
∴HE=FI,
∵DH+HE=DE,
∴AF+FI=2IJ;
(3)如图,连接AF、DG,
∵AM=AD,∠DAM的角平分线交DE于点N,交MC延长线于点G,
∴AG⊥DM,DN=MN,
∴AG垂直平分DM,则DG=GM,
∵∠ADC=45°,AD=AC,
∴∠ADC=∠ACD=45°,则∠DAC=180°﹣45°﹣45°=90°,
设∠CAM=2β,
∵AM=AD=AC,
∴∠AMD(180°﹣∠DAM)=45°﹣β,,
∴∠CMD=∠AMC﹣∠AMD=(90°﹣β)﹣(45°﹣β)=45°,
又∵DG=GM,
∴∠GDM=∠GMD=45°,
则∠DGC=180°﹣2×45°=90°,
设AD=AC=2a,则AM=2a,
∵F为CD的中点,∠DAC=90°,∠DGC=90°,
∴,
∵E在直线AC上运动时,,
当点F、A、M共线时取等号,即点M在点M'处时,FM有最大值为(2)a,
的最大值为.
【点评】本题考查等腰三角形的判定与性质、折叠性质、直角三角形的性质、三角形的外角性质、全等三角形的判定与性质、平行线的判定与性质、线段垂直平分线的性质、最短路径问题等知识,综合性极强的压轴题,需要学生有一定的综合能力和分析问题、解决问题的能力,利用数形结合思想进行灵活运用所学相关知识进行解决问题.
5.如图1,∠ACB=90°,AC=BC,过点C的直线L不经过三角形的内部,过点A、B作AD⊥DE,BE⊥DE,垂足为D,E.
(1)请你在图1中,写出一对全等三角形: △ADC≌△CEB; ;
(2)请证明你所写的结论;
(3)尝试探究:若AD=a,BE=b
图1中四边形ADEB的面积为 ;
图2中过点C的直线L经过三角形内部,其他条件不变,则四边形ADBE面积为 (用含a,b的代数式表示);
(4)拓展应用:如图3,A(﹣1,0)C(0,2)则点B坐标为 (﹣2,3) ;若点P(不与B重合),在坐标平面内,△ABC与△ACP全等,则点P的坐标为 (﹣3,1)或(2,1)或(1,﹣1) .
【考点】四边形综合题.
【专题】压轴题;推理能力.
【答案】(1)△ADC≌△CEB;
(2)见解析;
(3),;
(4)(﹣2,3),(﹣3,1)或(2,1)或(1,﹣1).
【分析】(1)依据图形直接写出即可;
(2)这是“一线三垂直”全等模型,通过同角的余角相等进行转化即可得证;
(3)①利用梯形面积公式可解;②同(2)可证△ADC≌△CEB,四边形ADEB的面积为△ADE和△BDE面积之和;
(4)在坐标系内构造全等三角形即可求解,注意分情况讨论.
【解答】(1)解:△ADC≌△CEB;
(2)证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=∠ACD+∠DAC,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
(3)解:①由(2)知△ADC≌△CEB,
∴AD=CE=a,BE=DC=b,
∴四边形ADEB的面积为:;
②同(2)可证△ADC≌△CEB,
∴AD=CE=a,BE=DC=b,
∴DE=CE﹣CD=a﹣b,
∴四边形ADEB的面积为:;
故答案为:,;
(4)解:如图所示,作BD⊥y轴于点D.
∵A(﹣1,0),C(0,2),
∴OA=1,OC=2,
∵∠ACB=90°,BD⊥y轴,
∴∠ACO+∠BCD=90°,∠CBD+∠BCD=90°,
∴∠CBD=∠ACO,
在△AOC和△CEB中,
,
∴△CDB≌△AOC(AAS),
∴CD=OA=1,BD=OC=2,
∴OD=OC+CD=2+1=3,
∴B(﹣2,3);
若△ABC与△ACP全等,则点P可能在第一、二、四象限,如图所示:
当点P在第二象限时,作P1H⊥x轴于点H,
∵∠CAP1=∠ACB=90°,P1H⊥x轴,
∴∠CAO+∠P1AH=90°,∠AP1H+∠P1AH=90°,
∴∠ACO=∠P1AH,
在△P1AH和△ACO中,
,
∴△ACO≌△P1AH(AAS),
∴P1H=OA=1,AH=OC=2,
∴OH=OA+AH=1+2=3,
∴P1(﹣3,1),
同理可得P2(2,1),P3(1,﹣1),
综上可知,B点坐标为(﹣2,3),点P的坐标为(﹣3,1)或(2,1)或(1,﹣1),
故答案为:(﹣2,3),(﹣3,1)或(2,1)或(1,﹣1).
【点评】本题主要考查了全等三角形的判定和性质以及坐标与图形等内容,熟练掌握“一线三垂直”模型是解题关键.
6.[问题提出]
(1)如图①,BD为矩形ABCD的对角线,点E为BD的中点,连接AE,若BC=10,CD=6,则AE的长为 ;
[问题探究]
(2)如图②,AC为 ABCD的对角线,且AC⊥AB,点E、F分别为边AD、BC的中点,连接AF,CE,试判断四边形AECF的形状,并说明理由;
[问题解决]
(3)如图③,△BCG是王叔叔家的果园平面示意图,王叔叔欲对该果园进行扩建,扩建部分为 ABCD,其中点D在GC的延长线上,E、F分别为边AD、BC的中点,在四边形AECF内种植某种新品种果树,经测量,AC∥BG,BG⊥DG,CE=160米,∠AFC=120°,P、H为两个临时仓库,其中H为CE的中点,点P在AC上,现要沿PE、PH修建两条运输通道,问运输通道的总长度(PE+PH)是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.
【考点】四边形综合题.
【专题】压轴题;推理能力;模型思想.
【答案】(1);(2)证明见解析;(3)PE+PH的最小值为米.
【分析】(1)先求解,可得;
(2)证明AD∥|BC,AD=BC,结合AE=CF,可得四边形AECF是平行四边形,结合AC⊥AB,F为边BC的中点,可得AF=BF=CF,从而可得结论;
(3)如图,连接EF,连接FH交AC于P,证明四边形ABGC是矩形,可得∠BAC=90°,结合(2)可得:四边形AFCE为菱形;可得PE+PH=PF+PH=FH,此时PE+PH最小,证明△ECF为等边三角形,可得CF=EF=160,证明FH⊥CE,CH=EH=80,再进一步即可得解.
【解答】解:(1)∵四边形ABCD是矩形,BC=10,CD=6,
∴AD=BC=10,AB=CD=6,∠BAD=90°,
∴,
∵点E为BD的中点,
∴.
故答案为:.
(2)四边形AECF是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别为边AD、BC的中点,
∴AE=CF,
∴四边形AECF是平行四边形,
∵AC⊥AB,F为边BC的中点,
∴AF=BF=CF,
∴四边形AECF是菱形;
(3)如图,连接EF,连接FH交AC于P,
∵四边形ABCD是平行四边形,
∴AB∥DG,
∵AC∥BG,
∴四边形ABGC是平行四边形,
∵BG⊥DG,
∴∠BGC=90°,
∴四边形ABGC是矩形,
∴∠BAC=90°,
∵E、F分别为边AD、BC的中点,
结合(2)可得:四边形AFCE为菱形;
∴AF∥CE,AF=CF=CE=AE,AC⊥EF,AC,EF互相垂直平分,
∴PE+PH=PF+PH≥FH,
当F、P、H三点共线时,PE+PH最小,
∵∠AFC=120°,
∴∠ECF=60°,
∴△ECF为等边三角形,而CE=160,
∴CF=EF=160,
∵H为CE的中点,
∴FH⊥CE,CH=EH=80,
∴.
∴PE+PH的最小值为米.
【点评】本题考查的是勾股定理的应用,直角三角形斜边上的中线的性质,平行四边形的判定与性质,矩形的判定与性质,菱形的判定 与性质,等边三角形的判定与性质,掌握几何基础知识是解本题的关键.
7.在菱形ABCD中,∠B=α(0°<α≤90°),点O′在对角线AC上运动(点O′不与点A,点C重合),,以点O′为顶点作菱形A'B'C'O';且菱形A'B'C'O'与菱形ABCD的形状、大小完全相同,即A′B′=AB,∠B′=∠B,在菱形A'B'C'O'绕点O′旋转的过程中,O'A'与边BC交于点E,O′C′与边CD交于点F.
【特例感知】
(1)如图1,当α=90°,时,则CE,CF,BC之间满足的数量关系是 CF+CE=BC ;
【类比探究】
(2)如图2,菱形的边长为8,α=60°,求CE+CF的值(用含k的代数式表示);
【拓展应用】
(3)在(2)的条件下,连接O′B,O′B=7,,求CE的长度.
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;推理能力.
【答案】(1)CF+CE=BC;
(2)CE+CF=8k;
(3)CE的长度为或.
【分析】(1)连接O′B,当α=90°,时,四边形ABCD和A′B′C′O′均为正方形,且O′为AC的中点,可证得△BO′E≌△CO′F(ASA),得出BE=CF,即可求得答案;
(2)过点O′作O′G∥AB,交BC于G,可证得△ABC、△ACD、△O′CG均为等边三角形,得出O′G=CG=O′C=k AC=8k,再证得△O′EG≌△O′FC(ASA),即可得出答案;
(3)连接BD交AC于O,运用勾股定理求得OO′=1,分两种情况:当点O′在线段AO上时,当点O′在线段OC上时,分别求得CE即可.
【解答】解:(1)当α=90°,时,
四边形ABCD和A′B′C′O′均为正方形,且O′为AC的中点,
如图1,连接O′B,
则O′B=O′C,∠O′BE=∠O′CF=45°,∠BO′E+∠CO′E=∠CO′E+∠CO′F=90°,
∴∠BO′E=∠CO′F,
∴△BO′E≌△CO′F(ASA),
∴BE=CF,
∵BE+CE=BC,
∴CF+CE=BC,
故答案为:CF+CE=BC;
(2)如图2,过点O′作O′G∥AB,交BC于G,
∵四边形ABCD和四边形A′B′C′O′是形状、大小完全相同的菱形,且边长为8,α=60°,
∴AB=BC=CD=AD=A′B′=B′C′=C′O′=O′A′=8,∠B=∠D=∠B′=∠A′O′C′=60°,
∴△ABC、△ACD均为等边三角形,
∴∠BAC=∠ACB=∠ACD=60°,AC=AB=8,
∵O′G∥AB,
∴∠CO′G=∠BAC=60°=∠O′CG,
∴△O′CG是等边三角形,
∴O′G=CG=O′C=k AC=8k,
∵∠EO′G+∠CO′E=∠CO′E+∠CO′F′=60°,
∴∠EO′G=∠CO′F,
∴△O′EG≌△O′FC(ASA),
∴EG=CF,
∵CE+EG=CG,
∴CE+CF=8k;
(3)连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,即∠BOC=90°,
∴OCACBC=4,
∴OB4,
∴OO′1,
当点O′在线段AO上时,如图2,过点O′作O′H⊥BC于H,
则O′C=OO′+OC=1+4=5,
∴k,
由(2)知:CE+CF=8k,
∴CE+CF=85,
∵CF,
∴CE=5;
当点O′在线段OC上时,如图3,
则O′C=OC﹣OO′=4﹣1=3,
∴k,
∴CE+CF=83,
∴CE=3;
综上所述,CE的长度为或.
【点评】本题是四边形综合题,考查了正方形的性质,菱形的性质,等边三角形的判定和性质,直角三角形的性质,勾股定理,全等三角形的判定和性质,正确添加辅助线,运用分类讨论思想是解题关键.
8.【材料背景】
如图1,在△ABC中,以边AB为底边向外作等腰Rt△ABD,其中∠ADB=90°,且AD=DB,那么点D就被称为边AB的“外展等直点”.
【建构与探究】
如图2,正方形网格是由边长为“1”的正方形组成,点O、A、B、C都在格点上,∠OAB=90°,点C为OB的中点.
(1)连接OA、OB、AB,请分别作边OA、AB的“外展等直点”P和Q,连接PC、QC和PQ,则△PCQ的形状为 等腰直角三角形 ;
(2)如图3,点E、F在格点上,请在线段EF上的格点中任取一点D(不与点A重合),连接OD、BD,分别作△OBD的边OD和边BD的“外展等直点”G、H,连接GC、HC和GH,请判断△GHC的形状,并说明理由.
【应用与拓展】
(3)如图4,点M、N为平面内某三角形两条边的“外展等直点”,已知M(﹣2,﹣1),N(3,1),请直接写出该三角形第三条边的中点K的坐标.
【考点】四边形综合题.
【专题】作图题;压轴题;新定义;几何直观.
【答案】(1)作图见解析,等腰直角三角形;(2)具体见解析;(3)K1(,),K2(,).
【分析】(1)根据“外展等值点”的定义即可画出点P、Q,再根据图形可知△PCQ是等腰直角三角形;
(2)先在格点上选取点D,根据“外展等值点”的定义即可画出点G、H,再利用“一线三垂直”的全等即可得证;
(3)由第二问可知△MNK为等腰直角三角形,所以会有两个K点,再构造“一线三垂直”的全等求解即可.
【解答】解:(1)点P、Q即为所求,
由图可知PC=CQ=3,且∠PCQ=90°,
∴△PCQ是等腰直角三角形.
故答案为:等腰直角三角形.
(2)选取点D如图所示,G、H即为所求.
参考一:
△GHC形状为等腰直角三角形,理由如下:
如图,GI=CJ=CI=HJ=3,∠GIC=∠CHH=90°
∴△GIC≌△CJH(SAS),
∴GC=CH,且∠GCH=180°﹣45°﹣45°=90°,
∴△GHC为等腰直角三角形.
参考二:
如图,GI=CJ=3,CI=HJ=1,∠GIC=∠CJH=90°,
∴△GIC≌△CJH(SAS),
∴GC=HC,∠IGC=∠JCH,则∠GCH=90°,
∴△GHC为等腰直角三角形.
参考三:
如图,GI=CJ=1,CI=HJ=3,∠GIC=∠CHH=90°,
∴△GIC≌△CJH(SAS),
∴GC=HC,∠IGC=∠JCH,则∠GCH=90°,
∴△GHC为等腰直角三角形.
(3)由第二问可知△MNK为等腰直角三角形,如图则会在MN上方和下方各有一个K点,
过K1作EF∥x轴,作ME⊥EF于点E,NF⊥EF于点F,
∵∠MK1N=90°,
∴∠MK1E=∠FNK1=90°﹣∠FK1N,
∵∠E=∠F=90°,MK1=NK1,
∴△MEK1≌△K1FN(AAS),
∴ME=FK1,EK1=FN,
∵M(﹣2,﹣1),N(3,1),
∴EF=EK1+FK1=5,EM﹣FN=2,
即ME+FN=5,ME﹣FN=2,
∴ME,FN,
∴K1(,);
同理可得K2(,).
综上,三角形第三条边的中点K的坐标为K1(,),K2(,).
【点评】本题主要考查格点作图、等腰三角形的判定和性质、全等三角形的判定和性质等内容,熟练掌握相关知识点和理解题意是解题的关键.
9.综合与实践
问题情境:“综合与实践”课上,老师提出如下问题:如图1,在 ABCD中,∠ADC=90°,点O是边AD的中点,连接AC.保持 ABCD不动,将△ADC从图1的位置开始,绕点O顺时针旋转得到△EFG,点A,D,C的对应点分别为点E,F,G.当线段AB与线段FG相交于点M(点M不与点A,B,F,G重合)时,连接OM.老师要求各个小组结合所学的图形变换的知识展开数学探究.
初步思考:(1)如图2,连接FD,“勤学”小组在旋转的过程中发现FD∥OM,请你证明这一结论;
操作探究:(2)如图3,连接BG,“善思”小组在旋转的过程中发现OM垂直平分BG,请你证明这一结论;
拓展延伸:(3)已知,CD=2,在旋转的过程中,当以点F,C,D为顶点的三角形是等腰三角形时,请直接写出此时线段AM的长度.
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】(1)证明见解答;
(2)证明见解答;
(3)线段AM的长度为2或1或.
【分析】(1)连接CF,DF,由旋转得∠ADC=∠EFG,OD=OF,再证得Rt△OAM≌Rt△OFM(HL),得出∠AOM=∠FOM,进而得出∠AOM=∠ODF,利用平行线的判定即可证得结论;
(2)延长OM交BG于点N,由旋转得CD=GF,进而推出BM=GM,再证得∠BMN=∠GMN,利用等腰三角形的性质即可证得结论;
(3)分三种情况:当FC=FD时,当FC=CD时,当FD=CD时,分别求得AM即可.
【解答】(1)证明:如图1,连接CF,DF,
∵将△ADC绕点O顺时针旋转得到△EFG,
∴∠ADC=∠EFG,OD=OF,
∴∠ODF=∠OFD,
∵∠ADC=90°,
∴∠EFG=90°,
∵点O是边AD的中点,
∴OA=OD,
∴OA=OF.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAD+∠ADC=180°,
又∵∠ADC=90°,
∴∠BAD=180°﹣90°=90°,
∴∠BAD=∠EFG=90°,
∵在Rt△OAM和Rt△OFM中,
∴Rt△OAM≌Rt△OFM(HL),
∴∠AOM=∠FOM,
∵∠AOF是△OFD的一个外角,
∴∠AOF=∠AOM+∠FOM=∠ODF+∠OFD,
即2∠AOM=2∠ODF,
∴∠AOM=∠ODF,
∴FD∥OM;
(2)证明:如图2,延长OM交BG于点N,
由(1)知:Rt△OAM≌Rt△OFM,
∴AM=FM,∠AMO=∠FMO,
∵将△ADC绕点O顺时针旋转得到△EFG,
∴CD=GF,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AB=GF,
∴AB﹣AM=GF﹣MF,
即BM=GM,
∵∠AMO=∠FMO,∠AMO=∠BMN,∠FMO=∠GMN,
∴∠BMN=∠GMN,
∴OM垂直平分BG;
(3)解:∵以点F,C,D为顶点的三角形是等腰三角形,
∴FC=FD或FC=CD或FD=CD,
当FC=FD时,如图3,过点F作FH⊥CD于H,交AB于L,过点O作OK⊥FH于K,
则四边形AOKL、OKHD、ALHD均为矩形,
∴AL=OK=DH,LK=OA,
∵,CD=2,点O是边AD的中点,
∴LK=OA=OD,
∵FC=FD,FH⊥CD,
∴DHCD=1,
∴OK=AL=DH=1,
由旋转得OF=OD,
又∵∠OKF=90°,
∴FK1,
∴FK=OK,
∴∠OFK=∠FOK=45°,
∴∠MFL=90°﹣∠OFK=45°,
∴△FML是等腰直角三角形,
∴ML=FL=LK﹣FK1,
∴AM=AL﹣ML=1﹣(1)=2;
当FC=CD时,如图3,连接OC,
由旋转得OF=OD,
又∵OC=OC,
∴△OCF≌△OCD(SSS),
∴∠OFC=∠ODC=90°,
∵∠EFG=90°,
∴∠OFC+∠EFG=90°+90°=180°,
即C、F、G三点共线,
在Rt△OAM和Rt△OFM中,
,
∴Rt△OAM≌Rt△OFM(HL),
∴AM=FM,
设AM=x,
∵四边形ABCD是矩形,AD=2,CD=2,
∴AB=CD=2,BC=AD=2,
则BM=2﹣x,CM=CF+FM=2+x,
在Rt△BCM中,BM2+BC2=CM2,
∴(2﹣x)2+(2)2=(2+x)2,
解得:x=1,
∴AM=1;
当FD=CD时,如图5,过点O作OK⊥DF于K,
∵OF=OD,OK⊥DF,
∴DK=FKDF=1,
在Rt△ODK中,OK1,
∴OK=DK=FK,
∴△ODK和△OFK均为等腰直角三角形,
∴∠DOK=∠FOK=45°,
∴∠DOF=45°+45°=90°,
∴∠AOF=90°,
∴∠OAM=∠AOF=∠OFM=90°,
∴四边形AOFM是矩形,
∴AM=OF;
综上所述,线段AM的长度为2或1或.
【点评】本题是矩形综合题,主要考查了等腰三角形的判定和性质,等腰直角三角形的判定和性质,平行四边形的性质,矩形的判定和性质,全等三角形的判定和性质,旋转变换的性质等知识,熟练掌握旋转的性质,全等三角形的判定和性质是解题关键.
10.在数学探究课上,王宇同学通过作辅助图形的方法,计算动点条件下线段和的最小值,其过程如下:
(1)【观察发现】
如图1,在等边△ABC中,AC=2,CDBC,E,F分别是AB和AC上的动点,且总有BE=AF,阅读下面作辅助图形的方法及推理过程并填空,理解确定DE+DF最小值的方法.
∵在等边△ABC中,AC=2,CDBC,
∴点D为BC边上的中点,∠B=∠ACB.
∴AD⊥BC.
过点A作AG⊥AD,使AG=BD,连接GF.
∴AG∥BC.∴∠GAC=∠ACB=∠B.
又∵AF=BE,∴△AGF≌△BDE(SAS).
∴GF=DE.
连接DG,DF,当D,F,G三点共线时,GF+DF的最小值等于线段DG的长.
连接GC,可证四边形ADCG是矩形,
∴DG=AC.
∴DE+DF的最小值为 2 .
(2)【类比应用】
如图2,已知正方形ABCD的边长为6,O为对角线的交点,M,N分别是AB,AD上的动点,且总有BM=DN,连接OM,CN,求OM+CN的最小值.
(3)【拓展延伸】
如图3,矩形ABCD中,AB,AD=2,E是AD的中点,F,G分别是BC和DC上的动点,且总有BF=2DG,则EF+2AG的最小值为 2 .
【考点】四边形综合题.
【专题】压轴题;构造法;模型思想.
【答案】(1)2;(2);(3)2.
【分析】(1)根据题意可得四边形ADCG是矩形,从而得到DG=AC=2;
(2)类比第一问作辅助线,得出OM+CN=GN+CN,当G,N,C三点共线时,线段GC的长为GN+CN的最小值,进而求解即可;
(3)由BF=2DG和前述思路可以构造2AG,所有延长AB到H,使BH=2AD,连接FH,从而△ADG∽△HBF,得到FH=2AG,连接EH,当E、F、H三点共线时,线段EH的长为EF+2AG的最小值,利用勾股定理求EH即可.
【解答】解:(1)由作图可知,四边形ADCG是矩形,
∴DG=AC=2,
故答案为:2.
(2)如图,类比(1),过点D作 DG⊥BD,使DG=OB,连接GN,易得∠GDN=∠ADB=∠OBM.
在△GND和△OMB 中,
∵GD=OB,∠GDN=∠OBM,DN=BM,
∴△GND≌△OMB(SAS).
∴GN=OM.
∴OM+CN=GN+CN.
连接GC,当G,N,C三点共线时,线段GC的长为GN+CN的最小值.
过点G作GH⊥CD,交CD的延长线于点H.
在正方形ABCD中,BD为对角线,
∴∠ADB=45°
∵∠GDH+∠GDA=90°,∠ADB+∠GDA=90°
∴∠GDH=∠ADB=45°.
∴Rt△HGD为等腰直角三角形.
∵正方形ABCD的边长为6,
∴.
∴.
∴在 Rt△HGC 中,,
∴OM+CN的最小值为 .
(3)如图,延长AB到H,使BH=2AD,连接FH.
∵,∠ADG=∠HBF,
∴△ADG∽△HBF,
∴,
∴FH=2AG,
∴EF+2AG=EF+FH,
连接EH,当E、F、H三点共线时,线段EH的长为EF+2AG的最小值.
∵AEAD,AH=AB+BH=5,
∴EH2.
故答案为:2.
【点评】本题主要考查矩形的性质、正方形的性质、勾股定理、轴对称的性质、全等三角形的判定和性质相似三角形的判定和性质等知识,熟练掌握相关知识和添加合适的辅助线是解题关键.
11.综合与实践课上,老师和同学们开展了一场以“最小值”为主题的探究活动.
【提出问题】老师提出了一个问题:如图1,在矩形ABCD中,AB=3,BC=6,P为AD边上的一动点,以PC为边向右作等边△PCE,连接BE,求BE的最小值;
【探究发现】小明发现:如图4所示,以BC为边向下构造一个等边△BCM,便可得到△PCM≌△ECB,进而将 BE的最小值转化为PM的最小值.
(1)按照小明的想法,请求出BE的最小值;
【拓展应用】
(2)小刚受此启发,举一反三,提出新问题:如图2,若将图1当中构造的等边三角形,改为以PC为边向右构造正方形PCFG,则运动过程中,BG的最小值是 6 .
(3)小红同学深入研究了小刚的问题,并又提出了新的问题:如图3,若将图2当中构造的正方形改为以PC为边向右构造菱形PCHI,使.∠CPI=120°,也可求得BI的最小值请你直接写出BI最小值为 3+3 .
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;图形的相似;推理能力.
【答案】(1)BE的最小值为33;
(2)6;
(3)3+3.
【分析】(1)过点M作MK⊥AD于K,交BC于L,可证得△BCE≌△MCP(SAS),得出BE=MP,由M为定点,可得当MP⊥AD时,即点P与点K重合时,MP=MK最小,再利用解直角三角形求得MK即可;
(2)以BC为边向下作正方形BCKL,连接BK、CL交于点O,连接OP,CG,过点O作OP′⊥AD于P′,交BC于T,可推出∠BCG=∠OCP,,证得△BCG∽△OCP,得出,即BGOP,故当BG取得最小值时,OPBG最小,利用解直角三角形求得OT,进而可求得BG的最小值;
(3)连接CI、PH交于O,在BC下方作射线BM、射线CN,使∠CBM=∠BCN=30°,射线BM、射线CN交于点Q,过点Q作QP′⊥AD于P′,交BC于K,连接PQ,可证得△BCI∽△QCP,得出,即BIQP,故当QP取得最小值时,BIQP最小,由点Q为定点,可得当QP⊥AD,即点P与点P′重合时,QP=QP′=QK+KP′最小,运用解直角三角形即可求得答案.
【解答】解:(1)如图,过点M作MK⊥AD于K,交BC于L,
∵△PCE和△BCM都是等边三角形,
∴CE=CP,CB=CM,∠PCE=∠MCB=∠MBC=60°,
∴∠PCE+∠PCB=∠MCB+∠PCB,
即∠BCE=∠MCP,
在△BCE和△MCP中,
,
∴△BCE≌△MCP(SAS),
∴BE=MP,
∴当MP最小时,BE最小,
∵M为定点,
∴当MP⊥AD时,即点P与点K重合时,MP=MK最小,
∵四边形ABCD是矩形,
∴AD∥BC,BC=6,∠A=∠ABC=90°,
∴ML⊥BC,
∵∠AKL=∠A=∠ABC=90°,
∴四边形ABLK是矩形,
∴KL=AB=3,
在Rt△MCL中,ML=CM sin∠MCB=6sin60°=3,
∴MK=ML+KL=33,
∴BE的最小值为33;
(2)如图,以BC为边向下作正方形BCKL,连接BK、CL交于点O,连接OP,CG,过点O作OP′⊥AD于P′,交BC于T,
∵四边形CPGF、BCKL是正方形,
∴∠PCG=∠BCO=45°,CGCP,OC=OBBC=3,△BOC是等腰直角三角形,
∴∠PCG+∠PCB=∠BCO+∠PCB,
即∠BCG=∠OCP,
∵,
∴△BCG∽△OCP,
∴,
∴BGOP,
∴当BG取得最小值时,OPBG最小,
∵点O为定点,
∴当OP⊥AD时,即点P与点P′重合时,OP=OP′最小,
∵BC∥AD,
∴OP′⊥BC,即∠CTO=90°,
∴OT=OC sin∠BCO=3sin45°=3,
∵∠A=∠ABC=∠AP′O=90°,
∴四边形ABTP′是矩形,
∴TP′=AB=3,
∴OP′=OT+TP′=3+3=6,
∴OP的最小值为6,
∴BG的最小值为6,
故答案为:6;
(3)如图,连接CI、PH交于O,在BC下方作射线BM、射线CN,使∠CBM=∠BCN=30°,射线BM、射线CN交于点Q,
过点Q作QP′⊥AD于P′,交BC于K,连接PQ,
∵四边形PCHI是菱形,∠CPI=120°,
∴PH⊥CI,PC=PI,∠PCI=∠PIC=30°,CI=2CO,
在Rt△CPO中,CO=PC cos∠PCI=PC cos30°PC,
∴CI=2COPC,
∵∠CBQ=∠BCQ=30°,
∴QB=QC,
∵QP′⊥AD,AD∥BC,
∴QK⊥BC,
∴BK=CKBC=3,
∴QK=CK tan∠BCQ=3tan30°,CQ2,
∴,,
∴,
∵∠BCI=∠BCP+30°,∠QCP=∠BCP+30°,
∴∠BCI=∠QCP,
∴△BCI∽△QCP,
∴,
∴BIQP,
∴当QP取得最小值时,BIQP最小,
∵点Q为定点,
∴当QP⊥AD,即点P与点P′重合时,QP=QP′=QK+KP′最小,
由(2)知:KP′=AB=3,
∴QP′=QK+KP′3,
∴BI的最小值(3)=3+3,
故答案为:3+3.
【点评】本题是四边形综合题,考查了矩形的性质,正方形的性质,菱形的性质,等边三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形等,解题的关键是正确地作出解题所需要的辅助线,构造全等三角形和相似三角形,此题难度较大,属于中考压轴题.
12.综合实践
如图1,点E为正方形ABCD内一点,∠AEB=90°,点E′为正方形ABCD外一点,且BE'⊥CE',BE=BE',延长AE交CE'于点F,连接DE.
(1)试判断四边形BE'FE的形状,并说明理由;
(2)如图2,若DA=DE,请猜想线段CF与E′F的数量关系,并加以证明;
(3)如图1,若AB=15,BE=9,请求出DE的长.
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;矩形 菱形 正方形;推理能力.
【答案】(1)四边形BE'FE是正方形,证明见解答;
(2)CF=E′F,证明见解答;
(3)DE的长为3.
【分析】(1)利用HL证明Rt△ABE≌Rt△CBE′,再证得四边形BE'FE是矩形,即可得出答案;
(2)过点D作DG⊥AE于点G,则∠AGD=∠AEB=90°,进而证得△DAG≌△ABE(AAS),Rt△ABE≌Rt△CBE′(HL),再根据线段的和差关系即可得出答案;
(3)过点E作EG⊥AB于G,EH⊥AD于H,则四边形AGEH是矩形,运用勾股定理求得AE=12,再运用面积法得出EG,AG,再运用勾股定理即可.
【解答】解:(1)四边形BE'FE是正方形,理由如下:
如图1,
∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵BE'⊥CE',
∴∠BE′C=90°,
又∠AEB=90°,
在Rt△ABE和Rt△CBE′中,
,
∴Rt△ABE≌Rt△CBE′(HL),
∴∠ABE=∠CBE′,
∴∠CBE′+∠CBE=∠ABE+∠CBE,
即∠EBE′=∠ABC=90°,
∵∠BEF=180°﹣∠AEB=90°,
∴∠BEF=∠EBE′=∠BE′F=90°,
∴四边形BE'FE是矩形,
∵BE=BE',
∴四边形BE'FE是正方形;
(2)猜想:CF=E′F,
证明:如图2,过点D作DG⊥AE于点G,则∠AGD=∠AEB=90°,
∵DA=DE,
∴AG=EGAE,
∵四边形ABCD是正方形,∴AD=AB,∠BAD=90°,
∴∠DAG+∠BAE=90°,
∵∠ABE+∠BAE=90°,
∴∠DAG=∠ABE,
在△DAG和△ABE中,
,
∴△DAG≌△ABE(AAS),
∴AG=BE,
∴AE=2BE,
在Rt△ABE和Rt△CBE′中,
,
∴Rt△ABE≌Rt△CBE′(HL),
∴AE=CE′,∠ABE=∠CBE′,
∵∠ABE+∠CBE=90°,
∴∠CBE′+∠CBE=90°,即∠EBE′=90°,
∴∠BEF=∠EBE′=∠BE′C=90°,
又BE=BE',
∴四边形BEFE′上正方形,
∴E′F=BE,
∴CF+E′F=CE′=2E′F,
∴CF=E′F;
(3)如图3,过点E作EG⊥AB于G,EH⊥AD于H,
则四边形AGEH是矩形,
∴AH=EG,EH=AG,
在Rt△ABE中,AB=15,BE=9,
∴AE12,
∵EG⊥AB,
∴EG,
在Rt△AEG中,AG,
∴EH,AH,
∴DH=AD﹣AH=15,
∴DE3,
故DE的长为3.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形的性质,旋转的性质,勾股定理,证明△DAG≌△ABE≌△CBE′是关键.
13.在一次数学活动课上,老师带领同学们探究图形的变换问题.老师先提出这样一个问题:
有一张矩形纸片ABCD,其中AB=4,,你能用这张矩形纸片折出一个等边三角形吗?
【操作】小明同学是这样操作的:如图①,先将矩形ABCD沿MN对折;展开后,再将点C沿BE折叠,使点C落在MN上的点F处;再展开,连接BF,CF,则△BCF为等边三角形.
【验证】(1)求证:△BCF为等边三角形;
【应用】(2)连接AF,DF,如图②,求AF的长;
【拓展】(3)将图②中的△BCF绕着点F顺时针旋转α(0°<α<90°)得到△B′C′F(点B,C的对应点分别为B′,C′),连接AB′,DC′,当△AFB'为等腰三角形时,直接写出线段DC′的长.
【考点】四边形综合题.
【专题】压轴题;几何直观.
【答案】(1)证明过程详见解析;(2)2;(3)2或2.
【分析】(1)由折叠很容易得出BF=CF=BC,即可得证;
(2)根据勾股定理先求出FN长度,进而求出FM长度,再用勾股定理求出AF即可;
(3)由题可知AF≠FB',所以需要分两种情况讨论,即AF=AB',B'A=BF,分别画出图形,再进行计算即可.
【解答】(1)证明:∵矩形沿MN对折,
∴MN是BC的垂直平分线,
∴BF=CF,
∵折叠,
∴BC=BF,
∴BC=BF=CF,
∴△BCF是等边三角形.
(2)解:设MN交AD于M,交BC于N,
∵BC=2,
∴BF=2,BN,
∴FN3,
∵AB=4,
∴MN=4,
∴FM=MN﹣FN=1,
∵AM,
∴AF2.
(3)∵旋转,
∴FB'=FB=2,
∵AF=2,
∴等腰三角形AFB'中AF≠FB',
∴可分两种情况讨论,
①当AF=AB'时,如图所示,
由(2)知,AF=2,FB=2,AB=4,
∴AF2+BF2=AB2,
∴△AFB是直角三角形,即∠AFB=90°,
∵AF=AB',
∴AB垂直平分FB',
∴此时FB旋转60°到FB',
∴点C对应点C'落到点B的位置,
此时DC'2.
②当B'A=BF时,如图所示,
过B'作B'K⊥AF于K,DR⊥CF于R,
∴KFAF=1,
∴B′K,
∴DRB'K,
∵DF=AF=2,
∴FR,
∴C'R,
在Rt△DRC'中,DC'2.
综上,线段DC′的长为2或2.
【点评】本题主要考查折叠的性质、等边三角形的判定和性质、勾股定理、旋转的性质等内容,熟练掌握相关知识是解题的关键.
14.[回顾课本]苏教版八年级下册数学教材“9.5三角形的中位线”一课中给出了“三角形的中位线定理”的证明思路,请根据分析完成证明过程.
已知:如图1,DE是△ABC的中位线,求证:DE∥BC,.
分析:因为点E是AC的中点,可以考虑把△ADE绕点E按顺时针方向旋转180°,得到△CFE,这样就需要证明四边形BCFD是平行四边形……
[探究发现]
如图2,等边△ABC的边长为2,点D、E分别为AB、AC边中点,点F为BC边上任意一点(不与B、C重合),沿DE、DF剪开分成①、②、③三块后,将②、③分别绕点D顺时针、点E逆时针旋转180°恰好能与①拼成 DIHG,求 DIHG周长的最小值.
[拓展作图]
如图3,已知四边形ABCD,现要求只剪两次将其剪成四块,使得剪成的四块能通过适当的摆放拼成一个平行四边形,请在图3中画出两条剪痕,并对剪痕作适当的说明.
【考点】四边形综合题.
【专题】几何综合题;压轴题;等腰三角形与直角三角形;多边形与平行四边形;平移、旋转与对称;推理能力.
【答案】[回顾课本]证明见解答;
[探究发现] DIHG周长的最小值为4;[拓展作图]作图见解答.
【分析】【回顾课本】以点E为旋转中心,把△ADE绕点E,按顺时针方向旋转180°,得△CFE,则D,E,F同在一直线上,DE=EF,且△ADE≌△CFE,得出∠ADE=∠F,AD=CF,证明四边形BCFD是平行四边形,则可得出结论;【探究发现】当DF⊥BC时最小,此时DF,则可得出答案;【拓展作图】取AB,BC,CD,DA边的中点,沿EG,FH剪开分成①,②,③,④四块即可.
【解答】[回顾课本]
证明:∵△ADE绕点E按顺时针方向旋转180°,得到△CFE,
∴CF=AD,EF=DE,∠ECF=∠A,
∴CF∥AB,
∵D是AB的中点,
∴AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DF∥BC,DF=BC,
即DE∥BC,2DE=BC,
∴DE∥BC,DEBC;
[探究发现]
解:由题可知: DIHG周长=2DI+2DG=2BC+2DF=4+2DF,
当DF⊥BC时最小,此时DF,
∴ DIHG周长的最小值为4;
[拓展作图]
如图,取点E,F,G,H分别是AB,BC,CD,DA边的中点,沿EG,FH剪开分成①,②,③,④四块后,将①,③分别绕点F,E旋转180°至⑦,⑤,再将②平移至⑥,恰好能与④拼成平行四边形LJKN即可,
理由:∵E、F、G、H分别是AB、BC、CD、DA边的中点,
∴AE=BE,BF=CF,CG=DG,AH=DH,
由旋转得:∠J=∠FLG,∠N=∠ELH,
∴KJ∥NL、KN∥JL,
∴四边形JKNL是平行四边形.
【点评】本题是四边形综合题,主要考查了平行四边形的判定与性质,等边三角形的性质,三角形中位线定理,熟练掌握以上知识是解题的关键.
15.函数是刻画现实世界的有效模型,函数和现实情境之间的转换可以帮助我们简化问题的处理.
(1)下列情境中,可以用反比例函数刻画的是 AC ;
A.甲、乙两地相距200km,行驶时间和行驶速度之间的关系;
B.单价为3元的练习本,购买数量和总价的关系;
C.面积为8的矩形,长和宽的关系.
(2)求函数的最小值时,直接求解困难较大,我们可以给函数赋予这样的数学情境:如图1,线段BC=3,AB=1,CD=2,AB⊥BC,CD⊥BC,则AP+PD可表示为 ,(用含有x的代数式表示)请你结合图形,继续完成求解过程.
(3)如图2,四边形ABCD为矩形,AB=6,BC=9,P为矩形ABCD内(不包含边界)一点,过P分别向AB、BC作垂线,垂足为M,N,若四边形MBNP的面积为6,则称点P为“美丽点”,在矩形BEFG中,BE=9,BG=4,过F点的直线l交直线BC于点Q,若直线l上存在“美丽点”,求FQ的取值范围.
【考点】四边形综合题.
【专题】代数几何综合题;压轴题;反比例函数及其应用;矩形 菱形 正方形;运算能力;推理能力;应用意识.
【答案】(1)AC;
(2);最小值为;
(3)9≤FQ<9.
【分析】(1)分别求出各问题中的关系式,根据反比例函数的定义判断即可;
(2)利用勾股定理表示出AP+PD,得到当A、P、D三点共线时,AP+PD的值最小,即AP+PD=AD,利用勾股定理求出AD,即可得到最小值;
(3)以点B为原点,BC、BA分别为x轴,y轴建立平面直角坐标系,设反比例函数y的图象交AD于点T,交FG于点N,求出FQ最大值和最小值即可.
【解答】解:(1)A.∵时间×速度=路程,即tv=200,
∴行驶时间和行驶速度之间的关系为t,
故A属于反比例函数;
B.∵单价×数量(x)=总价(y),
∴y=3x,即购买数量和总价的关系是正比例函数,不属于反比例函数;
C.∵矩形的面积(S)=长(a)×宽(b),即8=ab,
∴a,即面积为8的矩形,长和宽的关系属于反比例函数;
故答案为:AC;
(2)设BP=x,则PC=3﹣x,如图1,
∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°,
∴AP+PD,
故答案为:;
由图形可知,当A、P、D三点共线时,AP+PD的值最小,即AP+PD=AD,
如图2,过点D作DE⊥AB,交AB的延长线于点E,则四边形BCDE上矩形,
∴BE=CD=2,DE=BC=3,
∴AE=AB+BE=1+2=3,
∴AD3,
∴AP+PD的最小值为3,
故函数的最小值为3;
(3)如图3,以点B为原点,BC、BA分别为x轴,y轴建立平面直角坐标系,
∵点P为“美丽点”,
∴S矩形BMPN=6,
∴点P在反比例函数y的图象上,
设反比例函数y的图象交AD于点T,交FG于点N,
当y=6时,x=1,
∴T(1,6),
设直线FT的解析式为y=kx+b,将F(4,9),T(1,6)代入得,
解得:,
∴直线FT的解析式为y=x+5,
当y=0时,x=﹣5,故Q(﹣5,0),
∴FQ9,此时,FQ最大;
当点Q与点G重合时,FQ=9,此时,FQ最小,
∴FQ的取值范围是9≤FQ<9.
【点评】本题是反比例函数综合题,考查了实际问题与反比例函数的关系,反比例函数的实际应用,勾股定理,矩形的判定和性质,最值的确定,正确理解实际问题与反比例函数的关系是解题关键.
16.【探索发现】
(1)如图1,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等,边A1O与边AB相交于点E,边C1O与边CB相交于点F,连接EF.在实验与探究中,小新发现无论正方形A1B1C1O绕点O怎样转动,AE,CF,EF之间一直存在某种数量关系,小新发现通过证明△AOE≌△BOF即可推导出来.
①请你猜想AE,CF,EF之间的数量关系是 AE2+CF2=EF2 .
②小新对图1的进一步研究中发现,延长EO与DC交于一点G,通过证明△AOE≌△COG也可推导出AE,CF,EF之间的数量关系,请你证明△AOE≌△COG.
【类比迁移】
(2)如图2,矩形ABCD的中心O是矩形A1B1C1O的一个顶点,A1O与边AB相交于点E,C1O与边CB相交于点F,连接EF,矩形A1B1C1O可绕着点O旋转,判断AE,CF,EF之间的数量关系并进行证明;
【拓展应用】
(3)如图3,在Rt△ACB中,∠C=90°,AC=5cm,BC=12cm,点D是边AB的中点,∠EDF=90°,它的两条边DE和DF分别与直线AC,BC相交于点E,F,∠EDF可绕着点D旋转,当AE=4cm时,请直接写出线段CF的长度.
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;矩形 菱形 正方形;推理能力.
【答案】(1)①AE2+CF2=EF2,证明见解答;②证明见解答;
(2)AE2+CF2=EF2,证明见解答;
(3)线段CF的长度为cm或cm.
【分析】(1)①先证明△AOE≌△BOF(ASA),可得AE=BF,推出BE=CF,再运用勾股定理即可证得结论;
②延长EO交DC于点G,由正方形性质可得OA=OC,∠OAE=∠OCG=45°,再利用ASA可证得△AOE≌△COG;
(2)延长EO交CD于点G,连接FG,可证得△AEO≌△CGO(AAS),得出AE=CG,OE=OG,再由线段垂直平分线的性质可得EF=FG,再运用勾股定理即可求得答案;
(3)设CF=x cm,分两种情况讨论:①当点E在线段AC上时,②当点E在CA延长线上时,结合勾股定理,即可求解.
【解答】(1)①解:猜想:AE2+CF2=EF2,理由如下:
如图1,
∵四边形ABCD和四边形A1B1C1O均为正方形,
∴OA=OB,AB=BC,∠OAE=∠OBF=45°,∠AOB=∠A1OC1=90°,
∴∠AOB﹣∠BOE=∠A1OC1﹣∠BOE,
即∠AOE=∠BOF,
∴△AOE≌△BOF(ASA),
∴AE=BF,
∴AB﹣AE=BC﹣BF,即BE=CF,
在Rt△BEF中,BF2+BE2=EF2,
∴AE2+CF2=EF2,
故答案为:AE2+CF2=EF2.
②证明:如图1′,延长EO交DC于点G,
∵四边形ABCD为正方形,
∴OA=OC,∠OAE=∠OCG=45°,
在△AOE和△COG中,
,
∴△AOE≌△COG(ASA).
(2)解:结论:AE2+CF2=EF2,
证明:如图2,延长EO交CD于点G,连接FG,
∵O是矩形ABCD的中心,
∴点O是AC的中点.
∴AO=CO,
∵四边形ABCD是矩形,
∴∠BCD=90°,AB∥CD,
∴∠BAO=∠DCO,∠AEO=∠CGO,
∴△AEO≌△CGO(AAS),
∴AE=CG,OE=OG,
∵四边形A1B1C1O是矩形,
∴∠A1OC1=90°,即OF⊥EG,
∴OF垂直平分EG,
∴EF=FG,
在Rt△FCG中,CG2+CF2=GF2,
∴AE2+CF2=EF2;
(3)解:设CF=x cm,①当E在线段AC上时,如图3,连接EF,
∵AE=4cm,AC=5cm,BC=12cm,
∴CE=1cm,在Rt△FCE中,∠C=90°,
∴CE2+CF2=EF2,
∴12+x2=EF2,
又由(2)易知EF2=AE2十 BF2,
∴EF2=42+BF2,
∴12+x2=42+(12﹣x)2,
解得:x,
∴此时线段CF的长度为cm;
②当点E在CA延长线上时,如图4,过点B作BG⊥BC,交ED的延长线于G,连接EF,GF,
同理可证EF2=AE2十 BF2,
∴EF2=42+(12﹣x)2,
在Rt△FCE中,EF2=x2+(5+4)2,
∴x2+(5+4)2=42+(12﹣x)2,
解得:x,
∴此时线段CF的长度为cm;
综上所述,线段CF的长度为cm或cm.
【点评】本题是四边形综合题,考查了正方形的性质,矩形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形根据勾股定理列方程解决问题.
17.综合与实践
问题情境:第二十四届国际数学家大会合徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图1,在综合实践课上,同学们绘制了“弦图”并进行探究,获得了以下结论:该图是由四个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH拼成的大正方形ABCD,且∠ABF>∠BAF.
特殊化探究:连接BH.设BF=a,AF=b.
“运河小组”从线段长度的特殊化提出问题:
(1)若AB=5,FG=1,求△ABF的面积.
“武林小组”从a与b关系的特殊化提出问题:
(2)若b=2a,求证:∠BAE=∠BHE.
深入探究:老师进一步提出问题:
(3)如图2,连接BE,延长FA到点I,使AI=AB,作矩形BFIJ.设矩形BFIJ的面积为S1,正方形ABCD的面积为S2,若BE平分∠ABF,求证:S1=S2.
请你解答这三个问题.
【考点】四边形综合题.
【专题】压轴题;几何直观.
【答案】(1)6;(2)证明过程见解析;(3)证明过程见解析.
【分析】(1)根据”弦图“关系,设参数,利用勾股定理建立方程求解即可;
(2)由b=2a可知E是AF中点,从而可证△HGB≌△BFA,得到∠GBH=∠BAF,再证∠BHE=∠GBH即可得证;
(3)用代数法思路证:设DH=CG=BF=AE=a,正方形HEFG的边长为b,AI=AB=AD=c,先将S1表示出来,再证△BEF≌△BEM(AAS)得到EN的表示,从而达到S1和S2的关系.
【解答】(1)解:设BF=a,则BG=a+1,
∵△ABF≌△BCG,
∴AF=BG=a+1,
∵AB=5,
∴在Rt△ABF中,BF2+AF2=AB2,
即a2+(a+1)2=25,
解得a=3(负值舍去),
∴BF=3,AF=4,
∴S△ABFBF AF=6.
(2)证明:∵b=2a,
∴AF=2BF=2AE,
∴AE=EF,
∵四边形EHGF是正方形,
∴HG=HE=EF=GF=BF,
∵AF=BG,∠AFB=∠HGE=90°,
∴△HGB≌△BFA(SAS),
∴∠GBH=∠BAF,
∵DE∥BG,
∴∠BHE=∠HBG,
∴∠BAE=∠BHE.
(3)证明:设DH=CG=BF=AE=a,正方形HEFG的边长为b,AI=AB=AD=c,
如图,过E分别作AB,AD的垂线,垂足分别为M、N,
S1=a(a+b+c)=a(a+b)+ac=AD EN+ac,
∵BE平分∠ABF,
∴∠FBE=∠MBE,
∵∠BME=∠BFE=90°,BE=BE,
∴△BEF≌△BEM(AAS),
∴BM=BF=a,
∴NE=AM=c﹣a,
∴S1=AD EN+ac=c(c﹣a)+ac=c2=S2.
∴S1=S2.
【点评】本题主要考查了正方形的性质、全等三角形的判定和性质、勾股定理等内容,熟练掌握相关知识是解题的关键.
18.数学活动课上,某小组将一个含45°的三角尺AEF和一个正方形纸板ABCD如图1摆放,若AE=1,AB=2.将三角尺AEF绕点A逆时针方向旋转α(0°≤α≤90°)角,观察图形的变化,完成探究活动.
【初步探究】
如图2,连接BE,DF并延长,延长线相交于点G,BG交AD于点M.
问题1 BE和DF的数量关系是 BE=DF ,位置关系是 BE⊥DF .
【深入探究】
应用问题1的结论解决下面的问题.
问题2 如图3,连接BD,点O是BD的中点,连接OA,OG.求证OA=OD=OG.
【尝试应用】
问题3 如图4,请直接写出当旋转角α从0°变化到60°时,点G经过路线的长度.
【考点】四边形综合题.
【专题】压轴题;几何直观.
【答案】(1)BE=DF,BE⊥DF;(2)证明过程详见解析;(3)π.
【分析】(1)先证△AEB≌△AFD,得到BE=DF,再根据△AMB和△DMG内角和推导,证∠G=90°即可;
(2)利用直角三角形斜边上的中线等于斜边的一半即可得证;
(3)由(2)知点OA=OD=OG,则点G的运动轨迹是以O为圆心,OA为半径的弧上,再根据α的变化求圆心角即可得解.
【解答】(1)解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵△AEF是含有45°的直角三角尺,
∴△AEF是等腰直角三角形,
∴AE=AF,∠EAF=90°,
∵∠BAD﹣∠DAE=∠EAF﹣∠DAE,
∴∠BAE=∠DAF,
∴△ABE≌△ADF(SAS),
∴BE=DF,∠ABE=∠ADF,
∵∠AMB=∠DMG,
∴∠G=∠BAM=90°,即BE⊥DF,
故答案为:BE=DF,BE⊥DF.
(2)∵△BAD是直角三角形,O是BD中点,
∴OABD=OD,
由(1)知∠G=90°,
∴△BGD是直角三角形,
∴OGBD=OD,
∴OA=OD=OG.
(3)由(2)知,OA=OD=OG,
∴点G的运动轨迹是以O为圆心,OA为半径的弧,
连接OA,OG,
∵旋转角α从0°变化到60°,
∴此时点G的运动路线就是,
取AB中点H,连接EH,
∵∠BAE=60°,AE=1,AB=2,
∴AE=AHAB=BH,
∴△AEH为等边三角形,
∴EH=AH=BH,∠AHE=∠AEH=60°
∴∠HBE=∠BEH,
∵∠AHE=∠HBE+∠BEH,
∴∠HBE=∠BEHAHE=30°,
即∠ABE=30°,
∴∠OBG=45°﹣30°=15°,
∵OB=OGBD,
∴∠DOG=30°,
∴∠AOG=180°﹣∠AOB﹣∠DOG=60°,
∵AB=2,
∴BDAB=2,
∴OA=OG,
∴的长度π.
即点G经过路线的长度为π.
【点评】本题主要考查了正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、直角三角形的性质、弧长公式等内容,熟练掌握相关知识是解题的关键.
19.【教材呈现】如图是华师版九年级上册数学教材第78页的部分内容.
例1:求证:三角形的一条中位线与第三边上的中线互相平分. 已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC. 求证:AE、DF互相平分. 证明:连接DE、EF.
请根据教材提示,结合图①,写出完整的解题过程.
【拓展】如图②,设图①中的AE与DF的交点为G,连接CD,分别交AE、EF于点H、K.
(1) .
(2)若四边形FGHK的面积为3,则四边形ADEF的面积为 18 .
【考点】四边形综合题.
【专题】代数几何综合题;压轴题;多边形与平行四边形;几何直观.
【答案】【教材呈现】见解答;
【拓展】(1);(2)18.
【分析】【教材呈现】证明DE∥AC,且DEAC=AF,即可求解;
【拓展】(1)证明△DHG∽△CHE,则,即DHHC,进而求解;
(2)S△DHE+S△DHG=S四边形GFKH+S△EHK,即2a+S△DHG=3+a,故S△DHG=3﹣a,而K是平行四边形DFCE的对角线的交点,故K是EF的中点,同理S△DHE+S△EHK=S四边形GFKH+S△DGH,则3a=6﹣a,解得a,即可求解.
【解答】【教材呈现】证明:连接DE、EF,
则DE是△ABC的中位线,故DE∥AC,且DEAC=AF,
故四边形DAFE为平行四边形,
∴AE、DF互相平分;
【拓展】(1)解:同理可得,四边形DFCE为平行四边形,则KD=KC,DF=EC=BE,
∵DGBE,FGEC,
∴DG=FGEC,
∵DF∥BC,
∴△DHG∽△CHE,
∴,即DHHC,
设DH=x,则HC=2x,CD=DH+HC=3x,则CKCDx,
故,
故答案为;
(2)解:设△HKE的面积为a,
∵DH=x,HKx,则△DHE的面积为2a,
∵G是DF的中点,
∴S△DHE+S△DHG=S四边形GFKH+S△EHK,
即2a+S△DHG=3+a,故S△DHG=3﹣a,
∵K是平行四边形DFCE的对角线的交点,故K是EF的中点,
同理S△DHE+S△EHK=S四边形GFKH+S△DGH,
即3a=6﹣a,解得a,
故S△EFG=a+3,
∵四边形ADEF为平行四边形,
故四边形ADEF的面积=4S△EFG=18,
故答案为18.
【点评】本题为四边形综合题,涉及到三角形中位线的性质、平行四边形的性质、三角形面积的计算等,综合性比较强,难度较大.
20.【模型定义】
它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.他们得知这种模型称为“手拉手模型”.如果把小等腰三角形的腰长看作是小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手.
【模型探究】
(1)如图1,若△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,易证△CDA≌△CEB,则∠AEB的度数为 60° ;
【模型应用】
(2)如图2,P为等边△ABC内一点,PA:PB:PC=3:4:5,且PA=3,以BP为边构造等边△BPQ,这样就有两个等边三角形共顶点B,然后连接CQ,∠APB的度数是 150° ;S四边形BPCQ= 46 ;
(3)如图3,点P是等腰直角△ACB中内一点,∠ACB=90°,且CP=1,,AP=2,以CP为直角边构造等腰直角△DCP,点C为直角顶点,则∠CPB的度数是 135° ;AC的长为 ;
【深化模型】
(4)如图4,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°;⑥CO平分∠BCD,恒成立的结论有 ①②③⑤ .
【拓展提高】
(5)如图5,在△ABC中,∠ACB=90°,∠BAC=30°,AB=6,若点P是△ABC内一点,则PA+PB+PC的最小值为 3 .
(6)如图6,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;等腰三角形与直角三角形;平移、旋转与对称;推理能力.
【答案】(1)60°.
(2)150°;46;
(3)135°;;
(4)①②③⑤.
(5)3;
(6).
【分析】(1)先证明△ACD≌△BCE(SAS),可得∠ADC=∠BEC,再利用等边三角形性质可得∠CDE=∠CED=60°,进而得出∠ADC=∠BEC=120°,即可求得答案.
(2)先证明△ABP≌△CBQ(SAS),可得AP=CQ,∠APB=∠CQB,由等边三角形性质可得:PQ=BQ=PB=4,∠PBQ=∠BQP=60°,再运用勾股定理逆定理可得∠PQC=90°,再利用S四边形BPCQ=S△BPQ+S△CPQ即可求得答案.
(3)连接AD,先证明△CAD≌△CBP(SAS),可得:AD=BP,∠CDA=∠CPB,再运用勾股定理逆定理可得∠ADP=90°,推出∠APC=90°,运用勾股定理即可求得答案.
(4)利用SAS证得△DCA≌△ECB,可得AD=BE,故结论①正确.利用ASA证得△ACP≌△BCQ,可得CP=CQ,故结论③正确.利用等边三角形的性质推出∠ACB=∠CPQ,再运用平行线的判定可得PQ∥AE,故结论②正确.没有条件证出BO=OE,故结论④错误.利用三角形外角性质可得∠AOB=∠ACB=60°,故结论⑤正确.由PC=QC,∠AOC=∠EOC,OC=OC,不能说明△POC与△QOC全等,∠BCO≠∠DCO,故结论⑥错误.
(5)将△BAP绕点B逆时针旋转60°得到△BA′P′,连接PP′,A′C,过点A′作A′K⊥BC,交CB的延长线于点K,可得PA+PB+PC=P′A′+PP′+PC≥A′C,再运用勾股定理即可得出答案.
(6)过点A作EA⊥AD,且AE=AD,连接CE,DE,运用勾股定理可得CE,利用SAS可证得△BAD≌△CAE,即可得出答案.
【解答】解:(1)如图1,
∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
即∠ACD+∠BCD=∠BCD+∠BCE,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
∴∠AEB=∠BEC﹣∠CED=60°.
故答案为:60°.
(2)如图2,
∵△ABC与△BPQ都是等边三角形,
∴AB=BC,BP=BQ=PQ,∠ABC=∠PBQ=∠BQP=60°,
∴∠ABC﹣∠PBC=∠PBQ﹣∠PBC,即∠ABP=∠CBQ,
在△ABP和△CBQ中,
,
∴△ABP≌△CBQ(SAS),
∴AP=CQ,∠APB=∠CQB,
∵PA:PB:PC=3:4:5,且PA=3,
∴PB=4,PC=5,CQ=3,
∵△BPQ是等边三角形,
∴PQ=BQ=PB=4,∠PBQ=∠BQP=60°,
在△CPQ中,CQ2+PQ2=32+42=25=PC2,
∴∠PQC=90°,
∴∠BQC=∠BQP+∠PQC=60°+90°=150°,
∴∠APB=150°;
S四边形BPCQ=S△BPQ+S△CPQ423×4=46;
故答案为:150°;46;
(3)如图3,连接AD,
∵△ACB、△DCP均为等腰直角三角形,
∴∠ACB=∠DCP=90°,CA=CB,CD=CP,
∴∠DCP﹣∠ACP=∠ACB﹣∠ACP,
即∠ACD=∠BCP,
在△CAD和△CBP中,
,
∴△CAD≌△CBP(SAS),
∴AD=BP,∠CDA=∠CPB,
在等腰直角三角形DCP中,CP=1,∠DCP=90°,
∴CD=1,DP,∠CDP=∠CPD=45°,
在△ADP中,AD2+DP2=()2+()2=4,AP2=22=4,
∴AD2+DP2=AP2,
∴∠ADP=90°,
∴∠CDA=∠CDP+∠ADP=45°+90°=135°,
∴∠CPB=135°;
∵AD=DP,∠ADP=90°,
∴∠APD=45°,
∴∠APC=∠APD+∠CPD=45°+45°=90°,
∴AC,
故答案为:135°;;
(4)∵△ABC和△CDE是等边三角形,
∴BC=AC,DE=DC=CE,∠BCA=∠DCE=60°,
∴∠BCA+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE.
在△DCA和△ECB中,
,
∴△DCA≌△ECB(SAS),
∴AD=BE,故结论①正确.
∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠ACB=∠ECD=60°,
∴∠BCD=60°,
∴∠ACP=∠BCQ=60°.
在△ACP与△BCQ中,
,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,故结论③正确.
∵∠PCQ=60°,
∴△PCQ是等边三角形,
∴∠CPQ=60°,
∴∠ACB=∠CPQ,
∴PQ∥AE,故结论②正确.
没有条件证出BO=OE,故结论④错误.
∵∠CAD=∠CBE,∠APC=∠OPB,
∴∠AOB=∠ACB=60°,故结论⑤正确.
∵PC=QC,∠AOC=∠EOC,OC=OC,
∴不能说明△POC与△QOC全等,
∴∠BCO≠∠DCO,故结论⑥错误.
综上所述,正确的结论有①②③⑤,
故答案为:①②③⑤.
(5)如图5,将△BAP绕点B逆时针旋转60°得到△BA′P′,连接PP′,A′C,
过点A′作A′K⊥BC,交CB的延长线于点K,
则∠A′BP′=∠ABP,BP′=BP,A′B=AB,P′A′=PA,
在△ABC中,∠ACB=90°,∠BAC=30°,AB=6,
∴∠ABC=60°,BCAB=3,
∵BP′=BP,∠P′BP=60°,
∴△BPP′是等边三角形,
∴PP′=BP,
∴PA+PB+PC=P′A′+PP′+PC≥A′C,
∵∠PBC+∠ABP=∠ABC=60°,
∴∠PBC+∠A′BP′=60°,
∴∠A′BC=∠PBC+∠A′BP′+∠P′BP=120°,
∴∠A′BK=180°﹣∠A′BC=60°,
∵∠A′KB=90°,
∴∠BA′K=30°,
∴BKA′B=3,
在Rt△A′BK中,A′K3,
∴CK=BC+BK=3+3=6,
在Rt△A′CK中,A′C3,
∴PA+PB+PC的最小值为3,
故答案为:3;
(6)过点A作EA⊥AD,且AE=AD,连接CE,DE,如图6所示:
则△ADE是等腰直角三角形,∠EAD=90°,
∴DEAD=4,∠EDA=45°,
∵∠ADC=45°,
∴∠EDC=45°+45°=90°,
在Rt△DCE中,CE,
∵∠ACB=∠ABC=45°,
∴∠BAC=90°,AB=AC,
∵∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
故答案为:.
【点评】此题是三角形综合题,主要考查了等腰三角形的性质,直角三角形的性质,等腰直角三角形的性质,等边三角形的性质,三角形的内角和定理,三角形外角的性质,全等三角形的判定和性质,勾股定理,旋转变换的性质等,熟练掌握全等三角形的判定和性质是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学一轮复习 四边形
一.解答题(共20小题)
1.【问题情境】如图1,小明把三角板EFG(∠GFE=30°)放置到矩形ABCD中,使得顶点E、F、G分别落在AD、CD、AB上,你发现线段ED与AG有什么数量关系?直接写出结论: (不用证明).
【变式探究】如图2,小明把三角板EFG(∠GFE=30°)放置到矩形ABCD中,使得顶点E、F、G分别在AD、BC、AB边上,若GA=4,AE=6,求BG的长.
【拓展应用】如图3,小明把三角形EFG放置到平行四边形ABCD中,使得顶点E、F、G分别在AD、BC、AB边上,若,,∠FEG=∠BAD,求出的值.
2.综合与实践——平行四边形旋转中的数学问题
问题情境:
已知 ABCD与 A'B'C'D'中,AB=A'B'=6,BC=B'C'=8,∠ABC=∠A'B'C'=60°,同学们利用这样的两张平行四边形纸片开展操作实验,从中发现了许多有趣的数学问题,请你和他们一起进行探究.
拼图思考:
(1)希望小组的同学将 ABCD与 A'B'C'D'按图1的方式摆放,其中,点B与点B'重合,点A'落在BC边上,点C'落在BA边的延长线上,他们提出了如下问题,请你解答:
①连接BE,求证:BE平分∠ABA';
②点D,D′之间的距离为: ;
操作探究:
(2)创新小组的同学在图1的基础上进行了如下操作:保持 ABCD不动,将 A'B'C'D'绕点B沿顺时针方向旋转,连接DD′.
①当线段C'D'与DC交于点P时,连接CC';如图2,求证:点P在DD'的垂直平分线上;
②在 A'B'C'D'旋转的过程中,当点C′恰好落在线段DC的延长线上时,请在图3中补全图形,并直接写出此时点D,D'之间的距离.
3.【问题探究】
(1)如图1,在正方形ABCD中,对角线AC与BD相交于点O,在线段AO上任取一点P(端点除外),连接PD,PB.
①求证:PD=PB;
②将线段DP绕点P逆时针旋转,使点D落在BA的延长线上的点Q处,当点P在线段AO上的位置发生变化时,∠DPQ的大小是否发生变化?请说明理由;
③在探究AQ与OP的数量关系时,小颖作了如图2的辅助线:作PM⊥AB于点M,作PN⊥AD于点N,作PE⊥AO交AB于点E,作EF⊥OB于点F,请你直接写出AQ与OP的数量关系.
【迁移探究】
(2)如图3,将(1)中正方形ABCD换成菱形ABCD,且∠ABC=60°,其他条件不变,试探究AQ与CP的数量关系,并说明理由.
4.在 ABCD中,点E是对角线AC上一点.
(1)如图1,∠DAC=90°,将△ADE沿DE翻折,使得A点的对应点F落在CD上,若AD=3,AC=4,求EF的长;
(2)如图2,∠ADC=45°,AD=AC,点G是DE的中点,AF⊥DE交CD于F点,I是AC上一点,连接FI,延长FI交DE的延长线于点J.若∠J=2∠DAG,AG=EJ,求证:AF+FI=2IJ;
(3)如图3,∠ADC=45°,AD=AC,延长DE至M点使AM=AD,∠DAM的角平分线交DE于点N,交MC延长线于点G,取CD中点F,连接GF,FM.当E在直线AC上运动时,直接写出的最大值.
5.如图1,∠ACB=90°,AC=BC,过点C的直线L不经过三角形的内部,过点A、B作AD⊥DE,BE⊥DE,垂足为D,E.
(1)请你在图1中,写出一对全等三角形: ;
(2)请证明你所写的结论;
(3)尝试探究:若AD=a,BE=b
图1中四边形ADEB的面积为 ;
图2中过点C的直线L经过三角形内部,其他条件不变,则四边形ADBE面积为 (用含a,b的代数式表示);
(4)拓展应用:如图3,A(﹣1,0)C(0,2)则点B坐标为 ;若点P(不与B重合),在坐标平面内,△ABC与△ACP全等,则点P的坐标为 .
6.[问题提出]
(1)如图①,BD为矩形ABCD的对角线,点E为BD的中点,连接AE,若BC=10,CD=6,则AE的长为 ;
[问题探究]
(2)如图②,AC为 ABCD的对角线,且AC⊥AB,点E、F分别为边AD、BC的中点,连接AF,CE,试判断四边形AECF的形状,并说明理由;
[问题解决]
(3)如图③,△BCG是王叔叔家的果园平面示意图,王叔叔欲对该果园进行扩建,扩建部分为 ABCD,其中点D在GC的延长线上,E、F分别为边AD、BC的中点,在四边形AECF内种植某种新品种果树,经测量,AC∥BG,BG⊥DG,CE=160米,∠AFC=120°,P、H为两个临时仓库,其中H为CE的中点,点P在AC上,现要沿PE、PH修建两条运输通道,问运输通道的总长度(PE+PH)是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.
7.在菱形ABCD中,∠B=α(0°<α≤90°),点O′在对角线AC上运动(点O′不与点A,点C重合),,以点O′为顶点作菱形A'B'C'O';且菱形A'B'C'O'与菱形ABCD的形状、大小完全相同,即A′B′=AB,∠B′=∠B,在菱形A'B'C'O'绕点O′旋转的过程中,O'A'与边BC交于点E,O′C′与边CD交于点F.
【特例感知】
(1)如图1,当α=90°,时,则CE,CF,BC之间满足的数量关系是 ;
【类比探究】
(2)如图2,菱形的边长为8,α=60°,求CE+CF的值(用含k的代数式表示);
【拓展应用】
(3)在(2)的条件下,连接O′B,O′B=7,,求CE的长度.
8.【材料背景】
如图1,在△ABC中,以边AB为底边向外作等腰Rt△ABD,其中∠ADB=90°,且AD=DB,那么点D就被称为边AB的“外展等直点”.
【建构与探究】
如图2,正方形网格是由边长为“1”的正方形组成,点O、A、B、C都在格点上,∠OAB=90°,点C为OB的中点.
(1)连接OA、OB、AB,请分别作边OA、AB的“外展等直点”P和Q,连接PC、QC和PQ,则△PCQ的形状为 ;
(2)如图3,点E、F在格点上,请在线段EF上的格点中任取一点D(不与点A重合),连接OD、BD,分别作△OBD的边OD和边BD的“外展等直点”G、H,连接GC、HC和GH,请判断△GHC的形状,并说明理由.
【应用与拓展】
(3)如图4,点M、N为平面内某三角形两条边的“外展等直点”,已知M(﹣2,﹣1),N(3,1),请直接写出该三角形第三条边的中点K的坐标.
9.综合与实践
问题情境:“综合与实践”课上,老师提出如下问题:如图1,在 ABCD中,∠ADC=90°,点O是边AD的中点,连接AC.保持 ABCD不动,将△ADC从图1的位置开始,绕点O顺时针旋转得到△EFG,点A,D,C的对应点分别为点E,F,G.当线段AB与线段FG相交于点M(点M不与点A,B,F,G重合)时,连接OM.老师要求各个小组结合所学的图形变换的知识展开数学探究.
初步思考:(1)如图2,连接FD,“勤学”小组在旋转的过程中发现FD∥OM,请你证明这一结论;
操作探究:(2)如图3,连接BG,“善思”小组在旋转的过程中发现OM垂直平分BG,请你证明这一结论;
拓展延伸:(3)已知,CD=2,在旋转的过程中,当以点F,C,D为顶点的三角形是等腰三角形时,请直接写出此时线段AM的长度.
10.在数学探究课上,王宇同学通过作辅助图形的方法,计算动点条件下线段和的最小值,其过程如下:
(1)【观察发现】
如图1,在等边△ABC中,AC=2,CDBC,E,F分别是AB和AC上的动点,且总有BE=AF,阅读下面作辅助图形的方法及推理过程并填空,理解确定DE+DF最小值的方法.
∵在等边△ABC中,AC=2,CDBC,
∴点D为BC边上的中点,∠B=∠ACB.
∴AD⊥BC.
过点A作AG⊥AD,使AG=BD,连接GF.
∴AG∥BC.∴∠GAC=∠ACB=∠B.
又∵AF=BE,∴△AGF≌△BDE(SAS).
∴GF=DE.
连接DG,DF,当D,F,G三点共线时,GF+DF的最小值等于线段DG的长.
连接GC,可证四边形ADCG是矩形,
∴DG=AC.
∴DE+DF的最小值为 .
(2)【类比应用】
如图2,已知正方形ABCD的边长为6,O为对角线的交点,M,N分别是AB,AD上的动点,且总有BM=DN,连接OM,CN,求OM+CN的最小值.
(3)【拓展延伸】
如图3,矩形ABCD中,AB,AD=2,E是AD的中点,F,G分别是BC和DC上的动点,且总有BF=2DG,则EF+2AG的最小值为 .
11.综合与实践课上,老师和同学们开展了一场以“最小值”为主题的探究活动.
【提出问题】老师提出了一个问题:如图1,在矩形ABCD中,AB=3,BC=6,P为AD边上的一动点,以PC为边向右作等边△PCE,连接BE,求BE的最小值;
【探究发现】小明发现:如图4所示,以BC为边向下构造一个等边△BCM,便可得到△PCM≌△ECB,进而将 BE的最小值转化为PM的最小值.
(1)按照小明的想法,请求出BE的最小值;
【拓展应用】
(2)小刚受此启发,举一反三,提出新问题:如图2,若将图1当中构造的等边三角形,改为以PC为边向右构造正方形PCFG,则运动过程中,BG的最小值是 .
(3)小红同学深入研究了小刚的问题,并又提出了新的问题:如图3,若将图2当中构造的正方形改为以PC为边向右构造菱形PCHI,使.∠CPI=120°,也可求得BI的最小值请你直接写出BI最小值为 .
12.综合实践
如图1,点E为正方形ABCD内一点,∠AEB=90°,点E′为正方形ABCD外一点,且BE'⊥CE',BE=BE',延长AE交CE'于点F,连接DE.
(1)试判断四边形BE'FE的形状,并说明理由;
(2)如图2,若DA=DE,请猜想线段CF与E′F的数量关系,并加以证明;
(3)如图1,若AB=15,BE=9,请求出DE的长.
13.在一次数学活动课上,老师带领同学们探究图形的变换问题.老师先提出这样一个问题:
有一张矩形纸片ABCD,其中AB=4,,你能用这张矩形纸片折出一个等边三角形吗?
【操作】小明同学是这样操作的:如图①,先将矩形ABCD沿MN对折;展开后,再将点C沿BE折叠,使点C落在MN上的点F处;再展开,连接BF,CF,则△BCF为等边三角形.
【验证】(1)求证:△BCF为等边三角形;
【应用】(2)连接AF,DF,如图②,求AF的长;
【拓展】(3)将图②中的△BCF绕着点F顺时针旋转α(0°<α<90°)得到△B′C′F(点B,C的对应点分别为B′,C′),连接AB′,DC′,当△AFB'为等腰三角形时,直接写出线段DC′的长.
14.[回顾课本]苏教版八年级下册数学教材“9.5三角形的中位线”一课中给出了“三角形的中位线定理”的证明思路,请根据分析完成证明过程.
已知:如图1,DE是△ABC的中位线,求证:DE∥BC,.
分析:因为点E是AC的中点,可以考虑把△ADE绕点E按顺时针方向旋转180°,得到△CFE,这样就需要证明四边形BCFD是平行四边形……
[探究发现]
如图2,等边△ABC的边长为2,点D、E分别为AB、AC边中点,点F为BC边上任意一点(不与B、C重合),沿DE、DF剪开分成①、②、③三块后,将②、③分别绕点D顺时针、点E逆时针旋转180°恰好能与①拼成 DIHG,求 DIHG周长的最小值.
[拓展作图]
如图3,已知四边形ABCD,现要求只剪两次将其剪成四块,使得剪成的四块能通过适当的摆放拼成一个平行四边形,请在图3中画出两条剪痕,并对剪痕作适当的说明.
15.函数是刻画现实世界的有效模型,函数和现实情境之间的转换可以帮助我们简化问题的处理.
(1)下列情境中,可以用反比例函数刻画的是 ;
A.甲、乙两地相距200km,行驶时间和行驶速度之间的关系;
B.单价为3元的练习本,购买数量和总价的关系;
C.面积为8的矩形,长和宽的关系.
(2)求函数的最小值时,直接求解困难较大,我们可以给函数赋予这样的数学情境:如图1,线段BC=3,AB=1,CD=2,AB⊥BC,CD⊥BC,则AP+PD可表示为 ,(用含有x的代数式表示)请你结合图形,继续完成求解过程.
(3)如图2,四边形ABCD为矩形,AB=6,BC=9,P为矩形ABCD内(不包含边界)一点,过P分别向AB、BC作垂线,垂足为M,N,若四边形MBNP的面积为6,则称点P为“美丽点”,在矩形BEFG中,BE=9,BG=4,过F点的直线l交直线BC于点Q,若直线l上存在“美丽点”,求FQ的取值范围.
16.【探索发现】
(1)如图1,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等,边A1O与边AB相交于点E,边C1O与边CB相交于点F,连接EF.在实验与探究中,小新发现无论正方形A1B1C1O绕点O怎样转动,AE,CF,EF之间一直存在某种数量关系,小新发现通过证明△AOE≌△BOF即可推导出来.
①请你猜想AE,CF,EF之间的数量关系是 .
②小新对图1的进一步研究中发现,延长EO与DC交于一点G,通过证明△AOE≌△COG也可推导出AE,CF,EF之间的数量关系,请你证明△AOE≌△COG.
【类比迁移】
(2)如图2,矩形ABCD的中心O是矩形A1B1C1O的一个顶点,A1O与边AB相交于点E,C1O与边CB相交于点F,连接EF,矩形A1B1C1O可绕着点O旋转,判断AE,CF,EF之间的数量关系并进行证明;
【拓展应用】
(3)如图3,在Rt△ACB中,∠C=90°,AC=5cm,BC=12cm,点D是边AB的中点,∠EDF=90°,它的两条边DE和DF分别与直线AC,BC相交于点E,F,∠EDF可绕着点D旋转,当AE=4cm时,请直接写出线段CF的长度.
17.综合与实践
问题情境:第二十四届国际数学家大会合徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图1,在综合实践课上,同学们绘制了“弦图”并进行探究,获得了以下结论:该图是由四个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH拼成的大正方形ABCD,且∠ABF>∠BAF.
特殊化探究:连接BH.设BF=a,AF=b.
“运河小组”从线段长度的特殊化提出问题:
(1)若AB=5,FG=1,求△ABF的面积.
“武林小组”从a与b关系的特殊化提出问题:
(2)若b=2a,求证:∠BAE=∠BHE.
深入探究:老师进一步提出问题:
(3)如图2,连接BE,延长FA到点I,使AI=AB,作矩形BFIJ.设矩形BFIJ的面积为S1,正方形ABCD的面积为S2,若BE平分∠ABF,求证:S1=S2.
请你解答这三个问题.
18.数学活动课上,某小组将一个含45°的三角尺AEF和一个正方形纸板ABCD如图1摆放,若AE=1,AB=2.将三角尺AEF绕点A逆时针方向旋转α(0°≤α≤90°)角,观察图形的变化,完成探究活动.
【初步探究】
如图2,连接BE,DF并延长,延长线相交于点G,BG交AD于点M.
问题1 BE和DF的数量关系是 ,位置关系是 .
【深入探究】
应用问题1的结论解决下面的问题.
问题2 如图3,连接BD,点O是BD的中点,连接OA,OG.求证OA=OD=OG.
【尝试应用】
问题3 如图4,请直接写出当旋转角α从0°变化到60°时,点G经过路线的长度.
19.【教材呈现】如图是华师版九年级上册数学教材第78页的部分内容.
例1:求证:三角形的一条中位线与第三边上的中线互相平分. 已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC. 求证:AE、DF互相平分. 证明:连接DE、EF.
请根据教材提示,结合图①,写出完整的解题过程.
【拓展】如图②,设图①中的AE与DF的交点为G,连接CD,分别交AE、EF于点H、K.
(1) .
(2)若四边形FGHK的面积为3,则四边形ADEF的面积为 .
20.【模型定义】
它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.他们得知这种模型称为“手拉手模型”.如果把小等腰三角形的腰长看作是小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手.
【模型探究】
(1)如图1,若△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,易证△CDA≌△CEB,则∠AEB的度数为 ;
【模型应用】
(2)如图2,P为等边△ABC内一点,PA:PB:PC=3:4:5,且PA=3,以BP为边构造等边△BPQ,这样就有两个等边三角形共顶点B,然后连接CQ,∠APB的度数是 ;S四边形BPCQ= ;
(3)如图3,点P是等腰直角△ACB中内一点,∠ACB=90°,且CP=1,,AP=2,以CP为直角边构造等腰直角△DCP,点C为直角顶点,则∠CPB的度数是 ;AC的长为 ;
【深化模型】
(4)如图4,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°;⑥CO平分∠BCD,恒成立的结论有 .
【拓展提高】
(5)如图5,在△ABC中,∠ACB=90°,∠BAC=30°,AB=6,若点P是△ABC内一点,则PA+PB+PC的最小值为 .
(6)如图6,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
中考数学一轮复习 四边形
参考答案与试题解析
一.解答题(共20小题)
1.【问题情境】如图1,小明把三角板EFG(∠GFE=30°)放置到矩形ABCD中,使得顶点E、F、G分别落在AD、CD、AB上,你发现线段ED与AG有什么数量关系?直接写出结论: DEAG (不用证明).
【变式探究】如图2,小明把三角板EFG(∠GFE=30°)放置到矩形ABCD中,使得顶点E、F、G分别在AD、BC、AB边上,若GA=4,AE=6,求BG的长.
【拓展应用】如图3,小明把三角形EFG放置到平行四边形ABCD中,使得顶点E、F、G分别在AD、BC、AB边上,若,,∠FEG=∠BAD,求出的值.
【考点】四边形综合题.
【专题】几何综合题;压轴题;矩形 菱形 正方形;图形的相似;推理能力.
【答案】【问题情境】DEAG;
【变式探究】BG=64;
【拓展应用】的值为.
【分析】【问题情境】由四边形ABCD是矩形,可得∠A=∠B=90°,推出△AEG∽△DFE,可得DEAG;
【变式探究】过点F作FH⊥AD于H,则∠EHF=90°,可得△AEG∽△HFE,得出,,进而求得:EH=4,FH=6,再由四边形ABFH是矩形,可得AB=FH=6,即可求得答案;
【拓展应用】延长AD至M,连接FM交CD于P,使∠AMF=∠BAD,可得△AEG∽△MFE,推出,再根据平行四边形性质和等腰三角形性质即可求得答案.
【解答】解:【问题情境】结论:EDAG,理由如下:
如图1,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,
∴∠AGE+∠AEG=90°,
∵∠FEG=90°,∠GFE=30°,
∴∠DEF+∠AEG=90°,tan30°,
∴∠AGE=∠DEF,
∴△AEG∽△DFE,
∴,
∴DEAG,
故答案为:DEAG;
【变式探究】如图2,过点F作FH⊥AD于H,
则∠EHF=90°,
∴∠FEH+∠EFH=90°,
∵∠FEG=90°,
∴∠FEH+∠AEG=90°,
∴∠AEG=∠EFH,
∵∠A=∠EHF=90°,
∴△AEG∽△HFE,
∴,,
∴EH=4,FH=6,
∵∠A=∠B=∠AHF=90°,
∴四边形ABFH是矩形,
∴AB=FH=6,
∴BG=AB﹣AG=64;
【拓展应用】如图3,延长AD至M,连接FM交CD于P,使∠AMF=∠BAD,
∵∠FEG=∠BAD,
∴∠FEG=∠BAD=∠AMF,
∴∠AEG+∠AGE=∠FEM+∠AEG,
∴∠AGE=∠FEM,
∴△AEG∽△MFE,
∴,
∵,,
∴ABAD,AEAD,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD∥BC,∠BAD=∠C,
∴∠CDM=∠BAD=∠AMF=∠C=∠CFP,
∴PD=PM,PC=PF,
∴PC+PD=PF+PM,
即CD=FM=AB,
∴.
【点评】本题是三角形的综合题,熟练掌握三角形全等的判定及性质,轴对称求最短距离的方法是解题的关键.
2.综合与实践——平行四边形旋转中的数学问题
问题情境:
已知 ABCD与 A'B'C'D'中,AB=A'B'=6,BC=B'C'=8,∠ABC=∠A'B'C'=60°,同学们利用这样的两张平行四边形纸片开展操作实验,从中发现了许多有趣的数学问题,请你和他们一起进行探究.
拼图思考:
(1)希望小组的同学将 ABCD与 A'B'C'D'按图1的方式摆放,其中,点B与点B'重合,点A'落在BC边上,点C'落在BA边的延长线上,他们提出了如下问题,请你解答:
①连接BE,求证:BE平分∠ABA';
②点D,D′之间的距离为: 2 ;
操作探究:
(2)创新小组的同学在图1的基础上进行了如下操作:保持 ABCD不动,将 A'B'C'D'绕点B沿顺时针方向旋转,连接DD′.
①当线段C'D'与DC交于点P时,连接CC';如图2,求证:点P在DD'的垂直平分线上;
②在 A'B'C'D'旋转的过程中,当点C′恰好落在线段DC的延长线上时,请在图3中补全图形,并直接写出此时点D,D'之间的距离.
【考点】四边形综合题.
【专题】压轴题;推理能力.
【答案】(1)①证明见解析;②2;
(2)①证明见解析;②20.
【分析】(1)①借助△BAE与△BAE全等求证;②连接DD,判断△DDE′求解即可;
(2)①连接BD,BD,判断△BDD为等腰三角形,利用三线合一求证;②画出满足条件的图形,利用等边三角形求解.
【解答】(1)①证明:∵四边形ABCD、A'B'C'D'是平行四边形,
∴AD∥BC,A'D'∥B'C',
∴四边形A'EAB是平行四边形,∠AEB=∠EBC,
∴AE=B'A',
∵BA=B'A',
∴BA=AE,
∴四边形A'EAB是菱形,
∴BE平分∠ABA'.
②解:连接DD,如图,
由①知四边形ABAE是菱形,
∴AE=AE=CD=6,
∴AD﹣AE=AD﹣AE,
∴ED=ED'=8﹣6=2,
∵∠DED=∠ABA=60°,
∴△EDD为等边三角形,
∴DD'=ED=2.
故答案为:2.
(2)①证明:∵BC=BC',
∴∠BCC'=∠BC'C,
在 ABCD和 A'B'C'D'中,
∵∠ABC=∠AB'C=60°,AB=A'B',
∴∠BCD=∠B'C'D'=120°,CD=C'D',
∴∠PCC'=∠PC'C
∴PC=PC',
∴PD=PD',
∴点P在DD'的垂直平分线上.
②解:如图,
ABCD与 ABCD中,AB=AB=6,BC=B'C'=8,∠ABC=ABC'=60°,
∴CD=C'D'=6,BC=BC'=8,∠CBC'=180°﹣60°﹣60°=60°,
∴△BCC'是等边三角形,
∴CC'=8,
∴DD'=6+6+8=20.
【点评】本题主要考查平行四边形的性质,图形的旋转,全等三角形的判定与性质,等腰三角的性质定,等边三角形的判定与性质.关键是借助三角形全等和等腰三角形的三线合一进行解题.
3.【问题探究】
(1)如图1,在正方形ABCD中,对角线AC与BD相交于点O,在线段AO上任取一点P(端点除外),连接PD,PB.
①求证:PD=PB;
②将线段DP绕点P逆时针旋转,使点D落在BA的延长线上的点Q处,当点P在线段AO上的位置发生变化时,∠DPQ的大小是否发生变化?请说明理由;
③在探究AQ与OP的数量关系时,小颖作了如图2的辅助线:作PM⊥AB于点M,作PN⊥AD于点N,作PE⊥AO交AB于点E,作EF⊥OB于点F,请你直接写出AQ与OP的数量关系.
【迁移探究】
(2)如图3,将(1)中正方形ABCD换成菱形ABCD,且∠ABC=60°,其他条件不变,试探究AQ与CP的数量关系,并说明理由.
【考点】四边形综合题.
【专题】几何综合题;压轴题;推理能力.
【答案】(1)①证明见解答;②∠DPQ的大小不发生变化,∠DPQ=90°;③AQOP;
(2)AQ=CP.
【分析】(1)①根据正方形的性质可得CD=CB,∠DCA=∠BCA=45°,利用SAS证明△DCP≌△BCP即可证得结论;
②过点P作PM⊥AB于M,作PN⊥AD于N,可证得四边形AMPN是正方形,再利用HL证明Rt△DPN≌Rt△QPM,可得∠DPN=∠QPM,再利用角的关系即可证得结论;
③先得出△BEF是等腰直角三角形,BEEF,再证得四边形EFOP是矩形,得出EF=OP,即可求得答案;
(2)过点P作PM⊥AB于M,PE∥BC交AB于E,过点E作EG∥AC交BC于G,结合菱形的性质可得:四边形PEGC是平行四边形,再得出△ABC、△PAE和△BGE都是等边三角形,即可得出答案.
【解答】(1)①证明:∵四边形ABCD是正方形,
∴CD=CB,∠DCA=∠BCA=45°,
∵CP=CP,
∴△DCP≌△BCP(SAS),
∴PD=PB;
②解:∠DPQ的大小不发生变化,∠DPQ=90°;
理由如下:
过点P作PM⊥AB于M,作PN⊥AD于N,如图1,
∵四边形ABCD是正方形,
∴∠DAC=∠BAC=45°,
又∵PM⊥AB,PN⊥AD,
∴PM=PN,
∴四边形AMPN是正方形,
∴∠MPN=90°,
∵PD=PQ,PM=PN,
∴Rt△DPN≌Rt△QPM(HL),
∴∠DPN=∠QPM,
∵∠QPN+∠QPM=90°,
∴∠QPN+∠DPN=90°,
即∠DPQ=90°;
③解:AQOP,理由如下:如图2,
由①②知:PB=PD=PQ,AM=PM,
∵PM⊥AB,
∴BM=QM,
∵∠BAC=45°,
∴∠PEA=45°=∠PAE,
∵PM⊥AE,
∴AM=EM=PM,
∴BM﹣EM=QM﹣AM,
即BE=AQ,
∵∠BFE=90°,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴BEEF,
∵∠POF=∠OPE=∠OFE=90°,
∴四边形EFOP是矩形,
∴EF=OP,
∴AQOP;
(2)解:AQ=CP.理由如下:
∵四边形ABCD是菱形,
∴AC垂直平分BD,
∴PD=PB,
由旋转知:PD=PQ,
∴PQ=PB,
过点P作PM⊥AB于M,PE∥BC交AB于E,过点E作EG∥AC交BC于G,如图3,
则四边形PEGC是平行四边形,
∴PC=EG,
∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAC=60°,
∴△ABC是等边三角形,
同理可得:△PAE和△BGE都是等边三角形,
∴BE=EG=PC,
∵PM⊥AB,
∴MQ=MB,MA=ME,
∴MQ﹣MA=MB﹣ME,
即AQ=BE,
∴AQ=CP.
【点评】本题是正方形和菱形综合题,考查了正方形和菱形的性质,平行四边形的判定和性质,矩形的判定和性质,等边三角形的判定和性质,等腰直角三角形的判定和性质,全等三角形的判定和性质,添加辅助线构造全等三角形和直角三角形是解题关键.
4.在 ABCD中,点E是对角线AC上一点.
(1)如图1,∠DAC=90°,将△ADE沿DE翻折,使得A点的对应点F落在CD上,若AD=3,AC=4,求EF的长;
(2)如图2,∠ADC=45°,AD=AC,点G是DE的中点,AF⊥DE交CD于F点,I是AC上一点,连接FI,延长FI交DE的延长线于点J.若∠J=2∠DAG,AG=EJ,求证:AF+FI=2IJ;
(3)如图3,∠ADC=45°,AD=AC,延长DE至M点使AM=AD,∠DAM的角平分线交DE于点N,交MC延长线于点G,取CD中点F,连接GF,FM.当E在直线AC上运动时,直接写出的最大值.
【考点】四边形综合题.
【专题】压轴题;推理能力.
【答案】(1);
(2)证明过程详见解析;
(3).
【分析】(1)先由勾股定理求得CD=5,再由折叠性质得DF=AD=3,EF=AE,设EF=AE=x,在Rt△EFC中,利用勾股定理列方程求得x值即可;
(2)先根据等腰三角形的性质得到∠ADC=∠ACD=45°,∠DAC=90°,再根据直角三角形斜边中线性质得到,进而得到∠ADG=∠DAG,设∠ADG=∠DAG=α,利用三角形的外角性质结合已知得到∠AGE=∠J=2α,GE=EJ,证明△AEG≌△IEJ(ASA),AG∥FJ得到DE=2AG=2IJ,在DE截取DH=AF,连接AH,证明△ADH≌△CAF(SAS)得到AH=CF,∠DAH=∠ACF=45°,再证明△AHE≌△CFI(AAS)得到HE=FI,进而可得结论;
(3)连接AF,DG,根据等腰三角形的性质得到AG垂直平分DM,则DG=GM,∠DAC=90°,设∠CAM=2β,再根据等腰三角形的等边对等角进行角度运算得∠CMD=45°,进而推导出∠DGC=90°,设AD=AC=2a,则AM=2a,利用直角三角形斜边中线性质得到,利用三角形的三边关系得到,当点F、A、M共线时取等号,进而求得FM的最大值即可求解.
【解答】(1)解:∵AD=3,AC=4,∠DAC=90°,
∴,
由折叠性质得DF=AD=3,EF=AE,
设EF=AE=x,
在Rt△EFC中,CE=AC﹣AE=4﹣x,CF=CD﹣DF=2,
由勾股定理得x2+22=(4﹣x)2,
解得,
∴.
(2)证明:∵∠ADC=45°,AD=AC,
∴∠ADC=∠ACD=45°,则∠DAC=180°﹣45°﹣45°=90°,
∵点G是DE的中点,
∴,
∴∠ADG=∠DAG,设∠ADG=∠DAG=α,
∴∠AGE=∠ADG+∠DAG=2∠DAG=2α,
又∵∠J=2∠DAG,AG=EJ,
∴∠AGE=∠J=2α,GE=EJ,
又∵∠AEG=∠IEJ,
∴△AEG≌△IEJ(ASA),AG∥FJ,
∴AG=IJ,则DE=2AG=2IJ,
∵AF⊥DE,∠DAC=90°,
∴∠FAC+∠AED=∠ADE+∠AED=90°,
∴∠ADE=∠FAC=α,
在DE截取DH=AF,连接AH,
在△ADH和△CAF中,
,
∴△ADH≌△CAF(SAS),
∴AH=CF,∠DAH=∠ACF=45°,
∵∠HAE=∠DAC﹣∠DAH=90°﹣45°=45°,
∴∠HAE=∠FCI=45°,
∵AG∥FJ,∠GAE=90°﹣∠DAG=90°﹣α,
∴∠CIF=∠GAE=90°﹣α,
∵∠AEH=90°﹣∠ADG=90°﹣α,
∴∠AEH=∠CIF,
在△AHE和△CFI中,
,
∴△AHE≌△CFI(AAS),
∴HE=FI,
∵DH+HE=DE,
∴AF+FI=2IJ;
(3)如图,连接AF、DG,
∵AM=AD,∠DAM的角平分线交DE于点N,交MC延长线于点G,
∴AG⊥DM,DN=MN,
∴AG垂直平分DM,则DG=GM,
∵∠ADC=45°,AD=AC,
∴∠ADC=∠ACD=45°,则∠DAC=180°﹣45°﹣45°=90°,
设∠CAM=2β,
∵AM=AD=AC,
∴∠AMD(180°﹣∠DAM)=45°﹣β,,
∴∠CMD=∠AMC﹣∠AMD=(90°﹣β)﹣(45°﹣β)=45°,
又∵DG=GM,
∴∠GDM=∠GMD=45°,
则∠DGC=180°﹣2×45°=90°,
设AD=AC=2a,则AM=2a,
∵F为CD的中点,∠DAC=90°,∠DGC=90°,
∴,
∵E在直线AC上运动时,,
当点F、A、M共线时取等号,即点M在点M'处时,FM有最大值为(2)a,
的最大值为.
【点评】本题考查等腰三角形的判定与性质、折叠性质、直角三角形的性质、三角形的外角性质、全等三角形的判定与性质、平行线的判定与性质、线段垂直平分线的性质、最短路径问题等知识,综合性极强的压轴题,需要学生有一定的综合能力和分析问题、解决问题的能力,利用数形结合思想进行灵活运用所学相关知识进行解决问题.
5.如图1,∠ACB=90°,AC=BC,过点C的直线L不经过三角形的内部,过点A、B作AD⊥DE,BE⊥DE,垂足为D,E.
(1)请你在图1中,写出一对全等三角形: △ADC≌△CEB; ;
(2)请证明你所写的结论;
(3)尝试探究:若AD=a,BE=b
图1中四边形ADEB的面积为 ;
图2中过点C的直线L经过三角形内部,其他条件不变,则四边形ADBE面积为 (用含a,b的代数式表示);
(4)拓展应用:如图3,A(﹣1,0)C(0,2)则点B坐标为 (﹣2,3) ;若点P(不与B重合),在坐标平面内,△ABC与△ACP全等,则点P的坐标为 (﹣3,1)或(2,1)或(1,﹣1) .
【考点】四边形综合题.
【专题】压轴题;推理能力.
【答案】(1)△ADC≌△CEB;
(2)见解析;
(3),;
(4)(﹣2,3),(﹣3,1)或(2,1)或(1,﹣1).
【分析】(1)依据图形直接写出即可;
(2)这是“一线三垂直”全等模型,通过同角的余角相等进行转化即可得证;
(3)①利用梯形面积公式可解;②同(2)可证△ADC≌△CEB,四边形ADEB的面积为△ADE和△BDE面积之和;
(4)在坐标系内构造全等三角形即可求解,注意分情况讨论.
【解答】(1)解:△ADC≌△CEB;
(2)证明:∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=∠ACD+∠DAC,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
(3)解:①由(2)知△ADC≌△CEB,
∴AD=CE=a,BE=DC=b,
∴四边形ADEB的面积为:;
②同(2)可证△ADC≌△CEB,
∴AD=CE=a,BE=DC=b,
∴DE=CE﹣CD=a﹣b,
∴四边形ADEB的面积为:;
故答案为:,;
(4)解:如图所示,作BD⊥y轴于点D.
∵A(﹣1,0),C(0,2),
∴OA=1,OC=2,
∵∠ACB=90°,BD⊥y轴,
∴∠ACO+∠BCD=90°,∠CBD+∠BCD=90°,
∴∠CBD=∠ACO,
在△AOC和△CEB中,
,
∴△CDB≌△AOC(AAS),
∴CD=OA=1,BD=OC=2,
∴OD=OC+CD=2+1=3,
∴B(﹣2,3);
若△ABC与△ACP全等,则点P可能在第一、二、四象限,如图所示:
当点P在第二象限时,作P1H⊥x轴于点H,
∵∠CAP1=∠ACB=90°,P1H⊥x轴,
∴∠CAO+∠P1AH=90°,∠AP1H+∠P1AH=90°,
∴∠ACO=∠P1AH,
在△P1AH和△ACO中,
,
∴△ACO≌△P1AH(AAS),
∴P1H=OA=1,AH=OC=2,
∴OH=OA+AH=1+2=3,
∴P1(﹣3,1),
同理可得P2(2,1),P3(1,﹣1),
综上可知,B点坐标为(﹣2,3),点P的坐标为(﹣3,1)或(2,1)或(1,﹣1),
故答案为:(﹣2,3),(﹣3,1)或(2,1)或(1,﹣1).
【点评】本题主要考查了全等三角形的判定和性质以及坐标与图形等内容,熟练掌握“一线三垂直”模型是解题关键.
6.[问题提出]
(1)如图①,BD为矩形ABCD的对角线,点E为BD的中点,连接AE,若BC=10,CD=6,则AE的长为 ;
[问题探究]
(2)如图②,AC为 ABCD的对角线,且AC⊥AB,点E、F分别为边AD、BC的中点,连接AF,CE,试判断四边形AECF的形状,并说明理由;
[问题解决]
(3)如图③,△BCG是王叔叔家的果园平面示意图,王叔叔欲对该果园进行扩建,扩建部分为 ABCD,其中点D在GC的延长线上,E、F分别为边AD、BC的中点,在四边形AECF内种植某种新品种果树,经测量,AC∥BG,BG⊥DG,CE=160米,∠AFC=120°,P、H为两个临时仓库,其中H为CE的中点,点P在AC上,现要沿PE、PH修建两条运输通道,问运输通道的总长度(PE+PH)是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.
【考点】四边形综合题.
【专题】压轴题;推理能力;模型思想.
【答案】(1);(2)证明见解析;(3)PE+PH的最小值为米.
【分析】(1)先求解,可得;
(2)证明AD∥|BC,AD=BC,结合AE=CF,可得四边形AECF是平行四边形,结合AC⊥AB,F为边BC的中点,可得AF=BF=CF,从而可得结论;
(3)如图,连接EF,连接FH交AC于P,证明四边形ABGC是矩形,可得∠BAC=90°,结合(2)可得:四边形AFCE为菱形;可得PE+PH=PF+PH=FH,此时PE+PH最小,证明△ECF为等边三角形,可得CF=EF=160,证明FH⊥CE,CH=EH=80,再进一步即可得解.
【解答】解:(1)∵四边形ABCD是矩形,BC=10,CD=6,
∴AD=BC=10,AB=CD=6,∠BAD=90°,
∴,
∵点E为BD的中点,
∴.
故答案为:.
(2)四边形AECF是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别为边AD、BC的中点,
∴AE=CF,
∴四边形AECF是平行四边形,
∵AC⊥AB,F为边BC的中点,
∴AF=BF=CF,
∴四边形AECF是菱形;
(3)如图,连接EF,连接FH交AC于P,
∵四边形ABCD是平行四边形,
∴AB∥DG,
∵AC∥BG,
∴四边形ABGC是平行四边形,
∵BG⊥DG,
∴∠BGC=90°,
∴四边形ABGC是矩形,
∴∠BAC=90°,
∵E、F分别为边AD、BC的中点,
结合(2)可得:四边形AFCE为菱形;
∴AF∥CE,AF=CF=CE=AE,AC⊥EF,AC,EF互相垂直平分,
∴PE+PH=PF+PH≥FH,
当F、P、H三点共线时,PE+PH最小,
∵∠AFC=120°,
∴∠ECF=60°,
∴△ECF为等边三角形,而CE=160,
∴CF=EF=160,
∵H为CE的中点,
∴FH⊥CE,CH=EH=80,
∴.
∴PE+PH的最小值为米.
【点评】本题考查的是勾股定理的应用,直角三角形斜边上的中线的性质,平行四边形的判定与性质,矩形的判定与性质,菱形的判定 与性质,等边三角形的判定与性质,掌握几何基础知识是解本题的关键.
7.在菱形ABCD中,∠B=α(0°<α≤90°),点O′在对角线AC上运动(点O′不与点A,点C重合),,以点O′为顶点作菱形A'B'C'O';且菱形A'B'C'O'与菱形ABCD的形状、大小完全相同,即A′B′=AB,∠B′=∠B,在菱形A'B'C'O'绕点O′旋转的过程中,O'A'与边BC交于点E,O′C′与边CD交于点F.
【特例感知】
(1)如图1,当α=90°,时,则CE,CF,BC之间满足的数量关系是 CF+CE=BC ;
【类比探究】
(2)如图2,菱形的边长为8,α=60°,求CE+CF的值(用含k的代数式表示);
【拓展应用】
(3)在(2)的条件下,连接O′B,O′B=7,,求CE的长度.
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;推理能力.
【答案】(1)CF+CE=BC;
(2)CE+CF=8k;
(3)CE的长度为或.
【分析】(1)连接O′B,当α=90°,时,四边形ABCD和A′B′C′O′均为正方形,且O′为AC的中点,可证得△BO′E≌△CO′F(ASA),得出BE=CF,即可求得答案;
(2)过点O′作O′G∥AB,交BC于G,可证得△ABC、△ACD、△O′CG均为等边三角形,得出O′G=CG=O′C=k AC=8k,再证得△O′EG≌△O′FC(ASA),即可得出答案;
(3)连接BD交AC于O,运用勾股定理求得OO′=1,分两种情况:当点O′在线段AO上时,当点O′在线段OC上时,分别求得CE即可.
【解答】解:(1)当α=90°,时,
四边形ABCD和A′B′C′O′均为正方形,且O′为AC的中点,
如图1,连接O′B,
则O′B=O′C,∠O′BE=∠O′CF=45°,∠BO′E+∠CO′E=∠CO′E+∠CO′F=90°,
∴∠BO′E=∠CO′F,
∴△BO′E≌△CO′F(ASA),
∴BE=CF,
∵BE+CE=BC,
∴CF+CE=BC,
故答案为:CF+CE=BC;
(2)如图2,过点O′作O′G∥AB,交BC于G,
∵四边形ABCD和四边形A′B′C′O′是形状、大小完全相同的菱形,且边长为8,α=60°,
∴AB=BC=CD=AD=A′B′=B′C′=C′O′=O′A′=8,∠B=∠D=∠B′=∠A′O′C′=60°,
∴△ABC、△ACD均为等边三角形,
∴∠BAC=∠ACB=∠ACD=60°,AC=AB=8,
∵O′G∥AB,
∴∠CO′G=∠BAC=60°=∠O′CG,
∴△O′CG是等边三角形,
∴O′G=CG=O′C=k AC=8k,
∵∠EO′G+∠CO′E=∠CO′E+∠CO′F′=60°,
∴∠EO′G=∠CO′F,
∴△O′EG≌△O′FC(ASA),
∴EG=CF,
∵CE+EG=CG,
∴CE+CF=8k;
(3)连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,即∠BOC=90°,
∴OCACBC=4,
∴OB4,
∴OO′1,
当点O′在线段AO上时,如图2,过点O′作O′H⊥BC于H,
则O′C=OO′+OC=1+4=5,
∴k,
由(2)知:CE+CF=8k,
∴CE+CF=85,
∵CF,
∴CE=5;
当点O′在线段OC上时,如图3,
则O′C=OC﹣OO′=4﹣1=3,
∴k,
∴CE+CF=83,
∴CE=3;
综上所述,CE的长度为或.
【点评】本题是四边形综合题,考查了正方形的性质,菱形的性质,等边三角形的判定和性质,直角三角形的性质,勾股定理,全等三角形的判定和性质,正确添加辅助线,运用分类讨论思想是解题关键.
8.【材料背景】
如图1,在△ABC中,以边AB为底边向外作等腰Rt△ABD,其中∠ADB=90°,且AD=DB,那么点D就被称为边AB的“外展等直点”.
【建构与探究】
如图2,正方形网格是由边长为“1”的正方形组成,点O、A、B、C都在格点上,∠OAB=90°,点C为OB的中点.
(1)连接OA、OB、AB,请分别作边OA、AB的“外展等直点”P和Q,连接PC、QC和PQ,则△PCQ的形状为 等腰直角三角形 ;
(2)如图3,点E、F在格点上,请在线段EF上的格点中任取一点D(不与点A重合),连接OD、BD,分别作△OBD的边OD和边BD的“外展等直点”G、H,连接GC、HC和GH,请判断△GHC的形状,并说明理由.
【应用与拓展】
(3)如图4,点M、N为平面内某三角形两条边的“外展等直点”,已知M(﹣2,﹣1),N(3,1),请直接写出该三角形第三条边的中点K的坐标.
【考点】四边形综合题.
【专题】作图题;压轴题;新定义;几何直观.
【答案】(1)作图见解析,等腰直角三角形;(2)具体见解析;(3)K1(,),K2(,).
【分析】(1)根据“外展等值点”的定义即可画出点P、Q,再根据图形可知△PCQ是等腰直角三角形;
(2)先在格点上选取点D,根据“外展等值点”的定义即可画出点G、H,再利用“一线三垂直”的全等即可得证;
(3)由第二问可知△MNK为等腰直角三角形,所以会有两个K点,再构造“一线三垂直”的全等求解即可.
【解答】解:(1)点P、Q即为所求,
由图可知PC=CQ=3,且∠PCQ=90°,
∴△PCQ是等腰直角三角形.
故答案为:等腰直角三角形.
(2)选取点D如图所示,G、H即为所求.
参考一:
△GHC形状为等腰直角三角形,理由如下:
如图,GI=CJ=CI=HJ=3,∠GIC=∠CHH=90°
∴△GIC≌△CJH(SAS),
∴GC=CH,且∠GCH=180°﹣45°﹣45°=90°,
∴△GHC为等腰直角三角形.
参考二:
如图,GI=CJ=3,CI=HJ=1,∠GIC=∠CJH=90°,
∴△GIC≌△CJH(SAS),
∴GC=HC,∠IGC=∠JCH,则∠GCH=90°,
∴△GHC为等腰直角三角形.
参考三:
如图,GI=CJ=1,CI=HJ=3,∠GIC=∠CHH=90°,
∴△GIC≌△CJH(SAS),
∴GC=HC,∠IGC=∠JCH,则∠GCH=90°,
∴△GHC为等腰直角三角形.
(3)由第二问可知△MNK为等腰直角三角形,如图则会在MN上方和下方各有一个K点,
过K1作EF∥x轴,作ME⊥EF于点E,NF⊥EF于点F,
∵∠MK1N=90°,
∴∠MK1E=∠FNK1=90°﹣∠FK1N,
∵∠E=∠F=90°,MK1=NK1,
∴△MEK1≌△K1FN(AAS),
∴ME=FK1,EK1=FN,
∵M(﹣2,﹣1),N(3,1),
∴EF=EK1+FK1=5,EM﹣FN=2,
即ME+FN=5,ME﹣FN=2,
∴ME,FN,
∴K1(,);
同理可得K2(,).
综上,三角形第三条边的中点K的坐标为K1(,),K2(,).
【点评】本题主要考查格点作图、等腰三角形的判定和性质、全等三角形的判定和性质等内容,熟练掌握相关知识点和理解题意是解题的关键.
9.综合与实践
问题情境:“综合与实践”课上,老师提出如下问题:如图1,在 ABCD中,∠ADC=90°,点O是边AD的中点,连接AC.保持 ABCD不动,将△ADC从图1的位置开始,绕点O顺时针旋转得到△EFG,点A,D,C的对应点分别为点E,F,G.当线段AB与线段FG相交于点M(点M不与点A,B,F,G重合)时,连接OM.老师要求各个小组结合所学的图形变换的知识展开数学探究.
初步思考:(1)如图2,连接FD,“勤学”小组在旋转的过程中发现FD∥OM,请你证明这一结论;
操作探究:(2)如图3,连接BG,“善思”小组在旋转的过程中发现OM垂直平分BG,请你证明这一结论;
拓展延伸:(3)已知,CD=2,在旋转的过程中,当以点F,C,D为顶点的三角形是等腰三角形时,请直接写出此时线段AM的长度.
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;推理能力.
【答案】(1)证明见解答;
(2)证明见解答;
(3)线段AM的长度为2或1或.
【分析】(1)连接CF,DF,由旋转得∠ADC=∠EFG,OD=OF,再证得Rt△OAM≌Rt△OFM(HL),得出∠AOM=∠FOM,进而得出∠AOM=∠ODF,利用平行线的判定即可证得结论;
(2)延长OM交BG于点N,由旋转得CD=GF,进而推出BM=GM,再证得∠BMN=∠GMN,利用等腰三角形的性质即可证得结论;
(3)分三种情况:当FC=FD时,当FC=CD时,当FD=CD时,分别求得AM即可.
【解答】(1)证明:如图1,连接CF,DF,
∵将△ADC绕点O顺时针旋转得到△EFG,
∴∠ADC=∠EFG,OD=OF,
∴∠ODF=∠OFD,
∵∠ADC=90°,
∴∠EFG=90°,
∵点O是边AD的中点,
∴OA=OD,
∴OA=OF.
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAD+∠ADC=180°,
又∵∠ADC=90°,
∴∠BAD=180°﹣90°=90°,
∴∠BAD=∠EFG=90°,
∵在Rt△OAM和Rt△OFM中,
∴Rt△OAM≌Rt△OFM(HL),
∴∠AOM=∠FOM,
∵∠AOF是△OFD的一个外角,
∴∠AOF=∠AOM+∠FOM=∠ODF+∠OFD,
即2∠AOM=2∠ODF,
∴∠AOM=∠ODF,
∴FD∥OM;
(2)证明:如图2,延长OM交BG于点N,
由(1)知:Rt△OAM≌Rt△OFM,
∴AM=FM,∠AMO=∠FMO,
∵将△ADC绕点O顺时针旋转得到△EFG,
∴CD=GF,
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AB=GF,
∴AB﹣AM=GF﹣MF,
即BM=GM,
∵∠AMO=∠FMO,∠AMO=∠BMN,∠FMO=∠GMN,
∴∠BMN=∠GMN,
∴OM垂直平分BG;
(3)解:∵以点F,C,D为顶点的三角形是等腰三角形,
∴FC=FD或FC=CD或FD=CD,
当FC=FD时,如图3,过点F作FH⊥CD于H,交AB于L,过点O作OK⊥FH于K,
则四边形AOKL、OKHD、ALHD均为矩形,
∴AL=OK=DH,LK=OA,
∵,CD=2,点O是边AD的中点,
∴LK=OA=OD,
∵FC=FD,FH⊥CD,
∴DHCD=1,
∴OK=AL=DH=1,
由旋转得OF=OD,
又∵∠OKF=90°,
∴FK1,
∴FK=OK,
∴∠OFK=∠FOK=45°,
∴∠MFL=90°﹣∠OFK=45°,
∴△FML是等腰直角三角形,
∴ML=FL=LK﹣FK1,
∴AM=AL﹣ML=1﹣(1)=2;
当FC=CD时,如图3,连接OC,
由旋转得OF=OD,
又∵OC=OC,
∴△OCF≌△OCD(SSS),
∴∠OFC=∠ODC=90°,
∵∠EFG=90°,
∴∠OFC+∠EFG=90°+90°=180°,
即C、F、G三点共线,
在Rt△OAM和Rt△OFM中,
,
∴Rt△OAM≌Rt△OFM(HL),
∴AM=FM,
设AM=x,
∵四边形ABCD是矩形,AD=2,CD=2,
∴AB=CD=2,BC=AD=2,
则BM=2﹣x,CM=CF+FM=2+x,
在Rt△BCM中,BM2+BC2=CM2,
∴(2﹣x)2+(2)2=(2+x)2,
解得:x=1,
∴AM=1;
当FD=CD时,如图5,过点O作OK⊥DF于K,
∵OF=OD,OK⊥DF,
∴DK=FKDF=1,
在Rt△ODK中,OK1,
∴OK=DK=FK,
∴△ODK和△OFK均为等腰直角三角形,
∴∠DOK=∠FOK=45°,
∴∠DOF=45°+45°=90°,
∴∠AOF=90°,
∴∠OAM=∠AOF=∠OFM=90°,
∴四边形AOFM是矩形,
∴AM=OF;
综上所述,线段AM的长度为2或1或.
【点评】本题是矩形综合题,主要考查了等腰三角形的判定和性质,等腰直角三角形的判定和性质,平行四边形的性质,矩形的判定和性质,全等三角形的判定和性质,旋转变换的性质等知识,熟练掌握旋转的性质,全等三角形的判定和性质是解题关键.
10.在数学探究课上,王宇同学通过作辅助图形的方法,计算动点条件下线段和的最小值,其过程如下:
(1)【观察发现】
如图1,在等边△ABC中,AC=2,CDBC,E,F分别是AB和AC上的动点,且总有BE=AF,阅读下面作辅助图形的方法及推理过程并填空,理解确定DE+DF最小值的方法.
∵在等边△ABC中,AC=2,CDBC,
∴点D为BC边上的中点,∠B=∠ACB.
∴AD⊥BC.
过点A作AG⊥AD,使AG=BD,连接GF.
∴AG∥BC.∴∠GAC=∠ACB=∠B.
又∵AF=BE,∴△AGF≌△BDE(SAS).
∴GF=DE.
连接DG,DF,当D,F,G三点共线时,GF+DF的最小值等于线段DG的长.
连接GC,可证四边形ADCG是矩形,
∴DG=AC.
∴DE+DF的最小值为 2 .
(2)【类比应用】
如图2,已知正方形ABCD的边长为6,O为对角线的交点,M,N分别是AB,AD上的动点,且总有BM=DN,连接OM,CN,求OM+CN的最小值.
(3)【拓展延伸】
如图3,矩形ABCD中,AB,AD=2,E是AD的中点,F,G分别是BC和DC上的动点,且总有BF=2DG,则EF+2AG的最小值为 2 .
【考点】四边形综合题.
【专题】压轴题;构造法;模型思想.
【答案】(1)2;(2);(3)2.
【分析】(1)根据题意可得四边形ADCG是矩形,从而得到DG=AC=2;
(2)类比第一问作辅助线,得出OM+CN=GN+CN,当G,N,C三点共线时,线段GC的长为GN+CN的最小值,进而求解即可;
(3)由BF=2DG和前述思路可以构造2AG,所有延长AB到H,使BH=2AD,连接FH,从而△ADG∽△HBF,得到FH=2AG,连接EH,当E、F、H三点共线时,线段EH的长为EF+2AG的最小值,利用勾股定理求EH即可.
【解答】解:(1)由作图可知,四边形ADCG是矩形,
∴DG=AC=2,
故答案为:2.
(2)如图,类比(1),过点D作 DG⊥BD,使DG=OB,连接GN,易得∠GDN=∠ADB=∠OBM.
在△GND和△OMB 中,
∵GD=OB,∠GDN=∠OBM,DN=BM,
∴△GND≌△OMB(SAS).
∴GN=OM.
∴OM+CN=GN+CN.
连接GC,当G,N,C三点共线时,线段GC的长为GN+CN的最小值.
过点G作GH⊥CD,交CD的延长线于点H.
在正方形ABCD中,BD为对角线,
∴∠ADB=45°
∵∠GDH+∠GDA=90°,∠ADB+∠GDA=90°
∴∠GDH=∠ADB=45°.
∴Rt△HGD为等腰直角三角形.
∵正方形ABCD的边长为6,
∴.
∴.
∴在 Rt△HGC 中,,
∴OM+CN的最小值为 .
(3)如图,延长AB到H,使BH=2AD,连接FH.
∵,∠ADG=∠HBF,
∴△ADG∽△HBF,
∴,
∴FH=2AG,
∴EF+2AG=EF+FH,
连接EH,当E、F、H三点共线时,线段EH的长为EF+2AG的最小值.
∵AEAD,AH=AB+BH=5,
∴EH2.
故答案为:2.
【点评】本题主要考查矩形的性质、正方形的性质、勾股定理、轴对称的性质、全等三角形的判定和性质相似三角形的判定和性质等知识,熟练掌握相关知识和添加合适的辅助线是解题关键.
11.综合与实践课上,老师和同学们开展了一场以“最小值”为主题的探究活动.
【提出问题】老师提出了一个问题:如图1,在矩形ABCD中,AB=3,BC=6,P为AD边上的一动点,以PC为边向右作等边△PCE,连接BE,求BE的最小值;
【探究发现】小明发现:如图4所示,以BC为边向下构造一个等边△BCM,便可得到△PCM≌△ECB,进而将 BE的最小值转化为PM的最小值.
(1)按照小明的想法,请求出BE的最小值;
【拓展应用】
(2)小刚受此启发,举一反三,提出新问题:如图2,若将图1当中构造的等边三角形,改为以PC为边向右构造正方形PCFG,则运动过程中,BG的最小值是 6 .
(3)小红同学深入研究了小刚的问题,并又提出了新的问题:如图3,若将图2当中构造的正方形改为以PC为边向右构造菱形PCHI,使.∠CPI=120°,也可求得BI的最小值请你直接写出BI最小值为 3+3 .
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;图形的相似;推理能力.
【答案】(1)BE的最小值为33;
(2)6;
(3)3+3.
【分析】(1)过点M作MK⊥AD于K,交BC于L,可证得△BCE≌△MCP(SAS),得出BE=MP,由M为定点,可得当MP⊥AD时,即点P与点K重合时,MP=MK最小,再利用解直角三角形求得MK即可;
(2)以BC为边向下作正方形BCKL,连接BK、CL交于点O,连接OP,CG,过点O作OP′⊥AD于P′,交BC于T,可推出∠BCG=∠OCP,,证得△BCG∽△OCP,得出,即BGOP,故当BG取得最小值时,OPBG最小,利用解直角三角形求得OT,进而可求得BG的最小值;
(3)连接CI、PH交于O,在BC下方作射线BM、射线CN,使∠CBM=∠BCN=30°,射线BM、射线CN交于点Q,过点Q作QP′⊥AD于P′,交BC于K,连接PQ,可证得△BCI∽△QCP,得出,即BIQP,故当QP取得最小值时,BIQP最小,由点Q为定点,可得当QP⊥AD,即点P与点P′重合时,QP=QP′=QK+KP′最小,运用解直角三角形即可求得答案.
【解答】解:(1)如图,过点M作MK⊥AD于K,交BC于L,
∵△PCE和△BCM都是等边三角形,
∴CE=CP,CB=CM,∠PCE=∠MCB=∠MBC=60°,
∴∠PCE+∠PCB=∠MCB+∠PCB,
即∠BCE=∠MCP,
在△BCE和△MCP中,
,
∴△BCE≌△MCP(SAS),
∴BE=MP,
∴当MP最小时,BE最小,
∵M为定点,
∴当MP⊥AD时,即点P与点K重合时,MP=MK最小,
∵四边形ABCD是矩形,
∴AD∥BC,BC=6,∠A=∠ABC=90°,
∴ML⊥BC,
∵∠AKL=∠A=∠ABC=90°,
∴四边形ABLK是矩形,
∴KL=AB=3,
在Rt△MCL中,ML=CM sin∠MCB=6sin60°=3,
∴MK=ML+KL=33,
∴BE的最小值为33;
(2)如图,以BC为边向下作正方形BCKL,连接BK、CL交于点O,连接OP,CG,过点O作OP′⊥AD于P′,交BC于T,
∵四边形CPGF、BCKL是正方形,
∴∠PCG=∠BCO=45°,CGCP,OC=OBBC=3,△BOC是等腰直角三角形,
∴∠PCG+∠PCB=∠BCO+∠PCB,
即∠BCG=∠OCP,
∵,
∴△BCG∽△OCP,
∴,
∴BGOP,
∴当BG取得最小值时,OPBG最小,
∵点O为定点,
∴当OP⊥AD时,即点P与点P′重合时,OP=OP′最小,
∵BC∥AD,
∴OP′⊥BC,即∠CTO=90°,
∴OT=OC sin∠BCO=3sin45°=3,
∵∠A=∠ABC=∠AP′O=90°,
∴四边形ABTP′是矩形,
∴TP′=AB=3,
∴OP′=OT+TP′=3+3=6,
∴OP的最小值为6,
∴BG的最小值为6,
故答案为:6;
(3)如图,连接CI、PH交于O,在BC下方作射线BM、射线CN,使∠CBM=∠BCN=30°,射线BM、射线CN交于点Q,
过点Q作QP′⊥AD于P′,交BC于K,连接PQ,
∵四边形PCHI是菱形,∠CPI=120°,
∴PH⊥CI,PC=PI,∠PCI=∠PIC=30°,CI=2CO,
在Rt△CPO中,CO=PC cos∠PCI=PC cos30°PC,
∴CI=2COPC,
∵∠CBQ=∠BCQ=30°,
∴QB=QC,
∵QP′⊥AD,AD∥BC,
∴QK⊥BC,
∴BK=CKBC=3,
∴QK=CK tan∠BCQ=3tan30°,CQ2,
∴,,
∴,
∵∠BCI=∠BCP+30°,∠QCP=∠BCP+30°,
∴∠BCI=∠QCP,
∴△BCI∽△QCP,
∴,
∴BIQP,
∴当QP取得最小值时,BIQP最小,
∵点Q为定点,
∴当QP⊥AD,即点P与点P′重合时,QP=QP′=QK+KP′最小,
由(2)知:KP′=AB=3,
∴QP′=QK+KP′3,
∴BI的最小值(3)=3+3,
故答案为:3+3.
【点评】本题是四边形综合题,考查了矩形的性质,正方形的性质,菱形的性质,等边三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形等,解题的关键是正确地作出解题所需要的辅助线,构造全等三角形和相似三角形,此题难度较大,属于中考压轴题.
12.综合实践
如图1,点E为正方形ABCD内一点,∠AEB=90°,点E′为正方形ABCD外一点,且BE'⊥CE',BE=BE',延长AE交CE'于点F,连接DE.
(1)试判断四边形BE'FE的形状,并说明理由;
(2)如图2,若DA=DE,请猜想线段CF与E′F的数量关系,并加以证明;
(3)如图1,若AB=15,BE=9,请求出DE的长.
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;矩形 菱形 正方形;推理能力.
【答案】(1)四边形BE'FE是正方形,证明见解答;
(2)CF=E′F,证明见解答;
(3)DE的长为3.
【分析】(1)利用HL证明Rt△ABE≌Rt△CBE′,再证得四边形BE'FE是矩形,即可得出答案;
(2)过点D作DG⊥AE于点G,则∠AGD=∠AEB=90°,进而证得△DAG≌△ABE(AAS),Rt△ABE≌Rt△CBE′(HL),再根据线段的和差关系即可得出答案;
(3)过点E作EG⊥AB于G,EH⊥AD于H,则四边形AGEH是矩形,运用勾股定理求得AE=12,再运用面积法得出EG,AG,再运用勾股定理即可.
【解答】解:(1)四边形BE'FE是正方形,理由如下:
如图1,
∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵BE'⊥CE',
∴∠BE′C=90°,
又∠AEB=90°,
在Rt△ABE和Rt△CBE′中,
,
∴Rt△ABE≌Rt△CBE′(HL),
∴∠ABE=∠CBE′,
∴∠CBE′+∠CBE=∠ABE+∠CBE,
即∠EBE′=∠ABC=90°,
∵∠BEF=180°﹣∠AEB=90°,
∴∠BEF=∠EBE′=∠BE′F=90°,
∴四边形BE'FE是矩形,
∵BE=BE',
∴四边形BE'FE是正方形;
(2)猜想:CF=E′F,
证明:如图2,过点D作DG⊥AE于点G,则∠AGD=∠AEB=90°,
∵DA=DE,
∴AG=EGAE,
∵四边形ABCD是正方形,∴AD=AB,∠BAD=90°,
∴∠DAG+∠BAE=90°,
∵∠ABE+∠BAE=90°,
∴∠DAG=∠ABE,
在△DAG和△ABE中,
,
∴△DAG≌△ABE(AAS),
∴AG=BE,
∴AE=2BE,
在Rt△ABE和Rt△CBE′中,
,
∴Rt△ABE≌Rt△CBE′(HL),
∴AE=CE′,∠ABE=∠CBE′,
∵∠ABE+∠CBE=90°,
∴∠CBE′+∠CBE=90°,即∠EBE′=90°,
∴∠BEF=∠EBE′=∠BE′C=90°,
又BE=BE',
∴四边形BEFE′上正方形,
∴E′F=BE,
∴CF+E′F=CE′=2E′F,
∴CF=E′F;
(3)如图3,过点E作EG⊥AB于G,EH⊥AD于H,
则四边形AGEH是矩形,
∴AH=EG,EH=AG,
在Rt△ABE中,AB=15,BE=9,
∴AE12,
∵EG⊥AB,
∴EG,
在Rt△AEG中,AG,
∴EH,AH,
∴DH=AD﹣AH=15,
∴DE3,
故DE的长为3.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形的性质,旋转的性质,勾股定理,证明△DAG≌△ABE≌△CBE′是关键.
13.在一次数学活动课上,老师带领同学们探究图形的变换问题.老师先提出这样一个问题:
有一张矩形纸片ABCD,其中AB=4,,你能用这张矩形纸片折出一个等边三角形吗?
【操作】小明同学是这样操作的:如图①,先将矩形ABCD沿MN对折;展开后,再将点C沿BE折叠,使点C落在MN上的点F处;再展开,连接BF,CF,则△BCF为等边三角形.
【验证】(1)求证:△BCF为等边三角形;
【应用】(2)连接AF,DF,如图②,求AF的长;
【拓展】(3)将图②中的△BCF绕着点F顺时针旋转α(0°<α<90°)得到△B′C′F(点B,C的对应点分别为B′,C′),连接AB′,DC′,当△AFB'为等腰三角形时,直接写出线段DC′的长.
【考点】四边形综合题.
【专题】压轴题;几何直观.
【答案】(1)证明过程详见解析;(2)2;(3)2或2.
【分析】(1)由折叠很容易得出BF=CF=BC,即可得证;
(2)根据勾股定理先求出FN长度,进而求出FM长度,再用勾股定理求出AF即可;
(3)由题可知AF≠FB',所以需要分两种情况讨论,即AF=AB',B'A=BF,分别画出图形,再进行计算即可.
【解答】(1)证明:∵矩形沿MN对折,
∴MN是BC的垂直平分线,
∴BF=CF,
∵折叠,
∴BC=BF,
∴BC=BF=CF,
∴△BCF是等边三角形.
(2)解:设MN交AD于M,交BC于N,
∵BC=2,
∴BF=2,BN,
∴FN3,
∵AB=4,
∴MN=4,
∴FM=MN﹣FN=1,
∵AM,
∴AF2.
(3)∵旋转,
∴FB'=FB=2,
∵AF=2,
∴等腰三角形AFB'中AF≠FB',
∴可分两种情况讨论,
①当AF=AB'时,如图所示,
由(2)知,AF=2,FB=2,AB=4,
∴AF2+BF2=AB2,
∴△AFB是直角三角形,即∠AFB=90°,
∵AF=AB',
∴AB垂直平分FB',
∴此时FB旋转60°到FB',
∴点C对应点C'落到点B的位置,
此时DC'2.
②当B'A=BF时,如图所示,
过B'作B'K⊥AF于K,DR⊥CF于R,
∴KFAF=1,
∴B′K,
∴DRB'K,
∵DF=AF=2,
∴FR,
∴C'R,
在Rt△DRC'中,DC'2.
综上,线段DC′的长为2或2.
【点评】本题主要考查折叠的性质、等边三角形的判定和性质、勾股定理、旋转的性质等内容,熟练掌握相关知识是解题的关键.
14.[回顾课本]苏教版八年级下册数学教材“9.5三角形的中位线”一课中给出了“三角形的中位线定理”的证明思路,请根据分析完成证明过程.
已知:如图1,DE是△ABC的中位线,求证:DE∥BC,.
分析:因为点E是AC的中点,可以考虑把△ADE绕点E按顺时针方向旋转180°,得到△CFE,这样就需要证明四边形BCFD是平行四边形……
[探究发现]
如图2,等边△ABC的边长为2,点D、E分别为AB、AC边中点,点F为BC边上任意一点(不与B、C重合),沿DE、DF剪开分成①、②、③三块后,将②、③分别绕点D顺时针、点E逆时针旋转180°恰好能与①拼成 DIHG,求 DIHG周长的最小值.
[拓展作图]
如图3,已知四边形ABCD,现要求只剪两次将其剪成四块,使得剪成的四块能通过适当的摆放拼成一个平行四边形,请在图3中画出两条剪痕,并对剪痕作适当的说明.
【考点】四边形综合题.
【专题】几何综合题;压轴题;等腰三角形与直角三角形;多边形与平行四边形;平移、旋转与对称;推理能力.
【答案】[回顾课本]证明见解答;
[探究发现] DIHG周长的最小值为4;[拓展作图]作图见解答.
【分析】【回顾课本】以点E为旋转中心,把△ADE绕点E,按顺时针方向旋转180°,得△CFE,则D,E,F同在一直线上,DE=EF,且△ADE≌△CFE,得出∠ADE=∠F,AD=CF,证明四边形BCFD是平行四边形,则可得出结论;【探究发现】当DF⊥BC时最小,此时DF,则可得出答案;【拓展作图】取AB,BC,CD,DA边的中点,沿EG,FH剪开分成①,②,③,④四块即可.
【解答】[回顾课本]
证明:∵△ADE绕点E按顺时针方向旋转180°,得到△CFE,
∴CF=AD,EF=DE,∠ECF=∠A,
∴CF∥AB,
∵D是AB的中点,
∴AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DF∥BC,DF=BC,
即DE∥BC,2DE=BC,
∴DE∥BC,DEBC;
[探究发现]
解:由题可知: DIHG周长=2DI+2DG=2BC+2DF=4+2DF,
当DF⊥BC时最小,此时DF,
∴ DIHG周长的最小值为4;
[拓展作图]
如图,取点E,F,G,H分别是AB,BC,CD,DA边的中点,沿EG,FH剪开分成①,②,③,④四块后,将①,③分别绕点F,E旋转180°至⑦,⑤,再将②平移至⑥,恰好能与④拼成平行四边形LJKN即可,
理由:∵E、F、G、H分别是AB、BC、CD、DA边的中点,
∴AE=BE,BF=CF,CG=DG,AH=DH,
由旋转得:∠J=∠FLG,∠N=∠ELH,
∴KJ∥NL、KN∥JL,
∴四边形JKNL是平行四边形.
【点评】本题是四边形综合题,主要考查了平行四边形的判定与性质,等边三角形的性质,三角形中位线定理,熟练掌握以上知识是解题的关键.
15.函数是刻画现实世界的有效模型,函数和现实情境之间的转换可以帮助我们简化问题的处理.
(1)下列情境中,可以用反比例函数刻画的是 AC ;
A.甲、乙两地相距200km,行驶时间和行驶速度之间的关系;
B.单价为3元的练习本,购买数量和总价的关系;
C.面积为8的矩形,长和宽的关系.
(2)求函数的最小值时,直接求解困难较大,我们可以给函数赋予这样的数学情境:如图1,线段BC=3,AB=1,CD=2,AB⊥BC,CD⊥BC,则AP+PD可表示为 ,(用含有x的代数式表示)请你结合图形,继续完成求解过程.
(3)如图2,四边形ABCD为矩形,AB=6,BC=9,P为矩形ABCD内(不包含边界)一点,过P分别向AB、BC作垂线,垂足为M,N,若四边形MBNP的面积为6,则称点P为“美丽点”,在矩形BEFG中,BE=9,BG=4,过F点的直线l交直线BC于点Q,若直线l上存在“美丽点”,求FQ的取值范围.
【考点】四边形综合题.
【专题】代数几何综合题;压轴题;反比例函数及其应用;矩形 菱形 正方形;运算能力;推理能力;应用意识.
【答案】(1)AC;
(2);最小值为;
(3)9≤FQ<9.
【分析】(1)分别求出各问题中的关系式,根据反比例函数的定义判断即可;
(2)利用勾股定理表示出AP+PD,得到当A、P、D三点共线时,AP+PD的值最小,即AP+PD=AD,利用勾股定理求出AD,即可得到最小值;
(3)以点B为原点,BC、BA分别为x轴,y轴建立平面直角坐标系,设反比例函数y的图象交AD于点T,交FG于点N,求出FQ最大值和最小值即可.
【解答】解:(1)A.∵时间×速度=路程,即tv=200,
∴行驶时间和行驶速度之间的关系为t,
故A属于反比例函数;
B.∵单价×数量(x)=总价(y),
∴y=3x,即购买数量和总价的关系是正比例函数,不属于反比例函数;
C.∵矩形的面积(S)=长(a)×宽(b),即8=ab,
∴a,即面积为8的矩形,长和宽的关系属于反比例函数;
故答案为:AC;
(2)设BP=x,则PC=3﹣x,如图1,
∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°,
∴AP+PD,
故答案为:;
由图形可知,当A、P、D三点共线时,AP+PD的值最小,即AP+PD=AD,
如图2,过点D作DE⊥AB,交AB的延长线于点E,则四边形BCDE上矩形,
∴BE=CD=2,DE=BC=3,
∴AE=AB+BE=1+2=3,
∴AD3,
∴AP+PD的最小值为3,
故函数的最小值为3;
(3)如图3,以点B为原点,BC、BA分别为x轴,y轴建立平面直角坐标系,
∵点P为“美丽点”,
∴S矩形BMPN=6,
∴点P在反比例函数y的图象上,
设反比例函数y的图象交AD于点T,交FG于点N,
当y=6时,x=1,
∴T(1,6),
设直线FT的解析式为y=kx+b,将F(4,9),T(1,6)代入得,
解得:,
∴直线FT的解析式为y=x+5,
当y=0时,x=﹣5,故Q(﹣5,0),
∴FQ9,此时,FQ最大;
当点Q与点G重合时,FQ=9,此时,FQ最小,
∴FQ的取值范围是9≤FQ<9.
【点评】本题是反比例函数综合题,考查了实际问题与反比例函数的关系,反比例函数的实际应用,勾股定理,矩形的判定和性质,最值的确定,正确理解实际问题与反比例函数的关系是解题关键.
16.【探索发现】
(1)如图1,正方形ABCD的对角线相交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等,边A1O与边AB相交于点E,边C1O与边CB相交于点F,连接EF.在实验与探究中,小新发现无论正方形A1B1C1O绕点O怎样转动,AE,CF,EF之间一直存在某种数量关系,小新发现通过证明△AOE≌△BOF即可推导出来.
①请你猜想AE,CF,EF之间的数量关系是 AE2+CF2=EF2 .
②小新对图1的进一步研究中发现,延长EO与DC交于一点G,通过证明△AOE≌△COG也可推导出AE,CF,EF之间的数量关系,请你证明△AOE≌△COG.
【类比迁移】
(2)如图2,矩形ABCD的中心O是矩形A1B1C1O的一个顶点,A1O与边AB相交于点E,C1O与边CB相交于点F,连接EF,矩形A1B1C1O可绕着点O旋转,判断AE,CF,EF之间的数量关系并进行证明;
【拓展应用】
(3)如图3,在Rt△ACB中,∠C=90°,AC=5cm,BC=12cm,点D是边AB的中点,∠EDF=90°,它的两条边DE和DF分别与直线AC,BC相交于点E,F,∠EDF可绕着点D旋转,当AE=4cm时,请直接写出线段CF的长度.
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;矩形 菱形 正方形;推理能力.
【答案】(1)①AE2+CF2=EF2,证明见解答;②证明见解答;
(2)AE2+CF2=EF2,证明见解答;
(3)线段CF的长度为cm或cm.
【分析】(1)①先证明△AOE≌△BOF(ASA),可得AE=BF,推出BE=CF,再运用勾股定理即可证得结论;
②延长EO交DC于点G,由正方形性质可得OA=OC,∠OAE=∠OCG=45°,再利用ASA可证得△AOE≌△COG;
(2)延长EO交CD于点G,连接FG,可证得△AEO≌△CGO(AAS),得出AE=CG,OE=OG,再由线段垂直平分线的性质可得EF=FG,再运用勾股定理即可求得答案;
(3)设CF=x cm,分两种情况讨论:①当点E在线段AC上时,②当点E在CA延长线上时,结合勾股定理,即可求解.
【解答】(1)①解:猜想:AE2+CF2=EF2,理由如下:
如图1,
∵四边形ABCD和四边形A1B1C1O均为正方形,
∴OA=OB,AB=BC,∠OAE=∠OBF=45°,∠AOB=∠A1OC1=90°,
∴∠AOB﹣∠BOE=∠A1OC1﹣∠BOE,
即∠AOE=∠BOF,
∴△AOE≌△BOF(ASA),
∴AE=BF,
∴AB﹣AE=BC﹣BF,即BE=CF,
在Rt△BEF中,BF2+BE2=EF2,
∴AE2+CF2=EF2,
故答案为:AE2+CF2=EF2.
②证明:如图1′,延长EO交DC于点G,
∵四边形ABCD为正方形,
∴OA=OC,∠OAE=∠OCG=45°,
在△AOE和△COG中,
,
∴△AOE≌△COG(ASA).
(2)解:结论:AE2+CF2=EF2,
证明:如图2,延长EO交CD于点G,连接FG,
∵O是矩形ABCD的中心,
∴点O是AC的中点.
∴AO=CO,
∵四边形ABCD是矩形,
∴∠BCD=90°,AB∥CD,
∴∠BAO=∠DCO,∠AEO=∠CGO,
∴△AEO≌△CGO(AAS),
∴AE=CG,OE=OG,
∵四边形A1B1C1O是矩形,
∴∠A1OC1=90°,即OF⊥EG,
∴OF垂直平分EG,
∴EF=FG,
在Rt△FCG中,CG2+CF2=GF2,
∴AE2+CF2=EF2;
(3)解:设CF=x cm,①当E在线段AC上时,如图3,连接EF,
∵AE=4cm,AC=5cm,BC=12cm,
∴CE=1cm,在Rt△FCE中,∠C=90°,
∴CE2+CF2=EF2,
∴12+x2=EF2,
又由(2)易知EF2=AE2十 BF2,
∴EF2=42+BF2,
∴12+x2=42+(12﹣x)2,
解得:x,
∴此时线段CF的长度为cm;
②当点E在CA延长线上时,如图4,过点B作BG⊥BC,交ED的延长线于G,连接EF,GF,
同理可证EF2=AE2十 BF2,
∴EF2=42+(12﹣x)2,
在Rt△FCE中,EF2=x2+(5+4)2,
∴x2+(5+4)2=42+(12﹣x)2,
解得:x,
∴此时线段CF的长度为cm;
综上所述,线段CF的长度为cm或cm.
【点评】本题是四边形综合题,考查了正方形的性质,矩形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形根据勾股定理列方程解决问题.
17.综合与实践
问题情境:第二十四届国际数学家大会合徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图1,在综合实践课上,同学们绘制了“弦图”并进行探究,获得了以下结论:该图是由四个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH拼成的大正方形ABCD,且∠ABF>∠BAF.
特殊化探究:连接BH.设BF=a,AF=b.
“运河小组”从线段长度的特殊化提出问题:
(1)若AB=5,FG=1,求△ABF的面积.
“武林小组”从a与b关系的特殊化提出问题:
(2)若b=2a,求证:∠BAE=∠BHE.
深入探究:老师进一步提出问题:
(3)如图2,连接BE,延长FA到点I,使AI=AB,作矩形BFIJ.设矩形BFIJ的面积为S1,正方形ABCD的面积为S2,若BE平分∠ABF,求证:S1=S2.
请你解答这三个问题.
【考点】四边形综合题.
【专题】压轴题;几何直观.
【答案】(1)6;(2)证明过程见解析;(3)证明过程见解析.
【分析】(1)根据”弦图“关系,设参数,利用勾股定理建立方程求解即可;
(2)由b=2a可知E是AF中点,从而可证△HGB≌△BFA,得到∠GBH=∠BAF,再证∠BHE=∠GBH即可得证;
(3)用代数法思路证:设DH=CG=BF=AE=a,正方形HEFG的边长为b,AI=AB=AD=c,先将S1表示出来,再证△BEF≌△BEM(AAS)得到EN的表示,从而达到S1和S2的关系.
【解答】(1)解:设BF=a,则BG=a+1,
∵△ABF≌△BCG,
∴AF=BG=a+1,
∵AB=5,
∴在Rt△ABF中,BF2+AF2=AB2,
即a2+(a+1)2=25,
解得a=3(负值舍去),
∴BF=3,AF=4,
∴S△ABFBF AF=6.
(2)证明:∵b=2a,
∴AF=2BF=2AE,
∴AE=EF,
∵四边形EHGF是正方形,
∴HG=HE=EF=GF=BF,
∵AF=BG,∠AFB=∠HGE=90°,
∴△HGB≌△BFA(SAS),
∴∠GBH=∠BAF,
∵DE∥BG,
∴∠BHE=∠HBG,
∴∠BAE=∠BHE.
(3)证明:设DH=CG=BF=AE=a,正方形HEFG的边长为b,AI=AB=AD=c,
如图,过E分别作AB,AD的垂线,垂足分别为M、N,
S1=a(a+b+c)=a(a+b)+ac=AD EN+ac,
∵BE平分∠ABF,
∴∠FBE=∠MBE,
∵∠BME=∠BFE=90°,BE=BE,
∴△BEF≌△BEM(AAS),
∴BM=BF=a,
∴NE=AM=c﹣a,
∴S1=AD EN+ac=c(c﹣a)+ac=c2=S2.
∴S1=S2.
【点评】本题主要考查了正方形的性质、全等三角形的判定和性质、勾股定理等内容,熟练掌握相关知识是解题的关键.
18.数学活动课上,某小组将一个含45°的三角尺AEF和一个正方形纸板ABCD如图1摆放,若AE=1,AB=2.将三角尺AEF绕点A逆时针方向旋转α(0°≤α≤90°)角,观察图形的变化,完成探究活动.
【初步探究】
如图2,连接BE,DF并延长,延长线相交于点G,BG交AD于点M.
问题1 BE和DF的数量关系是 BE=DF ,位置关系是 BE⊥DF .
【深入探究】
应用问题1的结论解决下面的问题.
问题2 如图3,连接BD,点O是BD的中点,连接OA,OG.求证OA=OD=OG.
【尝试应用】
问题3 如图4,请直接写出当旋转角α从0°变化到60°时,点G经过路线的长度.
【考点】四边形综合题.
【专题】压轴题;几何直观.
【答案】(1)BE=DF,BE⊥DF;(2)证明过程详见解析;(3)π.
【分析】(1)先证△AEB≌△AFD,得到BE=DF,再根据△AMB和△DMG内角和推导,证∠G=90°即可;
(2)利用直角三角形斜边上的中线等于斜边的一半即可得证;
(3)由(2)知点OA=OD=OG,则点G的运动轨迹是以O为圆心,OA为半径的弧上,再根据α的变化求圆心角即可得解.
【解答】(1)解:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵△AEF是含有45°的直角三角尺,
∴△AEF是等腰直角三角形,
∴AE=AF,∠EAF=90°,
∵∠BAD﹣∠DAE=∠EAF﹣∠DAE,
∴∠BAE=∠DAF,
∴△ABE≌△ADF(SAS),
∴BE=DF,∠ABE=∠ADF,
∵∠AMB=∠DMG,
∴∠G=∠BAM=90°,即BE⊥DF,
故答案为:BE=DF,BE⊥DF.
(2)∵△BAD是直角三角形,O是BD中点,
∴OABD=OD,
由(1)知∠G=90°,
∴△BGD是直角三角形,
∴OGBD=OD,
∴OA=OD=OG.
(3)由(2)知,OA=OD=OG,
∴点G的运动轨迹是以O为圆心,OA为半径的弧,
连接OA,OG,
∵旋转角α从0°变化到60°,
∴此时点G的运动路线就是,
取AB中点H,连接EH,
∵∠BAE=60°,AE=1,AB=2,
∴AE=AHAB=BH,
∴△AEH为等边三角形,
∴EH=AH=BH,∠AHE=∠AEH=60°
∴∠HBE=∠BEH,
∵∠AHE=∠HBE+∠BEH,
∴∠HBE=∠BEHAHE=30°,
即∠ABE=30°,
∴∠OBG=45°﹣30°=15°,
∵OB=OGBD,
∴∠DOG=30°,
∴∠AOG=180°﹣∠AOB﹣∠DOG=60°,
∵AB=2,
∴BDAB=2,
∴OA=OG,
∴的长度π.
即点G经过路线的长度为π.
【点评】本题主要考查了正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、直角三角形的性质、弧长公式等内容,熟练掌握相关知识是解题的关键.
19.【教材呈现】如图是华师版九年级上册数学教材第78页的部分内容.
例1:求证:三角形的一条中位线与第三边上的中线互相平分. 已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC. 求证:AE、DF互相平分. 证明:连接DE、EF.
请根据教材提示,结合图①,写出完整的解题过程.
【拓展】如图②,设图①中的AE与DF的交点为G,连接CD,分别交AE、EF于点H、K.
(1) .
(2)若四边形FGHK的面积为3,则四边形ADEF的面积为 18 .
【考点】四边形综合题.
【专题】代数几何综合题;压轴题;多边形与平行四边形;几何直观.
【答案】【教材呈现】见解答;
【拓展】(1);(2)18.
【分析】【教材呈现】证明DE∥AC,且DEAC=AF,即可求解;
【拓展】(1)证明△DHG∽△CHE,则,即DHHC,进而求解;
(2)S△DHE+S△DHG=S四边形GFKH+S△EHK,即2a+S△DHG=3+a,故S△DHG=3﹣a,而K是平行四边形DFCE的对角线的交点,故K是EF的中点,同理S△DHE+S△EHK=S四边形GFKH+S△DGH,则3a=6﹣a,解得a,即可求解.
【解答】【教材呈现】证明:连接DE、EF,
则DE是△ABC的中位线,故DE∥AC,且DEAC=AF,
故四边形DAFE为平行四边形,
∴AE、DF互相平分;
【拓展】(1)解:同理可得,四边形DFCE为平行四边形,则KD=KC,DF=EC=BE,
∵DGBE,FGEC,
∴DG=FGEC,
∵DF∥BC,
∴△DHG∽△CHE,
∴,即DHHC,
设DH=x,则HC=2x,CD=DH+HC=3x,则CKCDx,
故,
故答案为;
(2)解:设△HKE的面积为a,
∵DH=x,HKx,则△DHE的面积为2a,
∵G是DF的中点,
∴S△DHE+S△DHG=S四边形GFKH+S△EHK,
即2a+S△DHG=3+a,故S△DHG=3﹣a,
∵K是平行四边形DFCE的对角线的交点,故K是EF的中点,
同理S△DHE+S△EHK=S四边形GFKH+S△DGH,
即3a=6﹣a,解得a,
故S△EFG=a+3,
∵四边形ADEF为平行四边形,
故四边形ADEF的面积=4S△EFG=18,
故答案为18.
【点评】本题为四边形综合题,涉及到三角形中位线的性质、平行四边形的性质、三角形面积的计算等,综合性比较强,难度较大.
20.【模型定义】
它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.他们得知这种模型称为“手拉手模型”.如果把小等腰三角形的腰长看作是小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手.
【模型探究】
(1)如图1,若△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,易证△CDA≌△CEB,则∠AEB的度数为 60° ;
【模型应用】
(2)如图2,P为等边△ABC内一点,PA:PB:PC=3:4:5,且PA=3,以BP为边构造等边△BPQ,这样就有两个等边三角形共顶点B,然后连接CQ,∠APB的度数是 150° ;S四边形BPCQ= 46 ;
(3)如图3,点P是等腰直角△ACB中内一点,∠ACB=90°,且CP=1,,AP=2,以CP为直角边构造等腰直角△DCP,点C为直角顶点,则∠CPB的度数是 135° ;AC的长为 ;
【深化模型】
(4)如图4,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°;⑥CO平分∠BCD,恒成立的结论有 ①②③⑤ .
【拓展提高】
(5)如图5,在△ABC中,∠ACB=90°,∠BAC=30°,AB=6,若点P是△ABC内一点,则PA+PB+PC的最小值为 3 .
(6)如图6,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为 .
【考点】四边形综合题.
【专题】几何综合题;压轴题;图形的全等;等腰三角形与直角三角形;平移、旋转与对称;推理能力.
【答案】(1)60°.
(2)150°;46;
(3)135°;;
(4)①②③⑤.
(5)3;
(6).
【分析】(1)先证明△ACD≌△BCE(SAS),可得∠ADC=∠BEC,再利用等边三角形性质可得∠CDE=∠CED=60°,进而得出∠ADC=∠BEC=120°,即可求得答案.
(2)先证明△ABP≌△CBQ(SAS),可得AP=CQ,∠APB=∠CQB,由等边三角形性质可得:PQ=BQ=PB=4,∠PBQ=∠BQP=60°,再运用勾股定理逆定理可得∠PQC=90°,再利用S四边形BPCQ=S△BPQ+S△CPQ即可求得答案.
(3)连接AD,先证明△CAD≌△CBP(SAS),可得:AD=BP,∠CDA=∠CPB,再运用勾股定理逆定理可得∠ADP=90°,推出∠APC=90°,运用勾股定理即可求得答案.
(4)利用SAS证得△DCA≌△ECB,可得AD=BE,故结论①正确.利用ASA证得△ACP≌△BCQ,可得CP=CQ,故结论③正确.利用等边三角形的性质推出∠ACB=∠CPQ,再运用平行线的判定可得PQ∥AE,故结论②正确.没有条件证出BO=OE,故结论④错误.利用三角形外角性质可得∠AOB=∠ACB=60°,故结论⑤正确.由PC=QC,∠AOC=∠EOC,OC=OC,不能说明△POC与△QOC全等,∠BCO≠∠DCO,故结论⑥错误.
(5)将△BAP绕点B逆时针旋转60°得到△BA′P′,连接PP′,A′C,过点A′作A′K⊥BC,交CB的延长线于点K,可得PA+PB+PC=P′A′+PP′+PC≥A′C,再运用勾股定理即可得出答案.
(6)过点A作EA⊥AD,且AE=AD,连接CE,DE,运用勾股定理可得CE,利用SAS可证得△BAD≌△CAE,即可得出答案.
【解答】解:(1)如图1,
∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
即∠ACD+∠BCD=∠BCD+∠BCE,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
∴∠AEB=∠BEC﹣∠CED=60°.
故答案为:60°.
(2)如图2,
∵△ABC与△BPQ都是等边三角形,
∴AB=BC,BP=BQ=PQ,∠ABC=∠PBQ=∠BQP=60°,
∴∠ABC﹣∠PBC=∠PBQ﹣∠PBC,即∠ABP=∠CBQ,
在△ABP和△CBQ中,
,
∴△ABP≌△CBQ(SAS),
∴AP=CQ,∠APB=∠CQB,
∵PA:PB:PC=3:4:5,且PA=3,
∴PB=4,PC=5,CQ=3,
∵△BPQ是等边三角形,
∴PQ=BQ=PB=4,∠PBQ=∠BQP=60°,
在△CPQ中,CQ2+PQ2=32+42=25=PC2,
∴∠PQC=90°,
∴∠BQC=∠BQP+∠PQC=60°+90°=150°,
∴∠APB=150°;
S四边形BPCQ=S△BPQ+S△CPQ423×4=46;
故答案为:150°;46;
(3)如图3,连接AD,
∵△ACB、△DCP均为等腰直角三角形,
∴∠ACB=∠DCP=90°,CA=CB,CD=CP,
∴∠DCP﹣∠ACP=∠ACB﹣∠ACP,
即∠ACD=∠BCP,
在△CAD和△CBP中,
,
∴△CAD≌△CBP(SAS),
∴AD=BP,∠CDA=∠CPB,
在等腰直角三角形DCP中,CP=1,∠DCP=90°,
∴CD=1,DP,∠CDP=∠CPD=45°,
在△ADP中,AD2+DP2=()2+()2=4,AP2=22=4,
∴AD2+DP2=AP2,
∴∠ADP=90°,
∴∠CDA=∠CDP+∠ADP=45°+90°=135°,
∴∠CPB=135°;
∵AD=DP,∠ADP=90°,
∴∠APD=45°,
∴∠APC=∠APD+∠CPD=45°+45°=90°,
∴AC,
故答案为:135°;;
(4)∵△ABC和△CDE是等边三角形,
∴BC=AC,DE=DC=CE,∠BCA=∠DCE=60°,
∴∠BCA+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE.
在△DCA和△ECB中,
,
∴△DCA≌△ECB(SAS),
∴AD=BE,故结论①正确.
∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠ACB=∠ECD=60°,
∴∠BCD=60°,
∴∠ACP=∠BCQ=60°.
在△ACP与△BCQ中,
,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,故结论③正确.
∵∠PCQ=60°,
∴△PCQ是等边三角形,
∴∠CPQ=60°,
∴∠ACB=∠CPQ,
∴PQ∥AE,故结论②正确.
没有条件证出BO=OE,故结论④错误.
∵∠CAD=∠CBE,∠APC=∠OPB,
∴∠AOB=∠ACB=60°,故结论⑤正确.
∵PC=QC,∠AOC=∠EOC,OC=OC,
∴不能说明△POC与△QOC全等,
∴∠BCO≠∠DCO,故结论⑥错误.
综上所述,正确的结论有①②③⑤,
故答案为:①②③⑤.
(5)如图5,将△BAP绕点B逆时针旋转60°得到△BA′P′,连接PP′,A′C,
过点A′作A′K⊥BC,交CB的延长线于点K,
则∠A′BP′=∠ABP,BP′=BP,A′B=AB,P′A′=PA,
在△ABC中,∠ACB=90°,∠BAC=30°,AB=6,
∴∠ABC=60°,BCAB=3,
∵BP′=BP,∠P′BP=60°,
∴△BPP′是等边三角形,
∴PP′=BP,
∴PA+PB+PC=P′A′+PP′+PC≥A′C,
∵∠PBC+∠ABP=∠ABC=60°,
∴∠PBC+∠A′BP′=60°,
∴∠A′BC=∠PBC+∠A′BP′+∠P′BP=120°,
∴∠A′BK=180°﹣∠A′BC=60°,
∵∠A′KB=90°,
∴∠BA′K=30°,
∴BKA′B=3,
在Rt△A′BK中,A′K3,
∴CK=BC+BK=3+3=6,
在Rt△A′CK中,A′C3,
∴PA+PB+PC的最小值为3,
故答案为:3;
(6)过点A作EA⊥AD,且AE=AD,连接CE,DE,如图6所示:
则△ADE是等腰直角三角形,∠EAD=90°,
∴DEAD=4,∠EDA=45°,
∵∠ADC=45°,
∴∠EDC=45°+45°=90°,
在Rt△DCE中,CE,
∵∠ACB=∠ABC=45°,
∴∠BAC=90°,AB=AC,
∵∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
故答案为:.
【点评】此题是三角形综合题,主要考查了等腰三角形的性质,直角三角形的性质,等腰直角三角形的性质,等边三角形的性质,三角形的内角和定理,三角形外角的性质,全等三角形的判定和性质,勾股定理,旋转变换的性质等,熟练掌握全等三角形的判定和性质是解本题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
