2026年中考数学核心考点一轮复习 图形的旋转(含解析)
文档属性
| 名称 | 2026年中考数学核心考点一轮复习 图形的旋转(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 15:10:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学一轮复习 图形的旋转
一.解答题(共20小题)
1.综合与实践
【问题情境】
数学活动课上,老师发给每位同学一个直角三角形纸片ABC,∠BAC=90°,AB=3,AC=4.
【问题发现】
奋进小组将三角形纸片ABC进行以下操作:第一步:折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE;第二步:然后将△DEC绕点D顺时针方向旋转得到△DFG.点E,C的对应点分别是点F,G,直线GF与边AC交于点M(点M不与点A重合),与边AB交于点N.
如图1小明发现,折痕DE的长很容易求出,并且MF和ME的数量关系也能证明.
如图2小红发现,在△DEC绕点D旋转的过程中,当直线GF经过点B时或直线GF∥BC时,AM的长都可求…
【问题提出与解决】
奋进小组根据小明和小红的发现,讨论后提出问题1和问题2,请你解答.
问题1:如图1,按照如上操作
(1)折痕DE的长为 ;
(2)在△DEC绕点D旋转的过程中,直接写出MF与ME的数量关系;
问题2:在△DEC绕点D旋转的过程中,如图2,探究当直线GF∥BC时,求AM的长;
【拓展应用】
小刚受到探究过程的启发,在△DEC绕点D旋转的过程中,尝试画图,并提出问题3,请你解答.
问题3:在△DEC绕点D旋转的过程中,连接AF,当AF取最小值时,请直接写出△AMD的面积.
2.在Rt△ABC中,∠ACB=90°,AC=1,BC=3.
(1)问题发现
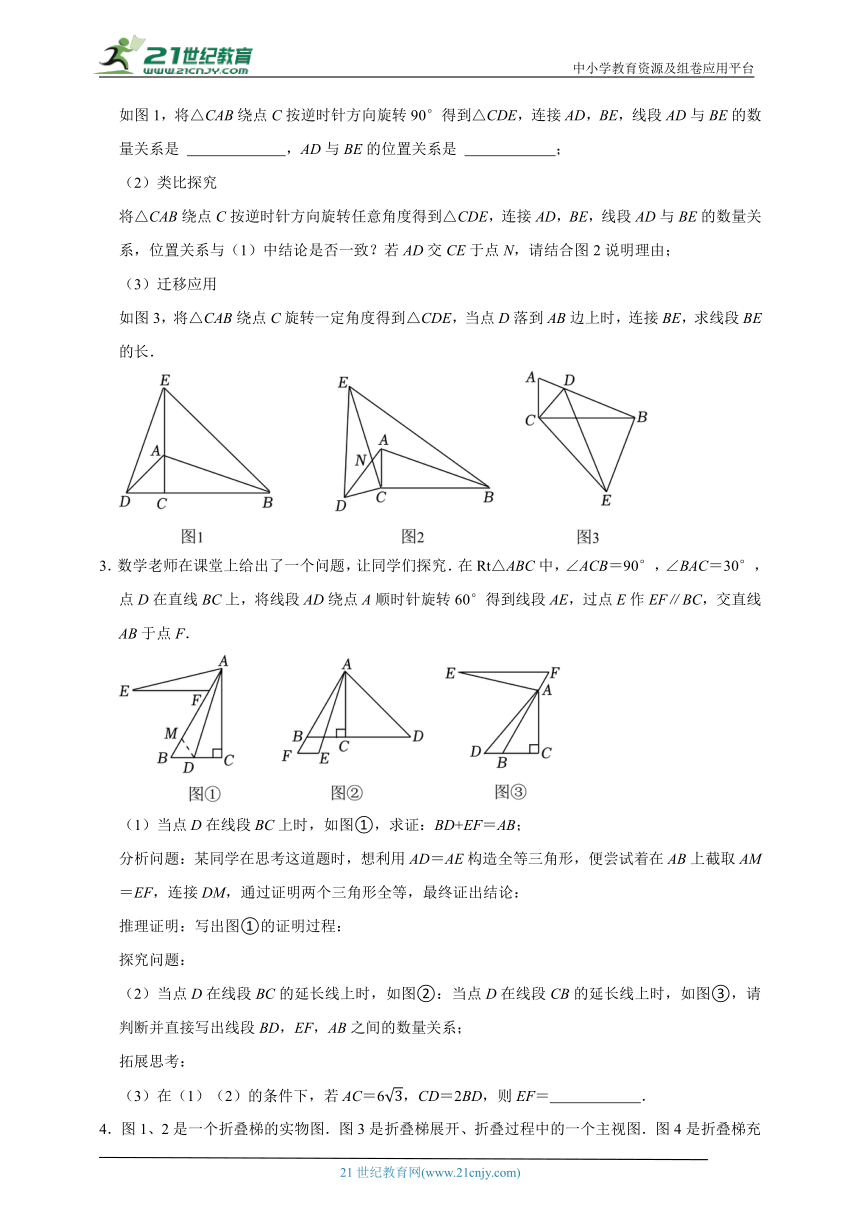
如图1,将△CAB绕点C按逆时针方向旋转90°得到△CDE,连接AD,BE,线段AD与BE的数量关系是 ,AD与BE的位置关系是 ;
(2)类比探究
将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,连接AD,BE,线段AD与BE的数量关系,位置关系与(1)中结论是否一致?若AD交CE于点N,请结合图2说明理由;
(3)迁移应用
如图3,将△CAB绕点C旋转一定角度得到△CDE,当点D落到AB边上时,连接BE,求线段BE的长.
3.数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.
(1)当点D在线段BC上时,如图①,求证:BD+EF=AB;
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
(2)当点D在线段BC的延长线上时,如图②:当点D在线段CB的延长线上时,如图③,请判断并直接写出线段BD,EF,AB之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若AC=6,CD=2BD,则EF= .
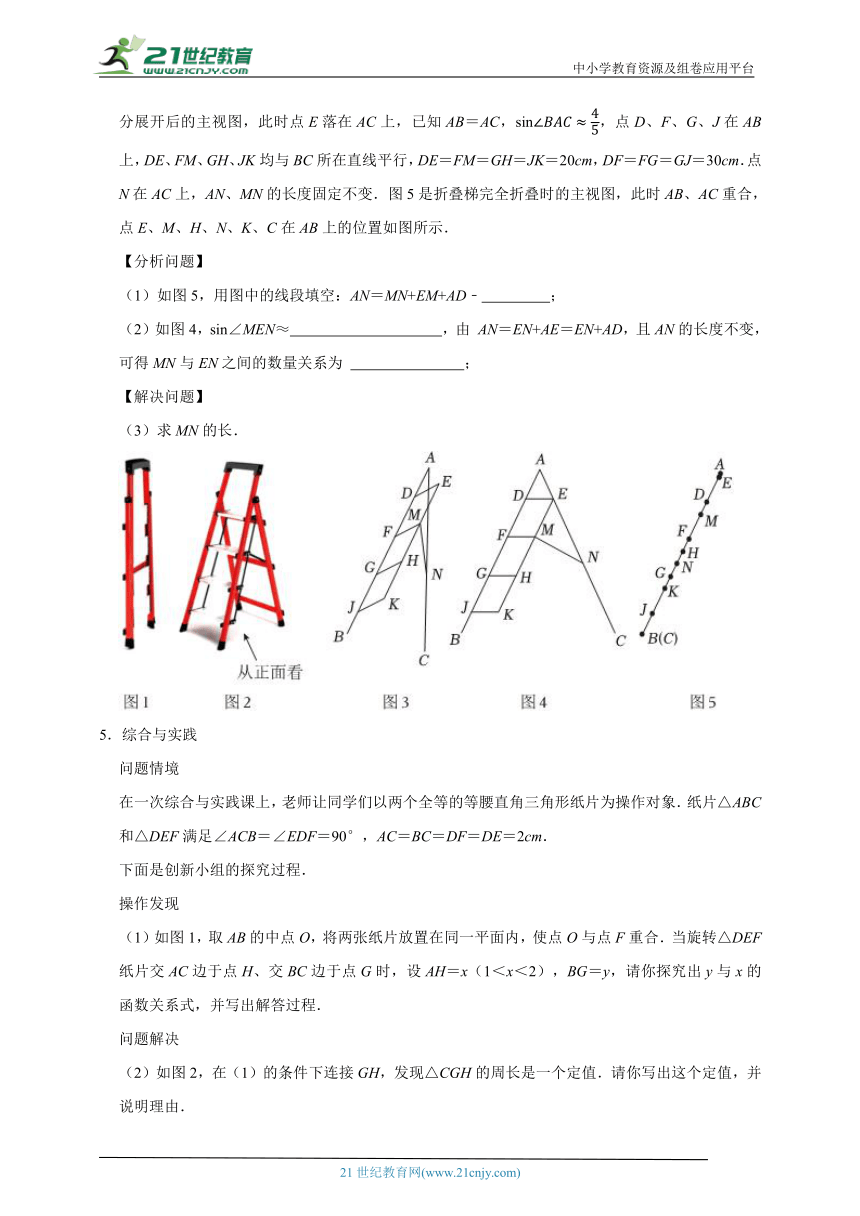
4.图1、2是一个折叠梯的实物图.图3是折叠梯展开、折叠过程中的一个主视图.图4是折叠梯充分展开后的主视图,此时点E落在AC上,已知AB=AC,sin,点D、F、G、J在AB上,DE、FM、GH、JK均与BC所在直线平行,DE=FM=GH=JK=20cm,DF=FG=GJ=30cm.点N在AC上,AN、MN的长度固定不变.图5是折叠梯完全折叠时的主视图,此时AB、AC重合,点E、M、H、N、K、C在AB上的位置如图所示.
【分析问题】
(1)如图5,用图中的线段填空:AN=MN+EM+AD﹣ ;
(2)如图4,sin∠MEN≈ ,由 AN=EN+AE=EN+AD,且AN的长度不变,可得MN与EN之间的数量关系为 ;
【解决问题】
(3)求MN的长.
5.综合与实践
问题情境
在一次综合与实践课上,老师让同学们以两个全等的等腰直角三角形纸片为操作对象.纸片△ABC和△DEF满足∠ACB=∠EDF=90°,AC=BC=DF=DE=2cm.
下面是创新小组的探究过程.
操作发现
(1)如图1,取AB的中点O,将两张纸片放置在同一平面内,使点O与点F重合.当旋转△DEF纸片交AC边于点H、交BC边于点G时,设AH=x(1<x<2),BG=y,请你探究出y与x的函数关系式,并写出解答过程.
问题解决
(2)如图2,在(1)的条件下连接GH,发现△CGH的周长是一个定值.请你写出这个定值,并说明理由.
拓展延伸
(3)如图3,当点F在AB边上运动(不包括端点A、B),且始终保持∠AFE=60°.请你直接写出△DEF纸片的斜边EF与△ABC纸片的直角边所夹锐角的正切值 (结果保留根号).
6.在等腰直角△ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD.将线段AD绕点D按顺时针方向旋转90°得线段ED,连接BE.
【尝试发现】
(1)如图1,当点D在线段BC上时,线段BE与CD的数量关系为 ;
【类比探究】
(2)当点D在线段BC的延长线上时,先在图2中补全图形,再探究线段BE与CD的数量关系并证明;
【联系拓广】
(3)若AC=BC=1,CD=2,请直接写出sin∠ECD的值.
7.如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B,点P在CB上.
(1)【动手操作】
如图②,若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形,图中∠PBE的度数为 度;
(2)【问题探究】
根据(1)所画图形,探究线段PA与PE的数量关系,并说明理由;
(3)【拓展延伸】
如图③,若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD交于点E,探究线段BA,BP,BE之间的数量关系,并说明理由.
8.【问题呈现】
△CAB和△CDE都是直角三角形,∠ACB=∠DCE=90°,CB=mCA,CE=mCD,连接AD,BE,探究AD,BE的位置关系.
【问题探究】
(1)如图1,当m=1时,直接写出AD,BE的位置关系: .
(2)如图2,当m≠1时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.
【拓展应用】
(3)当m,AB=4,DE=4时,将△CDE绕点C旋转,使A,D,E三点恰好在同一直线上,求BE的长.
9.1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.
(1)下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
当△ABC的三个内角均小于120°时,
如图1,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′,
由PC=P′C,∠PCP′=60°,可知△PCP′为 三角形,故PP′=PC,又P′A′=PA,故PA+PB+PC=P′A′+PB+PP′≥A′B,
由 可知,当B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,如图2,最小值为A′B,此时的P点为该三角形的“费马点”,
且有∠APC=∠BPC=∠APB= ;
已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点.如图3,若∠BAC≥120°,则该三角形的“费马点”为 点.
(2)如图4,在△ABC中,三个内角均小于120°,且AC=3,BC=4,∠ACB=30°,已知点P为△ABC的“费马点”,求PA+PB+PC的值;
(3)如图5,设村庄A,B,C的连线构成一个三角形,且已知AC=4km,BC=2km,∠ACB=60°.现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/km,a元/km,a元/km,选取合适的P的位置,可以使总的铺设成本最低为 元.(结果用含a的式子表示)
10.【模型建立】
(1)如图1,△ABC和△BDE都是等边三角形,点C关于AD的对称点F在BD边上.
①求证:AE=CD;
②用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型应用】
(2)如图2,△ABC是直角三角形,AB=AC,CD⊥BD,垂足为D,点C关于AD的对称点F在BD边上.用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型迁移】
(3)在(2)的条件下,若AD=4,BD=3CD,求cos∠AFB的值.
11.综合与实践
问题情境
数学活动课上,老师发给每名同学一个等腰三角形纸片ABC,AB=AC,∠BAC>90°,要求同学们将纸片沿一条直线折叠,探究图形中的结论.
问题发现
奋进小组在边AC上取一点D,连接BD,将这个纸片沿BD翻折,点A的对应点为E,如图1所示.
如图2,小明发现,当点E落在边BC上时,∠DEC=2∠ACB.
如图3,小红发现,当点D是AC的中点时,连接CE,若已知AB和CE的长,则可求BD的长.
……
问题提出与解决
奋进小组根据小明和小红的发现,讨论后提出问题1,请你解答.
问题1:在△ABC中,AB=AC,∠BAC>90°,点D是边AC上一点,将△ABD沿BD翻折得到△EBD.
(1)如图2,当点E在边BC上时,求证:∠DEC=2∠ACB.
(2)如图3,当点D是AC的中点时,连接CE,若AB=4,CE=3,求BD的长.
拓展延伸
小刚受到探究过程的启发,将等腰三角形的顶角改为锐角,尝试画图,并提出问题2,请你解答.
问题2:如图4,点D是△ABC外一点,AB=AC=BD=4,CD=1,∠ABD=2∠BDC,求BC的长.
12.如图1,在△ABC中,AB=AC,点M,N分别为边AB,BC的中点,连接MN.
初步尝试:(1)MN与AC的数量关系是 ,MN与AC的位置关系是 .
特例研讨:(2)如图2,若∠BAC=90°,BC=4,先将△BMN绕点B顺时针旋转α(α为锐角),得到△BEF,当点A,E,F在同一直线上时,AE与BC相交于点D,连接CF.
①求∠BCF的度数;
②求CD的长.
深入探究:(3)若∠BAC<90°,将△BMN绕点B顺时针旋转α,得到△BEF,连接AE,CF.当旋转角α满足0°<α<360°,点C,E,F在同一直线上时,利用所提供的备用图探究∠BAE与∠ABF的数量关系,并说明理由.
13.【问题情境】如图,在△ABC中,AB=AC,∠ACB=α,点D在边BC上.将线段DB绕点D顺时针旋转得到线段DE(旋转角小于180°),连接BE,CE,以CE为底边在其上方作等腰三角形FEC,使∠FCE=α,连接AF.
【尝试探究】
(1)如图1,当α=60°时,易知AF=BE;
如图2,当α=45°时,则AF与BE的数量关系为 ;
(2)如图3,写出AF与BE的数量关系(用含α的三角函数表示),并说明理由;
【拓展应用】
(3)如图4,当α=30°且点B,E,F三点共线时.若BC=4,BDBC,请直接写出AF的长.
14.【特例感知】
(1)如图1,△AOB和△COD是等腰直角三角形,∠AOB=∠COD=90°,点C在OA上,点D在BO的延长线上,连接AD,BC,线段AD与BC的数量关系是 ;
【类比迁移】
(2)如图2,将图1中的△COD绕着点O顺时针旋转α(0°<α<90°),那么第(1)问的结论是否仍然成立?如果成立,证明你的结论;如果不成立,说明理由.
【方法运用】
(3)如图3,若AB=8,点C是线段AB外一动点,AC=3,连接BC.
①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值是 ;
②若以BC为斜边作Rt△BCD(B,C,D三点按顺时针排列),∠CDB=90°,连接AD,当∠CBD=∠DAB=30°时,直接写出AD的值.
15.【问题情境】
在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中∠ACB=∠DEB=90°,∠B=30°,BE=AC=3.
【问题探究】
小昕同学将三角板DEB绕点B按顺时针方向旋转.
(1)如图2,当点E落在边AB上时,延长DE交BC于点F,求BF的长.
(2)若点C、E、D在同一条直线上,求点D到直线BC的距离.
(3)连接DC,取DC的中点G,三角板DEB由初始位置(图1),旋转到点C、B、D首次在同一条直线上(如图3),求点G所经过的路径长.
(4)如图4,G为DC的中点,则在旋转过程中,点G到直线AB的距离的最大值是 .
16.在△ABC中,点D,E分别是AB,AC边上的点,DE∥BC.
基础理解:
(1)如图1,若AD=4,BD=3,求的值;
证明与拓展:
(2)如图2,将△ADE绕点A逆时针旋转度,得到△AD1E1,连接BD1,CE1.
①求证:;
②如图3,若∠BAC=90°,AB<AC,AD=6,△ADE在旋转过程中,点D1恰好落在DE上时,连接EE1,,则△E1D1E的面积为 .
17.数学课上,有这样一道探究题.
如图,已知△ABC中,AB=AC=m,BC=n,∠BAC=α(0°<α<180°),点P为平面内不与点A、C重合的任意一点,连接CP,将线段CP绕点P顺时针旋转α,得线段PD,连接CD、AP点E、F分别为BC、CD的中点,设直线AP与直线EF相交所成的较小角为β,探究的值和β的度数与m、n、α的关系.
请你参与学习小组的探究过程,并完成以下任务:
(1)填空:
【问题发现】
小明研究了α=60°时,如图1,求出了的值和β的度数分别为 ,β= ;
小红研究了α=90°时,如图2,求出了的值和β的度数分别为 ,β= ;
【类比探究】
他们又共同研究了α=120°时,如图3,也求出了的值和β的度数;
【归纳总结】
最后他们终于共同探究得出规律: (用含m、n的式子表示);β= (用含α的式子表示).
(2)求出α=120°时的值和β的度数.
18.在一平面内,线段AB=20,线段BC=CD=DA=10,将这四条线段顺次首尾相接.把AB固定,让AD绕点A从AB开始逆时针旋转角α(α>0°)到某一位置时,BC,CD将会跟随出现到相应的位置.
论证:如图1,当AD∥BC时,设AB与CD交于点O,求证:AO=10;
发现:当旋转角α=60°时,∠ADC的度数可能是多少?
尝试:取线段CD的中点M,当点M与点B距离最大时,求点M到AB的距离;
拓展:①如图2,设点D与B的距离为d,若∠BCD的平分线所在直线交AB于点P,直接写出BP的长(用含d的式子表示);
②当点C在AB下方,且AD与CD垂直时,直接写出α的余弦值.
19.[初步尝试]
(1)如图①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 ;
[思考说理]
(2)如图②,在三角形纸片ABC中,AC=BC=6,AB=10,将△ABC折叠,使点B与点C重合,折痕为MN,求的值;
[拓展延伸]
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B′处,折痕为CM.
①求线段AC的长;
②若点O是边AC的中点,点P为线段OB′上的一个动点,将△APM沿PM折叠得到△A′PM,点A的对应点为点A′,A′M与CP交于点F,求的取值范围.
20.(1)【操作发现】
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①请按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的对应点为点B′,点C的对应点为点C′.连接BB′;
②在①中所画图形中,∠AB′B= °.
(2)【问题解决】
如图2,在Rt△ABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接DE,求∠ADE的度数.
(3)【拓展延伸】
如图3,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k为常数),求BD的长(用含k的式子表示).
中考数学一轮复习 图形的旋转
参考答案与试题解析
一.解答题(共20小题)
1.综合与实践
【问题情境】
数学活动课上,老师发给每位同学一个直角三角形纸片ABC,∠BAC=90°,AB=3,AC=4.
【问题发现】
奋进小组将三角形纸片ABC进行以下操作:第一步:折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE;第二步:然后将△DEC绕点D顺时针方向旋转得到△DFG.点E,C的对应点分别是点F,G,直线GF与边AC交于点M(点M不与点A重合),与边AB交于点N.
如图1小明发现,折痕DE的长很容易求出,并且MF和ME的数量关系也能证明.
如图2小红发现,在△DEC绕点D旋转的过程中,当直线GF经过点B时或直线GF∥BC时,AM的长都可求…
【问题提出与解决】
奋进小组根据小明和小红的发现,讨论后提出问题1和问题2,请你解答.
问题1:如图1,按照如上操作
(1)折痕DE的长为 ;
(2)在△DEC绕点D旋转的过程中,直接写出MF与ME的数量关系;
问题2:在△DEC绕点D旋转的过程中,如图2,探究当直线GF∥BC时,求AM的长;
【拓展应用】
小刚受到探究过程的启发,在△DEC绕点D旋转的过程中,尝试画图,并提出问题3,请你解答.
问题3:在△DEC绕点D旋转的过程中,连接AF,当AF取最小值时,请直接写出△AMD的面积.
【考点】几何变换综合题.
【专题】三角形.
【答案】问题1:(1);(2)MF=ME;问题2:AM;问题3:.
【分析】问题1:(1)由折叠的性质可知AE=CE,DE⊥AC,再证DE是△ABC的中位线,即可得出结论;
(2)连接DM,由旋转知DE=DF,∠DFM=∠DEM=90°,再证△DMF≌△DME即可得出结论;
问题2:过点A作AH⊥BC于H,交FG于K.则四边形DFKH是矩形,得出,由三角形面积求出AH,然后证△AKM∽△AHC,得出,即可得出结论;
问题3:连接AD、DM,则AF+DF≥AD,当A、F、D三点共线时,AF+DF=AD,此时AF+DF的值最小,AF最小,由直角三角形斜边中线的性质得,证明△AMF∽△CBA,由相似三角形的性质得出AM的长,利用三角形面积公式即可解答.
【解答】解:问题1:(1)∵折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE,
∴AE=CE,DE⊥AC,
∵∠BAC=90°,
∴DE∥AB,
∴,
∴CD=BD,
∴DE为△ABC的中位线,
∴,
故答案为:;
(2)如图,连接DM,
∵将△DEC绕点D顺时针方向旋转得到△DFG,
∴DE=DF,∠DFM=∠DEM=90°,
在Rt△DMF和Rt△DME中,
,
∴Rt△DMF≌Rt△DME(HL),
∴MF=ME;
问题2:①过点A作AH⊥BC于H,交FG于K,
∵GF∥BC,
∴∠HKF=90°,
∵∠DFG=90°,
∴四边形DFKH是矩形,
∴,
∵AB=3,AC=4,
∴,
∵,
∴3×4=5AH,
解得:,
∴,
∵GF∥BC,
∴△AKM∽△AHC,
∴,
解得:AM;
问题3:如图,连接AD、DM,
∵AF+DF≥AD,
∴A、F、D三点共线时,AF+DF=AD,此时AF+DF的值最小,AF最小,
∵∠BAC=90°,BD=CD,
∴,
∴,∠DAC=∠C,
∵∠AFM=∠BAC,
∴△AMF∽△CBA,
∴,即,
解得:,
∴.
【点评】本题考查旋转的性质、全等三角形的判定与性质、相似三角形的判定与性质、矩形的判定与性质、三角形的三边关系及勾股定理,熟练掌握相关性质及判定定理是解题关键.
2.在Rt△ABC中,∠ACB=90°,AC=1,BC=3.
(1)问题发现
如图1,将△CAB绕点C按逆时针方向旋转90°得到△CDE,连接AD,BE,线段AD与BE的数量关系是 BE=3AD ,AD与BE的位置关系是 AD⊥BE ;
(2)类比探究
将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,连接AD,BE,线段AD与BE的数量关系,位置关系与(1)中结论是否一致?若AD交CE于点N,请结合图2说明理由;
(3)迁移应用
如图3,将△CAB绕点C旋转一定角度得到△CDE,当点D落到AB边上时,连接BE,求线段BE的长.
【考点】几何变换综合题.
【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.
【答案】(1)BE=3AD,AD⊥BE;
(2)线段AD与BE的数量关系,位置关系与(1)中结论一致,理由见解析过程;
(3).
【分析】(1)由旋转的性质可得AC=DC=1,BC=CE=3,∠ECB=∠ACD=90°,由等腰直角三角形的性质可得AD,BE=3,∠CAD=∠ADC=45°,∠CBE=∠CEB=45°,可证AD⊥BE;
(2)通过证明△BCE∽△ACD,可得,∠CDA=∠CEB,可证BE=3AD,AD⊥BE;
(3)由勾股定理可求AB的长,通过证明△ACN∽△ABC,可求AN的长,由等腰三角形的性质可求AD的长,即可求解.
【解答】解:(1)如图1,延长DA交BE于H,
∵将△CAB绕点C按逆时针方向旋转90°得到△CDE,
∴AC=DC=1,BC=CE=3,∠ECB=∠ACD=90°,
∴AD,BE=3,∠CAD=∠ADC=45°,∠CBE=∠CEB=45°,
∴BE=3AD,∠CAD=∠EAH=45°,
∴∠EHA=90°,
∴AD⊥BE,
故答案为:BE=3AD,AD⊥BE;
(2)线段AD与BE的数量关系,位置关系与(1)中结论一致,理由如下:
如图2,延长DA交BE于H,
∵将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,
∴AC=DC=1,BC=CE=3,∠ECB=∠ACD,
∴,
∴△BCE∽△ACD,
∴,∠CDA=∠CEB,
∴BE=3AD,
∵∠CEB+∠ENH=∠CDA+∠CND=90°,
∴∠EHD=90°,
∴AD⊥BE;
(3)如图3,过点C作CN⊥AB于N,
∵∠ACB=90°,AC=1,BC=3,
∴AB,
∵CN⊥AB,
∴∠ANC=90°=∠ACB,
又∵∠A=∠A,
∴△ACN∽△ABC,
∴,
∴AN 1,
∴AN,
∵AC=DC,CN⊥AB,
∴AD=2AN,
由(2)可知:BE=3AD.
【点评】本题是几何变换综合题,考查了旋转的性质,相似三角形的判定和性质,等腰直角三角形的性质,勾股定理等知识,灵活运用这些性质解决问题是解题的关键.
3.数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.
(1)当点D在线段BC上时,如图①,求证:BD+EF=AB;
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
(2)当点D在线段BC的延长线上时,如图②:当点D在线段CB的延长线上时,如图③,请判断并直接写出线段BD,EF,AB之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若AC=6,CD=2BD,则EF= 10或18 .
【考点】几何变换综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)证明见解析过程;
(2)图②:AB=BD﹣EF,图③:AB=EF﹣BD;
(3)10或18.
【分析】(1)在AB边上截取AM=EF,连接DM,根据题意证明出△DAM≌△AEF(SAS),得到AF=DM,然后证明出△BMD是等边三角形,得到BD=BM=DM,进而求解即可;
(2)图②:在BD上取点H,使BH=AB,连接AH并延长到点G使AG=AF,连接DG,首先证明出△ABH是等边三角形,得到∠BAH=60°,然后求出∠BAH=∠DAE,然后证明出△FAE≌△GAD(SAS),得到EF=DG,∠AFE=∠G,然后证明出△DHG是等边三角形,得到DH=DG=EF,进而求解即可;
图③:在EF上取点H使AH=AF,同理证明出△EAH≌△ADB(AAS),得到BD=AH,AB=EH,进而求解即可;
(3)根据勾股定理和含30°角直角三角形的性质求出BC=6,AB=12,然后结合CD=2BD,分别(1)(2)的条件下求出BD的长度,进而求解即可.
【解答】(1)证明:在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.在AB边上截取AM=EF,连接DM.如图1,
∴∠B=90°﹣∠BAC=90°﹣30°=60°.
∵EF∥BC,
∴∠EFB=∠B=60°.
又∵∠EAD=60°,
∴∠EFB=∠EAD.
又∵∠BAD=∠EAD﹣∠EAF,∠AEF=∠EFB﹣∠EAF,
∴∠BAD=∠AEF.
又∵AD=AE,AM=EF,
∴△DAM≌△AEF(SAS).
∴AF=DM.
∴∠AMD=∠EFA=180°﹣∠EFB=180°﹣60°=120°.
∴∠BMD=180°﹣∠AMD=180°﹣120°=60°.
∵∠B=60°,
∴∠BMD=∠B=∠BDM.
∴△BMD是等边三角形.
∴BD=BM=DM,
∵AB=AM+BM,
∴AB=EF+BD;
(2)解:图②:AB=BD﹣EF,证明如下:
如图2.1所示,在BD上取点H,使BH=AB,连接AH并延长到点G使AG=AF,连接DG,
∵∠ABC=60°,
∴△ABH是等边三角形,
∴∠BAH=60°,
∵线段AD绕点A顺时针旋转60°得到线段AE,
∴∠DAE=60°,AE=AD,
∴∠BAH=∠DAE,
∴∠BAH﹣∠EAH=∠DAE﹣∠EAH,即∠BAE=∠HAD,
又∵AG=AF,
∴△FAE≌△GAD(SAS),
∴EF=DG,∠AFE=∠G,
∵BD∥EF,
∴∠ABC=∠F=∠G=60°,
∵∠DHG=∠AHB=60°,
∴△DHG是等边三角形,
∴DH=DG=EF,
∴AB=BH=BD﹣DH=BD﹣EF;
图③:AB=EF﹣BD,证明如下:
如图2.2所示,在EF上取点H使AH=AF,
∵EF∥BC,
∴∠F=∠ABC=60°,
∵AH=AF,
∴△AHF是等边三角形,
∴∠AHF=∠HAF=60°,
∴∠AHE=120°,
∵将线段AD绕点A顺时针旋转60°得到线段AE,
∴AD=AE,∠DAE=60°,
∴∠DAB+∠EAH=180°﹣∠EAD﹣∠HAF=60°,
∵∠D+∠DAB=∠ABC=60°,
∴∠D=∠EAH,
∵∠DBA=180°﹣∠ABC=120°=∠EHA,
又∵AD=AE,
∴△EAH≌△ADB(AAS),
∴BD=AH,AB=EH,
∵AH=FH,
∴BD=HF,
∴AB=EH=EF﹣FH=EF﹣BD;
(3)解:如图3.1所示,
∵∠BAC=30°,∠C=90°,
∴AB=2BC,AB2=BC2+AC2,
∴,
∴BC=6,
∴AB=2BC=12,
∵CD=2BD,BC=BD+CD,
∴BDBC=2,CD=4,
由(1)可知,BD+EF=AB,
∴EF=AB﹣BD=12﹣2=10;
如图3.2所示,当点D在线段BC的延长线上时,
∵CD<BD,与CD=2BD矛盾,
∴不符合题意;
如图3.3所示,当点D在线段CB的延长线上时,
∵CD=2BD=BD+BC,BC=6,
∴BD=BC=6,
由(2)可知,AB=EF﹣BD,
∵AB=2BC=12,
∴EF=AB+BD=12+6=18.
综上所述,EF=10或18,
故答案为:10或18.
【点评】此题考查了全等三角形的性质和判定,勾股定理,等边三角形的性质和判定,含30°角直角三角形的性质,解题的关键是掌握以上知识点.
4.图1、2是一个折叠梯的实物图.图3是折叠梯展开、折叠过程中的一个主视图.图4是折叠梯充分展开后的主视图,此时点E落在AC上,已知AB=AC,sin,点D、F、G、J在AB上,DE、FM、GH、JK均与BC所在直线平行,DE=FM=GH=JK=20cm,DF=FG=GJ=30cm.点N在AC上,AN、MN的长度固定不变.图5是折叠梯完全折叠时的主视图,此时AB、AC重合,点E、M、H、N、K、C在AB上的位置如图所示.
【分析问题】
(1)如图5,用图中的线段填空:AN=MN+EM+AD﹣ DE ;
(2)如图4,sin∠MEN≈ ,由 AN=EN+AE=EN+AD,且AN的长度不变,可得MN与EN之间的数量关系为 MN+10=EN ;
【解决问题】
(3)求MN的长.
【考点】几何变换综合题.
【专题】解直角三角形及其应用;运算能力;推理能力.
【答案】(1)DE;
(2),MN+10=EN;
(3)40cm.
【分析】(1)AN=MN+EM+AE=MN+EM+(AD﹣DE)=MN+EM+AD﹣DE;
(2)可推出四边形DEMF是平行四边形,从而EM∥DF,从而∠MEN=∠BAC,进而得出sin∠MEN=sin∠BAC,根据AN=MN+EM+AD﹣DE,AN=EN+AD得出MN+EM+AD﹣DE=EN+AD,进一步得出结果;
(3)作MW⊥AC于W,解直角三角形EMN求得MW和EW,进而表示出WN,在直角三角形MNW中根据勾股定理列出方程,进而得出结果.
【解答】解:(1)∵AE=AD﹣DE,
∴AN=MN+EM+AE=MN+EM+(AD﹣DE)=MN+EM+AD﹣DE,
故答案为:DE;
(2)∵DE、FM、GH、JK均与BC所在直线平行,
∴DE∥FM,
∵DE=FM=20cm,
∴四边形DEMF是平行四边形,
∴EM∥DF,
∴∠MEN=∠BAC,
∴sin∠MEN=sin∠BAC,
∵AN=MN+EM+AD﹣DE,AN=EN+AD,
∴MN+EM+AD﹣DE=EN+AD,
∴MN+EM﹣DE=EN,
∴MN+30﹣20=EN,
∴MN+10=EN,
故答案为:,MN+10=EN;
(3)如图,
作MW⊥AC于W,
∴∠MWN=∠MWE=90°,
∴MW2+WN2=MN2,MW=EM sin∠MEN=3024,
∴EW18,
设MN=a,则EN=a+10,WN=EN﹣EW=a+10﹣18=a﹣8,
∴242+(a﹣8)2=a2,
∴a=40,
∴MN=40cm.
【点评】本题考查了解直角三角形的应用,平行四边形的判定和性质等知识,解决问题的关键是理解题意,熟练应用有关基础知识.
5.综合与实践
问题情境
在一次综合与实践课上,老师让同学们以两个全等的等腰直角三角形纸片为操作对象.纸片△ABC和△DEF满足∠ACB=∠EDF=90°,AC=BC=DF=DE=2cm.
下面是创新小组的探究过程.
操作发现
(1)如图1,取AB的中点O,将两张纸片放置在同一平面内,使点O与点F重合.当旋转△DEF纸片交AC边于点H、交BC边于点G时,设AH=x(1<x<2),BG=y,请你探究出y与x的函数关系式,并写出解答过程.
问题解决
(2)如图2,在(1)的条件下连接GH,发现△CGH的周长是一个定值.请你写出这个定值,并说明理由.
拓展延伸
(3)如图3,当点F在AB边上运动(不包括端点A、B),且始终保持∠AFE=60°.请你直接写出△DEF纸片的斜边EF与△ABC纸片的直角边所夹锐角的正切值 2或2 (结果保留根号).
【考点】几何变换综合题.
【专题】分类讨论;等腰三角形与直角三角形;图形的相似;解直角三角形及其应用;应用意识.
【答案】(1)y与x的函数关系式为;
(2)△CHG 的周长为2;
(3)2或2.
【分析】(1)证明△AFH∽△BGF,可得AH BG=AF BF,求出,可得,故,=2,从而y与x的函数关系式为;
(2)求出CH=2﹣x,CG=2﹣y,可得,将xy=2代入得,而1<x<2,1<y<2,知x+y>2,故GH=x+y﹣2,可得△CHG 的周长=CH+CG+GH=2﹣x+2﹣y+x+y﹣2=2;
(3)分两种情况:①过点F作 FN⊥AC于点N,作FH的垂直平分线交FN于点M,连接MH,求出∠AHF=75°,可得∠NMH=30°,设NH=k,则MH=MF=2k,从而FN=MF+MN=(2)k,;②过点F作FN⊥BC于点N,作FG的垂直平分线交BG于点M,连接FM,同理可得GN=GM+MN=(2)k,.
【解答】解:(1)如图:
∵∠ACB=∠EDF=90°,且 AC=BC=DF=DE=2cm,
∴∠A=∠B=∠DFE=45°,
∴∠AFH+∠BFG=∠BFG+∠FGB=135°,
∴∠AFH=∠FGB,
∴△AFH∽△BGF,
∴,
∴AH BG=AF BF,
在 Rt△ACB 中,AC=BC=2,
∴,
∵O是AB的中点,点O与点F重合,
∴,
∴,
∴,
∴y与x的函数关系式为;
(2)△CGH的周长定值为2,理由如下:
∵AC=BC=2,AH=x,BG=y,
∴CH=2﹣x,CG=2﹣y,
在Rt△HCG 中,
∴,
将(1)中xy=2代入得:,
∵1<x<2,y,
∴1<y<2,
∴x+y>2,
∴GH=x+y﹣2,
∴△CHG 的周长=CH+CG+GH=2﹣x+2﹣y+x+y﹣2=2;
(3)①过点F作 FN⊥AC于点N,作FH的垂直平分线交FN于点M,连接MH,如图:
∵∠AFE=60°,∠A=45°,
∴∠AHF=75°,
∴FM=MH,
∵∠FNH=90°,
∴∠NFH=15°,
∵FM=MH,
∴∠NFH=∠MHF=15°,
∴∠NMH=30°,
在 Rt△MNH中,设NH=k,
∴MH=MF=2k,
∴MNk,
∴FN=MF+MN=(2)k,
在Rt△FNH中,
;
②过点F作FN⊥BC于点N,作FG的垂直平分线交BG于点M,连接FM,
∵∠AFE=60°,∠B=45°,
∴∠FGB=∠AFE﹣∠B=15°,
∵GM=MF,
∴∠FGB=∠GFM=15°,
∴∠FMB=30°,
在 Rt△FNM中,设FN=k,
∴GM=MF=2k,
由勾股定理得MNk,
∴GN=GM+MN=(2)k,
在 Rt△FNG 中,
,
综上所述,tan 或 ,
故答案为:2或2.
【点评】本题考查几何变换综合应用,涉及相似三角形判定与性质,等腰直角三角形性质及应用,锐角三角函数,勾股定理及应用等知识,解题的关键是作辅助线,构造直角三角形解决问题.
6.在等腰直角△ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD.将线段AD绕点D按顺时针方向旋转90°得线段ED,连接BE.
【尝试发现】
(1)如图1,当点D在线段BC上时,线段BE与CD的数量关系为 ;
【类比探究】
(2)当点D在线段BC的延长线上时,先在图2中补全图形,再探究线段BE与CD的数量关系并证明;
【联系拓广】
(3)若AC=BC=1,CD=2,请直接写出sin∠ECD的值.
【考点】几何变换综合题.
【专题】图形的全等;推理能力.
【答案】(1);(2),补图及证明见解析;(3)或.
【分析】(1)过点E作EM⊥CB延长线于点M,利用一线三垂直全等模型证明△ACD≌△DME,再证明BM=EM即可;
(2)同(1)中方法证明△ACD≌△DME,再证明BM=EM即可;
(3)过点E作EM⊥CB,求出EM,CE即可.
【解答】解:(1)如图,过点E作EM⊥CB延长线于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴BM=DM﹣BD=AC﹣BD=BC﹣BD=CD,
∴BM=EM,
∵EM⊥CB,
∴,
故答案为:;
(2)补全图形如图,,理由如下:
过点E作EM⊥BC于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴DM=BC,
∴DM﹣CM=BC﹣CM,
∴CD=BM,
∴EM=BM,
∵EM⊥CB,
∴;
(3)如图,当点D在CB延长线上时,过点E作EM⊥CB延长线于点M,
由(2)得DM=AC=1,EM=CD=2,
∴CM=CD+DM=3,
∴,
∴;
当点D在BC延长线上时,过点E作EM⊥CB于点M,
同理可得:△ACD≌△DME,
∴DM=AC=1,ME=CD=2,
∴CM=2﹣1=1,
∴CE,
∴sin∠ECD,
综上,sin∠ECD或.
【点评】本题考查三角形全等的判定与性质,三角函数,掌握一线三垂直全等模型是解题的关键.
7.如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B,点P在CB上.
(1)【动手操作】
如图②,若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形,图中∠PBE的度数为 135 度;
(2)【问题探究】
根据(1)所画图形,探究线段PA与PE的数量关系,并说明理由;
(3)【拓展延伸】
如图③,若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD交于点E,探究线段BA,BP,BE之间的数量关系,并说明理由.
【考点】几何变换综合题.
【专题】图形的全等;等腰三角形与直角三角形;平移、旋转与对称;推理能力;应用意识.
【答案】见试题解答内容
【分析】(1)根据题意画出图形,由CA=CB,∠C=90°,得∠ABC=45°,而BD⊥AB,即得∠PBE=∠ABC+∠ABD=135°;
(2)过P作PM∥AB交AC于M,证明△PCM是等腰直角三角形,得CP=CM,∠PMC=45°,即可证△APM≌△PEB(ASA),故PA=PE;
(3)当P在线段BC上时,过P作PM∥AB交AC于M,结合(2)可得ABBP+BE;当P在线段CB的延长线上时,过P作PN⊥BC交BE于N,证明△BPN是等腰直角三角形,可得∠ABP=135°,BP=NP,BNBP,∠PNB=45°,即可证△EPN≌△APB(ASA),EN=BA,根据BE=EN+BN,即得BE=BABP.
【解答】解:(1)画出图形如下:
∵CA=CB,∠C=90°,
∴∠ABC=45°,
∵BD⊥AB,
∴∠ABD=90°,
∴∠PBE=∠ABC+∠ABD=45°+90°=135°;
故答案为:135;
(2)PA=PE,理由如下:
过P作PM∥AB交AC于M,如图:
∴∠MPC=∠ABC=45°,
∴△PCM是等腰直角三角形,
∴CP=CM,∠PMC=45°,
∴CA﹣CM=CB﹣CP,即AM=BP,∠AMP=135°=∠PBE,
∵∠APE=90°,
∴∠EPB=90°﹣∠APC=∠PAC,
∴△APM≌△PEB(ASA),
∴PA=PE;
(3)当P在线段BC上时,过P作PM∥AB交AC于M,如图:
由(2)可知,BE=PM,BP=AM,
∵AB(AM+CM),
∴ABBPCM,
∵PMCM,
∴ABBP+BE;
当P在线段CB的延长线上时,过P作PN⊥BC交BE于N,如图:
∵∠ABD=90°,∠ABC=45°,
∴∠PBN=180°﹣∠ABC﹣∠ABD=45°,
∴△BPN是等腰直角三角形,∠ABP=135°,
∴BP=NP,BNBP,∠PNB=45°,
∴∠PNE=135°=∠ABP,
∵∠APE=90°,
∴∠EPN=90°﹣∠APN=∠APB,
∴△EPN≌△APB(ASA),
∴EN=BA,
∵BE=EN+BN,
∴BE=BABP;
综上所述,当P在线段BC上时,ABBP+BE;当P在线段CB的延长线上时,BE=BABP.
【点评】本题考查几何变换综合应用,涉及等腰直角三角形,旋转变换,全等三角形的判定与性质等知识,解题的关键是作辅助线,构造全等三角形解决问题.
8.【问题呈现】
△CAB和△CDE都是直角三角形,∠ACB=∠DCE=90°,CB=mCA,CE=mCD,连接AD,BE,探究AD,BE的位置关系.
【问题探究】
(1)如图1,当m=1时,直接写出AD,BE的位置关系: AD⊥BE .
(2)如图2,当m≠1时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.
【拓展应用】
(3)当m,AB=4,DE=4时,将△CDE绕点C旋转,使A,D,E三点恰好在同一直线上,求BE的长.
【考点】几何变换综合题.
【专题】图形的全等;等腰三角形与直角三角形;图形的相似;推理能力.
【答案】(1)BE⊥AD;
(2)成立,理由见解析过程;
(3)BE=6或4.
【分析】(1)由“SAS”可证△ACD≌△BCE,可得∠DAC=∠CBE,由余角的性质可证AD⊥BE;
(2)通过证明△DCA∽△ECB,可得∠DAC=∠CBE,由余角的性质可证AD⊥BE;
(3)分两种情况讨论,由相似三角形的性质可得BEAD,由勾股定理可求解.
【解答】解:(1)如图1,延长BE交AC于点H,交AD于N,
当m=1时,DC=CE,CB=CA,
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠DAC=∠CBE,
∵∠CAB+∠ABE+∠CBE=90°,
∴∠CAB+∠ABE+∠DAC=90°,
∴∠ANB=90°,
∴AD⊥BE,
故答案为:AD⊥BE;
(2)(1)中的结论成立,理由如下:
如图2,延长BE交AC于点H,交AD于N,
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
又∵,
∴△DCA∽△ECB,
∴∠DAC=∠CBE,
∵∠CAB+∠ABE+∠CBE=90°,
∴∠CAB+∠ABE+∠DAC=90°,
∴∠ANB=90°,
∴AD⊥BE,
(3)如图3,当点E在线段AD上时,连接BE,
∵△DCA∽△ECB,
∴m,
∴BEAD(4+AE),
∵AD⊥BE,
∴AB2=AE2+BE2,
∴112=AE2+3(4+AE)2,
∴AE=2或AE=﹣8(舍去),
∴BE=6,
当点D在线段AE上时,连接BE,
∵△DCA∽△ECB,
∴m,
∴BEAD(AE﹣4),
∵AD⊥BE,
∴AB2=AE2+BE2,
∴112=AE2+3(AE﹣4)2,
∴AE=8或AE=﹣2(舍去),
∴BE=4,
综上所述:BE=6或4.
【点评】本题是几何变换综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,等腰三角形的性质,灵活运用这些性质解决问题是解题的关键.
9.1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.
(1)下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
当△ABC的三个内角均小于120°时,
如图1,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′,
由PC=P′C,∠PCP′=60°,可知△PCP′为 等边 三角形,故PP′=PC,又P′A′=PA,故PA+PB+PC=P′A′+PB+PP′≥A′B,
由 两点之间线段最短 可知,当B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,如图2,最小值为A′B,此时的P点为该三角形的“费马点”,
且有∠APC=∠BPC=∠APB= 120° ;
已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点.如图3,若∠BAC≥120°,则该三角形的“费马点”为 A 点.
(2)如图4,在△ABC中,三个内角均小于120°,且AC=3,BC=4,∠ACB=30°,已知点P为△ABC的“费马点”,求PA+PB+PC的值;
(3)如图5,设村庄A,B,C的连线构成一个三角形,且已知AC=4km,BC=2km,∠ACB=60°.现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/km,a元/km,a元/km,选取合适的P的位置,可以使总的铺设成本最低为 元.(结果用含a的式子表示)
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】(1)等边;两点之间线段最短;120°;A;
(2)5;
(3)a.
【分析】(1)根据旋转的性质和两点之间线段最短进行推理分析后即可得出结论,然后填空即可;
(2)根据(1)的方法将△APC绕点C顺时针旋转60°得到△A'P'C,即可得出可知当B、P、P'、A'在同一条直线上时,PA+PB+PC取最小值,最小值为A'B,再根据∠ACB=30°可证明∠BCA'=90°,根据勾股定理即可求出A'B;
(3)根据总铺设成本,将△APC绕点C顺时针旋转90°得到△A'P'C,得到等腰直角△PP'C,推出PP'PC,即可得出当B、P、P'、A'在同一条直线上时,P'A'+PB+PP'取最小值,即PA+PBPC取最小值为A'B的长,然后根据已知条件和旋转的性质求出A'B即可.
【解答】解:(1)∵PC=P'C,∠PCP'=60°,
∴△PCP'为等边三角形,
∴PP'=PC,∠P'PC=∠PP'C=60°,
又∵P'A'=PA,
∴PA+PB+PC=PA'+PB+PP'≥A'B,
根据两点之间线段最短可知,当B、P、P'、A'在同一条直线上时,PA+PB+PC取最小值,最小值为A'B,
此时的P点为该三角形的“费马点”,
∴∠BPC+∠P'PC=180°,∠A'P'C+∠PP'C=180°,
∴∠BPC=120°,∠A'P'C=120°,
∵将△APC绕点C顺时针旋转60°得到△A′P′C,
∴△APC≌△A'P'C,
∴∠APC=∠AP'C'=120°,
∴∠APB=360°﹣120°﹣120°=120°,
∴∠APC=∠BPC=∠APB=120°,
∵∠BAC≥120°,
∴BC>AC,BC>AB,
∴BC+AB>AC+AB,BC+AC>AB+AC,
∴三个顶点中顶点A到另外两个顶点的距离和最小,
又∵已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点,
∴该三角形的“费马点”为点A.
故答案为:等边;两点之间线段最短;120°;A;
(2)如图4,将△APC绕点C顺时针旋转60°得到△A'P'C,连接PP',
由(1)可知当B、P、P'、A'在同一条直线上时,PA+PB+PC取最小值,最小值为A'B,
∵∠ACP=∠A'CP',
∴∠ACP+∠BCP=∠A'CP'+∠BCP=∠ACB=30°,
又∵∠PCP'=60°,
∴∠BCA'=90°,
根据旋转的性质可知:AC=A'C=3,
∴A'B,
即PA+PB+PC的最小值为5;
(3)∵总铺设成本=PA×a+PB×a+PCa,
∴当PA+PBPC最小时,总铺设成本最低,
将△APC绕点C顺时针旋转90°得到△A'P'C,连接PP',A'B,
由旋转性质可知:P'C=PC,∠PCP'=∠ACA'=90°,P'A'=PA,A'C=AC=4km,
∴PP'PC,
∴PA+PBPC=P'A'+PB+PP',
当B、P、P'、A'在同一条直线上时,P'A'+PB+PP'取最小值,
即PA+PBPC取最小值为A'B,
过点A'作A'H⊥BC于H,
∵∠ACB=60°,∠ACA'=90°,
∴∠A'CH=30°,
∴A'HA'C=2km,
∴HC(km),
∴BH=BC+CH(km),
∴A'B2(km),
即PA+PBPC的最小值为km,
总铺设成本为:总铺设成本a(元).
故答案为:a.
【点评】本题是几何变换综合题,主要考查旋转的性质,全等三角形的判定和性质,两点之间线段最短以及等边三角形的性质,深入理解题意是解决问题的关键.
10.【模型建立】
(1)如图1,△ABC和△BDE都是等边三角形,点C关于AD的对称点F在BD边上.
①求证:AE=CD;
②用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型应用】
(2)如图2,△ABC是直角三角形,AB=AC,CD⊥BD,垂足为D,点C关于AD的对称点F在BD边上.用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型迁移】
(3)在(2)的条件下,若AD=4,BD=3CD,求cos∠AFB的值.
【考点】几何变换综合题.
【专题】几何变换;几何直观.
【答案】(1)①证明见解答过程;
②AD=BD+DF.理由见解答过程;
(2)BD+DFAD.理由见解答过程;
(3).
【分析】(1)①根据△ABC和△BDE都是等边三角形推出判定△ABE和△CBD全等,然后根据全等三角形的对应边相等即可得证;
②根据等边三角形的性质和对称的性质即可推出线段AD,BD,DF的数量关系;
(2)过点B作BE⊥AD于E,根据等腰直角三角形的性质推出判定△ABE∽△CBD,然后根据等腰直角三角形的性质和对称性即可推出线段AD,BD,DF的数量关系;
(3)过点A作AG⊥BD于G,推出△ADG是等腰直角三角形,求出AG、FG、AF的长后即可求出cos∠AFB的值.
【解答】(1)证明:①∵△ABC和△BDE都是等边三角形,
∴AB=CB,EB=DB,∠ABC=∠EBD=60°,
∴∠ABE=∠CBD,
∴△ABE≌△CBD,
∴AE=CD;
②解:AD=BD+DF.
理由如下:
∵△BDE是等边三角形,
∴BD=DE,
∵点C与点F关于AD对称,
∴CD=DF,
∵AD=AE+DE,
∴AD=BD+DF;
(2)BD+DFAD.
理由如下:
如图1,过点B作BE⊥AD于E,
∵点C与点F关于AD对称,
∴∠ADC=∠ADB,
又∵CD⊥BD,
∴∠ADC=∠ADB=45°,
又∵BE⊥AD,
∴△BDE是等腰直角三角形,
又∵△ABC是等腰直角三角形,
∴,∠ABC=∠EBD=45°,
∴∠ABE=∠CBD,
∴△ABE∽△CBD,
∴,CD=DF,
∴DFAE,
∵△BDE是等腰直角三角形,
∴BD,
∴BD+DF,
即:BD+DFAD.
(3)解:如图2,过点A作AG⊥BD于G,
又∵∠ADB=45°,
∴△AGD是等腰直角三角形,
又∵AD=4,
∴AG=DG=4,BD+DFAD=8,
∵BD=3CD,CD=DF,
∴DF=2,
又∵DG=4,
∴FG=DG﹣DF=2,
在Rt△AFG中,由勾股定理得:,
∴cos∠AFB.
【点评】本题是几何变换综合题,主要考查等边三角形的性质,等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质以及勾股定理,深入理解题意是解决问题的关键.
11.综合与实践
问题情境
数学活动课上,老师发给每名同学一个等腰三角形纸片ABC,AB=AC,∠BAC>90°,要求同学们将纸片沿一条直线折叠,探究图形中的结论.
问题发现
奋进小组在边AC上取一点D,连接BD,将这个纸片沿BD翻折,点A的对应点为E,如图1所示.
如图2,小明发现,当点E落在边BC上时,∠DEC=2∠ACB.
如图3,小红发现,当点D是AC的中点时,连接CE,若已知AB和CE的长,则可求BD的长.
……
问题提出与解决
奋进小组根据小明和小红的发现,讨论后提出问题1,请你解答.
问题1:在△ABC中,AB=AC,∠BAC>90°,点D是边AC上一点,将△ABD沿BD翻折得到△EBD.
(1)如图2,当点E在边BC上时,求证:∠DEC=2∠ACB.
(2)如图3,当点D是AC的中点时,连接CE,若AB=4,CE=3,求BD的长.
拓展延伸
小刚受到探究过程的启发,将等腰三角形的顶角改为锐角,尝试画图,并提出问题2,请你解答.
问题2:如图4,点D是△ABC外一点,AB=AC=BD=4,CD=1,∠ABD=2∠BDC,求BC的长.
【考点】几何变换综合题.
【专题】图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;运算能力;推理能力.
【答案】问题1,
(1)证明过程详见解答;
(2);
问题2,
.
【分析】问题1,
(1)由∠A+∠DEC=180°,∠A+∠ACB+∠ABC=∠A+2∠ACB=180°得出结论;
(2)作AG⊥BD于G,作DF⊥CE于F,根据等腰三角形的性质得出CF=EF,进而得出DF的值,可证得△ADG≌△DFC,从而AG=DF,DG=CF,进而在Rt△ABG中求得BG,进一步得出结果;
问题2,
连接AD,作BE⊥AD于E,作BF⊥CD,交DC的延长线于F,可证得四边形DEBF是矩形,从而BF=DE,DF=BE,在Rt△ACD中求得AD,进而求得BF=DE,进而在Rt△BDE中求得DF=BE,从而得出CF=DF﹣CD,进而在Rt△BCF中求得BG的值,进一步得出结果.
【解答】问题1,
(1)证明:∵将△ABD沿BD翻折得到△EBD,
∴∠BED=∠A,
∵∠BED+∠DEC=180°,
∴∠A+∠DEC=180°,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠A+∠ACB+∠ABC=∠A+2∠ACB=180°,
∴∠DEC=2∠ACB;
(2)解:如图1,
作AG⊥BD于G,作DF⊥CE于F,
∴∠AGD=∠DFC=90°,
由折叠得,
AD=DE,∠ADB=∠BDE,
∵点D是AC的中点,
∴CD=AD,
∴DE=CD,
∴∠DEC=∠DCE,CF=EFCE
∴DF2=CD2﹣CF2=22﹣()2,
∵∠ADB+∠BDE+∠EDC=180°,
∴2∠ADB+∠EDC=180°,
∵∠DEC+∠DCE+∠EDC=180°,
∴2∠DCE+∠EDC=180°,
∴∠ADB=∠DCE,
∴△ADG≌△DFC(AAS),
∴AG=DF,DG=CF,
在Rt△ABG中,由勾股定理得,
BG,
∴BD=BG+DG;
问题2,
解:如图2,
连接AD,作BE⊥AD于E,作BF⊥CD,交DC的延长线于F,
∵AB=BD,
∴∠ABD=2∠DBE,DE=AEAD,
∵∠ABD=2∠BDC,
∴∠BDE=∠BDC,
∴CD∥BE,
∴CD⊥AD,
∴∠BED=∠EDC=∠F=90°,
∴四边形DEBF是矩形,
∴BF=DE,DF=BE,
在Rt△ACD中,CD=1,AC=4,
∴AD,
∴BF=DE,
在Rt△BDE中,BD=4,DE,
∴DF=BE,
∴CF=DF﹣CD,
在Rt△BCF中,CF,BF,
∴BC.
【点评】本题考查了轴对称的性质,等腰三角形的性质,勾股定理,全等三角形的判定及性质,矩形的判定和性质等知识,解决问题的关键是作辅助线,构造全等三角形.
12.如图1,在△ABC中,AB=AC,点M,N分别为边AB,BC的中点,连接MN.
初步尝试:(1)MN与AC的数量关系是 MNAC ,MN与AC的位置关系是 MN∥AC .
特例研讨:(2)如图2,若∠BAC=90°,BC=4,先将△BMN绕点B顺时针旋转α(α为锐角),得到△BEF,当点A,E,F在同一直线上时,AE与BC相交于点D,连接CF.
①求∠BCF的度数;
②求CD的长.
深入探究:(3)若∠BAC<90°,将△BMN绕点B顺时针旋转α,得到△BEF,连接AE,CF.当旋转角α满足0°<α<360°,点C,E,F在同一直线上时,利用所提供的备用图探究∠BAE与∠ABF的数量关系,并说明理由.
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】(1);MN∥AC;
(2)①∠BCF=30°;②;
(3)∠BAE=∠ABF 或∠BAE+∠ABF=180°.
【分析】(1)AB=AC,点M,N分别为边AB,BC的中点,则MN是△ABC的中位线,即可得出结论;
(2)特例研讨:①连接EM,MN,NF,证明△BME是等边三角形,△BNF是等边三角形,得出∠FCB=30°;
②连接AN,证明△ADN∽△BDE,则 ,设DE=x,则,在Rt△ABE中,BE=2,,则,在Rt△ADN中,AD2=DN2+AN2,勾股定理求得,则;
(3)当点C,E,F在同一直线上时,且点E在FC上时,设∠ABC=∠ACB=θ,则∠BAC=180°﹣2θ,得出∠BEC+∠BAC=180°,则A.B,E,C 在同一个圆上,进而根据圆周角定理得出∠EAC=∠EBC=α﹣θ,表示∠BAE与∠ABF,即可求解;当F在EC上时,可得A,B,E,C在同一个圆上,设∠ABC=∠ACB=θ,则∠BAC=∠BEF=180°﹣2θ,设∠NBF=β,则∠EBM=β,则 α+β=360°,表示∠BAE 与∠ABF,即可求解.
【解答】解:(1)∵AB=AC,点M,N分别为边AB,BC的中点,
∴MN是△ABC的中位线,
∴,MN∥AC;
故答案为:MNAC,MN∥AC;
(2)特例研讨:①如图所示,连接EM,MN,NF,
∵MN是△BAC的中位线,
∴MN∥AC,
∴∠BMN=∠BAC=90°,
∵将△BMN绕点B顺时针旋转α(α为锐角),得到△BEF,
∴BE=BM,BF=BN;∠BEF=∠BMN=90°,
∵点A,E,F在同一直线上,
∴∠AEB=∠BEF=90°,
在Rt△ABE中,M是斜边AB的中点,
∴,
∴BM=ME=BE,
∴△BME是等边三角形,
∴∠ABE=60°,即旋转角α=60°,
∴∠NBF=60°,BN=BF,
∴△BNF是等边三角形,
又∵BN=NC,BN=NF,
∴NF=NC,
∴∠NCF=∠NFC,
∴∠BNF=∠NCF+∠NFC=2∠NFC=60°,
∴∠FCB=30°;
(2)如图所示,连接AN,
∵AB=AC,∠BAC=90° ,
∴,∠ACB=∠ABC=45°,
∵∠ADN=∠BDE,∠ANB=∠BED=90°,
∴△ADN∽△BDE,
∴,
设DE=x,则,
在Rt△ABE中,,则,
在Rt△ADN中,AD2=DN2+AN2,
∴,
解得: 或 (舍去),
∴;
(3)如图所示,当点C,E,F在同一直线上时,且点E在FC上时,
∵AB=AC,
∴∠ABC=∠ACB,设∠ABC=∠ACB=θ,则∠BAC=180°﹣2θ,
∵MN是△ABC的中位线,
∴MN∥AC,
∴∠MNB=∠MBN=θ,
∵将△BMN绕点B顺时针旋转α,得到△BEF,
∴△EBF≌△MBN,∠MBE=∠NBF=α,
∴∠EBF=∠EFB=θ,
∴∠BEF=180°﹣2θ,
∵点C,E,F在同一直线上,
∴∠BEC=2θ,
∴∠BEC+∠BAC=180°,
∴A,B,E,C在同一个圆上,
∴∠EAC=∠EBC=α﹣θ,
∴∠BAE=∠BAC﹣∠EAC=(180°﹣2θ)﹣(α﹣θ)=180°﹣α﹣θ,
∵∠ABF=α+θ,
∴∠BAE+∠ABF=180°,
如图所示,当F在EC上时,
∵∠BEF=∠BAC,BC=BC,
∴A,B,E,C在同一个圆上,设∠ABC=∠ACB=θ,则∠BAC=∠BEF=180°﹣2θ,
将△BMN绕点B顺时针旋转α,得到△BEF,设∠NBF=β,则∠EBM=β,则 α+β=360°,
∴∠ABF=θ﹣β,
∵∠BFE=∠EBF=θ,∠EFB=∠FBC+∠FCB,
∴∠ECB=∠FCB=∠EFB﹣∠FBC=θ﹣β,
∵,
∴∠EAB=∠ECB=θ﹣β,
∴∠BAE=∠ABF,
综上所述,∠BAE=∠ABF或∠BAE+∠ABF=180°.
【点评】本题属于几何变换综合题,考查了圆周角定理,圆内接四边形对角互补,相似三角形的性质与判定,旋转的性质,中位 线的性质与判定,等腰三角形的性质与判定,三角形内角和定理,三角形外角的性质,勾股定理,熟练掌 以上知识是解题的关键.
13.【问题情境】如图,在△ABC中,AB=AC,∠ACB=α,点D在边BC上.将线段DB绕点D顺时针旋转得到线段DE(旋转角小于180°),连接BE,CE,以CE为底边在其上方作等腰三角形FEC,使∠FCE=α,连接AF.
【尝试探究】
(1)如图1,当α=60°时,易知AF=BE;
如图2,当α=45°时,则AF与BE的数量关系为 BEAF ;
(2)如图3,写出AF与BE的数量关系(用含α的三角函数表示),并说明理由;
【拓展应用】
(3)如图4,当α=30°且点B,E,F三点共线时.若BC=4,BDBC,请直接写出AF的长.
【考点】几何变换综合题.
【专题】等腰三角形与直角三角形;图形的相似;解直角三角形及其应用;运算能力;推理能力.
【答案】(1)BEAF;
(2)BE=2AF cosα;
(3).
【分析】(1)可证明△ACF∽△BCE,从而,进而得出结果;
(2)过点A作AH⊥BC于点H,可推出cosα,进而证得△ACF∽△BCE,从而;
(3)作DM⊥BF于点M,过点C作CH⊥BF,交BF延长线于点H,设BM=x,则BE=2x,由DM∥CH得,从而BH=5BM=5x,EH=BH﹣BE=3x,进而表示出FE=FC=2x,FH=x.,在Rt△BHC中,由勾股定理列出方程(5x)2+()2=(4)2,从而x=2,进一步得出结果.
【解答】解:(1)当α=45°时,△ABC和△FEC是等腰直角三角形,
∴∠ACB=∠FCE=45°,
∴∠ACF=∠BCE,
∵,
∴△ACF∽△BCE,
∴,
故答案为:BEAF;
(2)如图1,
BE=2AF cosα,理由如下:
过点A作AH⊥BC于点H,
∵AB=AC,
∴BH=CH,∠ABC=∠ACB=α,
∴cosα
∴2cosα
同理可得:2cosα,
∴,
∵∠FCE=∠ACB,
∴∠ACF=∠BCE,
∴△ACF∽△BCE,
∴,
∴BE=2AF cosα;
(3)方法一
如图2,
作DM⊥BF于点M,过点C作CH⊥BF,交BF延长线于点H,
∴∠BMD=∠H=90°,
∴DM∥CH,
∵线段DB绕点D顺时针旋转得到线段DE,
∴DB=DE,
∴BM=EM,
∵∠FCE=∠FEC=30°,
∴∠CFH=∠FCE+∠FEC=60°,
∴EF=CF=2FH,
设BM=x,则BE=2x,
∵DM∥CH,
∵,
∴BH=5BM=5x,
∴EH=BH﹣BE=3x,
∵FE=2FH,
∴FE=FC=2x,FH=x.
∴
在Rt△BHC中,由勾股定理得,
∴BH2+CH2=BC2,
∴(5x)2+()2=(4)2,
∴x=2,
∴BE=2x=4,
由(2)得:,
方法二
如图3,
作CG∥BF交ED延长线于点G,过点D作DM⊥CG于点M,
过点E作EH⊥CG于点H,
∴∠DMG=∠EHG=90°,
∴DM∥EH,
∵线段DB绕点D顺时针旋转得到线段DE,
∴DB=DE,
∴∠DBE=∠DEB,
∵CG∥BF,
∴∠DBE=∠DCG,∠DEB=∠G,
∴DG=DC,
∵DM⊥CG,
∴GM=CM,
∵△FEC是以CE为底边的等腰三角形,∠FCE=30°,
∴∠FEC=∠FCE=30°,
∵CG∥BF,
∴∠ECG=∠FEC=30°,△BDE∽△CDG,
∴,
设BE=2x,则GC=8x,
∴GM=CM=4x,
∵DM∥EH,
∴,
∴HM=x,
∴HC=3x,
∴GH=GM+HM=5x,
在Rt△EHC中,∠ECH=30°,
∴,
在Rt△EHG中,由勾股定理得,
∴GH2+EH2=GE2,
∴(5x)2+()2=(4)2,
∴x=2,
∴BE=4,
∵△BEC∽△AFC,
∴.
【点评】本题考查了相似三角形的判定和性质,解直角三角形,等腰三角形的性质等知识,解决问题的关键是作辅助线,构造相似三角形.
14.【特例感知】
(1)如图1,△AOB和△COD是等腰直角三角形,∠AOB=∠COD=90°,点C在OA上,点D在BO的延长线上,连接AD,BC,线段AD与BC的数量关系是 AD=BC ;
【类比迁移】
(2)如图2,将图1中的△COD绕着点O顺时针旋转α(0°<α<90°),那么第(1)问的结论是否仍然成立?如果成立,证明你的结论;如果不成立,说明理由.
【方法运用】
(3)如图3,若AB=8,点C是线段AB外一动点,AC=3,连接BC.
①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值是 8+3 ;
②若以BC为斜边作Rt△BCD(B,C,D三点按顺时针排列),∠CDB=90°,连接AD,当∠CBD=∠DAB=30°时,直接写出AD的值.
【考点】几何变换综合题.
【专题】几何综合题;压轴题;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)证明△AOD≌△BOC(SAS),即可得出结论;
(2)利用旋转性质可证得∠BOC=∠AOD,再证明△AOD≌△BOC(SAS),即可得出结论;
(3)①过点A作AT⊥AB,使AT=AB,连接BT,AD,DT,BD,先证得△ABC∽△TBD,得出DT=3,即点D的运动轨迹是以T为圆心,3为半径的圆,当D在AT的延长线上时,AD的值最大,最大值为8+3;
②如图4,在AB上方作∠ABT=30°,过点A作AT⊥BT于点T,连接AD、BD、DT,过点T作TH⊥AD于点H,可证得△BAC∽△BTD,得出DTAC3,再求出DH、AH,即可求得AD;如图5,在AB下方作∠ABE=30°,过点A作AE⊥BE于点E,连接DE,可证得△BAC∽△BTD,得出DE,再由勾股定理即可求得AD.
【解答】解:(1)AD=BC.理由如下:
如图1,∵△AOB和△COD是等腰直角三角形,∠AOB=∠COD=90°,
∴OA=OB,OD=OC,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴AD=BC,
故答案为:AD=BC;
(2)AD=BC仍然成立.
证明:如图2,∵∠AOB=∠COD=90°,
∴∠AOB+∠AOC=∠AOC+∠COD=90°+α,
即∠BOC=∠AOD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴AD=BC;
(3)①过点A作AT⊥AB,使AT=AB,连接BT,AD,DT,BD,
∵△ABT和△CBD都是等腰直角三角形,
∴BTAB,BDBC,∠ABT=∠CBD=45°,
∴,∠ABC=∠TBD,
∴△ABC∽△TBD,
∴,
∴DTAC33,
∵AT=AB=8,DT=3,
∴点D的运动轨迹是以T为圆心,3为半径的圆,
∴当D在AT的延长线上时,AD的值最大,最大值为8+3,
故答案为:8+3;
②如图4,在AB上方作∠ABT=30°,过点A作AT⊥BT于点T,连接AD、BD、DT,过点T作TH⊥AD于点H,
∵cos30°,∠ABC=∠TBD=30°+∠TBC,
∴△BAC∽△BTD,
∴,
∴DTAC3,
在Rt△ABT中,AT=AB sin∠ABT=8sin30°=4,
∵∠BAT=90°﹣30°=60°,
∴∠TAH=∠BAT﹣∠DAB=60°﹣30°=30°,
∵TH⊥AD,
∴TH=AT sin∠TAH=4sin30°=2,AH=AT cos∠TAH=4cos30°=2,
在Rt△DTH中,DH,
∴AD=AH+DH=2;
如图5,在AB上方作∠ABE=30°,过点A作AE⊥BE于点E,连接DE,
则cos30°,
∵∠EBD=∠ABC=∠ABD+30°,
∴△BDE∽△BCA,
∴,
∴DEAC3,
∵∠BAE=90°﹣30°=60°,AE=AB sin30°=84,
∴∠DAE=∠DAB+∠BAE=30°+60°=90°,
∴AD;
综上所述,AD的值为2或.
【点评】本题是几何变换综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,等腰三角形的性质,瓜豆原理等知识点,关键是添加恰当辅助线,构造全等三角形或相似三角形解决问题,综合性较强,难度较大,属于中考压轴题.
15.【问题情境】
在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中∠ACB=∠DEB=90°,∠B=30°,BE=AC=3.
【问题探究】
小昕同学将三角板DEB绕点B按顺时针方向旋转.
(1)如图2,当点E落在边AB上时,延长DE交BC于点F,求BF的长.
(2)若点C、E、D在同一条直线上,求点D到直线BC的距离.
(3)连接DC,取DC的中点G,三角板DEB由初始位置(图1),旋转到点C、B、D首次在同一条直线上(如图3),求点G所经过的路径长.
(4)如图4,G为DC的中点,则在旋转过程中,点G到直线AB的距离的最大值是 .
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】(1)2;(2)±1;(3)π;(4).
【分析】(1)根据锐角三角函数求解,即可求出答案;
(2)①当点E在BC上方时,如图1过点D作DH⊥BC于H,根据锐角三角函数求出BC=3,DE,最后利用面积求解,即可求出答案;
②当点E在BC下方时,同①的方法,即可求出答案;
(3)先求出∠BOG=150°,再判断出点G是以点O为圆心,为半径的圆上,最后用弧长公式求解,即可求出答案;
(4)过点O作OK⊥AB于K,求出OK,即可求出答案.
【解答】解:(1)由题意得,∠BEF=∠BED=90°,
在Rt△BEF中,∠ABC=30°,BE=3,
∴BF2;
(2)①当点E在BC上方时,
如图1,过点D作DH⊥BC于H,
在Rt△ABC中,AC=3,
∴tan∠ABC,
∴BC3,
在Rt△BED中,∠EBD=∠ABC=30°,BE=3,
∴DE=BE tan∠DBE,
在Rt△BCE中,BE=3,BC=3,
根据勾股定理得,CE3,
∴CD=CE+DE=3,
∵S△BCDCD BEBC DH,
∴DH1,
②当点E在BC下方时,如图2,
过点D作DM⊥BC于M,
∵S△BDCBC DMCD BE,
∴DM1,
即点D到直线BC的距离为±1;
(3)如图3﹣1,连接CD,取CD的中点G,
取BC的中点O,连接GO,则OG∥AB,
∴∠COG=∠B=30°,
∴∠BOG=150°,
∵点G为CD的中点,点O为BC的中点,
∴GOBD,
∴点G是以点O为圆心,为半径的圆上,如图3﹣2,
∴三角板DEB由初始位置(图1),旋转到点C、B、D首次在同一条直线上时,点G所经过的轨迹为150°所对的圆弧,
∴点G所经过的路径长为π;
(4)如图4,过点O作OK⊥AB于K,
∵点O为BC的中点,BC=3,
∴OB,
∴OK=OB sin30°,
由(3)知,点G是以点O为圆心,为半径的圆上,
∴点G到直线AB的距离的最大值是,
故答案为:.
【点评】此题是几何变换综合题,主要考查了锐角三角函数,勾股定理,弧长公式,三角形的中位线定理,三角形的面积,画出图形是解本题的关键.
16.在△ABC中,点D,E分别是AB,AC边上的点,DE∥BC.
基础理解:
(1)如图1,若AD=4,BD=3,求的值;
证明与拓展:
(2)如图2,将△ADE绕点A逆时针旋转度,得到△AD1E1,连接BD1,CE1.
①求证:;
②如图3,若∠BAC=90°,AB<AC,AD=6,△ADE在旋转过程中,点D1恰好落在DE上时,连接EE1,,则△E1D1E的面积为 13.44 .
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】(1);
(2)①见解析;
②13.44.
【分析】(1)利用平行线分线段成比例定理可得;
(2)①根据旋转的性质得AD=AD1,AE=AE1,∠BAD1=∠CAE1,再根据平行线分线段成比例定理得,证明△ABD1∽△ACE1,即可证明结论;
②由得,AD1和AE1的长,过点A作AM⊥DE于M,利用三角形内角和定理说明∠D1EE1=90°,利用勾股定理即可解决问题.
【解答】(1)解:∵DE∥BC,AD=4,BD=3,
∴;
(2)①证明:∵将△ADE绕点A逆时针旋转度,得到△AD1E1,
∴AD=AD1,AE=AE1,∠BAD1=∠CAE1,
∵DE∥BC,
∴,
∴,
∴△ABD1∽△ACE1,
∴;
②解:由①可知,△ABD1∽△ACE1,
∴,
∵将△ADE绕点A逆时针旋转度,得到△AD1E1,
∴AD=AD1=6,∠D1AE1=∠DAE=90°,
∴AE=AE18,DE=D1E=10,
过点A作AM⊥DE于点M,
则DM=D1M=AD×cos∠ADE=3.6,
∴D1E=10﹣3.6×2=2.8,
∴∠D1AE1=∠DAE=90°,
∴∠DAD1=∠EAE1,
∵AD=AD1,AE=AE1,
∴∠ADE=∠AEE1,
∴∠AED+∠AEE1=∠AED+∠ADE=90°,
∴∠D1EE1=90°,
∴EE1=9.6,
∴△E1D1E的面积为,
故答案为:13.44.
【点评】本题是几何变换综合题,主要考查了平行线分线段成比例定理,相似三角形的判定与性质,旋转的性质,等腰三角形的性质,勾股定理等知识,说明∠D1EE1=90°是解题的关键.
17.数学课上,有这样一道探究题.
如图,已知△ABC中,AB=AC=m,BC=n,∠BAC=α(0°<α<180°),点P为平面内不与点A、C重合的任意一点,连接CP,将线段CP绕点P顺时针旋转α,得线段PD,连接CD、AP点E、F分别为BC、CD的中点,设直线AP与直线EF相交所成的较小角为β,探究的值和β的度数与m、n、α的关系.
请你参与学习小组的探究过程,并完成以下任务:
(1)填空:
【问题发现】
小明研究了α=60°时,如图1,求出了的值和β的度数分别为 ,β= 60° ;
小红研究了α=90°时,如图2,求出了的值和β的度数分别为 ,β= 45° ;
【类比探究】
他们又共同研究了α=120°时,如图3,也求出了的值和β的度数;
【归纳总结】
最后他们终于共同探究得出规律: (用含m、n的式子表示);β= (用含α的式子表示).
(2)求出α=120°时的值和β的度数.
【考点】几何变换综合题.
【专题】图形的相似;模型思想.
【答案】(1),60°,,45°,,,(2).
【分析】(1)当α=60°时,△ABC和△PDC都是等边三角形,可证△ACP∽△ECF,从而有,∠Q=β=∠ACB=60°;
当α=90°时,△ABC和△PDC都是等腰直角三角形,同理可证△ACP∽△ECF即可解决,依此可得出规律;
(2)当α=120°,可证,,从而有,由∠ECF=∠ACP,可得△PCA∽△FCE即可解决问题.
【解答】解:(1)如图1,连接AE,PF,延长EF、AP交于点Q,
当α=60°时,△ABC和△PDC都是等边三角形,
∴∠PCD=∠ACB=60°,PC=CD,AC=CB,
∵F、E分别是CD、BC的中点,
∴,,
∴,
又∵∠ACP=∠ECF,
∴△ACP∽△ECF,
∴,∠CEF=∠CAP,
∴∠Q=β=∠ACB=60°,
当α=90°时,△ABC和△PDC都是等腰直角三角形,
∴∠PCD=∠ACB=45°,PCCD,ACCB,
∵F、E分别是CD、BC的中点,
∴,,
∴,
又∵∠ACP=∠ECF,
∴△ACP∽△ECF,
∴,∠CEF=∠CAP,
∴∠Q=β=∠ACB=45°,
由此,可归纳出,β=∠ACB;
(2)当α=120°,连接AE,PF,延长EF、AP交于点Q,
∵AB=AC,E为BC的中点,
∴AE⊥BC,∠CAE=60°
∴sin60°,
同理可得:,
∴,
∴,
又∵∠ECF=∠ACP,
∴△PCA∽△FCE,
∴,∠CEF=∠CAP,
∴∠Q=β=∠ACB=30°.
【点评】本题主要考查了三角形相似的判定与性质,通过解决本题感受到:图形在变化但解决问题的方法不变,体会“变中不变”的思想.
18.在一平面内,线段AB=20,线段BC=CD=DA=10,将这四条线段顺次首尾相接.把AB固定,让AD绕点A从AB开始逆时针旋转角α(α>0°)到某一位置时,BC,CD将会跟随出现到相应的位置.
论证:如图1,当AD∥BC时,设AB与CD交于点O,求证:AO=10;
发现:当旋转角α=60°时,∠ADC的度数可能是多少?
尝试:取线段CD的中点M,当点M与点B距离最大时,求点M到AB的距离;
拓展:①如图2,设点D与B的距离为d,若∠BCD的平分线所在直线交AB于点P,直接写出BP的长(用含d的式子表示);
②当点C在AB下方,且AD与CD垂直时,直接写出α的余弦值.
【考点】几何变换综合题.
【专题】压轴题;动点型;方程思想;应用意识.
【答案】论证:见解答过程;
发现:60°或120°;
尝试:;
拓展:
①;
②.
【分析】论证:由△AOD≌△BOC,得AO=BO,而AB=20,可得AO=10;
发现:设AB的中点为O,当AD从初始位置AO绕A逆时针旋转60°时,BC也从初始位置BC'绕点B逆时针旋转60°,BC旋转到BO的位置,即C以O重合,从而可得∠ADC=60°;当AD从AO绕A逆时针旋转60°时,CD从CD'的位置开始也旋转60°,故△ADO和△CDO都是等边三角形,可得此时∠ADC=120°,
尝试:当点M与点B距离最大时,D、C、B共线,过D作DQ⊥AB于Q,过M作MN⊥AB于N,由已知可得AD=10,设AQ=x,则BQ=20﹣x,100﹣x2=400﹣(20﹣x)2,可得AQ,DQ,再由MN∥DQ,得,MN,即点M到AB的距离为;
拓展:
①设直线CP交DB于H,过G作DG⊥AB于G,连接DP,设BG=m,则AG=20﹣m,由AD2﹣AG2=BD2﹣BG2,可得m,BG,而△BHP∽△BGD,有,即可得BP;
②方法一:过B作BG⊥CD于G,设AN=t,则BN=20﹣t,DN,由△ADN∽△BGN,,表达出NG,BG,Rt△BCG中,CG,根据DN+NG+CG=10,列方程10,解得t,即可得cosα.
方法二:过C作CK⊥AB于K,过F作FH⊥AC于H,由AC2﹣AK2=BC2﹣BK2,可解得AK,即得CK,Rt△ACK中,tan∠KAC,Rt△AFH中,tan∠KAC,设FHn,则CH=FHn,AH=5n,根据AC=AH+CH=10,解得n,从而AF,Rt△ADF中,即可得cosα.
【解答】论证:
证明:∵AD∥BC,
∴∠A=∠B,∠C=∠D,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(ASA),
∴AO=BO,
∵AO+BO=AB=20,
∴AO=10;
发现:①设AB的中点为O,如图:
当AD从初始位置AO绕A逆时针旋转60°时,BC也从初始位置BC'绕点B逆时针旋转60°,
而BO=BC'=10,
∴△BC'O是等边三角形,
∴BC旋转到BO的位置,即C与O重合,
∵AO=AD=CD=10,
∴△ADC是等边三角形,
∴此时∠ADC=60°;
②如图:
当AD从AO绕A逆时针旋转60°时,CD从CD'的位置开始也旋转60°,故△ADO和△CDO都是等边三角形,
∴此时∠ADC=120°,
综上所述,∠ADC为60°或120°;
尝试:取线段CD的中点M,当点M与点B距离最大时,D、C、B共线,过D作DQ⊥AB于Q,过M作MN⊥AB于N,如图:
由已知可得AD=10,BD=BC+CD=20,BM=CM+BC=15,
设AQ=x,则BQ=20﹣x,
∵AD2﹣AQ2=DQ2=BD2﹣BQ2,
∴100﹣x2=400﹣(20﹣x)2,
解得x,
∴AQ,
∴DQ,
∵DQ⊥AB,MN⊥AB,
∴MN∥DQ,
∴,即,
∴MN,
∴点M到AB的距离为;
拓展:
①设直线CP交DB于H,过D作DG⊥AB于G,连接DP,连接BD,如图:
∵BC=DC=10,CP平分∠BCD,
∴∠BHC=∠DHC=90°,BHBDd,
设BG=m,则AG=20﹣m,
∵AD2﹣AG2=BD2﹣BG2,
∴100﹣(20﹣m)2=d2﹣m2,
∴m,
∴BG,
∵∠BHP=∠BGD=90°,∠PBH=∠DBG,
∴△BHP∽△BGD,
∴,
∴BP;
②方法一:
过B作BG⊥CD于G,如图:
设AN=t,则BN=20﹣t,DN,
∵∠D=∠BGN=90°,∠AND=∠BNG,
∴△ADN∽△BGN,
∴,
即,
∴NG,BG,
Rt△BCG中,BC=10,
∴CG,
∵CD=10,
∴DN+NG+CG=10,
即10,
∴t(20﹣t)2010t,
202010t,即2t﹣2,
两边平方,整理得:3t2﹣40t=﹣4t,
∵t≠0,
∴3t﹣40=﹣4,
解得t(大于20,舍去)或t,
∴AN,
∴cosα.
方法二:过C作CK⊥AB于K,过F作FH⊥AC于H,如图:
∵AD=CD=10,AD⊥DC,
∴AC2=200,
∵AC2﹣AK2=BC2﹣BK2,
∴200﹣AK2=100﹣(20﹣AK)2,
解得AK,
∴CK,
Rt△ACK中,tan∠KAC,
Rt△AFH中,tan∠KAC,
设FHn,则CH=FHn,AH=5n,
∵AC=AH+CH=10,
∴5nn=10,
解得n,
∴AFn ,
Rt△ADF中,
cosα.
【点评】本题考查几何变换的综合应用,涉及全等三角形的判定与性质、等边三角形判定与性质、相似三角形的判定与性质、勾股定理及分式方程、无理方程等知识,题目综合性强,解题的关键是用含字母的代数式表示相关线段的长度,计算是本题的另一个难点.
19.[初步尝试]
(1)如图①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 AM=BM ;
[思考说理]
(2)如图②,在三角形纸片ABC中,AC=BC=6,AB=10,将△ABC折叠,使点B与点C重合,折痕为MN,求的值;
[拓展延伸]
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B′处,折痕为CM.
①求线段AC的长;
②若点O是边AC的中点,点P为线段OB′上的一个动点,将△APM沿PM折叠得到△A′PM,点A的对应点为点A′,A′M与CP交于点F,求的取值范围.
【考点】几何变换综合题.
【专题】几何综合题;图形的相似;应用意识.
【答案】(1)AM=BM;
(2);
(3)①;
②.
【分析】(1)利用平行线分线段成比例定理解决问题即可.
(2)利用相似三角形的性质求出BM,AM即可.
(3)①证明△BCM∽△BAC,推出,由此即可解决问题.
②设PB′=x.证明△PFA′∽△MFC,推出,因为CM=5,推出,判断出x的取值范围,即可解决问题.
【解答】解:(1)如图①中,
∵△ABC折叠,使点B与点C重合,折痕为MN,
∴MN垂直平分线段BC,
∴CN=BN,
∵∠MNB=∠ACB=90°,
∴MN∥AC,
∵CN=BN,
∴AM=BM.
故答案为AM=BM.
(2)如图②中,
∵CA=CB=6,
∴∠A=∠B,
由题意MN垂直平分线段BC,
∴BM=CM,
∴∠B=∠MCB,
∴∠BCM=∠A,
∵∠B=∠B,
∴△BCM∽△BAC,
∴,
∴,
∴BM,
∴AM=AB﹣BM=10,
∴.
(3)①如图③中,
由折叠的性质可知,CB=CB′=6,∠BCM=∠ACM,
∵∠ACB=2∠A,
∴∠BCM=∠A,
∵∠B=∠B,
∴△BCM∽△BAC,
∴,
∴,
∴BM=4,
∴AM=CM=5,
∴,
∴AC.
②如图③﹣1中,设PB′=x.
∵AC,BC=CB′=6,
∴AB′6,
∴AP=AP′x,
∵∠A=∠A′=∠MCF,∠PFA′=∠MFC,PA=PA′,
∴△PFA′∽△MFC,
∴,
∵CM=5,
∴,
∵OA=OC,
∴0≤x,
∴.
当x时,.
综上所述,.
【点评】本题属于几何变换综合题,考查了相似三角形的判定和性质,解直角三角形,等腰三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是正确寻找相似三角形解决问题,属于中考压轴题.
20.(1)【操作发现】
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①请按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的对应点为点B′,点C的对应点为点C′.连接BB′;
②在①中所画图形中,∠AB′B= 45 °.
(2)【问题解决】
如图2,在Rt△ABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接DE,求∠ADE的度数.
(3)【拓展延伸】
如图3,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k为常数),求BD的长(用含k的式子表示).
【考点】几何变换综合题.
【专题】几何综合题;应用意识.
【答案】见试题解答内容
【分析】(1)①根据旋转角,旋转方向画出图形即可.
②只要证明△ABB′是等腰直角三角形即可.
(2)如图2,过点E作EH⊥CD交CD的延长线于H.证明△ABC≌△EAH(AAS)即可解决问题.
(3)如图3中,由AE⊥BC,BE=EC,推出AB=AC,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,只要证明∠GDC=90°,可得CG,由此即可解决问题.
【解答】解:(1)①如图1中,△AB′C′即为所求.
②由作图可知,△ABB′是等腰直角三角形,
∴∠AB′B=45°,
故答案为45.
(2)如图2中,过点E作EH⊥CD交CD的延长线于H.
∵∠C=∠BAE=∠H=90°,
∴∠B+∠CAB=90°,∠CAB+∠EAH=90°,
∴∠B=∠EAH,
∵AB=AE,
∴△ABC≌△EAH(AAS),
∴BC=AH,EH=AC,
∵BC=CD,
∴CD=AH,
∴DH=AC=EH,
∴∠EDH=45°,
∴∠ADE=135°.
(3)如图3中,连接AC,
∵AE⊥BC,BE=EC,
∴AB=AC,
将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,
∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=kAB,
∴DG=kBC=2k,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG.
∴BD=CG.
【点评】本题属于几何变换综合题,考查了等边三角形的判定和性质,等腰三角形的判定和性质,勾股定理,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是学会用旋转法添加辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学一轮复习 图形的旋转
一.解答题(共20小题)
1.综合与实践
【问题情境】
数学活动课上,老师发给每位同学一个直角三角形纸片ABC,∠BAC=90°,AB=3,AC=4.
【问题发现】
奋进小组将三角形纸片ABC进行以下操作:第一步:折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE;第二步:然后将△DEC绕点D顺时针方向旋转得到△DFG.点E,C的对应点分别是点F,G,直线GF与边AC交于点M(点M不与点A重合),与边AB交于点N.
如图1小明发现,折痕DE的长很容易求出,并且MF和ME的数量关系也能证明.
如图2小红发现,在△DEC绕点D旋转的过程中,当直线GF经过点B时或直线GF∥BC时,AM的长都可求…
【问题提出与解决】
奋进小组根据小明和小红的发现,讨论后提出问题1和问题2,请你解答.
问题1:如图1,按照如上操作
(1)折痕DE的长为 ;
(2)在△DEC绕点D旋转的过程中,直接写出MF与ME的数量关系;
问题2:在△DEC绕点D旋转的过程中,如图2,探究当直线GF∥BC时,求AM的长;
【拓展应用】
小刚受到探究过程的启发,在△DEC绕点D旋转的过程中,尝试画图,并提出问题3,请你解答.
问题3:在△DEC绕点D旋转的过程中,连接AF,当AF取最小值时,请直接写出△AMD的面积.
2.在Rt△ABC中,∠ACB=90°,AC=1,BC=3.
(1)问题发现
如图1,将△CAB绕点C按逆时针方向旋转90°得到△CDE,连接AD,BE,线段AD与BE的数量关系是 ,AD与BE的位置关系是 ;
(2)类比探究
将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,连接AD,BE,线段AD与BE的数量关系,位置关系与(1)中结论是否一致?若AD交CE于点N,请结合图2说明理由;
(3)迁移应用
如图3,将△CAB绕点C旋转一定角度得到△CDE,当点D落到AB边上时,连接BE,求线段BE的长.
3.数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.
(1)当点D在线段BC上时,如图①,求证:BD+EF=AB;
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
(2)当点D在线段BC的延长线上时,如图②:当点D在线段CB的延长线上时,如图③,请判断并直接写出线段BD,EF,AB之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若AC=6,CD=2BD,则EF= .
4.图1、2是一个折叠梯的实物图.图3是折叠梯展开、折叠过程中的一个主视图.图4是折叠梯充分展开后的主视图,此时点E落在AC上,已知AB=AC,sin,点D、F、G、J在AB上,DE、FM、GH、JK均与BC所在直线平行,DE=FM=GH=JK=20cm,DF=FG=GJ=30cm.点N在AC上,AN、MN的长度固定不变.图5是折叠梯完全折叠时的主视图,此时AB、AC重合,点E、M、H、N、K、C在AB上的位置如图所示.
【分析问题】
(1)如图5,用图中的线段填空:AN=MN+EM+AD﹣ ;
(2)如图4,sin∠MEN≈ ,由 AN=EN+AE=EN+AD,且AN的长度不变,可得MN与EN之间的数量关系为 ;
【解决问题】
(3)求MN的长.
5.综合与实践
问题情境
在一次综合与实践课上,老师让同学们以两个全等的等腰直角三角形纸片为操作对象.纸片△ABC和△DEF满足∠ACB=∠EDF=90°,AC=BC=DF=DE=2cm.
下面是创新小组的探究过程.
操作发现
(1)如图1,取AB的中点O,将两张纸片放置在同一平面内,使点O与点F重合.当旋转△DEF纸片交AC边于点H、交BC边于点G时,设AH=x(1<x<2),BG=y,请你探究出y与x的函数关系式,并写出解答过程.
问题解决
(2)如图2,在(1)的条件下连接GH,发现△CGH的周长是一个定值.请你写出这个定值,并说明理由.
拓展延伸
(3)如图3,当点F在AB边上运动(不包括端点A、B),且始终保持∠AFE=60°.请你直接写出△DEF纸片的斜边EF与△ABC纸片的直角边所夹锐角的正切值 (结果保留根号).
6.在等腰直角△ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD.将线段AD绕点D按顺时针方向旋转90°得线段ED,连接BE.
【尝试发现】
(1)如图1,当点D在线段BC上时,线段BE与CD的数量关系为 ;
【类比探究】
(2)当点D在线段BC的延长线上时,先在图2中补全图形,再探究线段BE与CD的数量关系并证明;
【联系拓广】
(3)若AC=BC=1,CD=2,请直接写出sin∠ECD的值.
7.如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B,点P在CB上.
(1)【动手操作】
如图②,若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形,图中∠PBE的度数为 度;
(2)【问题探究】
根据(1)所画图形,探究线段PA与PE的数量关系,并说明理由;
(3)【拓展延伸】
如图③,若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD交于点E,探究线段BA,BP,BE之间的数量关系,并说明理由.
8.【问题呈现】
△CAB和△CDE都是直角三角形,∠ACB=∠DCE=90°,CB=mCA,CE=mCD,连接AD,BE,探究AD,BE的位置关系.
【问题探究】
(1)如图1,当m=1时,直接写出AD,BE的位置关系: .
(2)如图2,当m≠1时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.
【拓展应用】
(3)当m,AB=4,DE=4时,将△CDE绕点C旋转,使A,D,E三点恰好在同一直线上,求BE的长.
9.1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.
(1)下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
当△ABC的三个内角均小于120°时,
如图1,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′,
由PC=P′C,∠PCP′=60°,可知△PCP′为 三角形,故PP′=PC,又P′A′=PA,故PA+PB+PC=P′A′+PB+PP′≥A′B,
由 可知,当B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,如图2,最小值为A′B,此时的P点为该三角形的“费马点”,
且有∠APC=∠BPC=∠APB= ;
已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点.如图3,若∠BAC≥120°,则该三角形的“费马点”为 点.
(2)如图4,在△ABC中,三个内角均小于120°,且AC=3,BC=4,∠ACB=30°,已知点P为△ABC的“费马点”,求PA+PB+PC的值;
(3)如图5,设村庄A,B,C的连线构成一个三角形,且已知AC=4km,BC=2km,∠ACB=60°.现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/km,a元/km,a元/km,选取合适的P的位置,可以使总的铺设成本最低为 元.(结果用含a的式子表示)
10.【模型建立】
(1)如图1,△ABC和△BDE都是等边三角形,点C关于AD的对称点F在BD边上.
①求证:AE=CD;
②用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型应用】
(2)如图2,△ABC是直角三角形,AB=AC,CD⊥BD,垂足为D,点C关于AD的对称点F在BD边上.用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型迁移】
(3)在(2)的条件下,若AD=4,BD=3CD,求cos∠AFB的值.
11.综合与实践
问题情境
数学活动课上,老师发给每名同学一个等腰三角形纸片ABC,AB=AC,∠BAC>90°,要求同学们将纸片沿一条直线折叠,探究图形中的结论.
问题发现
奋进小组在边AC上取一点D,连接BD,将这个纸片沿BD翻折,点A的对应点为E,如图1所示.
如图2,小明发现,当点E落在边BC上时,∠DEC=2∠ACB.
如图3,小红发现,当点D是AC的中点时,连接CE,若已知AB和CE的长,则可求BD的长.
……
问题提出与解决
奋进小组根据小明和小红的发现,讨论后提出问题1,请你解答.
问题1:在△ABC中,AB=AC,∠BAC>90°,点D是边AC上一点,将△ABD沿BD翻折得到△EBD.
(1)如图2,当点E在边BC上时,求证:∠DEC=2∠ACB.
(2)如图3,当点D是AC的中点时,连接CE,若AB=4,CE=3,求BD的长.
拓展延伸
小刚受到探究过程的启发,将等腰三角形的顶角改为锐角,尝试画图,并提出问题2,请你解答.
问题2:如图4,点D是△ABC外一点,AB=AC=BD=4,CD=1,∠ABD=2∠BDC,求BC的长.
12.如图1,在△ABC中,AB=AC,点M,N分别为边AB,BC的中点,连接MN.
初步尝试:(1)MN与AC的数量关系是 ,MN与AC的位置关系是 .
特例研讨:(2)如图2,若∠BAC=90°,BC=4,先将△BMN绕点B顺时针旋转α(α为锐角),得到△BEF,当点A,E,F在同一直线上时,AE与BC相交于点D,连接CF.
①求∠BCF的度数;
②求CD的长.
深入探究:(3)若∠BAC<90°,将△BMN绕点B顺时针旋转α,得到△BEF,连接AE,CF.当旋转角α满足0°<α<360°,点C,E,F在同一直线上时,利用所提供的备用图探究∠BAE与∠ABF的数量关系,并说明理由.
13.【问题情境】如图,在△ABC中,AB=AC,∠ACB=α,点D在边BC上.将线段DB绕点D顺时针旋转得到线段DE(旋转角小于180°),连接BE,CE,以CE为底边在其上方作等腰三角形FEC,使∠FCE=α,连接AF.
【尝试探究】
(1)如图1,当α=60°时,易知AF=BE;
如图2,当α=45°时,则AF与BE的数量关系为 ;
(2)如图3,写出AF与BE的数量关系(用含α的三角函数表示),并说明理由;
【拓展应用】
(3)如图4,当α=30°且点B,E,F三点共线时.若BC=4,BDBC,请直接写出AF的长.
14.【特例感知】
(1)如图1,△AOB和△COD是等腰直角三角形,∠AOB=∠COD=90°,点C在OA上,点D在BO的延长线上,连接AD,BC,线段AD与BC的数量关系是 ;
【类比迁移】
(2)如图2,将图1中的△COD绕着点O顺时针旋转α(0°<α<90°),那么第(1)问的结论是否仍然成立?如果成立,证明你的结论;如果不成立,说明理由.
【方法运用】
(3)如图3,若AB=8,点C是线段AB外一动点,AC=3,连接BC.
①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值是 ;
②若以BC为斜边作Rt△BCD(B,C,D三点按顺时针排列),∠CDB=90°,连接AD,当∠CBD=∠DAB=30°时,直接写出AD的值.
15.【问题情境】
在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中∠ACB=∠DEB=90°,∠B=30°,BE=AC=3.
【问题探究】
小昕同学将三角板DEB绕点B按顺时针方向旋转.
(1)如图2,当点E落在边AB上时,延长DE交BC于点F,求BF的长.
(2)若点C、E、D在同一条直线上,求点D到直线BC的距离.
(3)连接DC,取DC的中点G,三角板DEB由初始位置(图1),旋转到点C、B、D首次在同一条直线上(如图3),求点G所经过的路径长.
(4)如图4,G为DC的中点,则在旋转过程中,点G到直线AB的距离的最大值是 .
16.在△ABC中,点D,E分别是AB,AC边上的点,DE∥BC.
基础理解:
(1)如图1,若AD=4,BD=3,求的值;
证明与拓展:
(2)如图2,将△ADE绕点A逆时针旋转度,得到△AD1E1,连接BD1,CE1.
①求证:;
②如图3,若∠BAC=90°,AB<AC,AD=6,△ADE在旋转过程中,点D1恰好落在DE上时,连接EE1,,则△E1D1E的面积为 .
17.数学课上,有这样一道探究题.
如图,已知△ABC中,AB=AC=m,BC=n,∠BAC=α(0°<α<180°),点P为平面内不与点A、C重合的任意一点,连接CP,将线段CP绕点P顺时针旋转α,得线段PD,连接CD、AP点E、F分别为BC、CD的中点,设直线AP与直线EF相交所成的较小角为β,探究的值和β的度数与m、n、α的关系.
请你参与学习小组的探究过程,并完成以下任务:
(1)填空:
【问题发现】
小明研究了α=60°时,如图1,求出了的值和β的度数分别为 ,β= ;
小红研究了α=90°时,如图2,求出了的值和β的度数分别为 ,β= ;
【类比探究】
他们又共同研究了α=120°时,如图3,也求出了的值和β的度数;
【归纳总结】
最后他们终于共同探究得出规律: (用含m、n的式子表示);β= (用含α的式子表示).
(2)求出α=120°时的值和β的度数.
18.在一平面内,线段AB=20,线段BC=CD=DA=10,将这四条线段顺次首尾相接.把AB固定,让AD绕点A从AB开始逆时针旋转角α(α>0°)到某一位置时,BC,CD将会跟随出现到相应的位置.
论证:如图1,当AD∥BC时,设AB与CD交于点O,求证:AO=10;
发现:当旋转角α=60°时,∠ADC的度数可能是多少?
尝试:取线段CD的中点M,当点M与点B距离最大时,求点M到AB的距离;
拓展:①如图2,设点D与B的距离为d,若∠BCD的平分线所在直线交AB于点P,直接写出BP的长(用含d的式子表示);
②当点C在AB下方,且AD与CD垂直时,直接写出α的余弦值.
19.[初步尝试]
(1)如图①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 ;
[思考说理]
(2)如图②,在三角形纸片ABC中,AC=BC=6,AB=10,将△ABC折叠,使点B与点C重合,折痕为MN,求的值;
[拓展延伸]
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B′处,折痕为CM.
①求线段AC的长;
②若点O是边AC的中点,点P为线段OB′上的一个动点,将△APM沿PM折叠得到△A′PM,点A的对应点为点A′,A′M与CP交于点F,求的取值范围.
20.(1)【操作发现】
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①请按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的对应点为点B′,点C的对应点为点C′.连接BB′;
②在①中所画图形中,∠AB′B= °.
(2)【问题解决】
如图2,在Rt△ABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接DE,求∠ADE的度数.
(3)【拓展延伸】
如图3,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k为常数),求BD的长(用含k的式子表示).
中考数学一轮复习 图形的旋转
参考答案与试题解析
一.解答题(共20小题)
1.综合与实践
【问题情境】
数学活动课上,老师发给每位同学一个直角三角形纸片ABC,∠BAC=90°,AB=3,AC=4.
【问题发现】
奋进小组将三角形纸片ABC进行以下操作:第一步:折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE;第二步:然后将△DEC绕点D顺时针方向旋转得到△DFG.点E,C的对应点分别是点F,G,直线GF与边AC交于点M(点M不与点A重合),与边AB交于点N.
如图1小明发现,折痕DE的长很容易求出,并且MF和ME的数量关系也能证明.
如图2小红发现,在△DEC绕点D旋转的过程中,当直线GF经过点B时或直线GF∥BC时,AM的长都可求…
【问题提出与解决】
奋进小组根据小明和小红的发现,讨论后提出问题1和问题2,请你解答.
问题1:如图1,按照如上操作
(1)折痕DE的长为 ;
(2)在△DEC绕点D旋转的过程中,直接写出MF与ME的数量关系;
问题2:在△DEC绕点D旋转的过程中,如图2,探究当直线GF∥BC时,求AM的长;
【拓展应用】
小刚受到探究过程的启发,在△DEC绕点D旋转的过程中,尝试画图,并提出问题3,请你解答.
问题3:在△DEC绕点D旋转的过程中,连接AF,当AF取最小值时,请直接写出△AMD的面积.
【考点】几何变换综合题.
【专题】三角形.
【答案】问题1:(1);(2)MF=ME;问题2:AM;问题3:.
【分析】问题1:(1)由折叠的性质可知AE=CE,DE⊥AC,再证DE是△ABC的中位线,即可得出结论;
(2)连接DM,由旋转知DE=DF,∠DFM=∠DEM=90°,再证△DMF≌△DME即可得出结论;
问题2:过点A作AH⊥BC于H,交FG于K.则四边形DFKH是矩形,得出,由三角形面积求出AH,然后证△AKM∽△AHC,得出,即可得出结论;
问题3:连接AD、DM,则AF+DF≥AD,当A、F、D三点共线时,AF+DF=AD,此时AF+DF的值最小,AF最小,由直角三角形斜边中线的性质得,证明△AMF∽△CBA,由相似三角形的性质得出AM的长,利用三角形面积公式即可解答.
【解答】解:问题1:(1)∵折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE,
∴AE=CE,DE⊥AC,
∵∠BAC=90°,
∴DE∥AB,
∴,
∴CD=BD,
∴DE为△ABC的中位线,
∴,
故答案为:;
(2)如图,连接DM,
∵将△DEC绕点D顺时针方向旋转得到△DFG,
∴DE=DF,∠DFM=∠DEM=90°,
在Rt△DMF和Rt△DME中,
,
∴Rt△DMF≌Rt△DME(HL),
∴MF=ME;
问题2:①过点A作AH⊥BC于H,交FG于K,
∵GF∥BC,
∴∠HKF=90°,
∵∠DFG=90°,
∴四边形DFKH是矩形,
∴,
∵AB=3,AC=4,
∴,
∵,
∴3×4=5AH,
解得:,
∴,
∵GF∥BC,
∴△AKM∽△AHC,
∴,
解得:AM;
问题3:如图,连接AD、DM,
∵AF+DF≥AD,
∴A、F、D三点共线时,AF+DF=AD,此时AF+DF的值最小,AF最小,
∵∠BAC=90°,BD=CD,
∴,
∴,∠DAC=∠C,
∵∠AFM=∠BAC,
∴△AMF∽△CBA,
∴,即,
解得:,
∴.
【点评】本题考查旋转的性质、全等三角形的判定与性质、相似三角形的判定与性质、矩形的判定与性质、三角形的三边关系及勾股定理,熟练掌握相关性质及判定定理是解题关键.
2.在Rt△ABC中,∠ACB=90°,AC=1,BC=3.
(1)问题发现
如图1,将△CAB绕点C按逆时针方向旋转90°得到△CDE,连接AD,BE,线段AD与BE的数量关系是 BE=3AD ,AD与BE的位置关系是 AD⊥BE ;
(2)类比探究
将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,连接AD,BE,线段AD与BE的数量关系,位置关系与(1)中结论是否一致?若AD交CE于点N,请结合图2说明理由;
(3)迁移应用
如图3,将△CAB绕点C旋转一定角度得到△CDE,当点D落到AB边上时,连接BE,求线段BE的长.
【考点】几何变换综合题.
【专题】等腰三角形与直角三角形;平移、旋转与对称;图形的相似;推理能力.
【答案】(1)BE=3AD,AD⊥BE;
(2)线段AD与BE的数量关系,位置关系与(1)中结论一致,理由见解析过程;
(3).
【分析】(1)由旋转的性质可得AC=DC=1,BC=CE=3,∠ECB=∠ACD=90°,由等腰直角三角形的性质可得AD,BE=3,∠CAD=∠ADC=45°,∠CBE=∠CEB=45°,可证AD⊥BE;
(2)通过证明△BCE∽△ACD,可得,∠CDA=∠CEB,可证BE=3AD,AD⊥BE;
(3)由勾股定理可求AB的长,通过证明△ACN∽△ABC,可求AN的长,由等腰三角形的性质可求AD的长,即可求解.
【解答】解:(1)如图1,延长DA交BE于H,
∵将△CAB绕点C按逆时针方向旋转90°得到△CDE,
∴AC=DC=1,BC=CE=3,∠ECB=∠ACD=90°,
∴AD,BE=3,∠CAD=∠ADC=45°,∠CBE=∠CEB=45°,
∴BE=3AD,∠CAD=∠EAH=45°,
∴∠EHA=90°,
∴AD⊥BE,
故答案为:BE=3AD,AD⊥BE;
(2)线段AD与BE的数量关系,位置关系与(1)中结论一致,理由如下:
如图2,延长DA交BE于H,
∵将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,
∴AC=DC=1,BC=CE=3,∠ECB=∠ACD,
∴,
∴△BCE∽△ACD,
∴,∠CDA=∠CEB,
∴BE=3AD,
∵∠CEB+∠ENH=∠CDA+∠CND=90°,
∴∠EHD=90°,
∴AD⊥BE;
(3)如图3,过点C作CN⊥AB于N,
∵∠ACB=90°,AC=1,BC=3,
∴AB,
∵CN⊥AB,
∴∠ANC=90°=∠ACB,
又∵∠A=∠A,
∴△ACN∽△ABC,
∴,
∴AN 1,
∴AN,
∵AC=DC,CN⊥AB,
∴AD=2AN,
由(2)可知:BE=3AD.
【点评】本题是几何变换综合题,考查了旋转的性质,相似三角形的判定和性质,等腰直角三角形的性质,勾股定理等知识,灵活运用这些性质解决问题是解题的关键.
3.数学老师在课堂上给出了一个问题,让同学们探究.在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.
(1)当点D在线段BC上时,如图①,求证:BD+EF=AB;
分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论:
推理证明:写出图①的证明过程:
探究问题:
(2)当点D在线段BC的延长线上时,如图②:当点D在线段CB的延长线上时,如图③,请判断并直接写出线段BD,EF,AB之间的数量关系;
拓展思考:
(3)在(1)(2)的条件下,若AC=6,CD=2BD,则EF= 10或18 .
【考点】几何变换综合题.
【专题】代数几何综合题;几何直观;运算能力;推理能力.
【答案】(1)证明见解析过程;
(2)图②:AB=BD﹣EF,图③:AB=EF﹣BD;
(3)10或18.
【分析】(1)在AB边上截取AM=EF,连接DM,根据题意证明出△DAM≌△AEF(SAS),得到AF=DM,然后证明出△BMD是等边三角形,得到BD=BM=DM,进而求解即可;
(2)图②:在BD上取点H,使BH=AB,连接AH并延长到点G使AG=AF,连接DG,首先证明出△ABH是等边三角形,得到∠BAH=60°,然后求出∠BAH=∠DAE,然后证明出△FAE≌△GAD(SAS),得到EF=DG,∠AFE=∠G,然后证明出△DHG是等边三角形,得到DH=DG=EF,进而求解即可;
图③:在EF上取点H使AH=AF,同理证明出△EAH≌△ADB(AAS),得到BD=AH,AB=EH,进而求解即可;
(3)根据勾股定理和含30°角直角三角形的性质求出BC=6,AB=12,然后结合CD=2BD,分别(1)(2)的条件下求出BD的长度,进而求解即可.
【解答】(1)证明:在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D在直线BC上,将线段AD绕点A顺时针旋转60°得到线段AE,过点E作EF∥BC,交直线AB于点F.在AB边上截取AM=EF,连接DM.如图1,
∴∠B=90°﹣∠BAC=90°﹣30°=60°.
∵EF∥BC,
∴∠EFB=∠B=60°.
又∵∠EAD=60°,
∴∠EFB=∠EAD.
又∵∠BAD=∠EAD﹣∠EAF,∠AEF=∠EFB﹣∠EAF,
∴∠BAD=∠AEF.
又∵AD=AE,AM=EF,
∴△DAM≌△AEF(SAS).
∴AF=DM.
∴∠AMD=∠EFA=180°﹣∠EFB=180°﹣60°=120°.
∴∠BMD=180°﹣∠AMD=180°﹣120°=60°.
∵∠B=60°,
∴∠BMD=∠B=∠BDM.
∴△BMD是等边三角形.
∴BD=BM=DM,
∵AB=AM+BM,
∴AB=EF+BD;
(2)解:图②:AB=BD﹣EF,证明如下:
如图2.1所示,在BD上取点H,使BH=AB,连接AH并延长到点G使AG=AF,连接DG,
∵∠ABC=60°,
∴△ABH是等边三角形,
∴∠BAH=60°,
∵线段AD绕点A顺时针旋转60°得到线段AE,
∴∠DAE=60°,AE=AD,
∴∠BAH=∠DAE,
∴∠BAH﹣∠EAH=∠DAE﹣∠EAH,即∠BAE=∠HAD,
又∵AG=AF,
∴△FAE≌△GAD(SAS),
∴EF=DG,∠AFE=∠G,
∵BD∥EF,
∴∠ABC=∠F=∠G=60°,
∵∠DHG=∠AHB=60°,
∴△DHG是等边三角形,
∴DH=DG=EF,
∴AB=BH=BD﹣DH=BD﹣EF;
图③:AB=EF﹣BD,证明如下:
如图2.2所示,在EF上取点H使AH=AF,
∵EF∥BC,
∴∠F=∠ABC=60°,
∵AH=AF,
∴△AHF是等边三角形,
∴∠AHF=∠HAF=60°,
∴∠AHE=120°,
∵将线段AD绕点A顺时针旋转60°得到线段AE,
∴AD=AE,∠DAE=60°,
∴∠DAB+∠EAH=180°﹣∠EAD﹣∠HAF=60°,
∵∠D+∠DAB=∠ABC=60°,
∴∠D=∠EAH,
∵∠DBA=180°﹣∠ABC=120°=∠EHA,
又∵AD=AE,
∴△EAH≌△ADB(AAS),
∴BD=AH,AB=EH,
∵AH=FH,
∴BD=HF,
∴AB=EH=EF﹣FH=EF﹣BD;
(3)解:如图3.1所示,
∵∠BAC=30°,∠C=90°,
∴AB=2BC,AB2=BC2+AC2,
∴,
∴BC=6,
∴AB=2BC=12,
∵CD=2BD,BC=BD+CD,
∴BDBC=2,CD=4,
由(1)可知,BD+EF=AB,
∴EF=AB﹣BD=12﹣2=10;
如图3.2所示,当点D在线段BC的延长线上时,
∵CD<BD,与CD=2BD矛盾,
∴不符合题意;
如图3.3所示,当点D在线段CB的延长线上时,
∵CD=2BD=BD+BC,BC=6,
∴BD=BC=6,
由(2)可知,AB=EF﹣BD,
∵AB=2BC=12,
∴EF=AB+BD=12+6=18.
综上所述,EF=10或18,
故答案为:10或18.
【点评】此题考查了全等三角形的性质和判定,勾股定理,等边三角形的性质和判定,含30°角直角三角形的性质,解题的关键是掌握以上知识点.
4.图1、2是一个折叠梯的实物图.图3是折叠梯展开、折叠过程中的一个主视图.图4是折叠梯充分展开后的主视图,此时点E落在AC上,已知AB=AC,sin,点D、F、G、J在AB上,DE、FM、GH、JK均与BC所在直线平行,DE=FM=GH=JK=20cm,DF=FG=GJ=30cm.点N在AC上,AN、MN的长度固定不变.图5是折叠梯完全折叠时的主视图,此时AB、AC重合,点E、M、H、N、K、C在AB上的位置如图所示.
【分析问题】
(1)如图5,用图中的线段填空:AN=MN+EM+AD﹣ DE ;
(2)如图4,sin∠MEN≈ ,由 AN=EN+AE=EN+AD,且AN的长度不变,可得MN与EN之间的数量关系为 MN+10=EN ;
【解决问题】
(3)求MN的长.
【考点】几何变换综合题.
【专题】解直角三角形及其应用;运算能力;推理能力.
【答案】(1)DE;
(2),MN+10=EN;
(3)40cm.
【分析】(1)AN=MN+EM+AE=MN+EM+(AD﹣DE)=MN+EM+AD﹣DE;
(2)可推出四边形DEMF是平行四边形,从而EM∥DF,从而∠MEN=∠BAC,进而得出sin∠MEN=sin∠BAC,根据AN=MN+EM+AD﹣DE,AN=EN+AD得出MN+EM+AD﹣DE=EN+AD,进一步得出结果;
(3)作MW⊥AC于W,解直角三角形EMN求得MW和EW,进而表示出WN,在直角三角形MNW中根据勾股定理列出方程,进而得出结果.
【解答】解:(1)∵AE=AD﹣DE,
∴AN=MN+EM+AE=MN+EM+(AD﹣DE)=MN+EM+AD﹣DE,
故答案为:DE;
(2)∵DE、FM、GH、JK均与BC所在直线平行,
∴DE∥FM,
∵DE=FM=20cm,
∴四边形DEMF是平行四边形,
∴EM∥DF,
∴∠MEN=∠BAC,
∴sin∠MEN=sin∠BAC,
∵AN=MN+EM+AD﹣DE,AN=EN+AD,
∴MN+EM+AD﹣DE=EN+AD,
∴MN+EM﹣DE=EN,
∴MN+30﹣20=EN,
∴MN+10=EN,
故答案为:,MN+10=EN;
(3)如图,
作MW⊥AC于W,
∴∠MWN=∠MWE=90°,
∴MW2+WN2=MN2,MW=EM sin∠MEN=3024,
∴EW18,
设MN=a,则EN=a+10,WN=EN﹣EW=a+10﹣18=a﹣8,
∴242+(a﹣8)2=a2,
∴a=40,
∴MN=40cm.
【点评】本题考查了解直角三角形的应用,平行四边形的判定和性质等知识,解决问题的关键是理解题意,熟练应用有关基础知识.
5.综合与实践
问题情境
在一次综合与实践课上,老师让同学们以两个全等的等腰直角三角形纸片为操作对象.纸片△ABC和△DEF满足∠ACB=∠EDF=90°,AC=BC=DF=DE=2cm.
下面是创新小组的探究过程.
操作发现
(1)如图1,取AB的中点O,将两张纸片放置在同一平面内,使点O与点F重合.当旋转△DEF纸片交AC边于点H、交BC边于点G时,设AH=x(1<x<2),BG=y,请你探究出y与x的函数关系式,并写出解答过程.
问题解决
(2)如图2,在(1)的条件下连接GH,发现△CGH的周长是一个定值.请你写出这个定值,并说明理由.
拓展延伸
(3)如图3,当点F在AB边上运动(不包括端点A、B),且始终保持∠AFE=60°.请你直接写出△DEF纸片的斜边EF与△ABC纸片的直角边所夹锐角的正切值 2或2 (结果保留根号).
【考点】几何变换综合题.
【专题】分类讨论;等腰三角形与直角三角形;图形的相似;解直角三角形及其应用;应用意识.
【答案】(1)y与x的函数关系式为;
(2)△CHG 的周长为2;
(3)2或2.
【分析】(1)证明△AFH∽△BGF,可得AH BG=AF BF,求出,可得,故,=2,从而y与x的函数关系式为;
(2)求出CH=2﹣x,CG=2﹣y,可得,将xy=2代入得,而1<x<2,1<y<2,知x+y>2,故GH=x+y﹣2,可得△CHG 的周长=CH+CG+GH=2﹣x+2﹣y+x+y﹣2=2;
(3)分两种情况:①过点F作 FN⊥AC于点N,作FH的垂直平分线交FN于点M,连接MH,求出∠AHF=75°,可得∠NMH=30°,设NH=k,则MH=MF=2k,从而FN=MF+MN=(2)k,;②过点F作FN⊥BC于点N,作FG的垂直平分线交BG于点M,连接FM,同理可得GN=GM+MN=(2)k,.
【解答】解:(1)如图:
∵∠ACB=∠EDF=90°,且 AC=BC=DF=DE=2cm,
∴∠A=∠B=∠DFE=45°,
∴∠AFH+∠BFG=∠BFG+∠FGB=135°,
∴∠AFH=∠FGB,
∴△AFH∽△BGF,
∴,
∴AH BG=AF BF,
在 Rt△ACB 中,AC=BC=2,
∴,
∵O是AB的中点,点O与点F重合,
∴,
∴,
∴,
∴y与x的函数关系式为;
(2)△CGH的周长定值为2,理由如下:
∵AC=BC=2,AH=x,BG=y,
∴CH=2﹣x,CG=2﹣y,
在Rt△HCG 中,
∴,
将(1)中xy=2代入得:,
∵1<x<2,y,
∴1<y<2,
∴x+y>2,
∴GH=x+y﹣2,
∴△CHG 的周长=CH+CG+GH=2﹣x+2﹣y+x+y﹣2=2;
(3)①过点F作 FN⊥AC于点N,作FH的垂直平分线交FN于点M,连接MH,如图:
∵∠AFE=60°,∠A=45°,
∴∠AHF=75°,
∴FM=MH,
∵∠FNH=90°,
∴∠NFH=15°,
∵FM=MH,
∴∠NFH=∠MHF=15°,
∴∠NMH=30°,
在 Rt△MNH中,设NH=k,
∴MH=MF=2k,
∴MNk,
∴FN=MF+MN=(2)k,
在Rt△FNH中,
;
②过点F作FN⊥BC于点N,作FG的垂直平分线交BG于点M,连接FM,
∵∠AFE=60°,∠B=45°,
∴∠FGB=∠AFE﹣∠B=15°,
∵GM=MF,
∴∠FGB=∠GFM=15°,
∴∠FMB=30°,
在 Rt△FNM中,设FN=k,
∴GM=MF=2k,
由勾股定理得MNk,
∴GN=GM+MN=(2)k,
在 Rt△FNG 中,
,
综上所述,tan 或 ,
故答案为:2或2.
【点评】本题考查几何变换综合应用,涉及相似三角形判定与性质,等腰直角三角形性质及应用,锐角三角函数,勾股定理及应用等知识,解题的关键是作辅助线,构造直角三角形解决问题.
6.在等腰直角△ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD.将线段AD绕点D按顺时针方向旋转90°得线段ED,连接BE.
【尝试发现】
(1)如图1,当点D在线段BC上时,线段BE与CD的数量关系为 ;
【类比探究】
(2)当点D在线段BC的延长线上时,先在图2中补全图形,再探究线段BE与CD的数量关系并证明;
【联系拓广】
(3)若AC=BC=1,CD=2,请直接写出sin∠ECD的值.
【考点】几何变换综合题.
【专题】图形的全等;推理能力.
【答案】(1);(2),补图及证明见解析;(3)或.
【分析】(1)过点E作EM⊥CB延长线于点M,利用一线三垂直全等模型证明△ACD≌△DME,再证明BM=EM即可;
(2)同(1)中方法证明△ACD≌△DME,再证明BM=EM即可;
(3)过点E作EM⊥CB,求出EM,CE即可.
【解答】解:(1)如图,过点E作EM⊥CB延长线于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴BM=DM﹣BD=AC﹣BD=BC﹣BD=CD,
∴BM=EM,
∵EM⊥CB,
∴,
故答案为:;
(2)补全图形如图,,理由如下:
过点E作EM⊥BC于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴DM=BC,
∴DM﹣CM=BC﹣CM,
∴CD=BM,
∴EM=BM,
∵EM⊥CB,
∴;
(3)如图,当点D在CB延长线上时,过点E作EM⊥CB延长线于点M,
由(2)得DM=AC=1,EM=CD=2,
∴CM=CD+DM=3,
∴,
∴;
当点D在BC延长线上时,过点E作EM⊥CB于点M,
同理可得:△ACD≌△DME,
∴DM=AC=1,ME=CD=2,
∴CM=2﹣1=1,
∴CE,
∴sin∠ECD,
综上,sin∠ECD或.
【点评】本题考查三角形全等的判定与性质,三角函数,掌握一线三垂直全等模型是解题的关键.
7.如图①,小红在学习了三角形相关知识后,对等腰直角三角形进行了探究,在等腰直角三角形ABC中,CA=CB,∠C=90°,过点B作射线BD⊥AB,垂足为B,点P在CB上.
(1)【动手操作】
如图②,若点P在线段CB上,画出射线PA,并将射线PA绕点P逆时针旋转90°与BD交于点E,根据题意在图中画出图形,图中∠PBE的度数为 135 度;
(2)【问题探究】
根据(1)所画图形,探究线段PA与PE的数量关系,并说明理由;
(3)【拓展延伸】
如图③,若点P在射线CB上移动,将射线PA绕点P逆时针旋转90°与BD交于点E,探究线段BA,BP,BE之间的数量关系,并说明理由.
【考点】几何变换综合题.
【专题】图形的全等;等腰三角形与直角三角形;平移、旋转与对称;推理能力;应用意识.
【答案】见试题解答内容
【分析】(1)根据题意画出图形,由CA=CB,∠C=90°,得∠ABC=45°,而BD⊥AB,即得∠PBE=∠ABC+∠ABD=135°;
(2)过P作PM∥AB交AC于M,证明△PCM是等腰直角三角形,得CP=CM,∠PMC=45°,即可证△APM≌△PEB(ASA),故PA=PE;
(3)当P在线段BC上时,过P作PM∥AB交AC于M,结合(2)可得ABBP+BE;当P在线段CB的延长线上时,过P作PN⊥BC交BE于N,证明△BPN是等腰直角三角形,可得∠ABP=135°,BP=NP,BNBP,∠PNB=45°,即可证△EPN≌△APB(ASA),EN=BA,根据BE=EN+BN,即得BE=BABP.
【解答】解:(1)画出图形如下:
∵CA=CB,∠C=90°,
∴∠ABC=45°,
∵BD⊥AB,
∴∠ABD=90°,
∴∠PBE=∠ABC+∠ABD=45°+90°=135°;
故答案为:135;
(2)PA=PE,理由如下:
过P作PM∥AB交AC于M,如图:
∴∠MPC=∠ABC=45°,
∴△PCM是等腰直角三角形,
∴CP=CM,∠PMC=45°,
∴CA﹣CM=CB﹣CP,即AM=BP,∠AMP=135°=∠PBE,
∵∠APE=90°,
∴∠EPB=90°﹣∠APC=∠PAC,
∴△APM≌△PEB(ASA),
∴PA=PE;
(3)当P在线段BC上时,过P作PM∥AB交AC于M,如图:
由(2)可知,BE=PM,BP=AM,
∵AB(AM+CM),
∴ABBPCM,
∵PMCM,
∴ABBP+BE;
当P在线段CB的延长线上时,过P作PN⊥BC交BE于N,如图:
∵∠ABD=90°,∠ABC=45°,
∴∠PBN=180°﹣∠ABC﹣∠ABD=45°,
∴△BPN是等腰直角三角形,∠ABP=135°,
∴BP=NP,BNBP,∠PNB=45°,
∴∠PNE=135°=∠ABP,
∵∠APE=90°,
∴∠EPN=90°﹣∠APN=∠APB,
∴△EPN≌△APB(ASA),
∴EN=BA,
∵BE=EN+BN,
∴BE=BABP;
综上所述,当P在线段BC上时,ABBP+BE;当P在线段CB的延长线上时,BE=BABP.
【点评】本题考查几何变换综合应用,涉及等腰直角三角形,旋转变换,全等三角形的判定与性质等知识,解题的关键是作辅助线,构造全等三角形解决问题.
8.【问题呈现】
△CAB和△CDE都是直角三角形,∠ACB=∠DCE=90°,CB=mCA,CE=mCD,连接AD,BE,探究AD,BE的位置关系.
【问题探究】
(1)如图1,当m=1时,直接写出AD,BE的位置关系: AD⊥BE .
(2)如图2,当m≠1时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.
【拓展应用】
(3)当m,AB=4,DE=4时,将△CDE绕点C旋转,使A,D,E三点恰好在同一直线上,求BE的长.
【考点】几何变换综合题.
【专题】图形的全等;等腰三角形与直角三角形;图形的相似;推理能力.
【答案】(1)BE⊥AD;
(2)成立,理由见解析过程;
(3)BE=6或4.
【分析】(1)由“SAS”可证△ACD≌△BCE,可得∠DAC=∠CBE,由余角的性质可证AD⊥BE;
(2)通过证明△DCA∽△ECB,可得∠DAC=∠CBE,由余角的性质可证AD⊥BE;
(3)分两种情况讨论,由相似三角形的性质可得BEAD,由勾股定理可求解.
【解答】解:(1)如图1,延长BE交AC于点H,交AD于N,
当m=1时,DC=CE,CB=CA,
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠DAC=∠CBE,
∵∠CAB+∠ABE+∠CBE=90°,
∴∠CAB+∠ABE+∠DAC=90°,
∴∠ANB=90°,
∴AD⊥BE,
故答案为:AD⊥BE;
(2)(1)中的结论成立,理由如下:
如图2,延长BE交AC于点H,交AD于N,
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
又∵,
∴△DCA∽△ECB,
∴∠DAC=∠CBE,
∵∠CAB+∠ABE+∠CBE=90°,
∴∠CAB+∠ABE+∠DAC=90°,
∴∠ANB=90°,
∴AD⊥BE,
(3)如图3,当点E在线段AD上时,连接BE,
∵△DCA∽△ECB,
∴m,
∴BEAD(4+AE),
∵AD⊥BE,
∴AB2=AE2+BE2,
∴112=AE2+3(4+AE)2,
∴AE=2或AE=﹣8(舍去),
∴BE=6,
当点D在线段AE上时,连接BE,
∵△DCA∽△ECB,
∴m,
∴BEAD(AE﹣4),
∵AD⊥BE,
∴AB2=AE2+BE2,
∴112=AE2+3(AE﹣4)2,
∴AE=8或AE=﹣2(舍去),
∴BE=4,
综上所述:BE=6或4.
【点评】本题是几何变换综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,等腰三角形的性质,灵活运用这些性质解决问题是解题的关键.
9.1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.
(1)下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
当△ABC的三个内角均小于120°时,
如图1,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′,
由PC=P′C,∠PCP′=60°,可知△PCP′为 等边 三角形,故PP′=PC,又P′A′=PA,故PA+PB+PC=P′A′+PB+PP′≥A′B,
由 两点之间线段最短 可知,当B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,如图2,最小值为A′B,此时的P点为该三角形的“费马点”,
且有∠APC=∠BPC=∠APB= 120° ;
已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点.如图3,若∠BAC≥120°,则该三角形的“费马点”为 A 点.
(2)如图4,在△ABC中,三个内角均小于120°,且AC=3,BC=4,∠ACB=30°,已知点P为△ABC的“费马点”,求PA+PB+PC的值;
(3)如图5,设村庄A,B,C的连线构成一个三角形,且已知AC=4km,BC=2km,∠ACB=60°.现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/km,a元/km,a元/km,选取合适的P的位置,可以使总的铺设成本最低为 元.(结果用含a的式子表示)
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】(1)等边;两点之间线段最短;120°;A;
(2)5;
(3)a.
【分析】(1)根据旋转的性质和两点之间线段最短进行推理分析后即可得出结论,然后填空即可;
(2)根据(1)的方法将△APC绕点C顺时针旋转60°得到△A'P'C,即可得出可知当B、P、P'、A'在同一条直线上时,PA+PB+PC取最小值,最小值为A'B,再根据∠ACB=30°可证明∠BCA'=90°,根据勾股定理即可求出A'B;
(3)根据总铺设成本,将△APC绕点C顺时针旋转90°得到△A'P'C,得到等腰直角△PP'C,推出PP'PC,即可得出当B、P、P'、A'在同一条直线上时,P'A'+PB+PP'取最小值,即PA+PBPC取最小值为A'B的长,然后根据已知条件和旋转的性质求出A'B即可.
【解答】解:(1)∵PC=P'C,∠PCP'=60°,
∴△PCP'为等边三角形,
∴PP'=PC,∠P'PC=∠PP'C=60°,
又∵P'A'=PA,
∴PA+PB+PC=PA'+PB+PP'≥A'B,
根据两点之间线段最短可知,当B、P、P'、A'在同一条直线上时,PA+PB+PC取最小值,最小值为A'B,
此时的P点为该三角形的“费马点”,
∴∠BPC+∠P'PC=180°,∠A'P'C+∠PP'C=180°,
∴∠BPC=120°,∠A'P'C=120°,
∵将△APC绕点C顺时针旋转60°得到△A′P′C,
∴△APC≌△A'P'C,
∴∠APC=∠AP'C'=120°,
∴∠APB=360°﹣120°﹣120°=120°,
∴∠APC=∠BPC=∠APB=120°,
∵∠BAC≥120°,
∴BC>AC,BC>AB,
∴BC+AB>AC+AB,BC+AC>AB+AC,
∴三个顶点中顶点A到另外两个顶点的距离和最小,
又∵已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点,
∴该三角形的“费马点”为点A.
故答案为:等边;两点之间线段最短;120°;A;
(2)如图4,将△APC绕点C顺时针旋转60°得到△A'P'C,连接PP',
由(1)可知当B、P、P'、A'在同一条直线上时,PA+PB+PC取最小值,最小值为A'B,
∵∠ACP=∠A'CP',
∴∠ACP+∠BCP=∠A'CP'+∠BCP=∠ACB=30°,
又∵∠PCP'=60°,
∴∠BCA'=90°,
根据旋转的性质可知:AC=A'C=3,
∴A'B,
即PA+PB+PC的最小值为5;
(3)∵总铺设成本=PA×a+PB×a+PCa,
∴当PA+PBPC最小时,总铺设成本最低,
将△APC绕点C顺时针旋转90°得到△A'P'C,连接PP',A'B,
由旋转性质可知:P'C=PC,∠PCP'=∠ACA'=90°,P'A'=PA,A'C=AC=4km,
∴PP'PC,
∴PA+PBPC=P'A'+PB+PP',
当B、P、P'、A'在同一条直线上时,P'A'+PB+PP'取最小值,
即PA+PBPC取最小值为A'B,
过点A'作A'H⊥BC于H,
∵∠ACB=60°,∠ACA'=90°,
∴∠A'CH=30°,
∴A'HA'C=2km,
∴HC(km),
∴BH=BC+CH(km),
∴A'B2(km),
即PA+PBPC的最小值为km,
总铺设成本为:总铺设成本a(元).
故答案为:a.
【点评】本题是几何变换综合题,主要考查旋转的性质,全等三角形的判定和性质,两点之间线段最短以及等边三角形的性质,深入理解题意是解决问题的关键.
10.【模型建立】
(1)如图1,△ABC和△BDE都是等边三角形,点C关于AD的对称点F在BD边上.
①求证:AE=CD;
②用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型应用】
(2)如图2,△ABC是直角三角形,AB=AC,CD⊥BD,垂足为D,点C关于AD的对称点F在BD边上.用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型迁移】
(3)在(2)的条件下,若AD=4,BD=3CD,求cos∠AFB的值.
【考点】几何变换综合题.
【专题】几何变换;几何直观.
【答案】(1)①证明见解答过程;
②AD=BD+DF.理由见解答过程;
(2)BD+DFAD.理由见解答过程;
(3).
【分析】(1)①根据△ABC和△BDE都是等边三角形推出判定△ABE和△CBD全等,然后根据全等三角形的对应边相等即可得证;
②根据等边三角形的性质和对称的性质即可推出线段AD,BD,DF的数量关系;
(2)过点B作BE⊥AD于E,根据等腰直角三角形的性质推出判定△ABE∽△CBD,然后根据等腰直角三角形的性质和对称性即可推出线段AD,BD,DF的数量关系;
(3)过点A作AG⊥BD于G,推出△ADG是等腰直角三角形,求出AG、FG、AF的长后即可求出cos∠AFB的值.
【解答】(1)证明:①∵△ABC和△BDE都是等边三角形,
∴AB=CB,EB=DB,∠ABC=∠EBD=60°,
∴∠ABE=∠CBD,
∴△ABE≌△CBD,
∴AE=CD;
②解:AD=BD+DF.
理由如下:
∵△BDE是等边三角形,
∴BD=DE,
∵点C与点F关于AD对称,
∴CD=DF,
∵AD=AE+DE,
∴AD=BD+DF;
(2)BD+DFAD.
理由如下:
如图1,过点B作BE⊥AD于E,
∵点C与点F关于AD对称,
∴∠ADC=∠ADB,
又∵CD⊥BD,
∴∠ADC=∠ADB=45°,
又∵BE⊥AD,
∴△BDE是等腰直角三角形,
又∵△ABC是等腰直角三角形,
∴,∠ABC=∠EBD=45°,
∴∠ABE=∠CBD,
∴△ABE∽△CBD,
∴,CD=DF,
∴DFAE,
∵△BDE是等腰直角三角形,
∴BD,
∴BD+DF,
即:BD+DFAD.
(3)解:如图2,过点A作AG⊥BD于G,
又∵∠ADB=45°,
∴△AGD是等腰直角三角形,
又∵AD=4,
∴AG=DG=4,BD+DFAD=8,
∵BD=3CD,CD=DF,
∴DF=2,
又∵DG=4,
∴FG=DG﹣DF=2,
在Rt△AFG中,由勾股定理得:,
∴cos∠AFB.
【点评】本题是几何变换综合题,主要考查等边三角形的性质,等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质以及勾股定理,深入理解题意是解决问题的关键.
11.综合与实践
问题情境
数学活动课上,老师发给每名同学一个等腰三角形纸片ABC,AB=AC,∠BAC>90°,要求同学们将纸片沿一条直线折叠,探究图形中的结论.
问题发现
奋进小组在边AC上取一点D,连接BD,将这个纸片沿BD翻折,点A的对应点为E,如图1所示.
如图2,小明发现,当点E落在边BC上时,∠DEC=2∠ACB.
如图3,小红发现,当点D是AC的中点时,连接CE,若已知AB和CE的长,则可求BD的长.
……
问题提出与解决
奋进小组根据小明和小红的发现,讨论后提出问题1,请你解答.
问题1:在△ABC中,AB=AC,∠BAC>90°,点D是边AC上一点,将△ABD沿BD翻折得到△EBD.
(1)如图2,当点E在边BC上时,求证:∠DEC=2∠ACB.
(2)如图3,当点D是AC的中点时,连接CE,若AB=4,CE=3,求BD的长.
拓展延伸
小刚受到探究过程的启发,将等腰三角形的顶角改为锐角,尝试画图,并提出问题2,请你解答.
问题2:如图4,点D是△ABC外一点,AB=AC=BD=4,CD=1,∠ABD=2∠BDC,求BC的长.
【考点】几何变换综合题.
【专题】图形的全等;等腰三角形与直角三角形;矩形 菱形 正方形;平移、旋转与对称;运算能力;推理能力.
【答案】问题1,
(1)证明过程详见解答;
(2);
问题2,
.
【分析】问题1,
(1)由∠A+∠DEC=180°,∠A+∠ACB+∠ABC=∠A+2∠ACB=180°得出结论;
(2)作AG⊥BD于G,作DF⊥CE于F,根据等腰三角形的性质得出CF=EF,进而得出DF的值,可证得△ADG≌△DFC,从而AG=DF,DG=CF,进而在Rt△ABG中求得BG,进一步得出结果;
问题2,
连接AD,作BE⊥AD于E,作BF⊥CD,交DC的延长线于F,可证得四边形DEBF是矩形,从而BF=DE,DF=BE,在Rt△ACD中求得AD,进而求得BF=DE,进而在Rt△BDE中求得DF=BE,从而得出CF=DF﹣CD,进而在Rt△BCF中求得BG的值,进一步得出结果.
【解答】问题1,
(1)证明:∵将△ABD沿BD翻折得到△EBD,
∴∠BED=∠A,
∵∠BED+∠DEC=180°,
∴∠A+∠DEC=180°,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠A+∠ACB+∠ABC=∠A+2∠ACB=180°,
∴∠DEC=2∠ACB;
(2)解:如图1,
作AG⊥BD于G,作DF⊥CE于F,
∴∠AGD=∠DFC=90°,
由折叠得,
AD=DE,∠ADB=∠BDE,
∵点D是AC的中点,
∴CD=AD,
∴DE=CD,
∴∠DEC=∠DCE,CF=EFCE
∴DF2=CD2﹣CF2=22﹣()2,
∵∠ADB+∠BDE+∠EDC=180°,
∴2∠ADB+∠EDC=180°,
∵∠DEC+∠DCE+∠EDC=180°,
∴2∠DCE+∠EDC=180°,
∴∠ADB=∠DCE,
∴△ADG≌△DFC(AAS),
∴AG=DF,DG=CF,
在Rt△ABG中,由勾股定理得,
BG,
∴BD=BG+DG;
问题2,
解:如图2,
连接AD,作BE⊥AD于E,作BF⊥CD,交DC的延长线于F,
∵AB=BD,
∴∠ABD=2∠DBE,DE=AEAD,
∵∠ABD=2∠BDC,
∴∠BDE=∠BDC,
∴CD∥BE,
∴CD⊥AD,
∴∠BED=∠EDC=∠F=90°,
∴四边形DEBF是矩形,
∴BF=DE,DF=BE,
在Rt△ACD中,CD=1,AC=4,
∴AD,
∴BF=DE,
在Rt△BDE中,BD=4,DE,
∴DF=BE,
∴CF=DF﹣CD,
在Rt△BCF中,CF,BF,
∴BC.
【点评】本题考查了轴对称的性质,等腰三角形的性质,勾股定理,全等三角形的判定及性质,矩形的判定和性质等知识,解决问题的关键是作辅助线,构造全等三角形.
12.如图1,在△ABC中,AB=AC,点M,N分别为边AB,BC的中点,连接MN.
初步尝试:(1)MN与AC的数量关系是 MNAC ,MN与AC的位置关系是 MN∥AC .
特例研讨:(2)如图2,若∠BAC=90°,BC=4,先将△BMN绕点B顺时针旋转α(α为锐角),得到△BEF,当点A,E,F在同一直线上时,AE与BC相交于点D,连接CF.
①求∠BCF的度数;
②求CD的长.
深入探究:(3)若∠BAC<90°,将△BMN绕点B顺时针旋转α,得到△BEF,连接AE,CF.当旋转角α满足0°<α<360°,点C,E,F在同一直线上时,利用所提供的备用图探究∠BAE与∠ABF的数量关系,并说明理由.
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】(1);MN∥AC;
(2)①∠BCF=30°;②;
(3)∠BAE=∠ABF 或∠BAE+∠ABF=180°.
【分析】(1)AB=AC,点M,N分别为边AB,BC的中点,则MN是△ABC的中位线,即可得出结论;
(2)特例研讨:①连接EM,MN,NF,证明△BME是等边三角形,△BNF是等边三角形,得出∠FCB=30°;
②连接AN,证明△ADN∽△BDE,则 ,设DE=x,则,在Rt△ABE中,BE=2,,则,在Rt△ADN中,AD2=DN2+AN2,勾股定理求得,则;
(3)当点C,E,F在同一直线上时,且点E在FC上时,设∠ABC=∠ACB=θ,则∠BAC=180°﹣2θ,得出∠BEC+∠BAC=180°,则A.B,E,C 在同一个圆上,进而根据圆周角定理得出∠EAC=∠EBC=α﹣θ,表示∠BAE与∠ABF,即可求解;当F在EC上时,可得A,B,E,C在同一个圆上,设∠ABC=∠ACB=θ,则∠BAC=∠BEF=180°﹣2θ,设∠NBF=β,则∠EBM=β,则 α+β=360°,表示∠BAE 与∠ABF,即可求解.
【解答】解:(1)∵AB=AC,点M,N分别为边AB,BC的中点,
∴MN是△ABC的中位线,
∴,MN∥AC;
故答案为:MNAC,MN∥AC;
(2)特例研讨:①如图所示,连接EM,MN,NF,
∵MN是△BAC的中位线,
∴MN∥AC,
∴∠BMN=∠BAC=90°,
∵将△BMN绕点B顺时针旋转α(α为锐角),得到△BEF,
∴BE=BM,BF=BN;∠BEF=∠BMN=90°,
∵点A,E,F在同一直线上,
∴∠AEB=∠BEF=90°,
在Rt△ABE中,M是斜边AB的中点,
∴,
∴BM=ME=BE,
∴△BME是等边三角形,
∴∠ABE=60°,即旋转角α=60°,
∴∠NBF=60°,BN=BF,
∴△BNF是等边三角形,
又∵BN=NC,BN=NF,
∴NF=NC,
∴∠NCF=∠NFC,
∴∠BNF=∠NCF+∠NFC=2∠NFC=60°,
∴∠FCB=30°;
(2)如图所示,连接AN,
∵AB=AC,∠BAC=90° ,
∴,∠ACB=∠ABC=45°,
∵∠ADN=∠BDE,∠ANB=∠BED=90°,
∴△ADN∽△BDE,
∴,
设DE=x,则,
在Rt△ABE中,,则,
在Rt△ADN中,AD2=DN2+AN2,
∴,
解得: 或 (舍去),
∴;
(3)如图所示,当点C,E,F在同一直线上时,且点E在FC上时,
∵AB=AC,
∴∠ABC=∠ACB,设∠ABC=∠ACB=θ,则∠BAC=180°﹣2θ,
∵MN是△ABC的中位线,
∴MN∥AC,
∴∠MNB=∠MBN=θ,
∵将△BMN绕点B顺时针旋转α,得到△BEF,
∴△EBF≌△MBN,∠MBE=∠NBF=α,
∴∠EBF=∠EFB=θ,
∴∠BEF=180°﹣2θ,
∵点C,E,F在同一直线上,
∴∠BEC=2θ,
∴∠BEC+∠BAC=180°,
∴A,B,E,C在同一个圆上,
∴∠EAC=∠EBC=α﹣θ,
∴∠BAE=∠BAC﹣∠EAC=(180°﹣2θ)﹣(α﹣θ)=180°﹣α﹣θ,
∵∠ABF=α+θ,
∴∠BAE+∠ABF=180°,
如图所示,当F在EC上时,
∵∠BEF=∠BAC,BC=BC,
∴A,B,E,C在同一个圆上,设∠ABC=∠ACB=θ,则∠BAC=∠BEF=180°﹣2θ,
将△BMN绕点B顺时针旋转α,得到△BEF,设∠NBF=β,则∠EBM=β,则 α+β=360°,
∴∠ABF=θ﹣β,
∵∠BFE=∠EBF=θ,∠EFB=∠FBC+∠FCB,
∴∠ECB=∠FCB=∠EFB﹣∠FBC=θ﹣β,
∵,
∴∠EAB=∠ECB=θ﹣β,
∴∠BAE=∠ABF,
综上所述,∠BAE=∠ABF或∠BAE+∠ABF=180°.
【点评】本题属于几何变换综合题,考查了圆周角定理,圆内接四边形对角互补,相似三角形的性质与判定,旋转的性质,中位 线的性质与判定,等腰三角形的性质与判定,三角形内角和定理,三角形外角的性质,勾股定理,熟练掌 以上知识是解题的关键.
13.【问题情境】如图,在△ABC中,AB=AC,∠ACB=α,点D在边BC上.将线段DB绕点D顺时针旋转得到线段DE(旋转角小于180°),连接BE,CE,以CE为底边在其上方作等腰三角形FEC,使∠FCE=α,连接AF.
【尝试探究】
(1)如图1,当α=60°时,易知AF=BE;
如图2,当α=45°时,则AF与BE的数量关系为 BEAF ;
(2)如图3,写出AF与BE的数量关系(用含α的三角函数表示),并说明理由;
【拓展应用】
(3)如图4,当α=30°且点B,E,F三点共线时.若BC=4,BDBC,请直接写出AF的长.
【考点】几何变换综合题.
【专题】等腰三角形与直角三角形;图形的相似;解直角三角形及其应用;运算能力;推理能力.
【答案】(1)BEAF;
(2)BE=2AF cosα;
(3).
【分析】(1)可证明△ACF∽△BCE,从而,进而得出结果;
(2)过点A作AH⊥BC于点H,可推出cosα,进而证得△ACF∽△BCE,从而;
(3)作DM⊥BF于点M,过点C作CH⊥BF,交BF延长线于点H,设BM=x,则BE=2x,由DM∥CH得,从而BH=5BM=5x,EH=BH﹣BE=3x,进而表示出FE=FC=2x,FH=x.,在Rt△BHC中,由勾股定理列出方程(5x)2+()2=(4)2,从而x=2,进一步得出结果.
【解答】解:(1)当α=45°时,△ABC和△FEC是等腰直角三角形,
∴∠ACB=∠FCE=45°,
∴∠ACF=∠BCE,
∵,
∴△ACF∽△BCE,
∴,
故答案为:BEAF;
(2)如图1,
BE=2AF cosα,理由如下:
过点A作AH⊥BC于点H,
∵AB=AC,
∴BH=CH,∠ABC=∠ACB=α,
∴cosα
∴2cosα
同理可得:2cosα,
∴,
∵∠FCE=∠ACB,
∴∠ACF=∠BCE,
∴△ACF∽△BCE,
∴,
∴BE=2AF cosα;
(3)方法一
如图2,
作DM⊥BF于点M,过点C作CH⊥BF,交BF延长线于点H,
∴∠BMD=∠H=90°,
∴DM∥CH,
∵线段DB绕点D顺时针旋转得到线段DE,
∴DB=DE,
∴BM=EM,
∵∠FCE=∠FEC=30°,
∴∠CFH=∠FCE+∠FEC=60°,
∴EF=CF=2FH,
设BM=x,则BE=2x,
∵DM∥CH,
∵,
∴BH=5BM=5x,
∴EH=BH﹣BE=3x,
∵FE=2FH,
∴FE=FC=2x,FH=x.
∴
在Rt△BHC中,由勾股定理得,
∴BH2+CH2=BC2,
∴(5x)2+()2=(4)2,
∴x=2,
∴BE=2x=4,
由(2)得:,
方法二
如图3,
作CG∥BF交ED延长线于点G,过点D作DM⊥CG于点M,
过点E作EH⊥CG于点H,
∴∠DMG=∠EHG=90°,
∴DM∥EH,
∵线段DB绕点D顺时针旋转得到线段DE,
∴DB=DE,
∴∠DBE=∠DEB,
∵CG∥BF,
∴∠DBE=∠DCG,∠DEB=∠G,
∴DG=DC,
∵DM⊥CG,
∴GM=CM,
∵△FEC是以CE为底边的等腰三角形,∠FCE=30°,
∴∠FEC=∠FCE=30°,
∵CG∥BF,
∴∠ECG=∠FEC=30°,△BDE∽△CDG,
∴,
设BE=2x,则GC=8x,
∴GM=CM=4x,
∵DM∥EH,
∴,
∴HM=x,
∴HC=3x,
∴GH=GM+HM=5x,
在Rt△EHC中,∠ECH=30°,
∴,
在Rt△EHG中,由勾股定理得,
∴GH2+EH2=GE2,
∴(5x)2+()2=(4)2,
∴x=2,
∴BE=4,
∵△BEC∽△AFC,
∴.
【点评】本题考查了相似三角形的判定和性质,解直角三角形,等腰三角形的性质等知识,解决问题的关键是作辅助线,构造相似三角形.
14.【特例感知】
(1)如图1,△AOB和△COD是等腰直角三角形,∠AOB=∠COD=90°,点C在OA上,点D在BO的延长线上,连接AD,BC,线段AD与BC的数量关系是 AD=BC ;
【类比迁移】
(2)如图2,将图1中的△COD绕着点O顺时针旋转α(0°<α<90°),那么第(1)问的结论是否仍然成立?如果成立,证明你的结论;如果不成立,说明理由.
【方法运用】
(3)如图3,若AB=8,点C是线段AB外一动点,AC=3,连接BC.
①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值是 8+3 ;
②若以BC为斜边作Rt△BCD(B,C,D三点按顺时针排列),∠CDB=90°,连接AD,当∠CBD=∠DAB=30°时,直接写出AD的值.
【考点】几何变换综合题.
【专题】几何综合题;压轴题;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)证明△AOD≌△BOC(SAS),即可得出结论;
(2)利用旋转性质可证得∠BOC=∠AOD,再证明△AOD≌△BOC(SAS),即可得出结论;
(3)①过点A作AT⊥AB,使AT=AB,连接BT,AD,DT,BD,先证得△ABC∽△TBD,得出DT=3,即点D的运动轨迹是以T为圆心,3为半径的圆,当D在AT的延长线上时,AD的值最大,最大值为8+3;
②如图4,在AB上方作∠ABT=30°,过点A作AT⊥BT于点T,连接AD、BD、DT,过点T作TH⊥AD于点H,可证得△BAC∽△BTD,得出DTAC3,再求出DH、AH,即可求得AD;如图5,在AB下方作∠ABE=30°,过点A作AE⊥BE于点E,连接DE,可证得△BAC∽△BTD,得出DE,再由勾股定理即可求得AD.
【解答】解:(1)AD=BC.理由如下:
如图1,∵△AOB和△COD是等腰直角三角形,∠AOB=∠COD=90°,
∴OA=OB,OD=OC,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴AD=BC,
故答案为:AD=BC;
(2)AD=BC仍然成立.
证明:如图2,∵∠AOB=∠COD=90°,
∴∠AOB+∠AOC=∠AOC+∠COD=90°+α,
即∠BOC=∠AOD,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(SAS),
∴AD=BC;
(3)①过点A作AT⊥AB,使AT=AB,连接BT,AD,DT,BD,
∵△ABT和△CBD都是等腰直角三角形,
∴BTAB,BDBC,∠ABT=∠CBD=45°,
∴,∠ABC=∠TBD,
∴△ABC∽△TBD,
∴,
∴DTAC33,
∵AT=AB=8,DT=3,
∴点D的运动轨迹是以T为圆心,3为半径的圆,
∴当D在AT的延长线上时,AD的值最大,最大值为8+3,
故答案为:8+3;
②如图4,在AB上方作∠ABT=30°,过点A作AT⊥BT于点T,连接AD、BD、DT,过点T作TH⊥AD于点H,
∵cos30°,∠ABC=∠TBD=30°+∠TBC,
∴△BAC∽△BTD,
∴,
∴DTAC3,
在Rt△ABT中,AT=AB sin∠ABT=8sin30°=4,
∵∠BAT=90°﹣30°=60°,
∴∠TAH=∠BAT﹣∠DAB=60°﹣30°=30°,
∵TH⊥AD,
∴TH=AT sin∠TAH=4sin30°=2,AH=AT cos∠TAH=4cos30°=2,
在Rt△DTH中,DH,
∴AD=AH+DH=2;
如图5,在AB上方作∠ABE=30°,过点A作AE⊥BE于点E,连接DE,
则cos30°,
∵∠EBD=∠ABC=∠ABD+30°,
∴△BDE∽△BCA,
∴,
∴DEAC3,
∵∠BAE=90°﹣30°=60°,AE=AB sin30°=84,
∴∠DAE=∠DAB+∠BAE=30°+60°=90°,
∴AD;
综上所述,AD的值为2或.
【点评】本题是几何变换综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,等腰三角形的性质,瓜豆原理等知识点,关键是添加恰当辅助线,构造全等三角形或相似三角形解决问题,综合性较强,难度较大,属于中考压轴题.
15.【问题情境】
在一次数学兴趣小组活动中,小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中∠ACB=∠DEB=90°,∠B=30°,BE=AC=3.
【问题探究】
小昕同学将三角板DEB绕点B按顺时针方向旋转.
(1)如图2,当点E落在边AB上时,延长DE交BC于点F,求BF的长.
(2)若点C、E、D在同一条直线上,求点D到直线BC的距离.
(3)连接DC,取DC的中点G,三角板DEB由初始位置(图1),旋转到点C、B、D首次在同一条直线上(如图3),求点G所经过的路径长.
(4)如图4,G为DC的中点,则在旋转过程中,点G到直线AB的距离的最大值是 .
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】(1)2;(2)±1;(3)π;(4).
【分析】(1)根据锐角三角函数求解,即可求出答案;
(2)①当点E在BC上方时,如图1过点D作DH⊥BC于H,根据锐角三角函数求出BC=3,DE,最后利用面积求解,即可求出答案;
②当点E在BC下方时,同①的方法,即可求出答案;
(3)先求出∠BOG=150°,再判断出点G是以点O为圆心,为半径的圆上,最后用弧长公式求解,即可求出答案;
(4)过点O作OK⊥AB于K,求出OK,即可求出答案.
【解答】解:(1)由题意得,∠BEF=∠BED=90°,
在Rt△BEF中,∠ABC=30°,BE=3,
∴BF2;
(2)①当点E在BC上方时,
如图1,过点D作DH⊥BC于H,
在Rt△ABC中,AC=3,
∴tan∠ABC,
∴BC3,
在Rt△BED中,∠EBD=∠ABC=30°,BE=3,
∴DE=BE tan∠DBE,
在Rt△BCE中,BE=3,BC=3,
根据勾股定理得,CE3,
∴CD=CE+DE=3,
∵S△BCDCD BEBC DH,
∴DH1,
②当点E在BC下方时,如图2,
过点D作DM⊥BC于M,
∵S△BDCBC DMCD BE,
∴DM1,
即点D到直线BC的距离为±1;
(3)如图3﹣1,连接CD,取CD的中点G,
取BC的中点O,连接GO,则OG∥AB,
∴∠COG=∠B=30°,
∴∠BOG=150°,
∵点G为CD的中点,点O为BC的中点,
∴GOBD,
∴点G是以点O为圆心,为半径的圆上,如图3﹣2,
∴三角板DEB由初始位置(图1),旋转到点C、B、D首次在同一条直线上时,点G所经过的轨迹为150°所对的圆弧,
∴点G所经过的路径长为π;
(4)如图4,过点O作OK⊥AB于K,
∵点O为BC的中点,BC=3,
∴OB,
∴OK=OB sin30°,
由(3)知,点G是以点O为圆心,为半径的圆上,
∴点G到直线AB的距离的最大值是,
故答案为:.
【点评】此题是几何变换综合题,主要考查了锐角三角函数,勾股定理,弧长公式,三角形的中位线定理,三角形的面积,画出图形是解本题的关键.
16.在△ABC中,点D,E分别是AB,AC边上的点,DE∥BC.
基础理解:
(1)如图1,若AD=4,BD=3,求的值;
证明与拓展:
(2)如图2,将△ADE绕点A逆时针旋转度,得到△AD1E1,连接BD1,CE1.
①求证:;
②如图3,若∠BAC=90°,AB<AC,AD=6,△ADE在旋转过程中,点D1恰好落在DE上时,连接EE1,,则△E1D1E的面积为 13.44 .
【考点】几何变换综合题.
【专题】几何综合题;推理能力.
【答案】(1);
(2)①见解析;
②13.44.
【分析】(1)利用平行线分线段成比例定理可得;
(2)①根据旋转的性质得AD=AD1,AE=AE1,∠BAD1=∠CAE1,再根据平行线分线段成比例定理得,证明△ABD1∽△ACE1,即可证明结论;
②由得,AD1和AE1的长,过点A作AM⊥DE于M,利用三角形内角和定理说明∠D1EE1=90°,利用勾股定理即可解决问题.
【解答】(1)解:∵DE∥BC,AD=4,BD=3,
∴;
(2)①证明:∵将△ADE绕点A逆时针旋转度,得到△AD1E1,
∴AD=AD1,AE=AE1,∠BAD1=∠CAE1,
∵DE∥BC,
∴,
∴,
∴△ABD1∽△ACE1,
∴;
②解:由①可知,△ABD1∽△ACE1,
∴,
∵将△ADE绕点A逆时针旋转度,得到△AD1E1,
∴AD=AD1=6,∠D1AE1=∠DAE=90°,
∴AE=AE18,DE=D1E=10,
过点A作AM⊥DE于点M,
则DM=D1M=AD×cos∠ADE=3.6,
∴D1E=10﹣3.6×2=2.8,
∴∠D1AE1=∠DAE=90°,
∴∠DAD1=∠EAE1,
∵AD=AD1,AE=AE1,
∴∠ADE=∠AEE1,
∴∠AED+∠AEE1=∠AED+∠ADE=90°,
∴∠D1EE1=90°,
∴EE1=9.6,
∴△E1D1E的面积为,
故答案为:13.44.
【点评】本题是几何变换综合题,主要考查了平行线分线段成比例定理,相似三角形的判定与性质,旋转的性质,等腰三角形的性质,勾股定理等知识,说明∠D1EE1=90°是解题的关键.
17.数学课上,有这样一道探究题.
如图,已知△ABC中,AB=AC=m,BC=n,∠BAC=α(0°<α<180°),点P为平面内不与点A、C重合的任意一点,连接CP,将线段CP绕点P顺时针旋转α,得线段PD,连接CD、AP点E、F分别为BC、CD的中点,设直线AP与直线EF相交所成的较小角为β,探究的值和β的度数与m、n、α的关系.
请你参与学习小组的探究过程,并完成以下任务:
(1)填空:
【问题发现】
小明研究了α=60°时,如图1,求出了的值和β的度数分别为 ,β= 60° ;
小红研究了α=90°时,如图2,求出了的值和β的度数分别为 ,β= 45° ;
【类比探究】
他们又共同研究了α=120°时,如图3,也求出了的值和β的度数;
【归纳总结】
最后他们终于共同探究得出规律: (用含m、n的式子表示);β= (用含α的式子表示).
(2)求出α=120°时的值和β的度数.
【考点】几何变换综合题.
【专题】图形的相似;模型思想.
【答案】(1),60°,,45°,,,(2).
【分析】(1)当α=60°时,△ABC和△PDC都是等边三角形,可证△ACP∽△ECF,从而有,∠Q=β=∠ACB=60°;
当α=90°时,△ABC和△PDC都是等腰直角三角形,同理可证△ACP∽△ECF即可解决,依此可得出规律;
(2)当α=120°,可证,,从而有,由∠ECF=∠ACP,可得△PCA∽△FCE即可解决问题.
【解答】解:(1)如图1,连接AE,PF,延长EF、AP交于点Q,
当α=60°时,△ABC和△PDC都是等边三角形,
∴∠PCD=∠ACB=60°,PC=CD,AC=CB,
∵F、E分别是CD、BC的中点,
∴,,
∴,
又∵∠ACP=∠ECF,
∴△ACP∽△ECF,
∴,∠CEF=∠CAP,
∴∠Q=β=∠ACB=60°,
当α=90°时,△ABC和△PDC都是等腰直角三角形,
∴∠PCD=∠ACB=45°,PCCD,ACCB,
∵F、E分别是CD、BC的中点,
∴,,
∴,
又∵∠ACP=∠ECF,
∴△ACP∽△ECF,
∴,∠CEF=∠CAP,
∴∠Q=β=∠ACB=45°,
由此,可归纳出,β=∠ACB;
(2)当α=120°,连接AE,PF,延长EF、AP交于点Q,
∵AB=AC,E为BC的中点,
∴AE⊥BC,∠CAE=60°
∴sin60°,
同理可得:,
∴,
∴,
又∵∠ECF=∠ACP,
∴△PCA∽△FCE,
∴,∠CEF=∠CAP,
∴∠Q=β=∠ACB=30°.
【点评】本题主要考查了三角形相似的判定与性质,通过解决本题感受到:图形在变化但解决问题的方法不变,体会“变中不变”的思想.
18.在一平面内,线段AB=20,线段BC=CD=DA=10,将这四条线段顺次首尾相接.把AB固定,让AD绕点A从AB开始逆时针旋转角α(α>0°)到某一位置时,BC,CD将会跟随出现到相应的位置.
论证:如图1,当AD∥BC时,设AB与CD交于点O,求证:AO=10;
发现:当旋转角α=60°时,∠ADC的度数可能是多少?
尝试:取线段CD的中点M,当点M与点B距离最大时,求点M到AB的距离;
拓展:①如图2,设点D与B的距离为d,若∠BCD的平分线所在直线交AB于点P,直接写出BP的长(用含d的式子表示);
②当点C在AB下方,且AD与CD垂直时,直接写出α的余弦值.
【考点】几何变换综合题.
【专题】压轴题;动点型;方程思想;应用意识.
【答案】论证:见解答过程;
发现:60°或120°;
尝试:;
拓展:
①;
②.
【分析】论证:由△AOD≌△BOC,得AO=BO,而AB=20,可得AO=10;
发现:设AB的中点为O,当AD从初始位置AO绕A逆时针旋转60°时,BC也从初始位置BC'绕点B逆时针旋转60°,BC旋转到BO的位置,即C以O重合,从而可得∠ADC=60°;当AD从AO绕A逆时针旋转60°时,CD从CD'的位置开始也旋转60°,故△ADO和△CDO都是等边三角形,可得此时∠ADC=120°,
尝试:当点M与点B距离最大时,D、C、B共线,过D作DQ⊥AB于Q,过M作MN⊥AB于N,由已知可得AD=10,设AQ=x,则BQ=20﹣x,100﹣x2=400﹣(20﹣x)2,可得AQ,DQ,再由MN∥DQ,得,MN,即点M到AB的距离为;
拓展:
①设直线CP交DB于H,过G作DG⊥AB于G,连接DP,设BG=m,则AG=20﹣m,由AD2﹣AG2=BD2﹣BG2,可得m,BG,而△BHP∽△BGD,有,即可得BP;
②方法一:过B作BG⊥CD于G,设AN=t,则BN=20﹣t,DN,由△ADN∽△BGN,,表达出NG,BG,Rt△BCG中,CG,根据DN+NG+CG=10,列方程10,解得t,即可得cosα.
方法二:过C作CK⊥AB于K,过F作FH⊥AC于H,由AC2﹣AK2=BC2﹣BK2,可解得AK,即得CK,Rt△ACK中,tan∠KAC,Rt△AFH中,tan∠KAC,设FHn,则CH=FHn,AH=5n,根据AC=AH+CH=10,解得n,从而AF,Rt△ADF中,即可得cosα.
【解答】论证:
证明:∵AD∥BC,
∴∠A=∠B,∠C=∠D,
在△AOD和△BOC中,
,
∴△AOD≌△BOC(ASA),
∴AO=BO,
∵AO+BO=AB=20,
∴AO=10;
发现:①设AB的中点为O,如图:
当AD从初始位置AO绕A逆时针旋转60°时,BC也从初始位置BC'绕点B逆时针旋转60°,
而BO=BC'=10,
∴△BC'O是等边三角形,
∴BC旋转到BO的位置,即C与O重合,
∵AO=AD=CD=10,
∴△ADC是等边三角形,
∴此时∠ADC=60°;
②如图:
当AD从AO绕A逆时针旋转60°时,CD从CD'的位置开始也旋转60°,故△ADO和△CDO都是等边三角形,
∴此时∠ADC=120°,
综上所述,∠ADC为60°或120°;
尝试:取线段CD的中点M,当点M与点B距离最大时,D、C、B共线,过D作DQ⊥AB于Q,过M作MN⊥AB于N,如图:
由已知可得AD=10,BD=BC+CD=20,BM=CM+BC=15,
设AQ=x,则BQ=20﹣x,
∵AD2﹣AQ2=DQ2=BD2﹣BQ2,
∴100﹣x2=400﹣(20﹣x)2,
解得x,
∴AQ,
∴DQ,
∵DQ⊥AB,MN⊥AB,
∴MN∥DQ,
∴,即,
∴MN,
∴点M到AB的距离为;
拓展:
①设直线CP交DB于H,过D作DG⊥AB于G,连接DP,连接BD,如图:
∵BC=DC=10,CP平分∠BCD,
∴∠BHC=∠DHC=90°,BHBDd,
设BG=m,则AG=20﹣m,
∵AD2﹣AG2=BD2﹣BG2,
∴100﹣(20﹣m)2=d2﹣m2,
∴m,
∴BG,
∵∠BHP=∠BGD=90°,∠PBH=∠DBG,
∴△BHP∽△BGD,
∴,
∴BP;
②方法一:
过B作BG⊥CD于G,如图:
设AN=t,则BN=20﹣t,DN,
∵∠D=∠BGN=90°,∠AND=∠BNG,
∴△ADN∽△BGN,
∴,
即,
∴NG,BG,
Rt△BCG中,BC=10,
∴CG,
∵CD=10,
∴DN+NG+CG=10,
即10,
∴t(20﹣t)2010t,
202010t,即2t﹣2,
两边平方,整理得:3t2﹣40t=﹣4t,
∵t≠0,
∴3t﹣40=﹣4,
解得t(大于20,舍去)或t,
∴AN,
∴cosα.
方法二:过C作CK⊥AB于K,过F作FH⊥AC于H,如图:
∵AD=CD=10,AD⊥DC,
∴AC2=200,
∵AC2﹣AK2=BC2﹣BK2,
∴200﹣AK2=100﹣(20﹣AK)2,
解得AK,
∴CK,
Rt△ACK中,tan∠KAC,
Rt△AFH中,tan∠KAC,
设FHn,则CH=FHn,AH=5n,
∵AC=AH+CH=10,
∴5nn=10,
解得n,
∴AFn ,
Rt△ADF中,
cosα.
【点评】本题考查几何变换的综合应用,涉及全等三角形的判定与性质、等边三角形判定与性质、相似三角形的判定与性质、勾股定理及分式方程、无理方程等知识,题目综合性强,解题的关键是用含字母的代数式表示相关线段的长度,计算是本题的另一个难点.
19.[初步尝试]
(1)如图①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 AM=BM ;
[思考说理]
(2)如图②,在三角形纸片ABC中,AC=BC=6,AB=10,将△ABC折叠,使点B与点C重合,折痕为MN,求的值;
[拓展延伸]
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B′处,折痕为CM.
①求线段AC的长;
②若点O是边AC的中点,点P为线段OB′上的一个动点,将△APM沿PM折叠得到△A′PM,点A的对应点为点A′,A′M与CP交于点F,求的取值范围.
【考点】几何变换综合题.
【专题】几何综合题;图形的相似;应用意识.
【答案】(1)AM=BM;
(2);
(3)①;
②.
【分析】(1)利用平行线分线段成比例定理解决问题即可.
(2)利用相似三角形的性质求出BM,AM即可.
(3)①证明△BCM∽△BAC,推出,由此即可解决问题.
②设PB′=x.证明△PFA′∽△MFC,推出,因为CM=5,推出,判断出x的取值范围,即可解决问题.
【解答】解:(1)如图①中,
∵△ABC折叠,使点B与点C重合,折痕为MN,
∴MN垂直平分线段BC,
∴CN=BN,
∵∠MNB=∠ACB=90°,
∴MN∥AC,
∵CN=BN,
∴AM=BM.
故答案为AM=BM.
(2)如图②中,
∵CA=CB=6,
∴∠A=∠B,
由题意MN垂直平分线段BC,
∴BM=CM,
∴∠B=∠MCB,
∴∠BCM=∠A,
∵∠B=∠B,
∴△BCM∽△BAC,
∴,
∴,
∴BM,
∴AM=AB﹣BM=10,
∴.
(3)①如图③中,
由折叠的性质可知,CB=CB′=6,∠BCM=∠ACM,
∵∠ACB=2∠A,
∴∠BCM=∠A,
∵∠B=∠B,
∴△BCM∽△BAC,
∴,
∴,
∴BM=4,
∴AM=CM=5,
∴,
∴AC.
②如图③﹣1中,设PB′=x.
∵AC,BC=CB′=6,
∴AB′6,
∴AP=AP′x,
∵∠A=∠A′=∠MCF,∠PFA′=∠MFC,PA=PA′,
∴△PFA′∽△MFC,
∴,
∵CM=5,
∴,
∵OA=OC,
∴0≤x,
∴.
当x时,.
综上所述,.
【点评】本题属于几何变换综合题,考查了相似三角形的判定和性质,解直角三角形,等腰三角形的判定和性质,平行线分线段成比例定理等知识,解题的关键是正确寻找相似三角形解决问题,属于中考压轴题.
20.(1)【操作发现】
如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.
①请按要求画图:将△ABC绕点A顺时针方向旋转90°,点B的对应点为点B′,点C的对应点为点C′.连接BB′;
②在①中所画图形中,∠AB′B= 45 °.
(2)【问题解决】
如图2,在Rt△ABC中,BC=1,∠C=90°,延长CA到D,使CD=1,将斜边AB绕点A顺时针旋转90°到AE,连接DE,求∠ADE的度数.
(3)【拓展延伸】
如图3,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=1,CD=3,AD=kAB(k为常数),求BD的长(用含k的式子表示).
【考点】几何变换综合题.
【专题】几何综合题;应用意识.
【答案】见试题解答内容
【分析】(1)①根据旋转角,旋转方向画出图形即可.
②只要证明△ABB′是等腰直角三角形即可.
(2)如图2,过点E作EH⊥CD交CD的延长线于H.证明△ABC≌△EAH(AAS)即可解决问题.
(3)如图3中,由AE⊥BC,BE=EC,推出AB=AC,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,只要证明∠GDC=90°,可得CG,由此即可解决问题.
【解答】解:(1)①如图1中,△AB′C′即为所求.
②由作图可知,△ABB′是等腰直角三角形,
∴∠AB′B=45°,
故答案为45.
(2)如图2中,过点E作EH⊥CD交CD的延长线于H.
∵∠C=∠BAE=∠H=90°,
∴∠B+∠CAB=90°,∠CAB+∠EAH=90°,
∴∠B=∠EAH,
∵AB=AE,
∴△ABC≌△EAH(AAS),
∴BC=AH,EH=AC,
∵BC=CD,
∴CD=AH,
∴DH=AC=EH,
∴∠EDH=45°,
∴∠ADE=135°.
(3)如图3中,连接AC,
∵AE⊥BC,BE=EC,
∴AB=AC,
将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,
∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=kAB,
∴DG=kBC=2k,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG.
∴BD=CG.
【点评】本题属于几何变换综合题,考查了等边三角形的判定和性质,等腰三角形的判定和性质,勾股定理,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是学会用旋转法添加辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
