2026年中考数学核心考点一轮复习 圆(含解析)
文档属性
| 名称 | 2026年中考数学核心考点一轮复习 圆(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 15:08:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考数学一轮复习 圆
一.解答题(共20小题)
1.定义:两个角对应互余,且这两个角的夹边对应相等的两个三角形叫做余等三角形.如图1,在△ABC和△DEF中,若∠A+∠E=∠B+∠D=90°,且AB=DE,则△ABC和△DEF是余等三角形.
(1)图2,等腰直角△ABC,其中∠ACB=90°,AC=BC,点D是AB上任意一点(不与点 A、B重合),则图中△ 和△ 是余等三角形,并求证:AD2+BD2=2CD2.
(2)图3,四边形ABCD是⊙O的内接四边形,⊙O的半径为5,且AD2+BC2=100,
①求证:△ABC和△ADC是余等三角形.
②图4,连接BD交AC于点I,连接OI,E为AI上一点,连接EO并延长交BI于点F,若∠ADB=67.5°,IE=IF,设OI=x,S△EIF=y,求y关于x的函数关系式.
2.问题提出
(1)如图①,已知直线a∥b,点A,B在直线a上,点C,D在直线b上,则S△ACD S△BCD(填“>”“<”或“=”);
问题探究
(2)如图②,⊙O的直径为20,点A,B,C都在⊙O上,AB=12,求△ABC面积的最大值;
问题解决
(3)如图③,在△ABC中,∠ACB=90°,AB=20,BC=10,根据设计要求,点D为∠ABC内部一点,且∠ADB=60°,过点C作CE∥AD交BD于点E,连接AE,CD,试求满足设计要求的四边形ADCE的最大面积.
3.问题探究
(1)如图1,⊙O1与⊙O2的半径分别为1和2,均与直线R1R2相切,切点分别为R1、R2,R1R2=4,S、T分别为两圆上的动点,求线段ST的最小值.
问题解决
(2)春意盎然,万物复苏,到了种植的季节,学校里的校园农场热闹起来,同学们积极参与到校园农场建设中.已知校园农场为矩形区域,如图2所示,记作矩形ABCD,经过测量,AD=40米,米,为方便耕作,需要在农场上设计两条小路.已知点E、F分别是线段AD、BC上的动点,且满足BF=2AE.在线段EF上任取一点G,始终满足∠DGF为直角,把满足条件的所有点G设计成第一条弯弯的小路,这条小路成了校园农场一道亮丽的风景线.为了方便休息,在这条弯弯的小路上建造凉亭N.在农场西南角如图顶点B位置搭建一个弓形阳光房,米,曲线BP是圆心角为120°的圆弧.在弧BP上取一点M作为阳光房的门,在门和凉亭之间建造第二条小路即线段MN.
①试画出第一条弯弯小路的位置(不要求尺规作图),并求这条小路的长度;
②当小路MN最短时,求三角形区域NAD的面积.
(注:小路和门的宽度忽略不计)
4.综合与探究
【课本回顾】如图1,在△ABC中,中线AD,BE,CF于点P,点P叫做△ABC的重心.
【知识探究】
(1)如图2,数学兴趣小组发现,当△ABC的中线AD,BE交于点P时,不管△ABC的边长如何变化,线段AP与PD存在固定的数量关系,并经过讨论得到如下两种解决思路:
思路一 思路二
第一步 如图3,取AD中点M,连接EM,证明△BDP∽△EMP; 如图4,作AN平行BC交BE延长线于点N,先证明△BCE≌△NAE,再证明△BDP∽△NAP;
第二步 利用相似三角形的性质及中位线的性质,得到线段AP与PD之间的数量关系. 利用全等三角形的性质及相似三角形的性质,得到线段AP与PD之间的数量关系.
图形表达
在上述两种思路中,可以选择其中一种,并完成具体解题过程;(若用其他思路解决问题,则写第3种)
【问题解决】
(2)在⊙O中,AB为直径,点C是⊙O上一点(不与点A,B重合).
①如图Ⅱ,若点M是弦BC的中点,AM交OC于点E,则的值为 ;
②如图Ⅲ,在①的条件下,若AM⊥OC,求sinB的值;
③如图IV,若AB=10,BC=8,D为弦BC上一动点,过D作DF⊥OC,交OC于点H,交AB于点F.设BD=x,FO=y,直接写出y与x的函数关系式.
5.问题探究
(1)如图1,在Rt△ABC中,BC=8,AC=6,点D是AB的中点,点P是BC上一动点,根据北师大版七年级下册123页的问题解决可知,DP+AP有最小值,则DP+AP的最小值为 ;
(2)在(1)的条件下,点P是平面内一动点,∠BPC=90°,求AP的最小值.
问题解决
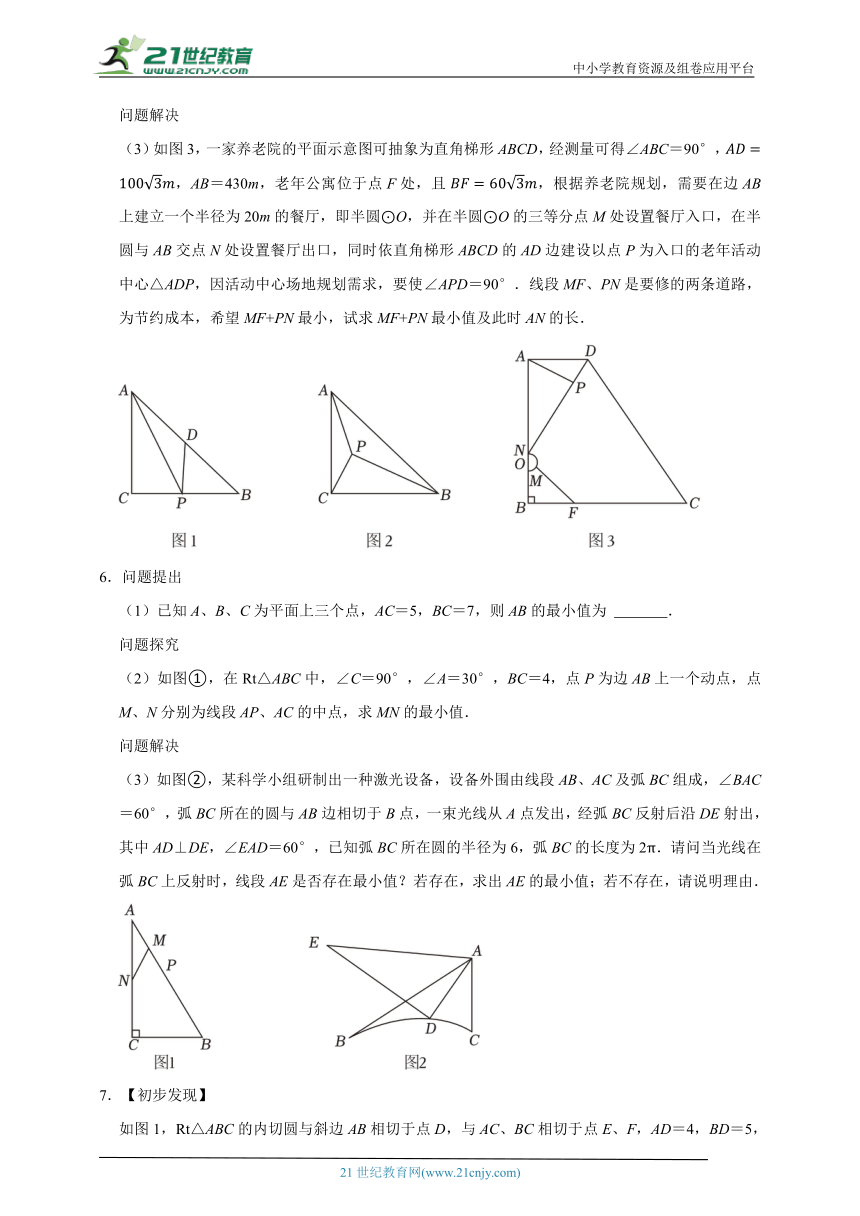
(3)如图3,一家养老院的平面示意图可抽象为直角梯形ABCD,经测量可得∠ABC=90°,,AB=430m,老年公寓位于点F处,且,根据养老院规划,需要在边AB上建立一个半径为20m的餐厅,即半圆⊙O,并在半圆⊙O的三等分点M处设置餐厅入口,在半圆与AB交点N处设置餐厅出口,同时依直角梯形ABCD的AD边建设以点P为入口的老年活动中心△ADP,因活动中心场地规划需求,要使∠APD=90°.线段MF、PN是要修的两条道路,为节约成本,希望MF+PN最小,试求MF+PN最小值及此时AN的长.
6.问题提出
(1)已知A、B、C为平面上三个点,AC=5,BC=7,则AB的最小值为 .
问题探究
(2)如图①,在Rt△ABC中,∠C=90°,∠A=30°,BC=4,点P为边AB上一个动点,点M、N分别为线段AP、AC的中点,求MN的最小值.
问题解决
(3)如图②,某科学小组研制出一种激光设备,设备外围由线段AB、AC及弧BC组成,∠BAC=60°,弧BC所在的圆与AB边相切于B点,一束光线从A点发出,经弧BC反射后沿DE射出,其中AD⊥DE,∠EAD=60°,已知弧BC所在圆的半径为6,弧BC的长度为2π.请问当光线在弧BC上反射时,线段AE是否存在最小值?若存在,求出AE的最小值;若不存在,请说明理由.
7.【初步发现】
如图1,Rt△ABC的内切圆与斜边AB相切于点D,与AC、BC相切于点E、F,AD=4,BD=5,求△ABC的面积.
解:设线段CE的长为x,根据切线长定理,得AE=AD=4,BF=BD=5,CF=CE=x,
在RtAABC中,根据勾股定理,
得(x+4)2+(x+5)2=(4+5)2,
整理,得x2+9x=20,
所以S△ABC(x+4)(x+5)=(x2+9x+20)=20
请同学们想一想,AD×BD=4×a5=20,△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
【深入探索】
已知:如图2,△ABC的内切圆与AB相切于点D,与AC、BC相切于点 E、F,AD=m,BD=n.
(1)若∠C=90°,求证:△ABC的面积等于mn;
(2)若AC.BC=2mn,求证:∠C=90°.
【拓展延伸】
已知:△ABC的内切圆与AB、AC、BC相切于点D、E、F,∠C=60°,AD=4,BD=5.请直接写出△ABC的面积.
8.【问题提出】
唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——将军饮马问题:
(1)如图1,△ABC中,∠C=90°,AC=BC=2,E是AB的中点,P是BC边上的一动点,则PA+PE的最小值为 ;
【问题探究】
(2)如图2,已知△ABC和△DEF都是等腰直角三角形,∠ABC=∠EDF=90°,AB=6,DE=3,EF在直线AC上运动时,求BE+BD的最小值;
【拓展应用】
(3)如图3,是某公园的示意图,AB、AC、BD是三处栅栏,CD是该公园附近的一条道路(宽度不计),半圆AM及其内部是一个带舞台的广场.已知∠BAC=∠ABD=90°,CD所对的圆心角为120°,AC与所在的圆相切于点C,点E、G在AC上,点F、H在BD上,点M在AB上,矩形EFHG是一条河流在该公园内的一段(EF∥AB),其中半圆AM的直径为300m,AB=600m,AC=700,河岸EF离AB的距离为,河宽EG为,为方便运输设备,现计划垂直于河岸造桥QS,使得PQ、QS与ST之和最短,求出此时EQ的长.(结果保留根号)
9.定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= 度;
(2)如图1,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,
①求证:△BDC是“近直角三角形”;
②在边AC上是否存在点E(异于点D),使得△BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
(3)如图2,在Rt△ABC中,∠BAC=90°,点D为AC边上一点,以BD为直径的圆交BC于点E,连接AE交BD于点F,若△BCD为“近直角三角形”,且AB=5,AF=3,求tan∠C的值.
10.综合与实践
【问题情境】在数学综合实践课上,“希望小组”的同学们以三角形为背景,探究图形变化过程中的几何问题,如图,在△ABC中,AB=AC,∠BAC=90°,点D为平面内一点(点A,B,D三点不共线),AE为△ABD的中线.
【初步尝试】(1)如图1,小林同学发现:延长AE至点M,使得ME=AE,连接DM.始终存在以下两个结论,请你在①,②中挑选一个进行证明:
①DM=AC;②∠MDA+∠DAB=180°;
【类比探究】(2)如图2,将AD绕点A顺时针旋转90°得到AF,连接CF.小斌同学沿着小林同学的思考进一步探究后发现:AECF,请你帮他证明;
【拓展延伸】(3)如图3,在(2)的条件下,王老师提出新的探究方向:点D在以点A为圆心,AD为半径的圆上运动(AD>AB),直线AE与直线CF相交于点G,连接BG,在点D的运动过程中BG存在最大值.若AB=4,请直接写出BG的最大值.
11.(1)【学习心得】
小赵同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.我们把这个过程称为“化隐圆为显圆”.
①已知:如图1,OA=OB=OC,若∠AOB=50°,求∠ACB的度数.
解:若以点O为圆心,OA为半径作辅助圆,∠AOB是⊙O的圆心角,而∠ACB是圆周角,从而可容易得到∠ACB= °.
②如图2,点P为正方形ABCD内一点,且∠BPC=90°,若AB=4,求AP的最小值.
解:∵BC=4,∠BPC=90°,∴点P在以BC为直径的圆上,
设圆心为点O,则O、P、A三点共线时AP最小,最小值为 .
(2)【问题解决】
①如图3,在平行四边形ABCD中,已知AB=4,BC=6,∠ABC=60°,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点Q,则线段QC的最小值为 .
②如图4,△ABC中,∠BAC=90°,AB=4,AC=3,D为AC上一动点,以AD为直径的⊙O交BD于E,求线段CE的最小值.
(3)【问题拓展】
如图5,在平面直角坐标系中,已知两点A(2,3),B(6,7),x轴上有一动点P,当∠APB最大时,直接写出点P的坐标 .
12.问题提出:如图①,在Rt△ABC中,∠C=90°,CB=4,CA=6,⊙C的半径为2,P为圆上一动点,连接AP、BP,求的最小值.
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图①,连接CP,在CB上取一点D,使CD=1,则.又∠PCD=∠BCP,所以△PCD∽△BCP.所以.
所以PDPB,所以.
请你完成余下的思考,并直接写出答案:的最小值为 ;
(2)自主探索:在“问题提出”的条件不变的前提下,求的最小值;
(3)拓展延伸:如图②,已知在扇形COD中,∠COD=90°,OC=6,OA=3,OB=5,P是上一点,求2PA+PB的最小值.
13.概念认识:
平面内,M为图形T上任意一点,N为⊙O上任意一点,将M、N两点间距离的最小值称为图形T到⊙O的“最近距离”,记作d(T﹣⊙O).例:如图1,在直线l上有A、C、O三点,以AC为对角线作正方形ABCD,以点O为圆心作圆,与l交于E、F两点,若将正方形ABCD记为图形T,则C、E两点间的距离称为图形T到⊙的“最近距离”.
数学理解:
(1)在平面内有A、B两点,以点A为圆心,5为半径作⊙A,将点B记为图形T,若d(T﹣⊙A)=2,则AB= .
(2)如图2,在平面直角坐标系中,以O(0,0)为圆心,半径为2作圆.
①将点C(4,3)记为图形T,则d(T﹣⊙O)= .
②将一次函数y=kx+2的图记为图形T,若d(T﹣⊙)>0,求k的取值范围.
推广运用:
(3)在平面直角坐标系中,P的坐标为(t,0),⊙P的半径为2,D、E两点的坐标分别为(5,5)、(5,﹣5),将△DOE记为图形T,若d(T﹣⊙P)=1,则t= .
14.问题提出:
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?
初步思考:
(1)给出了一些特殊的四边形:①矩形②菱形③等腰梯形④正方形,能过它们四个顶点作一个圆的是 (填写序号),过某个四边形四个顶点作一个圆的四边形相对的两个内角的关系是 .
进一步研究:
(2)如果过某个四边形的四个顶点不能作一个圆,那么其相对的两个内角之间有上面的关系吗?请结合图1的两幅图说明其中的道理.(提示:考虑∠B+∠D与180°之间的关系)
由上面的探究,请用文字语言直接写出过某个四边形的四个顶点能作一个圆的条件 .
拓展延伸
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图2,AB是⊙O的直径,点C在⊙O上,求作:CN⊥AB.
作法:①连接CA,CB;
②在上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M:
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图2中作图,并说明CN⊥AB的理由,(提示:可以利用(2)中的结论)
15.综合与实践
数学实践课堂上,张老师带领学生们从一道题入手,开始研究,并对此题做适当变式,尝试举一反三,开阔学生思维.
(1)原型题:如图1,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,AP=PC,AP⊥PC,则△ABP≌△ ,请你说明理由.
(2)利用结论,直接应用:
如图2,四边形ABCD、EFGH、NHMC都是正方形,边长分别为a、b、c,A、B、N、E、F五点在同一条直线上,则△CBN≌△ ,c= (用含a、b的式子表示).
如图3,四边形ABCD中,AB∥DC,AB⊥BC,AB=2,CD=4,以BC上一点O为圆心的圆经过A、D两点,且∠AOD=90°,则圆心O到弦AD的距离为 .
(3)弱化条件,变化引申:
如图4,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°,且DM交AC于点F,ME交BC于点G,连接FG,则△AMF与△BGM的关系为: ,若,AF=3,则FG= .
16.问题提出:
(1)如图1,点B、C在⊙O上且BC=2,过点O作OE⊥BC,交BC于点A,交⊙O于点E,连接BE、CE,若∠CBE=30°,则线段AE的长度为 .
问题探究:
(2)如图2,在△ABC中,BC=2,∠BAC=45°,求边AC长度的最大值;
问题解决:
(3)如图3,某城市拟在河流m、n所夹半岛区域建一个湿地公园,公园的周长由亲水廊桥AB、、CD和绿化带BC四部分构成.其中B、C两定点间的距离为2000米.根据规划要求,A、D两点间的距离为600米,A、D两点到直线BC的距离相等,的中点E到BC的距离比点A到BC的距离多100米;若修建时需保证∠B与∠C的和为120度,请判断这个湿地公园的周长是否存在最大值?若存在,请求出最大值.若不存在,请说明理由.(结果保留π)
17.在一次数学探究活动中,李老师设计了一份活动单:
已知线段BC=2,使用作图工具作∠BAC=30°,尝试操作后思考: (1)这样的点A唯一吗? (2)点A的位置有什么特征?你有什么感悟?
“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以BC为弦的圆弧上(点B、C除外),….小华同学画出了符合要求的一条圆弧(如图1).
(1)小华同学提出了下列问题,请你帮助解决.
①该弧所在圆的半径长为 ;
②△ABC面积的最大值为 ;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为A′,请你利用图1证明∠BA′C>30°.
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形ABCD的边长AB=2,BC=3,点P在直线CD的左侧,且tan∠DPC.
①线段PB长的最小值为 ;
②若S△PCDS△PAD,则线段PD长为 .
18.问题提出
(1)如图①,△ABC内接于⊙O,过点C作⊙O的切线l.在l上任取一个不同于点C的点P,连接PB、PA,比较∠ACB与∠APB的大小,并说明理由.
问题探究
(2)如图2,正方形ABCD,边长为2,在CD边上是否存在点P,使∠APB最大?若存在,确定点P的位置,并求此时sin∠APB的值;若不存在,请说明理由.
问题解决
(3)如图③,四边形ABCD为某工作室的平面示意图,线段BC、CD、DA为三面墙,MN为入户门处,其中AD∥BC,AD⊥AB,∠C=60°,BM=AN=4米,BC=30米,AD=20米.出于安全考虑,负责人想在墙上安装监控装置P,用来监控并记录进出的人员,为了让监控效果最佳,要求∠MPN最大,试问在墙上是否存在一点P,使得∠MPN最大?若存在,请求出此时sin∠MPN的值及P点的位置;若不存在,请说明理由.
19.【阅读材料】克罗狄斯 托勒密(约90﹣168年)是希腊著名的数学家、天文学家和地理学家,托勒密定理是欧几里得几何中的重要定理.定理内容如下:任意一个凸四边形,两组对边乘积的和不小于两条对角线的乘积,当且仅当四边形四个顶点共圆时,等号成立.即:四边形ABCD中,有AB CD+BC AD≥AC BD,当A,B,C,D四点共圆时,有AB CD+BC AD=AC BD.
【尝试证明】
(1)如图1,四边形ABCD内接于⊙O,求证:AB CD+BC AD=AC BD.
证明:在AC上取点E,连接DE,使∠CDE=∠BDA.
∵∠DCA=∠DBA,
∴ ,
∴,
∴AB CD=EC BD①,
∵∠CDE=∠BDA,
∴∠CDE+∠BDE=∠BDA+∠BDE,即∠ADE=∠BDC,
又∵∠DAE=∠DBC,
∴△ADE∽△BDC,
∴,
∴ ②,①+②得AB CD+BC AD=(EC+AE) BD,即 .
【直接应用】
(2)如图2,AB为⊙O的直径,AB=5,AD=4,BF=1,求DF的长.
【灵活运用】
(3)如图3,在等腰三角形ABC中,AB=AC=8,BC=12,点D在底边BC上,且∠DAC=∠ACD,将三角形ACD沿着AD所在的直线翻折,使得点C落在点E处,连接EB,求BE的长.
20.【问题提出】
在绿化公园时,需要安装一定数量的自动喷洒装置,定时喷水养护,某公司准备在一块边长为18m的正方形草坪(如图1)中安装自动喷洒装置,为了既节约安装成本,又尽可能提高喷洒覆盖率,需要设计合适的安装方案.
说明:一个自动喷洒装置的喷洒范围是半径为r(m)的圆面.喷洒覆盖率,s为待喷洒区域面积,k为待喷洒区域中的实际喷洒面积.
【数学建模】
这个问题可以转化为用圆面覆盖正方形面积的数学问题.
【探索发现】
(1)如图2,在该草坪中心位置设计安装1个喷洒半径为9m的自动喷洒装置,该方案的喷洒覆盖率ρ= .
(2)如图3,在该草坪内设计安装4个喷洒半径均为的自动喷洒装置;如图4,设计安装9个喷洒半径均为3m的自动喷洒装置;…,以此类推,如图5,设计安装n2个喷洒半径均为的自动喷洒装置.与(1)中的方案相比,采用这种增加装置个数且减小喷洒半径的方案,能否提高喷洒覆盖率?请判断并给出理由.
(3)如图6所示,该公司设计了用4个相同的自动喷洒装置喷洒的方案,且使得该草坪的喷洒覆盖率ρ=1.已知AE=BF=CG=DH,设AE=x(m),⊙O1的面积为y(m2),求y关于x的函数表达式,并求当y取得最小值时r的值.
【问题解决】
(4)该公司现有喷洒半径为的自动喷洒装置若干个,至少安装几个这样的喷洒装置可使该草坪的喷洒覆盖率ρ=1?(直接写出结果即可)
中考数学一轮复习 圆
参考答案与试题解析
一.解答题(共20小题)
1.定义:两个角对应互余,且这两个角的夹边对应相等的两个三角形叫做余等三角形.如图1,在△ABC和△DEF中,若∠A+∠E=∠B+∠D=90°,且AB=DE,则△ABC和△DEF是余等三角形.
(1)图2,等腰直角△ABC,其中∠ACB=90°,AC=BC,点D是AB上任意一点(不与点 A、B重合),则图中△ ACD 和△ BCD 是余等三角形,并求证:AD2+BD2=2CD2.
(2)图3,四边形ABCD是⊙O的内接四边形,⊙O的半径为5,且AD2+BC2=100,
①求证:△ABC和△ADC是余等三角形.
②图4,连接BD交AC于点I,连接OI,E为AI上一点,连接EO并延长交BI于点F,若∠ADB=67.5°,IE=IF,设OI=x,S△EIF=y,求y关于x的函数关系式.
【考点】圆的综合题.
【专题】压轴题;新定义;与圆有关的计算;推理能力;应用意识.
【答案】(1)ACD,BCD,证明见解答过程;
(2)①证明见解答过程;
②y.
【分析】(1)由△ABC是等腰直角三角形,根据余等三角形定义,可得△ACD和△BCD是余等三角形,过D作DE⊥AC于E,过D作DF⊥BC于F,证明△ADE和△BDF是等腰直角三角形,得DE,DF,CE,Rt△DCE中,用勾股定理即可得AD2+BD2=2CD2;
(2)①连接DO并延长交⊙O于E,连接AE、CE,根据AD2+BC2=100,可得AE=BC,从而△AEC≌△CBA,可得∠EAC=∠BCA,∠BCA+∠CAD=90°,同理可得:∠BAC+∠ACD=90°,而AC=AC,根据余等三角形,可知△ABC和△ADC是余等三角形;
②连接OA、OB,过O作OM⊥BD于M,过O作ON⊥AC于N,证明△EFI是等腰直角三角形,△MOF是等腰直角三角形,可得∠AEO=∠BFO=135°,由∠ADB=67.5°,有∠AOB=2∠ADB=135°,∠AOE=45°﹣∠BOF=∠OBF,从而△AOE≌△OBF,得OE=BF,设OE=BF=a,OM=FM=b,则ON=MIa,OF=AEb,在Rt△OIM中,(a)2+b2=x2得a2+2b2=2x2,在Rt△OBM中,(a+b)2+b2=52,得a2+2b2+2ab=25,故2ab=25﹣2x2,而yEI FI(a+b)2(a2+2b2)abx2.
【解答】解:(1)∵△ABC是等腰直角三角形,
∴∠A+∠B=90°,∠ACD+∠BCD=90°,AC=BC,
∴△ACD和△BCD是余等三角形,
过D作DE⊥AC于E,过D作DF⊥BC于F,如图:
∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∴△ADE和△BDF是等腰直角三角形,
∴DE,DF,
∵DE⊥AC,DF⊥BC,∠ACB=90°,
∴四边形CEDF是矩形,
∴CE=DF,
Rt△DCE中,DE2+CE2=CD2,
∴()2+()2=CD2,
∴AD2+BD2=2CD2;
故答案为:ACD,BCD;
(2)①连接DO并延长交⊙O于E,连接AE、CE,如图:
∵DE是⊙O直径,
∴∠EAD=90°,
在Rt△EAD中,AD2+AE2=DE2=100,
∵AD2+BC2=100,
∴AE=BC,
∴∠ACE=∠BAC,
∵∠AEC=∠CBA,AC=AC,
∴△AEC≌△CBA(AAS),
∴∠EAC=∠BCA,
∵∠EAC+∠CAD=90°,
∴∠BCA+∠CAD=90°,
同理可得:∠BAC+∠ACD=90°,
而AC=AC,
∴△ABC和△ADC是余等三角形;
②连接OA、OB,过O作OM⊥BD于M,过O作ON⊥AC于N,如图:
由①知:∠BAC+∠ACD=90°,
又∠ACD=∠ABD,
∴∠BAC+∠ABD=90°,
∴AC⊥BD,
∵IE=IF,
∴△EFI是等腰直角三角形,
∵OM⊥BD,
∴△MOF是等腰直角三角形,
∴OM=FM,
∵△EFI是等腰直角三角形,
∴∠AEO=∠BFO=135°,
∵∠ADB=67.5°,
∴∠AOB=2∠ADB=135°,
∴∠AOE=45°﹣∠BOF=∠OBF,
且OA=OB,
∴△AOE≌△OBF(AAS),
∴OE=BF,
设OE=BF=a,OM=FM=b,则ON=MIa,OF=AEb,
在Rt△OIM中,(a)2+b2=x2,化简得a2+2b2=2x2,
在Rt△OBM中,(a+b)2+b2=52,化简得a2+2b2+2ab=25,
∴2ab=25﹣2x2,
∴yEI FI(a+b)2(a2+2b2)abx2.
【点评】本题考查圆的性质及综合应用,涉及新定义、等腰直角三角形性质及判定、全等三角形性质及判定、勾股定理应用等知识,题目综合性强,解题的关键是作辅助线,构造直角三角形、全等三角形解决问题.
2.问题提出
(1)如图①,已知直线a∥b,点A,B在直线a上,点C,D在直线b上,则S△ACD = S△BCD(填“>”“<”或“=”);
问题探究
(2)如图②,⊙O的直径为20,点A,B,C都在⊙O上,AB=12,求△ABC面积的最大值;
问题解决
(3)如图③,在△ABC中,∠ACB=90°,AB=20,BC=10,根据设计要求,点D为∠ABC内部一点,且∠ADB=60°,过点C作CE∥AD交BD于点E,连接AE,CD,试求满足设计要求的四边形ADCE的最大面积.
【考点】圆的综合题.
【专题】几何综合题;压轴题;几何直观;运算能力;推理能力.
【答案】(1)=;
(2)△ABC面积的最大值为108;
(3)四边形ADCE的最大面积是75.
【分析】(1)由平行线的性质,根据同底等高的两三角形面积相等作答;
(2)AB长不变,只要AB边上的高最大,△ABC面积最大;由图知当C是优弧的中点时,AB边上的高最大,△ABC面积最大,求得优弧的中点到AB的距离就可求得△ABC最大面积;
(3)过C作CF∥BD交AD的延长线于F,得∠F=∠ADB=60°,先证得四边形ADCE的面积=△ACF的面积;根据∠F=60°得点F在以AC为边向△ABC外作的等边△AGC的外接圆上,受解决(2)的启发得,当F运动到点G时,△ACF的面积最大,即四边形ADCE的面积最大.最后计算出△ACF的面积即是四边形ADCE的面积最大值.
【解答】解:(1)如图①所示,分别过A、B两点向直线b作垂线,垂足为M、N.
∵a∥b,
∴∠MAB=∠AMN=90°,
∴四边形AMNB是矩形,
∴AM=BN,
∴CD AM=CD BN
又S△ACDCD AM,S△BCDCD BN,
∴S△ACD=S△BCD;
故答案为:=;
(2)取优弧的中点记为C1,过C1作AB的垂线,垂足为D,由垂径定理知C1D过O且AD=BD,如图②所示.
过点C作AB的平行线a,
∵当直线a向上平移时,a距AB的距离增大,即△ABC的AB边上的高增大,
∴当a运动到最高点C时,△ABC的AB边上的高最大,
又∵AB为常数,
∴当C运动到C1时,△ABC的面积最大,
下面计算△ABC1的面积:
连接OB,
在Rt△OBD中,
∵AB=12,⊙O的直径为20,
∴BD=6,BO=10,OC1=10,
由勾股定理得:
OD8,
∴C1D=OD+OC1=8+10=18,
∴△ABC1的面积为:AB C1D12×18=108,
∴△ABC面积的最大值为108;
(3)过点C作CF∥BD交AD的延长线于F,如图③﹣1所示,
∵CF∥BD,
∴∠F=∠ADB=60°,
∵AD∥CE,
∴四边形DECF是平行四边形,
∴DF=CE,FC=DE,
∵DC=CD
∴△DFC≌△CED(SSS),
∴S△DFC=S△CED,
又由(1)的结论知S△DAC=S△DAE,
∴S四边形ADCE=S△DAE+S△CED=S△DAC+S△DFC=S△AFC,
所以只需求得S△AFC最大值即得S四边形ADCE的最大值.
以AC为边向△ABC外作等边△AGC,再作等边△AGC的外接圆,过G作GJ⊥AC于J,如图③﹣2所示,
∵∠F=60°,
∴点F在△AGC的外接圆上,
由第(2)问的解决知,当F运动到点G时,S△AFC最大=S△ACG;
在Rt△ABC中:
由勾股定理得AC10,
∴AJAC=5,
∴GJ1015,
∴S△ACGAC×GJ1015=75;
∴四边形ADCE的最大面积是75.
【点评】此题考查了三角形等积变形、定角对定边的三角形的面积最大值、等边三角形及其外接圆、平行四边形的判定和性质等考点,熟练掌握相关知识并能综合应用是解题关键.
3.问题探究
(1)如图1,⊙O1与⊙O2的半径分别为1和2,均与直线R1R2相切,切点分别为R1、R2,R1R2=4,S、T分别为两圆上的动点,求线段ST的最小值.
问题解决
(2)春意盎然,万物复苏,到了种植的季节,学校里的校园农场热闹起来,同学们积极参与到校园农场建设中.已知校园农场为矩形区域,如图2所示,记作矩形ABCD,经过测量,AD=40米,米,为方便耕作,需要在农场上设计两条小路.已知点E、F分别是线段AD、BC上的动点,且满足BF=2AE.在线段EF上任取一点G,始终满足∠DGF为直角,把满足条件的所有点G设计成第一条弯弯的小路,这条小路成了校园农场一道亮丽的风景线.为了方便休息,在这条弯弯的小路上建造凉亭N.在农场西南角如图顶点B位置搭建一个弓形阳光房,米,曲线BP是圆心角为120°的圆弧.在弧BP上取一点M作为阳光房的门,在门和凉亭之间建造第二条小路即线段MN.
①试画出第一条弯弯小路的位置(不要求尺规作图),并求这条小路的长度;
②当小路MN最短时,求三角形区域NAD的面积.
(注:小路和门的宽度忽略不计)
【考点】圆的综合题.
【专题】压轴题;与圆有关的位置关系;推理能力.
【答案】(1)3;
(2)①π米;
②(100200)平方米.
【分析】(1)连接O1R1,O2R2,O1O2,过点O1作O1H⊥O2R2,设O1O2交⊙O1与⊙O2分别为S,T,则此时线段ST的长度最小,利用勾股定理可得O1O2,即可得出答案;
(2)①如图2,延长BA至点S,使AS=AB,连接SC交AD于点T,过点D作DG′⊥CT,连接SD,作出SD中点O,连接OA、OG′,以点O为圆心,OA为半径,作出,则为第一条弯弯小路的位置,再证得△SAE∽△SBF,利用相似三角形性质可得SB=2AB=40米,运用三角函数定义可求得∠BSC=30°,进而可得∠AOG′=60°,再运用弧长公式即可求得答案.
②以BP为底作等腰三角形BPQ,且使∠BQP=120°,则、是以点Q为圆心,PQ为半径的圆的一部分,连接OQ交AD于点R,分别交、于点M、N,此时MN最短,连接AN、DN,过点N作NJ⊥AD,连接OT,过点Q作QZOT交AB于点Y,垂足为点Z,运用解直角三角形即可求得答案.
【解答】∵′解:(1)如图1,连接O1R1,O2R2,O1O2,过点O1作O1H⊥O2R2,设O1O2交⊙O1与⊙O2分别为S,T,则此时线段ST的长度最小,
∵⊙O1与⊙O2的半径分别为1和2,均与直线R1R2相切,切点分别为R1、R2,R1R2=4,
∴O1R1⊥R1R2,O2R2⊥R1R2,
∴四边形O1R1R2H是矩形,
∴O1H=R1R2=4,R2H=O1R1=1,
∴O2H=O2R2=2﹣1=1,
∴O1O2,
∴线段ST的最小值1﹣23=14.
(2)①如图2,延长BA至点S,使AS=AB,连接SC交AD于点T,过点D作DG′⊥CT,连接SD,作出SD中点O,连接OA、OG′,以点O为圆心,OA为半径,作出,则为第一条弯弯小路的位置,
∵四边形ABCD是矩形,
∴AD=BC=40米,AB=CD=20米,AD∥BC,
∴△SAE∽△SBF,
∴,
∴SB=2AB=40米,
∴tan∠BSC,
∴∠BSC=30°,
∴∠AOG′=60°,
∵SD20米,
∴OASD=10米,
∴的长为:π米,
∴这条小路的长度为π米.
②如图3,以BP为底作等腰三角形BPQ,且使∠BQP=120°,则是以点Q为圆心,PQ为半径的圆的一部分,连接OQ交AD于点R,分别交、于点M、N,此时MN最短,连接AN、DN,过点N作NJ⊥AD,连接OT,过点Q作QZOT交AB于点Y,垂足为点Z,
∵OS=OD,TA=TD,
∴OT∥AS,OTAS=10米,
由题意得:在Rt△QBY中,∠QBY=30°,BYBP=5米,
∴QY=BY tan30°=55米,AY=TZ=15米,
∵YZ=AT=20米,
∴QZ=25米,OZ=25米,
∴tan∠QOZ,
∴∠QOZ=30°,
∴OR20米,
∴NR=ON﹣OR=1020(米),
∵∠OTA=∠NJR=90°,
∴NJ∥OT,
∴∠JNR=∠TOR=30°,
∴NJ=NR cos30°=(1020)510(米),
∴S△NADNJ AD(510)×40=100200(平方米).
【点评】此题属于圆的综合题,考查了三角形的面积,三角函数,最短路线,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.
4.综合与探究
【课本回顾】如图1,在△ABC中,中线AD,BE,CF于点P,点P叫做△ABC的重心.
【知识探究】
(1)如图2,数学兴趣小组发现,当△ABC的中线AD,BE交于点P时,不管△ABC的边长如何变化,线段AP与PD存在固定的数量关系,并经过讨论得到如下两种解决思路:
思路一 思路二
第一步 如图3,取AD中点M,连接EM,证明△BDP∽△EMP; 如图4,作AN平行BC交BE延长线于点N,先证明△BCE≌△NAE,再证明△BDP∽△NAP;
第二步 利用相似三角形的性质及中位线的性质,得到线段AP与PD之间的数量关系. 利用全等三角形的性质及相似三角形的性质,得到线段AP与PD之间的数量关系.
图形表达
在上述两种思路中,可以选择其中一种,并完成具体解题过程;(若用其他思路解决问题,则写第3种)
【问题解决】
(2)在⊙O中,AB为直径,点C是⊙O上一点(不与点A,B重合).
①如图Ⅱ,若点M是弦BC的中点,AM交OC于点E,则的值为 ;
②如图Ⅲ,在①的条件下,若AM⊥OC,求sinB的值;
③如图IV,若AB=10,BC=8,D为弦BC上一动点,过D作DF⊥OC,交OC于点H,交AB于点F.设BD=x,FO=y,直接写出y与x的函数关系式.
【考点】圆的综合题.
【专题】压轴题;推理能力.
【答案】(1)证明过程见解析;(2)①;②;③.
【分析】(1)根据提供的思路证明即可;
(2)①证明E为△ABC的重心即可得解;②由前述结论可得OC=3OE,根据这一关系设参数,利用勾股定理将AE、AC和OM表示出来即可得解;③作FQ⊥BC,将FQ和BQ用含y的式子表示出来,再用建立关于x和y的等式即可.
【解答】解:(1)线段AP与PD存在固定的数量关系为AP=2DP,理由:
思路一:取AD中点M,连接EM,如图,
∵AM=MD,AE=EC,
∴ME为△ADC的中位线,
∴ME∥CD,MECD.
∵BD=CD,
∴MECD.
∵ME∥BD,
∴△BDP∽△EMP,
∴,
∴PD=2MP,
∴MD=3MP,
∴AM=MD=3MP,
∴AP=4MP,
∴AP=2PD.
思路二:作AN∥BC交BE延长线于点N,如图,
∵AN∥BC,
∴∠EBC=∠N.
在△BCE和△NAE中,
,
△BCE≌△NAE(AAS),
∴BC=AN,
∵BD=CD,
∴AN=2BD.
∵∠EBC=∠N,∠BPD=∠NPA,
∴△BDP∽△NAP,
∴,
∴AP=2PD;
(2)①连接AC,如图,
∵BM=MC,OA=OB,
∴E为△ABC的重心,
∴CE=2OE,
∴OEOC,
∴.
故答案为:;
②连接OM、AC,
由(1)知:OC=3OE,
设OE=k,则OC=3k,
∴OA=OB=OC=3k,EC=2OE=2k,
∵AM⊥OC,
∴.
∴,
由(1)知:.
∴.
③如图,连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴,
如图所示,过点F作FQ⊥BC于点Q,交OC于T,
∵OB=OC,
∴∠OBC=∠OCB,
∵DF⊥OC,
∴∠FHT=∠FQC=90°,
∵∠FTH=∠CTQ,
∴∠DFQ=∠OCB=∠OBC,
在Rt△FBQ中,BF=5+y,
在Rt△ABC中,,,,
∴,
∵tan∠DFQ=tanB,
∴,
即,整理得.
∴y与x的函数关系式为.
【点评】本题主要考查了解直角三角形,直径所对的圆周角是直角,勾股定理,相似三角形的性质与判定,三角形中位线定理等等,正确作出辅助线构造相似三角形和直角三角形是解题的关键.
5.问题探究
(1)如图1,在Rt△ABC中,BC=8,AC=6,点D是AB的中点,点P是BC上一动点,根据北师大版七年级下册123页的问题解决可知,DP+AP有最小值,则DP+AP的最小值为 ;
(2)在(1)的条件下,点P是平面内一动点,∠BPC=90°,求AP的最小值.
问题解决
(3)如图3,一家养老院的平面示意图可抽象为直角梯形ABCD,经测量可得∠ABC=90°,,AB=430m,老年公寓位于点F处,且,根据养老院规划,需要在边AB上建立一个半径为20m的餐厅,即半圆⊙O,并在半圆⊙O的三等分点M处设置餐厅入口,在半圆与AB交点N处设置餐厅出口,同时依直角梯形ABCD的AD边建设以点P为入口的老年活动中心△ADP,因活动中心场地规划需求,要使∠APD=90°.线段MF、PN是要修的两条道路,为节约成本,希望MF+PN最小,试求MF+PN最小值及此时AN的长.
【考点】圆的综合题.
【专题】压轴题;模型思想.
【答案】(1).
(2)4.
(3)()m;200m.
【分析】(1)通过以BC为对称轴作点D的对称点D′,问题转化为求AP+PD′的最小值AD′,过点D'作BC的平行线交AC的延长线于点E,在Rt△AED′中应用勾股定理即可求出答案.
(2)由∠BPC=90°得出点P的轨迹是以BC为直径的⊙O.当点P在线段AO上时,AP的长度即为最小值.
(3)根据题意,M、N两点的相对位置是固定的,故平移线段MF至NG,使M、N两点重合,这样问题就会转化为求GN+NP的最小值.根据(1)、(2)的方法可知,点P在以AD为直径的半圆上,以AB为对称轴作点G的对称点G′,当G′,N,E三点共线时,G′N+NP最小,进而问题得到解决.
【解答】解:(1)如图,以BC为对称轴,作点D的对称点D′,DD′交BC于点F.过点D'作BC的平行线交AC的延长线于点E,连接PD′、AD′.
∵点D和D′关于BC对称,
∴DP=PD′,
∴DP+AP=PD′+AP,
当A,P,D′三点共线时,PD'+AP的最小值为AD′,
∴DP+AP的最小值为AD′.
∵DF⊥BC,AC⊥BC,
∴DD′∥AE,
∴DF为Rt△ABC的中位线,
∴DF=FD′AC6=3,CFBC8=4.
又∵ED′∥BC,
∴四边形CED′F为矩形,ED′=CF=4,CE=FD′=3.
∴AE=AC+CE=6+3=9.
∴AD′.
故DP+AP的最小值为.
(2)如图,根据直径所对应的圆周角为直角,则动点P的轨迹为以BC为直径的⊙O.
∵AP+PO≥AO,
∴当点P在线段AO上时,AP+PO的最小值为AO.
∵PO为定值,PO=COBC8=4,
在Rt△ACO中,AO,
∴AP的最小值为:AO﹣PO4.
(3)对于半圆形餐厅,局部放大图如图,连接MN,OM,作MQ⊥ON,Q为垂足.
如图,平移线段MF至NG,点M与点N重合,以AB为对称轴作点G的对称点G′.G′G交AB于点I.
根据线段平移的性质,四边形MNGF为平行四边形,MF=G′N=NG.NM=GF.
由于点M,N的相对位置固定不变,动点P的轨迹是以AD为直径的半圆,半径AEm上.根据(1),(2)的方法,对于定点G′、E和动点P,当P,G′,E三点共线时,G′P长度最小,即MF+PN为最小值.
在如图中,半圆形餐厅的半径OM=20m,∠QOM180°=60°.
∴∠ONM=∠OMN60°=30°,
∴QM=OM sin60°=20×sin60°m,QN=QM÷tan30°tan30°=30m.
根据平移的性质,点F移至点G,相当于先向左平移了QM长度,再向上平移了QN长度.
∴IG=IG′=BF﹣QM(m),
根据轴对称的性质,G′G⊥AB,
∴IB=QN=30m.
过点G′作AB的平行线交DA的延长线于H,易得四边形AIG′H为矩形,
∴AH=IG′m,G′H=AI=AB﹣IB=430﹣30=400(m),
∴HE=AH+AE(m).
在Rt△EHG′中,G′Em,
∴G′P最小值为:G′E﹣AE=()m.
即MF+NP的最小值为()m.
∵AH=AEm,G′H∥AN′,
∴AN′为△EHG′的中位线,AN′G′H=200m.
当MF+NP取最小值时,动点N位置为AB和G′E的交点N′.
故MF+NP的最小值为()m,此时AN的长度为200m.
【点评】本题为难度较大的圆综合题,考查了“将军饮马模型“和“定点到圆上动点的距离极值问题”,平移MF使点M与点N重合,是本题的关键.
6.问题提出
(1)已知A、B、C为平面上三个点,AC=5,BC=7,则AB的最小值为 2 .
问题探究
(2)如图①,在Rt△ABC中,∠C=90°,∠A=30°,BC=4,点P为边AB上一个动点,点M、N分别为线段AP、AC的中点,求MN的最小值.
问题解决
(3)如图②,某科学小组研制出一种激光设备,设备外围由线段AB、AC及弧BC组成,∠BAC=60°,弧BC所在的圆与AB边相切于B点,一束光线从A点发出,经弧BC反射后沿DE射出,其中AD⊥DE,∠EAD=60°,已知弧BC所在圆的半径为6,弧BC的长度为2π.请问当光线在弧BC上反射时,线段AE是否存在最小值?若存在,求出AE的最小值;若不存在,请说明理由.
【考点】圆的综合题.
【专题】压轴题;几何直观.
【答案】(1)2;(2),(3).
【分析】(1)当A、B、C三点共线时,且A在线段BC上时,AB最小;
(2)有题干条件得出MN是中位线,要求MN最小,实际上可求CP最小,点到直线的距离垂线段最短,所以当CP⊥AB时,PC长的值最小,再用等面积求解即可.
(3)要求AE最小,在直角三角形AED中进行转化,可求AD最小,要求AD最小则是点到塬上的最短距离,用三边关系即可确定三点共线时最小,再求解即可.
【解答】解:(1)当A、B、C三点共线时,且A在线段BC上时,AB最小,
此时AB=BC﹣AC=2,
故答案为2;
(2)连接PC.
∵M,N分别为线段AP,AC的中点,
∴,
∴当PC长的值最小时,MN长的值也最小.
∵P为边AB上的一个动点,
∴当CP⊥AB时,PC长的值最小.
当CP⊥AB时,.
∵在△ABC中,∠ACB=90°,∠A=30°,BC=4,
∴,AB=2BC=8.
∴,
解得.
∴MN长的最小值为.
(3)存在.
如图,设所在圆的圆心为点O,连接AO,BO,CO,DO,BC.
∵的长度是2π,且⊙O的半径是6,
∴,
解得n=60,即∠BOC=60°,
∵BO=CO,
∴△BOC是等边三角形,
∴∠CBO=60°,BC=BO=6.
∵AB是⊙O的切线,∠ABO=90°,∠ABC=30°,
∵∠BAC=60°,∠ACB=90°.
在Rt△ABC中,,
即,
解得.
在Rt△ABO中,.
∵AD+DO≥AO,即AD≥AO﹣DO,
∴AD长的最小值为.
在Rt△AED中,,
∴当AD长的值最小时,AE长的值也最小.
由,
解得.
∴AE长的最小值为.
【点评】本题主要考查了线段和差、中位线定理、解直角三角形、三角形三边关系、点圆最值等内容,熟练掌握相关知识点是解题的关键.
7.【初步发现】
如图1,Rt△ABC的内切圆与斜边AB相切于点D,与AC、BC相切于点E、F,AD=4,BD=5,求△ABC的面积.
解:设线段CE的长为x,根据切线长定理,得AE=AD=4,BF=BD=5,CF=CE=x,
在RtAABC中,根据勾股定理,
得(x+4)2+(x+5)2=(4+5)2,
整理,得x2+9x=20,
所以S△ABC(x+4)(x+5)=(x2+9x+20)=20
请同学们想一想,AD×BD=4×a5=20,△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
【深入探索】
已知:如图2,△ABC的内切圆与AB相切于点D,与AC、BC相切于点 E、F,AD=m,BD=n.
(1)若∠C=90°,求证:△ABC的面积等于mn;
(2)若AC.BC=2mn,求证:∠C=90°.
【拓展延伸】
已知:△ABC的内切圆与AB、AC、BC相切于点D、E、F,∠C=60°,AD=4,BD=5.请直接写出△ABC的面积.
【考点】圆的综合题.
【专题】压轴题;几何直观.
【答案】(1)(2)证明过程详见解析;(3)20.
【分析】(1)根据切线长定理得到AE=AD=m,BF=BD=n,CF=CE=x,再利用勾股定理建立等式即可;
(2)将AC和BC、AB表示出来,再利用勾股逆定理定理证明即可;
(3)过点C作CG⊥AB于点G,根据切线长定理CF=CE=x,表示出AG、CG、BG,再利用勾股定理建立方程,最后利用面积公式求解即可.
【解答】(1)证明:设线段CE的长为x,
根据切线长定理,得AE=AD=m,BF=BD=n,CF=CE=x,
∵∠C=90°,在Rt△ABC中,根据勾股定理,得(x+m)2+(x+n)2=(m+n)2
整理得x2+(m+n)x=mn,
∴S△ABC(x+m)(x+n)[x2+(m+n)x+mn],
∴,
∴△ABC的面积为mn;
(2)证明:由(1)可知:AE=AD=m,BF=BD=n,CF=CE=x,
∴AC=m+x,BC=n+x,
∴AC2+BC2=(m+x)2+(n+x)2=m2+2mx+x2+n2+2nx+x2=2x2+2x(m+n)+m2+n2,
∵AC BC=2mn,
∴(m+x)(n+x)=2mn,
∴x2+(m+n)x+mn=2mn,即x2+(m+n)x=mn,
∴2x2+2(m+n)x=2mn,
∴AC2+BC2=2mn+m2+n2=(m+n)2,
又∵AB2=(m+n)2,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,且∠C=90°;
(3)解:如图,过点C作CG⊥AB于点G,
设CF=CE=x,在Rt△ACG中,AC=x+4,∠C=60°,
∴4),CG(x+4),
∴BG=BC﹣CG=(x+5)(x+4),
在Rt△ABG中,根据勾股定理可得AG2+BG2=AB2,
即[(x+4)]2+[(x+5)(x+4)]2=(4+5)2,
整理得x2+9x﹣60=0,
∴x2+9x=60,
∴S△ABCBC AG(x+5) (x+4)(x2+9x+20)=20.
【点评】本题主要考查了三角形内切圆的性质、三角形的面积公式、勾股定理及逆定理、直角三角形的性质等内容,熟练掌握相关知识是解题的关键.
8.【问题提出】
唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——将军饮马问题:
(1)如图1,△ABC中,∠C=90°,AC=BC=2,E是AB的中点,P是BC边上的一动点,则PA+PE的最小值为 ;
【问题探究】
(2)如图2,已知△ABC和△DEF都是等腰直角三角形,∠ABC=∠EDF=90°,AB=6,DE=3,EF在直线AC上运动时,求BE+BD的最小值;
【拓展应用】
(3)如图3,是某公园的示意图,AB、AC、BD是三处栅栏,CD是该公园附近的一条道路(宽度不计),半圆AM及其内部是一个带舞台的广场.已知∠BAC=∠ABD=90°,CD所对的圆心角为120°,AC与所在的圆相切于点C,点E、G在AC上,点F、H在BD上,点M在AB上,矩形EFHG是一条河流在该公园内的一段(EF∥AB),其中半圆AM的直径为300m,AB=600m,AC=700,河岸EF离AB的距离为,河宽EG为,为方便运输设备,现计划垂直于河岸造桥QS,使得PQ、QS与ST之和最短,求出此时EQ的长.(结果保留根号)
【考点】圆的综合题.
【专题】几何综合题;压轴题;几何直观;推理能力.
【答案】(1);
(2);
(3)250m.
【分析】(1)如图所示,过点 E 作ED⊥AC于 D ,作点 A 关于BC的对称点A′,连接A′P,A′E,则PA′=PA,A′C=AC=2,故当P、A′、E三点共线时,PA′+PE最小,此时PA+PE最小,最小值为A′E的长,证明AED∽△ABC,求出DEBC=1,ADAC=1,则CD=1,A′D=3,由勾股定理可得A′E,即PA+PE的最小值为,
(2)如图所示,连接BE,BD,过点 D 作DG⊥EF于 G,DB′∥BC交直线AB于B′,先得到BAC=∠DEF=45°,DG=DE sin∠DEG,可证明四边形BEDB′是平行四边形,得到B′D=BE,BB′=DE=3,则AB′=3;再证明点 D 在与AC平行,且与AC之间的距离为的直线上.过点 D 作MN∥AC分别交直线AB、BC于 M 、 N ,则点 D 在直线MN上运动,证明四边形AEDM是平行四边形,得到AM=DE=3,B′M=6,BM=9,如图所示,作点 B 关于直线MN的对称点B″,连接B″D,B″B′,则B″M=BM=9,B″D=BD,可得当B′、D、B″三点共线时,B′D+B″D最小,即此时BE+BD最小,最小值为B″B′,即可得到BE+BD的最小值为;
(3)如图所示,过点 M 作MR⊥EF于 R ,则四边形AMRE是矩形,可得ER=AM=300m,MR=AEm,将点 P 沿着垂直于EF的方向平移到P′,使得PP′=QSm,则四边形P′PQS是平行四边形,可得PQ=P′S;如图所示,以ER为直径画圆,圆心设为 O ,连接ON,OP′,可得四边形ONMR是平行四边形,根据ON=MR=QS=PP′,ON∥MR,可证明四边形ONPP′是平行四边形,
因此OP′=NP=150m;过点 C 作CI⊥BD交BD延长线于 I ,在CI上取一点O′使得∠CO′D=120°,则O′即为所在圆圆心,
证明四边形ABIC是矩形,得到CI=AB=600m,解直角三角形得到r=400;如图所示,连接OO′,可得当P′S+ST最小时,PQ+QS+ST最小,进而推出当O、P′、S、T、O′五点共线时P′S+ST有最小值,最小值为OO′﹣OP′﹣O′T;过点 O 作OK⊥CT于 K ,则四边形OECK是矩形,则OK=CE=AC﹣AE=500m,CK=OE=150m,O′K=250m,得到OO′m,则PQ+QS+ST的最小值为()米.设此时OO′与GH交于 V ,OK与GH交于 W ,证明△OWV∽△OKO′,根据,可得WV=100,则GV=250m,即EQ=GV=250m.
【解答】解:(1)如图所示,过点 E 作ED⊥AC于 D ,作点 A 关于BC的对称点A′,连接A′P,A′E,
∴PA′=PA,A′C=AC=2,
∴PA+PE=PA′+PE,
∴当P、A′、E三点共线时,PA′+PE最小,即此时PA+PE最小,最小值为A′E的长,
∵∠C=90°,ED⊥AC,
∴DE∥BC,
∴△AED∽△ABC,
∴,
∵ E 是AB的中点,
∴,
∴DEBC=1,ADAC=1,
∴CD=1,
∴A′D=3,
∴A′E,
∴PA+PE的最小值为,
故答案为:;
(2)如图所示,连接BE,BD,过点 D 作DG⊥EF于 G,DB′∥BC交直线AB于B′,
∵△ABC和△DEF都是等腰直角三角形,∠ABC=∠EDF=9°,AB=6,DE=3,
∴∠BAC=∠DEF=45°,DG=DE sin∠DEG,
∴DE∥AB,
∴四边形BEDB′是平行四边形,
∴B′D=BE,BB′=DE=3,
∴AB′=3;
∵DG,即点 D 到直线AC的距离为定值,
∴点 D 在与AC平行,且与AC之间的距离为的直线上,
过点 D 作MN∥AC分别交直线AB、BC于 M 、 N ,则点 D 在直线MN上运动,
∴∠BMN=BAC=45°,
∵DE∥AM,AE∥DM,
∴四边形AEDM是平行四边形,
∴AM=DE=3,
∴B′M=6,BM=9,
如图所示,作点 B 关于直线MN的对称点B″,连接B″D,B″B′,
∴B″M=BM=9,B″D=BD,∠DMB″=∠DMB=45°,
∴∠B′MB″=90°,
∵BE+BD=B′D+B″D,
∴当B′、D、B″三点共线时,B′D+B″D最小,即此时BE+BD最小,最小值为B″B′,
∴BE+BD的最小值为;
(3)如图所示,过点 M 作MR⊥EF于 R ,则四边形AMRE是矩形,
∴ER=AM=300m,MR=AEm,
将点 P 沿着垂直于EF的方向平移到P′,使得PP′=QSm,
∴四边形P′PQS是平行四边形,
∴PQ=P′S;
如图所示,以ER为直径画圆,圆心设为 O ,连接ON,OP′,
∴OR=MN,
又∵OR∥MN,
∴四边形ONMR是平行四边形,
∴ON=MR=QS=PP′,ON∥MR,
∴ON∥QS∥MR∥PP′,
∴四边形ONPP′是平行四边形,
∴OP′=NP=150m;
过点 C 作CI⊥BD交BD延长线于 I ,在CI上取一点O′使得∠CO′D=120°,
∵AC与所在的圆相切于点 C ,
∴的圆心在射线CI上,
又∵所对的圆心角为120°,
∴O′即为所在圆圆心,
∵∠ABI=∠BAC=90°,CI⊥BI,
∴四边形ABIC是矩形,
∴CI=AB=600m,
设O′D=O′C=rm,则O′I=(600﹣r)m,
∵∠IO′D=180°﹣120°=60°,
∴O′I=O′D cos60°rm,
∴r=600﹣r,
∴r=400;
如图所示,连接OO′,
∵PQ+QS+ST=P′S+ST,
∴当P′S+ST最小时,PQ+QS+ST最小,
∵P′S+ST≥P′T≥P′O′﹣O′T,P′O′≥OO′﹣OP′,
∴P′S+ST≥OO′﹣OP′﹣O′T,
∴当O、P′、S、T、O′五点共线时P′S+ST有最小值,最小值为OO′﹣OP′﹣O′T;
过点 O 作OK⊥CT于 K ,则四边形OECK是矩形,
∴OK=CE=AC﹣AE=500m,CK=OE=150m,
∴O′K=250m,
∴OO′m,
∴PQ+QS+ST的最小值为()米.
设此时OO′与GH交于 V ,OK与GH交于 W ,
∵WV∥O′K,
∴△OWV∽△OKO′,
∴,即,
∴WV=100,
∴GV=250m,
∴EQ=GV=250m.
【点评】本题主要考查了矩形的性质与判定,一点到圆上一点距离的最值问题,平行四边形的性质与判定,勾股定理,解直角三角形,轴对称的性质,相似三角形的性质与判定等等,解题的关键在于构造将军饮马模型,确定取得最值的情形.
9.定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= 20 度;
(2)如图1,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,
①求证:△BDC是“近直角三角形”;
②在边AC上是否存在点E(异于点D),使得△BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
(3)如图2,在Rt△ABC中,∠BAC=90°,点D为AC边上一点,以BD为直径的圆交BC于点E,连接AE交BD于点F,若△BCD为“近直角三角形”,且AB=5,AF=3,求tan∠C的值.
【考点】圆的综合题.
【专题】压轴题;创新意识.
【答案】见试题解答内容
【分析】(1)∠B不可能是α或β,当∠A=α时,∠C=β=50°,α+2β=90°,不成立;故∠A=β,∠C=α,α+2β=90°,则β=20°,答案为20;
(2)①如图1,设∠=ABD∠DBC=β,∠C=α,则α+2β=90°,故△BDC是“近直角三角形”;
②∠ABE=∠C,则△ABC∽△AEB,即,即,解得:AE,即可求解
(3)①如图2所示,当∠ABD=∠DBC=β时,设BH=x,则HE=5﹣x,则AH2=AE2﹣HE2=AB2﹣HB2,即52﹣x2=62﹣(5﹣x)2,解得:x,即可求解;
②如图3所示,当∠ABD=∠C=β时,AF:EF=AG:DE=3:2,则DE=2k,则AG=3k=R(圆的半径)=BG,点H是BE的中点,则GHDE=k,在△BGH中,BH2k,由三角函数可求解.
【解答】解:(1)∠B不可能是α或β,
当∠A=α时,∠C=β=50°,α+2β=90°,不成立;
故∠A=β,∠C=α,α+2β=90°,则β=20°,
故答案为20;
(2)①如图1,设∠ABD=∠DBC=β,∠C=α,
则α+2β=90°,故△BDC是“近直角三角形”;
②存在,理由:
在边AC上是否存在点E(异于点D),使得△BCE是“近直角三角形”,
AB=3,AC=4,则BC=5,
则∠ABE=∠C,则△ABC∽△AEB,
即,即,解得:AE,
则CE=4;
(3)①如图2所示,当∠ABD=∠DBC=β时,
则AE⊥BF,则AF=FE=3,则AE=6,
AB=BE=5,
过点A作AH⊥BC于点H,
设BH=x,则HE=5﹣x,
则AH2=AE2﹣HE2=AB2﹣HB2,即52﹣x2=62﹣(5﹣x)2,解得:x;
cos∠ABEcos2β,则tan2β,
则tanα;
②如图3所示,当∠ABD=∠C=β时,
过点A作AH⊥BE交BE于点H,交BD于点G,则点G是圆的圆心(BE的中垂线与直径的交点),
∵∠AEB=∠DAE+∠C=α+β=∠ABC,故AE=AB=5,则EF=AE﹣AF=5﹣3=2,
∵DE⊥BC,AH⊥BC,
∴ED∥AH,则AF:EF=AG:DE=3:2,
则DE=2k,则AG=3k=R(圆的半径)=BG,点H是BE的中点,则GHDE=k,
在△BGH中,BH2k,
在△ABH中,AB=5,BH=2k,AH=AG+HG=4k,
∵∠C+∠ABC=90°,∠ABC+∠BAH=90°,
∴∠C=∠BAH,
∴tanC=tan∠BAH,
综上,tanC的值为或.
【点评】此题属于圆的综合题,涉及了平行四边形的性质、全等三角形的判定与性质、三角函数值的知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.
10.综合与实践
【问题情境】在数学综合实践课上,“希望小组”的同学们以三角形为背景,探究图形变化过程中的几何问题,如图,在△ABC中,AB=AC,∠BAC=90°,点D为平面内一点(点A,B,D三点不共线),AE为△ABD的中线.
【初步尝试】(1)如图1,小林同学发现:延长AE至点M,使得ME=AE,连接DM.始终存在以下两个结论,请你在①,②中挑选一个进行证明:
①DM=AC;②∠MDA+∠DAB=180°;
【类比探究】(2)如图2,将AD绕点A顺时针旋转90°得到AF,连接CF.小斌同学沿着小林同学的思考进一步探究后发现:AECF,请你帮他证明;
【拓展延伸】(3)如图3,在(2)的条件下,王老师提出新的探究方向:点D在以点A为圆心,AD为半径的圆上运动(AD>AB),直线AE与直线CF相交于点G,连接BG,在点D的运动过程中BG存在最大值.若AB=4,请直接写出BG的最大值.
【考点】圆的综合题.
【专题】几何综合题;压轴题;图形的全等;推理能力.
【答案】(1)证明见解答;
(2)证明见解答;
(3)BG的最大值为22.
【分析】(1)利用SAS证明△ABE≌△MDE,可得AB=DM,再结合AB=AC,即可证得DM=AC;由全等三角形性质可得∠BAE=∠DME,再运用平行线的判定和性质即可证得∠MDA+∠DAB=180°;
(2)延长AE至点M,使得ME=AE,连接DM.利用SAS证得△ACF≌△DMA,可得CF=AM,再由AEAM,可证得AECF;
(3)延长DA至M,使AM=AD,设AM交CF于N,连接BM交CF于K,取AC中点P,连接GP,可证得△ACF≌△ABM(SAS),利用三角形中位线定理可得AE∥BM,即AG∥BM,利用直角三角形性质可得GPACAB=2,得出点G在以P为圆心,2为半径的⊙P上运动,连接BP并延长交⊙P于G′,可得BG′的长为BG的最大值,再运用勾股定理即可求得答案.
【解答】(1)证明:①∵AE为△ABD的中线,
∴BE=DE,
在△ABE和△MDE中,
,
∴△ABE≌△MDE(SAS),
∴AB=DM,
∵AB=AC,
∴DM=AC;
②由①知△ABE≌△MDE,
∴∠BAE=∠DME,
∴AB∥DM,
∴∠MDA+∠DAB=180°;
(2)证明:延长AE至点M,使得ME=AE,连接DM.
由旋转得:AF=AD,∠DAF=90°,
∵∠BAC=90°,∠DAF+∠BAC+∠BAD+∠CAF=360°,
∴∠BAD+∠CAF=180°,
由(1)②得:∠MDA+∠DAB=180°,DM=AB=AC,
∴∠CAF=∠MDA,
在△ACF和△DMA中,
,
∴△ACF≌△DMA(SAS),
∴CF=AM,
∵AEAM,
∴AECF;
(3)如图3,延长AE至M,使EM=AE,连接BM,
在△ADE和△MBE中,
,
∴△ADE≌△MBE(SAS),
∴AD=BM,∠DAE=∠M,
∴AD∥BM,
∴∠BAD+∠ABM=180°,
∵∠DAF+∠BAC=180°,
∴∠BAD+∠CAF=180°,
∴∠ABM=∠CAF,
∵AF=AD,
∴AF=BM,
在△ABM和△CAF中,
,
∴△ABM≌△CAF(SAS),
∴∠BAM=∠ACF,
∵∠BAC=90°,
∴∠BAM+∠CAG=90°,
∴∠ACF+∠CAG=90°,
∴∠AGC=90°,
点G在以AC为直径的⊙O上运动,当且仅当B、O、G三点共线时,BG取得最大值,
此时BG=OB+OG,
在Rt△ABO中,O为AC的中点,则OAAC=2,
∴OB2,
在Rt△ACG中,O为斜边AC的中点,
∴OGAC=2,
∴BG的最大值为22.
【点评】本题是几何综合题,考查了三角形的全等的性质与判定,两直线垂直的判定,三角形中位线定理,勾股定理,圆的性质,熟练掌握全等三角形的判定定理是解决本题的关键.
11.(1)【学习心得】
小赵同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.我们把这个过程称为“化隐圆为显圆”.
①已知:如图1,OA=OB=OC,若∠AOB=50°,求∠ACB的度数.
解:若以点O为圆心,OA为半径作辅助圆,∠AOB是⊙O的圆心角,而∠ACB是圆周角,从而可容易得到∠ACB= 25 °.
②如图2,点P为正方形ABCD内一点,且∠BPC=90°,若AB=4,求AP的最小值.
解:∵BC=4,∠BPC=90°,∴点P在以BC为直径的圆上,
设圆心为点O,则O、P、A三点共线时AP最小,最小值为 22 .
(2)【问题解决】
①如图3,在平行四边形ABCD中,已知AB=4,BC=6,∠ABC=60°,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点Q,则线段QC的最小值为 24 .
②如图4,△ABC中,∠BAC=90°,AB=4,AC=3,D为AC上一动点,以AD为直径的⊙O交BD于E,求线段CE的最小值.
(3)【问题拓展】
如图5,在平面直角坐标系中,已知两点A(2,3),B(6,7),x轴上有一动点P,当∠APB最大时,直接写出点P的坐标 1 .
【考点】圆的综合题.
【专题】几何综合题;压轴题;运算能力;推理能力.
【答案】(1)①25.②22.
(2)①24.②线段CE的最小值为2.
(3)1.
【分析】(1)①利用圆周角定理即可求得答案;
②由正方形性质可得:∠ABC=90°,BC=AB=4,OBBC=2,由勾股定理得:AO=2,推出点P在以BC为直径的⊙O上,则O、P、A三点共线时AP最小,即可求得答案;
(2)①过点A作AH⊥BC于H,利用解直角三角形得AH=AB sin∠ABC=2,BH=AB cos∠ABC=2,CH=BC﹣BH=4,由勾股定理得AC=2,再由AQ=AB=4,可得点Q在以A为圆心AB为半径的⊙A上,即当C、Q、A三点共线时QC最小,QC的最小值=AC﹣AQ=24;
②连接AE,由AD是⊙O的直径,可得∠AED=90°,推出∠AEB=90°,即点E在以AB为直径的圆上,进而可得当C、E、Q三点共线时,CE最小,运用勾股定理即可求得答案;
(3)当∠APB最大时,过A、B两点的⊙O′与x轴相切,利用待定系数法可得直线AB的解析式为y=x+1,线段AB的垂直平分线为y=﹣x+9,设O′(m,﹣m+9),根据O′A=O′B=O′P,建立方程求解即可得出答案.
【解答】解:(1)①如图1,以点O为圆心,OA为半径作辅助圆⊙O,
∵,∠AOB=50°,
∴∠ACB∠AOB=25°,
故答案为:25.
②点P为正方形ABCD内一点,且∠BPC=90°,若AB=4,求AP的最小值.
如图②,以BC为直径作⊙O,
∵四边形ABCD是正方形,
∴∠ABC=90°,BC=AB=4,
∴OBBC=2,
在Rt△ABO中,AO2,
∵BC=4,∠BPC=90°,
∴点P在以BC为直径的⊙O上,
则O、P、A三点共线时AP最小,
∴AP的最小值=AO﹣OP=22,
故答案为:22.
(2)①如图3,过点A作AH⊥BC于H,
∵AB=4,BC=6,∠ABC=60°,
则AH=AB sin∠ABC=4sin60°=2,BH=AB cos∠ABC=4cos60°=2,
∴CH=BC﹣BH=6﹣2=4,
在Rt△ACH中,AC2,
∵点B与点Q关于直线AP对称,
∴AQ=AB=4,
∴点Q在以A为圆心AB为半径的⊙A上,
∴当C、Q、A三点共线时QC最小,QC的最小值=AC﹣AQ=24,
故答案为:24.
②如图4,连接AE,
∵AD是⊙O的直径,
∴∠AED=90°,
∴∠AEB=180°﹣∠AED=90°,
即点E在以AB为直径的圆上,
以AB为直径作⊙Q,交⊙O于E,当C、E、Q三点共线时,CE最小,
∵△ABC中,∠BAC=90°,AB=4,AC=3,
∴QE=AQAB=2,
∴CQ,
∴CE=CQ﹣QE2,
故线段CE的最小值为2.
(3)当∠APB最大时,过A、B两点的⊙O′与x轴相切,
设直线AB的解析式为y=kx+b,把A(2,3),B(6,7)代入,
得:,
解得:,
∴直线AB的解析式为y=x+1,
∵线段AB的中点坐标为(4,5),圆心O′在AB的垂直平分线上,
∴线段AB的垂直平分线为y=﹣x+9,
设O′(m,﹣m+9),
∵O′A=O′B=O′P,
∴(m﹣2)2+(﹣m+9﹣3)2=(﹣m+9)2,
解得:m1或m1(舍去),
∴点P的坐标为(1,0),
故答案为:1.
【点评】本题是圆的综合题,考查了圆的有关知识,正方形的性质,平行四边形的性质,解直角三角形等知识,灵活运用这些性质解决问题是解题的关键.
12.问题提出:如图①,在Rt△ABC中,∠C=90°,CB=4,CA=6,⊙C的半径为2,P为圆上一动点,连接AP、BP,求的最小值.
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图①,连接CP,在CB上取一点D,使CD=1,则.又∠PCD=∠BCP,所以△PCD∽△BCP.所以.
所以PDPB,所以.
请你完成余下的思考,并直接写出答案:的最小值为 ;
(2)自主探索:在“问题提出”的条件不变的前提下,求的最小值;
(3)拓展延伸:如图②,已知在扇形COD中,∠COD=90°,OC=6,OA=3,OB=5,P是上一点,求2PA+PB的最小值.
【考点】圆的综合题.
【专题】压轴题;与圆有关的计算;数据分析观念.
【答案】(1);
(2);
(3)13.
【分析】(1)利用勾股定理即可求解;
(2)连接CP,在CA上取点D,使CD,则有,可证△PCD∽△ACP,得到PDAP,即AP+BP=BP+PD,从而AP+BP的最小值为BD;
(3)延长OA到点E,使CE=6,连接PE、OP,可证△OAP∽△OPE,得到EP=2PA,得到2PA+PB=EP+PB,当E、P、B三点共线时,得到最小值.
【解答】解:(1)如图1,
连接AD,
∵APBP=AP+PD,要使APBP最小,
∴AP+AD最小,当点A,P,D在同一条直线时,AP+AD最小,
即:APBP最小值为AD,
在Rt△ACD中,CD=1,AC=6,
∴AD,
APBP的最小值为,
故答案为:;
(2)如图2,
连接CP,在CA上取点D,使CD,
∴,
∵∠PCD=∠ACP,
∴△PCD∽△ACP,
∴,
∴PDAP,
∴AP+BP=BP+PD,
∴同(1)的方法得出AP+BP的最小值为BD;
(3)如图3,
延长OA到点E,使CE=6,
∴OE=OC+CE=12,
连接PE、OP,
∵OA=3,OP
∴,
∵∠AOP=∠AOP,
∴△OAP∽△OPE,
∴,
∴EP=2PA,
∴2PA+PB=EP+PB,
∴当E、P、B三点共线时,取得最小值为:BE13.
【点评】此题是圆的综合题,主要考查了勾股定理,相似三角形的判定和性质,极值的确定,还考查了学生的阅读理解能力,解本题的关键是根据材料中的思路构造出△PCD∽△ACP和△OAP∽△OPE,也是解本题的难点.
13.概念认识:
平面内,M为图形T上任意一点,N为⊙O上任意一点,将M、N两点间距离的最小值称为图形T到⊙O的“最近距离”,记作d(T﹣⊙O).例:如图1,在直线l上有A、C、O三点,以AC为对角线作正方形ABCD,以点O为圆心作圆,与l交于E、F两点,若将正方形ABCD记为图形T,则C、E两点间的距离称为图形T到⊙的“最近距离”.
数学理解:
(1)在平面内有A、B两点,以点A为圆心,5为半径作⊙A,将点B记为图形T,若d(T﹣⊙A)=2,则AB= 3或7 .
(2)如图2,在平面直角坐标系中,以O(0,0)为圆心,半径为2作圆.
①将点C(4,3)记为图形T,则d(T﹣⊙O)= 3 .
②将一次函数y=kx+2的图记为图形T,若d(T﹣⊙)>0,求k的取值范围.
推广运用:
(3)在平面直角坐标系中,P的坐标为(t,0),⊙P的半径为2,D、E两点的坐标分别为(5,5)、(5,﹣5),将△DOE记为图形T,若d(T﹣⊙P)=1,则t= 8或﹣3 .
【考点】圆的综合题.
【专题】压轴题;运算能力;推理能力.
【答案】(1)3或7;
(2)①3,②﹣1<k<1且k≠0;
(3)8或﹣3.
【分析】(1)根据图形T到⊙O的“最近距离”的定义即可解决问题.
(2)①如图2中,连接OC交⊙O于E.求出EC的长即可.
②如图,设直线y=kx+2与⊙O相切于E,K.连接OK,OE.求出直线DE,直线DK的解析式即可解决问题.
(3)分两种情形:①如图3﹣1中,当点P在∠DOE内部时,作PM⊥OD于M,交⊙P于K.②如图3﹣2中,当点P在∠DOE的外侧时,分别求解即可.
【解答】解:(1)如图1中,
∵d(T﹣⊙A)=2,
∴CB=CB′=2,
∵AC=5,
∴AB′=5﹣2=3,AB=5+2=7.
故答案为:3或7.
(2)①如图2中,连接OC交⊙O于E.
∵C(4,3),
∴OC5,
∵OE=2,
∴EC=3,
∴d(T﹣⊙O)=3.
故答案为:3.
②如图,设直线y=kx+2与⊙O相切于E,K.连接OK,OE.
∵OE⊥DE,OK⊥DK,OD=2,OE=OK=2,
∴DK2,DE2,
∴DE=OE=DK=OK,
∴四边形DEOK是菱形,
∵∠DKO=∠DEO=90°,
∴四边形DEOK是正方形,
∴∠ODE=∠ODK=45°,
∴直线DE的解析式为y=﹣x+2,直线DK的解析式为y=x+2,
∵d(T﹣⊙O)>0,
∴观察图象可知满足条件的k的值为﹣1<k<1且k≠0.
(3)如图3﹣1中,当点P在DE的右边时.
∵D(5,5),
∴∠DOP=45°,
∵d(T﹣⊙P)=1,
∴OP=5+1+2=8
∴t=8.
如图3﹣2中,当点P在∠DOE的外侧时,由题意可知OM=1,OP=1+2=3,t=﹣3.
综上所述,满足条件的t的值为8或﹣3.
【点评】本题属于圆综合题,考查了直线与圆的位置关系,图形T到⊙O的“最近距离”的定义,解直角三角形等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考压轴题.
14.问题提出:
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?
初步思考:
(1)给出了一些特殊的四边形:①矩形②菱形③等腰梯形④正方形,能过它们四个顶点作一个圆的是 ①③④ (填写序号),过某个四边形四个顶点作一个圆的四边形相对的两个内角的关系是 互补(对角之和等于180°) .
进一步研究:
(2)如果过某个四边形的四个顶点不能作一个圆,那么其相对的两个内角之间有上面的关系吗?请结合图1的两幅图说明其中的道理.(提示:考虑∠B+∠D与180°之间的关系)
由上面的探究,请用文字语言直接写出过某个四边形的四个顶点能作一个圆的条件 对角互补 .
拓展延伸
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图2,AB是⊙O的直径,点C在⊙O上,求作:CN⊥AB.
作法:①连接CA,CB;
②在上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M:
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图2中作图,并说明CN⊥AB的理由,(提示:可以利用(2)中的结论)
【考点】圆的综合题.
【专题】压轴题;几何直观;推理能力.
【答案】(1)①②③;互补(对角之和等于180°);
(2)对角互补;
(3)图见解析,理由见解析.
【分析】(1)(2)根据圆内接四边形的对角互补可知这些四边形的对角互补;
(3)先画出图形,根据AB是圆O的直径可得出点E是△ABF三条高的交点,进而得到FM⊥AB;接下来根据(2)中的结论可得点E、M、B、D在同一个圆上,则有∠EMD=∠DBE,再结合点N、C、B、D在⊙O上,推出∠DBE=∠CND,等量代换,结合平行线的判定可证明FM∥CN,至此问题不难解答.
【解答】解:(1)
①如答图1,矩形ABCD中,∠A=∠B=∠C=∠D=90°,则∠A+∠C=∠B+∠D=180°,A,B,C,D四点共圆.
②如答图2,在菱形ABCD中,∠A=∠C,∠B=∠D,A,B,C,D四点不共圆.
③如答图3,在等腰梯形中,∠B+∠C=180°,∠A+∠D=180°,∠A=∠B,∠C=∠D,则∠A+∠C=∠B+∠D=180°,A,B,C,D四点共圆.
④如答图4,在正方形ABCD中,∠A=∠B=∠C=∠D=90°,则∠A+∠C=∠B+∠D=180°,A,B,C,D四点共圆.
综上所述,相对的两个角之间的关系是:互补(对角之和等于180°);
故答案为:①②③;互补(对角之和等于180°);
(2)如果四边形没有外接圆,那么相对的两个内角之间没有有上面的关系.
如答图4:连接BE,
∵∠A+∠E=180°,∠BCD>∠E,
∴∠A+∠BCD>180°;
如答图5:连接DE,
∵∠A+∠BED=180°,∠BED>∠C,
∴∠A+∠C<180°.
综上所述,某个四边形的四个顶点能作一个圆的条件是:对角互补.
故答案为:对角互补;
(3)答图6即为所求作.
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,即BC⊥AF,AD⊥BF,
∴根据三角形的三条高交于同一点可得:FM⊥AB.
∴∠EMB=90°.
∴∠EMB+∠EDB=180°.
∴由(2)中的结论可得:点E、D、B、M在同一个圆上,如答图⑥所示.
∴∠EMD=∠EBD.
∵∠CND=∠CBD,
∴∠CND=∠EMD.
∴CN∥EM.
∴∠CHB=∠EMB.
∵∠EMB=90°,
∴∠CHB=90°,即CN⊥AB.
【点评】本题属于圆的综合题,综合考查了圆周角定理、三角形外角的性质、平行线的判定与性质、圆周角的度数与所对弧的度数之间的关系等知识,考查了操作与探究的能力,考查了运用已有的经验解决问题的能力,是一条体现新课程理念的好题.
15.综合与实践
数学实践课堂上,张老师带领学生们从一道题入手,开始研究,并对此题做适当变式,尝试举一反三,开阔学生思维.
(1)原型题:如图1,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,AP=PC,AP⊥PC,则△ABP≌△ PDC ,请你说明理由.
(2)利用结论,直接应用:
如图2,四边形ABCD、EFGH、NHMC都是正方形,边长分别为a、b、c,A、B、N、E、F五点在同一条直线上,则△CBN≌△ NEH ,c= (用含a、b的式子表示).
如图3,四边形ABCD中,AB∥DC,AB⊥BC,AB=2,CD=4,以BC上一点O为圆心的圆经过A、D两点,且∠AOD=90°,则圆心O到弦AD的距离为 .
(3)弱化条件,变化引申:
如图4,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°,且DM交AC于点F,ME交BC于点G,连接FG,则△AMF与△BGM的关系为: △AMF∽△BGM ,若,AF=3,则FG= .
【考点】圆的综合题.
【专题】几何综合题;压轴题;运算能力;推理能力.
【答案】(1)△ABP≌△PDC;
(2)△CBN≌△NEH,c,圆心O到弦AD的距离为.
(3)△AMF∽△BGM,FG.
【分析】(1)先证明∠BAP=∠CPD,根据AAS定理可证明△ABP≌△PDC.
(2)先证明△CBN≌△NEH,再利用勾股定理说明a、b、c间关系;根据AAS证明△AOB≌△ODC,则有OB=CD=4;再根据勾股定理求得OA.可证明三角形AOD是等腰直角三角形,则可得出答案.
(3)利用三角形外角可得∠AFM=∠DME+∠E=∠A+∠E=∠BMG,进而证得△AMF∽△BGM,再由∠A=∠B=45°,可得出△ABC是等腰直角三角形,根据M为线段AB的中点,可得AM=BMAB42,运用相似三角形性质和勾股定理即可求得答案.
【解答】(1)证明:∵AB⊥BD,CD⊥BD,
∴∠ABP=∠PDC=90°,
∴∠BAP+∠APB=90°,
∵AP⊥PC,
∴∠CPD+∠APB=90°,
∴∠BAP=∠CPD,
在△ABP和△PDC中,
,
∴△ABP≌△PDC(AAS);
故答案为:PDC.
(2)证明:∵四边形ABCD、EFGH、NHMC都是正方形,边长分别为a、b、c,
∴∠CBN=∠NEH=∠CNH=90°,CN=NH=c,BC=a,EH=b,
∵∠BCN+∠BNC=∠ENH+∠BNC=90°,
∴∠BCN=∠ENH,
在△CBN和△NEH中,
,
∴△CBN≌△NEH(AAS),
∴BN=EH=b,
在Rt△CBN中,CN2=BC2+BN2,
∴c2=a2+b2,
∵a、b、c均为正数,
∴c,
故答案为:NEH,.
如图3,∵AB∥DC,AB⊥BC,
∴∠B=∠C=90°,
∴∠BAO+∠AOB=90°,
∵∠AOD=90°,
∴∠COD+∠AOB=90°,
∴∠BAO=∠COD,
∵以点O为圆心的圆经过A、D两点,
∴OA=OD,
∴△AOB≌△ODC(AAS),
∴AB=OC=2,OB=CD=4,
在Rt△AOB中,OA2,
∴OD=OA=2,
∵∠AOD=90°,
∴△AOD是等腰直角三角形,
∴ADAB22,∠OAD=∠ODA=45°,
过点O作OH⊥AD于点H,
根据垂径定理可得:AH=DH,
∵OHAD,
∴OH,
故答案为:.
(3)∵∠AFM=∠DME+∠E(外角定理),
∠DME=∠A=∠B(已知),
∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,
∴△AMF∽△BGM,
∵∠DME=∠A=∠B=45°
∴AC=BC,∠ACB=90°,
∴AC⊥BC,
∵M为线段AB的中点,
∴AM=BMAB42,
∵△AMF∽△BGM,
∴,
∴BG,
又∵AC=BC=4cos45°=4,
∴CG=BC﹣BG=4,CF=AC﹣AF=4﹣3=1,
在Rt△FCG中,由勾股定理得:
FG.
【点评】本题是有关圆的综合题,考查了全等三角形的判定和性质,直角三角形的性质,勾股定理,等腰直角三角形的性质与判定,相似三角形的判定与性质,垂径定理,圆的性质等,此题难度适中,熟练掌握全等三角形的判定和性质以及相似三角形的判定和性质是解题关键.
16.问题提出:
(1)如图1,点B、C在⊙O上且BC=2,过点O作OE⊥BC,交BC于点A,交⊙O于点E,连接BE、CE,若∠CBE=30°,则线段AE的长度为 .
问题探究:
(2)如图2,在△ABC中,BC=2,∠BAC=45°,求边AC长度的最大值;
问题解决:
(3)如图3,某城市拟在河流m、n所夹半岛区域建一个湿地公园,公园的周长由亲水廊桥AB、、CD和绿化带BC四部分构成.其中B、C两定点间的距离为2000米.根据规划要求,A、D两点间的距离为600米,A、D两点到直线BC的距离相等,的中点E到BC的距离比点A到BC的距离多100米;若修建时需保证∠B与∠C的和为120度,请判断这个湿地公园的周长是否存在最大值?若存在,请求出最大值.若不存在,请说明理由.(结果保留π)
【考点】圆的综合题.
【专题】压轴题;构造法;推理能力;模型思想.
【答案】(1);
(2)2;
(3)4800.
【分析】(1)利用角度关系直接求解即可;
(2)构造外接圆,圆内最长的为直径,即可求解;
(3)关键在于构造出两个外接圆,然后利用弦的长度和角度关系将相关量表示出来即可求解.
【解答】解:(1)∵BC=2,OE⊥BC,
∴AB=AC=1,
∵∠CBE=30°,
∴tan∠CBE=tan30°,
∴AE.
(2)如图1,构造△ABC的外接圆⊙O,连接OB,OC,
∴∠BOC=2∠BAC=90°,
∵OB=OC,
∴OB,
∴⊙O的直径为,
∵AC为弦长,
∴AC,
∴AC的最大值为.
(3)如图2,构造△AED的外接圆⊙O,连接OE,AD交AD于点F,连接OA,OD,过点D作DG∥AB交BC于点G,构造△DGC的外接圆⊙M,
∵点E为的中点,
∴OE⊥AD,
∴AFAD=300,
∵的中点E到BC的距离比点A到BC的距离多100米,
∴EF=100,
设OA=r,则:
OF=r﹣100,
∵AF2+OF2=OA2,
∴3002+(r﹣100)2=r2,
解得:r=200,
∴sin∠AOF,
∴∠AOF=60°,
∴∠AOD=120°,
的长度为:,
∵DG∥AB,AD∥BC,
∴四边形ABGD为平行四边形,
∴DG=AB,∠DGC=∠B,BG=AD,
∴CG=BC﹣BG=1400,
∵∠B+∠C=120°,
∴∠DGC+∠C=120°,
∴∠GDC=60°,
当D到CG的距离最远时,
AB+DC=DG+DC最大,
此时有DM⊥CG,
∴DG=DC=CG=1400,
此时周长最大为:BC+CDAB=2000+28002π×2004800,
∴公园周长最大值为4800米.
【点评】本题考查了圆的综合运用,涉及垂径定理,圆周角定理,还有平行四边形等相关知识点,综合性比较强,对解题思维要求较高,属于中考压轴题.
17.在一次数学探究活动中,李老师设计了一份活动单:
已知线段BC=2,使用作图工具作∠BAC=30°,尝试操作后思考: (1)这样的点A唯一吗? (2)点A的位置有什么特征?你有什么感悟?
“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以BC为弦的圆弧上(点B、C除外),….小华同学画出了符合要求的一条圆弧(如图1).
(1)小华同学提出了下列问题,请你帮助解决.
①该弧所在圆的半径长为 2 ;
②△ABC面积的最大值为 ;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为A′,请你利用图1证明∠BA′C>30°.
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形ABCD的边长AB=2,BC=3,点P在直线CD的左侧,且tan∠DPC.
①线段PB长的最小值为 ;
②若S△PCDS△PAD,则线段PD长为 .
【考点】圆的综合题.
【专题】压轴题;矩形 菱形 正方形;圆的有关概念及性质;推理能力.
【答案】见试题解答内容
【分析】(1)①设O为圆心,连接BO,CO,根据圆周角定理得到∠BOC=60°,证明△OBC是等边三角形,可得半径;
②过点O作BC的垂线,垂足为E,延长EO,交圆于D,以BC为底,则当A与D重合时,△ABC的面积最大,求出OE,根据三角形面积公式计算即可;
(2)延长BA′,交圆于点D,连接CD,利用三角形外角的性质和圆周角定理证明即可;
(3)①根据,连接PD,设点Q为PD中点,以点Q为圆心,PD为半径画圆,可得点P在优弧CPD上,连接BQ,与圆Q交于P′,可得BP′即为BP的最小值,再计算出BQ和圆Q的半径,相减即可得到BP′;
②根据AD,CD和 推出点P在∠ADC的平分线上,从而找到点P的位置,过点C作CF⊥PD,垂足为F,解直角三角形即可求出DP.
【解答】解:(1)①设O为圆心,连接BO,CO,
∵∠BAC=30°,
∴∠BOC=60°,又OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=2,即半径为2;
②∵△ABC以BC为底边,BC=2,
∴当点A到BC的距离最大时,△ABC的面积最大,
如图,过点O作BC的垂线,垂足为E,延长EO,交圆于D,
∴BE=CE=1,DO=BO=2,
∴OE,
∴DE,
∴△ABC的最大面积为;
(2)如图,延长BA′,交圆于点D,连接CD,
∵点D在圆上,
∴∠BDC=∠BAC,
∵∠BA′C=∠BDC+∠A′CD,
∴∠BA′C>∠BDC,
∴∠BA′C>∠BAC,即∠BA′C>30°;
(3)①如图,当点P在BC上,且PC时,
∵∠PCD=90°,AB=CD=2,AD=BC=3,
∴tan∠DPC,为定值,
连接PD,设点Q为PD中点,以点Q为圆心,PD为半径画圆,
∴当点P在优弧CPD上时,tan∠DPC,连接BQ,与圆Q交于P′,
此时BP′即为BP的最小值,过点Q作QE⊥BE,垂足为E,
∵点Q是PD中点,
∴点E为PC中点,即QECD=1,PE=CEPC,
∴BE=BC﹣CE=3,
∴BQ,
∵PD,
∴圆Q的半径为,
∴BP′=BQ﹣P′Q,即BP的最小值为;
②∵AD=3,CD=2,S△PCDS△PAD,
则,
∴△PAD中AD边上的高=△PCD中CD边上的高,
即点P到AD的距离和点P到CD的距离相等,
则点P到AD和CD的距离相等,即点P在∠ADC的平分线上,如图,
过点C作CF⊥PD,垂足为F,
∵PD平分∠ADC,
∴∠ADP=∠CDP=45°,
∴△CDF为等腰直角三角形,又CD=2,
∴CF=DF,
∵tan∠DPC,
∴PF,
∴PD=DF+PF.
解法二:如图,作直径DG,连接PG,
∵△CDF为等腰直角三角形,又CD=2,
∴∠CDF=∠CED=45°,
∴CD=CE=2,
∴DE=2,
∵∠DPC=∠GDC,
∴tan∠DGC=tan∠DPC,
∴CG=1.5,EG=0.5,
∵DG是直径,
∴∠DPG=∠EPG=90°,
∴PEEG,
∴PD=DE﹣PE=2.
【点评】本题是圆的综合题,考查了圆周角定理,三角形的面积,等边三角形的判定和性质,最值问题,解直角三角形,三角形外角的性质,勾股定理,知识点较多,难度较大,解题时要根据已知条件找到点P的轨迹.
18.问题提出
(1)如图①,△ABC内接于⊙O,过点C作⊙O的切线l.在l上任取一个不同于点C的点P,连接PB、PA,比较∠ACB与∠APB的大小,并说明理由.
问题探究
(2)如图2,正方形ABCD,边长为2,在CD边上是否存在点P,使∠APB最大?若存在,确定点P的位置,并求此时sin∠APB的值;若不存在,请说明理由.
问题解决
(3)如图③,四边形ABCD为某工作室的平面示意图,线段BC、CD、DA为三面墙,MN为入户门处,其中AD∥BC,AD⊥AB,∠C=60°,BM=AN=4米,BC=30米,AD=20米.出于安全考虑,负责人想在墙上安装监控装置P,用来监控并记录进出的人员,为了让监控效果最佳,要求∠MPN最大,试问在墙上是否存在一点P,使得∠MPN最大?若存在,请求出此时sin∠MPN的值及P点的位置;若不存在,请说明理由.
【考点】圆的综合题.
【专题】压轴题;圆的有关概念及性质;与圆有关的位置关系;模型思想;应用意识.
【答案】(1)∠ACB>∠APB,理由见解答过程;
(2)存在,P是边CD的中点,sin∠APB;
(3)监控装置P应在AD上,距A6米的地方,此时sin∠MPN,
或监控装置P应在BC上,距B6米的地方,此时sin∠MPN.
【分析】(1)设AP交⊙O于D,连接AD,由∠ACB=∠ADB,∠ADB>∠APB,即可证∠ACB>∠APB;
(2)过A、B两点作⊙O与CD相切于P,连接PO并延长交AB于E,过A作AF⊥BP于F,此时∠APB最大,由⊙O与CD相切于P,可得EP⊥AB,四边形AEPD、四边形BEPC是矩形,从而AE=BEAB=1,PE=AD=2,P是边CD的中点,在Rt△BEP中,求出BP,同理AP,再由S△ABP得AF,即可在Rt△APF中,得到sin∠APB;
(3)分三种情况:①当P在BC上时,作过M、N的⊙O与BC相切于P,此时∠MPN最大,过O作OE垂直AB于E,过D作DF⊥BC于F,连接OP、OM、ON,由四边形ABFD是矩形,DF=AB=10,由BM=AN=4,可得ME=NEMN,BE=BM+ME=5,由四边形BPOE是矩形,得OP=BE=5,BP=OE,Rt△MOE中,用勾股定理得OE6,即BP=6,此时监控装置P在距B6米的墙上,再根据∠MPN=∠MOE,在Rt△MOE中,求得sin∠MPN;②当P在AD上时,作过M、N的⊙O与AD相切于P,此时∠MPN最大,同①的道理:AP=6,即此时监控装置P在距A6米的墙上,sin∠MPN;③当P在CD上时,作过M、N的⊙O与CD相切于P,此时∠MPN最大,过O作OE垂直AB于E,直线OE交CD于G,过D作DF⊥BC于F,连接OP、OM、ON,设PG=x,则DP=10﹣x,OG=2x,OPx,OE=GE﹣OG=25﹣2x,OM=OPx,Rt△MOE中,ME2+OE2=OM2有()2+(25﹣2x)2=(x)2,解得∴PG=50﹣12,DP=1240,即此时监控装置P在距D(1240)米的墙上,sin∠MPN=sin∠MOE,比较,可得到答案.
【解答】解:(1)∠ACB>∠APB,理由如下:
设AP交⊙O于D,连接AD,如图:
∵弧AB=弧AB,
∴∠ACB=∠ADB,
而∠ADB是△BDP的一个外角,
∴∠ADB>∠APB,
∴∠ACB>∠APB;
(2)存在,P是边CD的中点,理由如下:
过A、B两点作⊙O与CD相切于P,连接PO并延长交AB于E,过A作AF⊥BP于F,如图:
由(1)知此时∠APB最大,
∵⊙O与CD相切于P,
∴EP⊥CD,
∵正方形ABCD,边长为2,
∴CD∥AB,AB=AD=2,∠DAB=∠ABC=90°,
∴EP⊥AB,四边形AEPD、四边形BEPC是矩形,
∴AE=BEAB=1,PE=AD=2,
∴CP=BE=AE=DP,即P是边CD的中点,
Rt△BEP中,BP,
同理AP,
由S△ABPAB PEBP AF得:AF,
在Rt△APF中,sin∠APB;
(3)存在,理由如下:
①当P在BC上时,作过M、N的⊙O与BC相切于P,此时∠MPN最大,过O作OE垂直AB于E,过D作DF⊥BC于F,连接OP、OM、ON,如图:
∵AD∥BC,AD⊥AB,DF⊥BC,
∴四边形ABFD是矩形,
∴AB=DF,AD=BF,
∵BC=30,AD=20,
∴CF=BC﹣BF=BC﹣AD=10,
Rt△DCF中,DF=CF tanC=10 tan60°=10,
∴AB=10,
∵BM=AN=4,
∴MN=AB﹣BM﹣AN=2,
∵OE⊥AB,
∴ME=NEMN,
∴BE=BM+ME=5,
∵⊙O与BC相切于P,
∴∠OPB=90°,
∴四边形BPOE是矩形,
∴OP=BE=5,BP=OE,
∴OM=OP=5,
Rt△MOE中,OE6,
∴BP=6,即此时监控装置P在距B6米的墙上,
∵OE⊥AB,OM=ON,
∴∠MOE∠MON,
又弧MN=弧MN,
∴∠MPN∠MON,
∴∠MPN=∠MOE,
Rt△MOE中,sin∠MOE,
∴sin∠MPN;
②当P在AD上时,作过M、N的⊙O与AD相切于P,此时∠MPN最大,如图:
同①的道理:AP=6,即此时监控装置P在距A6米的墙上,sin∠MPN;
③当P在CD上时,作过M、N的⊙O与CD相切于P,此时∠MPN最大,过O作OE垂直AB于E,直线OE交CD于G,过D作DF⊥BC于F,连接OP、OM、ON,
由①知:ME,BE=AE=5,CF=10,
Rt△CDF中,CD20,
∵AD∥BC,AD⊥AB,OE⊥BC,
∴BC∥GE∥AD,
∴∠OGP=∠C=60°,GE为梯形ABCD的中位线,
∴DGCD=10,GE25,
设PG=x,则DP=10﹣x,
Rt△POG中,OG=2x,OPx,
∴OE=GE﹣OG=25﹣2x,OM=OPx,
Rt△MOE中,ME2+OE2=OM2,
∴()2+(25﹣2x)2=(x)2,
解得:x=50+12(大于CD,舍去)或x=50﹣12,
∴PG=50﹣12,DP=1240,即此时监控装置P在距D(1240)米的墙上,
OM=OP=5012,
∴sin∠MPN=sin∠MOE,
∵,
∴监控装置P在CD上时的∠MPN较小,
∴监控装置P应在AD上,距A6米的地方,此时sin∠MPN,
或监控装置P应在BC上,距B6米的地方,此时sin∠MPN.
【点评】本题考查圆的综合知识,涉及圆周角、圆心角、垂径定理、圆的切线、解直角三角形、勾股定理等知识,综合性很强,解题的关键是掌握圆的基本性质,根据已知画出符合条件的图形,
中考数学一轮复习 圆
一.解答题(共20小题)
1.定义:两个角对应互余,且这两个角的夹边对应相等的两个三角形叫做余等三角形.如图1,在△ABC和△DEF中,若∠A+∠E=∠B+∠D=90°,且AB=DE,则△ABC和△DEF是余等三角形.
(1)图2,等腰直角△ABC,其中∠ACB=90°,AC=BC,点D是AB上任意一点(不与点 A、B重合),则图中△ 和△ 是余等三角形,并求证:AD2+BD2=2CD2.
(2)图3,四边形ABCD是⊙O的内接四边形,⊙O的半径为5,且AD2+BC2=100,
①求证:△ABC和△ADC是余等三角形.
②图4,连接BD交AC于点I,连接OI,E为AI上一点,连接EO并延长交BI于点F,若∠ADB=67.5°,IE=IF,设OI=x,S△EIF=y,求y关于x的函数关系式.
2.问题提出
(1)如图①,已知直线a∥b,点A,B在直线a上,点C,D在直线b上,则S△ACD S△BCD(填“>”“<”或“=”);
问题探究
(2)如图②,⊙O的直径为20,点A,B,C都在⊙O上,AB=12,求△ABC面积的最大值;
问题解决
(3)如图③,在△ABC中,∠ACB=90°,AB=20,BC=10,根据设计要求,点D为∠ABC内部一点,且∠ADB=60°,过点C作CE∥AD交BD于点E,连接AE,CD,试求满足设计要求的四边形ADCE的最大面积.
3.问题探究
(1)如图1,⊙O1与⊙O2的半径分别为1和2,均与直线R1R2相切,切点分别为R1、R2,R1R2=4,S、T分别为两圆上的动点,求线段ST的最小值.
问题解决
(2)春意盎然,万物复苏,到了种植的季节,学校里的校园农场热闹起来,同学们积极参与到校园农场建设中.已知校园农场为矩形区域,如图2所示,记作矩形ABCD,经过测量,AD=40米,米,为方便耕作,需要在农场上设计两条小路.已知点E、F分别是线段AD、BC上的动点,且满足BF=2AE.在线段EF上任取一点G,始终满足∠DGF为直角,把满足条件的所有点G设计成第一条弯弯的小路,这条小路成了校园农场一道亮丽的风景线.为了方便休息,在这条弯弯的小路上建造凉亭N.在农场西南角如图顶点B位置搭建一个弓形阳光房,米,曲线BP是圆心角为120°的圆弧.在弧BP上取一点M作为阳光房的门,在门和凉亭之间建造第二条小路即线段MN.
①试画出第一条弯弯小路的位置(不要求尺规作图),并求这条小路的长度;
②当小路MN最短时,求三角形区域NAD的面积.
(注:小路和门的宽度忽略不计)
4.综合与探究
【课本回顾】如图1,在△ABC中,中线AD,BE,CF于点P,点P叫做△ABC的重心.
【知识探究】
(1)如图2,数学兴趣小组发现,当△ABC的中线AD,BE交于点P时,不管△ABC的边长如何变化,线段AP与PD存在固定的数量关系,并经过讨论得到如下两种解决思路:
思路一 思路二
第一步 如图3,取AD中点M,连接EM,证明△BDP∽△EMP; 如图4,作AN平行BC交BE延长线于点N,先证明△BCE≌△NAE,再证明△BDP∽△NAP;
第二步 利用相似三角形的性质及中位线的性质,得到线段AP与PD之间的数量关系. 利用全等三角形的性质及相似三角形的性质,得到线段AP与PD之间的数量关系.
图形表达
在上述两种思路中,可以选择其中一种,并完成具体解题过程;(若用其他思路解决问题,则写第3种)
【问题解决】
(2)在⊙O中,AB为直径,点C是⊙O上一点(不与点A,B重合).
①如图Ⅱ,若点M是弦BC的中点,AM交OC于点E,则的值为 ;
②如图Ⅲ,在①的条件下,若AM⊥OC,求sinB的值;
③如图IV,若AB=10,BC=8,D为弦BC上一动点,过D作DF⊥OC,交OC于点H,交AB于点F.设BD=x,FO=y,直接写出y与x的函数关系式.
5.问题探究
(1)如图1,在Rt△ABC中,BC=8,AC=6,点D是AB的中点,点P是BC上一动点,根据北师大版七年级下册123页的问题解决可知,DP+AP有最小值,则DP+AP的最小值为 ;
(2)在(1)的条件下,点P是平面内一动点,∠BPC=90°,求AP的最小值.
问题解决
(3)如图3,一家养老院的平面示意图可抽象为直角梯形ABCD,经测量可得∠ABC=90°,,AB=430m,老年公寓位于点F处,且,根据养老院规划,需要在边AB上建立一个半径为20m的餐厅,即半圆⊙O,并在半圆⊙O的三等分点M处设置餐厅入口,在半圆与AB交点N处设置餐厅出口,同时依直角梯形ABCD的AD边建设以点P为入口的老年活动中心△ADP,因活动中心场地规划需求,要使∠APD=90°.线段MF、PN是要修的两条道路,为节约成本,希望MF+PN最小,试求MF+PN最小值及此时AN的长.
6.问题提出
(1)已知A、B、C为平面上三个点,AC=5,BC=7,则AB的最小值为 .
问题探究
(2)如图①,在Rt△ABC中,∠C=90°,∠A=30°,BC=4,点P为边AB上一个动点,点M、N分别为线段AP、AC的中点,求MN的最小值.
问题解决
(3)如图②,某科学小组研制出一种激光设备,设备外围由线段AB、AC及弧BC组成,∠BAC=60°,弧BC所在的圆与AB边相切于B点,一束光线从A点发出,经弧BC反射后沿DE射出,其中AD⊥DE,∠EAD=60°,已知弧BC所在圆的半径为6,弧BC的长度为2π.请问当光线在弧BC上反射时,线段AE是否存在最小值?若存在,求出AE的最小值;若不存在,请说明理由.
7.【初步发现】
如图1,Rt△ABC的内切圆与斜边AB相切于点D,与AC、BC相切于点E、F,AD=4,BD=5,求△ABC的面积.
解:设线段CE的长为x,根据切线长定理,得AE=AD=4,BF=BD=5,CF=CE=x,
在RtAABC中,根据勾股定理,
得(x+4)2+(x+5)2=(4+5)2,
整理,得x2+9x=20,
所以S△ABC(x+4)(x+5)=(x2+9x+20)=20
请同学们想一想,AD×BD=4×a5=20,△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
【深入探索】
已知:如图2,△ABC的内切圆与AB相切于点D,与AC、BC相切于点 E、F,AD=m,BD=n.
(1)若∠C=90°,求证:△ABC的面积等于mn;
(2)若AC.BC=2mn,求证:∠C=90°.
【拓展延伸】
已知:△ABC的内切圆与AB、AC、BC相切于点D、E、F,∠C=60°,AD=4,BD=5.请直接写出△ABC的面积.
8.【问题提出】
唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——将军饮马问题:
(1)如图1,△ABC中,∠C=90°,AC=BC=2,E是AB的中点,P是BC边上的一动点,则PA+PE的最小值为 ;
【问题探究】
(2)如图2,已知△ABC和△DEF都是等腰直角三角形,∠ABC=∠EDF=90°,AB=6,DE=3,EF在直线AC上运动时,求BE+BD的最小值;
【拓展应用】
(3)如图3,是某公园的示意图,AB、AC、BD是三处栅栏,CD是该公园附近的一条道路(宽度不计),半圆AM及其内部是一个带舞台的广场.已知∠BAC=∠ABD=90°,CD所对的圆心角为120°,AC与所在的圆相切于点C,点E、G在AC上,点F、H在BD上,点M在AB上,矩形EFHG是一条河流在该公园内的一段(EF∥AB),其中半圆AM的直径为300m,AB=600m,AC=700,河岸EF离AB的距离为,河宽EG为,为方便运输设备,现计划垂直于河岸造桥QS,使得PQ、QS与ST之和最短,求出此时EQ的长.(结果保留根号)
9.定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= 度;
(2)如图1,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,
①求证:△BDC是“近直角三角形”;
②在边AC上是否存在点E(异于点D),使得△BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
(3)如图2,在Rt△ABC中,∠BAC=90°,点D为AC边上一点,以BD为直径的圆交BC于点E,连接AE交BD于点F,若△BCD为“近直角三角形”,且AB=5,AF=3,求tan∠C的值.
10.综合与实践
【问题情境】在数学综合实践课上,“希望小组”的同学们以三角形为背景,探究图形变化过程中的几何问题,如图,在△ABC中,AB=AC,∠BAC=90°,点D为平面内一点(点A,B,D三点不共线),AE为△ABD的中线.
【初步尝试】(1)如图1,小林同学发现:延长AE至点M,使得ME=AE,连接DM.始终存在以下两个结论,请你在①,②中挑选一个进行证明:
①DM=AC;②∠MDA+∠DAB=180°;
【类比探究】(2)如图2,将AD绕点A顺时针旋转90°得到AF,连接CF.小斌同学沿着小林同学的思考进一步探究后发现:AECF,请你帮他证明;
【拓展延伸】(3)如图3,在(2)的条件下,王老师提出新的探究方向:点D在以点A为圆心,AD为半径的圆上运动(AD>AB),直线AE与直线CF相交于点G,连接BG,在点D的运动过程中BG存在最大值.若AB=4,请直接写出BG的最大值.
11.(1)【学习心得】
小赵同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.我们把这个过程称为“化隐圆为显圆”.
①已知:如图1,OA=OB=OC,若∠AOB=50°,求∠ACB的度数.
解:若以点O为圆心,OA为半径作辅助圆,∠AOB是⊙O的圆心角,而∠ACB是圆周角,从而可容易得到∠ACB= °.
②如图2,点P为正方形ABCD内一点,且∠BPC=90°,若AB=4,求AP的最小值.
解:∵BC=4,∠BPC=90°,∴点P在以BC为直径的圆上,
设圆心为点O,则O、P、A三点共线时AP最小,最小值为 .
(2)【问题解决】
①如图3,在平行四边形ABCD中,已知AB=4,BC=6,∠ABC=60°,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点Q,则线段QC的最小值为 .
②如图4,△ABC中,∠BAC=90°,AB=4,AC=3,D为AC上一动点,以AD为直径的⊙O交BD于E,求线段CE的最小值.
(3)【问题拓展】
如图5,在平面直角坐标系中,已知两点A(2,3),B(6,7),x轴上有一动点P,当∠APB最大时,直接写出点P的坐标 .
12.问题提出:如图①,在Rt△ABC中,∠C=90°,CB=4,CA=6,⊙C的半径为2,P为圆上一动点,连接AP、BP,求的最小值.
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图①,连接CP,在CB上取一点D,使CD=1,则.又∠PCD=∠BCP,所以△PCD∽△BCP.所以.
所以PDPB,所以.
请你完成余下的思考,并直接写出答案:的最小值为 ;
(2)自主探索:在“问题提出”的条件不变的前提下,求的最小值;
(3)拓展延伸:如图②,已知在扇形COD中,∠COD=90°,OC=6,OA=3,OB=5,P是上一点,求2PA+PB的最小值.
13.概念认识:
平面内,M为图形T上任意一点,N为⊙O上任意一点,将M、N两点间距离的最小值称为图形T到⊙O的“最近距离”,记作d(T﹣⊙O).例:如图1,在直线l上有A、C、O三点,以AC为对角线作正方形ABCD,以点O为圆心作圆,与l交于E、F两点,若将正方形ABCD记为图形T,则C、E两点间的距离称为图形T到⊙的“最近距离”.
数学理解:
(1)在平面内有A、B两点,以点A为圆心,5为半径作⊙A,将点B记为图形T,若d(T﹣⊙A)=2,则AB= .
(2)如图2,在平面直角坐标系中,以O(0,0)为圆心,半径为2作圆.
①将点C(4,3)记为图形T,则d(T﹣⊙O)= .
②将一次函数y=kx+2的图记为图形T,若d(T﹣⊙)>0,求k的取值范围.
推广运用:
(3)在平面直角坐标系中,P的坐标为(t,0),⊙P的半径为2,D、E两点的坐标分别为(5,5)、(5,﹣5),将△DOE记为图形T,若d(T﹣⊙P)=1,则t= .
14.问题提出:
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?
初步思考:
(1)给出了一些特殊的四边形:①矩形②菱形③等腰梯形④正方形,能过它们四个顶点作一个圆的是 (填写序号),过某个四边形四个顶点作一个圆的四边形相对的两个内角的关系是 .
进一步研究:
(2)如果过某个四边形的四个顶点不能作一个圆,那么其相对的两个内角之间有上面的关系吗?请结合图1的两幅图说明其中的道理.(提示:考虑∠B+∠D与180°之间的关系)
由上面的探究,请用文字语言直接写出过某个四边形的四个顶点能作一个圆的条件 .
拓展延伸
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图2,AB是⊙O的直径,点C在⊙O上,求作:CN⊥AB.
作法:①连接CA,CB;
②在上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M:
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图2中作图,并说明CN⊥AB的理由,(提示:可以利用(2)中的结论)
15.综合与实践
数学实践课堂上,张老师带领学生们从一道题入手,开始研究,并对此题做适当变式,尝试举一反三,开阔学生思维.
(1)原型题:如图1,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,AP=PC,AP⊥PC,则△ABP≌△ ,请你说明理由.
(2)利用结论,直接应用:
如图2,四边形ABCD、EFGH、NHMC都是正方形,边长分别为a、b、c,A、B、N、E、F五点在同一条直线上,则△CBN≌△ ,c= (用含a、b的式子表示).
如图3,四边形ABCD中,AB∥DC,AB⊥BC,AB=2,CD=4,以BC上一点O为圆心的圆经过A、D两点,且∠AOD=90°,则圆心O到弦AD的距离为 .
(3)弱化条件,变化引申:
如图4,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°,且DM交AC于点F,ME交BC于点G,连接FG,则△AMF与△BGM的关系为: ,若,AF=3,则FG= .
16.问题提出:
(1)如图1,点B、C在⊙O上且BC=2,过点O作OE⊥BC,交BC于点A,交⊙O于点E,连接BE、CE,若∠CBE=30°,则线段AE的长度为 .
问题探究:
(2)如图2,在△ABC中,BC=2,∠BAC=45°,求边AC长度的最大值;
问题解决:
(3)如图3,某城市拟在河流m、n所夹半岛区域建一个湿地公园,公园的周长由亲水廊桥AB、、CD和绿化带BC四部分构成.其中B、C两定点间的距离为2000米.根据规划要求,A、D两点间的距离为600米,A、D两点到直线BC的距离相等,的中点E到BC的距离比点A到BC的距离多100米;若修建时需保证∠B与∠C的和为120度,请判断这个湿地公园的周长是否存在最大值?若存在,请求出最大值.若不存在,请说明理由.(结果保留π)
17.在一次数学探究活动中,李老师设计了一份活动单:
已知线段BC=2,使用作图工具作∠BAC=30°,尝试操作后思考: (1)这样的点A唯一吗? (2)点A的位置有什么特征?你有什么感悟?
“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以BC为弦的圆弧上(点B、C除外),….小华同学画出了符合要求的一条圆弧(如图1).
(1)小华同学提出了下列问题,请你帮助解决.
①该弧所在圆的半径长为 ;
②△ABC面积的最大值为 ;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为A′,请你利用图1证明∠BA′C>30°.
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形ABCD的边长AB=2,BC=3,点P在直线CD的左侧,且tan∠DPC.
①线段PB长的最小值为 ;
②若S△PCDS△PAD,则线段PD长为 .
18.问题提出
(1)如图①,△ABC内接于⊙O,过点C作⊙O的切线l.在l上任取一个不同于点C的点P,连接PB、PA,比较∠ACB与∠APB的大小,并说明理由.
问题探究
(2)如图2,正方形ABCD,边长为2,在CD边上是否存在点P,使∠APB最大?若存在,确定点P的位置,并求此时sin∠APB的值;若不存在,请说明理由.
问题解决
(3)如图③,四边形ABCD为某工作室的平面示意图,线段BC、CD、DA为三面墙,MN为入户门处,其中AD∥BC,AD⊥AB,∠C=60°,BM=AN=4米,BC=30米,AD=20米.出于安全考虑,负责人想在墙上安装监控装置P,用来监控并记录进出的人员,为了让监控效果最佳,要求∠MPN最大,试问在墙上是否存在一点P,使得∠MPN最大?若存在,请求出此时sin∠MPN的值及P点的位置;若不存在,请说明理由.
19.【阅读材料】克罗狄斯 托勒密(约90﹣168年)是希腊著名的数学家、天文学家和地理学家,托勒密定理是欧几里得几何中的重要定理.定理内容如下:任意一个凸四边形,两组对边乘积的和不小于两条对角线的乘积,当且仅当四边形四个顶点共圆时,等号成立.即:四边形ABCD中,有AB CD+BC AD≥AC BD,当A,B,C,D四点共圆时,有AB CD+BC AD=AC BD.
【尝试证明】
(1)如图1,四边形ABCD内接于⊙O,求证:AB CD+BC AD=AC BD.
证明:在AC上取点E,连接DE,使∠CDE=∠BDA.
∵∠DCA=∠DBA,
∴ ,
∴,
∴AB CD=EC BD①,
∵∠CDE=∠BDA,
∴∠CDE+∠BDE=∠BDA+∠BDE,即∠ADE=∠BDC,
又∵∠DAE=∠DBC,
∴△ADE∽△BDC,
∴,
∴ ②,①+②得AB CD+BC AD=(EC+AE) BD,即 .
【直接应用】
(2)如图2,AB为⊙O的直径,AB=5,AD=4,BF=1,求DF的长.
【灵活运用】
(3)如图3,在等腰三角形ABC中,AB=AC=8,BC=12,点D在底边BC上,且∠DAC=∠ACD,将三角形ACD沿着AD所在的直线翻折,使得点C落在点E处,连接EB,求BE的长.
20.【问题提出】
在绿化公园时,需要安装一定数量的自动喷洒装置,定时喷水养护,某公司准备在一块边长为18m的正方形草坪(如图1)中安装自动喷洒装置,为了既节约安装成本,又尽可能提高喷洒覆盖率,需要设计合适的安装方案.
说明:一个自动喷洒装置的喷洒范围是半径为r(m)的圆面.喷洒覆盖率,s为待喷洒区域面积,k为待喷洒区域中的实际喷洒面积.
【数学建模】
这个问题可以转化为用圆面覆盖正方形面积的数学问题.
【探索发现】
(1)如图2,在该草坪中心位置设计安装1个喷洒半径为9m的自动喷洒装置,该方案的喷洒覆盖率ρ= .
(2)如图3,在该草坪内设计安装4个喷洒半径均为的自动喷洒装置;如图4,设计安装9个喷洒半径均为3m的自动喷洒装置;…,以此类推,如图5,设计安装n2个喷洒半径均为的自动喷洒装置.与(1)中的方案相比,采用这种增加装置个数且减小喷洒半径的方案,能否提高喷洒覆盖率?请判断并给出理由.
(3)如图6所示,该公司设计了用4个相同的自动喷洒装置喷洒的方案,且使得该草坪的喷洒覆盖率ρ=1.已知AE=BF=CG=DH,设AE=x(m),⊙O1的面积为y(m2),求y关于x的函数表达式,并求当y取得最小值时r的值.
【问题解决】
(4)该公司现有喷洒半径为的自动喷洒装置若干个,至少安装几个这样的喷洒装置可使该草坪的喷洒覆盖率ρ=1?(直接写出结果即可)
中考数学一轮复习 圆
参考答案与试题解析
一.解答题(共20小题)
1.定义:两个角对应互余,且这两个角的夹边对应相等的两个三角形叫做余等三角形.如图1,在△ABC和△DEF中,若∠A+∠E=∠B+∠D=90°,且AB=DE,则△ABC和△DEF是余等三角形.
(1)图2,等腰直角△ABC,其中∠ACB=90°,AC=BC,点D是AB上任意一点(不与点 A、B重合),则图中△ ACD 和△ BCD 是余等三角形,并求证:AD2+BD2=2CD2.
(2)图3,四边形ABCD是⊙O的内接四边形,⊙O的半径为5,且AD2+BC2=100,
①求证:△ABC和△ADC是余等三角形.
②图4,连接BD交AC于点I,连接OI,E为AI上一点,连接EO并延长交BI于点F,若∠ADB=67.5°,IE=IF,设OI=x,S△EIF=y,求y关于x的函数关系式.
【考点】圆的综合题.
【专题】压轴题;新定义;与圆有关的计算;推理能力;应用意识.
【答案】(1)ACD,BCD,证明见解答过程;
(2)①证明见解答过程;
②y.
【分析】(1)由△ABC是等腰直角三角形,根据余等三角形定义,可得△ACD和△BCD是余等三角形,过D作DE⊥AC于E,过D作DF⊥BC于F,证明△ADE和△BDF是等腰直角三角形,得DE,DF,CE,Rt△DCE中,用勾股定理即可得AD2+BD2=2CD2;
(2)①连接DO并延长交⊙O于E,连接AE、CE,根据AD2+BC2=100,可得AE=BC,从而△AEC≌△CBA,可得∠EAC=∠BCA,∠BCA+∠CAD=90°,同理可得:∠BAC+∠ACD=90°,而AC=AC,根据余等三角形,可知△ABC和△ADC是余等三角形;
②连接OA、OB,过O作OM⊥BD于M,过O作ON⊥AC于N,证明△EFI是等腰直角三角形,△MOF是等腰直角三角形,可得∠AEO=∠BFO=135°,由∠ADB=67.5°,有∠AOB=2∠ADB=135°,∠AOE=45°﹣∠BOF=∠OBF,从而△AOE≌△OBF,得OE=BF,设OE=BF=a,OM=FM=b,则ON=MIa,OF=AEb,在Rt△OIM中,(a)2+b2=x2得a2+2b2=2x2,在Rt△OBM中,(a+b)2+b2=52,得a2+2b2+2ab=25,故2ab=25﹣2x2,而yEI FI(a+b)2(a2+2b2)abx2.
【解答】解:(1)∵△ABC是等腰直角三角形,
∴∠A+∠B=90°,∠ACD+∠BCD=90°,AC=BC,
∴△ACD和△BCD是余等三角形,
过D作DE⊥AC于E,过D作DF⊥BC于F,如图:
∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∴△ADE和△BDF是等腰直角三角形,
∴DE,DF,
∵DE⊥AC,DF⊥BC,∠ACB=90°,
∴四边形CEDF是矩形,
∴CE=DF,
Rt△DCE中,DE2+CE2=CD2,
∴()2+()2=CD2,
∴AD2+BD2=2CD2;
故答案为:ACD,BCD;
(2)①连接DO并延长交⊙O于E,连接AE、CE,如图:
∵DE是⊙O直径,
∴∠EAD=90°,
在Rt△EAD中,AD2+AE2=DE2=100,
∵AD2+BC2=100,
∴AE=BC,
∴∠ACE=∠BAC,
∵∠AEC=∠CBA,AC=AC,
∴△AEC≌△CBA(AAS),
∴∠EAC=∠BCA,
∵∠EAC+∠CAD=90°,
∴∠BCA+∠CAD=90°,
同理可得:∠BAC+∠ACD=90°,
而AC=AC,
∴△ABC和△ADC是余等三角形;
②连接OA、OB,过O作OM⊥BD于M,过O作ON⊥AC于N,如图:
由①知:∠BAC+∠ACD=90°,
又∠ACD=∠ABD,
∴∠BAC+∠ABD=90°,
∴AC⊥BD,
∵IE=IF,
∴△EFI是等腰直角三角形,
∵OM⊥BD,
∴△MOF是等腰直角三角形,
∴OM=FM,
∵△EFI是等腰直角三角形,
∴∠AEO=∠BFO=135°,
∵∠ADB=67.5°,
∴∠AOB=2∠ADB=135°,
∴∠AOE=45°﹣∠BOF=∠OBF,
且OA=OB,
∴△AOE≌△OBF(AAS),
∴OE=BF,
设OE=BF=a,OM=FM=b,则ON=MIa,OF=AEb,
在Rt△OIM中,(a)2+b2=x2,化简得a2+2b2=2x2,
在Rt△OBM中,(a+b)2+b2=52,化简得a2+2b2+2ab=25,
∴2ab=25﹣2x2,
∴yEI FI(a+b)2(a2+2b2)abx2.
【点评】本题考查圆的性质及综合应用,涉及新定义、等腰直角三角形性质及判定、全等三角形性质及判定、勾股定理应用等知识,题目综合性强,解题的关键是作辅助线,构造直角三角形、全等三角形解决问题.
2.问题提出
(1)如图①,已知直线a∥b,点A,B在直线a上,点C,D在直线b上,则S△ACD = S△BCD(填“>”“<”或“=”);
问题探究
(2)如图②,⊙O的直径为20,点A,B,C都在⊙O上,AB=12,求△ABC面积的最大值;
问题解决
(3)如图③,在△ABC中,∠ACB=90°,AB=20,BC=10,根据设计要求,点D为∠ABC内部一点,且∠ADB=60°,过点C作CE∥AD交BD于点E,连接AE,CD,试求满足设计要求的四边形ADCE的最大面积.
【考点】圆的综合题.
【专题】几何综合题;压轴题;几何直观;运算能力;推理能力.
【答案】(1)=;
(2)△ABC面积的最大值为108;
(3)四边形ADCE的最大面积是75.
【分析】(1)由平行线的性质,根据同底等高的两三角形面积相等作答;
(2)AB长不变,只要AB边上的高最大,△ABC面积最大;由图知当C是优弧的中点时,AB边上的高最大,△ABC面积最大,求得优弧的中点到AB的距离就可求得△ABC最大面积;
(3)过C作CF∥BD交AD的延长线于F,得∠F=∠ADB=60°,先证得四边形ADCE的面积=△ACF的面积;根据∠F=60°得点F在以AC为边向△ABC外作的等边△AGC的外接圆上,受解决(2)的启发得,当F运动到点G时,△ACF的面积最大,即四边形ADCE的面积最大.最后计算出△ACF的面积即是四边形ADCE的面积最大值.
【解答】解:(1)如图①所示,分别过A、B两点向直线b作垂线,垂足为M、N.
∵a∥b,
∴∠MAB=∠AMN=90°,
∴四边形AMNB是矩形,
∴AM=BN,
∴CD AM=CD BN
又S△ACDCD AM,S△BCDCD BN,
∴S△ACD=S△BCD;
故答案为:=;
(2)取优弧的中点记为C1,过C1作AB的垂线,垂足为D,由垂径定理知C1D过O且AD=BD,如图②所示.
过点C作AB的平行线a,
∵当直线a向上平移时,a距AB的距离增大,即△ABC的AB边上的高增大,
∴当a运动到最高点C时,△ABC的AB边上的高最大,
又∵AB为常数,
∴当C运动到C1时,△ABC的面积最大,
下面计算△ABC1的面积:
连接OB,
在Rt△OBD中,
∵AB=12,⊙O的直径为20,
∴BD=6,BO=10,OC1=10,
由勾股定理得:
OD8,
∴C1D=OD+OC1=8+10=18,
∴△ABC1的面积为:AB C1D12×18=108,
∴△ABC面积的最大值为108;
(3)过点C作CF∥BD交AD的延长线于F,如图③﹣1所示,
∵CF∥BD,
∴∠F=∠ADB=60°,
∵AD∥CE,
∴四边形DECF是平行四边形,
∴DF=CE,FC=DE,
∵DC=CD
∴△DFC≌△CED(SSS),
∴S△DFC=S△CED,
又由(1)的结论知S△DAC=S△DAE,
∴S四边形ADCE=S△DAE+S△CED=S△DAC+S△DFC=S△AFC,
所以只需求得S△AFC最大值即得S四边形ADCE的最大值.
以AC为边向△ABC外作等边△AGC,再作等边△AGC的外接圆,过G作GJ⊥AC于J,如图③﹣2所示,
∵∠F=60°,
∴点F在△AGC的外接圆上,
由第(2)问的解决知,当F运动到点G时,S△AFC最大=S△ACG;
在Rt△ABC中:
由勾股定理得AC10,
∴AJAC=5,
∴GJ1015,
∴S△ACGAC×GJ1015=75;
∴四边形ADCE的最大面积是75.
【点评】此题考查了三角形等积变形、定角对定边的三角形的面积最大值、等边三角形及其外接圆、平行四边形的判定和性质等考点,熟练掌握相关知识并能综合应用是解题关键.
3.问题探究
(1)如图1,⊙O1与⊙O2的半径分别为1和2,均与直线R1R2相切,切点分别为R1、R2,R1R2=4,S、T分别为两圆上的动点,求线段ST的最小值.
问题解决
(2)春意盎然,万物复苏,到了种植的季节,学校里的校园农场热闹起来,同学们积极参与到校园农场建设中.已知校园农场为矩形区域,如图2所示,记作矩形ABCD,经过测量,AD=40米,米,为方便耕作,需要在农场上设计两条小路.已知点E、F分别是线段AD、BC上的动点,且满足BF=2AE.在线段EF上任取一点G,始终满足∠DGF为直角,把满足条件的所有点G设计成第一条弯弯的小路,这条小路成了校园农场一道亮丽的风景线.为了方便休息,在这条弯弯的小路上建造凉亭N.在农场西南角如图顶点B位置搭建一个弓形阳光房,米,曲线BP是圆心角为120°的圆弧.在弧BP上取一点M作为阳光房的门,在门和凉亭之间建造第二条小路即线段MN.
①试画出第一条弯弯小路的位置(不要求尺规作图),并求这条小路的长度;
②当小路MN最短时,求三角形区域NAD的面积.
(注:小路和门的宽度忽略不计)
【考点】圆的综合题.
【专题】压轴题;与圆有关的位置关系;推理能力.
【答案】(1)3;
(2)①π米;
②(100200)平方米.
【分析】(1)连接O1R1,O2R2,O1O2,过点O1作O1H⊥O2R2,设O1O2交⊙O1与⊙O2分别为S,T,则此时线段ST的长度最小,利用勾股定理可得O1O2,即可得出答案;
(2)①如图2,延长BA至点S,使AS=AB,连接SC交AD于点T,过点D作DG′⊥CT,连接SD,作出SD中点O,连接OA、OG′,以点O为圆心,OA为半径,作出,则为第一条弯弯小路的位置,再证得△SAE∽△SBF,利用相似三角形性质可得SB=2AB=40米,运用三角函数定义可求得∠BSC=30°,进而可得∠AOG′=60°,再运用弧长公式即可求得答案.
②以BP为底作等腰三角形BPQ,且使∠BQP=120°,则、是以点Q为圆心,PQ为半径的圆的一部分,连接OQ交AD于点R,分别交、于点M、N,此时MN最短,连接AN、DN,过点N作NJ⊥AD,连接OT,过点Q作QZOT交AB于点Y,垂足为点Z,运用解直角三角形即可求得答案.
【解答】∵′解:(1)如图1,连接O1R1,O2R2,O1O2,过点O1作O1H⊥O2R2,设O1O2交⊙O1与⊙O2分别为S,T,则此时线段ST的长度最小,
∵⊙O1与⊙O2的半径分别为1和2,均与直线R1R2相切,切点分别为R1、R2,R1R2=4,
∴O1R1⊥R1R2,O2R2⊥R1R2,
∴四边形O1R1R2H是矩形,
∴O1H=R1R2=4,R2H=O1R1=1,
∴O2H=O2R2=2﹣1=1,
∴O1O2,
∴线段ST的最小值1﹣23=14.
(2)①如图2,延长BA至点S,使AS=AB,连接SC交AD于点T,过点D作DG′⊥CT,连接SD,作出SD中点O,连接OA、OG′,以点O为圆心,OA为半径,作出,则为第一条弯弯小路的位置,
∵四边形ABCD是矩形,
∴AD=BC=40米,AB=CD=20米,AD∥BC,
∴△SAE∽△SBF,
∴,
∴SB=2AB=40米,
∴tan∠BSC,
∴∠BSC=30°,
∴∠AOG′=60°,
∵SD20米,
∴OASD=10米,
∴的长为:π米,
∴这条小路的长度为π米.
②如图3,以BP为底作等腰三角形BPQ,且使∠BQP=120°,则是以点Q为圆心,PQ为半径的圆的一部分,连接OQ交AD于点R,分别交、于点M、N,此时MN最短,连接AN、DN,过点N作NJ⊥AD,连接OT,过点Q作QZOT交AB于点Y,垂足为点Z,
∵OS=OD,TA=TD,
∴OT∥AS,OTAS=10米,
由题意得:在Rt△QBY中,∠QBY=30°,BYBP=5米,
∴QY=BY tan30°=55米,AY=TZ=15米,
∵YZ=AT=20米,
∴QZ=25米,OZ=25米,
∴tan∠QOZ,
∴∠QOZ=30°,
∴OR20米,
∴NR=ON﹣OR=1020(米),
∵∠OTA=∠NJR=90°,
∴NJ∥OT,
∴∠JNR=∠TOR=30°,
∴NJ=NR cos30°=(1020)510(米),
∴S△NADNJ AD(510)×40=100200(平方米).
【点评】此题属于圆的综合题,考查了三角形的面积,三角函数,最短路线,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.
4.综合与探究
【课本回顾】如图1,在△ABC中,中线AD,BE,CF于点P,点P叫做△ABC的重心.
【知识探究】
(1)如图2,数学兴趣小组发现,当△ABC的中线AD,BE交于点P时,不管△ABC的边长如何变化,线段AP与PD存在固定的数量关系,并经过讨论得到如下两种解决思路:
思路一 思路二
第一步 如图3,取AD中点M,连接EM,证明△BDP∽△EMP; 如图4,作AN平行BC交BE延长线于点N,先证明△BCE≌△NAE,再证明△BDP∽△NAP;
第二步 利用相似三角形的性质及中位线的性质,得到线段AP与PD之间的数量关系. 利用全等三角形的性质及相似三角形的性质,得到线段AP与PD之间的数量关系.
图形表达
在上述两种思路中,可以选择其中一种,并完成具体解题过程;(若用其他思路解决问题,则写第3种)
【问题解决】
(2)在⊙O中,AB为直径,点C是⊙O上一点(不与点A,B重合).
①如图Ⅱ,若点M是弦BC的中点,AM交OC于点E,则的值为 ;
②如图Ⅲ,在①的条件下,若AM⊥OC,求sinB的值;
③如图IV,若AB=10,BC=8,D为弦BC上一动点,过D作DF⊥OC,交OC于点H,交AB于点F.设BD=x,FO=y,直接写出y与x的函数关系式.
【考点】圆的综合题.
【专题】压轴题;推理能力.
【答案】(1)证明过程见解析;(2)①;②;③.
【分析】(1)根据提供的思路证明即可;
(2)①证明E为△ABC的重心即可得解;②由前述结论可得OC=3OE,根据这一关系设参数,利用勾股定理将AE、AC和OM表示出来即可得解;③作FQ⊥BC,将FQ和BQ用含y的式子表示出来,再用建立关于x和y的等式即可.
【解答】解:(1)线段AP与PD存在固定的数量关系为AP=2DP,理由:
思路一:取AD中点M,连接EM,如图,
∵AM=MD,AE=EC,
∴ME为△ADC的中位线,
∴ME∥CD,MECD.
∵BD=CD,
∴MECD.
∵ME∥BD,
∴△BDP∽△EMP,
∴,
∴PD=2MP,
∴MD=3MP,
∴AM=MD=3MP,
∴AP=4MP,
∴AP=2PD.
思路二:作AN∥BC交BE延长线于点N,如图,
∵AN∥BC,
∴∠EBC=∠N.
在△BCE和△NAE中,
,
△BCE≌△NAE(AAS),
∴BC=AN,
∵BD=CD,
∴AN=2BD.
∵∠EBC=∠N,∠BPD=∠NPA,
∴△BDP∽△NAP,
∴,
∴AP=2PD;
(2)①连接AC,如图,
∵BM=MC,OA=OB,
∴E为△ABC的重心,
∴CE=2OE,
∴OEOC,
∴.
故答案为:;
②连接OM、AC,
由(1)知:OC=3OE,
设OE=k,则OC=3k,
∴OA=OB=OC=3k,EC=2OE=2k,
∵AM⊥OC,
∴.
∴,
由(1)知:.
∴.
③如图,连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴,
如图所示,过点F作FQ⊥BC于点Q,交OC于T,
∵OB=OC,
∴∠OBC=∠OCB,
∵DF⊥OC,
∴∠FHT=∠FQC=90°,
∵∠FTH=∠CTQ,
∴∠DFQ=∠OCB=∠OBC,
在Rt△FBQ中,BF=5+y,
在Rt△ABC中,,,,
∴,
∵tan∠DFQ=tanB,
∴,
即,整理得.
∴y与x的函数关系式为.
【点评】本题主要考查了解直角三角形,直径所对的圆周角是直角,勾股定理,相似三角形的性质与判定,三角形中位线定理等等,正确作出辅助线构造相似三角形和直角三角形是解题的关键.
5.问题探究
(1)如图1,在Rt△ABC中,BC=8,AC=6,点D是AB的中点,点P是BC上一动点,根据北师大版七年级下册123页的问题解决可知,DP+AP有最小值,则DP+AP的最小值为 ;
(2)在(1)的条件下,点P是平面内一动点,∠BPC=90°,求AP的最小值.
问题解决
(3)如图3,一家养老院的平面示意图可抽象为直角梯形ABCD,经测量可得∠ABC=90°,,AB=430m,老年公寓位于点F处,且,根据养老院规划,需要在边AB上建立一个半径为20m的餐厅,即半圆⊙O,并在半圆⊙O的三等分点M处设置餐厅入口,在半圆与AB交点N处设置餐厅出口,同时依直角梯形ABCD的AD边建设以点P为入口的老年活动中心△ADP,因活动中心场地规划需求,要使∠APD=90°.线段MF、PN是要修的两条道路,为节约成本,希望MF+PN最小,试求MF+PN最小值及此时AN的长.
【考点】圆的综合题.
【专题】压轴题;模型思想.
【答案】(1).
(2)4.
(3)()m;200m.
【分析】(1)通过以BC为对称轴作点D的对称点D′,问题转化为求AP+PD′的最小值AD′,过点D'作BC的平行线交AC的延长线于点E,在Rt△AED′中应用勾股定理即可求出答案.
(2)由∠BPC=90°得出点P的轨迹是以BC为直径的⊙O.当点P在线段AO上时,AP的长度即为最小值.
(3)根据题意,M、N两点的相对位置是固定的,故平移线段MF至NG,使M、N两点重合,这样问题就会转化为求GN+NP的最小值.根据(1)、(2)的方法可知,点P在以AD为直径的半圆上,以AB为对称轴作点G的对称点G′,当G′,N,E三点共线时,G′N+NP最小,进而问题得到解决.
【解答】解:(1)如图,以BC为对称轴,作点D的对称点D′,DD′交BC于点F.过点D'作BC的平行线交AC的延长线于点E,连接PD′、AD′.
∵点D和D′关于BC对称,
∴DP=PD′,
∴DP+AP=PD′+AP,
当A,P,D′三点共线时,PD'+AP的最小值为AD′,
∴DP+AP的最小值为AD′.
∵DF⊥BC,AC⊥BC,
∴DD′∥AE,
∴DF为Rt△ABC的中位线,
∴DF=FD′AC6=3,CFBC8=4.
又∵ED′∥BC,
∴四边形CED′F为矩形,ED′=CF=4,CE=FD′=3.
∴AE=AC+CE=6+3=9.
∴AD′.
故DP+AP的最小值为.
(2)如图,根据直径所对应的圆周角为直角,则动点P的轨迹为以BC为直径的⊙O.
∵AP+PO≥AO,
∴当点P在线段AO上时,AP+PO的最小值为AO.
∵PO为定值,PO=COBC8=4,
在Rt△ACO中,AO,
∴AP的最小值为:AO﹣PO4.
(3)对于半圆形餐厅,局部放大图如图,连接MN,OM,作MQ⊥ON,Q为垂足.
如图,平移线段MF至NG,点M与点N重合,以AB为对称轴作点G的对称点G′.G′G交AB于点I.
根据线段平移的性质,四边形MNGF为平行四边形,MF=G′N=NG.NM=GF.
由于点M,N的相对位置固定不变,动点P的轨迹是以AD为直径的半圆,半径AEm上.根据(1),(2)的方法,对于定点G′、E和动点P,当P,G′,E三点共线时,G′P长度最小,即MF+PN为最小值.
在如图中,半圆形餐厅的半径OM=20m,∠QOM180°=60°.
∴∠ONM=∠OMN60°=30°,
∴QM=OM sin60°=20×sin60°m,QN=QM÷tan30°tan30°=30m.
根据平移的性质,点F移至点G,相当于先向左平移了QM长度,再向上平移了QN长度.
∴IG=IG′=BF﹣QM(m),
根据轴对称的性质,G′G⊥AB,
∴IB=QN=30m.
过点G′作AB的平行线交DA的延长线于H,易得四边形AIG′H为矩形,
∴AH=IG′m,G′H=AI=AB﹣IB=430﹣30=400(m),
∴HE=AH+AE(m).
在Rt△EHG′中,G′Em,
∴G′P最小值为:G′E﹣AE=()m.
即MF+NP的最小值为()m.
∵AH=AEm,G′H∥AN′,
∴AN′为△EHG′的中位线,AN′G′H=200m.
当MF+NP取最小值时,动点N位置为AB和G′E的交点N′.
故MF+NP的最小值为()m,此时AN的长度为200m.
【点评】本题为难度较大的圆综合题,考查了“将军饮马模型“和“定点到圆上动点的距离极值问题”,平移MF使点M与点N重合,是本题的关键.
6.问题提出
(1)已知A、B、C为平面上三个点,AC=5,BC=7,则AB的最小值为 2 .
问题探究
(2)如图①,在Rt△ABC中,∠C=90°,∠A=30°,BC=4,点P为边AB上一个动点,点M、N分别为线段AP、AC的中点,求MN的最小值.
问题解决
(3)如图②,某科学小组研制出一种激光设备,设备外围由线段AB、AC及弧BC组成,∠BAC=60°,弧BC所在的圆与AB边相切于B点,一束光线从A点发出,经弧BC反射后沿DE射出,其中AD⊥DE,∠EAD=60°,已知弧BC所在圆的半径为6,弧BC的长度为2π.请问当光线在弧BC上反射时,线段AE是否存在最小值?若存在,求出AE的最小值;若不存在,请说明理由.
【考点】圆的综合题.
【专题】压轴题;几何直观.
【答案】(1)2;(2),(3).
【分析】(1)当A、B、C三点共线时,且A在线段BC上时,AB最小;
(2)有题干条件得出MN是中位线,要求MN最小,实际上可求CP最小,点到直线的距离垂线段最短,所以当CP⊥AB时,PC长的值最小,再用等面积求解即可.
(3)要求AE最小,在直角三角形AED中进行转化,可求AD最小,要求AD最小则是点到塬上的最短距离,用三边关系即可确定三点共线时最小,再求解即可.
【解答】解:(1)当A、B、C三点共线时,且A在线段BC上时,AB最小,
此时AB=BC﹣AC=2,
故答案为2;
(2)连接PC.
∵M,N分别为线段AP,AC的中点,
∴,
∴当PC长的值最小时,MN长的值也最小.
∵P为边AB上的一个动点,
∴当CP⊥AB时,PC长的值最小.
当CP⊥AB时,.
∵在△ABC中,∠ACB=90°,∠A=30°,BC=4,
∴,AB=2BC=8.
∴,
解得.
∴MN长的最小值为.
(3)存在.
如图,设所在圆的圆心为点O,连接AO,BO,CO,DO,BC.
∵的长度是2π,且⊙O的半径是6,
∴,
解得n=60,即∠BOC=60°,
∵BO=CO,
∴△BOC是等边三角形,
∴∠CBO=60°,BC=BO=6.
∵AB是⊙O的切线,∠ABO=90°,∠ABC=30°,
∵∠BAC=60°,∠ACB=90°.
在Rt△ABC中,,
即,
解得.
在Rt△ABO中,.
∵AD+DO≥AO,即AD≥AO﹣DO,
∴AD长的最小值为.
在Rt△AED中,,
∴当AD长的值最小时,AE长的值也最小.
由,
解得.
∴AE长的最小值为.
【点评】本题主要考查了线段和差、中位线定理、解直角三角形、三角形三边关系、点圆最值等内容,熟练掌握相关知识点是解题的关键.
7.【初步发现】
如图1,Rt△ABC的内切圆与斜边AB相切于点D,与AC、BC相切于点E、F,AD=4,BD=5,求△ABC的面积.
解:设线段CE的长为x,根据切线长定理,得AE=AD=4,BF=BD=5,CF=CE=x,
在RtAABC中,根据勾股定理,
得(x+4)2+(x+5)2=(4+5)2,
整理,得x2+9x=20,
所以S△ABC(x+4)(x+5)=(x2+9x+20)=20
请同学们想一想,AD×BD=4×a5=20,△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
【深入探索】
已知:如图2,△ABC的内切圆与AB相切于点D,与AC、BC相切于点 E、F,AD=m,BD=n.
(1)若∠C=90°,求证:△ABC的面积等于mn;
(2)若AC.BC=2mn,求证:∠C=90°.
【拓展延伸】
已知:△ABC的内切圆与AB、AC、BC相切于点D、E、F,∠C=60°,AD=4,BD=5.请直接写出△ABC的面积.
【考点】圆的综合题.
【专题】压轴题;几何直观.
【答案】(1)(2)证明过程详见解析;(3)20.
【分析】(1)根据切线长定理得到AE=AD=m,BF=BD=n,CF=CE=x,再利用勾股定理建立等式即可;
(2)将AC和BC、AB表示出来,再利用勾股逆定理定理证明即可;
(3)过点C作CG⊥AB于点G,根据切线长定理CF=CE=x,表示出AG、CG、BG,再利用勾股定理建立方程,最后利用面积公式求解即可.
【解答】(1)证明:设线段CE的长为x,
根据切线长定理,得AE=AD=m,BF=BD=n,CF=CE=x,
∵∠C=90°,在Rt△ABC中,根据勾股定理,得(x+m)2+(x+n)2=(m+n)2
整理得x2+(m+n)x=mn,
∴S△ABC(x+m)(x+n)[x2+(m+n)x+mn],
∴,
∴△ABC的面积为mn;
(2)证明:由(1)可知:AE=AD=m,BF=BD=n,CF=CE=x,
∴AC=m+x,BC=n+x,
∴AC2+BC2=(m+x)2+(n+x)2=m2+2mx+x2+n2+2nx+x2=2x2+2x(m+n)+m2+n2,
∵AC BC=2mn,
∴(m+x)(n+x)=2mn,
∴x2+(m+n)x+mn=2mn,即x2+(m+n)x=mn,
∴2x2+2(m+n)x=2mn,
∴AC2+BC2=2mn+m2+n2=(m+n)2,
又∵AB2=(m+n)2,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,且∠C=90°;
(3)解:如图,过点C作CG⊥AB于点G,
设CF=CE=x,在Rt△ACG中,AC=x+4,∠C=60°,
∴4),CG(x+4),
∴BG=BC﹣CG=(x+5)(x+4),
在Rt△ABG中,根据勾股定理可得AG2+BG2=AB2,
即[(x+4)]2+[(x+5)(x+4)]2=(4+5)2,
整理得x2+9x﹣60=0,
∴x2+9x=60,
∴S△ABCBC AG(x+5) (x+4)(x2+9x+20)=20.
【点评】本题主要考查了三角形内切圆的性质、三角形的面积公式、勾股定理及逆定理、直角三角形的性质等内容,熟练掌握相关知识是解题的关键.
8.【问题提出】
唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——将军饮马问题:
(1)如图1,△ABC中,∠C=90°,AC=BC=2,E是AB的中点,P是BC边上的一动点,则PA+PE的最小值为 ;
【问题探究】
(2)如图2,已知△ABC和△DEF都是等腰直角三角形,∠ABC=∠EDF=90°,AB=6,DE=3,EF在直线AC上运动时,求BE+BD的最小值;
【拓展应用】
(3)如图3,是某公园的示意图,AB、AC、BD是三处栅栏,CD是该公园附近的一条道路(宽度不计),半圆AM及其内部是一个带舞台的广场.已知∠BAC=∠ABD=90°,CD所对的圆心角为120°,AC与所在的圆相切于点C,点E、G在AC上,点F、H在BD上,点M在AB上,矩形EFHG是一条河流在该公园内的一段(EF∥AB),其中半圆AM的直径为300m,AB=600m,AC=700,河岸EF离AB的距离为,河宽EG为,为方便运输设备,现计划垂直于河岸造桥QS,使得PQ、QS与ST之和最短,求出此时EQ的长.(结果保留根号)
【考点】圆的综合题.
【专题】几何综合题;压轴题;几何直观;推理能力.
【答案】(1);
(2);
(3)250m.
【分析】(1)如图所示,过点 E 作ED⊥AC于 D ,作点 A 关于BC的对称点A′,连接A′P,A′E,则PA′=PA,A′C=AC=2,故当P、A′、E三点共线时,PA′+PE最小,此时PA+PE最小,最小值为A′E的长,证明AED∽△ABC,求出DEBC=1,ADAC=1,则CD=1,A′D=3,由勾股定理可得A′E,即PA+PE的最小值为,
(2)如图所示,连接BE,BD,过点 D 作DG⊥EF于 G,DB′∥BC交直线AB于B′,先得到BAC=∠DEF=45°,DG=DE sin∠DEG,可证明四边形BEDB′是平行四边形,得到B′D=BE,BB′=DE=3,则AB′=3;再证明点 D 在与AC平行,且与AC之间的距离为的直线上.过点 D 作MN∥AC分别交直线AB、BC于 M 、 N ,则点 D 在直线MN上运动,证明四边形AEDM是平行四边形,得到AM=DE=3,B′M=6,BM=9,如图所示,作点 B 关于直线MN的对称点B″,连接B″D,B″B′,则B″M=BM=9,B″D=BD,可得当B′、D、B″三点共线时,B′D+B″D最小,即此时BE+BD最小,最小值为B″B′,即可得到BE+BD的最小值为;
(3)如图所示,过点 M 作MR⊥EF于 R ,则四边形AMRE是矩形,可得ER=AM=300m,MR=AEm,将点 P 沿着垂直于EF的方向平移到P′,使得PP′=QSm,则四边形P′PQS是平行四边形,可得PQ=P′S;如图所示,以ER为直径画圆,圆心设为 O ,连接ON,OP′,可得四边形ONMR是平行四边形,根据ON=MR=QS=PP′,ON∥MR,可证明四边形ONPP′是平行四边形,
因此OP′=NP=150m;过点 C 作CI⊥BD交BD延长线于 I ,在CI上取一点O′使得∠CO′D=120°,则O′即为所在圆圆心,
证明四边形ABIC是矩形,得到CI=AB=600m,解直角三角形得到r=400;如图所示,连接OO′,可得当P′S+ST最小时,PQ+QS+ST最小,进而推出当O、P′、S、T、O′五点共线时P′S+ST有最小值,最小值为OO′﹣OP′﹣O′T;过点 O 作OK⊥CT于 K ,则四边形OECK是矩形,则OK=CE=AC﹣AE=500m,CK=OE=150m,O′K=250m,得到OO′m,则PQ+QS+ST的最小值为()米.设此时OO′与GH交于 V ,OK与GH交于 W ,证明△OWV∽△OKO′,根据,可得WV=100,则GV=250m,即EQ=GV=250m.
【解答】解:(1)如图所示,过点 E 作ED⊥AC于 D ,作点 A 关于BC的对称点A′,连接A′P,A′E,
∴PA′=PA,A′C=AC=2,
∴PA+PE=PA′+PE,
∴当P、A′、E三点共线时,PA′+PE最小,即此时PA+PE最小,最小值为A′E的长,
∵∠C=90°,ED⊥AC,
∴DE∥BC,
∴△AED∽△ABC,
∴,
∵ E 是AB的中点,
∴,
∴DEBC=1,ADAC=1,
∴CD=1,
∴A′D=3,
∴A′E,
∴PA+PE的最小值为,
故答案为:;
(2)如图所示,连接BE,BD,过点 D 作DG⊥EF于 G,DB′∥BC交直线AB于B′,
∵△ABC和△DEF都是等腰直角三角形,∠ABC=∠EDF=9°,AB=6,DE=3,
∴∠BAC=∠DEF=45°,DG=DE sin∠DEG,
∴DE∥AB,
∴四边形BEDB′是平行四边形,
∴B′D=BE,BB′=DE=3,
∴AB′=3;
∵DG,即点 D 到直线AC的距离为定值,
∴点 D 在与AC平行,且与AC之间的距离为的直线上,
过点 D 作MN∥AC分别交直线AB、BC于 M 、 N ,则点 D 在直线MN上运动,
∴∠BMN=BAC=45°,
∵DE∥AM,AE∥DM,
∴四边形AEDM是平行四边形,
∴AM=DE=3,
∴B′M=6,BM=9,
如图所示,作点 B 关于直线MN的对称点B″,连接B″D,B″B′,
∴B″M=BM=9,B″D=BD,∠DMB″=∠DMB=45°,
∴∠B′MB″=90°,
∵BE+BD=B′D+B″D,
∴当B′、D、B″三点共线时,B′D+B″D最小,即此时BE+BD最小,最小值为B″B′,
∴BE+BD的最小值为;
(3)如图所示,过点 M 作MR⊥EF于 R ,则四边形AMRE是矩形,
∴ER=AM=300m,MR=AEm,
将点 P 沿着垂直于EF的方向平移到P′,使得PP′=QSm,
∴四边形P′PQS是平行四边形,
∴PQ=P′S;
如图所示,以ER为直径画圆,圆心设为 O ,连接ON,OP′,
∴OR=MN,
又∵OR∥MN,
∴四边形ONMR是平行四边形,
∴ON=MR=QS=PP′,ON∥MR,
∴ON∥QS∥MR∥PP′,
∴四边形ONPP′是平行四边形,
∴OP′=NP=150m;
过点 C 作CI⊥BD交BD延长线于 I ,在CI上取一点O′使得∠CO′D=120°,
∵AC与所在的圆相切于点 C ,
∴的圆心在射线CI上,
又∵所对的圆心角为120°,
∴O′即为所在圆圆心,
∵∠ABI=∠BAC=90°,CI⊥BI,
∴四边形ABIC是矩形,
∴CI=AB=600m,
设O′D=O′C=rm,则O′I=(600﹣r)m,
∵∠IO′D=180°﹣120°=60°,
∴O′I=O′D cos60°rm,
∴r=600﹣r,
∴r=400;
如图所示,连接OO′,
∵PQ+QS+ST=P′S+ST,
∴当P′S+ST最小时,PQ+QS+ST最小,
∵P′S+ST≥P′T≥P′O′﹣O′T,P′O′≥OO′﹣OP′,
∴P′S+ST≥OO′﹣OP′﹣O′T,
∴当O、P′、S、T、O′五点共线时P′S+ST有最小值,最小值为OO′﹣OP′﹣O′T;
过点 O 作OK⊥CT于 K ,则四边形OECK是矩形,
∴OK=CE=AC﹣AE=500m,CK=OE=150m,
∴O′K=250m,
∴OO′m,
∴PQ+QS+ST的最小值为()米.
设此时OO′与GH交于 V ,OK与GH交于 W ,
∵WV∥O′K,
∴△OWV∽△OKO′,
∴,即,
∴WV=100,
∴GV=250m,
∴EQ=GV=250m.
【点评】本题主要考查了矩形的性质与判定,一点到圆上一点距离的最值问题,平行四边形的性质与判定,勾股定理,解直角三角形,轴对称的性质,相似三角形的性质与判定等等,解题的关键在于构造将军饮马模型,确定取得最值的情形.
9.定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= 20 度;
(2)如图1,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若BD是∠ABC的平分线,
①求证:△BDC是“近直角三角形”;
②在边AC上是否存在点E(异于点D),使得△BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.
(3)如图2,在Rt△ABC中,∠BAC=90°,点D为AC边上一点,以BD为直径的圆交BC于点E,连接AE交BD于点F,若△BCD为“近直角三角形”,且AB=5,AF=3,求tan∠C的值.
【考点】圆的综合题.
【专题】压轴题;创新意识.
【答案】见试题解答内容
【分析】(1)∠B不可能是α或β,当∠A=α时,∠C=β=50°,α+2β=90°,不成立;故∠A=β,∠C=α,α+2β=90°,则β=20°,答案为20;
(2)①如图1,设∠=ABD∠DBC=β,∠C=α,则α+2β=90°,故△BDC是“近直角三角形”;
②∠ABE=∠C,则△ABC∽△AEB,即,即,解得:AE,即可求解
(3)①如图2所示,当∠ABD=∠DBC=β时,设BH=x,则HE=5﹣x,则AH2=AE2﹣HE2=AB2﹣HB2,即52﹣x2=62﹣(5﹣x)2,解得:x,即可求解;
②如图3所示,当∠ABD=∠C=β时,AF:EF=AG:DE=3:2,则DE=2k,则AG=3k=R(圆的半径)=BG,点H是BE的中点,则GHDE=k,在△BGH中,BH2k,由三角函数可求解.
【解答】解:(1)∠B不可能是α或β,
当∠A=α时,∠C=β=50°,α+2β=90°,不成立;
故∠A=β,∠C=α,α+2β=90°,则β=20°,
故答案为20;
(2)①如图1,设∠ABD=∠DBC=β,∠C=α,
则α+2β=90°,故△BDC是“近直角三角形”;
②存在,理由:
在边AC上是否存在点E(异于点D),使得△BCE是“近直角三角形”,
AB=3,AC=4,则BC=5,
则∠ABE=∠C,则△ABC∽△AEB,
即,即,解得:AE,
则CE=4;
(3)①如图2所示,当∠ABD=∠DBC=β时,
则AE⊥BF,则AF=FE=3,则AE=6,
AB=BE=5,
过点A作AH⊥BC于点H,
设BH=x,则HE=5﹣x,
则AH2=AE2﹣HE2=AB2﹣HB2,即52﹣x2=62﹣(5﹣x)2,解得:x;
cos∠ABEcos2β,则tan2β,
则tanα;
②如图3所示,当∠ABD=∠C=β时,
过点A作AH⊥BE交BE于点H,交BD于点G,则点G是圆的圆心(BE的中垂线与直径的交点),
∵∠AEB=∠DAE+∠C=α+β=∠ABC,故AE=AB=5,则EF=AE﹣AF=5﹣3=2,
∵DE⊥BC,AH⊥BC,
∴ED∥AH,则AF:EF=AG:DE=3:2,
则DE=2k,则AG=3k=R(圆的半径)=BG,点H是BE的中点,则GHDE=k,
在△BGH中,BH2k,
在△ABH中,AB=5,BH=2k,AH=AG+HG=4k,
∵∠C+∠ABC=90°,∠ABC+∠BAH=90°,
∴∠C=∠BAH,
∴tanC=tan∠BAH,
综上,tanC的值为或.
【点评】此题属于圆的综合题,涉及了平行四边形的性质、全等三角形的判定与性质、三角函数值的知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.
10.综合与实践
【问题情境】在数学综合实践课上,“希望小组”的同学们以三角形为背景,探究图形变化过程中的几何问题,如图,在△ABC中,AB=AC,∠BAC=90°,点D为平面内一点(点A,B,D三点不共线),AE为△ABD的中线.
【初步尝试】(1)如图1,小林同学发现:延长AE至点M,使得ME=AE,连接DM.始终存在以下两个结论,请你在①,②中挑选一个进行证明:
①DM=AC;②∠MDA+∠DAB=180°;
【类比探究】(2)如图2,将AD绕点A顺时针旋转90°得到AF,连接CF.小斌同学沿着小林同学的思考进一步探究后发现:AECF,请你帮他证明;
【拓展延伸】(3)如图3,在(2)的条件下,王老师提出新的探究方向:点D在以点A为圆心,AD为半径的圆上运动(AD>AB),直线AE与直线CF相交于点G,连接BG,在点D的运动过程中BG存在最大值.若AB=4,请直接写出BG的最大值.
【考点】圆的综合题.
【专题】几何综合题;压轴题;图形的全等;推理能力.
【答案】(1)证明见解答;
(2)证明见解答;
(3)BG的最大值为22.
【分析】(1)利用SAS证明△ABE≌△MDE,可得AB=DM,再结合AB=AC,即可证得DM=AC;由全等三角形性质可得∠BAE=∠DME,再运用平行线的判定和性质即可证得∠MDA+∠DAB=180°;
(2)延长AE至点M,使得ME=AE,连接DM.利用SAS证得△ACF≌△DMA,可得CF=AM,再由AEAM,可证得AECF;
(3)延长DA至M,使AM=AD,设AM交CF于N,连接BM交CF于K,取AC中点P,连接GP,可证得△ACF≌△ABM(SAS),利用三角形中位线定理可得AE∥BM,即AG∥BM,利用直角三角形性质可得GPACAB=2,得出点G在以P为圆心,2为半径的⊙P上运动,连接BP并延长交⊙P于G′,可得BG′的长为BG的最大值,再运用勾股定理即可求得答案.
【解答】(1)证明:①∵AE为△ABD的中线,
∴BE=DE,
在△ABE和△MDE中,
,
∴△ABE≌△MDE(SAS),
∴AB=DM,
∵AB=AC,
∴DM=AC;
②由①知△ABE≌△MDE,
∴∠BAE=∠DME,
∴AB∥DM,
∴∠MDA+∠DAB=180°;
(2)证明:延长AE至点M,使得ME=AE,连接DM.
由旋转得:AF=AD,∠DAF=90°,
∵∠BAC=90°,∠DAF+∠BAC+∠BAD+∠CAF=360°,
∴∠BAD+∠CAF=180°,
由(1)②得:∠MDA+∠DAB=180°,DM=AB=AC,
∴∠CAF=∠MDA,
在△ACF和△DMA中,
,
∴△ACF≌△DMA(SAS),
∴CF=AM,
∵AEAM,
∴AECF;
(3)如图3,延长AE至M,使EM=AE,连接BM,
在△ADE和△MBE中,
,
∴△ADE≌△MBE(SAS),
∴AD=BM,∠DAE=∠M,
∴AD∥BM,
∴∠BAD+∠ABM=180°,
∵∠DAF+∠BAC=180°,
∴∠BAD+∠CAF=180°,
∴∠ABM=∠CAF,
∵AF=AD,
∴AF=BM,
在△ABM和△CAF中,
,
∴△ABM≌△CAF(SAS),
∴∠BAM=∠ACF,
∵∠BAC=90°,
∴∠BAM+∠CAG=90°,
∴∠ACF+∠CAG=90°,
∴∠AGC=90°,
点G在以AC为直径的⊙O上运动,当且仅当B、O、G三点共线时,BG取得最大值,
此时BG=OB+OG,
在Rt△ABO中,O为AC的中点,则OAAC=2,
∴OB2,
在Rt△ACG中,O为斜边AC的中点,
∴OGAC=2,
∴BG的最大值为22.
【点评】本题是几何综合题,考查了三角形的全等的性质与判定,两直线垂直的判定,三角形中位线定理,勾股定理,圆的性质,熟练掌握全等三角形的判定定理是解决本题的关键.
11.(1)【学习心得】
小赵同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.我们把这个过程称为“化隐圆为显圆”.
①已知:如图1,OA=OB=OC,若∠AOB=50°,求∠ACB的度数.
解:若以点O为圆心,OA为半径作辅助圆,∠AOB是⊙O的圆心角,而∠ACB是圆周角,从而可容易得到∠ACB= 25 °.
②如图2,点P为正方形ABCD内一点,且∠BPC=90°,若AB=4,求AP的最小值.
解:∵BC=4,∠BPC=90°,∴点P在以BC为直径的圆上,
设圆心为点O,则O、P、A三点共线时AP最小,最小值为 22 .
(2)【问题解决】
①如图3,在平行四边形ABCD中,已知AB=4,BC=6,∠ABC=60°,点P是BC边上一动点(点P不与B,C重合),连接AP,作点B关于直线AP的对称点Q,则线段QC的最小值为 24 .
②如图4,△ABC中,∠BAC=90°,AB=4,AC=3,D为AC上一动点,以AD为直径的⊙O交BD于E,求线段CE的最小值.
(3)【问题拓展】
如图5,在平面直角坐标系中,已知两点A(2,3),B(6,7),x轴上有一动点P,当∠APB最大时,直接写出点P的坐标 1 .
【考点】圆的综合题.
【专题】几何综合题;压轴题;运算能力;推理能力.
【答案】(1)①25.②22.
(2)①24.②线段CE的最小值为2.
(3)1.
【分析】(1)①利用圆周角定理即可求得答案;
②由正方形性质可得:∠ABC=90°,BC=AB=4,OBBC=2,由勾股定理得:AO=2,推出点P在以BC为直径的⊙O上,则O、P、A三点共线时AP最小,即可求得答案;
(2)①过点A作AH⊥BC于H,利用解直角三角形得AH=AB sin∠ABC=2,BH=AB cos∠ABC=2,CH=BC﹣BH=4,由勾股定理得AC=2,再由AQ=AB=4,可得点Q在以A为圆心AB为半径的⊙A上,即当C、Q、A三点共线时QC最小,QC的最小值=AC﹣AQ=24;
②连接AE,由AD是⊙O的直径,可得∠AED=90°,推出∠AEB=90°,即点E在以AB为直径的圆上,进而可得当C、E、Q三点共线时,CE最小,运用勾股定理即可求得答案;
(3)当∠APB最大时,过A、B两点的⊙O′与x轴相切,利用待定系数法可得直线AB的解析式为y=x+1,线段AB的垂直平分线为y=﹣x+9,设O′(m,﹣m+9),根据O′A=O′B=O′P,建立方程求解即可得出答案.
【解答】解:(1)①如图1,以点O为圆心,OA为半径作辅助圆⊙O,
∵,∠AOB=50°,
∴∠ACB∠AOB=25°,
故答案为:25.
②点P为正方形ABCD内一点,且∠BPC=90°,若AB=4,求AP的最小值.
如图②,以BC为直径作⊙O,
∵四边形ABCD是正方形,
∴∠ABC=90°,BC=AB=4,
∴OBBC=2,
在Rt△ABO中,AO2,
∵BC=4,∠BPC=90°,
∴点P在以BC为直径的⊙O上,
则O、P、A三点共线时AP最小,
∴AP的最小值=AO﹣OP=22,
故答案为:22.
(2)①如图3,过点A作AH⊥BC于H,
∵AB=4,BC=6,∠ABC=60°,
则AH=AB sin∠ABC=4sin60°=2,BH=AB cos∠ABC=4cos60°=2,
∴CH=BC﹣BH=6﹣2=4,
在Rt△ACH中,AC2,
∵点B与点Q关于直线AP对称,
∴AQ=AB=4,
∴点Q在以A为圆心AB为半径的⊙A上,
∴当C、Q、A三点共线时QC最小,QC的最小值=AC﹣AQ=24,
故答案为:24.
②如图4,连接AE,
∵AD是⊙O的直径,
∴∠AED=90°,
∴∠AEB=180°﹣∠AED=90°,
即点E在以AB为直径的圆上,
以AB为直径作⊙Q,交⊙O于E,当C、E、Q三点共线时,CE最小,
∵△ABC中,∠BAC=90°,AB=4,AC=3,
∴QE=AQAB=2,
∴CQ,
∴CE=CQ﹣QE2,
故线段CE的最小值为2.
(3)当∠APB最大时,过A、B两点的⊙O′与x轴相切,
设直线AB的解析式为y=kx+b,把A(2,3),B(6,7)代入,
得:,
解得:,
∴直线AB的解析式为y=x+1,
∵线段AB的中点坐标为(4,5),圆心O′在AB的垂直平分线上,
∴线段AB的垂直平分线为y=﹣x+9,
设O′(m,﹣m+9),
∵O′A=O′B=O′P,
∴(m﹣2)2+(﹣m+9﹣3)2=(﹣m+9)2,
解得:m1或m1(舍去),
∴点P的坐标为(1,0),
故答案为:1.
【点评】本题是圆的综合题,考查了圆的有关知识,正方形的性质,平行四边形的性质,解直角三角形等知识,灵活运用这些性质解决问题是解题的关键.
12.问题提出:如图①,在Rt△ABC中,∠C=90°,CB=4,CA=6,⊙C的半径为2,P为圆上一动点,连接AP、BP,求的最小值.
(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图①,连接CP,在CB上取一点D,使CD=1,则.又∠PCD=∠BCP,所以△PCD∽△BCP.所以.
所以PDPB,所以.
请你完成余下的思考,并直接写出答案:的最小值为 ;
(2)自主探索:在“问题提出”的条件不变的前提下,求的最小值;
(3)拓展延伸:如图②,已知在扇形COD中,∠COD=90°,OC=6,OA=3,OB=5,P是上一点,求2PA+PB的最小值.
【考点】圆的综合题.
【专题】压轴题;与圆有关的计算;数据分析观念.
【答案】(1);
(2);
(3)13.
【分析】(1)利用勾股定理即可求解;
(2)连接CP,在CA上取点D,使CD,则有,可证△PCD∽△ACP,得到PDAP,即AP+BP=BP+PD,从而AP+BP的最小值为BD;
(3)延长OA到点E,使CE=6,连接PE、OP,可证△OAP∽△OPE,得到EP=2PA,得到2PA+PB=EP+PB,当E、P、B三点共线时,得到最小值.
【解答】解:(1)如图1,
连接AD,
∵APBP=AP+PD,要使APBP最小,
∴AP+AD最小,当点A,P,D在同一条直线时,AP+AD最小,
即:APBP最小值为AD,
在Rt△ACD中,CD=1,AC=6,
∴AD,
APBP的最小值为,
故答案为:;
(2)如图2,
连接CP,在CA上取点D,使CD,
∴,
∵∠PCD=∠ACP,
∴△PCD∽△ACP,
∴,
∴PDAP,
∴AP+BP=BP+PD,
∴同(1)的方法得出AP+BP的最小值为BD;
(3)如图3,
延长OA到点E,使CE=6,
∴OE=OC+CE=12,
连接PE、OP,
∵OA=3,OP
∴,
∵∠AOP=∠AOP,
∴△OAP∽△OPE,
∴,
∴EP=2PA,
∴2PA+PB=EP+PB,
∴当E、P、B三点共线时,取得最小值为:BE13.
【点评】此题是圆的综合题,主要考查了勾股定理,相似三角形的判定和性质,极值的确定,还考查了学生的阅读理解能力,解本题的关键是根据材料中的思路构造出△PCD∽△ACP和△OAP∽△OPE,也是解本题的难点.
13.概念认识:
平面内,M为图形T上任意一点,N为⊙O上任意一点,将M、N两点间距离的最小值称为图形T到⊙O的“最近距离”,记作d(T﹣⊙O).例:如图1,在直线l上有A、C、O三点,以AC为对角线作正方形ABCD,以点O为圆心作圆,与l交于E、F两点,若将正方形ABCD记为图形T,则C、E两点间的距离称为图形T到⊙的“最近距离”.
数学理解:
(1)在平面内有A、B两点,以点A为圆心,5为半径作⊙A,将点B记为图形T,若d(T﹣⊙A)=2,则AB= 3或7 .
(2)如图2,在平面直角坐标系中,以O(0,0)为圆心,半径为2作圆.
①将点C(4,3)记为图形T,则d(T﹣⊙O)= 3 .
②将一次函数y=kx+2的图记为图形T,若d(T﹣⊙)>0,求k的取值范围.
推广运用:
(3)在平面直角坐标系中,P的坐标为(t,0),⊙P的半径为2,D、E两点的坐标分别为(5,5)、(5,﹣5),将△DOE记为图形T,若d(T﹣⊙P)=1,则t= 8或﹣3 .
【考点】圆的综合题.
【专题】压轴题;运算能力;推理能力.
【答案】(1)3或7;
(2)①3,②﹣1<k<1且k≠0;
(3)8或﹣3.
【分析】(1)根据图形T到⊙O的“最近距离”的定义即可解决问题.
(2)①如图2中,连接OC交⊙O于E.求出EC的长即可.
②如图,设直线y=kx+2与⊙O相切于E,K.连接OK,OE.求出直线DE,直线DK的解析式即可解决问题.
(3)分两种情形:①如图3﹣1中,当点P在∠DOE内部时,作PM⊥OD于M,交⊙P于K.②如图3﹣2中,当点P在∠DOE的外侧时,分别求解即可.
【解答】解:(1)如图1中,
∵d(T﹣⊙A)=2,
∴CB=CB′=2,
∵AC=5,
∴AB′=5﹣2=3,AB=5+2=7.
故答案为:3或7.
(2)①如图2中,连接OC交⊙O于E.
∵C(4,3),
∴OC5,
∵OE=2,
∴EC=3,
∴d(T﹣⊙O)=3.
故答案为:3.
②如图,设直线y=kx+2与⊙O相切于E,K.连接OK,OE.
∵OE⊥DE,OK⊥DK,OD=2,OE=OK=2,
∴DK2,DE2,
∴DE=OE=DK=OK,
∴四边形DEOK是菱形,
∵∠DKO=∠DEO=90°,
∴四边形DEOK是正方形,
∴∠ODE=∠ODK=45°,
∴直线DE的解析式为y=﹣x+2,直线DK的解析式为y=x+2,
∵d(T﹣⊙O)>0,
∴观察图象可知满足条件的k的值为﹣1<k<1且k≠0.
(3)如图3﹣1中,当点P在DE的右边时.
∵D(5,5),
∴∠DOP=45°,
∵d(T﹣⊙P)=1,
∴OP=5+1+2=8
∴t=8.
如图3﹣2中,当点P在∠DOE的外侧时,由题意可知OM=1,OP=1+2=3,t=﹣3.
综上所述,满足条件的t的值为8或﹣3.
【点评】本题属于圆综合题,考查了直线与圆的位置关系,图形T到⊙O的“最近距离”的定义,解直角三角形等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考压轴题.
14.问题提出:
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?
初步思考:
(1)给出了一些特殊的四边形:①矩形②菱形③等腰梯形④正方形,能过它们四个顶点作一个圆的是 ①③④ (填写序号),过某个四边形四个顶点作一个圆的四边形相对的两个内角的关系是 互补(对角之和等于180°) .
进一步研究:
(2)如果过某个四边形的四个顶点不能作一个圆,那么其相对的两个内角之间有上面的关系吗?请结合图1的两幅图说明其中的道理.(提示:考虑∠B+∠D与180°之间的关系)
由上面的探究,请用文字语言直接写出过某个四边形的四个顶点能作一个圆的条件 对角互补 .
拓展延伸
(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知:如图2,AB是⊙O的直径,点C在⊙O上,求作:CN⊥AB.
作法:①连接CA,CB;
②在上任取异于B、C的一点D,连接DA,DB;
③DA与CB相交于E点,延长AC、BD,交于F点;
④连接F、E并延长,交直径AB于M:
⑤连接D、M并延长,交⊙O于N.连接CN.
则CN⊥AB.
请按上述作法在图2中作图,并说明CN⊥AB的理由,(提示:可以利用(2)中的结论)
【考点】圆的综合题.
【专题】压轴题;几何直观;推理能力.
【答案】(1)①②③;互补(对角之和等于180°);
(2)对角互补;
(3)图见解析,理由见解析.
【分析】(1)(2)根据圆内接四边形的对角互补可知这些四边形的对角互补;
(3)先画出图形,根据AB是圆O的直径可得出点E是△ABF三条高的交点,进而得到FM⊥AB;接下来根据(2)中的结论可得点E、M、B、D在同一个圆上,则有∠EMD=∠DBE,再结合点N、C、B、D在⊙O上,推出∠DBE=∠CND,等量代换,结合平行线的判定可证明FM∥CN,至此问题不难解答.
【解答】解:(1)
①如答图1,矩形ABCD中,∠A=∠B=∠C=∠D=90°,则∠A+∠C=∠B+∠D=180°,A,B,C,D四点共圆.
②如答图2,在菱形ABCD中,∠A=∠C,∠B=∠D,A,B,C,D四点不共圆.
③如答图3,在等腰梯形中,∠B+∠C=180°,∠A+∠D=180°,∠A=∠B,∠C=∠D,则∠A+∠C=∠B+∠D=180°,A,B,C,D四点共圆.
④如答图4,在正方形ABCD中,∠A=∠B=∠C=∠D=90°,则∠A+∠C=∠B+∠D=180°,A,B,C,D四点共圆.
综上所述,相对的两个角之间的关系是:互补(对角之和等于180°);
故答案为:①②③;互补(对角之和等于180°);
(2)如果四边形没有外接圆,那么相对的两个内角之间没有有上面的关系.
如答图4:连接BE,
∵∠A+∠E=180°,∠BCD>∠E,
∴∠A+∠BCD>180°;
如答图5:连接DE,
∵∠A+∠BED=180°,∠BED>∠C,
∴∠A+∠C<180°.
综上所述,某个四边形的四个顶点能作一个圆的条件是:对角互补.
故答案为:对角互补;
(3)答图6即为所求作.
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,即BC⊥AF,AD⊥BF,
∴根据三角形的三条高交于同一点可得:FM⊥AB.
∴∠EMB=90°.
∴∠EMB+∠EDB=180°.
∴由(2)中的结论可得:点E、D、B、M在同一个圆上,如答图⑥所示.
∴∠EMD=∠EBD.
∵∠CND=∠CBD,
∴∠CND=∠EMD.
∴CN∥EM.
∴∠CHB=∠EMB.
∵∠EMB=90°,
∴∠CHB=90°,即CN⊥AB.
【点评】本题属于圆的综合题,综合考查了圆周角定理、三角形外角的性质、平行线的判定与性质、圆周角的度数与所对弧的度数之间的关系等知识,考查了操作与探究的能力,考查了运用已有的经验解决问题的能力,是一条体现新课程理念的好题.
15.综合与实践
数学实践课堂上,张老师带领学生们从一道题入手,开始研究,并对此题做适当变式,尝试举一反三,开阔学生思维.
(1)原型题:如图1,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,AP=PC,AP⊥PC,则△ABP≌△ PDC ,请你说明理由.
(2)利用结论,直接应用:
如图2,四边形ABCD、EFGH、NHMC都是正方形,边长分别为a、b、c,A、B、N、E、F五点在同一条直线上,则△CBN≌△ NEH ,c= (用含a、b的式子表示).
如图3,四边形ABCD中,AB∥DC,AB⊥BC,AB=2,CD=4,以BC上一点O为圆心的圆经过A、D两点,且∠AOD=90°,则圆心O到弦AD的距离为 .
(3)弱化条件,变化引申:
如图4,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°,且DM交AC于点F,ME交BC于点G,连接FG,则△AMF与△BGM的关系为: △AMF∽△BGM ,若,AF=3,则FG= .
【考点】圆的综合题.
【专题】几何综合题;压轴题;运算能力;推理能力.
【答案】(1)△ABP≌△PDC;
(2)△CBN≌△NEH,c,圆心O到弦AD的距离为.
(3)△AMF∽△BGM,FG.
【分析】(1)先证明∠BAP=∠CPD,根据AAS定理可证明△ABP≌△PDC.
(2)先证明△CBN≌△NEH,再利用勾股定理说明a、b、c间关系;根据AAS证明△AOB≌△ODC,则有OB=CD=4;再根据勾股定理求得OA.可证明三角形AOD是等腰直角三角形,则可得出答案.
(3)利用三角形外角可得∠AFM=∠DME+∠E=∠A+∠E=∠BMG,进而证得△AMF∽△BGM,再由∠A=∠B=45°,可得出△ABC是等腰直角三角形,根据M为线段AB的中点,可得AM=BMAB42,运用相似三角形性质和勾股定理即可求得答案.
【解答】(1)证明:∵AB⊥BD,CD⊥BD,
∴∠ABP=∠PDC=90°,
∴∠BAP+∠APB=90°,
∵AP⊥PC,
∴∠CPD+∠APB=90°,
∴∠BAP=∠CPD,
在△ABP和△PDC中,
,
∴△ABP≌△PDC(AAS);
故答案为:PDC.
(2)证明:∵四边形ABCD、EFGH、NHMC都是正方形,边长分别为a、b、c,
∴∠CBN=∠NEH=∠CNH=90°,CN=NH=c,BC=a,EH=b,
∵∠BCN+∠BNC=∠ENH+∠BNC=90°,
∴∠BCN=∠ENH,
在△CBN和△NEH中,
,
∴△CBN≌△NEH(AAS),
∴BN=EH=b,
在Rt△CBN中,CN2=BC2+BN2,
∴c2=a2+b2,
∵a、b、c均为正数,
∴c,
故答案为:NEH,.
如图3,∵AB∥DC,AB⊥BC,
∴∠B=∠C=90°,
∴∠BAO+∠AOB=90°,
∵∠AOD=90°,
∴∠COD+∠AOB=90°,
∴∠BAO=∠COD,
∵以点O为圆心的圆经过A、D两点,
∴OA=OD,
∴△AOB≌△ODC(AAS),
∴AB=OC=2,OB=CD=4,
在Rt△AOB中,OA2,
∴OD=OA=2,
∵∠AOD=90°,
∴△AOD是等腰直角三角形,
∴ADAB22,∠OAD=∠ODA=45°,
过点O作OH⊥AD于点H,
根据垂径定理可得:AH=DH,
∵OHAD,
∴OH,
故答案为:.
(3)∵∠AFM=∠DME+∠E(外角定理),
∠DME=∠A=∠B(已知),
∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,
∴△AMF∽△BGM,
∵∠DME=∠A=∠B=45°
∴AC=BC,∠ACB=90°,
∴AC⊥BC,
∵M为线段AB的中点,
∴AM=BMAB42,
∵△AMF∽△BGM,
∴,
∴BG,
又∵AC=BC=4cos45°=4,
∴CG=BC﹣BG=4,CF=AC﹣AF=4﹣3=1,
在Rt△FCG中,由勾股定理得:
FG.
【点评】本题是有关圆的综合题,考查了全等三角形的判定和性质,直角三角形的性质,勾股定理,等腰直角三角形的性质与判定,相似三角形的判定与性质,垂径定理,圆的性质等,此题难度适中,熟练掌握全等三角形的判定和性质以及相似三角形的判定和性质是解题关键.
16.问题提出:
(1)如图1,点B、C在⊙O上且BC=2,过点O作OE⊥BC,交BC于点A,交⊙O于点E,连接BE、CE,若∠CBE=30°,则线段AE的长度为 .
问题探究:
(2)如图2,在△ABC中,BC=2,∠BAC=45°,求边AC长度的最大值;
问题解决:
(3)如图3,某城市拟在河流m、n所夹半岛区域建一个湿地公园,公园的周长由亲水廊桥AB、、CD和绿化带BC四部分构成.其中B、C两定点间的距离为2000米.根据规划要求,A、D两点间的距离为600米,A、D两点到直线BC的距离相等,的中点E到BC的距离比点A到BC的距离多100米;若修建时需保证∠B与∠C的和为120度,请判断这个湿地公园的周长是否存在最大值?若存在,请求出最大值.若不存在,请说明理由.(结果保留π)
【考点】圆的综合题.
【专题】压轴题;构造法;推理能力;模型思想.
【答案】(1);
(2)2;
(3)4800.
【分析】(1)利用角度关系直接求解即可;
(2)构造外接圆,圆内最长的为直径,即可求解;
(3)关键在于构造出两个外接圆,然后利用弦的长度和角度关系将相关量表示出来即可求解.
【解答】解:(1)∵BC=2,OE⊥BC,
∴AB=AC=1,
∵∠CBE=30°,
∴tan∠CBE=tan30°,
∴AE.
(2)如图1,构造△ABC的外接圆⊙O,连接OB,OC,
∴∠BOC=2∠BAC=90°,
∵OB=OC,
∴OB,
∴⊙O的直径为,
∵AC为弦长,
∴AC,
∴AC的最大值为.
(3)如图2,构造△AED的外接圆⊙O,连接OE,AD交AD于点F,连接OA,OD,过点D作DG∥AB交BC于点G,构造△DGC的外接圆⊙M,
∵点E为的中点,
∴OE⊥AD,
∴AFAD=300,
∵的中点E到BC的距离比点A到BC的距离多100米,
∴EF=100,
设OA=r,则:
OF=r﹣100,
∵AF2+OF2=OA2,
∴3002+(r﹣100)2=r2,
解得:r=200,
∴sin∠AOF,
∴∠AOF=60°,
∴∠AOD=120°,
的长度为:,
∵DG∥AB,AD∥BC,
∴四边形ABGD为平行四边形,
∴DG=AB,∠DGC=∠B,BG=AD,
∴CG=BC﹣BG=1400,
∵∠B+∠C=120°,
∴∠DGC+∠C=120°,
∴∠GDC=60°,
当D到CG的距离最远时,
AB+DC=DG+DC最大,
此时有DM⊥CG,
∴DG=DC=CG=1400,
此时周长最大为:BC+CDAB=2000+28002π×2004800,
∴公园周长最大值为4800米.
【点评】本题考查了圆的综合运用,涉及垂径定理,圆周角定理,还有平行四边形等相关知识点,综合性比较强,对解题思维要求较高,属于中考压轴题.
17.在一次数学探究活动中,李老师设计了一份活动单:
已知线段BC=2,使用作图工具作∠BAC=30°,尝试操作后思考: (1)这样的点A唯一吗? (2)点A的位置有什么特征?你有什么感悟?
“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以BC为弦的圆弧上(点B、C除外),….小华同学画出了符合要求的一条圆弧(如图1).
(1)小华同学提出了下列问题,请你帮助解决.
①该弧所在圆的半径长为 2 ;
②△ABC面积的最大值为 ;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为A′,请你利用图1证明∠BA′C>30°.
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形ABCD的边长AB=2,BC=3,点P在直线CD的左侧,且tan∠DPC.
①线段PB长的最小值为 ;
②若S△PCDS△PAD,则线段PD长为 .
【考点】圆的综合题.
【专题】压轴题;矩形 菱形 正方形;圆的有关概念及性质;推理能力.
【答案】见试题解答内容
【分析】(1)①设O为圆心,连接BO,CO,根据圆周角定理得到∠BOC=60°,证明△OBC是等边三角形,可得半径;
②过点O作BC的垂线,垂足为E,延长EO,交圆于D,以BC为底,则当A与D重合时,△ABC的面积最大,求出OE,根据三角形面积公式计算即可;
(2)延长BA′,交圆于点D,连接CD,利用三角形外角的性质和圆周角定理证明即可;
(3)①根据,连接PD,设点Q为PD中点,以点Q为圆心,PD为半径画圆,可得点P在优弧CPD上,连接BQ,与圆Q交于P′,可得BP′即为BP的最小值,再计算出BQ和圆Q的半径,相减即可得到BP′;
②根据AD,CD和 推出点P在∠ADC的平分线上,从而找到点P的位置,过点C作CF⊥PD,垂足为F,解直角三角形即可求出DP.
【解答】解:(1)①设O为圆心,连接BO,CO,
∵∠BAC=30°,
∴∠BOC=60°,又OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=2,即半径为2;
②∵△ABC以BC为底边,BC=2,
∴当点A到BC的距离最大时,△ABC的面积最大,
如图,过点O作BC的垂线,垂足为E,延长EO,交圆于D,
∴BE=CE=1,DO=BO=2,
∴OE,
∴DE,
∴△ABC的最大面积为;
(2)如图,延长BA′,交圆于点D,连接CD,
∵点D在圆上,
∴∠BDC=∠BAC,
∵∠BA′C=∠BDC+∠A′CD,
∴∠BA′C>∠BDC,
∴∠BA′C>∠BAC,即∠BA′C>30°;
(3)①如图,当点P在BC上,且PC时,
∵∠PCD=90°,AB=CD=2,AD=BC=3,
∴tan∠DPC,为定值,
连接PD,设点Q为PD中点,以点Q为圆心,PD为半径画圆,
∴当点P在优弧CPD上时,tan∠DPC,连接BQ,与圆Q交于P′,
此时BP′即为BP的最小值,过点Q作QE⊥BE,垂足为E,
∵点Q是PD中点,
∴点E为PC中点,即QECD=1,PE=CEPC,
∴BE=BC﹣CE=3,
∴BQ,
∵PD,
∴圆Q的半径为,
∴BP′=BQ﹣P′Q,即BP的最小值为;
②∵AD=3,CD=2,S△PCDS△PAD,
则,
∴△PAD中AD边上的高=△PCD中CD边上的高,
即点P到AD的距离和点P到CD的距离相等,
则点P到AD和CD的距离相等,即点P在∠ADC的平分线上,如图,
过点C作CF⊥PD,垂足为F,
∵PD平分∠ADC,
∴∠ADP=∠CDP=45°,
∴△CDF为等腰直角三角形,又CD=2,
∴CF=DF,
∵tan∠DPC,
∴PF,
∴PD=DF+PF.
解法二:如图,作直径DG,连接PG,
∵△CDF为等腰直角三角形,又CD=2,
∴∠CDF=∠CED=45°,
∴CD=CE=2,
∴DE=2,
∵∠DPC=∠GDC,
∴tan∠DGC=tan∠DPC,
∴CG=1.5,EG=0.5,
∵DG是直径,
∴∠DPG=∠EPG=90°,
∴PEEG,
∴PD=DE﹣PE=2.
【点评】本题是圆的综合题,考查了圆周角定理,三角形的面积,等边三角形的判定和性质,最值问题,解直角三角形,三角形外角的性质,勾股定理,知识点较多,难度较大,解题时要根据已知条件找到点P的轨迹.
18.问题提出
(1)如图①,△ABC内接于⊙O,过点C作⊙O的切线l.在l上任取一个不同于点C的点P,连接PB、PA,比较∠ACB与∠APB的大小,并说明理由.
问题探究
(2)如图2,正方形ABCD,边长为2,在CD边上是否存在点P,使∠APB最大?若存在,确定点P的位置,并求此时sin∠APB的值;若不存在,请说明理由.
问题解决
(3)如图③,四边形ABCD为某工作室的平面示意图,线段BC、CD、DA为三面墙,MN为入户门处,其中AD∥BC,AD⊥AB,∠C=60°,BM=AN=4米,BC=30米,AD=20米.出于安全考虑,负责人想在墙上安装监控装置P,用来监控并记录进出的人员,为了让监控效果最佳,要求∠MPN最大,试问在墙上是否存在一点P,使得∠MPN最大?若存在,请求出此时sin∠MPN的值及P点的位置;若不存在,请说明理由.
【考点】圆的综合题.
【专题】压轴题;圆的有关概念及性质;与圆有关的位置关系;模型思想;应用意识.
【答案】(1)∠ACB>∠APB,理由见解答过程;
(2)存在,P是边CD的中点,sin∠APB;
(3)监控装置P应在AD上,距A6米的地方,此时sin∠MPN,
或监控装置P应在BC上,距B6米的地方,此时sin∠MPN.
【分析】(1)设AP交⊙O于D,连接AD,由∠ACB=∠ADB,∠ADB>∠APB,即可证∠ACB>∠APB;
(2)过A、B两点作⊙O与CD相切于P,连接PO并延长交AB于E,过A作AF⊥BP于F,此时∠APB最大,由⊙O与CD相切于P,可得EP⊥AB,四边形AEPD、四边形BEPC是矩形,从而AE=BEAB=1,PE=AD=2,P是边CD的中点,在Rt△BEP中,求出BP,同理AP,再由S△ABP得AF,即可在Rt△APF中,得到sin∠APB;
(3)分三种情况:①当P在BC上时,作过M、N的⊙O与BC相切于P,此时∠MPN最大,过O作OE垂直AB于E,过D作DF⊥BC于F,连接OP、OM、ON,由四边形ABFD是矩形,DF=AB=10,由BM=AN=4,可得ME=NEMN,BE=BM+ME=5,由四边形BPOE是矩形,得OP=BE=5,BP=OE,Rt△MOE中,用勾股定理得OE6,即BP=6,此时监控装置P在距B6米的墙上,再根据∠MPN=∠MOE,在Rt△MOE中,求得sin∠MPN;②当P在AD上时,作过M、N的⊙O与AD相切于P,此时∠MPN最大,同①的道理:AP=6,即此时监控装置P在距A6米的墙上,sin∠MPN;③当P在CD上时,作过M、N的⊙O与CD相切于P,此时∠MPN最大,过O作OE垂直AB于E,直线OE交CD于G,过D作DF⊥BC于F,连接OP、OM、ON,设PG=x,则DP=10﹣x,OG=2x,OPx,OE=GE﹣OG=25﹣2x,OM=OPx,Rt△MOE中,ME2+OE2=OM2有()2+(25﹣2x)2=(x)2,解得∴PG=50﹣12,DP=1240,即此时监控装置P在距D(1240)米的墙上,sin∠MPN=sin∠MOE,比较,可得到答案.
【解答】解:(1)∠ACB>∠APB,理由如下:
设AP交⊙O于D,连接AD,如图:
∵弧AB=弧AB,
∴∠ACB=∠ADB,
而∠ADB是△BDP的一个外角,
∴∠ADB>∠APB,
∴∠ACB>∠APB;
(2)存在,P是边CD的中点,理由如下:
过A、B两点作⊙O与CD相切于P,连接PO并延长交AB于E,过A作AF⊥BP于F,如图:
由(1)知此时∠APB最大,
∵⊙O与CD相切于P,
∴EP⊥CD,
∵正方形ABCD,边长为2,
∴CD∥AB,AB=AD=2,∠DAB=∠ABC=90°,
∴EP⊥AB,四边形AEPD、四边形BEPC是矩形,
∴AE=BEAB=1,PE=AD=2,
∴CP=BE=AE=DP,即P是边CD的中点,
Rt△BEP中,BP,
同理AP,
由S△ABPAB PEBP AF得:AF,
在Rt△APF中,sin∠APB;
(3)存在,理由如下:
①当P在BC上时,作过M、N的⊙O与BC相切于P,此时∠MPN最大,过O作OE垂直AB于E,过D作DF⊥BC于F,连接OP、OM、ON,如图:
∵AD∥BC,AD⊥AB,DF⊥BC,
∴四边形ABFD是矩形,
∴AB=DF,AD=BF,
∵BC=30,AD=20,
∴CF=BC﹣BF=BC﹣AD=10,
Rt△DCF中,DF=CF tanC=10 tan60°=10,
∴AB=10,
∵BM=AN=4,
∴MN=AB﹣BM﹣AN=2,
∵OE⊥AB,
∴ME=NEMN,
∴BE=BM+ME=5,
∵⊙O与BC相切于P,
∴∠OPB=90°,
∴四边形BPOE是矩形,
∴OP=BE=5,BP=OE,
∴OM=OP=5,
Rt△MOE中,OE6,
∴BP=6,即此时监控装置P在距B6米的墙上,
∵OE⊥AB,OM=ON,
∴∠MOE∠MON,
又弧MN=弧MN,
∴∠MPN∠MON,
∴∠MPN=∠MOE,
Rt△MOE中,sin∠MOE,
∴sin∠MPN;
②当P在AD上时,作过M、N的⊙O与AD相切于P,此时∠MPN最大,如图:
同①的道理:AP=6,即此时监控装置P在距A6米的墙上,sin∠MPN;
③当P在CD上时,作过M、N的⊙O与CD相切于P,此时∠MPN最大,过O作OE垂直AB于E,直线OE交CD于G,过D作DF⊥BC于F,连接OP、OM、ON,
由①知:ME,BE=AE=5,CF=10,
Rt△CDF中,CD20,
∵AD∥BC,AD⊥AB,OE⊥BC,
∴BC∥GE∥AD,
∴∠OGP=∠C=60°,GE为梯形ABCD的中位线,
∴DGCD=10,GE25,
设PG=x,则DP=10﹣x,
Rt△POG中,OG=2x,OPx,
∴OE=GE﹣OG=25﹣2x,OM=OPx,
Rt△MOE中,ME2+OE2=OM2,
∴()2+(25﹣2x)2=(x)2,
解得:x=50+12(大于CD,舍去)或x=50﹣12,
∴PG=50﹣12,DP=1240,即此时监控装置P在距D(1240)米的墙上,
OM=OP=5012,
∴sin∠MPN=sin∠MOE,
∵,
∴监控装置P在CD上时的∠MPN较小,
∴监控装置P应在AD上,距A6米的地方,此时sin∠MPN,
或监控装置P应在BC上,距B6米的地方,此时sin∠MPN.
【点评】本题考查圆的综合知识,涉及圆周角、圆心角、垂径定理、圆的切线、解直角三角形、勾股定理等知识,综合性很强,解题的关键是掌握圆的基本性质,根据已知画出符合条件的图形,
同课章节目录
