北师大版九年级数学下册第三章 圆 回顾与思考 课件(共24张PPT)
文档属性
| 名称 | 北师大版九年级数学下册第三章 圆 回顾与思考 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 07:22:23 | ||
图片预览

文档简介
(共24张PPT)
初中数学九年级(下)
第三章 圆回顾与思考
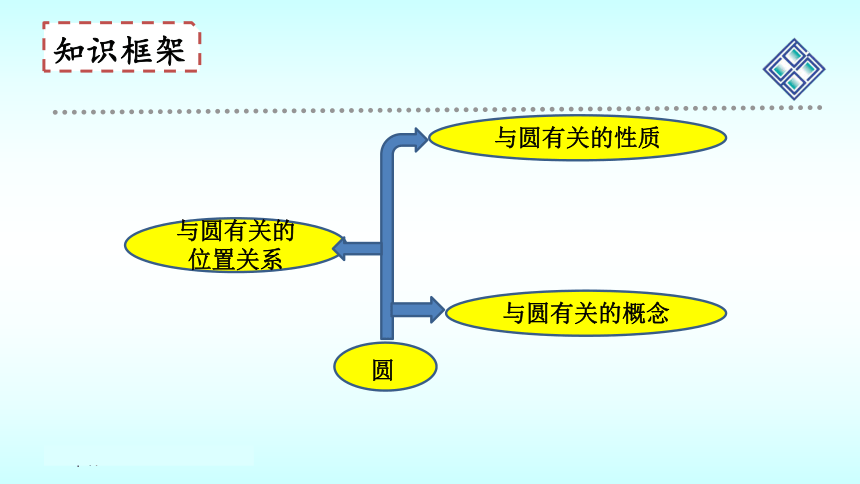
知识框架
圆
与圆有关的性质
与圆有关的概念
与圆有关的位置关系
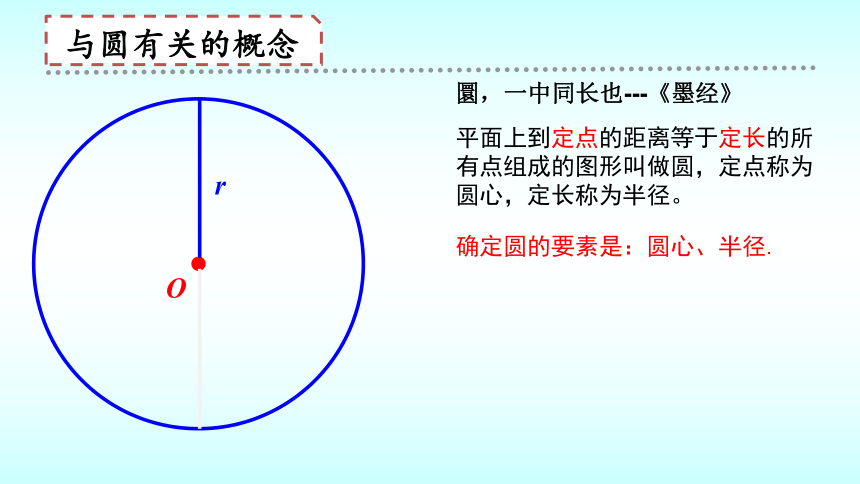
与圆有关的概念
·
r
O
圜,一中同长也---《墨经》
平面上到定点的距离等于定长的所有点组成的图形叫做圆,定点称为圆心,定长称为半径。
确定圆的要素是:圆心、半径.
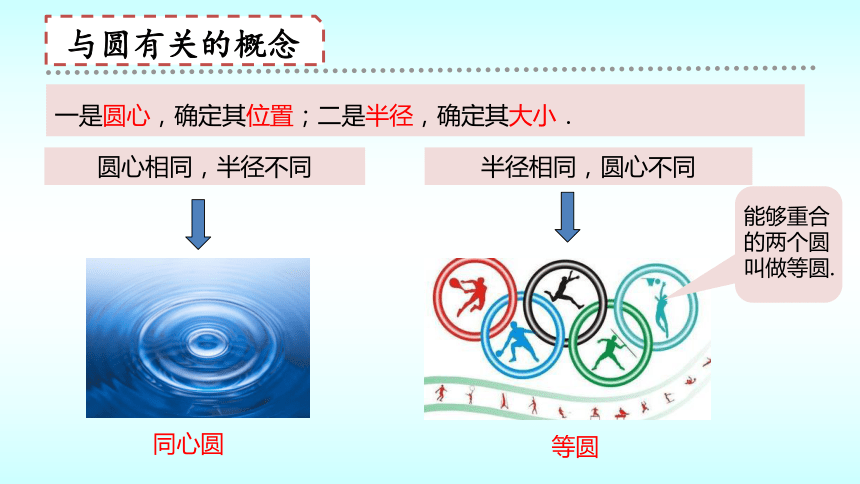
与圆有关的概念
圆心相同,半径不同
等圆
半径相同,圆心不同
能够重合的两个圆叫做等圆.
一是圆心,确定其位置;二是半径,确定其大小.
同心圆
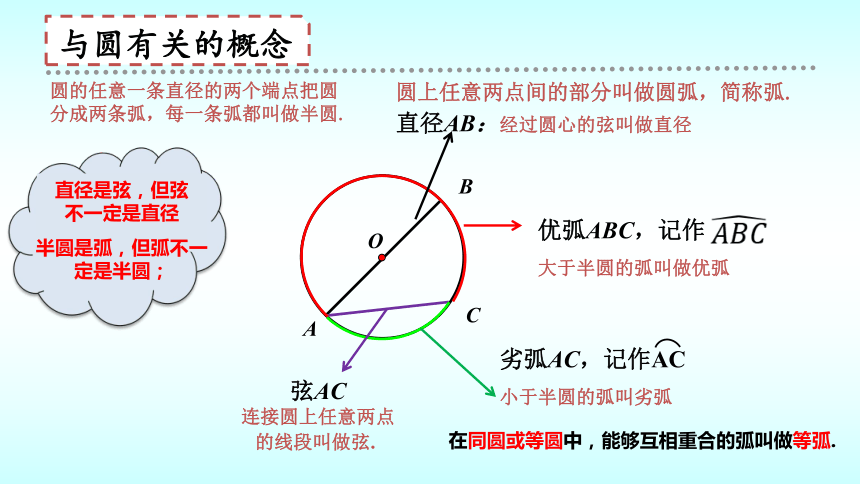
与圆有关的概念
·
C
O
A
B
直径AB:经过圆心的弦叫做直径
弦AC
连接圆上任意两点的线段叫做弦.
优弧ABC,记作
大于半圆的弧叫做优弧
劣弧AC,记作AC
小于半圆的弧叫劣弧
圆上任意两点间的部分叫做圆弧,简称弧.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
直径是弦,但弦不一定是直径
半圆是弧,但弧不一定是半圆;
在同圆或等圆中,能够互相重合的弧叫做等弧.
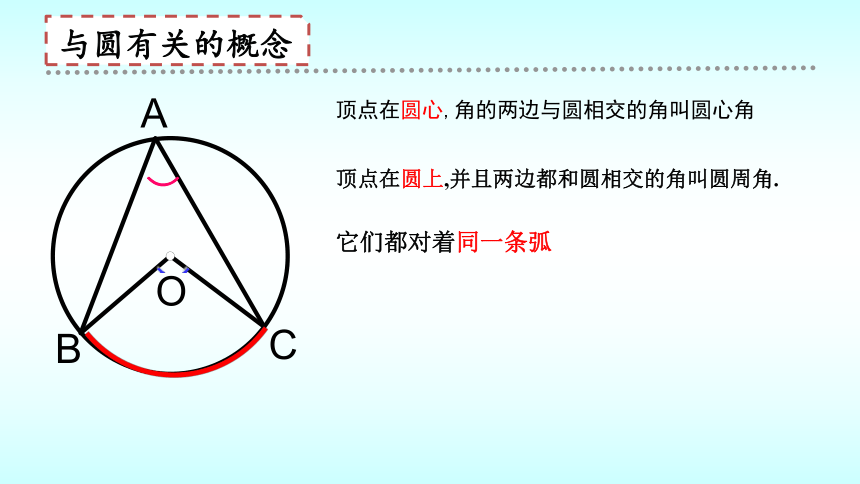
与圆有关的概念
它们都对着同一条弧
⌒
⌒
顶点在圆上,并且两边都和圆相交的角叫圆周角.
顶点在圆心,角的两边与圆相交的角叫圆心角
与圆有关的性质
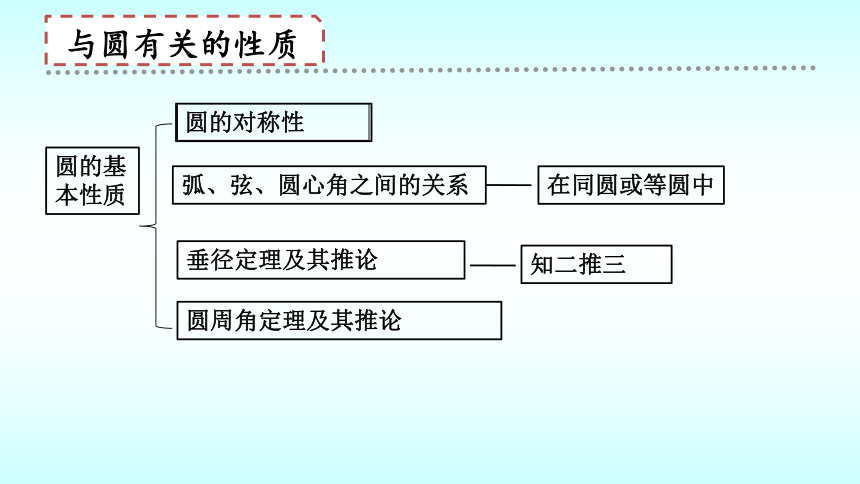
圆的基本性质
圆的对称性
弧、弦、圆心角之间的关系
垂径定理及其推论
圆周角定理及其推论
在同圆或等圆中
知二推三
与圆有关的性质
●O
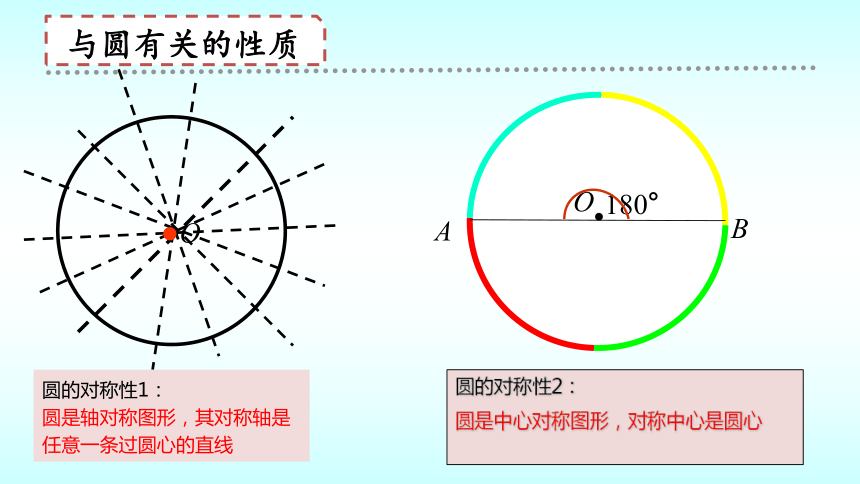
圆的对称性1:
圆是轴对称图形,其对称轴是任意一条过圆心的直线
.
O
A
B
180°
圆的对称性2:
圆是中心对称图形,对称中心是圆心
与圆有关的性质
·
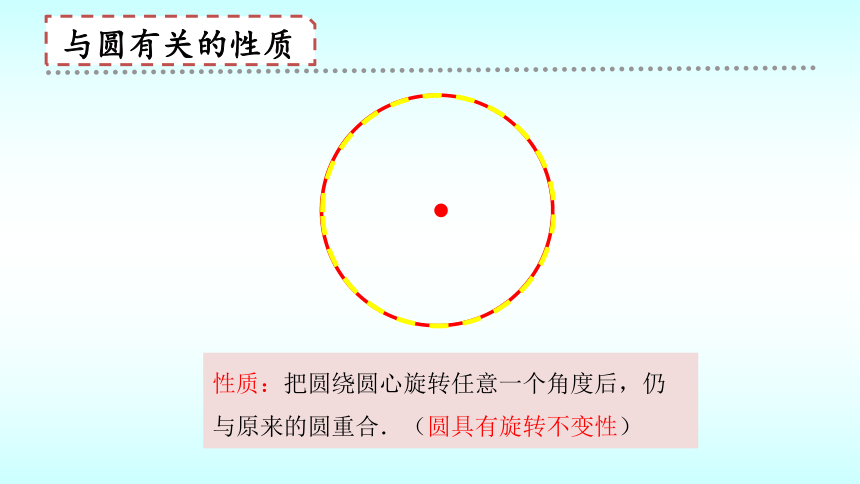
性质:把圆绕圆心旋转任意一个角度后,仍与原来的圆重合.(圆具有旋转不变性)
与圆有关的性质
·
O
A
B
C
D
A
B
O
A′
B′
O
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
与圆有关的性质
条件
CD为直径
CD⊥AB
结论
AE=BE
∠AOD=∠BOD
·
O
A
C
E
2.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理及其推论:知二推三
B
D
与圆有关的性质
4
5
3
C
OC为半径
OC⊥AB
OC平分AB
勾股定理
线段长
运用垂径定理及其推论解决一些问题,最常见的辅助线是连接半径,及过圆心作弦的垂线,利用勾股定理解决问题。
口诀“连半径,作垂直”
30o
40o
B
与圆有关的性质
如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( )
A.70° B.55° C.45° D.35°
圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
半径相等 等腰三角形
见直径,连周角,得90°
与圆有关的性质
如图,AB是⊙O 的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )。
∠BCD=110°
推论2:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
推论3:圆内接四边形的对角互补.
推论1:同弧或等弧所对的圆周角相等
与圆有关的位置关系
与圆有关的位置关系
点和圆的位置关系
直线和圆的位置关系
切线
切线的性质、 切线的判定
三角形的内切圆
切线长定理
三角形的外接圆
圆内接正多边形
与圆有关的位置关系
dd=r
d>r
点到圆心的距离与半径之间的数量关系可以判定点与圆的位置关系
点与圆的位置关系
可以转化为点到圆
心的距离与半径之
间的数量关系
点在圆外
点在圆内
点在圆上
用点到圆心的距离为d和圆的半径r
的大小关系刻画点的位置特征。
形
数
r
P
d
r
d
P
P
r
d
与圆有关的位置关系
已知☉O的半径为3,点A在☉O外,OA的取值范围是 ;
点B在☉O上,OB= ;点C(不与点O重合)在☉O内,则OC的取值范围是 .
3
0OA>3
与圆有关的位置关系
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
锐角三角形:内部
直角三角形:斜边中点
钝角三角形:外部
外心:三角形三条边的垂直平分线的交点.
●O
A
B
C
A
B
C
C
A
B
┐
●O
●O
考点突破
1.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
考点突破
2. 如图,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,∠CBE=40°,则∠AOC等于( )
A.20° B.40° C.80° D.100°
C
考点突破
3.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
B
不共线的三点确定一个圆
外心:三角形三条边的垂直平分线的交点.
考点突破
B′
60o
将军饮马
作定点的对称点,以动点所在直线为对称轴。
与圆有关的性质
与圆有关的概念
与圆有关的位置关系
谢 谢
初中数学九年级(下)
第三章 圆回顾与思考
知识框架
圆
与圆有关的性质
与圆有关的概念
与圆有关的位置关系
与圆有关的概念
·
r
O
圜,一中同长也---《墨经》
平面上到定点的距离等于定长的所有点组成的图形叫做圆,定点称为圆心,定长称为半径。
确定圆的要素是:圆心、半径.
与圆有关的概念
圆心相同,半径不同
等圆
半径相同,圆心不同
能够重合的两个圆叫做等圆.
一是圆心,确定其位置;二是半径,确定其大小.
同心圆
与圆有关的概念
·
C
O
A
B
直径AB:经过圆心的弦叫做直径
弦AC
连接圆上任意两点的线段叫做弦.
优弧ABC,记作
大于半圆的弧叫做优弧
劣弧AC,记作AC
小于半圆的弧叫劣弧
圆上任意两点间的部分叫做圆弧,简称弧.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
直径是弦,但弦不一定是直径
半圆是弧,但弧不一定是半圆;
在同圆或等圆中,能够互相重合的弧叫做等弧.
与圆有关的概念
它们都对着同一条弧
⌒
⌒
顶点在圆上,并且两边都和圆相交的角叫圆周角.
顶点在圆心,角的两边与圆相交的角叫圆心角
与圆有关的性质
圆的基本性质
圆的对称性
弧、弦、圆心角之间的关系
垂径定理及其推论
圆周角定理及其推论
在同圆或等圆中
知二推三
与圆有关的性质
●O
圆的对称性1:
圆是轴对称图形,其对称轴是任意一条过圆心的直线
.
O
A
B
180°
圆的对称性2:
圆是中心对称图形,对称中心是圆心
与圆有关的性质
·
性质:把圆绕圆心旋转任意一个角度后,仍与原来的圆重合.(圆具有旋转不变性)
与圆有关的性质
·
O
A
B
C
D
A
B
O
A′
B′
O
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
与圆有关的性质
条件
CD为直径
CD⊥AB
结论
AE=BE
∠AOD=∠BOD
·
O
A
C
E
2.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理及其推论:知二推三
B
D
与圆有关的性质
4
5
3
C
OC为半径
OC⊥AB
OC平分AB
勾股定理
线段长
运用垂径定理及其推论解决一些问题,最常见的辅助线是连接半径,及过圆心作弦的垂线,利用勾股定理解决问题。
口诀“连半径,作垂直”
30o
40o
B
与圆有关的性质
如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( )
A.70° B.55° C.45° D.35°
圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
半径相等 等腰三角形
见直径,连周角,得90°
与圆有关的性质
如图,AB是⊙O 的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )。
∠BCD=110°
推论2:直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
推论3:圆内接四边形的对角互补.
推论1:同弧或等弧所对的圆周角相等
与圆有关的位置关系
与圆有关的位置关系
点和圆的位置关系
直线和圆的位置关系
切线
切线的性质、 切线的判定
三角形的内切圆
切线长定理
三角形的外接圆
圆内接正多边形
与圆有关的位置关系
d
d>r
点到圆心的距离与半径之间的数量关系可以判定点与圆的位置关系
点与圆的位置关系
可以转化为点到圆
心的距离与半径之
间的数量关系
点在圆外
点在圆内
点在圆上
用点到圆心的距离为d和圆的半径r
的大小关系刻画点的位置特征。
形
数
r
P
d
r
d
P
P
r
d
与圆有关的位置关系
已知☉O的半径为3,点A在☉O外,OA的取值范围是 ;
点B在☉O上,OB= ;点C(不与点O重合)在☉O内,则OC的取值范围是 .
3
0
与圆有关的位置关系
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
锐角三角形:内部
直角三角形:斜边中点
钝角三角形:外部
外心:三角形三条边的垂直平分线的交点.
●O
A
B
C
A
B
C
C
A
B
┐
●O
●O
考点突破
1.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
考点突破
2. 如图,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,∠CBE=40°,则∠AOC等于( )
A.20° B.40° C.80° D.100°
C
考点突破
3.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
B
不共线的三点确定一个圆
外心:三角形三条边的垂直平分线的交点.
考点突破
B′
60o
将军饮马
作定点的对称点,以动点所在直线为对称轴。
与圆有关的性质
与圆有关的概念
与圆有关的位置关系
谢 谢
