第九章 统计 单元复习课件(共24张PPT)
文档属性
| 名称 | 第九章 统计 单元复习课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 17:29:57 | ||
图片预览







文档简介
(共24张PPT)
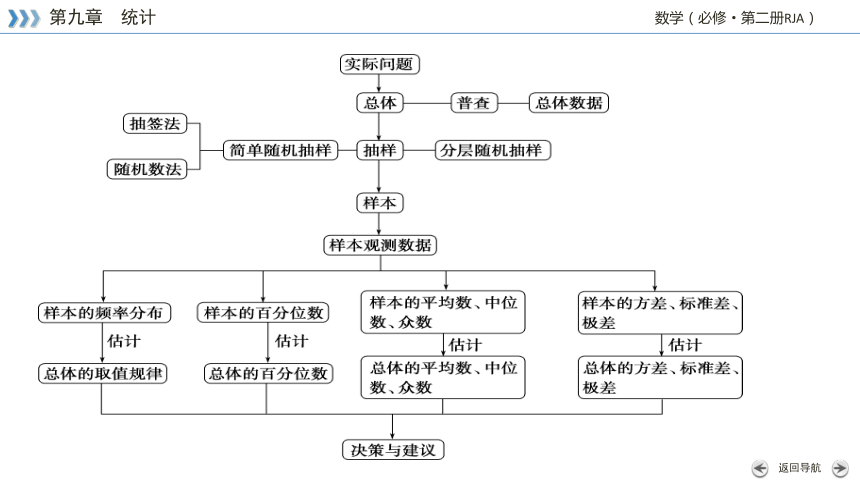
第九章
统 计
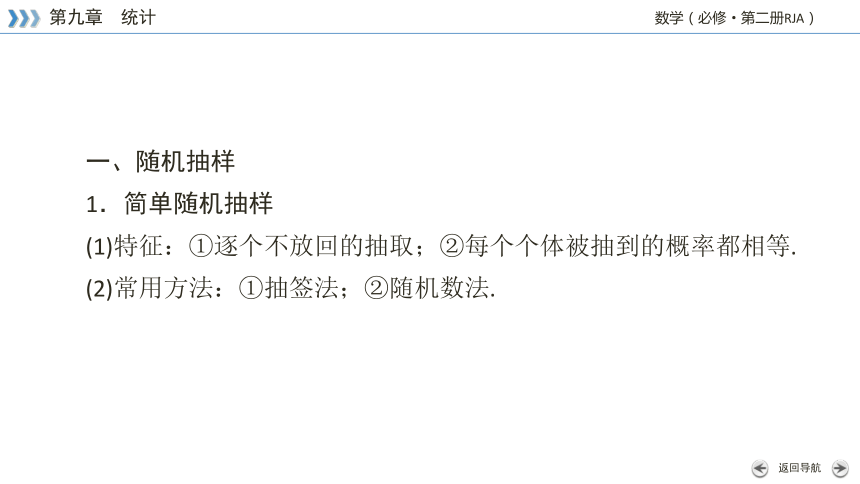
一、随机抽样
1.简单随机抽样
(1)特征:①逐个不放回的抽取;②每个个体被抽到的概率都相等.
(2)常用方法:①抽签法;②随机数法.
两种抽样方法的适用范围:当总体容量较小,样本容量也较小时,可采用抽签法;当总体容量较大,样本容量较小时,可采用随机数法;当总体中个体差异较显著时,可采用分层随机抽样.
要点一 抽样方法的选取及应用
答案 B
例1.①某小区有800户家庭,其中高收入家庭200户,中等收入家庭480户,低收入家庭120户,为了了解有关家用轿车购买力的某个指标,要从中抽取一个容量为100的样本;②从10名学生中抽取3人参加座谈会.方法:(1)简单随机抽样;(2)分层随机抽样. 则问题与方法配对正确的是( ).
(A)①(1),②(2) (B)①(2),②(1)
(C)① (1),②(1) (D)①(2),②(2)
解析 问题①中的总体是由差异明显的几部分组成的,故可采用分层随机抽样方法
问题②中总体的个数较少,故可采用简单随机抽样.
例2.某校高中部有三个年级,其中高三有学生1000人,现采用分层抽样法抽取一个容量为185的样本,已知在高一年级抽取了75人,高二年级抽取了60人,则高中部共有学生 人.
【方法指导】先求出抽取高三的样本数,再根据高三样本容量与总数之比得到抽取比例,由样本容量与总体之比等于抽取比例计算出总体.
练习:为了了解学生学习的情况,某校采用分层随机抽样的方法从高一1 200人、高二1 000人、高三n人中,抽取90人进行问卷调查.已知高一被抽取的人数为36,那么高三被抽取的人数为 ( )
A.20 B.24
C.30 D.32
[分析] 各层中抽样比例相同.
典1
B
二、用样本估计总体
1.频率分布直方图
例3下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料(单位:cm):
(1)列出样本的频率分布表(频率保留两位小数);
(2)画出频率分布直方图;
(3)估计身高低于134 cm的人数占总人数的百分比.
区间界限 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
区间界限 [142,146) [146,150) [150,154) [154,158]
人数 20 11 6 5
[解析] (1)列出样本频率分布表:
分组 频数 频率
[122,126) 5 0.04
[126,130) 8 0.07
[130,134) 10 0.08
[134,138) 22 0.18
[138,142) 33 0.28
[142,146) 20 0.17
[146,150) 11 0.09
[150,154) 6 0.05
[154,158] 5 0.04
合计 120 1.00
练习:某电子商务公司对10 000名网络购物者2018年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a=____;
(2)在这些购物者中,
消费金额在区间[0.5,0.9]内的
购物者的人数为________.
3
6 000
[解析] (1)由0.1×1.5+0.1×2.5+0.1a+0.1×2.0+0.1×0.8+0.1×0.2=1,解得a=3.
(2)消费金额在区间[0.3,0.5)内的频率为0.1×1.5+0.1×2.5=0.4,故在[0.5,0.9]内的频率为1-0.4=0.6.
因此,消费金额在区间[0.5,0.9]内的购物者的人数为0.6×10 000=6 000.
2.百分位数与总体百分位数的估计
(1)第p百分位数:一般地,一组数据的第p百分位数是这样一个值,它使得这组数数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
(2)可以用样本数据的百分位数估计总体的百分位数.
例4:数学兴趣小组调查了12位大学毕业生的起始月薪,具体如表:
试确定第85百分位数.
[分析] 首先从小到大排列各数,再计算i.
[解析] 将数据从小到大排列:3 710,3 755,3 850,3 880,3 880,3 890,3 920,3 940,3 950,4 050,4 130,4 325.计算i=n×p%=12×85%=10.2,显然i不是整数,所以将i=10.2向上取整,大于i的比邻整数11即为第85百分位数的位置,所以第85百分位数是4 130.
学生编号 起始月薪
1 3 850
2 3 950
3 4 050
4 3 880
5 3 755
6 3 710
7 3 890
8 4 130
9 3 940
10 4 325
11 3 920
12 3 880
练习:新华中学高一年级共有1 200人参加了学校组织的诗词背诵比赛,已知所有学生成绩的第70百分位数是75分,则成绩大于或等于75分的学生至少有______人 ( )
A.348 B.360
C.372 D.384
[解析] 将1 200人的成绩按照从小到大的顺序排列,75分排在第70百分位数,就是比75分少的人数占了70%,所以成绩大于或等于75分的学生至少占了30%,其人数为1 200×30%=360.
B
3.众数、中位数和平均数与总体集中趋势的估计
4.总体集中趋势的估计
例5:根据某市所在地区的收入水平、消费水平等情况,拟将家庭年收入低于1.5万元的家庭确定为“贫困户”,家庭年收入在[6.5,7.5)万元的家庭确定为“小康户”,家庭年收入在[7.5,8.5]万元的家庭确定为“富裕户”,该市扶贫办为了打好精准脱贫攻坚战,在所辖某县的100万户家庭中随机抽取200户家庭,对其2019年的全年收入进行调查,抽查结果的频率分布直方图如图所示.
4
练习:如图是某班一次考试结果的频率分布直方图,据此估计该班这次考试的平均分为_____.
75
第九章
统 计
一、随机抽样
1.简单随机抽样
(1)特征:①逐个不放回的抽取;②每个个体被抽到的概率都相等.
(2)常用方法:①抽签法;②随机数法.
两种抽样方法的适用范围:当总体容量较小,样本容量也较小时,可采用抽签法;当总体容量较大,样本容量较小时,可采用随机数法;当总体中个体差异较显著时,可采用分层随机抽样.
要点一 抽样方法的选取及应用
答案 B
例1.①某小区有800户家庭,其中高收入家庭200户,中等收入家庭480户,低收入家庭120户,为了了解有关家用轿车购买力的某个指标,要从中抽取一个容量为100的样本;②从10名学生中抽取3人参加座谈会.方法:(1)简单随机抽样;(2)分层随机抽样. 则问题与方法配对正确的是( ).
(A)①(1),②(2) (B)①(2),②(1)
(C)① (1),②(1) (D)①(2),②(2)
解析 问题①中的总体是由差异明显的几部分组成的,故可采用分层随机抽样方法
问题②中总体的个数较少,故可采用简单随机抽样.
例2.某校高中部有三个年级,其中高三有学生1000人,现采用分层抽样法抽取一个容量为185的样本,已知在高一年级抽取了75人,高二年级抽取了60人,则高中部共有学生 人.
【方法指导】先求出抽取高三的样本数,再根据高三样本容量与总数之比得到抽取比例,由样本容量与总体之比等于抽取比例计算出总体.
练习:为了了解学生学习的情况,某校采用分层随机抽样的方法从高一1 200人、高二1 000人、高三n人中,抽取90人进行问卷调查.已知高一被抽取的人数为36,那么高三被抽取的人数为 ( )
A.20 B.24
C.30 D.32
[分析] 各层中抽样比例相同.
典1
B
二、用样本估计总体
1.频率分布直方图
例3下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料(单位:cm):
(1)列出样本的频率分布表(频率保留两位小数);
(2)画出频率分布直方图;
(3)估计身高低于134 cm的人数占总人数的百分比.
区间界限 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
区间界限 [142,146) [146,150) [150,154) [154,158]
人数 20 11 6 5
[解析] (1)列出样本频率分布表:
分组 频数 频率
[122,126) 5 0.04
[126,130) 8 0.07
[130,134) 10 0.08
[134,138) 22 0.18
[138,142) 33 0.28
[142,146) 20 0.17
[146,150) 11 0.09
[150,154) 6 0.05
[154,158] 5 0.04
合计 120 1.00
练习:某电子商务公司对10 000名网络购物者2018年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a=____;
(2)在这些购物者中,
消费金额在区间[0.5,0.9]内的
购物者的人数为________.
3
6 000
[解析] (1)由0.1×1.5+0.1×2.5+0.1a+0.1×2.0+0.1×0.8+0.1×0.2=1,解得a=3.
(2)消费金额在区间[0.3,0.5)内的频率为0.1×1.5+0.1×2.5=0.4,故在[0.5,0.9]内的频率为1-0.4=0.6.
因此,消费金额在区间[0.5,0.9]内的购物者的人数为0.6×10 000=6 000.
2.百分位数与总体百分位数的估计
(1)第p百分位数:一般地,一组数据的第p百分位数是这样一个值,它使得这组数数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
(2)可以用样本数据的百分位数估计总体的百分位数.
例4:数学兴趣小组调查了12位大学毕业生的起始月薪,具体如表:
试确定第85百分位数.
[分析] 首先从小到大排列各数,再计算i.
[解析] 将数据从小到大排列:3 710,3 755,3 850,3 880,3 880,3 890,3 920,3 940,3 950,4 050,4 130,4 325.计算i=n×p%=12×85%=10.2,显然i不是整数,所以将i=10.2向上取整,大于i的比邻整数11即为第85百分位数的位置,所以第85百分位数是4 130.
学生编号 起始月薪
1 3 850
2 3 950
3 4 050
4 3 880
5 3 755
6 3 710
7 3 890
8 4 130
9 3 940
10 4 325
11 3 920
12 3 880
练习:新华中学高一年级共有1 200人参加了学校组织的诗词背诵比赛,已知所有学生成绩的第70百分位数是75分,则成绩大于或等于75分的学生至少有______人 ( )
A.348 B.360
C.372 D.384
[解析] 将1 200人的成绩按照从小到大的顺序排列,75分排在第70百分位数,就是比75分少的人数占了70%,所以成绩大于或等于75分的学生至少占了30%,其人数为1 200×30%=360.
B
3.众数、中位数和平均数与总体集中趋势的估计
4.总体集中趋势的估计
例5:根据某市所在地区的收入水平、消费水平等情况,拟将家庭年收入低于1.5万元的家庭确定为“贫困户”,家庭年收入在[6.5,7.5)万元的家庭确定为“小康户”,家庭年收入在[7.5,8.5]万元的家庭确定为“富裕户”,该市扶贫办为了打好精准脱贫攻坚战,在所辖某县的100万户家庭中随机抽取200户家庭,对其2019年的全年收入进行调查,抽查结果的频率分布直方图如图所示.
4
练习:如图是某班一次考试结果的频率分布直方图,据此估计该班这次考试的平均分为_____.
75
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
