1.1 认识负数 课件(共17张PPT) 2025-2026学年数学湘教版(2024)七年级上册
文档属性
| 名称 | 1.1 认识负数 课件(共17张PPT) 2025-2026学年数学湘教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 929.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 06:08:26 | ||
图片预览





文档简介
(共17张PPT)
第1章 有理数
1.1 认识负数
1.知道正数、负数和0的意义,体会引入负数的必要性.
2.会用正数、负数表示相反意义的量.
3.知道有理数的意义,会对有理数进行分类.
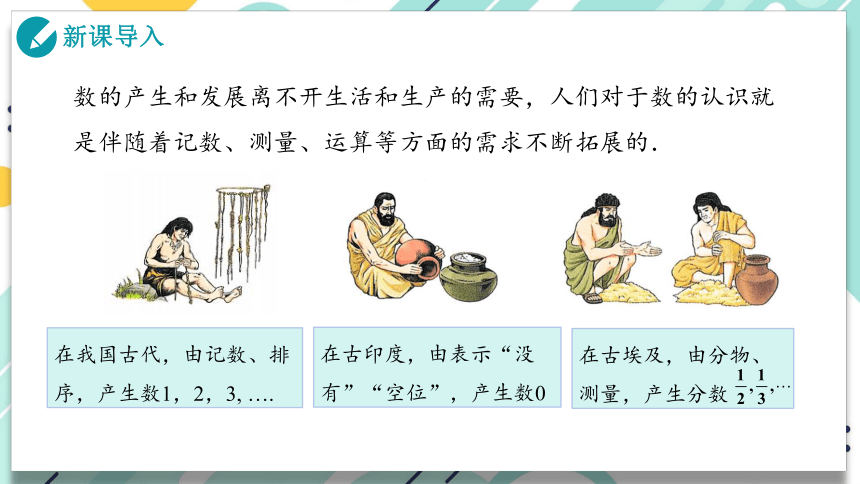
在我国古代,由记数、排序,产生数1,2,3, ….
在古印度,由表示“没有”“空位”,产生数0
在古埃及,由分物、测量,产生分数
数的产生和发展离不开生活和生产的需要,人们对于数的认识就是伴随着记数、测量、运算等方面的需求不断拓展的.
在预报北京市某天的天气时,播音员说:“北京,晴,局部多云,零下6 ℃到5 ℃”.
问题1:“零下6 ℃”和“5 ℃”是具有相反意义的量,生活中还有哪些具有相反意义的量(属性相同,表示的意义却相反)?说一说.
问题2:如何在数学上简洁的表示像“零下6 ℃”和“5 ℃”这样具有相反意义的量呢?和同伴交流.
水位“升高5厘米”和“水位降低5厘米”,收益“盈利10000元”和“亏损6000元”或“收入10000元”和“支出6000元”,价格“上涨1元”和“下跌1元”,等等.
正数和负数
为了表示某一问题中具有相反意义的两种量,我们把其中一种意义的量,如水位升高、价格上涨等规定为正的,用小学学过的大于 0 的数,如 2,0.6, 等
来表示它们,这样的数叫作正数.
把与它意义相反的量,如水位降低、价格下跌等规定为负的,用在正数前面添上“-”(读作“负号”)的数,如-3,-0. 4,- 等来表示它们,这样的数
叫作负数.
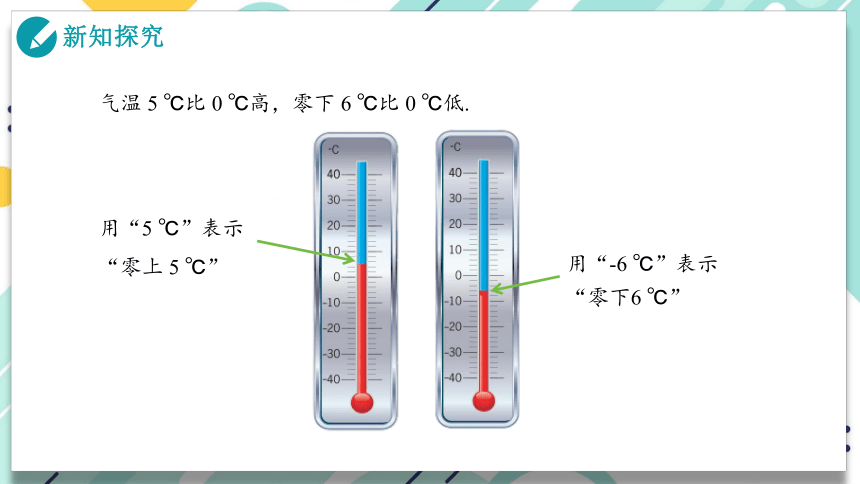
气温 5 ℃比 0 ℃高,零下 6 ℃比 0 ℃低.
用“5 ℃”表示“零上 5 ℃”
用“-6 ℃”表示“零下6 ℃”
正数的前面也可添上“+”(称作“正号”).
如 +3,+ 0. 618,+ 等.
注意:
0既不是正数,也不是负数.
正号可省略不写
读作:正3
正数和0统称为非负数.
负数和0统称为非正数.
2020 年 12 月 8 日,中国、尼泊尔两国向全世界正式宣布珠穆朗玛峰峰顶的最新高度为8848. 86 m.
2020年 11月 10日 8时 12分,我国“奋斗者”号载人潜水器在马里亚纳海沟成功坐底,坐底深度为10909 m,刷新中国载人深潜纪录.
将测量起点记作 0,珠穆朗玛峰峰顶的高度和“奋斗者”号载人潜水器的
坐底深度分别如何表示?
解:珠穆朗玛峰峰顶的高度表示为8848. 86 m.
“奋斗者”号载人潜水器的坐底深度表示为-10909 m.
议一议
小华、小楠从同一点 O 出发,沿一条笔直的东西向人行道分别去图书馆和
体育馆,已知图书馆在出发点 O 的东边 2 km 处,体育馆在出发点 O 的西边 4 km 处.
西
东
图书馆
O
体育馆
如果规定向东用正数表示,则小华应向______走______km,可记为______km,小楠应向______走______km,可记为______km.
+ 2
- 4
做一做
东
小华
小楠
2
西
4
像 1,2,3,…这样的正数称为正整数.
像 -1,-2,-3,…这样的负数称为负整数.
像 …这样的正数称为正分数.
像 …这样的负数称为负分数.
正整数前添负号
正整数前添负号
如 1.59 = ,0.125 = , = , = .
正有限小数和正无限循坏小数都可以化为正分数的形式.
负有限小数和负无限循环小数也可化成负分数的形式.
如
正整数、负整数、零统称为整数,正分数、负分数统称为分数.
小数和分数只是两种表现形式,数的本质是一样的.
正有理数、负有理数、零统称为有理数.
正整数可看作分母为1的正分数,负整数也可看作分母为1的正分数.
如
把可以化成正分数形式的数,称为正有理数.
把可以化成负分数形式的数,称为负有理数.
要注意分数的分子和分母必须是整数.
有理数的分类:
正整数 如 1,2,3.
正分数 如
负整数 如 -1,-2,-3.
负分数 如
有理数
正有理数
零
负有理数
有理数
整数
分数
正整数
零
负整数
正分数
负分数
1.按符号分
2.按定义分
还有其他的分类方式吗?
把下列各数填在相应的横线上:
(1)正有理数: ;
(2)零: ;
(3)负有理数: .
练一练
0
1.下列关于“0”的叙述中,正确的有( )
①0是正数与负数的分界 ②0比任何负数都大
③0只表示没有 ④0常用来表示某种量的基准
A.1个 B.2个 C.3个 D.4个
C
2.银行电子账单交易明细单上,存入的钱用正数表示,支出的钱用负数表示.8月15日张叔叔存入银行2000元,交易明细单上记作 元;8月28日他支出1600元,交易明细单上记作 元.
+2000
-1600
3.把下列各数填在相应的横线上:
-1 ,-0.5 ,0 , , ,-5.14 ,-78 ,-0.37 , .
整数: ;
分数: .
-1 ,0 ,-78
-0.5 , , ,-5.14 ,-0.37 ,
认识负数
正数、负数的概念
大于0的数叫作正数.
在正数前面添上“-”(称作“负号”)的数叫作负数
具有相反意义的量
①必须是同类量,而且是成对出现的;
②只要求意义相反,不要求数量一定相等.
有理数的分类
第1章 有理数
1.1 认识负数
1.知道正数、负数和0的意义,体会引入负数的必要性.
2.会用正数、负数表示相反意义的量.
3.知道有理数的意义,会对有理数进行分类.
在我国古代,由记数、排序,产生数1,2,3, ….
在古印度,由表示“没有”“空位”,产生数0
在古埃及,由分物、测量,产生分数
数的产生和发展离不开生活和生产的需要,人们对于数的认识就是伴随着记数、测量、运算等方面的需求不断拓展的.
在预报北京市某天的天气时,播音员说:“北京,晴,局部多云,零下6 ℃到5 ℃”.
问题1:“零下6 ℃”和“5 ℃”是具有相反意义的量,生活中还有哪些具有相反意义的量(属性相同,表示的意义却相反)?说一说.
问题2:如何在数学上简洁的表示像“零下6 ℃”和“5 ℃”这样具有相反意义的量呢?和同伴交流.
水位“升高5厘米”和“水位降低5厘米”,收益“盈利10000元”和“亏损6000元”或“收入10000元”和“支出6000元”,价格“上涨1元”和“下跌1元”,等等.
正数和负数
为了表示某一问题中具有相反意义的两种量,我们把其中一种意义的量,如水位升高、价格上涨等规定为正的,用小学学过的大于 0 的数,如 2,0.6, 等
来表示它们,这样的数叫作正数.
把与它意义相反的量,如水位降低、价格下跌等规定为负的,用在正数前面添上“-”(读作“负号”)的数,如-3,-0. 4,- 等来表示它们,这样的数
叫作负数.
气温 5 ℃比 0 ℃高,零下 6 ℃比 0 ℃低.
用“5 ℃”表示“零上 5 ℃”
用“-6 ℃”表示“零下6 ℃”
正数的前面也可添上“+”(称作“正号”).
如 +3,+ 0. 618,+ 等.
注意:
0既不是正数,也不是负数.
正号可省略不写
读作:正3
正数和0统称为非负数.
负数和0统称为非正数.
2020 年 12 月 8 日,中国、尼泊尔两国向全世界正式宣布珠穆朗玛峰峰顶的最新高度为8848. 86 m.
2020年 11月 10日 8时 12分,我国“奋斗者”号载人潜水器在马里亚纳海沟成功坐底,坐底深度为10909 m,刷新中国载人深潜纪录.
将测量起点记作 0,珠穆朗玛峰峰顶的高度和“奋斗者”号载人潜水器的
坐底深度分别如何表示?
解:珠穆朗玛峰峰顶的高度表示为8848. 86 m.
“奋斗者”号载人潜水器的坐底深度表示为-10909 m.
议一议
小华、小楠从同一点 O 出发,沿一条笔直的东西向人行道分别去图书馆和
体育馆,已知图书馆在出发点 O 的东边 2 km 处,体育馆在出发点 O 的西边 4 km 处.
西
东
图书馆
O
体育馆
如果规定向东用正数表示,则小华应向______走______km,可记为______km,小楠应向______走______km,可记为______km.
+ 2
- 4
做一做
东
小华
小楠
2
西
4
像 1,2,3,…这样的正数称为正整数.
像 -1,-2,-3,…这样的负数称为负整数.
像 …这样的正数称为正分数.
像 …这样的负数称为负分数.
正整数前添负号
正整数前添负号
如 1.59 = ,0.125 = , = , = .
正有限小数和正无限循坏小数都可以化为正分数的形式.
负有限小数和负无限循环小数也可化成负分数的形式.
如
正整数、负整数、零统称为整数,正分数、负分数统称为分数.
小数和分数只是两种表现形式,数的本质是一样的.
正有理数、负有理数、零统称为有理数.
正整数可看作分母为1的正分数,负整数也可看作分母为1的正分数.
如
把可以化成正分数形式的数,称为正有理数.
把可以化成负分数形式的数,称为负有理数.
要注意分数的分子和分母必须是整数.
有理数的分类:
正整数 如 1,2,3.
正分数 如
负整数 如 -1,-2,-3.
负分数 如
有理数
正有理数
零
负有理数
有理数
整数
分数
正整数
零
负整数
正分数
负分数
1.按符号分
2.按定义分
还有其他的分类方式吗?
把下列各数填在相应的横线上:
(1)正有理数: ;
(2)零: ;
(3)负有理数: .
练一练
0
1.下列关于“0”的叙述中,正确的有( )
①0是正数与负数的分界 ②0比任何负数都大
③0只表示没有 ④0常用来表示某种量的基准
A.1个 B.2个 C.3个 D.4个
C
2.银行电子账单交易明细单上,存入的钱用正数表示,支出的钱用负数表示.8月15日张叔叔存入银行2000元,交易明细单上记作 元;8月28日他支出1600元,交易明细单上记作 元.
+2000
-1600
3.把下列各数填在相应的横线上:
-1 ,-0.5 ,0 , , ,-5.14 ,-78 ,-0.37 , .
整数: ;
分数: .
-1 ,0 ,-78
-0.5 , , ,-5.14 ,-0.37 ,
认识负数
正数、负数的概念
大于0的数叫作正数.
在正数前面添上“-”(称作“负号”)的数叫作负数
具有相反意义的量
①必须是同类量,而且是成对出现的;
②只要求意义相反,不要求数量一定相等.
有理数的分类
同课章节目录
