1.4.1 课时1 有理数的加法法则 课件(共18张PPT) 2025-2026学年数学湘教版(2024)七年级上册
文档属性
| 名称 | 1.4.1 课时1 有理数的加法法则 课件(共18张PPT) 2025-2026学年数学湘教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 451.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 06:17:36 | ||
图片预览






文档简介
(共18张PPT)
课时1 有理数的加法法则
1.4.1 有理数的加法
1.经历有理数加法法则的探索过程,掌握有理数的加法法则.
2.能熟练进行有理数的加法运算.
知识点 1 两个负数相加
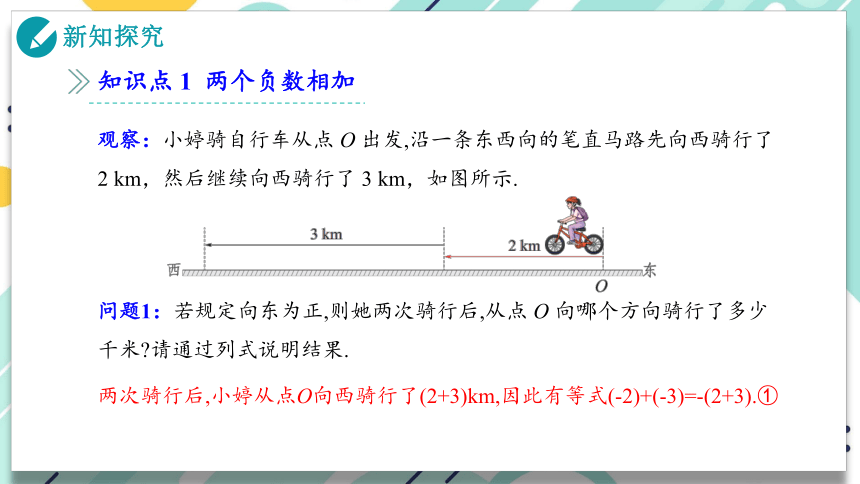
观察:小婷骑自行车从点 O 出发,沿一条东西向的笔直马路先向西骑行了 2 km,然后继续向西骑行了 3 km,如图所示.
两次骑行后,小婷从点O向西骑行了(2+3)km,因此有等式(-2)+(-3)=-(2+3).①
问题1:若规定向东为正,则她两次骑行后,从点 O 向哪个方向骑行了多少千米 请通过列式说明结果.
(-2)+(-3)=-(2+3).①
问题2:观察上述算式中两个加数的符号与和的符号,它们有什么关系 和的绝对值与两个加数的绝对值的和又有怎样的关系
都是负号.和的绝对值与两个加数的绝对值的和相等.
思考:由此你能提出什么猜想?
用字母表示:若 a < 0, b < 0,则 a + b = -( | a | + | b | )
两个负数相加,结果是负数,并把它们的绝对值相加.
例1 计算:
(1) (-8) + (-12); (2) (-3.75) + (-0.25) ;
解:(1) (-8) + (-12) =
(2) (-3.75) + (-0.25) =
-
(8 + 12)
= -20.
-(3.75+0.25)
= -4.
知识点 2 异号两数相加
(1)将前面“观察”中的条件改为“先向东骑行了4 km,然后因故掉头向西骑行了1 km”;在其他条件均不变的情况下,则她两次骑行后,从点O向哪个方向骑行了多少千米
如图,由于小婷掉头向西骑行1 km抵消了原来向东骑行4 km中的1 km,
因此两次骑行后,相当于从点O向东骑行了(4-1)km.
于是有等式4+(-1)=+(4-1).②
(2)将前面“观察”中的条件改为“先向西骑行了3 km,然后因故掉头向东骑行了1 km”.在其他条件均不变的情况下,则她两次骑行后,从点O
向哪个方向骑行了多少千米
如图,由于小婷掉头向东骑行1 km抵消了原来向西骑行3 km中的1 km,
因此两次骑行后,相当于从点O向西骑行了(3-1)km.
于是有等式(-3)+1=-(3-1).③
思考:观察上述两个算式,想一想异号两数相加时:
(1)和的符号怎么确定
(2)和的绝对值与两个加数的绝对值有什么关系
4+(-1)=+(4-1).②
(-3)+1=-(3-1).③
解:(1)和的符号与绝对值大的数的符号相同.
(2)和的绝对值等于较大的绝对值减去较小的绝对值.
用字母表示:
若 a > 0, b < 0, 且 | a | > | b |, 则 a + b = +( | a | - | b | )
若 a > 0, b < 0, 且 | a | < | b |, 则 a + b = -( | b | - | a | )
异号两数相加,当正数的绝对值较大时,得正数,
并用较大的绝对值减去较小的绝对值;
当负数的绝对值较大时,得负数,并用较大的绝对值减去较小的绝对值.
例2 计算:
(1) (-5) + 9; (2) 7 + (-10) ;
解:(1) (-5)+9=
(2) 7 + (-10) =
+
9-5
=4.
-
(10-7)
=-3.
有理数加法的计算步骤:
1.确定符号:判断同号还是异号两数相加.若是同号,取与加数相同的符号;若是异号,判断哪个数的绝对值较大,取绝对值较大数的符号.
2.确定绝对值:用两个加数的绝对值相加或相减来求和的绝对值.
知识点 3 与0有关的加法
议一议:
(1)异号两数相加,当它们的绝对值相等,即互为相反数时,
其和为多少
(2)一个数与0相加,和为多少
互为相反数的两个数相加得0.
一个数与0相加,仍得这个数.
如果两个数的和等于0,那么这两个数互为相反数.
1.计算:
(-5) + (-7) =
(-1.2) + (-0.8) =
-12
6 + (-4) =
(-9) + 5 =
12 + (-12) =
0 + (-5.6) =
2
0
-5.6
-4
-2
-1
0
2.判断题
(1)两个负数相加,结果一定是负数.
(2)一个正数和一个负数相加,结果一定是负数.
(2)如果两个数的和是0,那么它们互为相反数.
( )
( )
( )
√
×
√
3.某地白天温度上升了8 ℃,晚上又下降了5 ℃,求温度变化的最终结果.
解:8+(-5)=3.
答:温度最终上升了3 ℃.
有
理
数
的
加
法
法
则
同号
特殊
异号
两个负数相加,结果是负数,并把它们的绝对值相加.
1.当正数的绝对值较大时,得正数,并用较大的绝对值减去较小的绝对值;
2.当负数的绝对值较大时,得负数,并用较大的绝对值减去较小的绝对值.
1.互为相反数的两个数相加得0.
2.一个数与0相加,仍得这个数.
计算步骤:1.确定符号;2.确定绝对值.
课时1 有理数的加法法则
1.4.1 有理数的加法
1.经历有理数加法法则的探索过程,掌握有理数的加法法则.
2.能熟练进行有理数的加法运算.
知识点 1 两个负数相加
观察:小婷骑自行车从点 O 出发,沿一条东西向的笔直马路先向西骑行了 2 km,然后继续向西骑行了 3 km,如图所示.
两次骑行后,小婷从点O向西骑行了(2+3)km,因此有等式(-2)+(-3)=-(2+3).①
问题1:若规定向东为正,则她两次骑行后,从点 O 向哪个方向骑行了多少千米 请通过列式说明结果.
(-2)+(-3)=-(2+3).①
问题2:观察上述算式中两个加数的符号与和的符号,它们有什么关系 和的绝对值与两个加数的绝对值的和又有怎样的关系
都是负号.和的绝对值与两个加数的绝对值的和相等.
思考:由此你能提出什么猜想?
用字母表示:若 a < 0, b < 0,则 a + b = -( | a | + | b | )
两个负数相加,结果是负数,并把它们的绝对值相加.
例1 计算:
(1) (-8) + (-12); (2) (-3.75) + (-0.25) ;
解:(1) (-8) + (-12) =
(2) (-3.75) + (-0.25) =
-
(8 + 12)
= -20.
-(3.75+0.25)
= -4.
知识点 2 异号两数相加
(1)将前面“观察”中的条件改为“先向东骑行了4 km,然后因故掉头向西骑行了1 km”;在其他条件均不变的情况下,则她两次骑行后,从点O向哪个方向骑行了多少千米
如图,由于小婷掉头向西骑行1 km抵消了原来向东骑行4 km中的1 km,
因此两次骑行后,相当于从点O向东骑行了(4-1)km.
于是有等式4+(-1)=+(4-1).②
(2)将前面“观察”中的条件改为“先向西骑行了3 km,然后因故掉头向东骑行了1 km”.在其他条件均不变的情况下,则她两次骑行后,从点O
向哪个方向骑行了多少千米
如图,由于小婷掉头向东骑行1 km抵消了原来向西骑行3 km中的1 km,
因此两次骑行后,相当于从点O向西骑行了(3-1)km.
于是有等式(-3)+1=-(3-1).③
思考:观察上述两个算式,想一想异号两数相加时:
(1)和的符号怎么确定
(2)和的绝对值与两个加数的绝对值有什么关系
4+(-1)=+(4-1).②
(-3)+1=-(3-1).③
解:(1)和的符号与绝对值大的数的符号相同.
(2)和的绝对值等于较大的绝对值减去较小的绝对值.
用字母表示:
若 a > 0, b < 0, 且 | a | > | b |, 则 a + b = +( | a | - | b | )
若 a > 0, b < 0, 且 | a | < | b |, 则 a + b = -( | b | - | a | )
异号两数相加,当正数的绝对值较大时,得正数,
并用较大的绝对值减去较小的绝对值;
当负数的绝对值较大时,得负数,并用较大的绝对值减去较小的绝对值.
例2 计算:
(1) (-5) + 9; (2) 7 + (-10) ;
解:(1) (-5)+9=
(2) 7 + (-10) =
+
9-5
=4.
-
(10-7)
=-3.
有理数加法的计算步骤:
1.确定符号:判断同号还是异号两数相加.若是同号,取与加数相同的符号;若是异号,判断哪个数的绝对值较大,取绝对值较大数的符号.
2.确定绝对值:用两个加数的绝对值相加或相减来求和的绝对值.
知识点 3 与0有关的加法
议一议:
(1)异号两数相加,当它们的绝对值相等,即互为相反数时,
其和为多少
(2)一个数与0相加,和为多少
互为相反数的两个数相加得0.
一个数与0相加,仍得这个数.
如果两个数的和等于0,那么这两个数互为相反数.
1.计算:
(-5) + (-7) =
(-1.2) + (-0.8) =
-12
6 + (-4) =
(-9) + 5 =
12 + (-12) =
0 + (-5.6) =
2
0
-5.6
-4
-2
-1
0
2.判断题
(1)两个负数相加,结果一定是负数.
(2)一个正数和一个负数相加,结果一定是负数.
(2)如果两个数的和是0,那么它们互为相反数.
( )
( )
( )
√
×
√
3.某地白天温度上升了8 ℃,晚上又下降了5 ℃,求温度变化的最终结果.
解:8+(-5)=3.
答:温度最终上升了3 ℃.
有
理
数
的
加
法
法
则
同号
特殊
异号
两个负数相加,结果是负数,并把它们的绝对值相加.
1.当正数的绝对值较大时,得正数,并用较大的绝对值减去较小的绝对值;
2.当负数的绝对值较大时,得负数,并用较大的绝对值减去较小的绝对值.
1.互为相反数的两个数相加得0.
2.一个数与0相加,仍得这个数.
计算步骤:1.确定符号;2.确定绝对值.
同课章节目录
