1.4.2 有理数的减法 课件(共12张PPT) 2025-2026学年数学湘教版(2024)七年级上册
文档属性
| 名称 | 1.4.2 有理数的减法 课件(共12张PPT) 2025-2026学年数学湘教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 323.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 06:25:21 | ||
图片预览




文档简介
(共12张PPT)
1.4 有理数的加法和减法
1.4.2 有理数的减法
1.能将有理数的减法运算转化为有理数的加法运算.
2.能熟练地进行有理数的减法运算.
某天北京市的最高气温是 -1 ℃,最低气温是 -9 ℃.
问题1:借助温度计可知,-1 ℃比-9 ℃高出多少度?
.5
-10
0
10
-10
0
10
℃
高8 ℃
问题2:由此可以列出怎样的算式?
(-1)-(-9)=8
问题3:(-1)-(-9)与(-1)+9的结果相等吗?
相等
-1 ℃
-9 ℃
活动1:发现有理数减法的规律
知识点 1 有理数的减法
计算下列各题,看看有什么规律
(1)15-6= ;
(2)19-3= ;
(3)12-0= ;
(4)由11+(-3)=8,可得8-(-3)= ;
(5)由13+(-3)=10,可得10-(-3)= ;
9
16
12
11
13
思考:对比左、右两列算式,它们有什么区别和联系 由此你能得出什么结论
15+(-6)= .
19+(-3)= .
12+0= .
8+3= .
10+3= .
11
13
9
16
12
活动2:验证规律
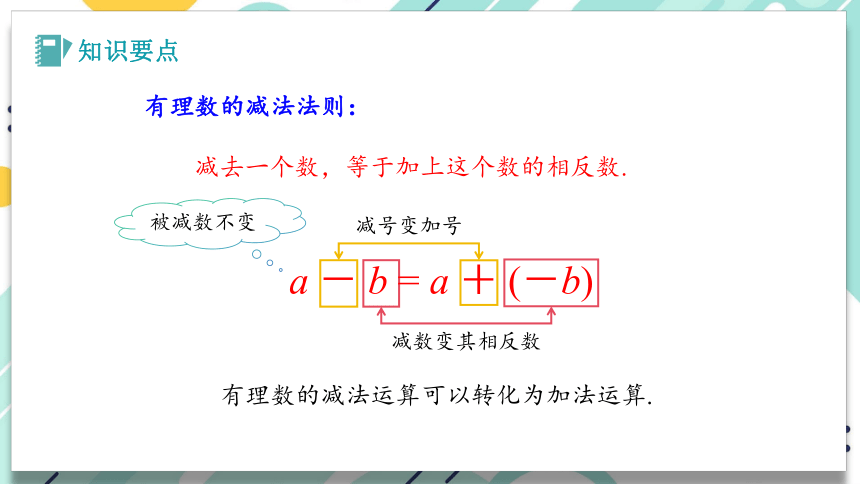
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
a - b = a + (-b)
被减数不变
减号变加号
减数变其相反数
有理数的减法运算可以转化为加法运算.
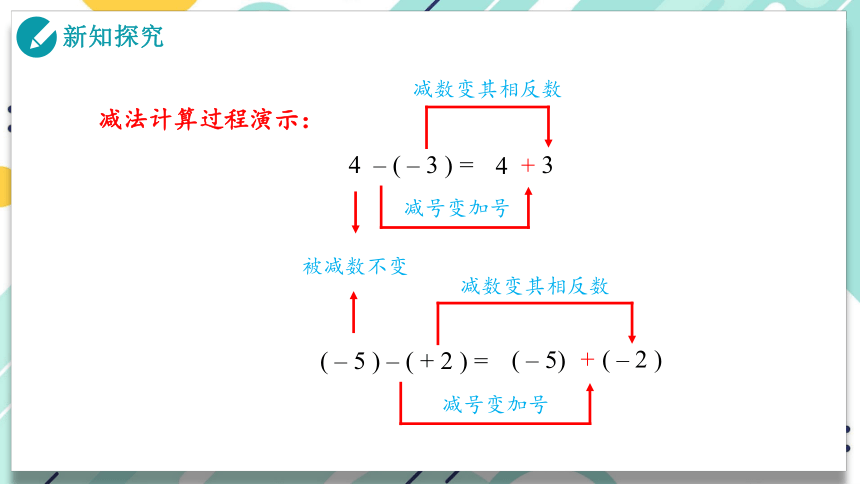
减法计算过程演示:
4 – ( – 3 ) =
4
( – 5 ) – ( + 2 ) =
( – 5)
减号变加号
减数变其相反数
减数变其相反数
减号变加号
被减数不变
+
3
+
( – 2 )
例1 计算:
解:
(1) 0 - (-3.18) = 0 + 3.18
(2) 5.3 - (-2.7) = 5.3 + 2.7
(3) (-10) - (-6) = (-10) + 6
(1) 0 - (-3.18); (2) 5.3 - (-2.7);
(3) (-10) - (-6); (4) .
(4)
= 3.18.
= 8.
+ (- )
= -10.2.
6.5
= - 4.
计算有理数减法的一般步骤:
(1)将减号变为加号,同时将减数变为它的相反数;
(2)利用有理数的加法法则计算.
两变:(1)改变运算符号:减号变加号;
(2)改变减数的符号:正数变负数,负数变正数.
两不变:(1)在运算过程中,被减数与减数的位置不变;
(2)被减数的符号不变.
注意:
月球表面的温度在白昼可升到 127 ℃,在黑夜可降到-183 ℃. 月球表面昼夜温差(最高气温-最低气温)可达多少
解:127-(-183)=127+183=310(℃).
答:月球表面昼夜温差可达 310 ℃.
知识点 2 有理数减法的应用
1.下列用算式表示“比-3 ℃低6 ℃的温度”正确的是 ( )
A.-3+6=3 B.-3-6=-9
C.-3+6=-9 D.-3-6=-3
2.下列说法正确的是 ( )
A.5 - (-5) = 0
B.0 - (-5) = -5
C.两个数相减,被减数一定大于减数
D.减去一个正数,差一定小于被减数
B
D
(3) 6.25 - (-0.75); (4) .
(3) 6.25 - (-0.75) = 6.25 + 0.75 = 7.
(4) .
3. 将下列减法转化为加法并计算:
(1) (-8) - (-3) ; (2) 10 - (-15);
(1) (-8) - (-3) = -8 + 3 = -5.
(2) 10 - (-15) = 10 + 15 = 25.
解:
有
理
数
的
减
法
法则
运算
a - b = a + (-b)
公式
本质
将减法转化为加法.
减数取其相反数.
两不变 被减数和减数的位置、被减数的符号.
两变 减号变加号、减数变其相反数.
应用
1.4 有理数的加法和减法
1.4.2 有理数的减法
1.能将有理数的减法运算转化为有理数的加法运算.
2.能熟练地进行有理数的减法运算.
某天北京市的最高气温是 -1 ℃,最低气温是 -9 ℃.
问题1:借助温度计可知,-1 ℃比-9 ℃高出多少度?
.5
-10
0
10
-10
0
10
℃
高8 ℃
问题2:由此可以列出怎样的算式?
(-1)-(-9)=8
问题3:(-1)-(-9)与(-1)+9的结果相等吗?
相等
-1 ℃
-9 ℃
活动1:发现有理数减法的规律
知识点 1 有理数的减法
计算下列各题,看看有什么规律
(1)15-6= ;
(2)19-3= ;
(3)12-0= ;
(4)由11+(-3)=8,可得8-(-3)= ;
(5)由13+(-3)=10,可得10-(-3)= ;
9
16
12
11
13
思考:对比左、右两列算式,它们有什么区别和联系 由此你能得出什么结论
15+(-6)= .
19+(-3)= .
12+0= .
8+3= .
10+3= .
11
13
9
16
12
活动2:验证规律
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
a - b = a + (-b)
被减数不变
减号变加号
减数变其相反数
有理数的减法运算可以转化为加法运算.
减法计算过程演示:
4 – ( – 3 ) =
4
( – 5 ) – ( + 2 ) =
( – 5)
减号变加号
减数变其相反数
减数变其相反数
减号变加号
被减数不变
+
3
+
( – 2 )
例1 计算:
解:
(1) 0 - (-3.18) = 0 + 3.18
(2) 5.3 - (-2.7) = 5.3 + 2.7
(3) (-10) - (-6) = (-10) + 6
(1) 0 - (-3.18); (2) 5.3 - (-2.7);
(3) (-10) - (-6); (4) .
(4)
= 3.18.
= 8.
+ (- )
= -10.2.
6.5
= - 4.
计算有理数减法的一般步骤:
(1)将减号变为加号,同时将减数变为它的相反数;
(2)利用有理数的加法法则计算.
两变:(1)改变运算符号:减号变加号;
(2)改变减数的符号:正数变负数,负数变正数.
两不变:(1)在运算过程中,被减数与减数的位置不变;
(2)被减数的符号不变.
注意:
月球表面的温度在白昼可升到 127 ℃,在黑夜可降到-183 ℃. 月球表面昼夜温差(最高气温-最低气温)可达多少
解:127-(-183)=127+183=310(℃).
答:月球表面昼夜温差可达 310 ℃.
知识点 2 有理数减法的应用
1.下列用算式表示“比-3 ℃低6 ℃的温度”正确的是 ( )
A.-3+6=3 B.-3-6=-9
C.-3+6=-9 D.-3-6=-3
2.下列说法正确的是 ( )
A.5 - (-5) = 0
B.0 - (-5) = -5
C.两个数相减,被减数一定大于减数
D.减去一个正数,差一定小于被减数
B
D
(3) 6.25 - (-0.75); (4) .
(3) 6.25 - (-0.75) = 6.25 + 0.75 = 7.
(4) .
3. 将下列减法转化为加法并计算:
(1) (-8) - (-3) ; (2) 10 - (-15);
(1) (-8) - (-3) = -8 + 3 = -5.
(2) 10 - (-15) = 10 + 15 = 25.
解:
有
理
数
的
减
法
法则
运算
a - b = a + (-b)
公式
本质
将减法转化为加法.
减数取其相反数.
两不变 被减数和减数的位置、被减数的符号.
两变 减号变加号、减数变其相反数.
应用
同课章节目录
