沪科版2025数学八年级上册11.1 第2课时 平面直角坐标系中点的坐标特征 课件(共25张PPT)
文档属性
| 名称 | 沪科版2025数学八年级上册11.1 第2课时 平面直角坐标系中点的坐标特征 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 09:32:05 | ||
图片预览





文档简介
(共25张PPT)
11.1 平面内点的坐标
第二课时 平面直角坐标系中点的坐标特征
学习目标及重难点
1. 理解各象限内及坐标轴上点的坐标特征;
2.会用象限或坐标轴说明直角坐标系内点的位置,能根据点的位置确定横、纵坐标的符号.
3.能在方格纸中建立适当的平面直角坐标系来描述点的位置.
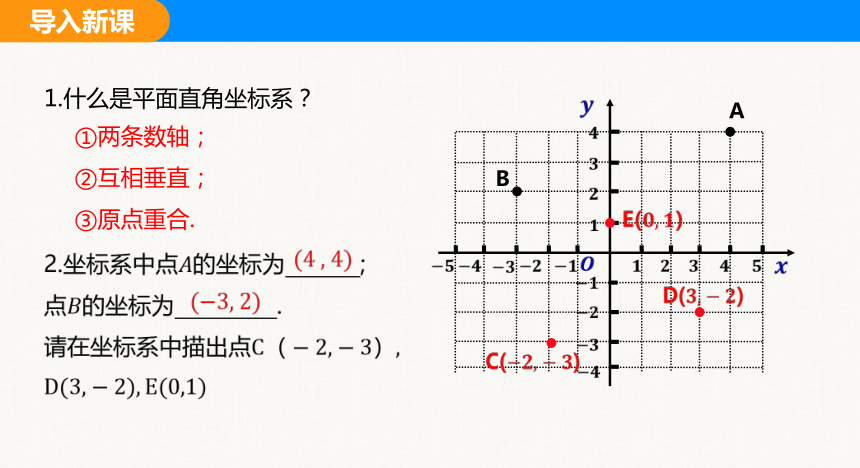
1.什么是平面直角坐标系?
①两条数轴;
②互相垂直;
③原点重合.
2.坐标系中点的坐标为 ;
点的坐标为 .
请在坐标系中描出点
B
D()
A
C()
E()
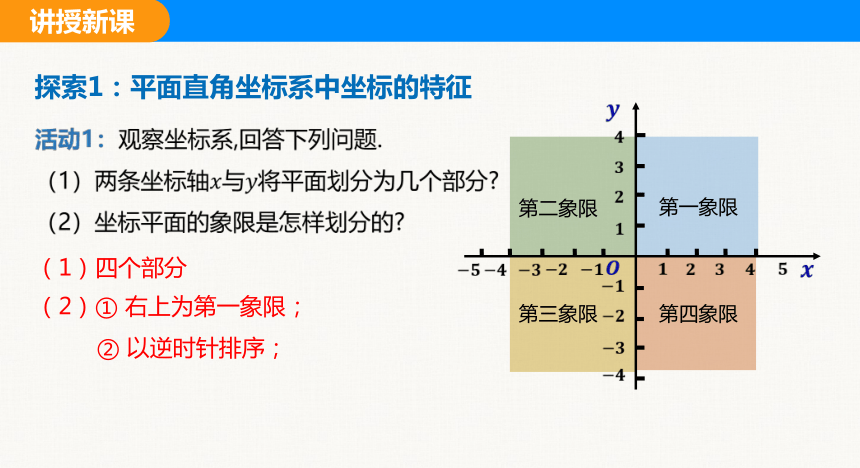
探索1:平面直角坐标系中坐标的特征
第一象限
第二象限
第三象限
第四象限
活动1:观察坐标系,回答下列问题.
(1)两条坐标轴与将平面划分为几个部分
(2)坐标平面的象限是怎样划分的
(1)四个部分
(2)① 右上为第一象限;
② 以逆时针排序;
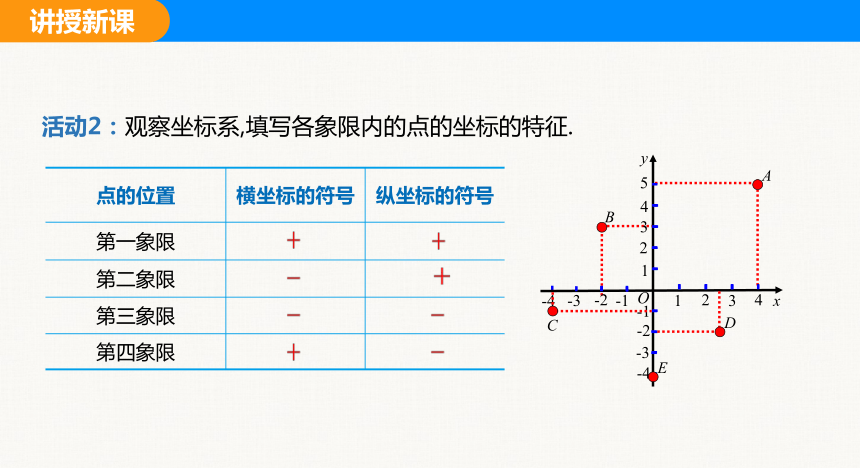
活动2:观察坐标系,填写各象限内的点的坐标的特征.
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
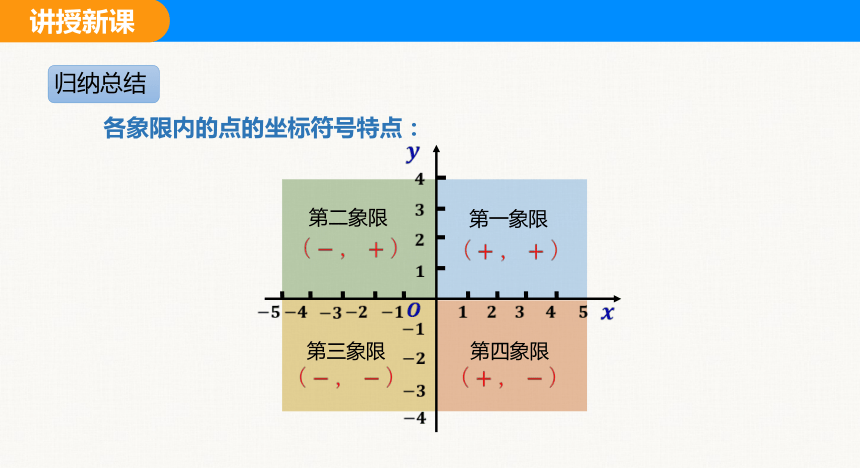
各象限内的点的坐标符号特点:
第一象限
第二象限
第三象限
第四象限
归纳总结
想一想:不看平面直角坐标系,你能迅速说出
所在的象限吗?
分析:位于第一象限; 位于第二象限;
位于第三象限; 位于第四象限;
第一、二、三、四象限内的点的坐标符号分别是:
为什么无法判断处于第几象限?
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动3:观察坐标系,填写坐标轴上的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
想一想:不看平面直角坐标系,你能迅速说出
所在的位置吗?你的方法又是什么?
分析:位于轴的负半轴; ;
位于轴的正半轴; 位于轴的正半轴;位于原点.
在x轴的正半轴上 , x轴的负半轴上 , y轴的正半轴上 , y轴的负半轴上的点的坐标符号分别是:
点的位置 横坐标符号 纵坐标符号
第一象限 + +
第二象限 +
第三象限
第四象限 +
在 轴上 在正半轴上 + 0
在负半轴上 0
在 轴上 在正半轴上 0 +
在负半轴上 0
原点 0 0
坐标平面内,各象限及坐标轴上点的坐标特征
在平面直角坐标系中描出下列各点,并指出它们分别在哪个象限或哪条坐标轴上:
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
x
O
D(-5,3)
B(4,-6)
A(-5,-3)
E(3.5,0)
F(-3.5,0)
-5
-6
y
C(0,-1)
随堂小练习
探索2:建立坐标系求图形中点的坐标
A
B
C
D
E
F
G
H
I
例1:如图,请建立合适的平面直角坐标系,使点 的坐标分别为,
,写出在此平面直角坐标系中其余各点的坐标,指出它们分别在哪个象限或在哪条坐标轴上.
y
6
4
2
-2
-4
-6
x
-6 -4 -2 2 4 6
(O)
A
B
C
D
E
F
G
H
I
解:因为点的坐标分别为所以可以选点作为原点.
如图,画出平面直角坐标系.
则在此平面直角坐标系中,点的坐标为,既在轴上又在轴上;
点的坐标为,在轴上;
点的坐标为在第二象限;
点的坐标为在轴上;
点的坐标为在第三象限;
点的坐标为在轴上;
点的坐标为,在第四象限.
例2:如图,正方形的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点在这个平面直角坐标系的坐标.
解: 如图,以顶点为原点,所在直线为轴,所在的直线为轴, 建立平面直角坐标系.
此时,正方形的四个顶点的坐标分别为:
A
B
C
D
(O)
-2 2 4 6
x
6
4
2
-2
y
你能另建一个平面直角坐标系,并写出此时顶点的坐标吗?
例2:如图,正方形的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点在这个平面直角坐标系的坐标.
A
B
C
D
(O)
-4 -2 2 4
x
4
2
-2
-4
y
建立合适的平面直角坐标系:
①以图形的顶点或者边的中点或图形的中心为原点建立;
②以与图形的边平行或垂直的直线为坐标轴建立坐标系等.
A
B
C
D
归纳总结
B
A
C
如图,等腰三角形 的底边的长为6,且三点都在对应的格点上. 请你试着建立一个平面直角坐标系,并写出三点的坐标.
x
y
O
答案不唯一
①以图形的顶点或者边的中点或图形的中心为原点建立;
②以与图形的边平行或垂直的直线为坐标轴建立坐标系等.
随堂小练习
1.在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
习题1
2.已知点在轴上,则点的坐标是( )
A. B. C. D.
A
习题2
3.右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是,白棋③的坐标是,则黑棋 的坐标是______________.
x
y
O
习题3
A
B
C
D
E
F
G
(0,0)
(4,0)
(-2,3)
(1,5)
(5,3)
(6,1)
x
y
解:要使得点的坐标为,点的坐标为,所以点在轴上,所在直线为轴,过点且垂直于轴的直线为轴,如图:
则另外五个顶点的坐标分别为
4.在图中建立一个平面直角坐标系,使点的坐标为,点的坐标为并写出这两个正方形中另外五个顶点的坐标.
习题4
(3,2)
5.已知点
(1)若点在轴上,求点的坐标;
(2)若点在第一象限,求的取值范围;
(3)若点到轴、轴的距离相等,求点的坐标.
解:(1)∵点在轴上,
∴,解得,
∴
∴点的坐标为
习题5
5.已知点
(1)若点在轴上,求点的坐标;
(2)若点在第一象限,求的取值范围;
(3)若点到轴、轴的距离相等,求点的坐标.
解:(2)由题意,得解得.
习题5
5.已知点
(3)若点到轴、轴的距离相等,求点的坐标.
习题5
解:(3)∵点到轴、轴的距离相等,
∴或,
解得或
当时,,
∴点的坐标为;
当时,,
∴点的坐标为.
综上所述,点的坐标为或.
平面直角坐标系中点的坐标特征
四个象限内的点
第一象限内的点
第二象限内的点
第三象限内的点
第四象限内的点
坐标轴上的点
轴上的点的纵坐标为
轴上的点的横坐标为
原点
11.1 平面内点的坐标
第二课时 平面直角坐标系中点的坐标特征
学习目标及重难点
1. 理解各象限内及坐标轴上点的坐标特征;
2.会用象限或坐标轴说明直角坐标系内点的位置,能根据点的位置确定横、纵坐标的符号.
3.能在方格纸中建立适当的平面直角坐标系来描述点的位置.
1.什么是平面直角坐标系?
①两条数轴;
②互相垂直;
③原点重合.
2.坐标系中点的坐标为 ;
点的坐标为 .
请在坐标系中描出点
B
D()
A
C()
E()
探索1:平面直角坐标系中坐标的特征
第一象限
第二象限
第三象限
第四象限
活动1:观察坐标系,回答下列问题.
(1)两条坐标轴与将平面划分为几个部分
(2)坐标平面的象限是怎样划分的
(1)四个部分
(2)① 右上为第一象限;
② 以逆时针排序;
活动2:观察坐标系,填写各象限内的点的坐标的特征.
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
点的位置 横坐标的符号 纵坐标的符号
第一象限
第二象限
第三象限
第四象限
各象限内的点的坐标符号特点:
第一象限
第二象限
第三象限
第四象限
归纳总结
想一想:不看平面直角坐标系,你能迅速说出
所在的象限吗?
分析:位于第一象限; 位于第二象限;
位于第三象限; 位于第四象限;
第一、二、三、四象限内的点的坐标符号分别是:
为什么无法判断处于第几象限?
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动3:观察坐标系,填写坐标轴上的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
想一想:不看平面直角坐标系,你能迅速说出
所在的位置吗?你的方法又是什么?
分析:位于轴的负半轴; ;
位于轴的正半轴; 位于轴的正半轴;位于原点.
在x轴的正半轴上 , x轴的负半轴上 , y轴的正半轴上 , y轴的负半轴上的点的坐标符号分别是:
点的位置 横坐标符号 纵坐标符号
第一象限 + +
第二象限 +
第三象限
第四象限 +
在 轴上 在正半轴上 + 0
在负半轴上 0
在 轴上 在正半轴上 0 +
在负半轴上 0
原点 0 0
坐标平面内,各象限及坐标轴上点的坐标特征
在平面直角坐标系中描出下列各点,并指出它们分别在哪个象限或哪条坐标轴上:
1
1
-1
-2
-3
-4
2
3
2
3
4
5
4
-1
-2
-3
-4
-5
x
O
D(-5,3)
B(4,-6)
A(-5,-3)
E(3.5,0)
F(-3.5,0)
-5
-6
y
C(0,-1)
随堂小练习
探索2:建立坐标系求图形中点的坐标
A
B
C
D
E
F
G
H
I
例1:如图,请建立合适的平面直角坐标系,使点 的坐标分别为,
,写出在此平面直角坐标系中其余各点的坐标,指出它们分别在哪个象限或在哪条坐标轴上.
y
6
4
2
-2
-4
-6
x
-6 -4 -2 2 4 6
(O)
A
B
C
D
E
F
G
H
I
解:因为点的坐标分别为所以可以选点作为原点.
如图,画出平面直角坐标系.
则在此平面直角坐标系中,点的坐标为,既在轴上又在轴上;
点的坐标为,在轴上;
点的坐标为在第二象限;
点的坐标为在轴上;
点的坐标为在第三象限;
点的坐标为在轴上;
点的坐标为,在第四象限.
例2:如图,正方形的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点在这个平面直角坐标系的坐标.
解: 如图,以顶点为原点,所在直线为轴,所在的直线为轴, 建立平面直角坐标系.
此时,正方形的四个顶点的坐标分别为:
A
B
C
D
(O)
-2 2 4 6
x
6
4
2
-2
y
你能另建一个平面直角坐标系,并写出此时顶点的坐标吗?
例2:如图,正方形的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点在这个平面直角坐标系的坐标.
A
B
C
D
(O)
-4 -2 2 4
x
4
2
-2
-4
y
建立合适的平面直角坐标系:
①以图形的顶点或者边的中点或图形的中心为原点建立;
②以与图形的边平行或垂直的直线为坐标轴建立坐标系等.
A
B
C
D
归纳总结
B
A
C
如图,等腰三角形 的底边的长为6,且三点都在对应的格点上. 请你试着建立一个平面直角坐标系,并写出三点的坐标.
x
y
O
答案不唯一
①以图形的顶点或者边的中点或图形的中心为原点建立;
②以与图形的边平行或垂直的直线为坐标轴建立坐标系等.
随堂小练习
1.在平面直角坐标系中,点所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
习题1
2.已知点在轴上,则点的坐标是( )
A. B. C. D.
A
习题2
3.右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是,白棋③的坐标是,则黑棋 的坐标是______________.
x
y
O
习题3
A
B
C
D
E
F
G
(0,0)
(4,0)
(-2,3)
(1,5)
(5,3)
(6,1)
x
y
解:要使得点的坐标为,点的坐标为,所以点在轴上,所在直线为轴,过点且垂直于轴的直线为轴,如图:
则另外五个顶点的坐标分别为
4.在图中建立一个平面直角坐标系,使点的坐标为,点的坐标为并写出这两个正方形中另外五个顶点的坐标.
习题4
(3,2)
5.已知点
(1)若点在轴上,求点的坐标;
(2)若点在第一象限,求的取值范围;
(3)若点到轴、轴的距离相等,求点的坐标.
解:(1)∵点在轴上,
∴,解得,
∴
∴点的坐标为
习题5
5.已知点
(1)若点在轴上,求点的坐标;
(2)若点在第一象限,求的取值范围;
(3)若点到轴、轴的距离相等,求点的坐标.
解:(2)由题意,得解得.
习题5
5.已知点
(3)若点到轴、轴的距离相等,求点的坐标.
习题5
解:(3)∵点到轴、轴的距离相等,
∴或,
解得或
当时,,
∴点的坐标为;
当时,,
∴点的坐标为.
综上所述,点的坐标为或.
平面直角坐标系中点的坐标特征
四个象限内的点
第一象限内的点
第二象限内的点
第三象限内的点
第四象限内的点
坐标轴上的点
轴上的点的纵坐标为
轴上的点的横坐标为
原点
