沪科版2025数学八年级上册12.1 第2课时 函数的表示方法---列表法和解析法 课件(共25张PPT)
文档属性
| 名称 | 沪科版2025数学八年级上册12.1 第2课时 函数的表示方法---列表法和解析法 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 09:32:38 | ||
图片预览






文档简介
(共25张PPT)
12.1 函数
第二课时 函数的表示方法——列表法和解析法
学习目标及重难点
1. 学会求函数自变量的取值范围 ;(重点)
2. 理解函数自变量与函数值的对应关系,会求指定条件下的函数值;(难点)
3. 会求具体问题中的函数表达式.(难点)
下列问题中的变量是不是的函数?
(1)
(2)
(3)
(6)
(7)
(4)
(5)
(8)
(9)
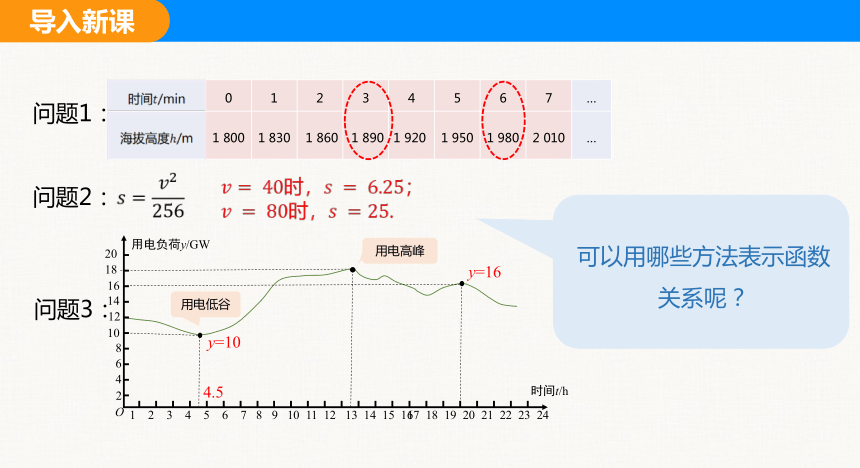
时间/min 0 1 2 3 4 5 6 7 …
海拔高度/m 1 800 1 830 1 860 1 890 1 920 1 950 1 980 2 010 …
问题1:
问题2:
问题3:
时间t/h
O
1 2 3 4 5 6 7 8
2
4
6
8
10
12
14
16
18
20
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
用电负荷y/GW
4.5
y=10
y=16
用电低谷
用电高峰
时,;
时,.
上节课我们研究了三个问题,它们都反映了两个变量间的函数关系.
可以用哪些方法表示函数关系呢?
时间/min 0 1 2 3 4 5 6 7 …
海拔高度/m 1 800 1 830 1 860 1 890 1 920 1 950 1 980 2 010 …
问题1:
问题2:
问题3:
时间t/h
O
1 2 3 4 5 6 7 8
2
4
6
8
10
12
14
16
18
20
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
用电负荷y/GW
4.5
y=10
y=16
用电低谷
用电高峰
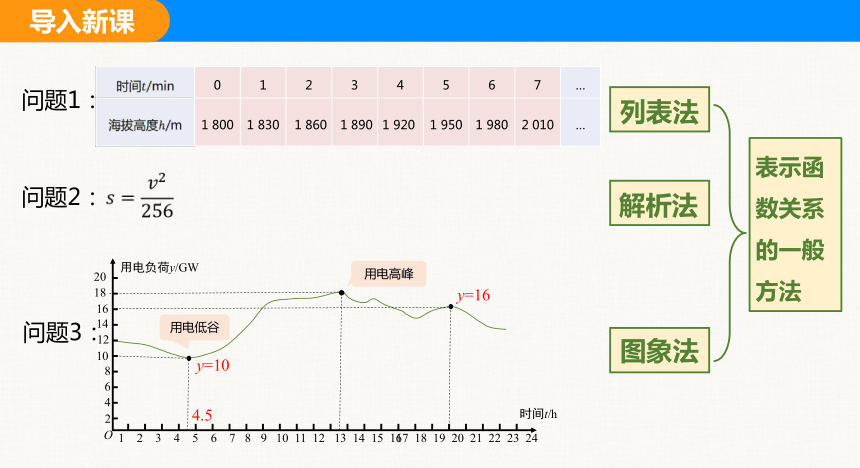
列表法
解析法
图象法
表示函数关系的一般方法
时间/min 0 1 2 3 4 5 6 7 …
海拔高度/m 1 800 1 830 1 860 1 890 1 920 1 950 1 980 2 010 …
问题1:
列表法:
通过列出自变量的值与对应函数值的表格来表示函数关系的方法叫作列表法.
探索1:用列表法、解析法表示函数
优点:
能够具体地反映自变量的值与函数值的对应关系.
想一想:列表法表示函数关系有什么优点与不足呢?
时间/min 0 1 2 3 4 5 6 7 …
海拔高度/m 1 800 1 830 1 860 1 890 1 920 1 950 1 980 2 010 …
问题1:
不足:
只能列出部分自变量的值与对应的函数值,难以反映函数变化的全貌.
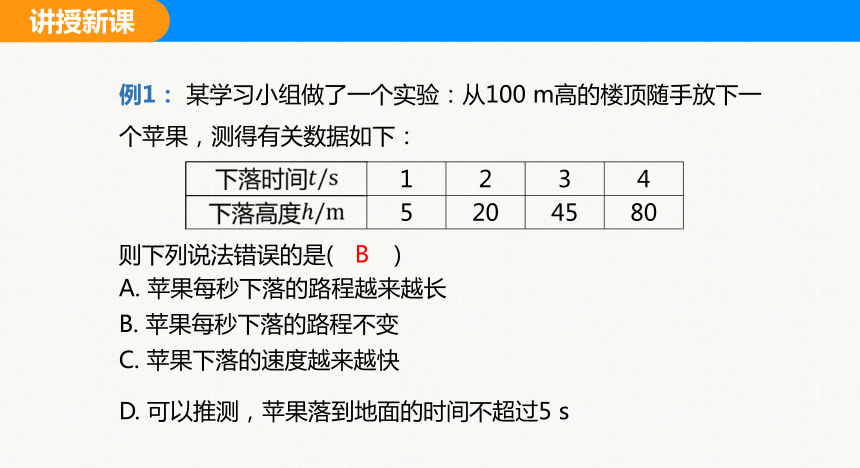
例1: 某学习小组做了一个实验:从100 m高的楼顶随手放下一
个苹果,测得有关数据如下:
下落时间 1 2 3 4
下落高度 5 20 45 80
则下列说法错误的是( B )
B
A. 苹果每秒下落的路程越来越长
B. 苹果每秒下落的路程不变
C. 苹果下落的速度越来越快
D. 可以推测,苹果落到地面的时间不超过5 s
解析法:
像这种用数学式子表示函数关系的方法叫作解析法.
其中的数学式子叫作函数表达式(或函数解析式).
问题2:
探索2:解析法
优点:
能够准确地反映函数与自变量间的数量关系.
问题2:
想一想:解析法表示函数关系有什么优点与不足呢?
不足:
有些自变量与函数间的关系很难或不能用解析式表示;涉及到具体数量还要进行计算.
例2: 一个正方形的边长为3 cm,它的边长减少 cm后,得到的新正方形的周长为 cm, 与 之间的函数表达式是( C )
A. B.
C. D. 以上都不对
C
注意:
在用函数表达式表示函数时,自变量的取值必须使函数关系式有意义.
例3:求下列函数中自变量的取值范围:
(1) ; (2);
(3) ; (4) .
解: (1)为全体实数;
(2)为全体实数;
(3);
(4).
注意:在确定函数中自变量的取值范围时,如果是实际问题,还必须使实际问题有意义.
如函数 中自变量 可取全体实数,如果指明这个式子是表示圆的面积 与其半径 的关系,那么自变量 的取值范围应是.
探索2:自变量的取值范围及求函数值
确定函数自变量的取值范围要注意:
1.要使函数的表达式有意义:
(1)当函数表达式是整式:自变量可取全体实数;
(2)当函数表达式是分式:自变量的取值应使分母不为零;
(3)当函数表达式含算术平方根:自变量的取值应使被开方数大于或等于零;
(4)当函数表达式是混合式:自变量的取值应根据实际列不等式组.
2.在实际问题中,还要使实际问题有意义.
如问题1、问题2中的时间、问题3中的速度等不能为负数.
例4: 当时,求下列函数的函数值:
(1) ; (2);
(3) ; (4) .
解:
(1)当时,
(2)当时,
(3)当时,
(4)当时,.
如果时,,那么叫作当自变量的值为时的函数值.
例5:一个游泳池内有水m ,现打开排水管以 m 的速度排水.
设排水时间为h,游泳池内剩余水量 m .
(1) 写出与 之间的函数表达式;
(2) 写出自变量 的取值范围;
(3) 开始排水后的h后,游泳池中还有多少水?
(4) 当游泳池中还剩 m 水时,已经排水多久?
解:(1)函数表达式为 ,即
例5:一个游泳池内有水m ,现打开排水管以 m 的速度排水.
设排水时间为h,游泳池内剩余水量 m .
(1) 写出与 之间的函数表达式;
(2) 写出自变量 的取值范围;
(3) 开始排水后的h后,游泳池中还有多少水?
(4) 当游泳池中还剩 m 水时,已经排水多久?
解: (2)游泳池中共有m 水,排水速度为 m ,全部排完只需,故自变量 的取值范围是.
例5:一个游泳池内有水m ,现打开排水管以 m 的速度排水.
设排水时间为h,游泳池内剩余水量 m .
(1) 写出与 之间的函数表达式;
(2) 写出自变量 的取值范围;
(3) 开始排水后的h后,游泳池中还有多少水?
(4) 当游泳池中还剩 m 水时,已经排水多久?
解: (3)将 代入函数表达式,得,
答:开始排水h后,游泳池中还有水 .
例5:一个游泳池内有水m ,现打开排水管以 m 的速度排水.
设排水时间为h,游泳池内剩余水量 m .
(1) 写出与 之间的函数表达式;
(2) 写出自变量 的取值范围;
(3) 开始排水后的h后,游泳池中还有多少水?
(4) 当游泳池中还剩 m 水时,已经排水多久?
解: (4)当时,由, 得,
答:当游泳池中还剩水时,已经排水h.
习题1
1.某数学兴趣小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
则下列说法错误的是( )
A.在这个变化中,自变量是温度
B.当温度每升高10 ℃,声速增加6 m/s
C.当空气温度为20 ℃时,声音5 s的时间可以传播1740 m
D.温度越高,声速越快
C
温度/℃ 20 10 0 10 20 30
声速/(m/s) 318 324 330 336 342 348
2.某服装厂开展优惠促销活动:“凡一次性购买服装超过
500元者,超过的部分按8折优惠”.在此活动中,小明到
该商场一次性购买标价 元的服装,则应付款
(元)与标价 (元)之间的关系式是( D )
A. B.
C. D.
D
习题2
习题3
3.求下列函数中自变量x的取值范围.
(1) ;(2) ;(3) ;
(4) ;(5)= .
解: (1)函数表达式右边是整式,所以的取值范围为全体实数;
(2)
习题3
3.求下列函数中自变量x的取值范围.
(1) ;(2) ;(3) ;
(4) ;(5)= .
解: (3) 由得,所以的取值范围是;
(4) 由
习题3
3.求下列函数中自变量x的取值范围.
(1) ;(2) ;(3) ;
(4) ;(5)= .
解:(5) 由
习题4
4.拖拉机开始工作时,油箱中有油30 L,每小时耗油5 L.
(1)写出油箱中的余油量(L)与工作时间(h)之间的函数表达式;
(2)求出自变量的取值范围;
(3)拖拉机工作3 h后,剩余多少油?
解:(1)函数表达式为即.
(2)由于油箱中有油L,每小时耗油 L,拖拉机可以工作,所以自变量的取值范围是
(3)当时,.
即拖拉机工作 h后,剩余油量为L.
表示函数关系的方法
确定自变量的取值范围的方法
函数
列表法
图象法
解析法
自变量的值与函数值
12.1 函数
第二课时 函数的表示方法——列表法和解析法
学习目标及重难点
1. 学会求函数自变量的取值范围 ;(重点)
2. 理解函数自变量与函数值的对应关系,会求指定条件下的函数值;(难点)
3. 会求具体问题中的函数表达式.(难点)
下列问题中的变量是不是的函数?
(1)
(2)
(3)
(6)
(7)
(4)
(5)
(8)
(9)
时间/min 0 1 2 3 4 5 6 7 …
海拔高度/m 1 800 1 830 1 860 1 890 1 920 1 950 1 980 2 010 …
问题1:
问题2:
问题3:
时间t/h
O
1 2 3 4 5 6 7 8
2
4
6
8
10
12
14
16
18
20
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
用电负荷y/GW
4.5
y=10
y=16
用电低谷
用电高峰
时,;
时,.
上节课我们研究了三个问题,它们都反映了两个变量间的函数关系.
可以用哪些方法表示函数关系呢?
时间/min 0 1 2 3 4 5 6 7 …
海拔高度/m 1 800 1 830 1 860 1 890 1 920 1 950 1 980 2 010 …
问题1:
问题2:
问题3:
时间t/h
O
1 2 3 4 5 6 7 8
2
4
6
8
10
12
14
16
18
20
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
用电负荷y/GW
4.5
y=10
y=16
用电低谷
用电高峰
列表法
解析法
图象法
表示函数关系的一般方法
时间/min 0 1 2 3 4 5 6 7 …
海拔高度/m 1 800 1 830 1 860 1 890 1 920 1 950 1 980 2 010 …
问题1:
列表法:
通过列出自变量的值与对应函数值的表格来表示函数关系的方法叫作列表法.
探索1:用列表法、解析法表示函数
优点:
能够具体地反映自变量的值与函数值的对应关系.
想一想:列表法表示函数关系有什么优点与不足呢?
时间/min 0 1 2 3 4 5 6 7 …
海拔高度/m 1 800 1 830 1 860 1 890 1 920 1 950 1 980 2 010 …
问题1:
不足:
只能列出部分自变量的值与对应的函数值,难以反映函数变化的全貌.
例1: 某学习小组做了一个实验:从100 m高的楼顶随手放下一
个苹果,测得有关数据如下:
下落时间 1 2 3 4
下落高度 5 20 45 80
则下列说法错误的是( B )
B
A. 苹果每秒下落的路程越来越长
B. 苹果每秒下落的路程不变
C. 苹果下落的速度越来越快
D. 可以推测,苹果落到地面的时间不超过5 s
解析法:
像这种用数学式子表示函数关系的方法叫作解析法.
其中的数学式子叫作函数表达式(或函数解析式).
问题2:
探索2:解析法
优点:
能够准确地反映函数与自变量间的数量关系.
问题2:
想一想:解析法表示函数关系有什么优点与不足呢?
不足:
有些自变量与函数间的关系很难或不能用解析式表示;涉及到具体数量还要进行计算.
例2: 一个正方形的边长为3 cm,它的边长减少 cm后,得到的新正方形的周长为 cm, 与 之间的函数表达式是( C )
A. B.
C. D. 以上都不对
C
注意:
在用函数表达式表示函数时,自变量的取值必须使函数关系式有意义.
例3:求下列函数中自变量的取值范围:
(1) ; (2);
(3) ; (4) .
解: (1)为全体实数;
(2)为全体实数;
(3);
(4).
注意:在确定函数中自变量的取值范围时,如果是实际问题,还必须使实际问题有意义.
如函数 中自变量 可取全体实数,如果指明这个式子是表示圆的面积 与其半径 的关系,那么自变量 的取值范围应是.
探索2:自变量的取值范围及求函数值
确定函数自变量的取值范围要注意:
1.要使函数的表达式有意义:
(1)当函数表达式是整式:自变量可取全体实数;
(2)当函数表达式是分式:自变量的取值应使分母不为零;
(3)当函数表达式含算术平方根:自变量的取值应使被开方数大于或等于零;
(4)当函数表达式是混合式:自变量的取值应根据实际列不等式组.
2.在实际问题中,还要使实际问题有意义.
如问题1、问题2中的时间、问题3中的速度等不能为负数.
例4: 当时,求下列函数的函数值:
(1) ; (2);
(3) ; (4) .
解:
(1)当时,
(2)当时,
(3)当时,
(4)当时,.
如果时,,那么叫作当自变量的值为时的函数值.
例5:一个游泳池内有水m ,现打开排水管以 m 的速度排水.
设排水时间为h,游泳池内剩余水量 m .
(1) 写出与 之间的函数表达式;
(2) 写出自变量 的取值范围;
(3) 开始排水后的h后,游泳池中还有多少水?
(4) 当游泳池中还剩 m 水时,已经排水多久?
解:(1)函数表达式为 ,即
例5:一个游泳池内有水m ,现打开排水管以 m 的速度排水.
设排水时间为h,游泳池内剩余水量 m .
(1) 写出与 之间的函数表达式;
(2) 写出自变量 的取值范围;
(3) 开始排水后的h后,游泳池中还有多少水?
(4) 当游泳池中还剩 m 水时,已经排水多久?
解: (2)游泳池中共有m 水,排水速度为 m ,全部排完只需,故自变量 的取值范围是.
例5:一个游泳池内有水m ,现打开排水管以 m 的速度排水.
设排水时间为h,游泳池内剩余水量 m .
(1) 写出与 之间的函数表达式;
(2) 写出自变量 的取值范围;
(3) 开始排水后的h后,游泳池中还有多少水?
(4) 当游泳池中还剩 m 水时,已经排水多久?
解: (3)将 代入函数表达式,得,
答:开始排水h后,游泳池中还有水 .
例5:一个游泳池内有水m ,现打开排水管以 m 的速度排水.
设排水时间为h,游泳池内剩余水量 m .
(1) 写出与 之间的函数表达式;
(2) 写出自变量 的取值范围;
(3) 开始排水后的h后,游泳池中还有多少水?
(4) 当游泳池中还剩 m 水时,已经排水多久?
解: (4)当时,由, 得,
答:当游泳池中还剩水时,已经排水h.
习题1
1.某数学兴趣小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
则下列说法错误的是( )
A.在这个变化中,自变量是温度
B.当温度每升高10 ℃,声速增加6 m/s
C.当空气温度为20 ℃时,声音5 s的时间可以传播1740 m
D.温度越高,声速越快
C
温度/℃ 20 10 0 10 20 30
声速/(m/s) 318 324 330 336 342 348
2.某服装厂开展优惠促销活动:“凡一次性购买服装超过
500元者,超过的部分按8折优惠”.在此活动中,小明到
该商场一次性购买标价 元的服装,则应付款
(元)与标价 (元)之间的关系式是( D )
A. B.
C. D.
D
习题2
习题3
3.求下列函数中自变量x的取值范围.
(1) ;(2) ;(3) ;
(4) ;(5)= .
解: (1)函数表达式右边是整式,所以的取值范围为全体实数;
(2)
习题3
3.求下列函数中自变量x的取值范围.
(1) ;(2) ;(3) ;
(4) ;(5)= .
解: (3) 由得,所以的取值范围是;
(4) 由
习题3
3.求下列函数中自变量x的取值范围.
(1) ;(2) ;(3) ;
(4) ;(5)= .
解:(5) 由
习题4
4.拖拉机开始工作时,油箱中有油30 L,每小时耗油5 L.
(1)写出油箱中的余油量(L)与工作时间(h)之间的函数表达式;
(2)求出自变量的取值范围;
(3)拖拉机工作3 h后,剩余多少油?
解:(1)函数表达式为即.
(2)由于油箱中有油L,每小时耗油 L,拖拉机可以工作,所以自变量的取值范围是
(3)当时,.
即拖拉机工作 h后,剩余油量为L.
表示函数关系的方法
确定自变量的取值范围的方法
函数
列表法
图象法
解析法
自变量的值与函数值
