沪科版2025数学八年级上册12.1 第3课时 函数的表示方法---图象法 课件(共23张PPT)
文档属性
| 名称 | 沪科版2025数学八年级上册12.1 第3课时 函数的表示方法---图象法 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 09:33:09 | ||
图片预览





文档简介
(共23张PPT)
12.1 函数
第三课时 函数的表示方法——图象法
学习目标及重难点
1.学会用列表、描点、连线画函数图象 ;(重点)
2.能用这三种表示函数的方法解决简单的实际问题.(难点)
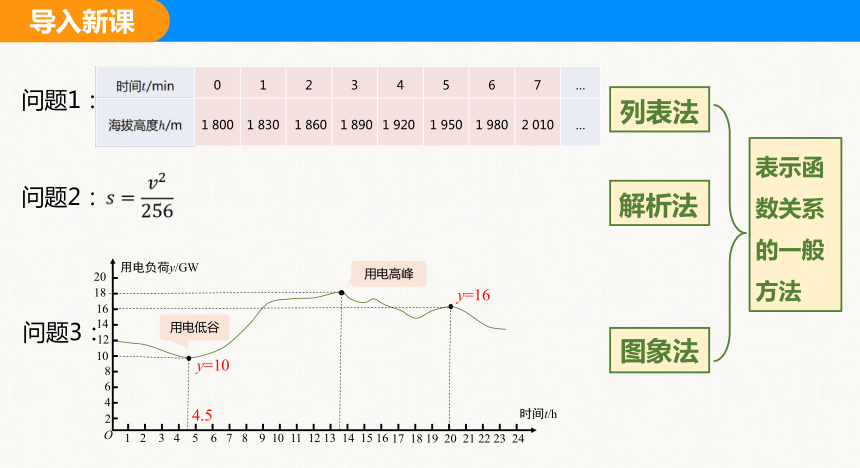
时间/min 0 1 2 3 4 5 6 7 …
海拔高度/m 1 800 1 830 1 860 1 890 1 920 1 950 1 980 2 010 …
问题1:
问题2:
问题3:
时间t/h
O
1 2 3 4 5 6 7 8
2
4
6
8
10
12
14
16
18
20
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
用电负荷y/GW
4.5
y=10
y=16
用电低谷
用电高峰
列表法
解析法
图象法
表示函数关系的一般方法
问题3:
时间t/h
O
1 2 3 4 5 6 7 8
2
4
6
8
10
12
14
16
18
20
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
用电负荷y/GW
4.5
y=10
y=16
用电低谷
用电高峰
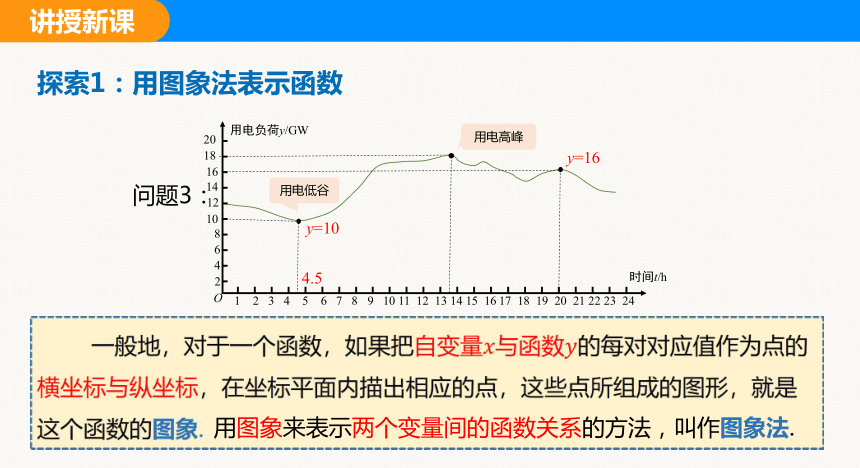
探索1:用图象法表示函数
一般地,对于一个函数,如果把自变量与函数的每对对应值作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.
用图象来表示两个变量间的函数关系的方法,叫作图象法.
问题3:
时间t/h
O
1 2 3 4 5 6 7 8
2
4
6
8
10
12
14
16
18
20
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
用电负荷y/GW
4.5
y=10
y=16
用电低谷
用电高峰
想一想:用图象法表示函数关系有什么优点和不足呢
优点:
直观、形象,容易从中了解函数的变化情况.
不足:
图像是近似的、局部的,由图像确定的函数值往往不够准确.
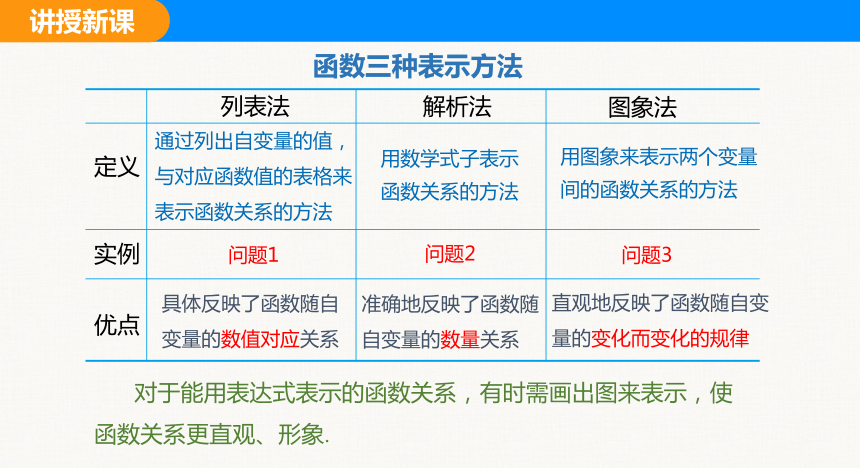
列表法
解析法
图象法
定义
实例
优点
通过列出自变量的值,与对应函数值的表格来表示函数关系的方法
问题1
具体反映了函数随自变量的数值对应关系
用数学式子表示函数关系的方法
问题2
准确地反映了函数随自变量的数量关系
用图象来表示两个变量间的函数关系的方法
问题3
直观地反映了函数随自变量的变化而变化的规律
函数三种表示方法
对于能用表达式表示的函数关系,有时需画出图来表示,使函数关系更直观、形象.
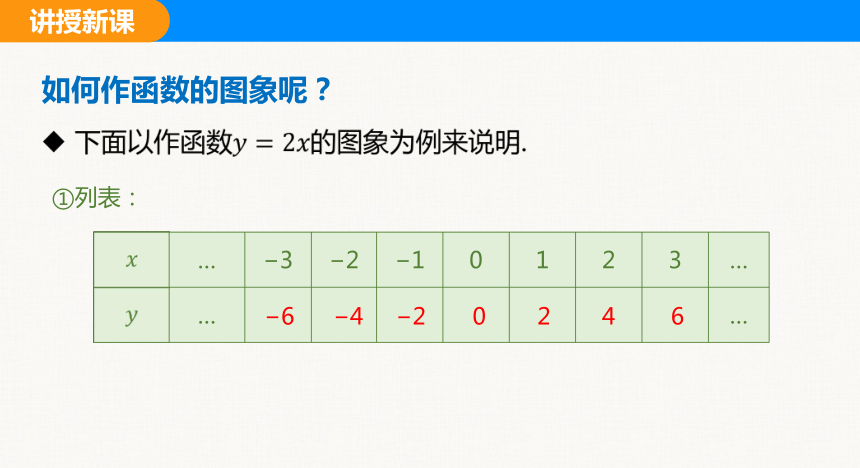
如何作函数的图象呢?
下面以作函数的图象为例来说明.
①列表:
… 3 2 1 0 1 2 3 …
… …
6
4
2
0
2
4
6
如何作函数的图象呢?
下面以作函数的图象为例来说明.
②任意一个有序实数对(x,y)与坐标平面内一点 M(x,y)一一对应.
因此,表中给出的有序实数对可在平面直角坐标系中描出相应的点.
… 3 2 1 0 1 2 3 …
… …
6
4
2
0
2
4
6
-1
1
1
2
2
3
3
4
4
5
6
7
0
-1
-2
-3
-4
-2
-3
-4
-5
-6
-7
x
y
③我们不能把所有点都描出,因此用平滑曲线连接画出的点,从而得到表示这个函数关系的近似图形.
y=2x
如何作函数的图象呢?
下面以作函数的图象为例来说明.
-1
1
1
2
2
3
3
4
4
5
6
7
0
-1
-2
-3
-4
-2
-3
-4
-5
-6
-7
x
y
因为函数中的自变量可以取一切实数,列表计算可以得到无数多个有序实数对,在坐标平面内可描出无数多个点,这些点组成了坐标系中的图形.
1. 列表:列表给出自变量与函数的一些对应值.
2. 描点:以表中各组对应值为坐标,在坐标平面内描出相应的点.
3. 连线:按照自变量的大小顺序,把所描各点用平滑曲线依次连接起来.
由函数表达式画图象,一般按下列步骤进行:
注意:描出的点越多,所得的图象就越准确.
归纳总结
例1: 画出前面问题2中的函数 的图像.
解:(1)列表:因为这里,我们分别取求出它们对应的值.列表如下:
O
x
y
10
20
30
40
50
-1
3
1
4
2
5
-1
6
(2)描点:如图,在坐标平面内描出
等点.
0 10 20 30 40 …
…
0
解:(1)列表:因为这里,我们分别取求出它们对应的值.列表如下:
O
x
y
10
20
30
40
50
-1
3
1
4
2
5
-1
6
(2)描点:如图,在坐标平面内描出
等点.
0 10 20 30 40 …
…
0
(3)连线:将以上各点按自变量 由小到大的顺序用平滑的曲线连接,就得到了 图象.
画出函数的图像(先列表,然后描点、连线)
解:(1)列表:
(3)连线:
-1
1
1
2
2
3
3
4
4
5
6
7
0
-1
-2
-3
-4
-2
-3
-4
-5
-6
-7
x
y
(2)描点 : 在坐标平面内描出相应的点.
……
……
……
……
随堂小练习
例2:已知函数.
(1)试判断点和点 是否在此函数的图象上;
(2)已知点在此函数的图象上,求的值.
分析:(1)将点的坐标分别代入,看点的坐标能否
满足这个表达式即可;
(2)将点的坐标代入,可得到一个关于的一元一次方
程,求出的值即可.
探索2:知道函数图象中自变量与函数的对应关系.
例2:已知函数.
(1)试判断点和点 是否在此函数的图象上;
(2)已知点在此函数的图象上,求的值.
解:(1)因为当时,,
所以点不在函数的图象上.
因为当 时,,
所以点在函数的图象上.
例2:已知函数.
(1)试判断点和点 是否在此函数的图象上;
(2)已知点在此函数的图象上,求的值.
解: (2)因为点在函数的图象上,
所以把代入,得.
解得.
(1) 判断点是否在函数图象上的方法是:将点
的值代入函数表达式,若能满足函数的表达式,则
这个点就在函数的图象上;若不满足函数的表达式,则
这个点不在函数的图象上.
(2) 坐标含字母的点在函数图象上求字母值的方法:将坐标
代入函数表达式中,得到一个关于该字母的方程,解这
个方程即得字母的值.
归纳总结
随堂小练习
1.下列各点在函数的图象上的是( )
A. B.
C. D.
2.已知点在函数的图象上,则的值为( )
A. B. C. D.
B
A
1.下列坐标系中的图形不能表示 是 的函数的是( )
A
习题1
习题2
2.下列函数中,其图象经过原点的是( )
A. B.
C. D.
D
3.已知点 在函数的图象上,则的值为( )
A. B.
C. D.
A
习题3
4.用解析法与图象法表示等边三角形的周长是边长的函数.
②描点:在坐标平面内描出相应的点.
③连线
①列表
解:因为等边三角形的周长是边长的倍,
所以周长与边长的函数关系可表示为.
a
l
1
3
2
6
3
9
4
12
……
……
……
……
O
2
x
y
1
2
3
4
5
8
6
4
10
12
习题4
函数关系的方法有三种:
2.解析法——用数学式子表示函数关系的方法.
1.列表法——通过列出自变量的值,与对应函数值的表格来表示函数关系的方法.
3.图象法——把自变量与函数的每对对应值作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象. 用图象来表示两个变量间的函数关系的方法,叫作图象法.
画函数的图象要经过(1)列表;(2)描点; (3)连线.
12.1 函数
第三课时 函数的表示方法——图象法
学习目标及重难点
1.学会用列表、描点、连线画函数图象 ;(重点)
2.能用这三种表示函数的方法解决简单的实际问题.(难点)
时间/min 0 1 2 3 4 5 6 7 …
海拔高度/m 1 800 1 830 1 860 1 890 1 920 1 950 1 980 2 010 …
问题1:
问题2:
问题3:
时间t/h
O
1 2 3 4 5 6 7 8
2
4
6
8
10
12
14
16
18
20
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
用电负荷y/GW
4.5
y=10
y=16
用电低谷
用电高峰
列表法
解析法
图象法
表示函数关系的一般方法
问题3:
时间t/h
O
1 2 3 4 5 6 7 8
2
4
6
8
10
12
14
16
18
20
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
用电负荷y/GW
4.5
y=10
y=16
用电低谷
用电高峰
探索1:用图象法表示函数
一般地,对于一个函数,如果把自变量与函数的每对对应值作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象.
用图象来表示两个变量间的函数关系的方法,叫作图象法.
问题3:
时间t/h
O
1 2 3 4 5 6 7 8
2
4
6
8
10
12
14
16
18
20
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
用电负荷y/GW
4.5
y=10
y=16
用电低谷
用电高峰
想一想:用图象法表示函数关系有什么优点和不足呢
优点:
直观、形象,容易从中了解函数的变化情况.
不足:
图像是近似的、局部的,由图像确定的函数值往往不够准确.
列表法
解析法
图象法
定义
实例
优点
通过列出自变量的值,与对应函数值的表格来表示函数关系的方法
问题1
具体反映了函数随自变量的数值对应关系
用数学式子表示函数关系的方法
问题2
准确地反映了函数随自变量的数量关系
用图象来表示两个变量间的函数关系的方法
问题3
直观地反映了函数随自变量的变化而变化的规律
函数三种表示方法
对于能用表达式表示的函数关系,有时需画出图来表示,使函数关系更直观、形象.
如何作函数的图象呢?
下面以作函数的图象为例来说明.
①列表:
… 3 2 1 0 1 2 3 …
… …
6
4
2
0
2
4
6
如何作函数的图象呢?
下面以作函数的图象为例来说明.
②任意一个有序实数对(x,y)与坐标平面内一点 M(x,y)一一对应.
因此,表中给出的有序实数对可在平面直角坐标系中描出相应的点.
… 3 2 1 0 1 2 3 …
… …
6
4
2
0
2
4
6
-1
1
1
2
2
3
3
4
4
5
6
7
0
-1
-2
-3
-4
-2
-3
-4
-5
-6
-7
x
y
③我们不能把所有点都描出,因此用平滑曲线连接画出的点,从而得到表示这个函数关系的近似图形.
y=2x
如何作函数的图象呢?
下面以作函数的图象为例来说明.
-1
1
1
2
2
3
3
4
4
5
6
7
0
-1
-2
-3
-4
-2
-3
-4
-5
-6
-7
x
y
因为函数中的自变量可以取一切实数,列表计算可以得到无数多个有序实数对,在坐标平面内可描出无数多个点,这些点组成了坐标系中的图形.
1. 列表:列表给出自变量与函数的一些对应值.
2. 描点:以表中各组对应值为坐标,在坐标平面内描出相应的点.
3. 连线:按照自变量的大小顺序,把所描各点用平滑曲线依次连接起来.
由函数表达式画图象,一般按下列步骤进行:
注意:描出的点越多,所得的图象就越准确.
归纳总结
例1: 画出前面问题2中的函数 的图像.
解:(1)列表:因为这里,我们分别取求出它们对应的值.列表如下:
O
x
y
10
20
30
40
50
-1
3
1
4
2
5
-1
6
(2)描点:如图,在坐标平面内描出
等点.
0 10 20 30 40 …
…
0
解:(1)列表:因为这里,我们分别取求出它们对应的值.列表如下:
O
x
y
10
20
30
40
50
-1
3
1
4
2
5
-1
6
(2)描点:如图,在坐标平面内描出
等点.
0 10 20 30 40 …
…
0
(3)连线:将以上各点按自变量 由小到大的顺序用平滑的曲线连接,就得到了 图象.
画出函数的图像(先列表,然后描点、连线)
解:(1)列表:
(3)连线:
-1
1
1
2
2
3
3
4
4
5
6
7
0
-1
-2
-3
-4
-2
-3
-4
-5
-6
-7
x
y
(2)描点 : 在坐标平面内描出相应的点.
……
……
……
……
随堂小练习
例2:已知函数.
(1)试判断点和点 是否在此函数的图象上;
(2)已知点在此函数的图象上,求的值.
分析:(1)将点的坐标分别代入,看点的坐标能否
满足这个表达式即可;
(2)将点的坐标代入,可得到一个关于的一元一次方
程,求出的值即可.
探索2:知道函数图象中自变量与函数的对应关系.
例2:已知函数.
(1)试判断点和点 是否在此函数的图象上;
(2)已知点在此函数的图象上,求的值.
解:(1)因为当时,,
所以点不在函数的图象上.
因为当 时,,
所以点在函数的图象上.
例2:已知函数.
(1)试判断点和点 是否在此函数的图象上;
(2)已知点在此函数的图象上,求的值.
解: (2)因为点在函数的图象上,
所以把代入,得.
解得.
(1) 判断点是否在函数图象上的方法是:将点
的值代入函数表达式,若能满足函数的表达式,则
这个点就在函数的图象上;若不满足函数的表达式,则
这个点不在函数的图象上.
(2) 坐标含字母的点在函数图象上求字母值的方法:将坐标
代入函数表达式中,得到一个关于该字母的方程,解这
个方程即得字母的值.
归纳总结
随堂小练习
1.下列各点在函数的图象上的是( )
A. B.
C. D.
2.已知点在函数的图象上,则的值为( )
A. B. C. D.
B
A
1.下列坐标系中的图形不能表示 是 的函数的是( )
A
习题1
习题2
2.下列函数中,其图象经过原点的是( )
A. B.
C. D.
D
3.已知点 在函数的图象上,则的值为( )
A. B.
C. D.
A
习题3
4.用解析法与图象法表示等边三角形的周长是边长的函数.
②描点:在坐标平面内描出相应的点.
③连线
①列表
解:因为等边三角形的周长是边长的倍,
所以周长与边长的函数关系可表示为.
a
l
1
3
2
6
3
9
4
12
……
……
……
……
O
2
x
y
1
2
3
4
5
8
6
4
10
12
习题4
函数关系的方法有三种:
2.解析法——用数学式子表示函数关系的方法.
1.列表法——通过列出自变量的值,与对应函数值的表格来表示函数关系的方法.
3.图象法——把自变量与函数的每对对应值作为点的横坐标与纵坐标,在坐标平面内描出相应的点,这些点所组成的图形,就是这个函数的图象. 用图象来表示两个变量间的函数关系的方法,叫作图象法.
画函数的图象要经过(1)列表;(2)描点; (3)连线.
