沪科版2025数学八年级上册12.1 第4课时 从函数图象中获取信息 课件(共29张PPT)
文档属性
| 名称 | 沪科版2025数学八年级上册12.1 第4课时 从函数图象中获取信息 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 09:33:20 | ||
图片预览



文档简介
(共29张PPT)
12.1 函数
第四课时 从函数图象中获取信息
学习目标及重难点
1. 提高识图能力、分析函数图象的能力 ;(重点)
2. 体会数形结合思想,并利用它解决问题,提高解决问题能力.(难点)
1.函数图象的定义.
2.画函数图象的步骤.
3.如何判断某一点是否在某个函数的图象上.
列表
描点
连线
若一个点在某个函数图象上.那么这一点的横、纵坐标一定满足这个函数的解析式,反之则不在.
复习回顾
如果给你一个函数图象,你能读出其中的信息吗?
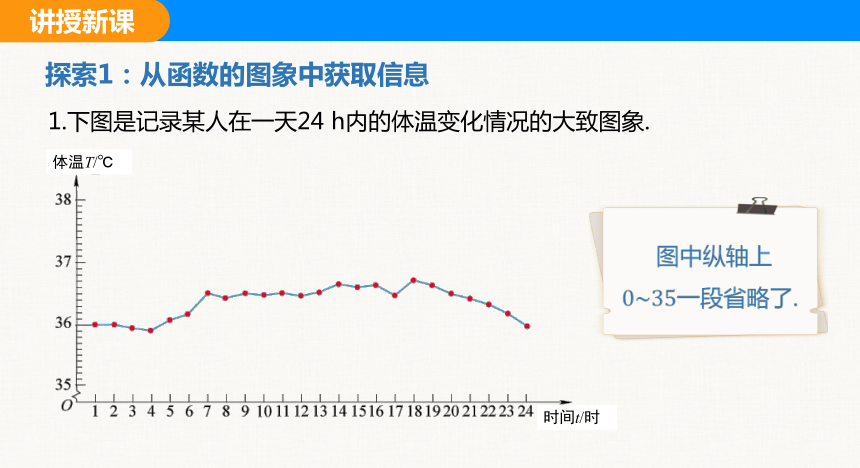
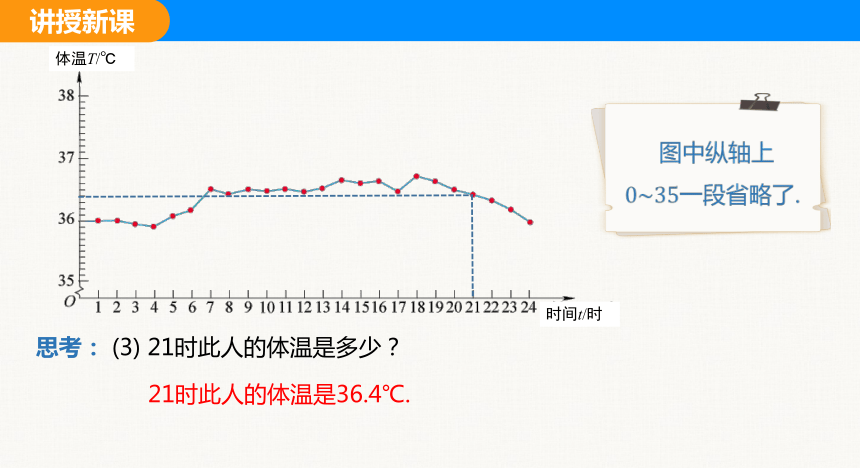
1.下图是记录某人在一天24 h内的体温变化情况的大致图象.
体温T/℃
时间t/时
探索1:从函数的图象中获取信息
图中纵轴上一段省略了.
体温T/℃
时间t/时
图中纵轴上一段省略了.
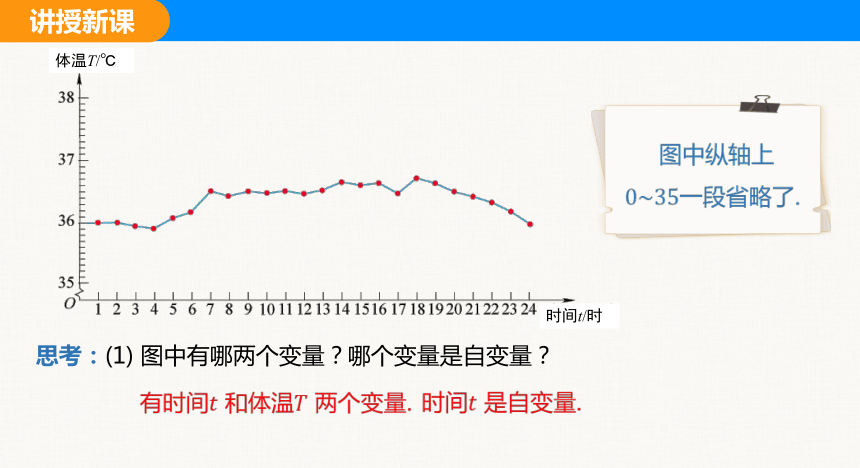
思考:(1) 图中有哪两个变量?哪个变量是自变量?
有时间 和体温 两个变量.
时间 是自变量.
体温T/℃
时间t/时
图中纵轴上一段省略了.
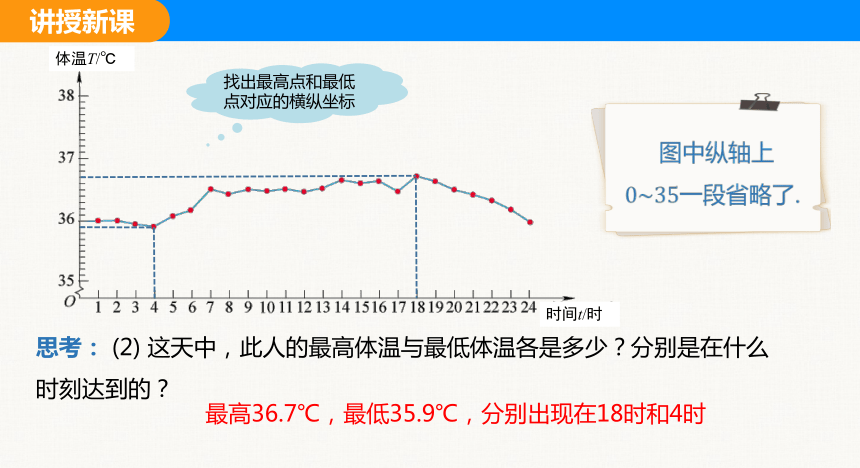
思考: (2) 这天中,此人的最高体温与最低体温各是多少?分别是在什么时刻达到的?
找出最高点和最低点对应的横纵坐标
最高36.7℃,最低35.9℃,分别出现在18时和4时
体温T/℃
时间t/时
图中纵轴上一段省略了.
思考: (3) 21时此人的体温是多少?
21时此人的体温是36.4℃.
体温T/℃
时间t/时
图中纵轴上一段省略了.
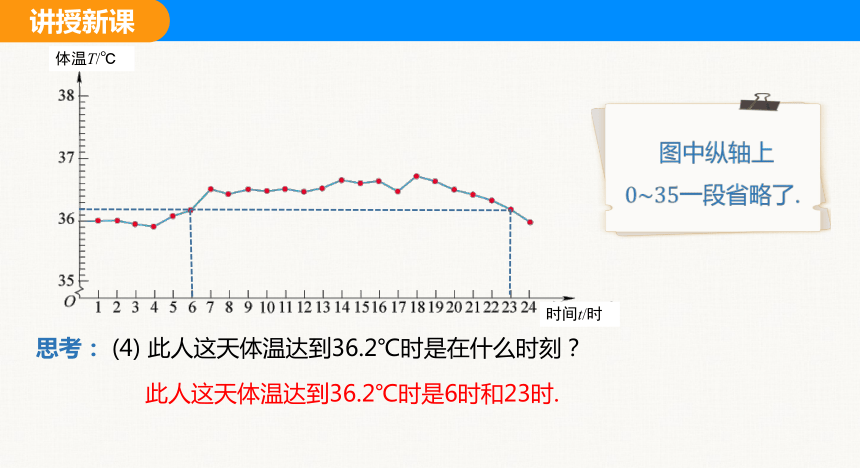
思考: (4) 此人这天体温达到36.2℃时是在什么时刻?
此人这天体温达到36.2℃时是6时和23时.
体温T/℃
时间t/时
图中纵轴上一段省略了.
思考: (5) 4时到7时,此人体温是如何变化的?18时到24时,此人体温又是如何变化的?
4时到7时,此人体温是不断上升的.
18时到24时,此人体温是不断下降的.
上升线表示函数值随自变量的增大而增大
下降线表示函数值随自变量的增大而减小
如何从图象中获得有用信息:
明确“两轴”的含义
通常横轴表示自变量,纵轴表示函数值.通过图象可明确自变量、函数值以及它们的取值范围.
明确图象上的点的意义
过一点分别向横轴和纵轴作垂线,两个垂足分别所表示的数就是自变量与函数值的一对对应值.
弄清上升线、下降线和水平线
上升(下降)线表示函数值随自变量的增大而增大(减小),水平线表示随自变量的变化函数值不变.
1
2
3
2.一只轮船在甲港与乙港之间往返运输,只行驶一个来回,途径丙港,如下图是这艘轮船离开甲港的距离随时间的变化曲线.
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
观察曲线回答下列问题(以下括号中字母表示轮船所在位置对应曲线上的点):
轮船离开甲港的距离是时间的函数.
对应点之间的间隔时间即为行驶时间,由图象中段平行于轴可知,轮船在乙港停留了一段时间.
甲港
丙港
乙港
丙港
甲港
乙港
思考:(1)从甲港()出发到丙港(),需用多长时间?
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
从甲港()出发到达丙港(),需用1个小时.
甲港
丙港
乙港
丙港
甲港
乙港
思考:(2)从丙港()到达乙港(),需用多长时间?
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
从丙港()到达乙港(),需用2个小时.
甲港
丙港
乙港
丙港
甲港
乙港
思考:(3)图中段表示该轮船在乙港停留多长时间?返回时,多长时间到达丙港()?
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
段表示该轮船在乙港停留了个小时,返回时4个小时到达丙港().
甲港
丙港
乙港
丙港
甲港
乙港
思考:(4)从丙港()返回到出发点甲港(),需多长时间?
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
从丙港()返回到出发点甲港()需2个小时.
甲港
丙港
乙港
丙港
甲港
乙港
思考:(5)轮船从甲港前往乙港的平均速度快,还是轮船返回的平均速度快呢?
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
轮船从甲港前往乙港的平均行驶速度快.
轮船往返行驶的路程一样,用的时间越少则平均速度越快.
甲港
丙港
乙港
丙港
甲港
乙港
海水受日、月引力影响而产生的涨落现象叫作潮汐,发生在早晨的叫潮,发生在黄昏的叫汐. 某海滨港口在某天的水位变化曲线如图所示.
随堂小练习
随堂小练习
(1) 在这一问题中,有哪几个变量?其中自变量是什么?
(2) 大约在什么时间水最深,深度约为多少?
有2个变量时间和水深;其中自变量是时间.
在3时和15时水最深,深度约为13米.
随堂小练习
(3) 大约在什么时间水最浅,深度约为多少?
在9时和21时水最浅,深度约为7米.
(4)从图中,你还能看出港口水位变化的其他情况吗?
0~3时在持续上涨,3~9时在持续下降,9~15时又在持续上涨,
15~21时又在持续下降,21~24时又在持续上涨 .
1.小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑到公园,打了一会儿太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离(米)与时间(分钟)之间关系的大致图象是( )
B
习题1
2.匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中为一折线).这个容器的形状是下列选项中哪一个( )
C
习题2
A.甲队率先到达终点
B.甲队比乙队多走了200米路程
C.乙队比甲队少用0.2分钟
D.比赛中两队从出发到2.2分钟时间段,乙队的速度比甲队的速度快
3.甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程(米)与时间(分钟)之间的函数关系图象如下图所示,请你根据图象判断,下列说法正确的是( )
C
习题3
4.小李与小陆从地出发,骑自行车沿同一条路行驶到地,他们离出发地的距离(单位:km)和行驶时间(单位:h)之间的函数关系的图象如图,据图中提供的信息,有下列说法:(1)他们都行驶了20 km;(2)小陆全程共用了1.5 h;(3)小李与小陆相遇后,小李的速度小于小陆的速度; (4)小李在途中停留了0.5 h.其中正确的有( )
A.4个 B.3个
C.2个 D.1个
A
习题4
5.已知有两个人分别骑自行车和摩托车沿着相同的路线从甲地到乙地去,如图反映的是这两个人在行驶过程中时间和路程的关系,请根据图象回答下列问题.
(1)甲地与乙地相距多少千米?两个人分别用了几小时才到达乙地?谁先到达乙地?先到者早到了多长时间?
解:(1)
甲地与乙地相距 100km.
骑摩托车的人用了 2h 到达乙地,
骑自行车的人用了 6h 到达乙地.
骑摩托车的人先到达乙地,早到了1 h.
习题5
(2)分别描述在这个过程中自行车和摩托车的行驶状态.
(3)求摩托车行驶的平均速度.
(3)摩托车行驶的平均速度是100÷2=50(km/h).
(2)骑自行车的人先匀速行驶了2 h,又休息了1 h,然后又匀速行驶了3 h到达乙地;
骑摩托车的人在骑自行车的人出发3 h后出发,匀速行驶2 h后到达乙地.
习题5
6.小红星期天从家里出发骑自行车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,如图是她本次去舅舅家所用的时间(分钟)与离家的距离(米)的关系示意图.
习题6
根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的距离是_________米,小红在商店停留了________分钟.
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快?最快的速度是多少米/分?
1500
4
12≤≤14
450米/分
习题6
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?
观察图象可知小红共行驶了(米),共用了分钟.
习题6
如何从图象中获得有用信息:
明确“两轴”的含义
通常横轴表示自变量,纵轴表示函数值.通过图象可明确自变量、函数值以及它们的取值范围.
明确图象上的点的意义
过一点分别向横轴和纵轴作垂线,两个垂足分别所表示的数就是自变量与函数值的一对对应值.
弄清上升线、下降线和水平线
上升(下降)线表示函数值随自变量的增大而增大(减小),水平线表示随自变量的变化函数值不变.
1
2
3
12.1 函数
第四课时 从函数图象中获取信息
学习目标及重难点
1. 提高识图能力、分析函数图象的能力 ;(重点)
2. 体会数形结合思想,并利用它解决问题,提高解决问题能力.(难点)
1.函数图象的定义.
2.画函数图象的步骤.
3.如何判断某一点是否在某个函数的图象上.
列表
描点
连线
若一个点在某个函数图象上.那么这一点的横、纵坐标一定满足这个函数的解析式,反之则不在.
复习回顾
如果给你一个函数图象,你能读出其中的信息吗?
1.下图是记录某人在一天24 h内的体温变化情况的大致图象.
体温T/℃
时间t/时
探索1:从函数的图象中获取信息
图中纵轴上一段省略了.
体温T/℃
时间t/时
图中纵轴上一段省略了.
思考:(1) 图中有哪两个变量?哪个变量是自变量?
有时间 和体温 两个变量.
时间 是自变量.
体温T/℃
时间t/时
图中纵轴上一段省略了.
思考: (2) 这天中,此人的最高体温与最低体温各是多少?分别是在什么时刻达到的?
找出最高点和最低点对应的横纵坐标
最高36.7℃,最低35.9℃,分别出现在18时和4时
体温T/℃
时间t/时
图中纵轴上一段省略了.
思考: (3) 21时此人的体温是多少?
21时此人的体温是36.4℃.
体温T/℃
时间t/时
图中纵轴上一段省略了.
思考: (4) 此人这天体温达到36.2℃时是在什么时刻?
此人这天体温达到36.2℃时是6时和23时.
体温T/℃
时间t/时
图中纵轴上一段省略了.
思考: (5) 4时到7时,此人体温是如何变化的?18时到24时,此人体温又是如何变化的?
4时到7时,此人体温是不断上升的.
18时到24时,此人体温是不断下降的.
上升线表示函数值随自变量的增大而增大
下降线表示函数值随自变量的增大而减小
如何从图象中获得有用信息:
明确“两轴”的含义
通常横轴表示自变量,纵轴表示函数值.通过图象可明确自变量、函数值以及它们的取值范围.
明确图象上的点的意义
过一点分别向横轴和纵轴作垂线,两个垂足分别所表示的数就是自变量与函数值的一对对应值.
弄清上升线、下降线和水平线
上升(下降)线表示函数值随自变量的增大而增大(减小),水平线表示随自变量的变化函数值不变.
1
2
3
2.一只轮船在甲港与乙港之间往返运输,只行驶一个来回,途径丙港,如下图是这艘轮船离开甲港的距离随时间的变化曲线.
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
观察曲线回答下列问题(以下括号中字母表示轮船所在位置对应曲线上的点):
轮船离开甲港的距离是时间的函数.
对应点之间的间隔时间即为行驶时间,由图象中段平行于轴可知,轮船在乙港停留了一段时间.
甲港
丙港
乙港
丙港
甲港
乙港
思考:(1)从甲港()出发到丙港(),需用多长时间?
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
从甲港()出发到达丙港(),需用1个小时.
甲港
丙港
乙港
丙港
甲港
乙港
思考:(2)从丙港()到达乙港(),需用多长时间?
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
从丙港()到达乙港(),需用2个小时.
甲港
丙港
乙港
丙港
甲港
乙港
思考:(3)图中段表示该轮船在乙港停留多长时间?返回时,多长时间到达丙港()?
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
段表示该轮船在乙港停留了个小时,返回时4个小时到达丙港().
甲港
丙港
乙港
丙港
甲港
乙港
思考:(4)从丙港()返回到出发点甲港(),需多长时间?
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
从丙港()返回到出发点甲港()需2个小时.
甲港
丙港
乙港
丙港
甲港
乙港
思考:(5)轮船从甲港前往乙港的平均速度快,还是轮船返回的平均速度快呢?
时间t/h
O
1 2 3 4 5 6 7 8 9 10
20
40
距离s/km
A
B
C
D
E
轮船从甲港前往乙港的平均行驶速度快.
轮船往返行驶的路程一样,用的时间越少则平均速度越快.
甲港
丙港
乙港
丙港
甲港
乙港
海水受日、月引力影响而产生的涨落现象叫作潮汐,发生在早晨的叫潮,发生在黄昏的叫汐. 某海滨港口在某天的水位变化曲线如图所示.
随堂小练习
随堂小练习
(1) 在这一问题中,有哪几个变量?其中自变量是什么?
(2) 大约在什么时间水最深,深度约为多少?
有2个变量时间和水深;其中自变量是时间.
在3时和15时水最深,深度约为13米.
随堂小练习
(3) 大约在什么时间水最浅,深度约为多少?
在9时和21时水最浅,深度约为7米.
(4)从图中,你还能看出港口水位变化的其他情况吗?
0~3时在持续上涨,3~9时在持续下降,9~15时又在持续上涨,
15~21时又在持续下降,21~24时又在持续上涨 .
1.小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑到公园,打了一会儿太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离(米)与时间(分钟)之间关系的大致图象是( )
B
习题1
2.匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中为一折线).这个容器的形状是下列选项中哪一个( )
C
习题2
A.甲队率先到达终点
B.甲队比乙队多走了200米路程
C.乙队比甲队少用0.2分钟
D.比赛中两队从出发到2.2分钟时间段,乙队的速度比甲队的速度快
3.甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程(米)与时间(分钟)之间的函数关系图象如下图所示,请你根据图象判断,下列说法正确的是( )
C
习题3
4.小李与小陆从地出发,骑自行车沿同一条路行驶到地,他们离出发地的距离(单位:km)和行驶时间(单位:h)之间的函数关系的图象如图,据图中提供的信息,有下列说法:(1)他们都行驶了20 km;(2)小陆全程共用了1.5 h;(3)小李与小陆相遇后,小李的速度小于小陆的速度; (4)小李在途中停留了0.5 h.其中正确的有( )
A.4个 B.3个
C.2个 D.1个
A
习题4
5.已知有两个人分别骑自行车和摩托车沿着相同的路线从甲地到乙地去,如图反映的是这两个人在行驶过程中时间和路程的关系,请根据图象回答下列问题.
(1)甲地与乙地相距多少千米?两个人分别用了几小时才到达乙地?谁先到达乙地?先到者早到了多长时间?
解:(1)
甲地与乙地相距 100km.
骑摩托车的人用了 2h 到达乙地,
骑自行车的人用了 6h 到达乙地.
骑摩托车的人先到达乙地,早到了1 h.
习题5
(2)分别描述在这个过程中自行车和摩托车的行驶状态.
(3)求摩托车行驶的平均速度.
(3)摩托车行驶的平均速度是100÷2=50(km/h).
(2)骑自行车的人先匀速行驶了2 h,又休息了1 h,然后又匀速行驶了3 h到达乙地;
骑摩托车的人在骑自行车的人出发3 h后出发,匀速行驶2 h后到达乙地.
习题5
6.小红星期天从家里出发骑自行车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,如图是她本次去舅舅家所用的时间(分钟)与离家的距离(米)的关系示意图.
习题6
根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的距离是_________米,小红在商店停留了________分钟.
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快?最快的速度是多少米/分?
1500
4
12≤≤14
450米/分
习题6
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?
观察图象可知小红共行驶了(米),共用了分钟.
习题6
如何从图象中获得有用信息:
明确“两轴”的含义
通常横轴表示自变量,纵轴表示函数值.通过图象可明确自变量、函数值以及它们的取值范围.
明确图象上的点的意义
过一点分别向横轴和纵轴作垂线,两个垂足分别所表示的数就是自变量与函数值的一对对应值.
弄清上升线、下降线和水平线
上升(下降)线表示函数值随自变量的增大而增大(减小),水平线表示随自变量的变化函数值不变.
1
2
3
