沪科版2025数学八年级上册12.2 第5课时 一次函数的简单应用——分段函数 课件(共25张PPT)
文档属性
| 名称 | 沪科版2025数学八年级上册12.2 第5课时 一次函数的简单应用——分段函数 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 09:37:19 | ||
图片预览




文档简介
(共25张PPT)
12.2 一次函数
第五课时 一次函数的简单应用——分段函数
学习目标及重难点
1.理解分段函数的特点;(重点)
2.会根据题意求出分段函数的表达式并画出函数图象.(重点)
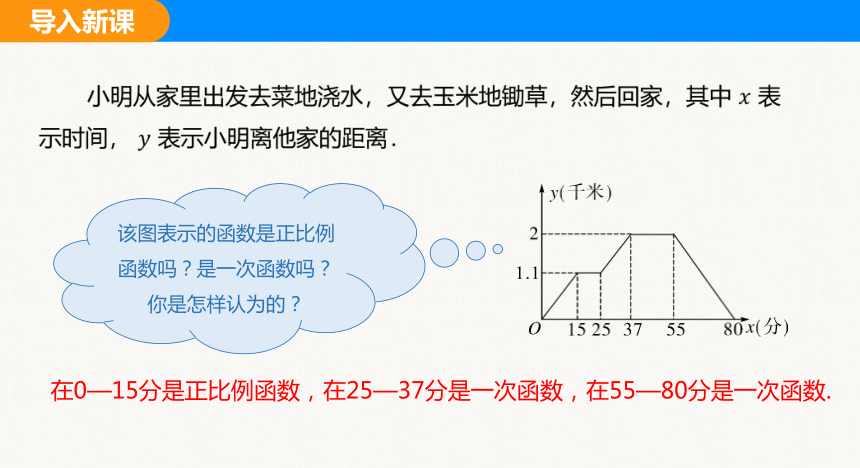
小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中 表示时间, 表示小明离他家的距离.
该图表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?
在0—15分是正比例函数,在25—37分是一次函数,在55—80分是一次函数.
例1:为节约用水,某城市对居民用水制定以下收费标准:一户的水费由使用费和污水处理费组成,每月用水量不超过16m 时,使用费为每立方米1.3元;超过16m 时,超过部分的使用费为每立方米2.0元;污水处理费为每立方米1.2元.设一户每月用水量为 m ,应缴水费为 元.
(1)求 与 之间的函数表式;
探索1:了解分段函数并解决相关问题
分析:用水量以m 为界,分成两段,收费标准不一样:
当 时,每立方米收费 元;
当 时,超过部分每立方米收费 元.
例1:为节约用水,某城市对居民用水制定以下收费标准:一户的水费由使用费和污水处理费组成,每月用水量不超过16m 时,使用费为每立方米1.3元;超过16m 时,超过部分的使用费为每立方米2.0元;污水处理费为每立方米1.2元.设一户每月用水量为 m ,应缴水费为 元.
(1)写出 与 之间的函数表式;
解:(1)当 时,
当 时,
.
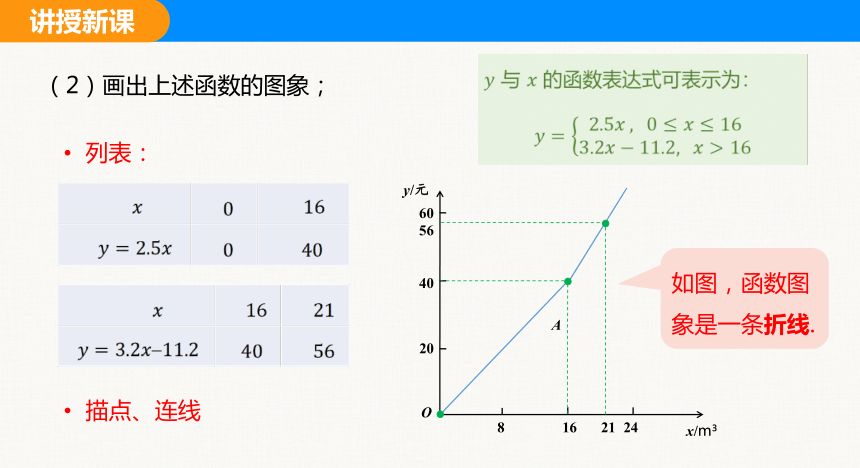
与 的函数表达式可表示为:
(2)画出上述函数的图象;
与 的函数表达式可表示为:
列表:
描点、连线
如图,函数图象是一条折线.
O
y/元
x/m
8
16
24
20
40
A
60
56
21
O
y/元
x/m
8
16
24
20
40
A
60
56
21
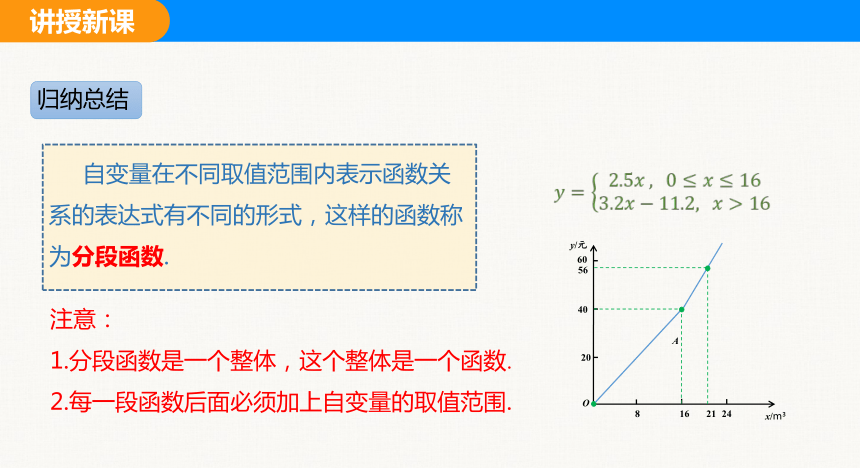
自变量在不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数.
注意:
1.分段函数是一个整体,这个整体是一个函数.
2.每一段函数后面必须加上自变量的取值范围.
归纳总结
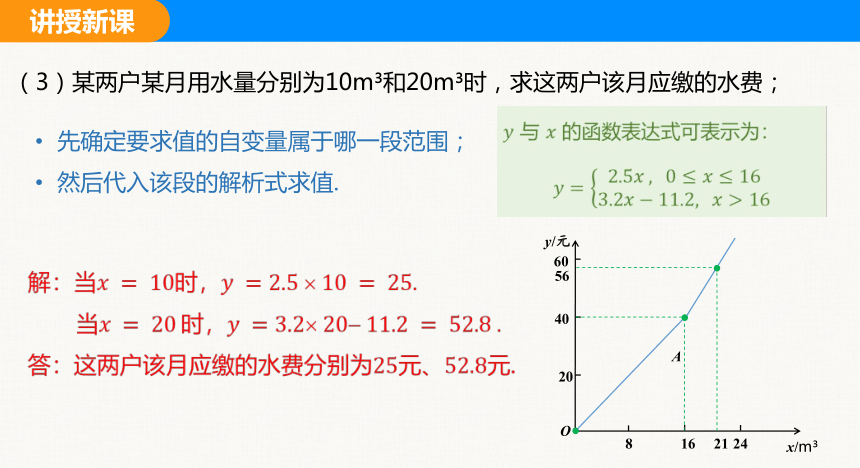
(3)某两户某月用水量分别为10m 和20m 时,求这两户该月应缴的水费;
与 的函数表达式可表示为:
O
y/元
x/m
8
16
24
20
40
A
60
56
21
先确定要求值的自变量属于哪一段范围;
然后代入该段的解析式求值.
解:当时,
当 时,
答:这两户该月应缴的水费分别为元、元.
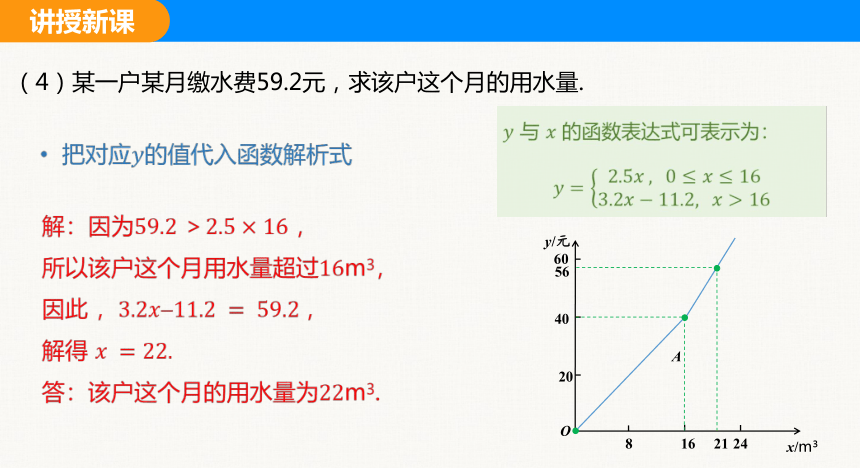
(4)某一户某月缴水费59.2元,求该户这个月的用水量.
与 的函数表达式可表示为:
O
y/元
x/m
8
16
24
20
40
A
60
56
21
把对应的值代入函数解析式
解:因为 ,
所以该户这个月用水量超过m3,
因此 ,,
解得
答:该户这个月的用水量为m3.
分段函数求值:
1.先确定要求值的自变量属于哪一段范围;
2.代入该段的解析式求值.
O
y/元
x/m
8
16
24
20
40
A
60
56
21
归纳总结
例2:某市出租车计费方法如图所示.根据图象信息,下列说法错误的是( )
A.出租车的起步价是10元
B.在3千米内只收起步价
C.超过3千米部分()每千米收3元
D.超过3千米时(),所需费用与之间的函数关系式是
探索2:分段函数的应用
C
要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论,读函数的图象时首先要理解横纵坐标表示的含义,理解问题叙述的过程.
某厂今年前5个月生产某种产品的总量(件)关于时间(月)的函数图象如图所示,则下列说法正确的是( )
A.1月至3月每月生产总量逐月增加,4,5两月每月生产总量逐月减少
B.1月至3月每月生产总量逐月增加,4,5两月每月生产量与3月持平
C.1月至3月每月生产总量逐月增加,4,5两月均停止生产
D.1月至3月每月生产总量不变,4,5两月均停止生产
D
随堂小练习
例3:某地实行阶梯电价,用户每月应缴电费 元与用电量 kW·h的关系如图所示. 求出 与 之间的函数表达式.
x/kW·h
y/元
正比例函数与一次函数构成的分段函数.
解:①当时,
设与之间的函数关系式为(),
代入(),可得
解得,
.
②当时,
设与之间的函数关系式为().
例3:某地实行阶梯电价,用户每月应缴电费 元与用电量 kW·h的关系如图所示. 求出 与 之间的函数表达式.
x/kW·h
y/元
正比例函数与一次函数构成的分段函数.
解:②当时,
设与之间的函数关系式为().
代入可得
解得
x/kW·h
y/元
正比例函数与一次函数构成的分段函数.
解:②当时,
设与之间的函数关系式为().
代入可得
解得
综上可得:
1.定类型:根据自变量在不同范围内的图象的特点,先确定函数的类型;
2.设函数式:设出函数的解析式;
3.列方程(组):根据图象中的已知点,列出方程 (组),求出该段内的解析式;
4.下结论:最后用“{”表示出各段解析式,注意自变量的取值范围.
由分段函数的图象确定函数解析式的方法:
归纳总结
某移动公司采用分段计费的方法来计算话费,月通话时间 (分钟)与相应话费 (元)之间的函数图象如图所示:
(1)月通话为100分钟时,应交话费 元;
(2)当100时,求与之间的函数关系式;
(3)月通话为280分钟时,应交话费多少元?
40
x/min
y/元
解:(2)
设与之间的函数关系式为
由图上知:时,
时,
随堂小练习
(2)当100时,求与之间的函数关系式;
x/min
y/元
解:(2)
设与之间的函数关系式为
由图上知:时,
时,
则有 , 解得
当100时,求与之间的函数关系式为
(2)当100时,求与之间的函数关系式;
(3)月通话为280分钟时,应交话费多少元?
x/min
y/元
解:(3)把代入 得,
,
即当月通话为分钟时,应交话费元.
1.某商户以每件8元的价格购进若干件四季如春植绒窗花到市场去销售,销售金额(元)与销售量(件)之间的函数关系图象如图所示,则降价后每件商品销售的价格为( )
A.5元 B.10元 C.12.5元 D.15元
B
习题1
2.小明早上从家骑自行车去上学,先走平路到达点,再走上坡路到达点,最后走下坡路到达学校,小明骑自行车所走的路程(单位:千米)与他所用的时间(单位:分钟)的关系如图所示,放学后,小明沿原路返回,且走平路、上坡路、下坡路的速度分别保持和上学时一致.下列说法错误的是( )
A.小明家距学校4千米
B.小明上学所用的时间为12分钟
C.小明上坡的速度是0.5千米分钟
D.小明放学回家所用的时间为15分钟
C
习题2
3.电信公司在某市推出新的收费套餐,收费标准为一次通话前3分钟为0.2元,3分钟后超过3分钟的部分按0.1元/min收费,则一次通话时间(分)与这次通话的费用(元)之间的函数表
达式是 .
=
习题3
(1)小明全家在旅游景点游玩了多少小时?
4.“五一”黄金周的某一 天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
解:由图象可知,小明全家在旅游景点游玩了4小时.
5
10
15
120
180
s(千米)
t(时)
O
A
B
C
D
8
14
习题4
(2)求出返程途中,(千米)与时间(时)的函数关系,并回答小明全家到家是什么时间?
解:设由图象过
令得
返程途中 与时间的函数关系是
小明全家当天17:00到家.
得
5
10
15
120
180
s(千米)
t(时)
O
A
B
C
D
8
14
习题4
分段函数
分段函数:
1.定义:
在自变量的不同取值范围内表示函数关系的表达式有不 同的形式,这样的函数称为分段函数.
2.图象:
画出函数在各段上的图象,再合起来就是分段函数的图象.
3.注意:
它是一个函数;要写明自变量取值范围.
分段函数求值:
1.先确定要求值的自变量属于哪一段范围;
2.代入该段的解析式求值.
由分段函数的图象确定解析式的方法:
1.定类型 2.设函数式 3.列方程(组) 4.下结论
12.2 一次函数
第五课时 一次函数的简单应用——分段函数
学习目标及重难点
1.理解分段函数的特点;(重点)
2.会根据题意求出分段函数的表达式并画出函数图象.(重点)
小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中 表示时间, 表示小明离他家的距离.
该图表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?
在0—15分是正比例函数,在25—37分是一次函数,在55—80分是一次函数.
例1:为节约用水,某城市对居民用水制定以下收费标准:一户的水费由使用费和污水处理费组成,每月用水量不超过16m 时,使用费为每立方米1.3元;超过16m 时,超过部分的使用费为每立方米2.0元;污水处理费为每立方米1.2元.设一户每月用水量为 m ,应缴水费为 元.
(1)求 与 之间的函数表式;
探索1:了解分段函数并解决相关问题
分析:用水量以m 为界,分成两段,收费标准不一样:
当 时,每立方米收费 元;
当 时,超过部分每立方米收费 元.
例1:为节约用水,某城市对居民用水制定以下收费标准:一户的水费由使用费和污水处理费组成,每月用水量不超过16m 时,使用费为每立方米1.3元;超过16m 时,超过部分的使用费为每立方米2.0元;污水处理费为每立方米1.2元.设一户每月用水量为 m ,应缴水费为 元.
(1)写出 与 之间的函数表式;
解:(1)当 时,
当 时,
.
与 的函数表达式可表示为:
(2)画出上述函数的图象;
与 的函数表达式可表示为:
列表:
描点、连线
如图,函数图象是一条折线.
O
y/元
x/m
8
16
24
20
40
A
60
56
21
O
y/元
x/m
8
16
24
20
40
A
60
56
21
自变量在不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数.
注意:
1.分段函数是一个整体,这个整体是一个函数.
2.每一段函数后面必须加上自变量的取值范围.
归纳总结
(3)某两户某月用水量分别为10m 和20m 时,求这两户该月应缴的水费;
与 的函数表达式可表示为:
O
y/元
x/m
8
16
24
20
40
A
60
56
21
先确定要求值的自变量属于哪一段范围;
然后代入该段的解析式求值.
解:当时,
当 时,
答:这两户该月应缴的水费分别为元、元.
(4)某一户某月缴水费59.2元,求该户这个月的用水量.
与 的函数表达式可表示为:
O
y/元
x/m
8
16
24
20
40
A
60
56
21
把对应的值代入函数解析式
解:因为 ,
所以该户这个月用水量超过m3,
因此 ,,
解得
答:该户这个月的用水量为m3.
分段函数求值:
1.先确定要求值的自变量属于哪一段范围;
2.代入该段的解析式求值.
O
y/元
x/m
8
16
24
20
40
A
60
56
21
归纳总结
例2:某市出租车计费方法如图所示.根据图象信息,下列说法错误的是( )
A.出租车的起步价是10元
B.在3千米内只收起步价
C.超过3千米部分()每千米收3元
D.超过3千米时(),所需费用与之间的函数关系式是
探索2:分段函数的应用
C
要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论,读函数的图象时首先要理解横纵坐标表示的含义,理解问题叙述的过程.
某厂今年前5个月生产某种产品的总量(件)关于时间(月)的函数图象如图所示,则下列说法正确的是( )
A.1月至3月每月生产总量逐月增加,4,5两月每月生产总量逐月减少
B.1月至3月每月生产总量逐月增加,4,5两月每月生产量与3月持平
C.1月至3月每月生产总量逐月增加,4,5两月均停止生产
D.1月至3月每月生产总量不变,4,5两月均停止生产
D
随堂小练习
例3:某地实行阶梯电价,用户每月应缴电费 元与用电量 kW·h的关系如图所示. 求出 与 之间的函数表达式.
x/kW·h
y/元
正比例函数与一次函数构成的分段函数.
解:①当时,
设与之间的函数关系式为(),
代入(),可得
解得,
.
②当时,
设与之间的函数关系式为().
例3:某地实行阶梯电价,用户每月应缴电费 元与用电量 kW·h的关系如图所示. 求出 与 之间的函数表达式.
x/kW·h
y/元
正比例函数与一次函数构成的分段函数.
解:②当时,
设与之间的函数关系式为().
代入可得
解得
x/kW·h
y/元
正比例函数与一次函数构成的分段函数.
解:②当时,
设与之间的函数关系式为().
代入可得
解得
综上可得:
1.定类型:根据自变量在不同范围内的图象的特点,先确定函数的类型;
2.设函数式:设出函数的解析式;
3.列方程(组):根据图象中的已知点,列出方程 (组),求出该段内的解析式;
4.下结论:最后用“{”表示出各段解析式,注意自变量的取值范围.
由分段函数的图象确定函数解析式的方法:
归纳总结
某移动公司采用分段计费的方法来计算话费,月通话时间 (分钟)与相应话费 (元)之间的函数图象如图所示:
(1)月通话为100分钟时,应交话费 元;
(2)当100时,求与之间的函数关系式;
(3)月通话为280分钟时,应交话费多少元?
40
x/min
y/元
解:(2)
设与之间的函数关系式为
由图上知:时,
时,
随堂小练习
(2)当100时,求与之间的函数关系式;
x/min
y/元
解:(2)
设与之间的函数关系式为
由图上知:时,
时,
则有 , 解得
当100时,求与之间的函数关系式为
(2)当100时,求与之间的函数关系式;
(3)月通话为280分钟时,应交话费多少元?
x/min
y/元
解:(3)把代入 得,
,
即当月通话为分钟时,应交话费元.
1.某商户以每件8元的价格购进若干件四季如春植绒窗花到市场去销售,销售金额(元)与销售量(件)之间的函数关系图象如图所示,则降价后每件商品销售的价格为( )
A.5元 B.10元 C.12.5元 D.15元
B
习题1
2.小明早上从家骑自行车去上学,先走平路到达点,再走上坡路到达点,最后走下坡路到达学校,小明骑自行车所走的路程(单位:千米)与他所用的时间(单位:分钟)的关系如图所示,放学后,小明沿原路返回,且走平路、上坡路、下坡路的速度分别保持和上学时一致.下列说法错误的是( )
A.小明家距学校4千米
B.小明上学所用的时间为12分钟
C.小明上坡的速度是0.5千米分钟
D.小明放学回家所用的时间为15分钟
C
习题2
3.电信公司在某市推出新的收费套餐,收费标准为一次通话前3分钟为0.2元,3分钟后超过3分钟的部分按0.1元/min收费,则一次通话时间(分)与这次通话的费用(元)之间的函数表
达式是 .
=
习题3
(1)小明全家在旅游景点游玩了多少小时?
4.“五一”黄金周的某一 天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
解:由图象可知,小明全家在旅游景点游玩了4小时.
5
10
15
120
180
s(千米)
t(时)
O
A
B
C
D
8
14
习题4
(2)求出返程途中,(千米)与时间(时)的函数关系,并回答小明全家到家是什么时间?
解:设由图象过
令得
返程途中 与时间的函数关系是
小明全家当天17:00到家.
得
5
10
15
120
180
s(千米)
t(时)
O
A
B
C
D
8
14
习题4
分段函数
分段函数:
1.定义:
在自变量的不同取值范围内表示函数关系的表达式有不 同的形式,这样的函数称为分段函数.
2.图象:
画出函数在各段上的图象,再合起来就是分段函数的图象.
3.注意:
它是一个函数;要写明自变量取值范围.
分段函数求值:
1.先确定要求值的自变量属于哪一段范围;
2.代入该段的解析式求值.
由分段函数的图象确定解析式的方法:
1.定类型 2.设函数式 3.列方程(组) 4.下结论
