沪科版2025数学八年级上册12.3 第2课时 一次函数与二元一次方程组 课件(共23张PPT)
文档属性
| 名称 | 沪科版2025数学八年级上册12.3 第2课时 一次函数与二元一次方程组 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 09:38:11 | ||
图片预览






文档简介
(共23张PPT)
12.3 一次函数与二元一次方程
第二课时 一次函数与二元一次方程组
学习目标及重难点
1.知道一次函数与二元一次方程组的关系,会用图象法解二元一次方程组;
2.通过一次函数,了解二元一次方程组无解的情形;
3.会根据二元一次方程的系数判断二元一次方程组解的情况.
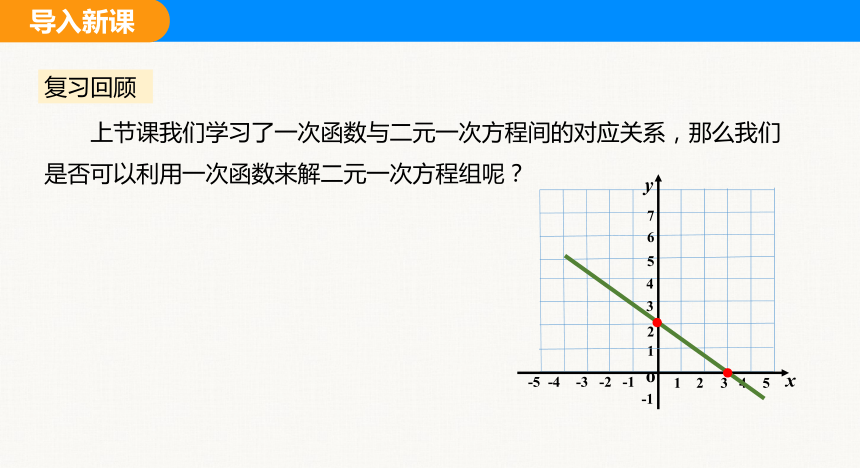
上节课我们学习了一次函数与二元一次方程间的对应关系,那么我们是否可以利用一次函数来解二元一次方程组呢?
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
复习回顾
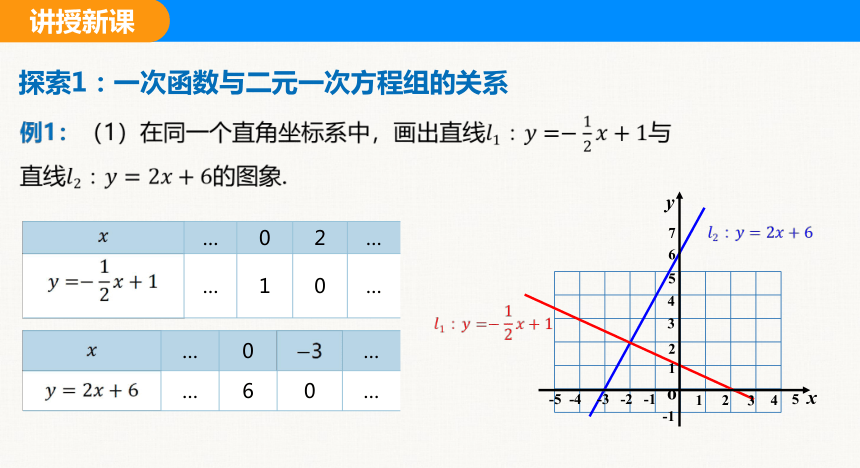
例1:(1)在同一个直角坐标系中,画出直线与
直线的图象.
探索1:一次函数与二元一次方程组的关系
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
… 0 2 …
… 1 0 …
… 0 3 …
… 6 0 …
例1:(1)在同一个直角坐标系中,画出直线与
直线的图象.
(2)如果直线 与 相交于点,写出点的坐标;
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
解(2)由图可知,直线与交于点,点的坐标为
例1:(3)说明点的坐标是否为下面方程组的解?
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
(3)方程 可以转化成一次函数 的形式,
因此,直线 :上任意一点的坐标都是方程 的解.
同理,得直线上任意一点的坐标都是方程 的解.
所以直线 与 的交点 的坐标是方程 与 的公共解,
也就是说,点的坐标是二元一次方程组的解.
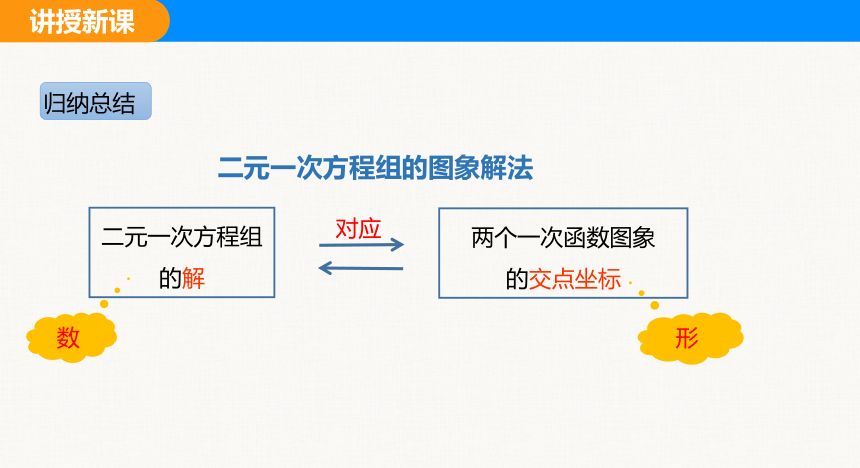
归纳总结
二元一次方程组的图象解法
形
对应
二元一次方程组
的解
两个一次函数图象
的交点坐标
数
若关于的二元一次方程组 的解为 ,一次函数与的图象的交点坐标为( )
A
A.(1,2) B.(2,1) C.(2,3) D.(1,3)
随堂小练习
例2:利用函数图象解方程组:
解:对于方程①,有
过和画出表示方程①的直线
同样,和也在表示方程②的直线上,
所以方程①、 ②对应的直线是通过和两点的直线,
y
1
2
3
4
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
… …
… …
探索2:利用一次函数图象解二元一次方程组
例2:利用函数图象解方程组:
解:对于方程①,有
过和画出表示方程①的直线
同样,和也在表示方程②的直线上,
所以方程①、 ②对应的直线是通过和两点的直线,
就是说,这两条直线重合,显然,直线上每一个点的坐标都是原方程组的解,所以原方程组有无穷多组解.
y
1
2
3
4
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
… …
… …
思考:你能归纳运用图象法解二元一次方程组的一般步骤吗?
一般步骤
①方程化成函数
②画出函数图象
③找出图象的交点坐标
④写出方程组的解
例3:利用函数图象法解方程组:
1
2
3
4
5
6
7
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
-5
8
解:方程对应直线
对应直线
作出直线两条直线平行,所以方程组无解.
思考:上述例题直观地说明二元一次方程组的解有三种情况.当把其中的各个二元一次方程组化为标准形式:
(其中,,,,,为常数)
比较每个例题里两个方程中 的系数之比、 的系数之比以及常数项之比,你发现了怎样的规律?
例1:
一组解
例2:
无穷多组解
例3:
无解
探索3:二元一次方程组解的情况与系数比的关系
思考:上述例题直观地说明二元一次方程组的解有三种情况.当把其中的各个二元一次方程组化为标准形式:
(其中,,,,,为常数)
比较每个例题里两个方程中 的系数之比、 的系数之比以及常数项之比,你发现了怎样的规律?
例1:
一组解
(1)当 时,方程组有一组解;
思考:上述例题直观地说明二元一次方程组的解有三种情况.当把其中的各个二元一次方程组化为标准形式:
(其中,,,,,为常数)
比较每个例题里两个方程中 的系数之比、 的系数之比以及常数项之比,你发现了怎样的规律?
例2:
无穷多组解
(2)当 时,方程组有无穷多组解;
思考:上述例题直观地说明二元一次方程组的解有三种情况.当把其中的各个二元一次方程组化为标准形式:
(其中,,,,,为常数)
比较每个例题里两个方程中 的系数之比、 的系数之比以及常数项之比,你发现了怎样的规律?
例3:
无解
(3)当 时,方程组无解.
(1)当 时,方程组有一组解;
(2)当 时,方程组有无穷多组解;
(3)当 时,方程组无解.
归纳总结
3x+5y=8
2x3y=7
既不解方程组也不画图,你能判断下列方程组的解的情况吗?
(1)
(2)
(3)
(4)
y=2x3
4x2y=6
3x4y=5
6x8y=12
2x+3y=5
y=x
一组解
无穷组解
无解
一组解
随堂小练习
1.已知直线 与的图象如图,则方程组
的解为( )
A.
B.
C.
D.
B
1
2
1
3
5
4
2
3
习题1
B
2.不解方程,下列方程组中无解的是( )
A. B.
C. D.
习题2
3. 已知直线与的交点坐标为,则方程组
的解是( )
A. B.
C. D.
D
习题3
解:直线与直线的交点坐标为,
所以原方程组的解为
4.利用函数图像解方程组:
习题4
通过以上学习你能发现二元一次方程组的解有几种情况?
二元一次方程组的解有以下三种情况
只有一组解(两直线只有一个交点)
有无穷多组解(两直线重合)
无解(两直线平行)
二元一次方程组
12.3 一次函数与二元一次方程
第二课时 一次函数与二元一次方程组
学习目标及重难点
1.知道一次函数与二元一次方程组的关系,会用图象法解二元一次方程组;
2.通过一次函数,了解二元一次方程组无解的情形;
3.会根据二元一次方程的系数判断二元一次方程组解的情况.
上节课我们学习了一次函数与二元一次方程间的对应关系,那么我们是否可以利用一次函数来解二元一次方程组呢?
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
复习回顾
例1:(1)在同一个直角坐标系中,画出直线与
直线的图象.
探索1:一次函数与二元一次方程组的关系
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
… 0 2 …
… 1 0 …
… 0 3 …
… 6 0 …
例1:(1)在同一个直角坐标系中,画出直线与
直线的图象.
(2)如果直线 与 相交于点,写出点的坐标;
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
解(2)由图可知,直线与交于点,点的坐标为
例1:(3)说明点的坐标是否为下面方程组的解?
x
y
o
1
2
3
4
5
-1
-2
-3
-4
-5
1
2
3
4
5
-1
6
7
(3)方程 可以转化成一次函数 的形式,
因此,直线 :上任意一点的坐标都是方程 的解.
同理,得直线上任意一点的坐标都是方程 的解.
所以直线 与 的交点 的坐标是方程 与 的公共解,
也就是说,点的坐标是二元一次方程组的解.
归纳总结
二元一次方程组的图象解法
形
对应
二元一次方程组
的解
两个一次函数图象
的交点坐标
数
若关于的二元一次方程组 的解为 ,一次函数与的图象的交点坐标为( )
A
A.(1,2) B.(2,1) C.(2,3) D.(1,3)
随堂小练习
例2:利用函数图象解方程组:
解:对于方程①,有
过和画出表示方程①的直线
同样,和也在表示方程②的直线上,
所以方程①、 ②对应的直线是通过和两点的直线,
y
1
2
3
4
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
… …
… …
探索2:利用一次函数图象解二元一次方程组
例2:利用函数图象解方程组:
解:对于方程①,有
过和画出表示方程①的直线
同样,和也在表示方程②的直线上,
所以方程①、 ②对应的直线是通过和两点的直线,
就是说,这两条直线重合,显然,直线上每一个点的坐标都是原方程组的解,所以原方程组有无穷多组解.
y
1
2
3
4
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
… …
… …
思考:你能归纳运用图象法解二元一次方程组的一般步骤吗?
一般步骤
①方程化成函数
②画出函数图象
③找出图象的交点坐标
④写出方程组的解
例3:利用函数图象法解方程组:
1
2
3
4
5
6
7
o
4
3
2
1
-1
-2
-3
-4
x
-1
-2
-3
-4
-5
8
解:方程对应直线
对应直线
作出直线两条直线平行,所以方程组无解.
思考:上述例题直观地说明二元一次方程组的解有三种情况.当把其中的各个二元一次方程组化为标准形式:
(其中,,,,,为常数)
比较每个例题里两个方程中 的系数之比、 的系数之比以及常数项之比,你发现了怎样的规律?
例1:
一组解
例2:
无穷多组解
例3:
无解
探索3:二元一次方程组解的情况与系数比的关系
思考:上述例题直观地说明二元一次方程组的解有三种情况.当把其中的各个二元一次方程组化为标准形式:
(其中,,,,,为常数)
比较每个例题里两个方程中 的系数之比、 的系数之比以及常数项之比,你发现了怎样的规律?
例1:
一组解
(1)当 时,方程组有一组解;
思考:上述例题直观地说明二元一次方程组的解有三种情况.当把其中的各个二元一次方程组化为标准形式:
(其中,,,,,为常数)
比较每个例题里两个方程中 的系数之比、 的系数之比以及常数项之比,你发现了怎样的规律?
例2:
无穷多组解
(2)当 时,方程组有无穷多组解;
思考:上述例题直观地说明二元一次方程组的解有三种情况.当把其中的各个二元一次方程组化为标准形式:
(其中,,,,,为常数)
比较每个例题里两个方程中 的系数之比、 的系数之比以及常数项之比,你发现了怎样的规律?
例3:
无解
(3)当 时,方程组无解.
(1)当 时,方程组有一组解;
(2)当 时,方程组有无穷多组解;
(3)当 时,方程组无解.
归纳总结
3x+5y=8
2x3y=7
既不解方程组也不画图,你能判断下列方程组的解的情况吗?
(1)
(2)
(3)
(4)
y=2x3
4x2y=6
3x4y=5
6x8y=12
2x+3y=5
y=x
一组解
无穷组解
无解
一组解
随堂小练习
1.已知直线 与的图象如图,则方程组
的解为( )
A.
B.
C.
D.
B
1
2
1
3
5
4
2
3
习题1
B
2.不解方程,下列方程组中无解的是( )
A. B.
C. D.
习题2
3. 已知直线与的交点坐标为,则方程组
的解是( )
A. B.
C. D.
D
习题3
解:直线与直线的交点坐标为,
所以原方程组的解为
4.利用函数图像解方程组:
习题4
通过以上学习你能发现二元一次方程组的解有几种情况?
二元一次方程组的解有以下三种情况
只有一组解(两直线只有一个交点)
有无穷多组解(两直线重合)
无解(两直线平行)
二元一次方程组
