沪科版2025数学八年级上册12.3 第3课时 一次函数与二元一次方程(组)的应用 课件(共23张PPT)
文档属性
| 名称 | 沪科版2025数学八年级上册12.3 第3课时 一次函数与二元一次方程(组)的应用 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 09:38:27 | ||
图片预览




文档简介
(共23张PPT)
12.3 一次函数与二元一次方程
第三课时 一次函数与二元一次方程(组)的应用
学习目标及重难点
1.深入了解一次函数的应用价值;(重点)
2.能将一个具体的实际问题转化为数学问题,利用数学模型解决实际问题.(难点)
二元一次方程组的图象解法
形
对应
二元一次方程组
的解
两个一次函数图象
的交点坐标
数
复习回顾
做一件事情,有时有不同的实施方案.比较这些方案,从中选择最佳方案作为行动计划,是非常必要的.应用数学的知识和方法对各种方案进行比较分析,可以帮助我们清晰地认识各种方案,作出理性的决策.
你能说说生活中需要选择方案的例子吗?
租车方案的选择
旅行社的选择
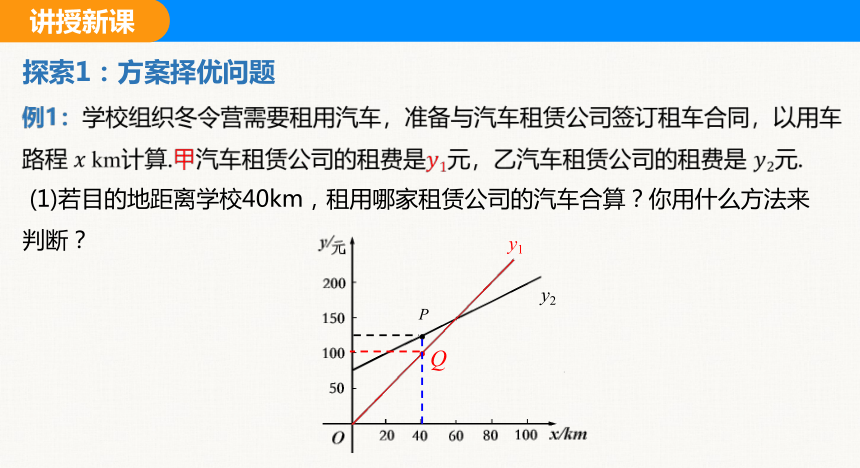
y1
y2
(1)若目的地距离学校40km,租用哪家租赁公司的汽车合算?你用什么方法来判断?
P
Q
例1:学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 km计算.甲汽车租赁公司的租费是元,乙汽车租赁公司的租费是 元.
探索1:方案择优问题
y1
y2
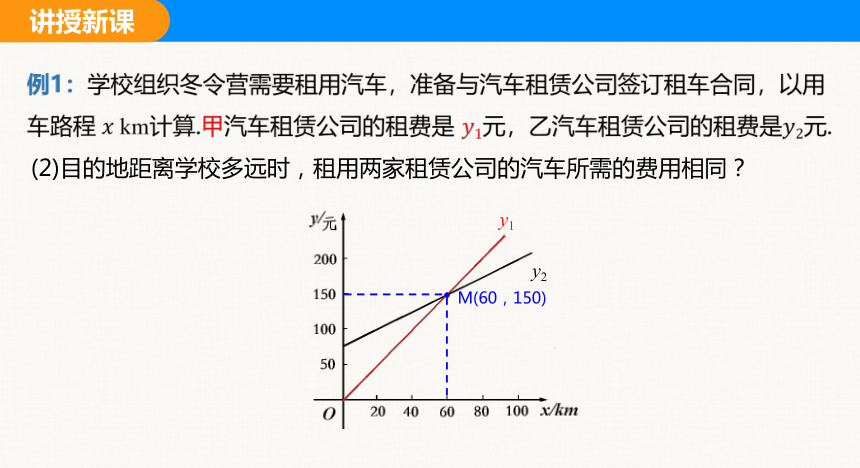
(2)目的地距离学校多远时,租用两家租赁公司的汽车所需的费用相同?
M(60,150)
例1:学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 km计算.甲汽车租赁公司的租费是 元,乙汽车租赁公司的租费是元.
y1
y2
M
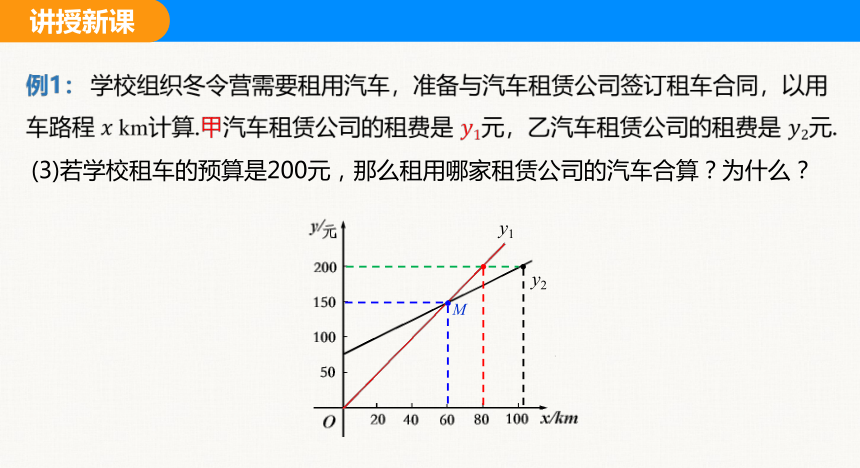
(3)若学校租车的预算是200元,那么租用哪家租赁公司的汽车合算?为什么?
例1: 学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 km计算.甲汽车租赁公司的租费是 元,乙汽车租赁公司的租费是 元.
y1
y2
M
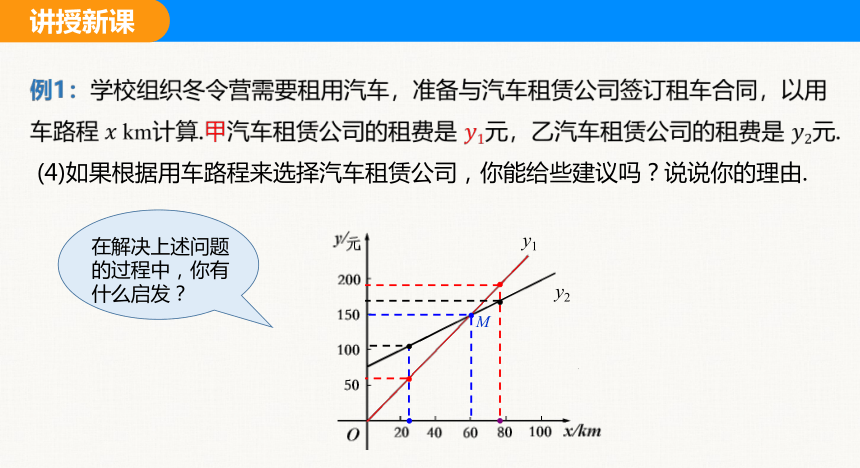
(4)如果根据用车路程来选择汽车租赁公司,你能给些建议吗?说说你的理由.
例1:学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 km计算.甲汽车租赁公司的租费是 元,乙汽车租赁公司的租费是 元.
在解决上述问题的过程中,你有什么启发?
例2:某单位想在节假日期间组织职工到外地 处旅游. 当地有甲、乙两家旅行社,它们服务质量基本相同,到此 地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客 8 折优惠;乙旅行社表示单位先交1 000元后,给予每位游客 6 折优惠. 该单位应选择哪个旅行社,使其支付的旅游总费用较少?
分析:假设该单位参加旅游人数为_____,
按甲旅行社的优惠条件,应付费用_________元;
按乙旅行社的优惠条件,应付费用_____________________元
如何比较与的大小?
例2:某单位想在节假日期间组织职工到外地 处旅游. 当地有甲、乙两家旅行社,它们服务质量基本相同,到此 地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客 8 折优惠;乙旅行社表示单位先交1 000元后,给予每位游客 6 折优惠. 该单位应选择哪个旅行社,使其支付的旅游总费用较少?
解:设该单位参加旅游人数为(其中,且为正整数),旅游总费用为元. 那么选甲旅行社,应付元;选乙旅行社,应付元.
记
y/元
800
1600
3200
2400
4000
4800
5600
观察图象,可得:
①当人数为时,
选择甲或乙旅行社费用都一样;
②当人数为时,
选择甲旅行社费用较少;
③当人数为人时,
选择乙旅行社费用较少.
x/人
50
60
O
10
20
30
40
70
y1= 80x
y2= 60x+1000
方法一:在同一直角坐标系中,作出两个函数的图象,与的图象交于点
方法二:设选择甲、乙旅行社费用之差为,
则
画出一次函数的图象如下图,它与 轴的交点为.
-200
-400
-600
-800
-1000
y
由图可知:
①当时,,即
选择甲或乙旅行社费用都一样;
②当时,,即
选择乙旅行社费用较少;
③当时,,即
选择甲旅行社费用较少.
O
20
40
60
x
y= 20x1000
(1) → 两图像的交点坐标;
(2) → 图像在上方;
(3)→ 图像在下方;
(4)→ 图像与轴的交点坐标;
(5) → 图像在轴上方;
(6)→ 图像在轴下方;
(7)差量 → →新函数→新图像.
归纳总结
方法三:
(1)当,即时,
所以当人数为时,选择甲或乙旅行社费用都一样;
(2)当,即时, 得
所以当人数为以上时 ,选择乙旅行社费用较少;
(3)当,即时,得
所以当人数为时,选择甲旅行社费用较少;
②列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
从数学的角度分析数学问题,建立函数模型
结合实际需求,选择最佳方案
①画出图像,找出交点位置,判断交点左右两侧的大小关系
利用一次函数进行方案决策:
6
4
L1
100
200
300
400
2
y/元
x/件
L2
O
1.如图所示,L1反映了某公司产品的销售收入和销售数量的关系, L2反映产品的销售成本与销售数量的关系,根据图象判断公司盈利时销售量( )
A.小于4件
B.大于4件
C.等于4件
D.大于或等于4件
B
习题1
2.某公司准备与汽车租赁公司签订租车合同,以每月用车路程km计算,甲汽车租赁公司每月收取的租赁费为元,乙汽车租赁公司每月收取的租赁费为元,若与之间的函数关系如图所示,其中对应的函数值为月固定租赁费,则下列判断错误的是( )
D
A.当月用车路程为km时,两家汽车租赁公司租赁费用相同
B.当月用车路程为km时,租赁乙汽车租赁公车比较合算
C.除去月固定租赁费,甲租赁公司每公里收取的费用比乙租赁公司多
D.甲租赁公司平均每公里收到的费用比乙租赁公司少
习题2
习题3
解:设小明的速度为米/秒,小刚的速度为
米/秒,由题意得
解得.
故这次越野跑的全程为米.
3.一次越野跑中,当小明跑了米时,小刚跑了米,小明、小刚所跑的路程 (米)与时间 (秒)之间的函数关系如图,则这次越野跑的全程为 米.
4. 某厂日产手套的总成本元与日产量副之间的函数表达式为,而手套的出厂价格为每副元,试问该厂至少应日产手套多少副才能不亏本?
解:
根据题意得:
解得
答:该厂至少应日产手套副才能不亏本.
习题4
5.某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间(分钟)与收费(元)之间的函数关系式如图.
(1)有月租时的收费方式是_______(选填“①”或“②”),月租费是_______元;
(2)分别求出①、②两种收费方式中与自变量之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
①
30
习题5
(2)分别求出①、②两种收费方式中与自变量之间的函数表达式;
(2) 设
将代入
得
∴.
将代入
得
故①、②两种收费方式中与自变量之间的函数表达式分别为
习题5
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
(3)由,
得,解得
当时,.
由图可知,
当通讯时间在分钟以内时,选择收费方式②实惠;
当通讯时间超过分钟时,选择收费方式①实惠;
当通讯时间等于分钟时,选择收费方式①、②一样实惠.
习题5
利用一次函数进行方案决策
列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
从数学的角度分析数学问题,建立函数模型
结合实际需求,选择最佳方案
12.3 一次函数与二元一次方程
第三课时 一次函数与二元一次方程(组)的应用
学习目标及重难点
1.深入了解一次函数的应用价值;(重点)
2.能将一个具体的实际问题转化为数学问题,利用数学模型解决实际问题.(难点)
二元一次方程组的图象解法
形
对应
二元一次方程组
的解
两个一次函数图象
的交点坐标
数
复习回顾
做一件事情,有时有不同的实施方案.比较这些方案,从中选择最佳方案作为行动计划,是非常必要的.应用数学的知识和方法对各种方案进行比较分析,可以帮助我们清晰地认识各种方案,作出理性的决策.
你能说说生活中需要选择方案的例子吗?
租车方案的选择
旅行社的选择
y1
y2
(1)若目的地距离学校40km,租用哪家租赁公司的汽车合算?你用什么方法来判断?
P
Q
例1:学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 km计算.甲汽车租赁公司的租费是元,乙汽车租赁公司的租费是 元.
探索1:方案择优问题
y1
y2
(2)目的地距离学校多远时,租用两家租赁公司的汽车所需的费用相同?
M(60,150)
例1:学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 km计算.甲汽车租赁公司的租费是 元,乙汽车租赁公司的租费是元.
y1
y2
M
(3)若学校租车的预算是200元,那么租用哪家租赁公司的汽车合算?为什么?
例1: 学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 km计算.甲汽车租赁公司的租费是 元,乙汽车租赁公司的租费是 元.
y1
y2
M
(4)如果根据用车路程来选择汽车租赁公司,你能给些建议吗?说说你的理由.
例1:学校组织冬令营需要租用汽车,准备与汽车租赁公司签订租车合同,以用车路程 km计算.甲汽车租赁公司的租费是 元,乙汽车租赁公司的租费是 元.
在解决上述问题的过程中,你有什么启发?
例2:某单位想在节假日期间组织职工到外地 处旅游. 当地有甲、乙两家旅行社,它们服务质量基本相同,到此 地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客 8 折优惠;乙旅行社表示单位先交1 000元后,给予每位游客 6 折优惠. 该单位应选择哪个旅行社,使其支付的旅游总费用较少?
分析:假设该单位参加旅游人数为_____,
按甲旅行社的优惠条件,应付费用_________元;
按乙旅行社的优惠条件,应付费用_____________________元
如何比较与的大小?
例2:某单位想在节假日期间组织职工到外地 处旅游. 当地有甲、乙两家旅行社,它们服务质量基本相同,到此 地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客 8 折优惠;乙旅行社表示单位先交1 000元后,给予每位游客 6 折优惠. 该单位应选择哪个旅行社,使其支付的旅游总费用较少?
解:设该单位参加旅游人数为(其中,且为正整数),旅游总费用为元. 那么选甲旅行社,应付元;选乙旅行社,应付元.
记
y/元
800
1600
3200
2400
4000
4800
5600
观察图象,可得:
①当人数为时,
选择甲或乙旅行社费用都一样;
②当人数为时,
选择甲旅行社费用较少;
③当人数为人时,
选择乙旅行社费用较少.
x/人
50
60
O
10
20
30
40
70
y1= 80x
y2= 60x+1000
方法一:在同一直角坐标系中,作出两个函数的图象,与的图象交于点
方法二:设选择甲、乙旅行社费用之差为,
则
画出一次函数的图象如下图,它与 轴的交点为.
-200
-400
-600
-800
-1000
y
由图可知:
①当时,,即
选择甲或乙旅行社费用都一样;
②当时,,即
选择乙旅行社费用较少;
③当时,,即
选择甲旅行社费用较少.
O
20
40
60
x
y= 20x1000
(1) → 两图像的交点坐标;
(2) → 图像在上方;
(3)→ 图像在下方;
(4)→ 图像与轴的交点坐标;
(5) → 图像在轴上方;
(6)→ 图像在轴下方;
(7)差量 → →新函数→新图像.
归纳总结
方法三:
(1)当,即时,
所以当人数为时,选择甲或乙旅行社费用都一样;
(2)当,即时, 得
所以当人数为以上时 ,选择乙旅行社费用较少;
(3)当,即时,得
所以当人数为时,选择甲旅行社费用较少;
②列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
从数学的角度分析数学问题,建立函数模型
结合实际需求,选择最佳方案
①画出图像,找出交点位置,判断交点左右两侧的大小关系
利用一次函数进行方案决策:
6
4
L1
100
200
300
400
2
y/元
x/件
L2
O
1.如图所示,L1反映了某公司产品的销售收入和销售数量的关系, L2反映产品的销售成本与销售数量的关系,根据图象判断公司盈利时销售量( )
A.小于4件
B.大于4件
C.等于4件
D.大于或等于4件
B
习题1
2.某公司准备与汽车租赁公司签订租车合同,以每月用车路程km计算,甲汽车租赁公司每月收取的租赁费为元,乙汽车租赁公司每月收取的租赁费为元,若与之间的函数关系如图所示,其中对应的函数值为月固定租赁费,则下列判断错误的是( )
D
A.当月用车路程为km时,两家汽车租赁公司租赁费用相同
B.当月用车路程为km时,租赁乙汽车租赁公车比较合算
C.除去月固定租赁费,甲租赁公司每公里收取的费用比乙租赁公司多
D.甲租赁公司平均每公里收到的费用比乙租赁公司少
习题2
习题3
解:设小明的速度为米/秒,小刚的速度为
米/秒,由题意得
解得.
故这次越野跑的全程为米.
3.一次越野跑中,当小明跑了米时,小刚跑了米,小明、小刚所跑的路程 (米)与时间 (秒)之间的函数关系如图,则这次越野跑的全程为 米.
4. 某厂日产手套的总成本元与日产量副之间的函数表达式为,而手套的出厂价格为每副元,试问该厂至少应日产手套多少副才能不亏本?
解:
根据题意得:
解得
答:该厂至少应日产手套副才能不亏本.
习题4
5.某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间(分钟)与收费(元)之间的函数关系式如图.
(1)有月租时的收费方式是_______(选填“①”或“②”),月租费是_______元;
(2)分别求出①、②两种收费方式中与自变量之间的函数表达式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
①
30
习题5
(2)分别求出①、②两种收费方式中与自变量之间的函数表达式;
(2) 设
将代入
得
∴.
将代入
得
故①、②两种收费方式中与自变量之间的函数表达式分别为
习题5
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
(3)由,
得,解得
当时,.
由图可知,
当通讯时间在分钟以内时,选择收费方式②实惠;
当通讯时间超过分钟时,选择收费方式①实惠;
当通讯时间等于分钟时,选择收费方式①、②一样实惠.
习题5
利用一次函数进行方案决策
列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
从数学的角度分析数学问题,建立函数模型
结合实际需求,选择最佳方案
