(小升初择校分班考)小升初重点校择校分班考模拟卷-2025年秋六年级数学人教版(含答案解析)
文档属性
| 名称 | (小升初择校分班考)小升初重点校择校分班考模拟卷-2025年秋六年级数学人教版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 281.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 18:14:48 | ||
图片预览




文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初重点校择校分班考模拟卷(人教版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.一个等腰三角形的两条边长分别是2cm和5cm,它的周长是( )
A.7cm B.9cm C.12cm D.不能确定
2.一个圆柱的底面半径扩大4倍,高不变,它的体积扩大( )
A.4倍 B.8倍 C.16倍
3.把一段a米(a>0)长的铁丝平均分成4段,每段铁丝长( )米
A. B. C. D.
4.如图由一个正方形和平行四边形组成,正方形的面积是a平方厘米,平行四边形的面积是( )平方厘米。
A. B.a C. D.2a
5.点m和点n位置如图所示,下面说法正确的是( )
A.n>m B.mn>m C.1 D.1
6.如图三幅图分别描述三个故事,这三幅图对应的故事正确的是( )
A.龟兔赛跑、司马光砸缸、乌鸦喝水
B.乌鸦喝水、司马光磁缸、龟兔赛跑
C.司马光砸缸、龟兔赛跑、乌鸦喝水
D.乌鸦喝水、龟兔赛跑、司马光砸缸
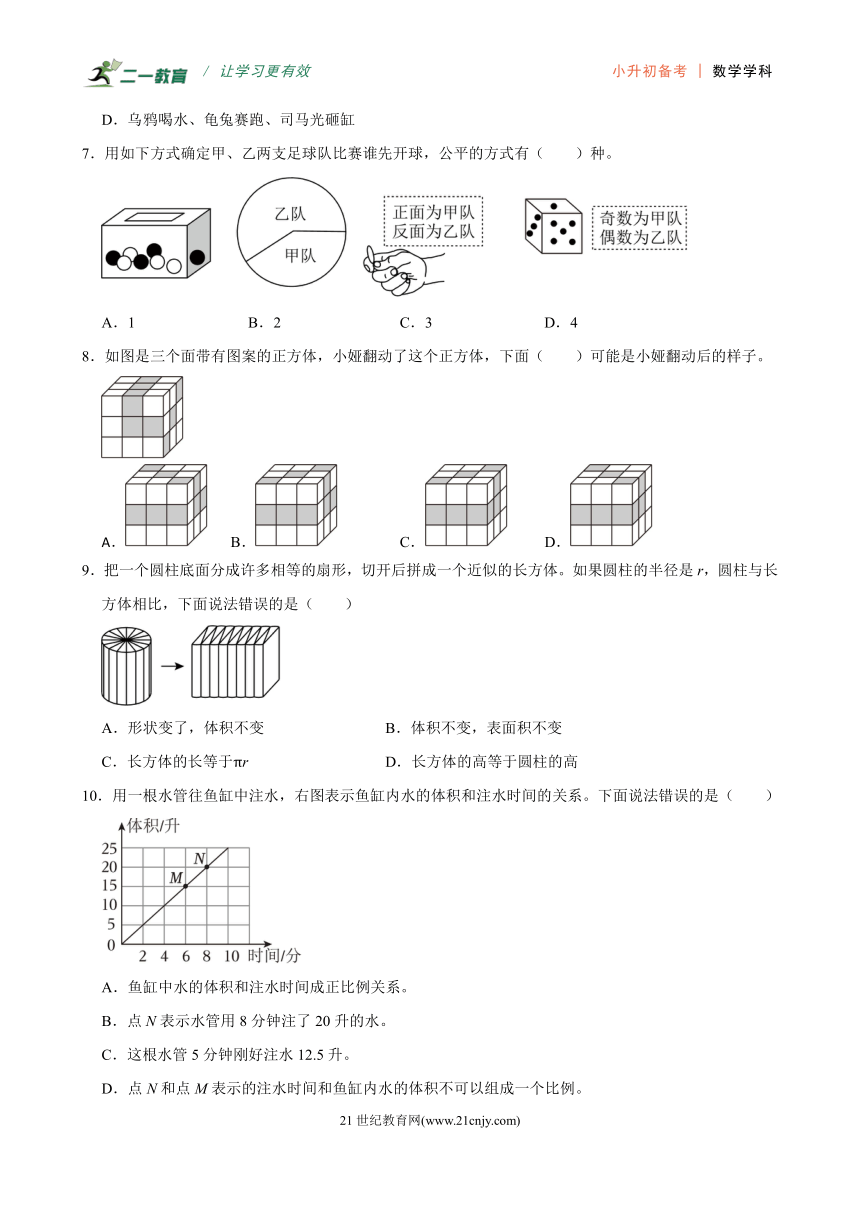
7.用如下方式确定甲、乙两支足球队比赛谁先开球,公平的方式有( )种。
A.1 B.2 C.3 D.4
8.如图是三个面带有图案的正方体,小娅翻动了这个正方体,下面( )可能是小娅翻动后的样子。
B. C. D.
9.把一个圆柱底面分成许多相等的扇形,切开后拼成一个近似的长方体。如果圆柱的半径是r,圆柱与长方体相比,下面说法错误的是( )
A.形状变了,体积不变 B.体积不变,表面积不变
C.长方体的长等于πr D.长方体的高等于圆柱的高
10.用一根水管往鱼缸中注水,右图表示鱼缸内水的体积和注水时间的关系。下面说法错误的是( )
A.鱼缸中水的体积和注水时间成正比例关系。
B.点N表示水管用8分钟注了20升的水。
C.这根水管5分钟刚好注水12.5升。
D.点N和点M表示的注水时间和鱼缸内水的体积不可以组成一个比例。
二.填空题
11.按如图的方式摆放桌子和椅子.25张桌子可以坐 人.
12.如果把一个圆柱的高截短3cm,表面积就减少了94.2cm2,这个圆柱的底面积是 cm2.
13.44公顷= 平方千米 4080米= 千米
3.2立方分米= 升= 毫升 时= 时 分
14.大小两个圆的半径之比是2:1,它们的直径之比是 ,周长之比 ,面积之比是 。
15.把化成循环小数是0.428571428571…,这个循环小数的小数部分第50位上的数字是 .
16.如图,长方形ABCD被分成两个长方形,且AB:AE=4:1,图阴影部分三角形的面积为4平方分米,长方形ABCD的面积是 平方分米.
17.如果a+1=b(a、b都是自然数,且不等于0),那么a和b的最大公因数是 ,最小公倍数 .
18.(1):0.75化成最简单的整数比是 ,比值是 ;
(2)根据3a=5b(a、b不为0),写出一个比例是 : = : 。
19.如图所示,在 号位置上面放一个同样的小方块,从左面看到的图形不变,在 号位置上面放一个同样的小方块,从前面看到的图形不变。
20.把一个半径是5cm的圆等分成若干份后拼成一个近似长方形,长方形的周长比原来圆的周长增加_____ cm,长方形的面积是 cm2。
21.观察如图线段图,按要求填空。(1)小伍根据等量关系 可以列出算式“80﹣80。
(2)小娅列出算式为“80×(1)”,其中“1”表示的意义: 。
22.某男装专卖店所有服装都打同样的折扣销售。王叔叔买了一件上衣,原价250元,现价200元。他还想买一条裤子,原价180元,现价 元。
三.判断题
23.一个三角形最小的角是46°,所以它是一个锐角三角形。
24.甲在乙的东偏北36°方向100m处,则乙在甲的西偏南36°方向100m处.
25.汽车所行驶的速度和时间成反比例关系。
26.在比例里外项之积减内项之积,所得的差是0. .
27.两个圆的半径比是2:3,那么它们周长的比是2:3,面积的比是4:9。
28.一个圆柱的侧面展开图是一个正方形,则这个圆柱的底面直径与高相等。
四.计算题
29.口算下列各题。
3.7+1.2= 50×80= 1 32=
0.2= 0 8×1.25= 625÷90≈
30.解比例。
::x
31.计算下面各题,能用简便算法的就用简便算法。
1+()÷4 9
137.4﹣8.47﹣1.53 0.25×64×1.25
五.操作题(共1小题)
32.画一画。
(1)请在上边方格图中描出下列各点并依次连成封闭图形。
A(1,6)B(1,9)、C(4,6)
(2)按2:1画出上题封闭图形放大后的图形A′B′C′
六.应用题
33.一个有盖的圆柱形铁桶,底面周长是25.12分米,高10分米,做这个铁桶至少要用铁皮多少平方分米?(接口处忽略不计)
34.一列火车行驶720km需要3小时.照这样计算,从甲地到乙地的铁路长约1200千米,这列火车需要行驶几小时?(用比例解答)
35.一个用钢铸成的圆锥形机器零件,底面直径4cm,高3cm,每立方厘米的钢约重7.8g,这个零件大约重多少克?(得数保留整数)
36.书店运来800本《趣味数学故事》,第一天卖出,第二天比第一天多卖出了20%,第二天卖出多少本?
37.某发电厂五月份用煤3000吨,是四月份的1.2倍:五月份比六月份多用560吨。六月份比四月份少用煤多少吨?
38.一个工厂有3个车间,已知第一车间有30人,并且人数是最多的。以下三个关于车间人数的信息只有一个是正确的:A.第一车间比总人数的少2人;B.第一车间人数占3个车间总人数的30%;C.第1车间,第2车间,第3车间人数比是4:2:3。
(1)以上3个信息中,正确的信息是 ;
(2)根据这个信息算一算,这个工厂3个车间总共有多少人?
参考答案及试题解析
一.选择题
1.【考点】三角形的周长和面积;等腰三角形与等边三角形.
【答案】C
【思路分析】根据三角形3条边之间的关系,在三角形中,任意两边之和大于第三边,任意两边之差小于第三边,由此可知,这个等腰三角形的底是2厘米,一条腰是5厘米,根据三角形的周长公式解答即可。
【解答】解:5×2+2
=10+2
=12(厘米)
答:它的周长是12厘米。
故选:C。
【名师点评】此题主要考查三角形周长公式的灵活运用,熟练掌握三角形的三边关系,是解答此题的关键。
2.【考点】圆柱的侧面积、表面积和体积.
【答案】C
【思路分析】圆柱的体积=底面积×高,圆柱的高不变,设圆柱底面半径为r,高为h,原来的体积为v,扩大后的体积为v1,则扩大后的半径为4r,代入圆柱的体积公式,从而可以求出它的体积扩大的倍数.
【解答】解:原来的体积:v=πr2h,
扩大后的体积:v1=π(4r)2h=16πr2h,
体积扩大:16πr2h÷πr2h=16倍,
于是可得:它的体积扩大16倍.
故选:C.
【名师点评】此题主要考查圆柱体的体积计算公式的灵活应用.
3.【考点】用字母表示数.
【答案】A
【思路分析】把这段铁丝的长度看作单位“1”,每段长(1÷4),由此解答本题。
【解答】解:由分析可知:每段铁丝长:a÷4=a。
故选:A。
【名师点评】解决本题的关键是找出题中单位“1”以及数量关系。
4.【考点】平行四边形的面积;用字母表示数;长方形、正方形的面积.
【答案】B
【思路分析】通过观察图形可知,平行四边形的底和高都等于正方形的边长,等底等高的平行四边形的面积与正方形的面积相等。据此解答即可。
【解答】解:因为平行四边形与正方形等底等高,所以平行四边形的面积等于正方形的面积。
答:平行四边形的面积是a平方厘米。
故选:B。
【名师点评】此题解答的关键是明确:等底等高的平行四边形的面积与正方形的面积相等。
5.【考点】数轴的认识.
【答案】D
【思路分析】根据图示可知,n小于1,m大于1,据此结合各个选项分析解答即可。
【解答】解:A、因为n小于1,m大于1,所以n>m,说法错误。
B、因为n小于1,m大于1,m乘一个比1小的数,所得的积一定比m小,所以mn>m,说法错误。
C、因为m大于1,所以 1,说法错误。
D、因为n小于1,所以1,说法正确。
故选:D。
【名师点评】本题考查了数轴知识和小数乘除运算知识,根据一个数(0除外)乘比1小的数,乘积比原来的数小;1除以一个比1大的数,商比1小,反之比1大,结合题意分析解答即可。
6.【考点】从统计图表中获取信息.
【答案】A
【思路分析】左图:两条折线,应该有2个“主角”,结合选项可知“龟兔赛跑”符合该图形,兔子跑的快,中途睡觉觉,乌龟匀速行驶后超过兔子,兔子醒来奋起直追;
中图:结合选项可知“司马光砸缸”符合该图形,水缸的水是满的,司马光砸缸后水慢慢流出;
右图:结合选项可知“乌鸦喝水”符合该图形,乌鸦口渴,瓶口太小喝不到水,乌鸦就把瓶子旁边的石子放进瓶子里,瓶子的水因为石子体积的增加水面慢慢的升高,乌鸦喝到水了。
据此选择。
【解答】解:根据分析可知,三幅图从左到右符合龟兔赛跑、司马光砸缸、乌鸦喝水的故事。
故选:A。
【名师点评】本题考查了学生能根据图像结合学习知识判断图像表达什么意思。
7.【考点】游戏规则的公平性.
【答案】C
【思路分析】逐项分析后即可判断。
【解答】解:A.箱子里面有4个黑球4个白球,摸到黑球和白球的可能性相同,都是,游戏规则公平,即用摸球的方式确定甲、乙两支足球队比赛谁先开球,公平;
B.转盘中乙队获胜的可能性大于50%,甲队获胜的可能性小于50%,游戏规则不公平,即用转转盘的方式确定甲、乙两支足球队比赛谁先开球,不公平;
C.抛硬币的方式,硬币抛起来下落后是正面和反面的可能性相同,都是,游戏规则公平,即用抛硬币的方式确定甲、乙两支足球队比赛谁先开球,公平;
D.掷骰子的方式,骰子上面奇数有1、3、5,偶数有2、4、6,掷出奇数和偶数的可能性相同,都是,游戏规则公平,即用掷骰子的方式确定甲、乙两支足球队比赛谁先开球,公平;
综上,公平的方式有A、C、D,三种。
故选:C。
【名师点评】此题考查了游戏的公平性,解决本题的关键是得到相应的可能性,可能性相等就公平,否则就不公平。
8.【考点】通过操作实验探索规律.
【答案】C
【思路分析】依据题意结合图示可知,把正方体向左翻转90°,再逆时针旋转90°,原来正方体上面的图案就转到了前面,原来正方体前面的图案就转到了右面,原来正方体右面的图案就转到了上面,由此解答本题。
【解答】解:由分析可知,可能是小娅翻动后的样子。
故选:C。
【名师点评】解答本题的关键是弄清三个图形的相对位置,可以找一个正方体模型操作一下。
9.【考点】圆柱的侧面积、表面积和体积.
【答案】B
【思路分析】依据题意结合图示可知,圆柱的高等于长方体的高,圆柱的底面半径等于长方体的宽,圆柱底面周长的一半等于长方体的长,由此解答本题。
【解答】解:由分析可知:圆柱的体积等于长方体的体积,圆柱的表面积加上2个长方形的面积等于长方体的表面积。
故选:B。
【名师点评】本题考查的是圆柱的表面积,体积的应用。
10.【考点】从统计图表中获取信息;辨识成正比例的量与成反比例的量.
【答案】D
【思路分析】逐项分析各个选项后即可判断。
【解答】解:A.因为鱼缸内水的体积和注水时间的图像是一条从0开始的射线,所以鱼缸中水的体积和注水时间成正比例关系,即原说法正确;
B.根据图象可知,点N表示水管用8分钟注了20升的水,即原说法正确;
C.因为鱼缸中水的体积和注水时间成正比例关系,且8分钟注了20升的水,所以20÷8×5=12.5(升),故这根水管5分钟刚好注水12.5升,即原说法正确;
D.因为鱼缸中水的体积和注水时间成正比例关系,所以图像上的每个点都可以组成正比例关系,即原说法错误。
所以,只有D选项的说法错误。
故选:D。
【名师点评】本题考查了学生能读懂统计图并根据统计图解决问题的能力。
二.填空题
11.【考点】数与形结合的规律.
【答案】见试题解答内容
【思路分析】第一张餐桌上可以摆放6把椅子,进一步观察发现:多一张餐桌,多放4把椅子.第n张餐桌共有6+4(n﹣1)=4n+2.把n=25代入,即可得解.
【解答】解:有1张桌子时有6把椅子,
有2张桌子时有10把椅子,10=6+4×1,
有3张桌子时有14把椅子,14=6+4×2,
多一张餐桌,多放4把椅子,
所以第25张餐桌共有6+4(25﹣1)
=4×25+2
=102(人)
答:25张桌子可以坐 102人.
故答案为:102.
【名师点评】本题考查了图形的变化类问题,注意结合图形进行观察,即可得到规律.
12.【考点】圆柱的侧面积、表面积和体积.
【答案】见试题解答内容
【思路分析】根据题意可知,把一个圆柱的高截短3cm,表面积就减少了94.2平方厘米,表面积减少是高为3厘米的圆柱的侧面积,根据圆柱的侧面积公式:S=Ch,据此可以求出圆柱的底面周长,根据圆的周长公式:C=2πr,求出底面半径,然后根据圆的面积公式:S=πr2,把数据代入公式解答.
【解答】解:94.2÷3=31.4(厘米)
31.4÷3.14÷2=5(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:这个圆柱的底面积是78.5平方厘米.
故答案为:78.5.
【名师点评】此题主要考查圆柱的侧面积公式、圆的周长公式、圆的面积公式的灵活运用,关键是熟记公式.
13.【考点】体积、容积进率及单位换算.
【答案】0.44,4.08,3,200,3,40。
【思路分析】根据1平方千米=100公顷,1千米=1000米,3小时看作3小时与小时之和,把小时乘进率60化成40分钟;把3.2立方分米换算成升数,用3.2乘进率1,因为1立方分米=1升;把3.2立方分米换算成毫升数,用3.2乘进率1000;即可得解。
【解答】解:
44公顷=0.44平方千米 4080米=4.08千米
3.2立方分米=3升200毫升 时=3时40分
故答案为:0.44,4.08,3,200,3,40。
【名师点评】此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,反之,则除以进率。
14.【考点】比的意义.
【答案】2:1,2:1,4:1。
【思路分析】可设大圆的半径为2,则小圆的半径为1,分别求出两个圆的直径、周长和面积,再求它们之间的比。
【解答】解:设大圆的半径为2,则小圆的半径为1,得:
直径比:(2×2):(1×2)=4:2=2:1
周长比:(2×2π):(2π)=4π:2π=2:1
面积比:π×22:π×12=4π:π=4:1
故答案为:2:1,2:1,4:1。
【名师点评】两个圆的直径的比和周长的比都等于半径的比,面积的比等于半径的平方的比。
15.【考点】算术中的规律.
【答案】见试题解答内容
【思路分析】此题首先分析循环小数0.428571428571…的循环节有几位数字,然后用50除以循环节的位数,余数是几,第50位上的数字就是循环节的第几位数字.
【解答】解:0.428571428571…,循环节为428571,有6位数字,
因为50÷6=8…2,循环节中第二个数是2,
所以这个循环小数的小数部分第50位上的数字是2.
故答案为:2.
【名师点评】此题属于探索规律的题目,找规律,要从给出的条件着手,仔细观察,发现解决问题的最佳办法,解决问题.
16.【考点】组合图形的面积.
【答案】见试题解答内容
【思路分析】由图形可知:阴影部分三角形的底等于长方形EFDB的长、三角形的高等于长方形EFDB的宽,所以阴影部分三角形的面积是长方形EFDB的面积的一半,由此可以求出长方形EFBD的面积,又知长方形ABCD被分成两个长方形,且AB:AE=4:1,所以,长方形EFDB与长方形ACFE面积的比=3:1,据此可以求出长方形ACFE的面积,然后把两个长方形的面积合并起来就是长方形ABCD的面积,据此解答.
【解答】解:4×2=8(平方分米),
82(平方分米),
8+210(平方分米),
答:长方形ABCD的面积是10平方分米.
故答案为:10.
【名师点评】此题解答关键的根据等底等高的三角形的面积是长方形(平行四边形)面积的一半,求出长方形EFDB的面积,再根据等长的两个长方形的宽的比等于两个长方形面积的比,求出长方形ACFE的面积,进而求出整个长方形的面积.
17.【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法.
【答案】见试题解答内容
【思路分析】如果a+1=b(a、b都是自然数,且不等于0),则说明这两个数是相邻的自然数,如5、6,那么这两个数互质,那么a和b的最大公因数是 1,最小公倍数是它们的积.
【解答】解:如果a+1=b(a、b都是自然数,且不等于0),则a和b互质,
所以a和b的最大公因数是 1,最小公倍数是ab.
故答案为:1,ab.
【名师点评】此题考查了两个数是相邻的自然数的最大公因数和最小公倍数,最大公因数是1,最小公倍数是它们的积.
18.【考点】求比值和化简比;比例的意义和基本性质.
【答案】(1)2:1,2;(2)a,b,5,3(答案不唯一)。
【思路分析】(1)依据比的性质,即比的前项和后同时乘或除以一个不等于零的数,比的大小不变,即可化简比;用比的前项除以后项得到的数就是它们的比值,据此即可求解;
(2)用比例的基本性质的逆运用求解即可。
【解答】解:(1):0.75
=(4):(0.75×4)
=6:3
=(6÷3):(3÷3)
=2:1
2:1
=2÷1
=2
(2)3a=5b(a、b不为0)
a:b=5:3
故答案为:2:1,2;a,b,5,3(答案不唯一)。
【名师点评】本题主要考查了求比值和化简比及比例基本性质的灵活运用。
19.【考点】从不同方向观察物体和几何体.
【答案】②,③。
【思路分析】根据观察物体的方法,在②号位置上面放一个同样的小方块,从左面看到的图形不变,都是分2层,底层2个小正方形,上层1个小正方形,左齐;在③号位置上面放一个同样的小方块,从前面看到的图形不变,都是分2层,底层2个小正方形,上层1个小正方形,左齐。据此解答即可。
【解答】解:在②号位置上面放一个同样的小方块,从左面看到的图形不变,在③号位置上面放一个同样的小方块,从前面看到的图形不变。
故答案为:②,③。
【名师点评】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
20.【考点】圆、圆环的面积.
【答案】10,78.5。
【思路分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形后面积不变,拼成的长方形的周长比圆的周长多两条半径的长度,已知圆的半径是5厘米,据此可以求出长方形的周长比圆的周长增加多少厘米,根据圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:5×2=10(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:长方形的周长比圆的周长增加10厘米,长方形的面积是78.5平方厘米。
故答案为:10,78.5。
【名师点评】此题考查的目的是理解掌握圆面积公式的推导过程及应用,圆的周长、长方形周长的意义及应用,圆的面积公式及应用。
21.【考点】分数乘法应用题.
【答案】(1)已行路程=总路程﹣剩下路程;(2)已行路程占总路程的几分之几。
【思路分析】(1)根据图示可得:已行路程=总路程﹣剩下路程;
(2)把总路程看作单位“1”,用1减剩下的路程占总路程的分率,就是已行路程占总路程的几分之几。
【解答】解:(1)小伍根据等量关系已行路程=总路程﹣剩下路程可以列出算式“80﹣80。
(2)小娅列出算式为“80×(1)”,其中“1”表示的意义:已行路程占总路程的几分之几。
故答案为:已行路程=总路程﹣剩下路程;已行路程占总路程的几分之几。
【名师点评】本题主要考查了分数乘法应用题,解题的关键是能根据图形找出单位“1”及数量关系。
22.【考点】百分数的实际应用.
【答案】144。
【思路分析】用上衣的现价除以原价,求出现价是原价的百分之几。把这条裤子的原价看作单位“1”,根据百分数乘法的意义,用这条裤子的原价乘降价的百分率就是这条裤子的现价。
【解答】解:200÷250
=0.8
=80%
180×80%=144(元)
答:现价144元。
故答案为:144。
【名师点评】求一个数是另一个数的百分之几,用这个数除以另一个数。求一个数的百分之几是多少,用这个数乘百分率。
三.判断题
23.【考点】三角形的分类.
【答案】√
【思路分析】三角形的内角和是180度,一个三角形最小的角是46°,说明另外两个角的和是180°﹣46°=134°,假设较大的角是47度,利用134度减去47度求出第三个角的度数即可判断。
【解答】解:假设较大的角是47°,180°﹣46°﹣47°=87°,这三个角都是锐角,所以三角形是锐角三角形,原题说法正确。
故答案为:√。
【名师点评】此题考查了根据角对三角形分类的方法:三个角都是锐角,这个三角形是锐角三角形;有一个角是钝角的三角形是钝角三角形;有一个角是直角的三角形是直角三角形。
24.【考点】用角度表示方向.
【答案】见试题解答内容
【思路分析】根据位置的相对性可知:它们的方向相反,角度相等,距离相等,据此解答.
【解答】解:东与西相对,北与南相对,所以:
甲在乙的东偏北36°方向100m处,则乙在甲的西偏南36°方向100m处;
原题说法正确.
故答案为:√.
【名师点评】本题考查了位置的相对性:A与B位置关系是相对的,它们方向相反,角度相等,距离相等.
25.【考点】辨识成正比例的量与成反比例的量.
【答案】×
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:汽车所行驶的速度×时间=路程(不一定),所以汽车所行驶的速度和时间不一定成反比例关系,当汽车行驶的路程一定时,汽车所行驶的速度和时间成反比例关系。
所以原题说法错误。
故答案为:×。
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
26.【考点】比例的意义和基本性质.
【答案】√
【思路分析】在比例里,两个内项的积等于两个外项的积,所以它们的差为0.
【解答】解:因为在比例里,两个内项的积等于两个外项的积,
所以在比例里外项之积减内项之积,所得的差是0,说法正确的;
故答案为:√.
【名师点评】此题主要考查比例的基本性质的灵活应用.
27.【考点】比的意义;比的应用.
【答案】√
【思路分析】设小圆的半径为2r,则大圆的半径为3r,分别代入圆的周长和面积公式,表示出各自的周长和面积,即可求解。
【解答】解:设小圆的半径为2r,则大圆的半径为3r,
小圆的周长=2π×2r=4πr,
大圆的周长=2π×3r=6πr,
周长的比是:4πr:6πr=2:3;
小圆的面积=π(2r)2=4πr2,
大圆的面积=π(3r)2=9πr2,
面积的比是:4πr2:9πr2=4:9。
故答案为:√。
【名师点评】此题主要考查圆的周长和面积的计算方法的灵活应用。
28.【考点】圆柱的展开图.
【答案】×
【思路分析】圆柱的侧面展开图是一个正方形,说明圆柱的底面周长等于高。据此求解即可。
【解答】解:圆柱的侧面展开图是一个正方形,说明圆柱的底面周长等于高。所以原题说法错误。
故答案为:×。
【名师点评】本题考查了圆柱体的展开图知识,结合题意分析解答即可。
四.计算题
29.【考点】分数除法;数的估算;小数的加法和减法;分数乘法.
【答案】4.9、、4000、、9、0.3、6、0、10、7。
【思路分析】根据分数乘除法和小数加减法的方法进行口算即可。
【解答】解:
3.7+1.2=4.9 50×80=4000 1 32=9
0.2=0.3 6 00 8×1.25=10 625÷90≈7
【名师点评】此题属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
30.【考点】解比例.
【答案】x;x=14
【思路分析】(1)根据比例的基本性质,把原式化为x,然后方程的两边同时除以求解;
(2)根据比例的基本性质,把原式化为4x=7×8,然后方程的两边同时除以4求解。
【解答】解:(1)::x
x
x
x
(2)
4x=7×8
4x÷4=7×8÷4
x=14
【名师点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
31.【考点】运算定律与简便运算.
【答案】1;;127.4;20。
【思路分析】(1)先算小括号里面的减法,再算括号外面的除法,最后算括号外面的加法;
(2)根据乘法分配律进行计算;
(3)根据减法的性质进行计算;
(4)根据乘法交换律和结合律进行计算。
【解答】解:(1)1+()÷4
=14
=1
=1
(2)9
=()
=1
(3)137.4﹣8.47﹣1.53
=137.4﹣(8.47+1.53)
=137.4﹣10
=127.4
(4)0.25×64×1.25
=0.25×(2×4×8)×1.25
=(0.25×4)×(8×1.25)×2
=1×10×2
=20
【名师点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
五.操作题(共1小题)
32.【考点】数对与位置;图形的放大与缩小.
【答案】(1)(2)作图如下:
【思路分析】(1)数对中第一个数字表示列,第二个数字表示行,据此即可在方格图中描出A、B、C各点,并将各点依次连接起来即可。
(2)按2:1放大就是把这个三角形的底和高同时扩大2倍,依此画图即可。
【解答】解:(1)封闭图形如下所示:
(2)扩大后的图形如图所示:
【名师点评】图形的放大和缩小是生活中常见的现象,把一个图形放大或缩小后所得到的图形与原图形相比,形状相同,大小不同。
六.应用题
33.【考点】圆柱的侧面积和表面积.
【答案】351.68平方分米。
【思路分析】已知铁桶有盖,所以只求这个圆柱的2个底面的面积与侧面积的和即可,根据圆的面积公式:S=πr2,圆柱的侧面积公式:S=Ch,把数据代入公式解答。
【解答】解:25.12÷3.14÷2=4(分米)
3.14×42×2+25.12×10
=100.48+251.2
=351.68(平方分米)
答:做这个铁桶至少要用铁皮351.68平方分米。
【名师点评】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
34.【考点】正、反比例应用题.
【答案】见试题解答内容
【思路分析】根据题意可知:速度(一定),所以路程和时间成正比例,设这列火车需要行驶x小时,据此列比例解答.
【解答】解:设这列火车需要行驶x小时,
720x=3×1200
x
x=5.
答:这列火车需要行驶5小时.
【名师点评】本题主要考查比例在日常生活中的应用,要正确判断两种相关联量成正比例、还是成反比例是解答关键.
35.【考点】关于圆锥的应用题.
【答案】98克。
【思路分析】利用圆锥体积公式:Vπr2h代入数据计算求出零件的体积,再乘每立方厘米的质量,据此解答。
【解答】解:(4÷2)2×3×7.8
=3.14×4×7.8
=12.56×7.8
≈98(克)
答:这个零件大约重98克。
【名师点评】解答即可。熟练掌握圆锥的体积公式,是解答此题的关键。
36.【考点】分数、百分数复合应用题.
【答案】240本。
【思路分析】先把总本数看作单位“1”,运用分数乘法意义,求出第一天卖出本数,再把第一天卖书本数看作单位“1”,第二天比第一天多卖出了20%,那么第二天就是第一天卖出的(1+20%),运用百分数乘法意义即可求出第二天卖出书本数。
【解答】解:800(1+20%)
=200×1.2
=240(本)
答:第二天卖出240本。
【名师点评】解答此题的关键是分清两个不同的单位“1”,已知单位“1”的量,求它的几分之几是多少用乘法求解。
37.【考点】整数、小数复合应用题.
【答案】60吨。
【思路分析】首先根据已知一个数几倍是多少,求这个数,用除法求出四月份用煤多少吨。再根据整数减法的意义,求出六月份的用煤量,据此即可得出答案。
【解答】解:3000÷1.2﹣(3000﹣560)
=2500﹣2440
=60(吨)
答:六月份比四月份少用煤60吨。
【名师点评】此题解答关键是求出四月份的用煤量和六月份用煤量,再根据整数减法解答即可。
38.【考点】比的应用.
【答案】A,80人。
【思路分析】(1)将两项中所给出的信息与“已知第一车间有30人,并且人数最多”这个条件相结合进行分析,找出其矛盾之处即能确定哪个信息是准确的。
A.第一车间比总人数的少2人,总人数为:(30+2)80(人),另两个车间共有80﹣30=50(人),50÷2=25(人),两个车间均可以少于30人;所以A正确。
B.第一车间人数占3个车间总人数的30%,则总人数为30÷30%=100(人),另两个车间共有100﹣30=70(人),至少有一个会高于30人,与第一车间人数最多相矛盾,所以B错误。
C.第一、第二、第三车间人数的比是4:2:3,30(人),不是整数,不可能有非整数人员,与实际不符,所以C错误。
(2)根据分数除法的意义,第一车间比总人数的少2人,用第一车间人数加2再除以所占比例,即得共有多少人。
【解答】解:(1)A.(30+2)80(人),另外两个车间共有80﹣30=50(人),50÷2=25(人),两个车间均可以少于30人;所以A正确;
B.30÷30%=100(人),另两个车间共有100﹣30=70(人),至少有一个会高于30人,与第一车间人数最多相矛盾,信息为错误;
C.第一、第二、第三车间人数的比是4:2:3,30(人),不是整数,不可能有非整数人员,与实际不符,所以C错误。所以以上三条信息中,正确的信息是A。
(2)(30+2)80(人)
答:这个工厂3个车间共有80人。
【名师点评】完成本题要注意根据所给条件认真分析,然后做出正确判断。
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初重点校择校分班考模拟卷(人教版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.一个等腰三角形的两条边长分别是2cm和5cm,它的周长是( )
A.7cm B.9cm C.12cm D.不能确定
2.一个圆柱的底面半径扩大4倍,高不变,它的体积扩大( )
A.4倍 B.8倍 C.16倍
3.把一段a米(a>0)长的铁丝平均分成4段,每段铁丝长( )米
A. B. C. D.
4.如图由一个正方形和平行四边形组成,正方形的面积是a平方厘米,平行四边形的面积是( )平方厘米。
A. B.a C. D.2a
5.点m和点n位置如图所示,下面说法正确的是( )
A.n>m B.mn>m C.1 D.1
6.如图三幅图分别描述三个故事,这三幅图对应的故事正确的是( )
A.龟兔赛跑、司马光砸缸、乌鸦喝水
B.乌鸦喝水、司马光磁缸、龟兔赛跑
C.司马光砸缸、龟兔赛跑、乌鸦喝水
D.乌鸦喝水、龟兔赛跑、司马光砸缸
7.用如下方式确定甲、乙两支足球队比赛谁先开球,公平的方式有( )种。
A.1 B.2 C.3 D.4
8.如图是三个面带有图案的正方体,小娅翻动了这个正方体,下面( )可能是小娅翻动后的样子。
B. C. D.
9.把一个圆柱底面分成许多相等的扇形,切开后拼成一个近似的长方体。如果圆柱的半径是r,圆柱与长方体相比,下面说法错误的是( )
A.形状变了,体积不变 B.体积不变,表面积不变
C.长方体的长等于πr D.长方体的高等于圆柱的高
10.用一根水管往鱼缸中注水,右图表示鱼缸内水的体积和注水时间的关系。下面说法错误的是( )
A.鱼缸中水的体积和注水时间成正比例关系。
B.点N表示水管用8分钟注了20升的水。
C.这根水管5分钟刚好注水12.5升。
D.点N和点M表示的注水时间和鱼缸内水的体积不可以组成一个比例。
二.填空题
11.按如图的方式摆放桌子和椅子.25张桌子可以坐 人.
12.如果把一个圆柱的高截短3cm,表面积就减少了94.2cm2,这个圆柱的底面积是 cm2.
13.44公顷= 平方千米 4080米= 千米
3.2立方分米= 升= 毫升 时= 时 分
14.大小两个圆的半径之比是2:1,它们的直径之比是 ,周长之比 ,面积之比是 。
15.把化成循环小数是0.428571428571…,这个循环小数的小数部分第50位上的数字是 .
16.如图,长方形ABCD被分成两个长方形,且AB:AE=4:1,图阴影部分三角形的面积为4平方分米,长方形ABCD的面积是 平方分米.
17.如果a+1=b(a、b都是自然数,且不等于0),那么a和b的最大公因数是 ,最小公倍数 .
18.(1):0.75化成最简单的整数比是 ,比值是 ;
(2)根据3a=5b(a、b不为0),写出一个比例是 : = : 。
19.如图所示,在 号位置上面放一个同样的小方块,从左面看到的图形不变,在 号位置上面放一个同样的小方块,从前面看到的图形不变。
20.把一个半径是5cm的圆等分成若干份后拼成一个近似长方形,长方形的周长比原来圆的周长增加_____ cm,长方形的面积是 cm2。
21.观察如图线段图,按要求填空。(1)小伍根据等量关系 可以列出算式“80﹣80。
(2)小娅列出算式为“80×(1)”,其中“1”表示的意义: 。
22.某男装专卖店所有服装都打同样的折扣销售。王叔叔买了一件上衣,原价250元,现价200元。他还想买一条裤子,原价180元,现价 元。
三.判断题
23.一个三角形最小的角是46°,所以它是一个锐角三角形。
24.甲在乙的东偏北36°方向100m处,则乙在甲的西偏南36°方向100m处.
25.汽车所行驶的速度和时间成反比例关系。
26.在比例里外项之积减内项之积,所得的差是0. .
27.两个圆的半径比是2:3,那么它们周长的比是2:3,面积的比是4:9。
28.一个圆柱的侧面展开图是一个正方形,则这个圆柱的底面直径与高相等。
四.计算题
29.口算下列各题。
3.7+1.2= 50×80= 1 32=
0.2= 0 8×1.25= 625÷90≈
30.解比例。
::x
31.计算下面各题,能用简便算法的就用简便算法。
1+()÷4 9
137.4﹣8.47﹣1.53 0.25×64×1.25
五.操作题(共1小题)
32.画一画。
(1)请在上边方格图中描出下列各点并依次连成封闭图形。
A(1,6)B(1,9)、C(4,6)
(2)按2:1画出上题封闭图形放大后的图形A′B′C′
六.应用题
33.一个有盖的圆柱形铁桶,底面周长是25.12分米,高10分米,做这个铁桶至少要用铁皮多少平方分米?(接口处忽略不计)
34.一列火车行驶720km需要3小时.照这样计算,从甲地到乙地的铁路长约1200千米,这列火车需要行驶几小时?(用比例解答)
35.一个用钢铸成的圆锥形机器零件,底面直径4cm,高3cm,每立方厘米的钢约重7.8g,这个零件大约重多少克?(得数保留整数)
36.书店运来800本《趣味数学故事》,第一天卖出,第二天比第一天多卖出了20%,第二天卖出多少本?
37.某发电厂五月份用煤3000吨,是四月份的1.2倍:五月份比六月份多用560吨。六月份比四月份少用煤多少吨?
38.一个工厂有3个车间,已知第一车间有30人,并且人数是最多的。以下三个关于车间人数的信息只有一个是正确的:A.第一车间比总人数的少2人;B.第一车间人数占3个车间总人数的30%;C.第1车间,第2车间,第3车间人数比是4:2:3。
(1)以上3个信息中,正确的信息是 ;
(2)根据这个信息算一算,这个工厂3个车间总共有多少人?
参考答案及试题解析
一.选择题
1.【考点】三角形的周长和面积;等腰三角形与等边三角形.
【答案】C
【思路分析】根据三角形3条边之间的关系,在三角形中,任意两边之和大于第三边,任意两边之差小于第三边,由此可知,这个等腰三角形的底是2厘米,一条腰是5厘米,根据三角形的周长公式解答即可。
【解答】解:5×2+2
=10+2
=12(厘米)
答:它的周长是12厘米。
故选:C。
【名师点评】此题主要考查三角形周长公式的灵活运用,熟练掌握三角形的三边关系,是解答此题的关键。
2.【考点】圆柱的侧面积、表面积和体积.
【答案】C
【思路分析】圆柱的体积=底面积×高,圆柱的高不变,设圆柱底面半径为r,高为h,原来的体积为v,扩大后的体积为v1,则扩大后的半径为4r,代入圆柱的体积公式,从而可以求出它的体积扩大的倍数.
【解答】解:原来的体积:v=πr2h,
扩大后的体积:v1=π(4r)2h=16πr2h,
体积扩大:16πr2h÷πr2h=16倍,
于是可得:它的体积扩大16倍.
故选:C.
【名师点评】此题主要考查圆柱体的体积计算公式的灵活应用.
3.【考点】用字母表示数.
【答案】A
【思路分析】把这段铁丝的长度看作单位“1”,每段长(1÷4),由此解答本题。
【解答】解:由分析可知:每段铁丝长:a÷4=a。
故选:A。
【名师点评】解决本题的关键是找出题中单位“1”以及数量关系。
4.【考点】平行四边形的面积;用字母表示数;长方形、正方形的面积.
【答案】B
【思路分析】通过观察图形可知,平行四边形的底和高都等于正方形的边长,等底等高的平行四边形的面积与正方形的面积相等。据此解答即可。
【解答】解:因为平行四边形与正方形等底等高,所以平行四边形的面积等于正方形的面积。
答:平行四边形的面积是a平方厘米。
故选:B。
【名师点评】此题解答的关键是明确:等底等高的平行四边形的面积与正方形的面积相等。
5.【考点】数轴的认识.
【答案】D
【思路分析】根据图示可知,n小于1,m大于1,据此结合各个选项分析解答即可。
【解答】解:A、因为n小于1,m大于1,所以n>m,说法错误。
B、因为n小于1,m大于1,m乘一个比1小的数,所得的积一定比m小,所以mn>m,说法错误。
C、因为m大于1,所以 1,说法错误。
D、因为n小于1,所以1,说法正确。
故选:D。
【名师点评】本题考查了数轴知识和小数乘除运算知识,根据一个数(0除外)乘比1小的数,乘积比原来的数小;1除以一个比1大的数,商比1小,反之比1大,结合题意分析解答即可。
6.【考点】从统计图表中获取信息.
【答案】A
【思路分析】左图:两条折线,应该有2个“主角”,结合选项可知“龟兔赛跑”符合该图形,兔子跑的快,中途睡觉觉,乌龟匀速行驶后超过兔子,兔子醒来奋起直追;
中图:结合选项可知“司马光砸缸”符合该图形,水缸的水是满的,司马光砸缸后水慢慢流出;
右图:结合选项可知“乌鸦喝水”符合该图形,乌鸦口渴,瓶口太小喝不到水,乌鸦就把瓶子旁边的石子放进瓶子里,瓶子的水因为石子体积的增加水面慢慢的升高,乌鸦喝到水了。
据此选择。
【解答】解:根据分析可知,三幅图从左到右符合龟兔赛跑、司马光砸缸、乌鸦喝水的故事。
故选:A。
【名师点评】本题考查了学生能根据图像结合学习知识判断图像表达什么意思。
7.【考点】游戏规则的公平性.
【答案】C
【思路分析】逐项分析后即可判断。
【解答】解:A.箱子里面有4个黑球4个白球,摸到黑球和白球的可能性相同,都是,游戏规则公平,即用摸球的方式确定甲、乙两支足球队比赛谁先开球,公平;
B.转盘中乙队获胜的可能性大于50%,甲队获胜的可能性小于50%,游戏规则不公平,即用转转盘的方式确定甲、乙两支足球队比赛谁先开球,不公平;
C.抛硬币的方式,硬币抛起来下落后是正面和反面的可能性相同,都是,游戏规则公平,即用抛硬币的方式确定甲、乙两支足球队比赛谁先开球,公平;
D.掷骰子的方式,骰子上面奇数有1、3、5,偶数有2、4、6,掷出奇数和偶数的可能性相同,都是,游戏规则公平,即用掷骰子的方式确定甲、乙两支足球队比赛谁先开球,公平;
综上,公平的方式有A、C、D,三种。
故选:C。
【名师点评】此题考查了游戏的公平性,解决本题的关键是得到相应的可能性,可能性相等就公平,否则就不公平。
8.【考点】通过操作实验探索规律.
【答案】C
【思路分析】依据题意结合图示可知,把正方体向左翻转90°,再逆时针旋转90°,原来正方体上面的图案就转到了前面,原来正方体前面的图案就转到了右面,原来正方体右面的图案就转到了上面,由此解答本题。
【解答】解:由分析可知,可能是小娅翻动后的样子。
故选:C。
【名师点评】解答本题的关键是弄清三个图形的相对位置,可以找一个正方体模型操作一下。
9.【考点】圆柱的侧面积、表面积和体积.
【答案】B
【思路分析】依据题意结合图示可知,圆柱的高等于长方体的高,圆柱的底面半径等于长方体的宽,圆柱底面周长的一半等于长方体的长,由此解答本题。
【解答】解:由分析可知:圆柱的体积等于长方体的体积,圆柱的表面积加上2个长方形的面积等于长方体的表面积。
故选:B。
【名师点评】本题考查的是圆柱的表面积,体积的应用。
10.【考点】从统计图表中获取信息;辨识成正比例的量与成反比例的量.
【答案】D
【思路分析】逐项分析各个选项后即可判断。
【解答】解:A.因为鱼缸内水的体积和注水时间的图像是一条从0开始的射线,所以鱼缸中水的体积和注水时间成正比例关系,即原说法正确;
B.根据图象可知,点N表示水管用8分钟注了20升的水,即原说法正确;
C.因为鱼缸中水的体积和注水时间成正比例关系,且8分钟注了20升的水,所以20÷8×5=12.5(升),故这根水管5分钟刚好注水12.5升,即原说法正确;
D.因为鱼缸中水的体积和注水时间成正比例关系,所以图像上的每个点都可以组成正比例关系,即原说法错误。
所以,只有D选项的说法错误。
故选:D。
【名师点评】本题考查了学生能读懂统计图并根据统计图解决问题的能力。
二.填空题
11.【考点】数与形结合的规律.
【答案】见试题解答内容
【思路分析】第一张餐桌上可以摆放6把椅子,进一步观察发现:多一张餐桌,多放4把椅子.第n张餐桌共有6+4(n﹣1)=4n+2.把n=25代入,即可得解.
【解答】解:有1张桌子时有6把椅子,
有2张桌子时有10把椅子,10=6+4×1,
有3张桌子时有14把椅子,14=6+4×2,
多一张餐桌,多放4把椅子,
所以第25张餐桌共有6+4(25﹣1)
=4×25+2
=102(人)
答:25张桌子可以坐 102人.
故答案为:102.
【名师点评】本题考查了图形的变化类问题,注意结合图形进行观察,即可得到规律.
12.【考点】圆柱的侧面积、表面积和体积.
【答案】见试题解答内容
【思路分析】根据题意可知,把一个圆柱的高截短3cm,表面积就减少了94.2平方厘米,表面积减少是高为3厘米的圆柱的侧面积,根据圆柱的侧面积公式:S=Ch,据此可以求出圆柱的底面周长,根据圆的周长公式:C=2πr,求出底面半径,然后根据圆的面积公式:S=πr2,把数据代入公式解答.
【解答】解:94.2÷3=31.4(厘米)
31.4÷3.14÷2=5(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:这个圆柱的底面积是78.5平方厘米.
故答案为:78.5.
【名师点评】此题主要考查圆柱的侧面积公式、圆的周长公式、圆的面积公式的灵活运用,关键是熟记公式.
13.【考点】体积、容积进率及单位换算.
【答案】0.44,4.08,3,200,3,40。
【思路分析】根据1平方千米=100公顷,1千米=1000米,3小时看作3小时与小时之和,把小时乘进率60化成40分钟;把3.2立方分米换算成升数,用3.2乘进率1,因为1立方分米=1升;把3.2立方分米换算成毫升数,用3.2乘进率1000;即可得解。
【解答】解:
44公顷=0.44平方千米 4080米=4.08千米
3.2立方分米=3升200毫升 时=3时40分
故答案为:0.44,4.08,3,200,3,40。
【名师点评】此题考查名数的换算,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,反之,则除以进率。
14.【考点】比的意义.
【答案】2:1,2:1,4:1。
【思路分析】可设大圆的半径为2,则小圆的半径为1,分别求出两个圆的直径、周长和面积,再求它们之间的比。
【解答】解:设大圆的半径为2,则小圆的半径为1,得:
直径比:(2×2):(1×2)=4:2=2:1
周长比:(2×2π):(2π)=4π:2π=2:1
面积比:π×22:π×12=4π:π=4:1
故答案为:2:1,2:1,4:1。
【名师点评】两个圆的直径的比和周长的比都等于半径的比,面积的比等于半径的平方的比。
15.【考点】算术中的规律.
【答案】见试题解答内容
【思路分析】此题首先分析循环小数0.428571428571…的循环节有几位数字,然后用50除以循环节的位数,余数是几,第50位上的数字就是循环节的第几位数字.
【解答】解:0.428571428571…,循环节为428571,有6位数字,
因为50÷6=8…2,循环节中第二个数是2,
所以这个循环小数的小数部分第50位上的数字是2.
故答案为:2.
【名师点评】此题属于探索规律的题目,找规律,要从给出的条件着手,仔细观察,发现解决问题的最佳办法,解决问题.
16.【考点】组合图形的面积.
【答案】见试题解答内容
【思路分析】由图形可知:阴影部分三角形的底等于长方形EFDB的长、三角形的高等于长方形EFDB的宽,所以阴影部分三角形的面积是长方形EFDB的面积的一半,由此可以求出长方形EFBD的面积,又知长方形ABCD被分成两个长方形,且AB:AE=4:1,所以,长方形EFDB与长方形ACFE面积的比=3:1,据此可以求出长方形ACFE的面积,然后把两个长方形的面积合并起来就是长方形ABCD的面积,据此解答.
【解答】解:4×2=8(平方分米),
82(平方分米),
8+210(平方分米),
答:长方形ABCD的面积是10平方分米.
故答案为:10.
【名师点评】此题解答关键的根据等底等高的三角形的面积是长方形(平行四边形)面积的一半,求出长方形EFDB的面积,再根据等长的两个长方形的宽的比等于两个长方形面积的比,求出长方形ACFE的面积,进而求出整个长方形的面积.
17.【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法.
【答案】见试题解答内容
【思路分析】如果a+1=b(a、b都是自然数,且不等于0),则说明这两个数是相邻的自然数,如5、6,那么这两个数互质,那么a和b的最大公因数是 1,最小公倍数是它们的积.
【解答】解:如果a+1=b(a、b都是自然数,且不等于0),则a和b互质,
所以a和b的最大公因数是 1,最小公倍数是ab.
故答案为:1,ab.
【名师点评】此题考查了两个数是相邻的自然数的最大公因数和最小公倍数,最大公因数是1,最小公倍数是它们的积.
18.【考点】求比值和化简比;比例的意义和基本性质.
【答案】(1)2:1,2;(2)a,b,5,3(答案不唯一)。
【思路分析】(1)依据比的性质,即比的前项和后同时乘或除以一个不等于零的数,比的大小不变,即可化简比;用比的前项除以后项得到的数就是它们的比值,据此即可求解;
(2)用比例的基本性质的逆运用求解即可。
【解答】解:(1):0.75
=(4):(0.75×4)
=6:3
=(6÷3):(3÷3)
=2:1
2:1
=2÷1
=2
(2)3a=5b(a、b不为0)
a:b=5:3
故答案为:2:1,2;a,b,5,3(答案不唯一)。
【名师点评】本题主要考查了求比值和化简比及比例基本性质的灵活运用。
19.【考点】从不同方向观察物体和几何体.
【答案】②,③。
【思路分析】根据观察物体的方法,在②号位置上面放一个同样的小方块,从左面看到的图形不变,都是分2层,底层2个小正方形,上层1个小正方形,左齐;在③号位置上面放一个同样的小方块,从前面看到的图形不变,都是分2层,底层2个小正方形,上层1个小正方形,左齐。据此解答即可。
【解答】解:在②号位置上面放一个同样的小方块,从左面看到的图形不变,在③号位置上面放一个同样的小方块,从前面看到的图形不变。
故答案为:②,③。
【名师点评】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
20.【考点】圆、圆环的面积.
【答案】10,78.5。
【思路分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形后面积不变,拼成的长方形的周长比圆的周长多两条半径的长度,已知圆的半径是5厘米,据此可以求出长方形的周长比圆的周长增加多少厘米,根据圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:5×2=10(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:长方形的周长比圆的周长增加10厘米,长方形的面积是78.5平方厘米。
故答案为:10,78.5。
【名师点评】此题考查的目的是理解掌握圆面积公式的推导过程及应用,圆的周长、长方形周长的意义及应用,圆的面积公式及应用。
21.【考点】分数乘法应用题.
【答案】(1)已行路程=总路程﹣剩下路程;(2)已行路程占总路程的几分之几。
【思路分析】(1)根据图示可得:已行路程=总路程﹣剩下路程;
(2)把总路程看作单位“1”,用1减剩下的路程占总路程的分率,就是已行路程占总路程的几分之几。
【解答】解:(1)小伍根据等量关系已行路程=总路程﹣剩下路程可以列出算式“80﹣80。
(2)小娅列出算式为“80×(1)”,其中“1”表示的意义:已行路程占总路程的几分之几。
故答案为:已行路程=总路程﹣剩下路程;已行路程占总路程的几分之几。
【名师点评】本题主要考查了分数乘法应用题,解题的关键是能根据图形找出单位“1”及数量关系。
22.【考点】百分数的实际应用.
【答案】144。
【思路分析】用上衣的现价除以原价,求出现价是原价的百分之几。把这条裤子的原价看作单位“1”,根据百分数乘法的意义,用这条裤子的原价乘降价的百分率就是这条裤子的现价。
【解答】解:200÷250
=0.8
=80%
180×80%=144(元)
答:现价144元。
故答案为:144。
【名师点评】求一个数是另一个数的百分之几,用这个数除以另一个数。求一个数的百分之几是多少,用这个数乘百分率。
三.判断题
23.【考点】三角形的分类.
【答案】√
【思路分析】三角形的内角和是180度,一个三角形最小的角是46°,说明另外两个角的和是180°﹣46°=134°,假设较大的角是47度,利用134度减去47度求出第三个角的度数即可判断。
【解答】解:假设较大的角是47°,180°﹣46°﹣47°=87°,这三个角都是锐角,所以三角形是锐角三角形,原题说法正确。
故答案为:√。
【名师点评】此题考查了根据角对三角形分类的方法:三个角都是锐角,这个三角形是锐角三角形;有一个角是钝角的三角形是钝角三角形;有一个角是直角的三角形是直角三角形。
24.【考点】用角度表示方向.
【答案】见试题解答内容
【思路分析】根据位置的相对性可知:它们的方向相反,角度相等,距离相等,据此解答.
【解答】解:东与西相对,北与南相对,所以:
甲在乙的东偏北36°方向100m处,则乙在甲的西偏南36°方向100m处;
原题说法正确.
故答案为:√.
【名师点评】本题考查了位置的相对性:A与B位置关系是相对的,它们方向相反,角度相等,距离相等.
25.【考点】辨识成正比例的量与成反比例的量.
【答案】×
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:汽车所行驶的速度×时间=路程(不一定),所以汽车所行驶的速度和时间不一定成反比例关系,当汽车行驶的路程一定时,汽车所行驶的速度和时间成反比例关系。
所以原题说法错误。
故答案为:×。
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
26.【考点】比例的意义和基本性质.
【答案】√
【思路分析】在比例里,两个内项的积等于两个外项的积,所以它们的差为0.
【解答】解:因为在比例里,两个内项的积等于两个外项的积,
所以在比例里外项之积减内项之积,所得的差是0,说法正确的;
故答案为:√.
【名师点评】此题主要考查比例的基本性质的灵活应用.
27.【考点】比的意义;比的应用.
【答案】√
【思路分析】设小圆的半径为2r,则大圆的半径为3r,分别代入圆的周长和面积公式,表示出各自的周长和面积,即可求解。
【解答】解:设小圆的半径为2r,则大圆的半径为3r,
小圆的周长=2π×2r=4πr,
大圆的周长=2π×3r=6πr,
周长的比是:4πr:6πr=2:3;
小圆的面积=π(2r)2=4πr2,
大圆的面积=π(3r)2=9πr2,
面积的比是:4πr2:9πr2=4:9。
故答案为:√。
【名师点评】此题主要考查圆的周长和面积的计算方法的灵活应用。
28.【考点】圆柱的展开图.
【答案】×
【思路分析】圆柱的侧面展开图是一个正方形,说明圆柱的底面周长等于高。据此求解即可。
【解答】解:圆柱的侧面展开图是一个正方形,说明圆柱的底面周长等于高。所以原题说法错误。
故答案为:×。
【名师点评】本题考查了圆柱体的展开图知识,结合题意分析解答即可。
四.计算题
29.【考点】分数除法;数的估算;小数的加法和减法;分数乘法.
【答案】4.9、、4000、、9、0.3、6、0、10、7。
【思路分析】根据分数乘除法和小数加减法的方法进行口算即可。
【解答】解:
3.7+1.2=4.9 50×80=4000 1 32=9
0.2=0.3 6 00 8×1.25=10 625÷90≈7
【名师点评】此题属于基本的计算,在平时注意积累经验,逐步提高运算的速度和准确性。
30.【考点】解比例.
【答案】x;x=14
【思路分析】(1)根据比例的基本性质,把原式化为x,然后方程的两边同时除以求解;
(2)根据比例的基本性质,把原式化为4x=7×8,然后方程的两边同时除以4求解。
【解答】解:(1)::x
x
x
x
(2)
4x=7×8
4x÷4=7×8÷4
x=14
【名师点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
31.【考点】运算定律与简便运算.
【答案】1;;127.4;20。
【思路分析】(1)先算小括号里面的减法,再算括号外面的除法,最后算括号外面的加法;
(2)根据乘法分配律进行计算;
(3)根据减法的性质进行计算;
(4)根据乘法交换律和结合律进行计算。
【解答】解:(1)1+()÷4
=14
=1
=1
(2)9
=()
=1
(3)137.4﹣8.47﹣1.53
=137.4﹣(8.47+1.53)
=137.4﹣10
=127.4
(4)0.25×64×1.25
=0.25×(2×4×8)×1.25
=(0.25×4)×(8×1.25)×2
=1×10×2
=20
【名师点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
五.操作题(共1小题)
32.【考点】数对与位置;图形的放大与缩小.
【答案】(1)(2)作图如下:
【思路分析】(1)数对中第一个数字表示列,第二个数字表示行,据此即可在方格图中描出A、B、C各点,并将各点依次连接起来即可。
(2)按2:1放大就是把这个三角形的底和高同时扩大2倍,依此画图即可。
【解答】解:(1)封闭图形如下所示:
(2)扩大后的图形如图所示:
【名师点评】图形的放大和缩小是生活中常见的现象,把一个图形放大或缩小后所得到的图形与原图形相比,形状相同,大小不同。
六.应用题
33.【考点】圆柱的侧面积和表面积.
【答案】351.68平方分米。
【思路分析】已知铁桶有盖,所以只求这个圆柱的2个底面的面积与侧面积的和即可,根据圆的面积公式:S=πr2,圆柱的侧面积公式:S=Ch,把数据代入公式解答。
【解答】解:25.12÷3.14÷2=4(分米)
3.14×42×2+25.12×10
=100.48+251.2
=351.68(平方分米)
答:做这个铁桶至少要用铁皮351.68平方分米。
【名师点评】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
34.【考点】正、反比例应用题.
【答案】见试题解答内容
【思路分析】根据题意可知:速度(一定),所以路程和时间成正比例,设这列火车需要行驶x小时,据此列比例解答.
【解答】解:设这列火车需要行驶x小时,
720x=3×1200
x
x=5.
答:这列火车需要行驶5小时.
【名师点评】本题主要考查比例在日常生活中的应用,要正确判断两种相关联量成正比例、还是成反比例是解答关键.
35.【考点】关于圆锥的应用题.
【答案】98克。
【思路分析】利用圆锥体积公式:Vπr2h代入数据计算求出零件的体积,再乘每立方厘米的质量,据此解答。
【解答】解:(4÷2)2×3×7.8
=3.14×4×7.8
=12.56×7.8
≈98(克)
答:这个零件大约重98克。
【名师点评】解答即可。熟练掌握圆锥的体积公式,是解答此题的关键。
36.【考点】分数、百分数复合应用题.
【答案】240本。
【思路分析】先把总本数看作单位“1”,运用分数乘法意义,求出第一天卖出本数,再把第一天卖书本数看作单位“1”,第二天比第一天多卖出了20%,那么第二天就是第一天卖出的(1+20%),运用百分数乘法意义即可求出第二天卖出书本数。
【解答】解:800(1+20%)
=200×1.2
=240(本)
答:第二天卖出240本。
【名师点评】解答此题的关键是分清两个不同的单位“1”,已知单位“1”的量,求它的几分之几是多少用乘法求解。
37.【考点】整数、小数复合应用题.
【答案】60吨。
【思路分析】首先根据已知一个数几倍是多少,求这个数,用除法求出四月份用煤多少吨。再根据整数减法的意义,求出六月份的用煤量,据此即可得出答案。
【解答】解:3000÷1.2﹣(3000﹣560)
=2500﹣2440
=60(吨)
答:六月份比四月份少用煤60吨。
【名师点评】此题解答关键是求出四月份的用煤量和六月份用煤量,再根据整数减法解答即可。
38.【考点】比的应用.
【答案】A,80人。
【思路分析】(1)将两项中所给出的信息与“已知第一车间有30人,并且人数最多”这个条件相结合进行分析,找出其矛盾之处即能确定哪个信息是准确的。
A.第一车间比总人数的少2人,总人数为:(30+2)80(人),另两个车间共有80﹣30=50(人),50÷2=25(人),两个车间均可以少于30人;所以A正确。
B.第一车间人数占3个车间总人数的30%,则总人数为30÷30%=100(人),另两个车间共有100﹣30=70(人),至少有一个会高于30人,与第一车间人数最多相矛盾,所以B错误。
C.第一、第二、第三车间人数的比是4:2:3,30(人),不是整数,不可能有非整数人员,与实际不符,所以C错误。
(2)根据分数除法的意义,第一车间比总人数的少2人,用第一车间人数加2再除以所占比例,即得共有多少人。
【解答】解:(1)A.(30+2)80(人),另外两个车间共有80﹣30=50(人),50÷2=25(人),两个车间均可以少于30人;所以A正确;
B.30÷30%=100(人),另两个车间共有100﹣30=70(人),至少有一个会高于30人,与第一车间人数最多相矛盾,信息为错误;
C.第一、第二、第三车间人数的比是4:2:3,30(人),不是整数,不可能有非整数人员,与实际不符,所以C错误。所以以上三条信息中,正确的信息是A。
(2)(30+2)80(人)
答:这个工厂3个车间共有80人。
【名师点评】完成本题要注意根据所给条件认真分析,然后做出正确判断。
21世纪教育网(www.21cnjy.com)
同课章节目录
