(小升初择校分班考)小升初重点校择校分班考押题卷-2025年秋六年级数学苏教版(含答案解析)
文档属性
| 名称 | (小升初择校分班考)小升初重点校择校分班考押题卷-2025年秋六年级数学苏教版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 294.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 21:01:55 | ||
图片预览



文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初重点校择校分班考押题卷(苏教版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.(2023 雨花台区)奇奇想要了解5月份家庭支出中各类支出的分布情况,可以制作成( )
A.条形统计图 B.折线统计图
C.扇形统计图 D.无法确定
2.(2023 扬州)下列各选项中的两种量,成反比例关系的是( )
A.正方形的周长和边长 B.路程一定,时间和速度
C.圆的半径和它的周长 D.运送一批货物,运走的吨数和剩下的吨数
3.(2023 建邺区)如果a是一个质数,那么2a+1一定是( )
A.奇数 B.偶数 C.质数 D.合数
4.(2023 浦口区)虚线框中与圆锥体积相等的图形有( )个。(单位:厘米)
A.1 B.2 C.3 D.4
5.(2023 江宁区)下面的描述中不符合生活常识的是( )
A.一枚1元硬币厚度约是2毫米
B.小明家餐桌的面积为200平方厘米
C.小红家距离学校约600米,他上班大约步行1100步
6.(2022 南京)下面图形中的涂色部分,可以用来表示2.35中的“3”的是( )图形。
A. B. C.
7.(2022 鼓楼区)小明和小方做种子发芽实验,小明50粒种子的发芽率是80%,小方30粒种子的发芽率是100%,那么他俩80粒种子的发芽率是( )
A.90% B.85% C.87.5% D.95%
8.(2021 蒲县)下列各图中的正方形面积相等,图( )的阴影面积与另外两图不同。
A. B. C.
9.(2023 淮安区)能与4:0.3组成比例的是( )
A.0.4:0.3 B.4:3 C.80:6 D.6:8
二.填空题
10.(2021 六合区)将圆等分成若干份,拼成一个近似的长方形,已知长方形的长比宽多6.42cm,圆的面积是 cm2.
11.(2023 江宁区)将如图的直角三角形分别绕三条边所在的直线旋转一周,得到3个不同的立体图形,其中体积最大是 立方厘米,最小是 立方厘米。
12.(2022 建邺区)乐乐骑车去新华书店买书,如图是他离开家的距离与时间的统计图。
(1)他在书店买书用去 分钟。
(2)返回时的速度是每小时 千米。
13.(2023 雨花台区)用边长1cm的小正方形拼成长方形(如图)。像这样,用5个小正方形拼成的长方形的周长是 厘米,用a个小正方形拼成的长方形的周长是 厘米。
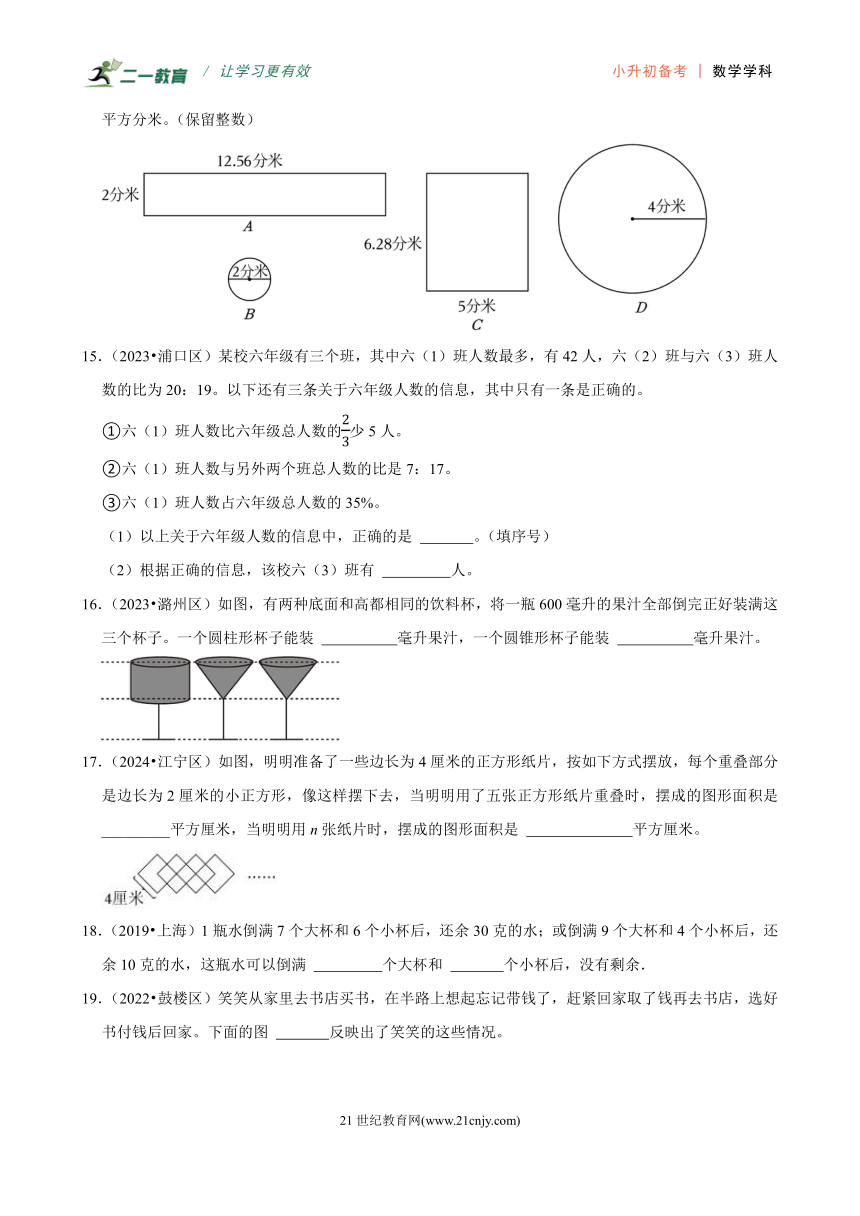
14.(2023 鼓楼区)制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。你认为( 和 )的材料搭配较合适。如果要在水桶的外表面涂上油漆,则油漆的面积有_______ 平方分米。(保留整数)
15.(2023 浦口区)某校六年级有三个班,其中六(1)班人数最多,有42人,六(2)班与六(3)班人数的比为20:19。以下还有三条关于六年级人数的信息,其中只有一条是正确的。
①六(1)班人数比六年级总人数的少5人。
②六(1)班人数与另外两个班总人数的比是7:17。
③六(1)班人数占六年级总人数的35%。
(1)以上关于六年级人数的信息中,正确的是 。(填序号)
(2)根据正确的信息,该校六(3)班有 人。
16.(2023 潞州区)如图,有两种底面和高都相同的饮料杯,将一瓶600毫升的果汁全部倒完正好装满这三个杯子。一个圆柱形杯子能装 毫升果汁,一个圆锥形杯子能装 毫升果汁。
17.(2024 江宁区)如图,明明准备了一些边长为4厘米的正方形纸片,按如下方式摆放,每个重叠部分是边长为2厘米的小正方形,像这样摆下去,当明明用了五张正方形纸片重叠时,摆成的图形面积是_________平方厘米,当明明用n张纸片时,摆成的图形面积是 平方厘米。
18.(2019 上海)1瓶水倒满7个大杯和6个小杯后,还余30克的水;或倒满9个大杯和4个小杯后,还余10克的水,这瓶水可以倒满 个大杯和 个小杯后,没有剩余.
19.(2022 鼓楼区)笑笑从家里去书店买书,在半路上想起忘记带钱了,赶紧回家取了钱再去书店,选好书付钱后回家。下面的图 反映出了笑笑的这些情况。
20.(2023 南京)“转化”思想是重要的数学思想方法之一。
(1)在学习圆柱体时,我们就是将圆柱体的体积转化成长方体的体积。请你根据圆柱体积的推导过程,完成下面填空。
当圆柱底面半径为r时,圆柱的底面积是 ,已知圆柱体的高为h,根据长方体的体积=底面积×高,所以圆柱体的体积公式的字母式是 。
(2)“转化”思想在我们的日常生活中无处不在,你能用“转化”的方法,算出1个土豆的体积吗?
①准备:1个圆柱形容器并注入一定量的水,测量出水面的高度;
②操作: ;
③计算:土豆的体积=容器的底面积× 。
21.(2023 浦口区)去年果园里有梨树和桃树共400棵,其中桃树占总数的40%.今年又种一些桃树,梨树棵数不变,这是梨树占总数的48%,现在这两种果树一共有 棵.
22.(2020 鼓楼区)将一根体积是48立方分米的圆柱形木料,削成与它等底等高的圆锥形,需要削去_______ 立方分米的木料。
三.判断题
23.(2023 吴江区)解比例的依据是比的基本性质. .
24.(2023 鼓楼区)一种盐水的含盐率是10%,盐与水的比是1:9. .
25.(2023 曲周县)两个圆柱的侧面积相等,它们的底面周长也一定相等. .
26.(2023 鼓楼区)一个圆锥的底面半径扩大3倍,高也扩大3倍,那么它的体积就扩大9倍。
27.(2023 鼓楼区)总路程一定,已行的路程和剩下的路程成反比例. .
28.(2023 鼓楼区)小红在小明的北偏东30°方向,那么小明在小红的南偏西30°方向。
四.计算题
29.(2022 高淳区)直接写出得数。
57+68= 72﹣0.2= 36×25%= 10.1÷5=
4: 0.52=
30.(2023 浦口区)解比例或解方程。
31.(2023 浦口区)怎样简便就怎样算。
2.5×1.25×16
五.操作题
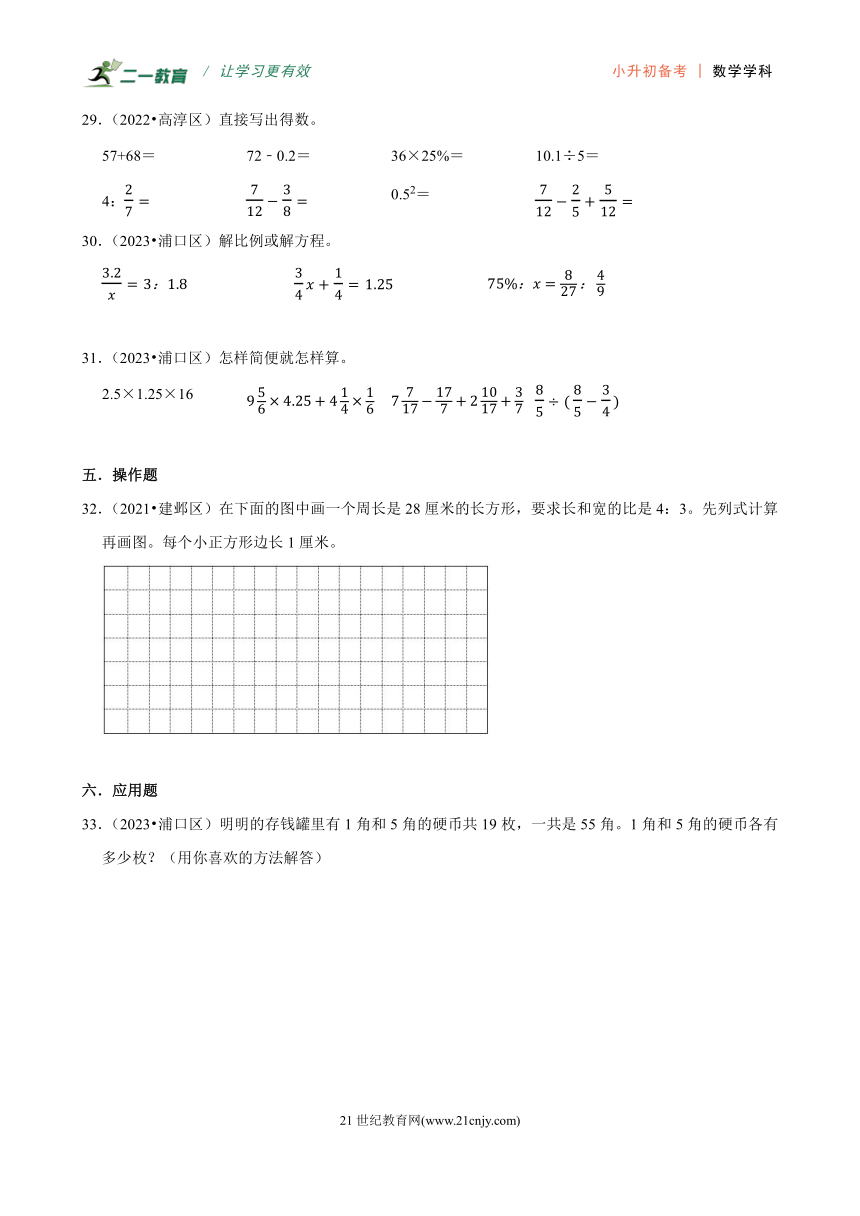
32.(2021 建邺区)在下面的图中画一个周长是28厘米的长方形,要求长和宽的比是4:3。先列式计算再画图。每个小正方形边长1厘米。
六.应用题
33.(2023 浦口区)明明的存钱罐里有1角和5角的硬币共19枚,一共是55角。1角和5角的硬币各有多少枚?(用你喜欢的方法解答)
34.(2020 鼓楼区)有一个近似于圆锥形的稻谷堆,底面半径是2米,高是1.5米。如果每立方米稻谷大约重0.5吨,那么这堆稻谷大约重多少吨?(得数保留整数)
35.(2021 建邺区)把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。这个长方体的宽是4厘米,高是20厘米,这个圆柱的体积是多少?
36.(2022 建邺区)在比例尺是的地图上,量得A、B两地的距离是6厘米。那么A、B两地的实际距离是多少?如果在一幅比例尺是1:5000000的地图上,A、B两地的图上距离是多少厘米?
37.(2022 建邺区)某公司委托快递公司托运360箱玻璃制品,合同规定每箱运费20元,若损坏一箱,不仅不需要给运费,快递公司还要赔偿损失120元。货物到达目的地后,快递公司获得6780元运费。损坏了多少箱?
38.(2020 鼓楼区)下面是王老师的一张储蓄存单,根据相关信息算一算,王老师存款到期时连本带息一共得到了多少元?
参考答案及试题解析
一.选择题
1.(2023 雨花台区)奇奇想要了解5月份家庭支出中各类支出的分布情况,可以制作成( )
A.条形统计图 B.折线统计图
C.扇形统计图 D.无法确定
【考点】统计图的选择.
【答案】C
【思路分析】条形统计图能很容易看出数量的多少;
折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;
扇形统计图能反映部分与整体的关系,由此根据情况选择即可。
【解答】解:奇奇想要了解5月份家庭支出中各类支出的分布情况,可以制作成扇形统计图。
故选:C。
【名师点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
2.(2023 扬州)下列各选项中的两种量,成反比例关系的是( )
A.正方形的周长和边长
B.路程一定,时间和速度
C.圆的半径和它的周长
D.运送一批货物,运走的吨数和剩下的吨数
【考点】辨识成正比例的量与成反比例的量.
【答案】B
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:A.正方形的周长÷边长=4(一定),商一定,所以正方形的周长和边长成正比例;
B.时间×速度=路程(一定),乘积一定,所以时间和速度成反比例;
C.圆的周长÷半径=2π(一定),商一定,所以圆的半径和它的周长成正比例;
D.运走的吨数+剩下的吨数=总吨数(一定),和一定,所以运走的吨数和剩下的吨数不成比例。
故选:B。
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
3.(2023 建邺区)如果a是一个质数,那么2a+1一定是( )
A.奇数 B.偶数 C.质数 D.合数
【考点】用字母表示数;奇数与偶数的初步认识;合数与质数的初步认识.
【答案】A
【思路分析】根据质数除了2以外都是奇数,奇数×2=偶数,2×2=偶数,可知2a是偶数,偶数+1=奇数,据此解答即可。
【解答】解:如果a是一个质数,那么2a+1一定是奇数。
故选:A。
【名师点评】本题考查奇数与偶数的认识以及质数的认识。
4.(2023 浦口区)虚线框中与圆锥体积相等的图形有( )个。(单位:厘米)
A.1 B.2 C.3 D.4
【考点】圆锥的体积;圆柱的体积.
【答案】D
【思路分析】根据圆柱、圆锥、长方体、棱柱的体积计算公式做题即可。
【解答】解:左面圆锥与圆柱的底面积相等,圆锥的高是圆柱高的3倍,所以体积相等;
长方体的体积=底面积×高,所以体积与圆柱相等,也和所给圆锥的体积相等;
根据圆锥的体积公式可知,两个圆锥的底面积和高的乘积相等,所以体积也相等;
三棱柱的体积等于底面积乘高,60×10=50×12=500(立方厘米),所以体积与圆柱和圆锥的体积都相等。
所以虚线框中与圆锥体积相等的图形有4个。
故选:D。
【名师点评】本题主要考查立体图形体积的计算。
5.(2023 江宁区)下面的描述中不符合生活常识的是( )
A.一枚1元硬币厚度约是2毫米
B.小明家餐桌的面积为200平方厘米
C.小红家距离学校约600米,他上班大约步行1100步
【考点】根据情景选择合适的计量单位;长度及长度的常用单位.
【答案】B
【思路分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【解答】解:一枚1元硬币厚度约是2毫米,符合生活常识。
小明家餐桌的面积为200平方分米,原题不符合生活常识。
小红家距离学校约600米,他上班大约步行1100步,符合生活常识。
故选:B。
【名师点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
6.(2022 南京)下面图形中的涂色部分,可以用来表示2.35中的“3”的是( )图形。
A. B. C.
【考点】小数的读写、意义及分类.
【答案】B
【思路分析】2.35中的“3”表示0.3,也就是把整个图形平均分成10份,阴影部分表示其中的3份。也表示把整个图形平均分成100份,阴影部分表示其中的30份。符合条件的图是B项。
【解答】解:可以用来表示2.35中的“3”。
故选:B。
【名师点评】此题主要考查了百分数的意义,要熟练掌握。
7.(2022 鼓楼区)小明和小方做种子发芽实验,小明50粒种子的发芽率是80%,小方30粒种子的发芽率是100%,那么他俩80粒种子的发芽率是( )
A.90% B.85% C.87.5% D.95%
【考点】百分数的实际应用.
【答案】C
【思路分析】发芽率是指发芽的种子数占种子总数的百分之几,100%=发芽率;要求他俩80粒种子的发芽率是多少,就要把小明和小方的种子发芽的粒数分别算出来;小明50粒种子的发芽率是80%,那么发芽的粒数为50×80%=40(粒),同理小方30粒种子的发芽粒数为30×100%=30(粒),小明和小方的种子发芽的粒数共40+30=70(粒),根据上述关系式列式解答即可.
【解答】解:50×80%+30×100%,
=40+30,
=70(粒);
100%=87.5%.
答:他俩80粒种子的发芽率是87.5%.
故选:C.
【名师点评】此题属于百分率问题,重点考查学生对“100%=发芽率”这个关系式的理解与运用.
8.(2021 蒲县)下列各图中的正方形面积相等,图( )的阴影面积与另外两图不同。
A. B. C.
【考点】组合图形的面积.
【答案】B
【思路分析】根据所给图形的特点,找到阴影部分的面积与正方形面积的关系,比较即可得出结论。
【解答】解:选项A和选项C的阴影部分的面积都等于正方形面积减去圆的面积;选项B的阴影部分面积等于正方形面积的一半。
所以B的阴影和另外两个的面积不同。
故选:B。
【名师点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后比较,得出结论。
9.(2023 淮安区)能与4:0.3组成比例的是( )
A.0.4:0.3 B.4:3 C.80:6 D.6:8
【考点】比例的意义和基本性质.
【答案】C
【思路分析】将题干中的比以及选项中的比化为最简整数比,然后找出相同的即可。
【解答】解:4:0.3=40:3
0.4:0.3=40:30=4:3
4:3=4:3
80:6=40:3
6:8=6:8=3:4
所以4:0.3=80:6。
故选:C。
【名师点评】本题主要考查了比例的意义,也可以根据比例的基本性质来进行判断。
二.填空题
10.(2021 六合区)将圆等分成若干份,拼成一个近似的长方形,已知长方形的长比宽多6.42cm,圆的面积是 28.26 cm2.
【考点】圆、圆环的面积.
【答案】28.26。
【思路分析】将圆等分成若干份,拼成一个近似的长方形,长方形的宽为圆的半径,长为圆的周长的一半,根据圆的周长公式C=2πr,长方形的长为宽的π倍,根据差倍公式,可以求出圆的半径,再根据圆的面积公式S=πr2,代入求解即可。
【解答】解:长方形的宽为圆的半径,长为圆的周长的一半,
根据圆的周长公式C=2πr,长方形的长为宽的π倍,
圆的半径为:
6.42÷(3.14﹣1)
=6.42÷2.14
=3(cm)
圆的面积为:
3.14×3×3
=9.42×3
=28.26(cm2)
答:圆的面积是28.26cm2。
故答案为:28.26。
【名师点评】本题主要考查了圆的面积,根据差倍公式求出圆的半径是本题解题的关键。
11.(2023 江宁区)将如图的直角三角形分别绕三条边所在的直线旋转一周,得到3个不同的立体图形,其中体积最大是 50.24 立方厘米,最小是 30.144 立方厘米。
【考点】圆锥的体积.
【答案】50.24,30.144。
【思路分析】根据圆锥的体积公式:Vπr2h,把数据代入公式求出它们的体积,然后进行比较即可。
【解答】解:①以4厘米为轴
π×32×4
π×9×4
=12π(立方厘米)
②以3厘米为轴
π×42×3
π×16×3
=16π(立方厘米)
③以5厘米为轴
底面半径:3×4÷2×2÷5
=12÷5
=2.4(厘米)
π×2.42×5
π×5.76×5
=9.6π(立方厘米)
16π>12π>9.6π
16π=50.24(立方厘米)
9.6π=30.144(立方厘米)
答:体积最大是50.24立方厘米,体积最小是30.144立方厘米。
故答案为:50.24,30.144。
【名师点评】此题主要考查圆锥的体积公式的灵活运用,关键是熟记公式。
12.(2022 建邺区)乐乐骑车去新华书店买书,如图是他离开家的距离与时间的统计图。
(1)他在书店买书用去 分钟。
(2)返回时的速度是每小时 千米。
【考点】单式折线统计图;从统计图表中获取信息.
【答案】(1)。(2)。
【思路分析】(1)从图中可以看出,他在书店买书的时间是:从小时到小时,作差即可。
(2)路程=速度×时间,速度=路程÷时间,路程是5千米,时间是2(小时),代入即可。
【解答】解:(1)
(小时)
答:他在书店买书用去小时。
(2)5
=5
(千米)
答:返回时的速度是每小时千米。
故答案为:(1)。(2)。
【名师点评】此题主要考查的是如何观察统计图并且从统计图中获取信息,然后再进行计算、解答即可。
13.(2023 雨花台区)用边长1cm的小正方形拼成长方形(如图)。像这样,用5个小正方形拼成的长方形的周长是 12 厘米,用a个小正方形拼成的长方形的周长是 (2a+2) 厘米。
【考点】数与形结合的规律.
【答案】12,(2a+2)。
【思路分析】单独一个正方形的周长是4厘米,每多一个正方形周长就增加2厘米,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,然后结合规律解答。
【解答】解:2个正方形拼成长方形的周长=4+(2﹣1)×2=6(厘米)
3个正方形拼成长方形的周长=4+(3﹣1)×2=8(厘米)
4个正方形拼成长方形的周长=4+(4﹣1)×2=10(厘米)
5个正方形拼成长方形的周长=4+(5﹣1)×2=12(厘米)
.......
由此得出规律:用a个正方形拼成长方形的周长=4+(a﹣1)×2=(2a+2)厘米
故答案为:12,(2a+2)。
【名师点评】此题属于数与形结合的规律,考查的目的是通过特例分析从而归纳总结出一般结论的能力,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,然后利用规律解决问题。
14.(2023 鼓楼区)制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。你认为( B 和 C )的材料搭配较合适。如果要在水桶的外表面涂上油漆,则油漆的面积有 35 平方分米。(保留整数)
【考点】关于圆柱的应用题.
【答案】B,C;35。
【思路分析】选择B和C的材料可以做成一个无盖的水桶。理由是长方形的长作为圆柱的底面周长,长方形的宽作为圆柱的高。根据圆柱的侧面积公式:S=Ch,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:B和C的材料搭配较合适。
(2)3.14×(2÷2)2+3.14×2×5
=3.14×1+31.4
=34.54
≈35(平方分米)
答:油漆的面积有35平方分米。
故答案为:B,C;35。
【名师点评】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆的周长公式、圆柱的侧面积公式、圆的面积公式及应用,关键是熟记公式。
15.(2023 浦口区)某校六年级有三个班,其中六(1)班人数最多,有42人,六(2)班与六(3)班人数的比为20:19。以下还有三条关于六年级人数的信息,其中只有一条是正确的。
①六(1)班人数比六年级总人数的少5人。
②六(1)班人数与另外两个班总人数的比是7:17。
③六(1)班人数占六年级总人数的35%。
(1)以上关于六年级人数的信息中,正确的是 ③ 。(填序号)
(2)根据正确的信息,该校六(3)班有 38 人。
【考点】比的应用.
【答案】(1)③;(2)38。
【思路分析】(1)①六(1)班人数比六年级总人数的少5人,即(42+5)正好是六年级总人数的,则总人数有[(42+5)]人,因为人数是整数,所以计算结果应是整数,但此结果不是整数,即本条信息错误;
②六(1)班与另外两班总人数的比是7:17,则六(1)班占另外两班总人数的,用六(1)班人数除以即是另外两班总人数之和,即42102(人),又因为六(2)班与六(3)班人数的比为20:19。即六(2)班人数占六(2)班与六(3)班人数之和的,因为人数是整数,所以计算结果应是整数,此结果不是整数,即本条信息错误;
③六(1)班人数占六年级总人数的35%,根据一个数的百分之几是多少,求这个数,用除法计算,用六(1)班的人数除以六(1)班人数占六年级总人数的百分数即是六年级的总人数,即42÷35%=120(人),则六(1)班和六(2)班人数之和为:120﹣42=78(人),结合六(2)班与六(3)班人数的比为20:19可知,六(3)班人数占六(2)班与六(3)班人数之和的,因为人数是整数,所以计算结果应是整数,此结果是整数,即本条信息正确;
(2)根据(1)中③的分析直接求解即可。
【解答】解:(1)①六(1)班人数比六年级总人数的少5人,即(42+5)正好是六年级总人数的,则总人数有[(42+5)]人,因为人数是整数,所以计算结果应是整数,但此结果不是整数,即本条信息错误;
②六(1)班与另外两班总人数的比是7:17,则六(1)班占另外两班总人数的,用六(1)班人数除以即是另外两班总人数之和,即42102(人),又因为六(2)班与六(3)班人数的比为20:19。即六(2)班人数占六(2)班与六(3)班人数之和的,因为人数是整数,所以计算结果应是整数,此结果不是整数,即本条信息错误;
③六(1)班人数占六年级总人数的35%,根据一个数的百分之几是多少,求这个数,用除法计算,用六(1)班的人数除以六(1)班人数占六年级总人数的百分数即是六年级的总人数,即42÷35%=120(人),则六(1)班和六(2)班人数之和为:120﹣42=78(人),结合六(2)班与六(3)班人数的比为20:19可知,六(3)班人数占六(2)班与六(3)班人数之和的,因为人数是整数,所以计算结果应是整数,此结果是整数,即本条信息正确;
综上,只有③信息是正确的;
(2)(42÷35%﹣42)
=(120﹣42)
=78
=38(人)
答:该校六(3)班有38人。
故答案为:(1)③;(2)38。
【名师点评】本题考查了比的应用。
16.(2023 潞州区)如图,有两种底面和高都相同的饮料杯,将一瓶600毫升的果汁全部倒完正好装满这三个杯子。一个圆柱形杯子能装 360 毫升果汁,一个圆锥形杯子能装 120 毫升果汁。
【考点】圆锥的体积.
【答案】360,120。
【思路分析】等底等高的圆柱的体积是圆锥体积的3;设圆锥形杯子能装x毫升果汁,则圆柱形杯子能装3x毫升果汁;两个圆锥形杯子能装x+x毫升果汁与一个圆柱形杯子能装3x毫升果汁,一共是600毫升,列方程:x+x+3x=600,解方程,即可求出一个圆锥形杯子能装果汁多少毫升,一个圆柱形杯子能装多少毫升果汁。
【解答】解:设一个圆锥形杯子能装x毫升果汁,则一个圆柱形杯子能装3x毫升果汁。
x+x+3x=600
2x+3x=600
5x=600
x=120
圆柱形杯子:120×3=360(毫升)
答:一个圆柱形杯子能装360毫升果汁,一个圆锥形杯子能装120毫升果汁。
故答案为:360,120。
【名师点评】利用等底等高的圆柱体积与圆锥体积之间的关系,设出未知数,找出相关的量,列方程,解方程。
17.(2024 江宁区)如图,明明准备了一些边长为4厘米的正方形纸片,按如下方式摆放,每个重叠部分是边长为2厘米的小正方形,像这样摆下去,当明明用了五张正方形纸片重叠时,摆成的图形面积是 64 平方厘米,当明明用n张纸片时,摆成的图形面积是 (12n+4) 平方厘米。
【考点】数与形结合的规律.
【答案】64;(12n+4)。
【思路分析】用2张纸片时,摆成图形的面积是2个大正方形的面积和﹣1个小正方形的面积;
用3张纸片时,摆成图形的面积是3个大正方形的面积和﹣2个小正方形的面积;
用4张纸片时,摆成图形的面积是4个大正方形的面积和﹣3个小正方形的面积;
用5张纸片时,摆成图形的面积是5个大正方形的面积和﹣4个小正方形的面积;
用n张纸片时,摆成图形的面积是n个正方形的面积和﹣(n﹣1)个小正方形的面积据此解答即可。
【解答】解:4×4=16(平方厘米)
2×2=4(平方厘米)
16×5﹣4×4
=80﹣16
=64(平方厘米)
16n﹣4(n﹣1)
=16n﹣4n+4
=(12n+4)(平方厘米)
答:当明明用了五张正方形纸片重叠时,摆成的图形面积是64平方厘米,当明明用n张纸片时,摆成的图形面积是(12n+4)平方厘米。
故答案为:64;(12n+4)。
【名师点评】本题主要考查数与形集合的规律发现每多1个正方形,面积的变化规律是解本题的关键。
18.(2019 上海)1瓶水倒满7个大杯和6个小杯后,还余30克的水;或倒满9个大杯和4个小杯后,还余10克的水,这瓶水可以倒满 10 个大杯和 3 个小杯后,没有剩余.
【考点】简单的等量代换问题.
【答案】见试题解答内容
【思路分析】把第二次倒的方法乘3,也就是说看成3瓶水,3瓶可以倒27个大杯和12个小杯还剩30克,减去第一次倒的后可得:2瓶水可以倒20个大杯和6个小杯,所以1瓶可以倒10个大杯和3个小杯.
【解答】解:倒满9个大杯和4个小杯后,还余10克的水,
所以当为3瓶水时,可以倒27个大杯和12个小杯还剩30克,
减去第一次倒的后可得:2瓶水可以倒20个大杯和6个小杯,
所以1瓶可以倒10个大杯和3个小杯.
故答案为:10,3.
【名师点评】此题的关键是根据第二次倒完后剩的10克,乘3,也就是看成是3瓶,然后和第一倒的进行整体相减,从而求解.
19.(2022 鼓楼区)笑笑从家里去书店买书,在半路上想起忘记带钱了,赶紧回家取了钱再去书店,选好书付钱后回家。下面的图 ② 反映出了笑笑的这些情况。
【考点】单式折线统计图.
【答案】②
【思路分析】图中横轴表示时间,纵轴表示路程,找准出发点,折线水平的部分表示在书店停留的时间,由此判断符合题意的图形即可。
【解答】解:首先排除选项①,因为图①中没有表示停留,是错误的。
再排除选项③,因为图③表示走到半路有停留的时间且没有表示返回家取钱,是错误的。
只有选项②比较准确的反映了笑笑的这些情况。
故答案为:②。
【名师点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
20.(2023 南京)“转化”思想是重要的数学思想方法之一。
(1)在学习圆柱体时,我们就是将圆柱体的体积转化成长方体的体积。请你根据圆柱体积的推导过程,完成下面填空。
当圆柱底面半径为r时,圆柱的底面积是 πr2 ,已知圆柱体的高为h,根据长方体的体积=底面积×高,所以圆柱体的体积公式的字母式是 V=πr2h 。
(2)“转化”思想在我们的日常生活中无处不在,你能用“转化”的方法,算出1个土豆的体积吗?
①准备:1个圆柱形容器并注入一定量的水,测量出水面的高度;
②操作: 把一个土豆放入有一些水的圆柱容器中(水未溢出),上升部分水的体积就等于这个土豆的体积 ;
③计算:土豆的体积=容器的底面积× 水面上升的高 。
【考点】圆柱的体积.
【答案】(1)πr2,V=πr2h;
(2)②把一个土豆放入有一些水的圆柱容器中(水未溢出),上升部分水的体积就等于这个土豆的体积;
③水面上升的高。
【思路分析】(1)根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体,拼成的长方体的底面积等于圆柱的底面积,拼成的长方体的高等于圆柱的高,根据长方体的体积公式推导出圆柱的体积公式。
(2)根据不规则物体体积的测量方法,把一个土豆放入有一些水的圆柱容器中(水未溢出),上升部分水的体积就等于这个土豆的体积,根据圆柱的体积公式:V=Sh,把数据的公式求出土豆的体积。
【解答】解:(1)在学习圆柱体时,我们就是将圆柱体的体积转化成长方体的体积。请你根据圆柱体积的推导过程,完成下面填空。
当圆柱底面半径为r时,圆柱的底面积是πr2,已知圆柱体的高为h,根据长方体的体积=底面积×高,所以圆柱体的体积公式的字母式是V=πr2h。
(2)“转化”思想在我们的日常生活中无处不在,我能用“转化”的方法,算出1个土豆的体积。
①准备:1个圆柱形容器并注入一定量的水,测量出水面的高度;
②操作:把一个土豆放入有一些水的圆柱容器中(水未溢出),上升部分水的体积就等于这个土豆的体积;
③计算:土豆的体积=容器的底面积×水面上升的高。
故答案为:πr2,V=πr2h;把一个土豆放入有一些水的圆柱容器中(水未溢出),上升部分水的体积就等于这个土豆的体积,水面上升的高。
【名师点评】此题考查的目的是理解掌握“转化”的思想方法在数学中的应用。
21.(2023 浦口区)去年果园里有梨树和桃树共400棵,其中桃树占总数的40%.今年又种一些桃树,梨树棵数不变,这是梨树占总数的48%,现在这两种果树一共有 500 棵.
【考点】分数和百分数应用题(多重条件).
【答案】见试题解答内容
【思路分析】去年果园里有梨树和桃树共400棵,其中桃树占总数的40%,则梨树占1﹣40%,所以梨树有400×(1﹣40%)棵,又今年又种一些桃树,梨树棵数不变,这是梨树占总数的48%,根据分数除法的意义,这时共有果树400×(1﹣40%)÷48%棵.
【解答】解:400×(1﹣40%)÷48%
=400×60%÷48%
=500(棵)
答:现在这两种果树一共有 500棵.
故答案为:500.
【名师点评】明确这一过程中梨树的棵数没有变,首先求出梨树的棵数是完成本题的关键.
22.(2020 鼓楼区)将一根体积是48立方分米的圆柱形木料,削成与它等底等高的圆锥形,需要削去 32 立方分米的木料。
【考点】圆柱的侧面积、表面积和体积.
【答案】32。
【思路分析】把一个圆柱体削成一个和它等底等高的圆锥,那么圆锥的体积就是圆柱体积的,求得圆锥体积,就可以求出削去的体积。
【解答】解:48﹣48
=48﹣16
=32(立方分米)
答:需要削去32立方分米的木料。
故答案为:32。
【名师点评】此题主要考查等底等高的圆柱与圆锥的关系:圆锥的体积等于与它等底等高圆柱体积的。
三.判断题
23.(2023 吴江区)解比例的依据是比的基本性质. × .
【考点】解比例.
【答案】见试题解答内容
【思路分析】根据比例的含义和解比例的方法,可得:解比例的依据是比例的基本性质,据此判断即可.
【解答】解:因为解比例的依据是比例的基本性质,不是比的基本性质,
所以题中说法不正确.
故答案为:×.
【名师点评】此题主要考查了解比例问题,要熟练掌握,注意比例的基本性质的应用.
24.(2023 鼓楼区)一种盐水的含盐率是10%,盐与水的比是1:9. √ .
【考点】比的应用.
【答案】见试题解答内容
【思路分析】根据“盐水的含盐率是10%,”把盐看做10份,盐水是100份,则水是(100﹣10)份,盐和盐水的比即可求出.
【解答】解:10:(100﹣10)
=10:90
=1:9;
答:盐与水的比是1:9;
故答案为:√.
【名师点评】解答此题的关键是把百分数转化成份数,根据要求的结果,找到对应份数,再根据比的基本性质,化成最简整数比即可.
25.(2023 曲周县)两个圆柱的侧面积相等,它们的底面周长也一定相等. × .
【考点】圆柱的侧面积、表面积和体积.
【答案】×
【思路分析】根据圆柱的侧面积计算公式“S=Ch”可知,圆柱的侧面积是由圆柱的底面周长和高决定的,因此,两个圆柱的侧面积相等,它们的底面周长不一定相等.
【解答】解:圆柱的侧面积是由圆柱的底面周长和高决定的,所以,两个圆柱的侧面积相等,它们的底面周长不一定相等.
因此,两个圆柱的侧面积相等,它们的底面周长也一定相等是错误的.
故答案为:×.
【名师点评】解答此题的关键是明白圆柱侧面积的意义,圆柱的侧面积是圆柱的底面周长和高的乘积,因此,圆柱侧面积相等,底面周长、高不一定相等.
26.(2023 鼓楼区)一个圆锥的底面半径扩大3倍,高也扩大3倍,那么它的体积就扩大9倍。 ×
【考点】圆锥的体积.
【答案】×
【思路分析】根据圆锥的体积V πr2h,半径扩大3倍,底面积扩大3×3=9倍,高也扩大3倍,则体积扩大9×3=27倍,据此判断。
【解答】解:由分析可知,一个圆锥的底面半径扩大3倍,高也扩大3倍,那么它的体积就扩大27倍。
所以题干说法错误。
故答案为:×。
【名师点评】此题考查了圆锥体积的计算方法,结合积的变化规律解答即可。
27.(2023 鼓楼区)总路程一定,已行的路程和剩下的路程成反比例. × .
【考点】辨识成正比例的量与成反比例的量.
【答案】×
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为已走的路程+剩下的路程=总路程(一定),是和一定,
所以已走的路程和剩下的路程不成反比例;
故答案为:×.
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
28.(2023 鼓楼区)小红在小明的北偏东30°方向,那么小明在小红的南偏西30°方向。 √
【考点】用角度表示方向.
【答案】√
【思路分析】根据位置的相对性可知,描述两个物体之间的相对位置时,方向相反,角度相等,或者先以小明为中心点,找到小红的位置后,再以小红为中心点找小明的位置,从而确定方向,据此解答。
【解答】解:通过分析可知,小红家在小明的北偏东30°方向,那么小明在小红的南偏西30°方向。画图如下:
原题说法正确。
故答案为:√。
【名师点评】本题考查了方向的认识,结合方向的相对性解答即可。
四.计算题
29.(2022 高淳区)直接写出得数。
57+68= 72﹣0.2= 36×25%= 10.1÷5=
4: 0.52=
【考点】整数、分数、小数、百分数四则混合运算;求比值和化简比;乘方;分数的加法和减法;分数乘法.
【答案】125,71.8,9,2.02,14,,0.25,。
【思路分析】根据整数、分数、小数以及百分数加减乘除法以及四则混合运算的顺序,直接进行口算即可。
【解答】解:
57+68=125 72﹣0.2=71.8 36×25%=9 10.1÷5=2.02
4:14 0.52=0.25
【名师点评】本题考查了基本的运算,注意运算数据和运算符号,细心计算即可。
30.(2023 浦口区)解比例或解方程。
【考点】解比例;百分数方程求解.
【答案】x=1.92;x;x。
【思路分析】化简比例方程后,在等式的两边同时除以3即可求解;
在等式的两边同时减去后再在等式两边同时乘即可求解;
根据比例的基本性质化简比例后,在方程两边同时乘即可求解。
【解答】解:3:1.8
3x=3.2×1.8
3x=5.76
3x÷3=5.76÷3
x=1.92
x1.25
x1.25
x=1
x1
x
75%:x:
x75%
x
x
x
【名师点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去,同时乘或同时除以一个数(0除外),两边仍相等。
31.(2023 浦口区)怎样简便就怎样算。
2.5×1.25×16
【考点】运算定律与简便运算;分数的四则混合运算.
【答案】50;42.5;8;。
【思路分析】把16看成4×4,再按照乘法交换律和结合律计算;
按照乘法分配律计算;
按照加法交换律和结合律计算;
先算小括号里面的减法,再算除法。
【解答】解:2.5×1.25×16
=(2.5×4)×(1.25×4)
=10×5
=50
=4.25×(9)
=4.25×10
=42.5
=(72)﹣()
=10﹣2
=8
【名师点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
五.操作题
32.(2021 建邺区)在下面的图中画一个周长是28厘米的长方形,要求长和宽的比是4:3。先列式计算再画图。每个小正方形边长1厘米。
【考点】画指定周长的长方形、正方形.
【答案】
【思路分析】先求出一组长和宽的和,利用周长除以2,然后把长和宽的和按照4:3进行比例分配求出长是多少,宽是多少,据此画图即可。
【解答】解:28÷2=14(厘米)
14÷(4+3)
=14÷7
=2(厘米)
长:4×2=8(厘米)
宽:3×2=6(厘米)
如图所示:
【名师点评】解决本题先根据周长分别求出长方形的长和宽。
六.应用题
33.(2023 浦口区)明明的存钱罐里有1角和5角的硬币共19枚,一共是55角。1角和5角的硬币各有多少枚?(用你喜欢的方法解答)
【考点】鸡兔同笼.
【答案】1角的硬币有10枚,5角的硬币有9枚。
【思路分析】设5角的硬币有x枚,1角的硬币有(19﹣x)枚,然后分别表示出1角和5角的各有多少钱加在一起就是55角,求出5角的数量,进一步求出1角钱的数量。
【解答】解:设5角的硬币有x枚,1角的硬币有(19﹣x)枚。
5x+1×(19﹣x)=55
5x+19﹣x=55
4x=36
x=9
19﹣9=10(枚)
答:1角的硬币有10枚,5角的硬币有9枚。
【名师点评】此题属于鸡兔同笼问题,解这类题可以用假设法进行分析,进而得出结论;也可以用方程进行解答。
34.(2020 鼓楼区)有一个近似于圆锥形的稻谷堆,底面半径是2米,高是1.5米。如果每立方米稻谷大约重0.5吨,那么这堆稻谷大约重多少吨?(得数保留整数)
【考点】关于圆锥的应用题.
【答案】3吨。
【思路分析】要求这堆稻谷的重量,先求得这堆稻谷的体积,这堆稻谷的形状是圆锥形的,利用圆锥的体积计算公式(VSh)先求得体积,进一步再求这堆稻谷的重量,问题得解。
【解答】解:3.14×2 ×1.5×0.5
3.14×4×1.5×0.5
3.14×6×0.5
=2×3.14×0.5
=3.14(吨)
≈3(吨)
答:这堆稻谷大约重3吨。
【名师点评】此题主要考查圆锥的体积计算公式:Vπr2h,运用公式计算时不要漏乘。
35.(2021 建邺区)把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。这个长方体的宽是4厘米,高是20厘米,这个圆柱的体积是多少?
【考点】圆柱的侧面积、表面积和体积.
【答案】1004.8立方厘米。
【思路分析】根据圆柱体积公式的推导过程可知,把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。这个长方体的宽等于圆柱的底面半径,这个长方体的高等于圆柱的高。根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×42×20
=3.14×16×20
=50.24×20
=1004.8(立方厘米)
答:这个圆柱的体积是1004.8立方厘米。
【名师点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用。
36.(2022 建邺区)在比例尺是的地图上,量得A、B两地的距离是6厘米。那么A、B两地的实际距离是多少?如果在一幅比例尺是1:5000000的地图上,A、B两地的图上距离是多少厘米?
【考点】图上距离与实际距离的换算(比例尺的应用).
【答案】18000000厘米;3.6厘米。
【思路分析】先根据“图上距离÷比例尺=实际距离”,求出A、B两地的实际距离,然后根据:实际距离×比例尺=图上距离,求出A、B两地在另一幅地图上的图上距离即可。
【解答】解:618000000(厘米)
答:A、B两地的实际距离是18000000厘米。
180000003.6(厘米)
答:在一幅比例尺是1:5000000的地图上,A、B两地的图上距离是3.6厘米。
【名师点评】根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论。
37.(2022 建邺区)某公司委托快递公司托运360箱玻璃制品,合同规定每箱运费20元,若损坏一箱,不仅不需要给运费,快递公司还要赔偿损失120元。货物到达目的地后,快递公司获得6780元运费。损坏了多少箱?
【考点】鸡兔同笼.
【答案】3箱。
【思路分析】假设运输时没有损坏,则应得到的运费是360×20=7200元,这与实际得到的运费就差了7200﹣6780=420(元),这是因为损坏一箱,不仅得不到运费20元,还要赔偿120元,即损坏一箱就要少得120+20=140元.据此可求出损坏的箱数。
【解答】解:(20×360﹣6780)÷(120+20)
=420÷140
=3(箱)
答:损坏了3箱。
【名师点评】本题的关键是让学生理解损坏一箱少得120+20=140(元),再根据假设没有损坏与实际得到钱数的差,列式求出损坏的箱数。
38.(2020 鼓楼区)下面是王老师的一张储蓄存单,根据相关信息算一算,王老师存款到期时连本带息一共得到了多少元?
【考点】存款利息与纳税相关问题.
【答案】10825元。
【思路分析】根据利息=本金×年利率×存期,本息=本金+利息,代入数据,即可得解。
【解答】解:10000+10000×2.75%×3
=10000+825
=10825(元)
答:王老师存款到期时连本带息一共得到了10825元。
【名师点评】这种类型属于利息问题,有固定的计算方法,利息=本金×利率×存期,本息=本金+利息,找清数据与问题,代入公式计算即可。
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初重点校择校分班考押题卷(苏教版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.(2023 雨花台区)奇奇想要了解5月份家庭支出中各类支出的分布情况,可以制作成( )
A.条形统计图 B.折线统计图
C.扇形统计图 D.无法确定
2.(2023 扬州)下列各选项中的两种量,成反比例关系的是( )
A.正方形的周长和边长 B.路程一定,时间和速度
C.圆的半径和它的周长 D.运送一批货物,运走的吨数和剩下的吨数
3.(2023 建邺区)如果a是一个质数,那么2a+1一定是( )
A.奇数 B.偶数 C.质数 D.合数
4.(2023 浦口区)虚线框中与圆锥体积相等的图形有( )个。(单位:厘米)
A.1 B.2 C.3 D.4
5.(2023 江宁区)下面的描述中不符合生活常识的是( )
A.一枚1元硬币厚度约是2毫米
B.小明家餐桌的面积为200平方厘米
C.小红家距离学校约600米,他上班大约步行1100步
6.(2022 南京)下面图形中的涂色部分,可以用来表示2.35中的“3”的是( )图形。
A. B. C.
7.(2022 鼓楼区)小明和小方做种子发芽实验,小明50粒种子的发芽率是80%,小方30粒种子的发芽率是100%,那么他俩80粒种子的发芽率是( )
A.90% B.85% C.87.5% D.95%
8.(2021 蒲县)下列各图中的正方形面积相等,图( )的阴影面积与另外两图不同。
A. B. C.
9.(2023 淮安区)能与4:0.3组成比例的是( )
A.0.4:0.3 B.4:3 C.80:6 D.6:8
二.填空题
10.(2021 六合区)将圆等分成若干份,拼成一个近似的长方形,已知长方形的长比宽多6.42cm,圆的面积是 cm2.
11.(2023 江宁区)将如图的直角三角形分别绕三条边所在的直线旋转一周,得到3个不同的立体图形,其中体积最大是 立方厘米,最小是 立方厘米。
12.(2022 建邺区)乐乐骑车去新华书店买书,如图是他离开家的距离与时间的统计图。
(1)他在书店买书用去 分钟。
(2)返回时的速度是每小时 千米。
13.(2023 雨花台区)用边长1cm的小正方形拼成长方形(如图)。像这样,用5个小正方形拼成的长方形的周长是 厘米,用a个小正方形拼成的长方形的周长是 厘米。
14.(2023 鼓楼区)制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。你认为( 和 )的材料搭配较合适。如果要在水桶的外表面涂上油漆,则油漆的面积有_______ 平方分米。(保留整数)
15.(2023 浦口区)某校六年级有三个班,其中六(1)班人数最多,有42人,六(2)班与六(3)班人数的比为20:19。以下还有三条关于六年级人数的信息,其中只有一条是正确的。
①六(1)班人数比六年级总人数的少5人。
②六(1)班人数与另外两个班总人数的比是7:17。
③六(1)班人数占六年级总人数的35%。
(1)以上关于六年级人数的信息中,正确的是 。(填序号)
(2)根据正确的信息,该校六(3)班有 人。
16.(2023 潞州区)如图,有两种底面和高都相同的饮料杯,将一瓶600毫升的果汁全部倒完正好装满这三个杯子。一个圆柱形杯子能装 毫升果汁,一个圆锥形杯子能装 毫升果汁。
17.(2024 江宁区)如图,明明准备了一些边长为4厘米的正方形纸片,按如下方式摆放,每个重叠部分是边长为2厘米的小正方形,像这样摆下去,当明明用了五张正方形纸片重叠时,摆成的图形面积是_________平方厘米,当明明用n张纸片时,摆成的图形面积是 平方厘米。
18.(2019 上海)1瓶水倒满7个大杯和6个小杯后,还余30克的水;或倒满9个大杯和4个小杯后,还余10克的水,这瓶水可以倒满 个大杯和 个小杯后,没有剩余.
19.(2022 鼓楼区)笑笑从家里去书店买书,在半路上想起忘记带钱了,赶紧回家取了钱再去书店,选好书付钱后回家。下面的图 反映出了笑笑的这些情况。
20.(2023 南京)“转化”思想是重要的数学思想方法之一。
(1)在学习圆柱体时,我们就是将圆柱体的体积转化成长方体的体积。请你根据圆柱体积的推导过程,完成下面填空。
当圆柱底面半径为r时,圆柱的底面积是 ,已知圆柱体的高为h,根据长方体的体积=底面积×高,所以圆柱体的体积公式的字母式是 。
(2)“转化”思想在我们的日常生活中无处不在,你能用“转化”的方法,算出1个土豆的体积吗?
①准备:1个圆柱形容器并注入一定量的水,测量出水面的高度;
②操作: ;
③计算:土豆的体积=容器的底面积× 。
21.(2023 浦口区)去年果园里有梨树和桃树共400棵,其中桃树占总数的40%.今年又种一些桃树,梨树棵数不变,这是梨树占总数的48%,现在这两种果树一共有 棵.
22.(2020 鼓楼区)将一根体积是48立方分米的圆柱形木料,削成与它等底等高的圆锥形,需要削去_______ 立方分米的木料。
三.判断题
23.(2023 吴江区)解比例的依据是比的基本性质. .
24.(2023 鼓楼区)一种盐水的含盐率是10%,盐与水的比是1:9. .
25.(2023 曲周县)两个圆柱的侧面积相等,它们的底面周长也一定相等. .
26.(2023 鼓楼区)一个圆锥的底面半径扩大3倍,高也扩大3倍,那么它的体积就扩大9倍。
27.(2023 鼓楼区)总路程一定,已行的路程和剩下的路程成反比例. .
28.(2023 鼓楼区)小红在小明的北偏东30°方向,那么小明在小红的南偏西30°方向。
四.计算题
29.(2022 高淳区)直接写出得数。
57+68= 72﹣0.2= 36×25%= 10.1÷5=
4: 0.52=
30.(2023 浦口区)解比例或解方程。
31.(2023 浦口区)怎样简便就怎样算。
2.5×1.25×16
五.操作题
32.(2021 建邺区)在下面的图中画一个周长是28厘米的长方形,要求长和宽的比是4:3。先列式计算再画图。每个小正方形边长1厘米。
六.应用题
33.(2023 浦口区)明明的存钱罐里有1角和5角的硬币共19枚,一共是55角。1角和5角的硬币各有多少枚?(用你喜欢的方法解答)
34.(2020 鼓楼区)有一个近似于圆锥形的稻谷堆,底面半径是2米,高是1.5米。如果每立方米稻谷大约重0.5吨,那么这堆稻谷大约重多少吨?(得数保留整数)
35.(2021 建邺区)把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。这个长方体的宽是4厘米,高是20厘米,这个圆柱的体积是多少?
36.(2022 建邺区)在比例尺是的地图上,量得A、B两地的距离是6厘米。那么A、B两地的实际距离是多少?如果在一幅比例尺是1:5000000的地图上,A、B两地的图上距离是多少厘米?
37.(2022 建邺区)某公司委托快递公司托运360箱玻璃制品,合同规定每箱运费20元,若损坏一箱,不仅不需要给运费,快递公司还要赔偿损失120元。货物到达目的地后,快递公司获得6780元运费。损坏了多少箱?
38.(2020 鼓楼区)下面是王老师的一张储蓄存单,根据相关信息算一算,王老师存款到期时连本带息一共得到了多少元?
参考答案及试题解析
一.选择题
1.(2023 雨花台区)奇奇想要了解5月份家庭支出中各类支出的分布情况,可以制作成( )
A.条形统计图 B.折线统计图
C.扇形统计图 D.无法确定
【考点】统计图的选择.
【答案】C
【思路分析】条形统计图能很容易看出数量的多少;
折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;
扇形统计图能反映部分与整体的关系,由此根据情况选择即可。
【解答】解:奇奇想要了解5月份家庭支出中各类支出的分布情况,可以制作成扇形统计图。
故选:C。
【名师点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
2.(2023 扬州)下列各选项中的两种量,成反比例关系的是( )
A.正方形的周长和边长
B.路程一定,时间和速度
C.圆的半径和它的周长
D.运送一批货物,运走的吨数和剩下的吨数
【考点】辨识成正比例的量与成反比例的量.
【答案】B
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:A.正方形的周长÷边长=4(一定),商一定,所以正方形的周长和边长成正比例;
B.时间×速度=路程(一定),乘积一定,所以时间和速度成反比例;
C.圆的周长÷半径=2π(一定),商一定,所以圆的半径和它的周长成正比例;
D.运走的吨数+剩下的吨数=总吨数(一定),和一定,所以运走的吨数和剩下的吨数不成比例。
故选:B。
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
3.(2023 建邺区)如果a是一个质数,那么2a+1一定是( )
A.奇数 B.偶数 C.质数 D.合数
【考点】用字母表示数;奇数与偶数的初步认识;合数与质数的初步认识.
【答案】A
【思路分析】根据质数除了2以外都是奇数,奇数×2=偶数,2×2=偶数,可知2a是偶数,偶数+1=奇数,据此解答即可。
【解答】解:如果a是一个质数,那么2a+1一定是奇数。
故选:A。
【名师点评】本题考查奇数与偶数的认识以及质数的认识。
4.(2023 浦口区)虚线框中与圆锥体积相等的图形有( )个。(单位:厘米)
A.1 B.2 C.3 D.4
【考点】圆锥的体积;圆柱的体积.
【答案】D
【思路分析】根据圆柱、圆锥、长方体、棱柱的体积计算公式做题即可。
【解答】解:左面圆锥与圆柱的底面积相等,圆锥的高是圆柱高的3倍,所以体积相等;
长方体的体积=底面积×高,所以体积与圆柱相等,也和所给圆锥的体积相等;
根据圆锥的体积公式可知,两个圆锥的底面积和高的乘积相等,所以体积也相等;
三棱柱的体积等于底面积乘高,60×10=50×12=500(立方厘米),所以体积与圆柱和圆锥的体积都相等。
所以虚线框中与圆锥体积相等的图形有4个。
故选:D。
【名师点评】本题主要考查立体图形体积的计算。
5.(2023 江宁区)下面的描述中不符合生活常识的是( )
A.一枚1元硬币厚度约是2毫米
B.小明家餐桌的面积为200平方厘米
C.小红家距离学校约600米,他上班大约步行1100步
【考点】根据情景选择合适的计量单位;长度及长度的常用单位.
【答案】B
【思路分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【解答】解:一枚1元硬币厚度约是2毫米,符合生活常识。
小明家餐桌的面积为200平方分米,原题不符合生活常识。
小红家距离学校约600米,他上班大约步行1100步,符合生活常识。
故选:B。
【名师点评】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
6.(2022 南京)下面图形中的涂色部分,可以用来表示2.35中的“3”的是( )图形。
A. B. C.
【考点】小数的读写、意义及分类.
【答案】B
【思路分析】2.35中的“3”表示0.3,也就是把整个图形平均分成10份,阴影部分表示其中的3份。也表示把整个图形平均分成100份,阴影部分表示其中的30份。符合条件的图是B项。
【解答】解:可以用来表示2.35中的“3”。
故选:B。
【名师点评】此题主要考查了百分数的意义,要熟练掌握。
7.(2022 鼓楼区)小明和小方做种子发芽实验,小明50粒种子的发芽率是80%,小方30粒种子的发芽率是100%,那么他俩80粒种子的发芽率是( )
A.90% B.85% C.87.5% D.95%
【考点】百分数的实际应用.
【答案】C
【思路分析】发芽率是指发芽的种子数占种子总数的百分之几,100%=发芽率;要求他俩80粒种子的发芽率是多少,就要把小明和小方的种子发芽的粒数分别算出来;小明50粒种子的发芽率是80%,那么发芽的粒数为50×80%=40(粒),同理小方30粒种子的发芽粒数为30×100%=30(粒),小明和小方的种子发芽的粒数共40+30=70(粒),根据上述关系式列式解答即可.
【解答】解:50×80%+30×100%,
=40+30,
=70(粒);
100%=87.5%.
答:他俩80粒种子的发芽率是87.5%.
故选:C.
【名师点评】此题属于百分率问题,重点考查学生对“100%=发芽率”这个关系式的理解与运用.
8.(2021 蒲县)下列各图中的正方形面积相等,图( )的阴影面积与另外两图不同。
A. B. C.
【考点】组合图形的面积.
【答案】B
【思路分析】根据所给图形的特点,找到阴影部分的面积与正方形面积的关系,比较即可得出结论。
【解答】解:选项A和选项C的阴影部分的面积都等于正方形面积减去圆的面积;选项B的阴影部分面积等于正方形面积的一半。
所以B的阴影和另外两个的面积不同。
故选:B。
【名师点评】本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后比较,得出结论。
9.(2023 淮安区)能与4:0.3组成比例的是( )
A.0.4:0.3 B.4:3 C.80:6 D.6:8
【考点】比例的意义和基本性质.
【答案】C
【思路分析】将题干中的比以及选项中的比化为最简整数比,然后找出相同的即可。
【解答】解:4:0.3=40:3
0.4:0.3=40:30=4:3
4:3=4:3
80:6=40:3
6:8=6:8=3:4
所以4:0.3=80:6。
故选:C。
【名师点评】本题主要考查了比例的意义,也可以根据比例的基本性质来进行判断。
二.填空题
10.(2021 六合区)将圆等分成若干份,拼成一个近似的长方形,已知长方形的长比宽多6.42cm,圆的面积是 28.26 cm2.
【考点】圆、圆环的面积.
【答案】28.26。
【思路分析】将圆等分成若干份,拼成一个近似的长方形,长方形的宽为圆的半径,长为圆的周长的一半,根据圆的周长公式C=2πr,长方形的长为宽的π倍,根据差倍公式,可以求出圆的半径,再根据圆的面积公式S=πr2,代入求解即可。
【解答】解:长方形的宽为圆的半径,长为圆的周长的一半,
根据圆的周长公式C=2πr,长方形的长为宽的π倍,
圆的半径为:
6.42÷(3.14﹣1)
=6.42÷2.14
=3(cm)
圆的面积为:
3.14×3×3
=9.42×3
=28.26(cm2)
答:圆的面积是28.26cm2。
故答案为:28.26。
【名师点评】本题主要考查了圆的面积,根据差倍公式求出圆的半径是本题解题的关键。
11.(2023 江宁区)将如图的直角三角形分别绕三条边所在的直线旋转一周,得到3个不同的立体图形,其中体积最大是 50.24 立方厘米,最小是 30.144 立方厘米。
【考点】圆锥的体积.
【答案】50.24,30.144。
【思路分析】根据圆锥的体积公式:Vπr2h,把数据代入公式求出它们的体积,然后进行比较即可。
【解答】解:①以4厘米为轴
π×32×4
π×9×4
=12π(立方厘米)
②以3厘米为轴
π×42×3
π×16×3
=16π(立方厘米)
③以5厘米为轴
底面半径:3×4÷2×2÷5
=12÷5
=2.4(厘米)
π×2.42×5
π×5.76×5
=9.6π(立方厘米)
16π>12π>9.6π
16π=50.24(立方厘米)
9.6π=30.144(立方厘米)
答:体积最大是50.24立方厘米,体积最小是30.144立方厘米。
故答案为:50.24,30.144。
【名师点评】此题主要考查圆锥的体积公式的灵活运用,关键是熟记公式。
12.(2022 建邺区)乐乐骑车去新华书店买书,如图是他离开家的距离与时间的统计图。
(1)他在书店买书用去 分钟。
(2)返回时的速度是每小时 千米。
【考点】单式折线统计图;从统计图表中获取信息.
【答案】(1)。(2)。
【思路分析】(1)从图中可以看出,他在书店买书的时间是:从小时到小时,作差即可。
(2)路程=速度×时间,速度=路程÷时间,路程是5千米,时间是2(小时),代入即可。
【解答】解:(1)
(小时)
答:他在书店买书用去小时。
(2)5
=5
(千米)
答:返回时的速度是每小时千米。
故答案为:(1)。(2)。
【名师点评】此题主要考查的是如何观察统计图并且从统计图中获取信息,然后再进行计算、解答即可。
13.(2023 雨花台区)用边长1cm的小正方形拼成长方形(如图)。像这样,用5个小正方形拼成的长方形的周长是 12 厘米,用a个小正方形拼成的长方形的周长是 (2a+2) 厘米。
【考点】数与形结合的规律.
【答案】12,(2a+2)。
【思路分析】单独一个正方形的周长是4厘米,每多一个正方形周长就增加2厘米,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,然后结合规律解答。
【解答】解:2个正方形拼成长方形的周长=4+(2﹣1)×2=6(厘米)
3个正方形拼成长方形的周长=4+(3﹣1)×2=8(厘米)
4个正方形拼成长方形的周长=4+(4﹣1)×2=10(厘米)
5个正方形拼成长方形的周长=4+(5﹣1)×2=12(厘米)
.......
由此得出规律:用a个正方形拼成长方形的周长=4+(a﹣1)×2=(2a+2)厘米
故答案为:12,(2a+2)。
【名师点评】此题属于数与形结合的规律,考查的目的是通过特例分析从而归纳总结出一般结论的能力,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,然后利用规律解决问题。
14.(2023 鼓楼区)制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。你认为( B 和 C )的材料搭配较合适。如果要在水桶的外表面涂上油漆,则油漆的面积有 35 平方分米。(保留整数)
【考点】关于圆柱的应用题.
【答案】B,C;35。
【思路分析】选择B和C的材料可以做成一个无盖的水桶。理由是长方形的长作为圆柱的底面周长,长方形的宽作为圆柱的高。根据圆柱的侧面积公式:S=Ch,圆的面积公式:S=πr2,把数据代入公式解答。
【解答】解:B和C的材料搭配较合适。
(2)3.14×(2÷2)2+3.14×2×5
=3.14×1+31.4
=34.54
≈35(平方分米)
答:油漆的面积有35平方分米。
故答案为:B,C;35。
【名师点评】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆的周长公式、圆柱的侧面积公式、圆的面积公式及应用,关键是熟记公式。
15.(2023 浦口区)某校六年级有三个班,其中六(1)班人数最多,有42人,六(2)班与六(3)班人数的比为20:19。以下还有三条关于六年级人数的信息,其中只有一条是正确的。
①六(1)班人数比六年级总人数的少5人。
②六(1)班人数与另外两个班总人数的比是7:17。
③六(1)班人数占六年级总人数的35%。
(1)以上关于六年级人数的信息中,正确的是 ③ 。(填序号)
(2)根据正确的信息,该校六(3)班有 38 人。
【考点】比的应用.
【答案】(1)③;(2)38。
【思路分析】(1)①六(1)班人数比六年级总人数的少5人,即(42+5)正好是六年级总人数的,则总人数有[(42+5)]人,因为人数是整数,所以计算结果应是整数,但此结果不是整数,即本条信息错误;
②六(1)班与另外两班总人数的比是7:17,则六(1)班占另外两班总人数的,用六(1)班人数除以即是另外两班总人数之和,即42102(人),又因为六(2)班与六(3)班人数的比为20:19。即六(2)班人数占六(2)班与六(3)班人数之和的,因为人数是整数,所以计算结果应是整数,此结果不是整数,即本条信息错误;
③六(1)班人数占六年级总人数的35%,根据一个数的百分之几是多少,求这个数,用除法计算,用六(1)班的人数除以六(1)班人数占六年级总人数的百分数即是六年级的总人数,即42÷35%=120(人),则六(1)班和六(2)班人数之和为:120﹣42=78(人),结合六(2)班与六(3)班人数的比为20:19可知,六(3)班人数占六(2)班与六(3)班人数之和的,因为人数是整数,所以计算结果应是整数,此结果是整数,即本条信息正确;
(2)根据(1)中③的分析直接求解即可。
【解答】解:(1)①六(1)班人数比六年级总人数的少5人,即(42+5)正好是六年级总人数的,则总人数有[(42+5)]人,因为人数是整数,所以计算结果应是整数,但此结果不是整数,即本条信息错误;
②六(1)班与另外两班总人数的比是7:17,则六(1)班占另外两班总人数的,用六(1)班人数除以即是另外两班总人数之和,即42102(人),又因为六(2)班与六(3)班人数的比为20:19。即六(2)班人数占六(2)班与六(3)班人数之和的,因为人数是整数,所以计算结果应是整数,此结果不是整数,即本条信息错误;
③六(1)班人数占六年级总人数的35%,根据一个数的百分之几是多少,求这个数,用除法计算,用六(1)班的人数除以六(1)班人数占六年级总人数的百分数即是六年级的总人数,即42÷35%=120(人),则六(1)班和六(2)班人数之和为:120﹣42=78(人),结合六(2)班与六(3)班人数的比为20:19可知,六(3)班人数占六(2)班与六(3)班人数之和的,因为人数是整数,所以计算结果应是整数,此结果是整数,即本条信息正确;
综上,只有③信息是正确的;
(2)(42÷35%﹣42)
=(120﹣42)
=78
=38(人)
答:该校六(3)班有38人。
故答案为:(1)③;(2)38。
【名师点评】本题考查了比的应用。
16.(2023 潞州区)如图,有两种底面和高都相同的饮料杯,将一瓶600毫升的果汁全部倒完正好装满这三个杯子。一个圆柱形杯子能装 360 毫升果汁,一个圆锥形杯子能装 120 毫升果汁。
【考点】圆锥的体积.
【答案】360,120。
【思路分析】等底等高的圆柱的体积是圆锥体积的3;设圆锥形杯子能装x毫升果汁,则圆柱形杯子能装3x毫升果汁;两个圆锥形杯子能装x+x毫升果汁与一个圆柱形杯子能装3x毫升果汁,一共是600毫升,列方程:x+x+3x=600,解方程,即可求出一个圆锥形杯子能装果汁多少毫升,一个圆柱形杯子能装多少毫升果汁。
【解答】解:设一个圆锥形杯子能装x毫升果汁,则一个圆柱形杯子能装3x毫升果汁。
x+x+3x=600
2x+3x=600
5x=600
x=120
圆柱形杯子:120×3=360(毫升)
答:一个圆柱形杯子能装360毫升果汁,一个圆锥形杯子能装120毫升果汁。
故答案为:360,120。
【名师点评】利用等底等高的圆柱体积与圆锥体积之间的关系,设出未知数,找出相关的量,列方程,解方程。
17.(2024 江宁区)如图,明明准备了一些边长为4厘米的正方形纸片,按如下方式摆放,每个重叠部分是边长为2厘米的小正方形,像这样摆下去,当明明用了五张正方形纸片重叠时,摆成的图形面积是 64 平方厘米,当明明用n张纸片时,摆成的图形面积是 (12n+4) 平方厘米。
【考点】数与形结合的规律.
【答案】64;(12n+4)。
【思路分析】用2张纸片时,摆成图形的面积是2个大正方形的面积和﹣1个小正方形的面积;
用3张纸片时,摆成图形的面积是3个大正方形的面积和﹣2个小正方形的面积;
用4张纸片时,摆成图形的面积是4个大正方形的面积和﹣3个小正方形的面积;
用5张纸片时,摆成图形的面积是5个大正方形的面积和﹣4个小正方形的面积;
用n张纸片时,摆成图形的面积是n个正方形的面积和﹣(n﹣1)个小正方形的面积据此解答即可。
【解答】解:4×4=16(平方厘米)
2×2=4(平方厘米)
16×5﹣4×4
=80﹣16
=64(平方厘米)
16n﹣4(n﹣1)
=16n﹣4n+4
=(12n+4)(平方厘米)
答:当明明用了五张正方形纸片重叠时,摆成的图形面积是64平方厘米,当明明用n张纸片时,摆成的图形面积是(12n+4)平方厘米。
故答案为:64;(12n+4)。
【名师点评】本题主要考查数与形集合的规律发现每多1个正方形,面积的变化规律是解本题的关键。
18.(2019 上海)1瓶水倒满7个大杯和6个小杯后,还余30克的水;或倒满9个大杯和4个小杯后,还余10克的水,这瓶水可以倒满 10 个大杯和 3 个小杯后,没有剩余.
【考点】简单的等量代换问题.
【答案】见试题解答内容
【思路分析】把第二次倒的方法乘3,也就是说看成3瓶水,3瓶可以倒27个大杯和12个小杯还剩30克,减去第一次倒的后可得:2瓶水可以倒20个大杯和6个小杯,所以1瓶可以倒10个大杯和3个小杯.
【解答】解:倒满9个大杯和4个小杯后,还余10克的水,
所以当为3瓶水时,可以倒27个大杯和12个小杯还剩30克,
减去第一次倒的后可得:2瓶水可以倒20个大杯和6个小杯,
所以1瓶可以倒10个大杯和3个小杯.
故答案为:10,3.
【名师点评】此题的关键是根据第二次倒完后剩的10克,乘3,也就是看成是3瓶,然后和第一倒的进行整体相减,从而求解.
19.(2022 鼓楼区)笑笑从家里去书店买书,在半路上想起忘记带钱了,赶紧回家取了钱再去书店,选好书付钱后回家。下面的图 ② 反映出了笑笑的这些情况。
【考点】单式折线统计图.
【答案】②
【思路分析】图中横轴表示时间,纵轴表示路程,找准出发点,折线水平的部分表示在书店停留的时间,由此判断符合题意的图形即可。
【解答】解:首先排除选项①,因为图①中没有表示停留,是错误的。
再排除选项③,因为图③表示走到半路有停留的时间且没有表示返回家取钱,是错误的。
只有选项②比较准确的反映了笑笑的这些情况。
故答案为:②。
【名师点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
20.(2023 南京)“转化”思想是重要的数学思想方法之一。
(1)在学习圆柱体时,我们就是将圆柱体的体积转化成长方体的体积。请你根据圆柱体积的推导过程,完成下面填空。
当圆柱底面半径为r时,圆柱的底面积是 πr2 ,已知圆柱体的高为h,根据长方体的体积=底面积×高,所以圆柱体的体积公式的字母式是 V=πr2h 。
(2)“转化”思想在我们的日常生活中无处不在,你能用“转化”的方法,算出1个土豆的体积吗?
①准备:1个圆柱形容器并注入一定量的水,测量出水面的高度;
②操作: 把一个土豆放入有一些水的圆柱容器中(水未溢出),上升部分水的体积就等于这个土豆的体积 ;
③计算:土豆的体积=容器的底面积× 水面上升的高 。
【考点】圆柱的体积.
【答案】(1)πr2,V=πr2h;
(2)②把一个土豆放入有一些水的圆柱容器中(水未溢出),上升部分水的体积就等于这个土豆的体积;
③水面上升的高。
【思路分析】(1)根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体,拼成的长方体的底面积等于圆柱的底面积,拼成的长方体的高等于圆柱的高,根据长方体的体积公式推导出圆柱的体积公式。
(2)根据不规则物体体积的测量方法,把一个土豆放入有一些水的圆柱容器中(水未溢出),上升部分水的体积就等于这个土豆的体积,根据圆柱的体积公式:V=Sh,把数据的公式求出土豆的体积。
【解答】解:(1)在学习圆柱体时,我们就是将圆柱体的体积转化成长方体的体积。请你根据圆柱体积的推导过程,完成下面填空。
当圆柱底面半径为r时,圆柱的底面积是πr2,已知圆柱体的高为h,根据长方体的体积=底面积×高,所以圆柱体的体积公式的字母式是V=πr2h。
(2)“转化”思想在我们的日常生活中无处不在,我能用“转化”的方法,算出1个土豆的体积。
①准备:1个圆柱形容器并注入一定量的水,测量出水面的高度;
②操作:把一个土豆放入有一些水的圆柱容器中(水未溢出),上升部分水的体积就等于这个土豆的体积;
③计算:土豆的体积=容器的底面积×水面上升的高。
故答案为:πr2,V=πr2h;把一个土豆放入有一些水的圆柱容器中(水未溢出),上升部分水的体积就等于这个土豆的体积,水面上升的高。
【名师点评】此题考查的目的是理解掌握“转化”的思想方法在数学中的应用。
21.(2023 浦口区)去年果园里有梨树和桃树共400棵,其中桃树占总数的40%.今年又种一些桃树,梨树棵数不变,这是梨树占总数的48%,现在这两种果树一共有 500 棵.
【考点】分数和百分数应用题(多重条件).
【答案】见试题解答内容
【思路分析】去年果园里有梨树和桃树共400棵,其中桃树占总数的40%,则梨树占1﹣40%,所以梨树有400×(1﹣40%)棵,又今年又种一些桃树,梨树棵数不变,这是梨树占总数的48%,根据分数除法的意义,这时共有果树400×(1﹣40%)÷48%棵.
【解答】解:400×(1﹣40%)÷48%
=400×60%÷48%
=500(棵)
答:现在这两种果树一共有 500棵.
故答案为:500.
【名师点评】明确这一过程中梨树的棵数没有变,首先求出梨树的棵数是完成本题的关键.
22.(2020 鼓楼区)将一根体积是48立方分米的圆柱形木料,削成与它等底等高的圆锥形,需要削去 32 立方分米的木料。
【考点】圆柱的侧面积、表面积和体积.
【答案】32。
【思路分析】把一个圆柱体削成一个和它等底等高的圆锥,那么圆锥的体积就是圆柱体积的,求得圆锥体积,就可以求出削去的体积。
【解答】解:48﹣48
=48﹣16
=32(立方分米)
答:需要削去32立方分米的木料。
故答案为:32。
【名师点评】此题主要考查等底等高的圆柱与圆锥的关系:圆锥的体积等于与它等底等高圆柱体积的。
三.判断题
23.(2023 吴江区)解比例的依据是比的基本性质. × .
【考点】解比例.
【答案】见试题解答内容
【思路分析】根据比例的含义和解比例的方法,可得:解比例的依据是比例的基本性质,据此判断即可.
【解答】解:因为解比例的依据是比例的基本性质,不是比的基本性质,
所以题中说法不正确.
故答案为:×.
【名师点评】此题主要考查了解比例问题,要熟练掌握,注意比例的基本性质的应用.
24.(2023 鼓楼区)一种盐水的含盐率是10%,盐与水的比是1:9. √ .
【考点】比的应用.
【答案】见试题解答内容
【思路分析】根据“盐水的含盐率是10%,”把盐看做10份,盐水是100份,则水是(100﹣10)份,盐和盐水的比即可求出.
【解答】解:10:(100﹣10)
=10:90
=1:9;
答:盐与水的比是1:9;
故答案为:√.
【名师点评】解答此题的关键是把百分数转化成份数,根据要求的结果,找到对应份数,再根据比的基本性质,化成最简整数比即可.
25.(2023 曲周县)两个圆柱的侧面积相等,它们的底面周长也一定相等. × .
【考点】圆柱的侧面积、表面积和体积.
【答案】×
【思路分析】根据圆柱的侧面积计算公式“S=Ch”可知,圆柱的侧面积是由圆柱的底面周长和高决定的,因此,两个圆柱的侧面积相等,它们的底面周长不一定相等.
【解答】解:圆柱的侧面积是由圆柱的底面周长和高决定的,所以,两个圆柱的侧面积相等,它们的底面周长不一定相等.
因此,两个圆柱的侧面积相等,它们的底面周长也一定相等是错误的.
故答案为:×.
【名师点评】解答此题的关键是明白圆柱侧面积的意义,圆柱的侧面积是圆柱的底面周长和高的乘积,因此,圆柱侧面积相等,底面周长、高不一定相等.
26.(2023 鼓楼区)一个圆锥的底面半径扩大3倍,高也扩大3倍,那么它的体积就扩大9倍。 ×
【考点】圆锥的体积.
【答案】×
【思路分析】根据圆锥的体积V πr2h,半径扩大3倍,底面积扩大3×3=9倍,高也扩大3倍,则体积扩大9×3=27倍,据此判断。
【解答】解:由分析可知,一个圆锥的底面半径扩大3倍,高也扩大3倍,那么它的体积就扩大27倍。
所以题干说法错误。
故答案为:×。
【名师点评】此题考查了圆锥体积的计算方法,结合积的变化规律解答即可。
27.(2023 鼓楼区)总路程一定,已行的路程和剩下的路程成反比例. × .
【考点】辨识成正比例的量与成反比例的量.
【答案】×
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为已走的路程+剩下的路程=总路程(一定),是和一定,
所以已走的路程和剩下的路程不成反比例;
故答案为:×.
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
28.(2023 鼓楼区)小红在小明的北偏东30°方向,那么小明在小红的南偏西30°方向。 √
【考点】用角度表示方向.
【答案】√
【思路分析】根据位置的相对性可知,描述两个物体之间的相对位置时,方向相反,角度相等,或者先以小明为中心点,找到小红的位置后,再以小红为中心点找小明的位置,从而确定方向,据此解答。
【解答】解:通过分析可知,小红家在小明的北偏东30°方向,那么小明在小红的南偏西30°方向。画图如下:
原题说法正确。
故答案为:√。
【名师点评】本题考查了方向的认识,结合方向的相对性解答即可。
四.计算题
29.(2022 高淳区)直接写出得数。
57+68= 72﹣0.2= 36×25%= 10.1÷5=
4: 0.52=
【考点】整数、分数、小数、百分数四则混合运算;求比值和化简比;乘方;分数的加法和减法;分数乘法.
【答案】125,71.8,9,2.02,14,,0.25,。
【思路分析】根据整数、分数、小数以及百分数加减乘除法以及四则混合运算的顺序,直接进行口算即可。
【解答】解:
57+68=125 72﹣0.2=71.8 36×25%=9 10.1÷5=2.02
4:14 0.52=0.25
【名师点评】本题考查了基本的运算,注意运算数据和运算符号,细心计算即可。
30.(2023 浦口区)解比例或解方程。
【考点】解比例;百分数方程求解.
【答案】x=1.92;x;x。
【思路分析】化简比例方程后,在等式的两边同时除以3即可求解;
在等式的两边同时减去后再在等式两边同时乘即可求解;
根据比例的基本性质化简比例后,在方程两边同时乘即可求解。
【解答】解:3:1.8
3x=3.2×1.8
3x=5.76
3x÷3=5.76÷3
x=1.92
x1.25
x1.25
x=1
x1
x
75%:x:
x75%
x
x
x
【名师点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去,同时乘或同时除以一个数(0除外),两边仍相等。
31.(2023 浦口区)怎样简便就怎样算。
2.5×1.25×16
【考点】运算定律与简便运算;分数的四则混合运算.
【答案】50;42.5;8;。
【思路分析】把16看成4×4,再按照乘法交换律和结合律计算;
按照乘法分配律计算;
按照加法交换律和结合律计算;
先算小括号里面的减法,再算除法。
【解答】解:2.5×1.25×16
=(2.5×4)×(1.25×4)
=10×5
=50
=4.25×(9)
=4.25×10
=42.5
=(72)﹣()
=10﹣2
=8
【名师点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
五.操作题
32.(2021 建邺区)在下面的图中画一个周长是28厘米的长方形,要求长和宽的比是4:3。先列式计算再画图。每个小正方形边长1厘米。
【考点】画指定周长的长方形、正方形.
【答案】
【思路分析】先求出一组长和宽的和,利用周长除以2,然后把长和宽的和按照4:3进行比例分配求出长是多少,宽是多少,据此画图即可。
【解答】解:28÷2=14(厘米)
14÷(4+3)
=14÷7
=2(厘米)
长:4×2=8(厘米)
宽:3×2=6(厘米)
如图所示:
【名师点评】解决本题先根据周长分别求出长方形的长和宽。
六.应用题
33.(2023 浦口区)明明的存钱罐里有1角和5角的硬币共19枚,一共是55角。1角和5角的硬币各有多少枚?(用你喜欢的方法解答)
【考点】鸡兔同笼.
【答案】1角的硬币有10枚,5角的硬币有9枚。
【思路分析】设5角的硬币有x枚,1角的硬币有(19﹣x)枚,然后分别表示出1角和5角的各有多少钱加在一起就是55角,求出5角的数量,进一步求出1角钱的数量。
【解答】解:设5角的硬币有x枚,1角的硬币有(19﹣x)枚。
5x+1×(19﹣x)=55
5x+19﹣x=55
4x=36
x=9
19﹣9=10(枚)
答:1角的硬币有10枚,5角的硬币有9枚。
【名师点评】此题属于鸡兔同笼问题,解这类题可以用假设法进行分析,进而得出结论;也可以用方程进行解答。
34.(2020 鼓楼区)有一个近似于圆锥形的稻谷堆,底面半径是2米,高是1.5米。如果每立方米稻谷大约重0.5吨,那么这堆稻谷大约重多少吨?(得数保留整数)
【考点】关于圆锥的应用题.
【答案】3吨。
【思路分析】要求这堆稻谷的重量,先求得这堆稻谷的体积,这堆稻谷的形状是圆锥形的,利用圆锥的体积计算公式(VSh)先求得体积,进一步再求这堆稻谷的重量,问题得解。
【解答】解:3.14×2 ×1.5×0.5
3.14×4×1.5×0.5
3.14×6×0.5
=2×3.14×0.5
=3.14(吨)
≈3(吨)
答:这堆稻谷大约重3吨。
【名师点评】此题主要考查圆锥的体积计算公式:Vπr2h,运用公式计算时不要漏乘。
35.(2021 建邺区)把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。这个长方体的宽是4厘米,高是20厘米,这个圆柱的体积是多少?
【考点】圆柱的侧面积、表面积和体积.
【答案】1004.8立方厘米。
【思路分析】根据圆柱体积公式的推导过程可知,把一个圆柱底面平均分成若干个扇形,沿高切开拼成一个近似长方体。这个长方体的宽等于圆柱的底面半径,这个长方体的高等于圆柱的高。根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:3.14×42×20
=3.14×16×20
=50.24×20
=1004.8(立方厘米)
答:这个圆柱的体积是1004.8立方厘米。
【名师点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用。
36.(2022 建邺区)在比例尺是的地图上,量得A、B两地的距离是6厘米。那么A、B两地的实际距离是多少?如果在一幅比例尺是1:5000000的地图上,A、B两地的图上距离是多少厘米?
【考点】图上距离与实际距离的换算(比例尺的应用).
【答案】18000000厘米;3.6厘米。
【思路分析】先根据“图上距离÷比例尺=实际距离”,求出A、B两地的实际距离,然后根据:实际距离×比例尺=图上距离,求出A、B两地在另一幅地图上的图上距离即可。
【解答】解:618000000(厘米)
答:A、B两地的实际距离是18000000厘米。
180000003.6(厘米)
答:在一幅比例尺是1:5000000的地图上,A、B两地的图上距离是3.6厘米。
【名师点评】根据图上距离、比例尺和实际距离三者的关系,进行分析解答即可得出结论。
37.(2022 建邺区)某公司委托快递公司托运360箱玻璃制品,合同规定每箱运费20元,若损坏一箱,不仅不需要给运费,快递公司还要赔偿损失120元。货物到达目的地后,快递公司获得6780元运费。损坏了多少箱?
【考点】鸡兔同笼.
【答案】3箱。
【思路分析】假设运输时没有损坏,则应得到的运费是360×20=7200元,这与实际得到的运费就差了7200﹣6780=420(元),这是因为损坏一箱,不仅得不到运费20元,还要赔偿120元,即损坏一箱就要少得120+20=140元.据此可求出损坏的箱数。
【解答】解:(20×360﹣6780)÷(120+20)
=420÷140
=3(箱)
答:损坏了3箱。
【名师点评】本题的关键是让学生理解损坏一箱少得120+20=140(元),再根据假设没有损坏与实际得到钱数的差,列式求出损坏的箱数。
38.(2020 鼓楼区)下面是王老师的一张储蓄存单,根据相关信息算一算,王老师存款到期时连本带息一共得到了多少元?
【考点】存款利息与纳税相关问题.
【答案】10825元。
【思路分析】根据利息=本金×年利率×存期,本息=本金+利息,代入数据,即可得解。
【解答】解:10000+10000×2.75%×3
=10000+825
=10825(元)
答:王老师存款到期时连本带息一共得到了10825元。
【名师点评】这种类型属于利息问题,有固定的计算方法,利息=本金×利率×存期,本息=本金+利息,找清数据与问题,代入公式计算即可。
21世纪教育网(www.21cnjy.com)
同课章节目录
