(小升初择校分班考)小升初重点校择校分班考培优卷-2025年秋六年级数学青岛版(六三学制)(含答案解析)
文档属性
| 名称 | (小升初择校分班考)小升初重点校择校分班考培优卷-2025年秋六年级数学青岛版(六三学制)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 196.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 21:06:26 | ||
图片预览



文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初重点校择校分班考培优卷青岛版(六三学制)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.某车间生产圆形铁片和长方形铁片,两个圆形铁片和一个长方形铁片可以制作成一个油桶(如图),已知该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或长方形铁片80片,为使生产的铁片恰好配套,设安排x人生产圆形铁片,可列方程为( )
A.80x=2×120(42﹣x) B.2×80x=120(42﹣x)
C.120x=2×80(42﹣x) D.2×120x=80(42﹣x)
2.如图,将一些小圆点按如图规律摆放,前4个图形中分别有小圆点6个,10个,16个,24个,依此规律,第20个图形中,小圆点有____个。( )
A.462 B.384 C.420 D.424
3.小明玩游戏:一张纸片,第一次将其撕成四小片,以后每次都将其中一片撕成更小的四片,如此进行下去,当小明撕了n次后,共有2023张纸片,则n的值是( )
A.505 B.506 C.674 D.675
4.下面图形中,( )可以折成正方体。
A. B. C. D.
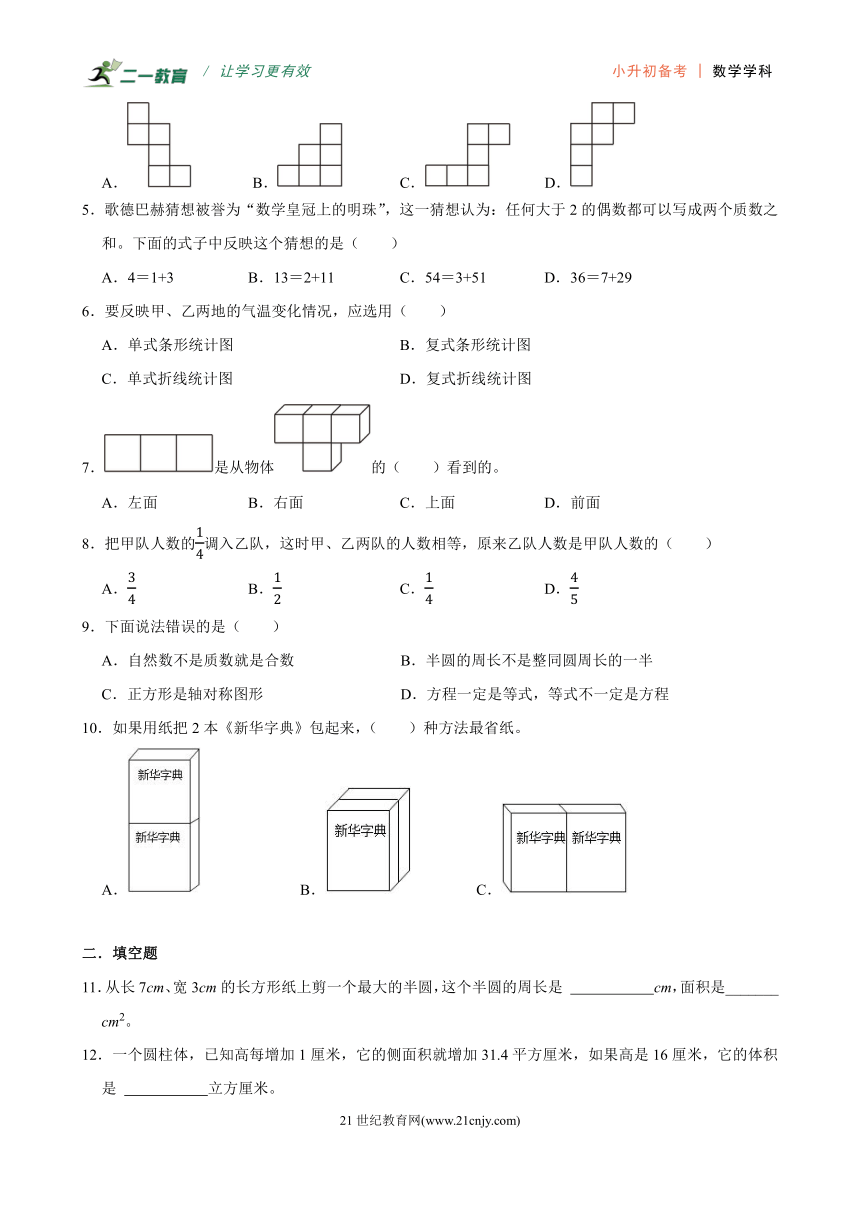
5.歌德巴赫猜想被誉为“数学皇冠上的明珠”,这一猜想认为:任何大于2的偶数都可以写成两个质数之和。下面的式子中反映这个猜想的是( )
A.4=1+3 B.13=2+11 C.54=3+51 D.36=7+29
6.要反映甲、乙两地的气温变化情况,应选用( )
A.单式条形统计图 B.复式条形统计图
C.单式折线统计图 D.复式折线统计图
7.是从物体的( )看到的。
A.左面 B.右面 C.上面 D.前面
8.把甲队人数的调入乙队,这时甲、乙两队的人数相等,原来乙队人数是甲队人数的( )
A. B. C. D.
9.下面说法错误的是( )
A.自然数不是质数就是合数 B.半圆的周长不是整同圆周长的一半
C.正方形是轴对称图形 D.方程一定是等式,等式不一定是方程
10.如果用纸把2本《新华字典》包起来,( )种方法最省纸。
A. B. C.
二.填空题
11.从长7cm、宽3cm的长方形纸上剪一个最大的半圆,这个半圆的周长是 cm,面积是_______ cm2。
12.一个圆柱体,已知高每增加1厘米,它的侧面积就增加31.4平方厘米,如果高是16厘米,它的体积是 立方厘米。
13.一个圆柱体的体积是42立方分米,底面积是6平方分米,它的高是 分米;和这个圆柱体等底等高的圆锥体的体积是 立方分米。
14.南极洲素有“寒极”之称,它的总贮冰量为29300000000立方米,约占全球总量的90%。横线上的数读作 ,把这个数改写为以“亿”为单位的数是 。
15.的分数单位是 ,至少再添上 个这样的分数单位就是最小的合数.
16.中国自古以来就使用十进制计数法,我看时代的数学家刘徽第一个将“小数”的概念用文字表达出来,请解决关于小数的问题:一个三位小数,“四舍五入”的近似数是6.80,这个三位小数最大是 ,最小是 。
17.把如图的比例尺换算成数值比例尺为 。北京到天津的实际距离120千米,画在比例尺是1:3000000的地图上,应画 厘米。
18.班级内的座位,小兰坐在(4,5)的位置上,小红坐在(4,3)的位置,小亮与她俩坐在同一条直线上,小亮可能坐在 的位置上。
19.如图,将一个底面直径为6厘米的圆柱滑底面半径切成若干等份,拼成一个长方体,表面积比原来增加了30平方厘米,原来圆柱的体积是 立方厘米,表面积是 平方厘米。
20.一位同学收集图片,收集的名山图片占40%,河流图片占20%。河流图片收集了80张,名山图片收集了 张。
21.在横线里填上“>”“<”或“=”。
升 50毫升 0.1
22.某小区在平地上挖一个圆柱形水池,水池深2米,底面直径6米,这个水池占地面积 平方米,在它的底面和四周涂上水泥,涂水泥的面积是 平方米。
三.判断题
23.如果2a=5b,那么a:b=2:5。
24.把一个圆柱体削成一个最大的圆锥体,削去部分的体积是圆柱体积的. .
25.每个平行四边形都能分成两个完全一样的三角形.
26.一件商品打六折,就是现价比原价便宜了40%。
27.走完同一段路程,甲用10分钟,乙用11分钟,甲和乙的速度比是10:11.
28.一个角的两条边越长,这个角就越大.
四.计算题
29.求未知数的值(要求写出过程)。
30.脱式计算。(能简算的要简算)
(1)1042﹣384÷16×13 (2)0.8×[(1.9+1.46)÷0.42]
(3)
(5)20.2×83+1.7×202 (6)
五.操作题
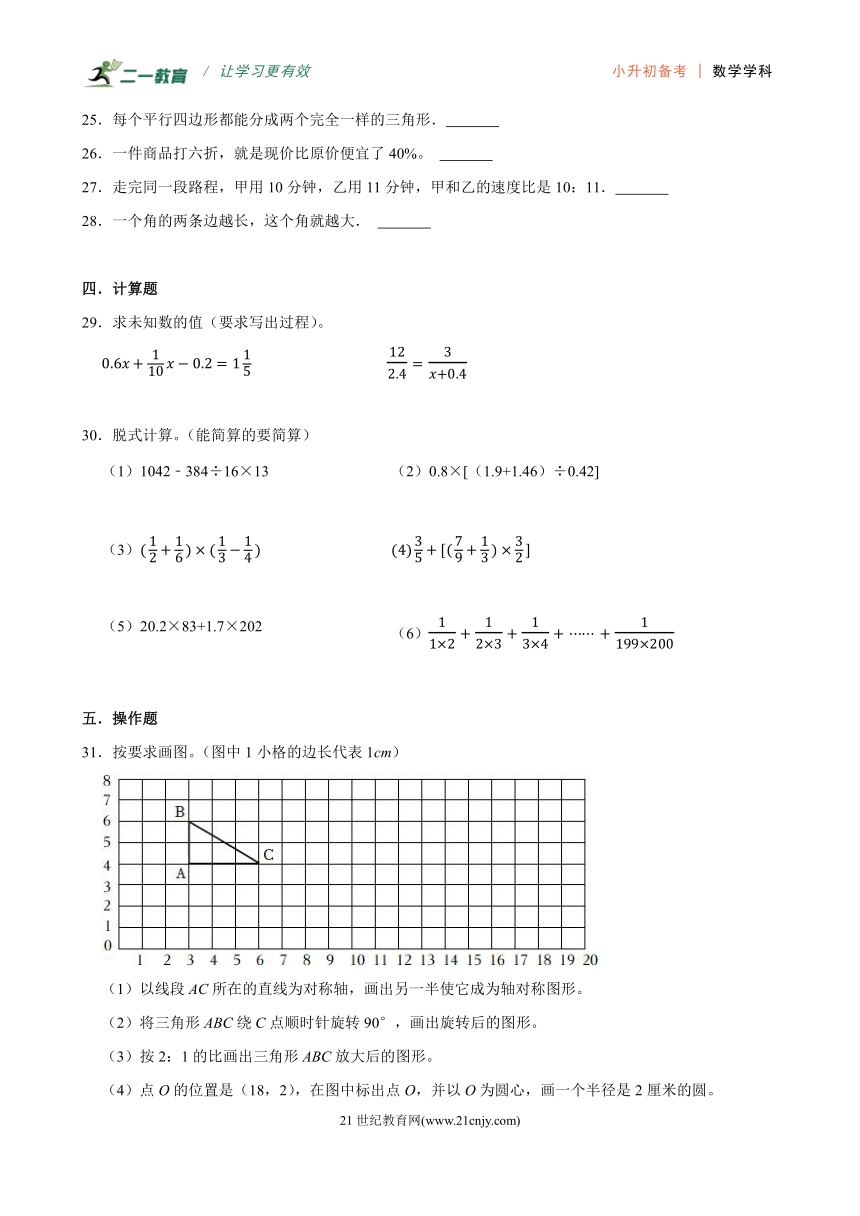
31.按要求画图。(图中1小格的边长代表1cm)
(1)以线段AC所在的直线为对称轴,画出另一半使它成为轴对称图形。
(2)将三角形ABC绕C点顺时针旋转90°,画出旋转后的图形。
(3)按2:1的比画出三角形ABC放大后的图形。
(4)点O的位置是(18,2),在图中标出点O,并以O为圆心,画一个半径是2厘米的圆。
六.应用题
32.学校买来400本故事书,图书室留下,其余的按2:3分给五、六年级,六年级分得多少本?
33.文文学校要整修操场,甲队单独修10天可以完成,乙队单独修5天可以完成,如果两队合修,多少天可以完成?
34.一个圆柱形玻璃容器的底面直径是4分米,高是6分米,向容器中倒入28升水,再把一个石块浸没在水中,这时量得水深25厘米,石块的体积是多少立方分米?
35.如图,是一块在电脑屏幕上出现的长方形色块,由A、B、C、D、E、F六个正方形组成,已知中间最小的正方形A的边长为2,那么这个长方形色块图的面积是多少?
36.如图所示是圆柱形玻璃花瓶的设计图,这个花瓶制作好的实际高度为12分米,图上没有标明比例尺,请你想办法计算出它的实际容积是多少升?(得数保留整数,瓶的厚度忽略不计)
37.“宜万”铁路,东起湖北省的宜昌,西至重庆市的万州,是我国铁路史上修建难度最大、公里造价最高、历时最长的山区铁路。铁路全场约380千米,其中桥梁和隧道相当于铁路全长的75%,平均每千米耗资约6000万元,比“天梯”青藏铁路还多。
(1)这段铁路中,桥梁和隧道一共长多少千米?
(2)青藏铁路平均每千米耗资多少万元?(用方程解答)
参考答案及试题解析
一.选择题
1.【考点】列方程解应用题(两步需要逆思考).
【答案】C
【思路分析】设安排x人生产圆形铁片,则共生产圆形铁片120x个,共生产长方形铁片80(42﹣x)个,根据等量关系:圆形的数量=长方形的数量×2,列出方程并解答即可。
【解答】解:设安排x人生产圆形铁片。
120x=2×80(42﹣x)
120x÷40=2×80×(42﹣x)÷40
3x=4×(42﹣x)
3x=168﹣4x
7x=168
x=24
42﹣24=18(人)
答:安排24人生产圆形铁片,18人生产长方形铁片。
故选:C。
【名师点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系列方程解答。
2.【考点】数与形结合的规律.
【答案】D
【思路分析】依据题意可知,第1个图中由小圆点(1×2+4)个,第2个图中由小圆点(2×3+4)个,第3个图中由小圆点(3×4+4)个,第4个图中由小圆点(4×5+4)个,第n个图中由小圆点[n×(n+1)+4]个,由此解答本题。
【解答】解:由分析可知,第20个图形中,小圆点有:20×21+4
=420+4
=424(个)
故选:D。
【名师点评】解决本题的关键是找出题中的规律,利用规律去解答。
3.【考点】数与形结合的规律.
【答案】C
【思路分析】依据题意结合图示可知,小明每撕一次,比上次多增加3张小纸片,因此撕了n次后,手中共有(3n+1)张纸片,由此解答本题。
【解答】解:由分析可知:3n+1=2023,则n=674。
故选:C。
【名师点评】解决本题的关键是找出题中的规律,利用规律去解答。
4.【考点】正方体的展开图.
【答案】A
【思路分析】根据正方体展开图的11种特征,即可确定哪个图形属于正方体展开图,能折叠成正方体,哪个图形不属于正方体展开图,不能折叠成正方体。
【解答】解:A、属于正方体展开图的“1﹣3﹣2”型,能折叠成正方体;
B、不属于正方体展开图,不能折成正方体;
C、不属于正方体展开图,不能折成正方体
D、不属于正方体展开图,不能折成正方体。
故选:A。
【名师点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
5.【考点】合数与质数的初步认识;奇数与偶数的初步认识.
【答案】D
【思路分析】根据任何大于2的偶数都可以写成两个质数之和,结合选项分析解答即可。
【解答】解:4=1+3中,1不是质数,所以不符合题意;
13=2+11中,13不是大于2的偶数,2和11是质数,所以不符合题意;
54=3+51中,51不是质数,所以不符合题意;
36=7+29,36是大于2的偶数,7和29是质数,所以符合题意。
故选:D。
【名师点评】本题考查了质数和合数、偶数和奇数的认识知识,结合题意分析解答即可。
6.【考点】统计图的选择.
【答案】D
【思路分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解答】解:根据统计图的特点可知:要反映甲、乙两地的气温变化情况,应选用复式折线统计图比较合适。
故选:D。
【名师点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
7.【考点】从不同方向观察物体和几何体.
【答案】C
【思路分析】根据观察物体的方法可知,从上面看是一行3个小正方形,据此解答即可。
【解答】解:分析可知,是从物体的上面看到的。
故选:C。
【名师点评】本题考查了从不同方向观察物体和几何图形,培养了学生的观察能力。
8.【考点】分数除法应用题.
【答案】B
【思路分析】把原来甲队人数看作单位“1”,则原来乙队人数相当于甲队人数的(12);再用原来乙队人数除以甲队人数。
【解答】解:(12)÷1
=(1)÷1
1
答:原来乙队人数是甲队人数的。
故选:B。
【名师点评】求一个数是另一个数的几分之几,用这个数除以另一个数。关键是把甲队原来的人数看作单位“1”,弄清乙队原来的人数。
9.【考点】合数与质数的初步认识;方程与等式的关系;圆、圆环的周长;轴对称图形的辨识.
【答案】A
【思路分析】A.自然数除了质数和合数还有0。
B.半圆的周长是整同圆周长的一半加半径。
C.正方形有4条对称轴,是轴对称图形。
D.等式是表示两个数或两个代数式相等关系的式子,方程是含有未知数的等式,所以方程一定是等式,等式不一定是方程。
【解答】解:自然数除了质数和合数还有0。
故选:A。
【名师点评】此题考查了自然数、半圆的周长、轴对称图形和方程以及等式的概念判断。
10.【考点】长方体和正方体的表面积.
【答案】B
【思路分析】根据题意可知,把2本《新华字典》包起来,最节省包装纸的方法是把2本《新华字典》的最大面重合进行包装。据此解答即可。
【解答】解:把2本《新华字典》包起来,最节省包装纸的方法是把2本《新华字典》的最大面重合进行包装。
故选:B。
【名师点评】此题考查的目的是理解掌握长方体的拼组方法及应用,长方体表面积的意义及应用。
二.填空题
11.【考点】圆、圆环的周长;圆、圆环的面积.
【答案】7.71,3.5325。
【思路分析】根据题意可知,从这个长方形硬纸上剪一个最大的半圆,这个半圆的直径等于长方形的长,因为宽小于长的一半,所以这个半圆的直径只能是3。根据半圆的周长公式:C=πd÷2+d,半圆的面积公式:S=πr2÷2,把数据代入公式解答。
【解答】解:3.14×3÷2+3
=4.71+3
=7.71(厘米)
3.14×(3÷2)2÷2
=3.14×2.25÷2
=7.065÷2
=3.5325(平方厘米)
答:这个半圆的周长是7.71厘米,面积是3.5325平方厘米。
故答案为:7.71,3.5325。
【名师点评】此题主要考查半圆的周长公式、面积公式的灵活运用,关键是熟记公式。
12.【考点】圆柱的侧面积、表面积和体积.
【答案】1256。
【思路分析】根据题意可知,圆柱的高增加1厘米,它的侧面积就增加31.4平方厘米,根据圆柱的侧面积公式:S=2πrh,据此可以求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式求出解答。
【解答】解:31.4÷1÷3.14÷2
=10÷2
=5(厘米)
3.14×52×16
=3.14×25×16
=78.5×16
=1256(立方厘米)
答:它的体积是1256立方厘米。
故答案为:1256。
【名师点评】此题主要考查圆柱的侧面积公式、圆的周长公式、圆柱的体积公式的灵活运用,关键是熟记公式。
13.【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【答案】7,14。
【思路分析】根据圆柱的体积公式:V=Sh,那么h=V÷S,把数据代入公式求出圆柱的高,等底等高的圆锥体的体积是圆柱体积的,据此解答即可。
【解答】解:42÷6=7(分米)
4214(立方分米)
答:圆柱的高是7分米,和这个圆柱体等底等高的圆锥体的体积是14立方分米。
故答案为:7,14。
【名师点评】此题主要考查圆柱体积公式的灵活运用,等底等高的圆柱与圆锥体积之间的关系及应用。
14.【考点】亿以上数的读写;亿以上数的改写与近似.
【答案】二百九十三亿,293亿。
【思路分析】读数时,把数先分级,从高位读起,亿级或万级的数按照万以内的数的读法去读,再在每级的末尾加一个“亿”或“万”字,每级末尾的0都不读,每一级的开头或中间无论有几个0,都读一个0;数的改写就是直接在原数的亿位后面点上小数点,同时要在改写的小数后面写上“亿”字,数的大小不变。
【解答】解:29300000000读作:二百九十三亿
29300000000改写为以“亿”为单位的数是293亿。
南极洲素有“寒极”之称,它的总贮冰量为29300000000立方米,约占全球总量的90%。横线上的数读作二百九十三亿,把这个数改写为以“亿”为单位的数是293亿。
故答案为:二百九十三亿,293亿。
【名师点评】此题考查了亿以内数的读法和数的改写,要求学生掌握此知识点。
15.【考点】分数的意义和读写;合数与质数的初步认识.
【答案】见试题解答内容
【思路分析】(1)判定一个分数的单位看分母,分母是几,分数单位就是几分之一;
(2)最小的合数是4,用4减去原分数的结果,再看有几个分数单位即可解答.
【解答】解:的分母是5,所以分数单位是;
(2)最小的合数是4,
4,
即至少再添上 16个这样的分数单位就是最小的合数;
故答案为:,16.
【名师点评】此题主要考查分数的单位:把单位“1”平均分成几份,表示其中一份的数就是它的分数单位.
16.【考点】小数的近似数及其求法.
【答案】6.804;6.795。
【思路分析】要考虑6.80是一个三位数的近似数,有两种情况:“四舍”得到的6.80最大是6.804,“五入”得到的6.80最小是6.795,由此解答问题即可。
【解答】解:一个三位小数,“四舍五入”的近似数是6.80,这个三位小数最大是6.804,最小是6.795。
故答案为:6.804;6.795。
【名师点评】取一个数的近似数,有两种情况:“四舍”得到的近似数比原数小,“五入”得到的近似数比原数大,根据题的要求灵活掌握解答方法。
17.【考点】图上距离与实际距离的换算(比例尺的应用).
【答案】1:3000,4。
【思路分析】由线段比例尺可知,图上1厘米代表实际距离30米,根据比例尺=图上距离:实际距离解答即可;根据图上距离=实际距离×比例尺,代入数据解答即可。
【解答】解:1厘米:30米
=1厘米:3000厘米
=1:3000
120千米=12000000厘米
120000004(厘米)
答:换算成数值比例尺为1:3000,应画4厘米。
故答案为:1:3000,4。
【名师点评】熟练掌握线段比例尺与数值比例尺的互化以及图上距离、实际距离、比例尺三者间的关系是解题的关键。
18.【考点】数对与位置.
【答案】(4,a)。
【思路分析】根据题干,小兰坐在(4,5)的位置上,小红坐在(4,3)的位置,所以小兰与小红都在第4列,不在同一行,因为小亮与她俩坐在同一直线上,所以小亮只能在第4列,即小亮的数对位置是(4,a),据此即可解答问题。
【解答】解:小兰坐在(4,5)的位置上,小红坐在(4,3)的位置,小亮与她俩坐在同一条直线上,小亮可能坐在(4,a)的位置上。
故答案为:(4,a)。
【名师点评】数对表示位置的方法是:第一个数字表示列,第二个数字表示行,据此即可解答问题。
19.【考点】圆柱的侧面积、表面积和体积.
【答案】141.3,150.72。
【思路分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体,这个长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,拼成的长方体的表面积比圆柱的表面积增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,已知表面积比原来增加了30平方厘米,据此可以求出圆柱的高,然后根据圆柱的体积公式:V=πr2h,圆柱的表面积=侧面积+底面积×2,把数据代入公式解答。
【解答】解:6÷2=3(厘米)
30÷2÷3
=15÷3
=5(厘米)
3.14×32×5
=3.14×9×5
=28.26×5
=141.3(立方厘米)
3.14×6×5+3.14×32×2
=18.84×5+3.14×9×2
=94.2+56.52
=150.72(平方厘米)
答:原来圆柱的体积是141.3立方厘米,表面积是150.72平方厘米。
故答案为:141.3,150.72。
【名师点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及运用,圆柱表面积公式的灵活运用,关键是熟记公式。
20.【考点】百分数的实际应用.
【答案】160。
【思路分析】将收集的图片总张数看作单位“1”,先用80除以20%,求出图片总张数;再乘40%,即可求出收集的名山图片张数。
【解答】解:80÷20%×40%
=400×40%
=160(张)
答:名山图片收集了160张。
故答案为:160。
【名师点评】已知一个数的几分之几是多少,求这个数,用除法计算;求一个数的几分之几是多少,用乘法计算。
21.【考点】分数大小的比较;体积、容积进率及单位换算.
【答案】=;=。
【思路分析】升和毫升之间的进率是1000,据此先统一单位,再比较大小;根据分数与除法的关系,求出1÷6的商,再与循环小0.1比较大小。
【解答】解:因为1000=50,所以升=50毫升;
因为1÷6=0.166……=0.1,所以0.1。
故答案为:=;=。
【名师点评】此题重点考查通过单位的换算比大小和利用分数与除法间的关系计算商再比大小的知识。
22.【考点】长方体和正方体的表面积.
【答案】28.26,65.94。
【思路分析】由题意知,水池占地面积就是圆柱的底面积,涂水泥的面积是内侧面和底面,要求涂水泥的面积,可用侧面积加上底面积,根据圆柱表面积公式列式解答即可。
【解答】解:6÷2=3(米)
32×3.14=28.26(平方米)
6×3.14×2=37.68(平方米)
37.68+28.26=65.94(平方米)
所以水池占地面积28.26平方米,涂水泥的面积是65.94平方米。
故答案为:28.26,65.94。
【名师点评】此题是考查圆柱形水池内表面积的计算,要注意是内侧面积加一个底面的面积。
三.判断题
23.【考点】比例的意义和基本性质.
【答案】×
【思路分析】此题根据比例的基本性质“两内项之积等于两外项之积”即可变形得出a与b是的比。
【解答】解:2a=5b,
根据比例的基本性质可得:a:b=5:2。
故答案为:×。
【名师点评】此题考查了比例的基本性质的应用。
24.【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【答案】见试题解答内容
【思路分析】把一个圆柱削成最大的圆锥,则圆锥与原来圆柱是等底等高的,则圆锥的体积是圆柱的体积,由此即可得出消去部分的体积是圆柱体积的1.
【解答】解:削成的最大圆锥与原来圆柱等底等高,则圆锥的体积是圆柱的体积的,
所以削去部分的体积是原圆柱体积的.
故答案为:√.
【名师点评】此题考查了圆柱内削成的最大圆锥的特点以及等底等高的圆柱与圆锥的体积的倍数关系的灵活应用.
25.【考点】平行四边形的特征及性质.
【答案】√
【思路分析】平行四边形分成两个完全一样的图形,有三种分法,据下图即可正确作答.
【解答】解:将一个平行四边形分成两个完全一样的平面图形,那么这两个完全一样的平面图形可能是平行四边形,也可能是梯形,还可能是三角形;分成的每个图形的面积都是的这个平行四边形面积的一半.
所以一个平行四边形能分成两个完全一样的三角形是正确的.
故答案为:√.
【名师点评】解答此题的关键是,依据题目要求,画出正确的图,即可正确作答.
26.【考点】百分数的实际应用.
【答案】√
【思路分析】打六折,就是现价是原价的60%,所以便宜了:1﹣60%=40%,所以就是比原价便宜了40%,所以题干正确。
【解答】解:1﹣60%=40%
因此一件商品打六折,就是现价比原价便宜了40%,原题说法正确。
故答案为:√。
【名师点评】解答此题的关键是把原价看作单位“1”。
27.【考点】比的意义.
【答案】见试题解答内容
【思路分析】把一段路程的长度看作“1”,根据路程÷时间=速度,分别求出甲乙的速度,再写出相应的比,根据比的基本性质化成最简整数比.
【解答】解:(1÷10):(1÷11)
:
=11:10
甲和乙的速度比是11:10,所以本题说法错误;
故答案为:×.
【名师点评】关键是把路程的长度看作“1”,再根据路程、时间与速度之间的关系求出甲乙的速度,写出相应的比化简即可.
28.【考点】角的概念和表示.
【答案】×
【思路分析】依据角的定义就可填出正确答案.
【解答】解:角的大小和边长无关.
故答案为:×.
【名师点评】此题主要考查角的定义.
四.计算题
29.【考点】分数方程求解.
【答案】x=2;x=0.2。
【思路分析】先化简,然后根据等式的性质,方程两边同时加上0.2,然后再同时除以0.7求解;
根据比例的基本性质,把比例化成普通方程,然后再根据等式的性质,方程两边同时除以12求解。
【解答】解:
0.7x﹣0.2=1.2
0.7x﹣0.2+0.2=1.2+0.2
0.7x=1.4
x=2
12×(x+0.4)=2.4×3
12x+4.8=7.2
12x+4.8﹣4.8=7.2﹣4.8
12x=2.4
x=0.2
【名师点评】本题考查了在解方程时应根据等式的性质,即等式两边同加上、同减去、同乘上或同除以某一个数(0除外),等式的两边仍相等,同时注意“=”上下要对齐。
30.【考点】运算定律与简便运算;小数四则混合运算;分数的四则混合运算.
【答案】(1)730;
(2)6.4;
(3);
(4);
(5)2020;
(6)。
【思路分析】(1)先算除法,再算乘法,最后算减法;
(2)先算小括号里面的加法,再算中括号里面的除法,最后算括号外面的乘法;
(3)先算小括号里面的加法和减法,再算括号外面的乘法;
(4)先算小括号里面的加法,再算中括号里面的乘法,最后算括号外面的加法;
(5)根据乘法分配律进行计算;
(6)根据分数的拆项公式进行计算。
【解答】解:(1)1042﹣384÷16×13
=1042﹣24×13
=1042﹣312
=730
(2)0.8×[(1.9+1.46)÷0.42]
=0.8×[3.36÷0.42]
=0.8×8
=6.4
(3)
(4)[()]
[]
(5)20.2×83+1.7×202
=202×8.3+1.7×202
=202×(8.3+1.7)
=202×10
=2020
(6)
=(1)+()+()+……+()
=1
=1
【名师点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
五.操作题
31.【考点】作轴对称图形;作旋转一定角度后的图形;图形的放大与缩小;数对与位置.
【答案】
【思路分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(AC所在的直线)的右边画出三角形ABC顶点B的对称点,然后连接即可画出另一半使它成为轴对称图形。
(2)根据旋转的特征,三角形ABC绕点C顺时针旋转90°,点C的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据图形放大与缩小的意义,把三角形ABC的各边均放大到原来的2倍,所得到的图形就是原图形按2:1放大后的图形。
(4)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可在方格图描出所点O的位置,然后以O为圆心,以2厘米为半径画圆即可。
【解答】解:根据题意画图如下:
【名师点评】此题考查的知识点:作轴对称图形、作旋转一定度数后的图形、图形的放大与缩小、画圆、数对与位置。
六.应用题
32.【考点】按比例分配应用题.
【答案】216本。
【思路分析】用400乘(1),求出剩下的数量,再把剩下的数量按2:3,进行分配,即可解答。
【解答】解:400×(1)
=400
=360(本)
360
=360
=216(本)
答:六年级分得216本。
【名师点评】本题考查的是按比例分配应用题,掌握按比例分配的方法是解答关键。
33.【考点】简单的工程问题.
【答案】6天。
【思路分析】把工作总量看作单位“1”,则甲队的工作效率是,乙队的工作效率是(),再根据工作时间=工作总量÷工作效率和,即可计算出两队合修多少天可以完成。
【解答】解:
1
=1
=6(天)
答:两队合修6天可以完成。
【名师点评】本题解题的关键是把工作总量看作单位“1”,根据工作时间=工作总量÷工作效率和,列式计算。
34.【考点】探索某些实物体积的测量方法.
【答案】3.4立方分米。
【思路分析】根据题意可知,把石块放入容器中上升部分水的体积就等于这块石块的体积,根据圆柱的体积公式:V=πr2h,把数据代入公式求出水与石块的体积和,然后减去水的体积就是石块的体积。
【解答】解:25厘米=2.5分米
28升=28立方分米
3.14×(4÷2)2×2.5﹣28
=3.14×4×2.5﹣28
=31.4﹣28
=3.4(立方分米)
答:石块的体积是3.4立方分米。
【名师点评】此题考查的目的是理解掌握不规则物体体积的测量方法及应用,圆柱的体积公式及应用,关键是熟记公式。
35.【考点】组合图形的面积.
【答案】572。
【思路分析】如图,
设右下方两个相等的正方形边长为x,则根据题意知,右上方最大的正方形边长为x+6,根据长方形的长=长方形的长,列出方程,求出长方形的长与宽,进一步解答即可。
【解答】解:设右下方两个相等的正方形边长为x,根据图意有:
x+4+x+6=x+x+x+2
2x+10=3x+2
x=8
原长方形的长为:8+8+8+2=26
原长方形的宽为:8+6+8=22
面积为:26×22=572
答:这个长方形色块图的面积是572。
【名师点评】解决此题关键是求出长方形的长和宽,进一步用长乘宽求得面积。
36.【考点】圆柱的体积.
【答案】603。
【思路分析】根据比例尺,求出比例尺,再根据实际距离=图上距离÷比例尺,求出实际半径,然后根据圆柱的容积(体积)公式:V=πr2h,把数据代入公式解答。
【解答】解:6厘米:12分米
=6厘米:120厘米
=1:20
2
=2×20
=40(厘米)
40厘米=4分米
3.14×42×12
=3.14×16×12
=50.24×12
=602.88(立方分米)
602.88立方分米≈603升
答:它的实际容积是603升。
【名师点评】此题主要考查圆柱容积(体积)公式的灵活运用,以及比例尺的意义及应用。
37.【考点】列方程解应用题(两步需要逆思考).
【答案】(1)285;(2)3200
【思路分析】(1)根据题目信息“铁路全场约380千米,其中桥梁和隧道相当于铁路全长的75%”可知,单位“1”是铁路全长已知的,直接用铁路全长×75%就可以求出桥梁和隧道一共多长。
(2)从题目信息“平均每千米耗资约6000万元,比“天梯”青藏铁路还多。”我们知道单位“1”是青藏铁路平均每千米耗资,未知,就设它为x万元,根据它和桥梁和隧道的耗资之间的关系列出方程解答。
【解答】解:(1)380×75%=285(千米)
答:这段铁路中,桥梁和隧道一共长285千米.。
(2)设青藏铁路平均每千米耗资x万元。
(1)x=6000
x=6000
x=3200
答:青藏铁路平均每千米耗资3200万元。
【名师点评】找出题中数量之间的相等关系。
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初重点校择校分班考培优卷青岛版(六三学制)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.某车间生产圆形铁片和长方形铁片,两个圆形铁片和一个长方形铁片可以制作成一个油桶(如图),已知该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或长方形铁片80片,为使生产的铁片恰好配套,设安排x人生产圆形铁片,可列方程为( )
A.80x=2×120(42﹣x) B.2×80x=120(42﹣x)
C.120x=2×80(42﹣x) D.2×120x=80(42﹣x)
2.如图,将一些小圆点按如图规律摆放,前4个图形中分别有小圆点6个,10个,16个,24个,依此规律,第20个图形中,小圆点有____个。( )
A.462 B.384 C.420 D.424
3.小明玩游戏:一张纸片,第一次将其撕成四小片,以后每次都将其中一片撕成更小的四片,如此进行下去,当小明撕了n次后,共有2023张纸片,则n的值是( )
A.505 B.506 C.674 D.675
4.下面图形中,( )可以折成正方体。
A. B. C. D.
5.歌德巴赫猜想被誉为“数学皇冠上的明珠”,这一猜想认为:任何大于2的偶数都可以写成两个质数之和。下面的式子中反映这个猜想的是( )
A.4=1+3 B.13=2+11 C.54=3+51 D.36=7+29
6.要反映甲、乙两地的气温变化情况,应选用( )
A.单式条形统计图 B.复式条形统计图
C.单式折线统计图 D.复式折线统计图
7.是从物体的( )看到的。
A.左面 B.右面 C.上面 D.前面
8.把甲队人数的调入乙队,这时甲、乙两队的人数相等,原来乙队人数是甲队人数的( )
A. B. C. D.
9.下面说法错误的是( )
A.自然数不是质数就是合数 B.半圆的周长不是整同圆周长的一半
C.正方形是轴对称图形 D.方程一定是等式,等式不一定是方程
10.如果用纸把2本《新华字典》包起来,( )种方法最省纸。
A. B. C.
二.填空题
11.从长7cm、宽3cm的长方形纸上剪一个最大的半圆,这个半圆的周长是 cm,面积是_______ cm2。
12.一个圆柱体,已知高每增加1厘米,它的侧面积就增加31.4平方厘米,如果高是16厘米,它的体积是 立方厘米。
13.一个圆柱体的体积是42立方分米,底面积是6平方分米,它的高是 分米;和这个圆柱体等底等高的圆锥体的体积是 立方分米。
14.南极洲素有“寒极”之称,它的总贮冰量为29300000000立方米,约占全球总量的90%。横线上的数读作 ,把这个数改写为以“亿”为单位的数是 。
15.的分数单位是 ,至少再添上 个这样的分数单位就是最小的合数.
16.中国自古以来就使用十进制计数法,我看时代的数学家刘徽第一个将“小数”的概念用文字表达出来,请解决关于小数的问题:一个三位小数,“四舍五入”的近似数是6.80,这个三位小数最大是 ,最小是 。
17.把如图的比例尺换算成数值比例尺为 。北京到天津的实际距离120千米,画在比例尺是1:3000000的地图上,应画 厘米。
18.班级内的座位,小兰坐在(4,5)的位置上,小红坐在(4,3)的位置,小亮与她俩坐在同一条直线上,小亮可能坐在 的位置上。
19.如图,将一个底面直径为6厘米的圆柱滑底面半径切成若干等份,拼成一个长方体,表面积比原来增加了30平方厘米,原来圆柱的体积是 立方厘米,表面积是 平方厘米。
20.一位同学收集图片,收集的名山图片占40%,河流图片占20%。河流图片收集了80张,名山图片收集了 张。
21.在横线里填上“>”“<”或“=”。
升 50毫升 0.1
22.某小区在平地上挖一个圆柱形水池,水池深2米,底面直径6米,这个水池占地面积 平方米,在它的底面和四周涂上水泥,涂水泥的面积是 平方米。
三.判断题
23.如果2a=5b,那么a:b=2:5。
24.把一个圆柱体削成一个最大的圆锥体,削去部分的体积是圆柱体积的. .
25.每个平行四边形都能分成两个完全一样的三角形.
26.一件商品打六折,就是现价比原价便宜了40%。
27.走完同一段路程,甲用10分钟,乙用11分钟,甲和乙的速度比是10:11.
28.一个角的两条边越长,这个角就越大.
四.计算题
29.求未知数的值(要求写出过程)。
30.脱式计算。(能简算的要简算)
(1)1042﹣384÷16×13 (2)0.8×[(1.9+1.46)÷0.42]
(3)
(5)20.2×83+1.7×202 (6)
五.操作题
31.按要求画图。(图中1小格的边长代表1cm)
(1)以线段AC所在的直线为对称轴,画出另一半使它成为轴对称图形。
(2)将三角形ABC绕C点顺时针旋转90°,画出旋转后的图形。
(3)按2:1的比画出三角形ABC放大后的图形。
(4)点O的位置是(18,2),在图中标出点O,并以O为圆心,画一个半径是2厘米的圆。
六.应用题
32.学校买来400本故事书,图书室留下,其余的按2:3分给五、六年级,六年级分得多少本?
33.文文学校要整修操场,甲队单独修10天可以完成,乙队单独修5天可以完成,如果两队合修,多少天可以完成?
34.一个圆柱形玻璃容器的底面直径是4分米,高是6分米,向容器中倒入28升水,再把一个石块浸没在水中,这时量得水深25厘米,石块的体积是多少立方分米?
35.如图,是一块在电脑屏幕上出现的长方形色块,由A、B、C、D、E、F六个正方形组成,已知中间最小的正方形A的边长为2,那么这个长方形色块图的面积是多少?
36.如图所示是圆柱形玻璃花瓶的设计图,这个花瓶制作好的实际高度为12分米,图上没有标明比例尺,请你想办法计算出它的实际容积是多少升?(得数保留整数,瓶的厚度忽略不计)
37.“宜万”铁路,东起湖北省的宜昌,西至重庆市的万州,是我国铁路史上修建难度最大、公里造价最高、历时最长的山区铁路。铁路全场约380千米,其中桥梁和隧道相当于铁路全长的75%,平均每千米耗资约6000万元,比“天梯”青藏铁路还多。
(1)这段铁路中,桥梁和隧道一共长多少千米?
(2)青藏铁路平均每千米耗资多少万元?(用方程解答)
参考答案及试题解析
一.选择题
1.【考点】列方程解应用题(两步需要逆思考).
【答案】C
【思路分析】设安排x人生产圆形铁片,则共生产圆形铁片120x个,共生产长方形铁片80(42﹣x)个,根据等量关系:圆形的数量=长方形的数量×2,列出方程并解答即可。
【解答】解:设安排x人生产圆形铁片。
120x=2×80(42﹣x)
120x÷40=2×80×(42﹣x)÷40
3x=4×(42﹣x)
3x=168﹣4x
7x=168
x=24
42﹣24=18(人)
答:安排24人生产圆形铁片,18人生产长方形铁片。
故选:C。
【名师点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系列方程解答。
2.【考点】数与形结合的规律.
【答案】D
【思路分析】依据题意可知,第1个图中由小圆点(1×2+4)个,第2个图中由小圆点(2×3+4)个,第3个图中由小圆点(3×4+4)个,第4个图中由小圆点(4×5+4)个,第n个图中由小圆点[n×(n+1)+4]个,由此解答本题。
【解答】解:由分析可知,第20个图形中,小圆点有:20×21+4
=420+4
=424(个)
故选:D。
【名师点评】解决本题的关键是找出题中的规律,利用规律去解答。
3.【考点】数与形结合的规律.
【答案】C
【思路分析】依据题意结合图示可知,小明每撕一次,比上次多增加3张小纸片,因此撕了n次后,手中共有(3n+1)张纸片,由此解答本题。
【解答】解:由分析可知:3n+1=2023,则n=674。
故选:C。
【名师点评】解决本题的关键是找出题中的规律,利用规律去解答。
4.【考点】正方体的展开图.
【答案】A
【思路分析】根据正方体展开图的11种特征,即可确定哪个图形属于正方体展开图,能折叠成正方体,哪个图形不属于正方体展开图,不能折叠成正方体。
【解答】解:A、属于正方体展开图的“1﹣3﹣2”型,能折叠成正方体;
B、不属于正方体展开图,不能折成正方体;
C、不属于正方体展开图,不能折成正方体
D、不属于正方体展开图,不能折成正方体。
故选:A。
【名师点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
5.【考点】合数与质数的初步认识;奇数与偶数的初步认识.
【答案】D
【思路分析】根据任何大于2的偶数都可以写成两个质数之和,结合选项分析解答即可。
【解答】解:4=1+3中,1不是质数,所以不符合题意;
13=2+11中,13不是大于2的偶数,2和11是质数,所以不符合题意;
54=3+51中,51不是质数,所以不符合题意;
36=7+29,36是大于2的偶数,7和29是质数,所以符合题意。
故选:D。
【名师点评】本题考查了质数和合数、偶数和奇数的认识知识,结合题意分析解答即可。
6.【考点】统计图的选择.
【答案】D
【思路分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解答】解:根据统计图的特点可知:要反映甲、乙两地的气温变化情况,应选用复式折线统计图比较合适。
故选:D。
【名师点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
7.【考点】从不同方向观察物体和几何体.
【答案】C
【思路分析】根据观察物体的方法可知,从上面看是一行3个小正方形,据此解答即可。
【解答】解:分析可知,是从物体的上面看到的。
故选:C。
【名师点评】本题考查了从不同方向观察物体和几何图形,培养了学生的观察能力。
8.【考点】分数除法应用题.
【答案】B
【思路分析】把原来甲队人数看作单位“1”,则原来乙队人数相当于甲队人数的(12);再用原来乙队人数除以甲队人数。
【解答】解:(12)÷1
=(1)÷1
1
答:原来乙队人数是甲队人数的。
故选:B。
【名师点评】求一个数是另一个数的几分之几,用这个数除以另一个数。关键是把甲队原来的人数看作单位“1”,弄清乙队原来的人数。
9.【考点】合数与质数的初步认识;方程与等式的关系;圆、圆环的周长;轴对称图形的辨识.
【答案】A
【思路分析】A.自然数除了质数和合数还有0。
B.半圆的周长是整同圆周长的一半加半径。
C.正方形有4条对称轴,是轴对称图形。
D.等式是表示两个数或两个代数式相等关系的式子,方程是含有未知数的等式,所以方程一定是等式,等式不一定是方程。
【解答】解:自然数除了质数和合数还有0。
故选:A。
【名师点评】此题考查了自然数、半圆的周长、轴对称图形和方程以及等式的概念判断。
10.【考点】长方体和正方体的表面积.
【答案】B
【思路分析】根据题意可知,把2本《新华字典》包起来,最节省包装纸的方法是把2本《新华字典》的最大面重合进行包装。据此解答即可。
【解答】解:把2本《新华字典》包起来,最节省包装纸的方法是把2本《新华字典》的最大面重合进行包装。
故选:B。
【名师点评】此题考查的目的是理解掌握长方体的拼组方法及应用,长方体表面积的意义及应用。
二.填空题
11.【考点】圆、圆环的周长;圆、圆环的面积.
【答案】7.71,3.5325。
【思路分析】根据题意可知,从这个长方形硬纸上剪一个最大的半圆,这个半圆的直径等于长方形的长,因为宽小于长的一半,所以这个半圆的直径只能是3。根据半圆的周长公式:C=πd÷2+d,半圆的面积公式:S=πr2÷2,把数据代入公式解答。
【解答】解:3.14×3÷2+3
=4.71+3
=7.71(厘米)
3.14×(3÷2)2÷2
=3.14×2.25÷2
=7.065÷2
=3.5325(平方厘米)
答:这个半圆的周长是7.71厘米,面积是3.5325平方厘米。
故答案为:7.71,3.5325。
【名师点评】此题主要考查半圆的周长公式、面积公式的灵活运用,关键是熟记公式。
12.【考点】圆柱的侧面积、表面积和体积.
【答案】1256。
【思路分析】根据题意可知,圆柱的高增加1厘米,它的侧面积就增加31.4平方厘米,根据圆柱的侧面积公式:S=2πrh,据此可以求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式求出解答。
【解答】解:31.4÷1÷3.14÷2
=10÷2
=5(厘米)
3.14×52×16
=3.14×25×16
=78.5×16
=1256(立方厘米)
答:它的体积是1256立方厘米。
故答案为:1256。
【名师点评】此题主要考查圆柱的侧面积公式、圆的周长公式、圆柱的体积公式的灵活运用,关键是熟记公式。
13.【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【答案】7,14。
【思路分析】根据圆柱的体积公式:V=Sh,那么h=V÷S,把数据代入公式求出圆柱的高,等底等高的圆锥体的体积是圆柱体积的,据此解答即可。
【解答】解:42÷6=7(分米)
4214(立方分米)
答:圆柱的高是7分米,和这个圆柱体等底等高的圆锥体的体积是14立方分米。
故答案为:7,14。
【名师点评】此题主要考查圆柱体积公式的灵活运用,等底等高的圆柱与圆锥体积之间的关系及应用。
14.【考点】亿以上数的读写;亿以上数的改写与近似.
【答案】二百九十三亿,293亿。
【思路分析】读数时,把数先分级,从高位读起,亿级或万级的数按照万以内的数的读法去读,再在每级的末尾加一个“亿”或“万”字,每级末尾的0都不读,每一级的开头或中间无论有几个0,都读一个0;数的改写就是直接在原数的亿位后面点上小数点,同时要在改写的小数后面写上“亿”字,数的大小不变。
【解答】解:29300000000读作:二百九十三亿
29300000000改写为以“亿”为单位的数是293亿。
南极洲素有“寒极”之称,它的总贮冰量为29300000000立方米,约占全球总量的90%。横线上的数读作二百九十三亿,把这个数改写为以“亿”为单位的数是293亿。
故答案为:二百九十三亿,293亿。
【名师点评】此题考查了亿以内数的读法和数的改写,要求学生掌握此知识点。
15.【考点】分数的意义和读写;合数与质数的初步认识.
【答案】见试题解答内容
【思路分析】(1)判定一个分数的单位看分母,分母是几,分数单位就是几分之一;
(2)最小的合数是4,用4减去原分数的结果,再看有几个分数单位即可解答.
【解答】解:的分母是5,所以分数单位是;
(2)最小的合数是4,
4,
即至少再添上 16个这样的分数单位就是最小的合数;
故答案为:,16.
【名师点评】此题主要考查分数的单位:把单位“1”平均分成几份,表示其中一份的数就是它的分数单位.
16.【考点】小数的近似数及其求法.
【答案】6.804;6.795。
【思路分析】要考虑6.80是一个三位数的近似数,有两种情况:“四舍”得到的6.80最大是6.804,“五入”得到的6.80最小是6.795,由此解答问题即可。
【解答】解:一个三位小数,“四舍五入”的近似数是6.80,这个三位小数最大是6.804,最小是6.795。
故答案为:6.804;6.795。
【名师点评】取一个数的近似数,有两种情况:“四舍”得到的近似数比原数小,“五入”得到的近似数比原数大,根据题的要求灵活掌握解答方法。
17.【考点】图上距离与实际距离的换算(比例尺的应用).
【答案】1:3000,4。
【思路分析】由线段比例尺可知,图上1厘米代表实际距离30米,根据比例尺=图上距离:实际距离解答即可;根据图上距离=实际距离×比例尺,代入数据解答即可。
【解答】解:1厘米:30米
=1厘米:3000厘米
=1:3000
120千米=12000000厘米
120000004(厘米)
答:换算成数值比例尺为1:3000,应画4厘米。
故答案为:1:3000,4。
【名师点评】熟练掌握线段比例尺与数值比例尺的互化以及图上距离、实际距离、比例尺三者间的关系是解题的关键。
18.【考点】数对与位置.
【答案】(4,a)。
【思路分析】根据题干,小兰坐在(4,5)的位置上,小红坐在(4,3)的位置,所以小兰与小红都在第4列,不在同一行,因为小亮与她俩坐在同一直线上,所以小亮只能在第4列,即小亮的数对位置是(4,a),据此即可解答问题。
【解答】解:小兰坐在(4,5)的位置上,小红坐在(4,3)的位置,小亮与她俩坐在同一条直线上,小亮可能坐在(4,a)的位置上。
故答案为:(4,a)。
【名师点评】数对表示位置的方法是:第一个数字表示列,第二个数字表示行,据此即可解答问题。
19.【考点】圆柱的侧面积、表面积和体积.
【答案】141.3,150.72。
【思路分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体,这个长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,拼成的长方体的表面积比圆柱的表面积增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,已知表面积比原来增加了30平方厘米,据此可以求出圆柱的高,然后根据圆柱的体积公式:V=πr2h,圆柱的表面积=侧面积+底面积×2,把数据代入公式解答。
【解答】解:6÷2=3(厘米)
30÷2÷3
=15÷3
=5(厘米)
3.14×32×5
=3.14×9×5
=28.26×5
=141.3(立方厘米)
3.14×6×5+3.14×32×2
=18.84×5+3.14×9×2
=94.2+56.52
=150.72(平方厘米)
答:原来圆柱的体积是141.3立方厘米,表面积是150.72平方厘米。
故答案为:141.3,150.72。
【名师点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及运用,圆柱表面积公式的灵活运用,关键是熟记公式。
20.【考点】百分数的实际应用.
【答案】160。
【思路分析】将收集的图片总张数看作单位“1”,先用80除以20%,求出图片总张数;再乘40%,即可求出收集的名山图片张数。
【解答】解:80÷20%×40%
=400×40%
=160(张)
答:名山图片收集了160张。
故答案为:160。
【名师点评】已知一个数的几分之几是多少,求这个数,用除法计算;求一个数的几分之几是多少,用乘法计算。
21.【考点】分数大小的比较;体积、容积进率及单位换算.
【答案】=;=。
【思路分析】升和毫升之间的进率是1000,据此先统一单位,再比较大小;根据分数与除法的关系,求出1÷6的商,再与循环小0.1比较大小。
【解答】解:因为1000=50,所以升=50毫升;
因为1÷6=0.166……=0.1,所以0.1。
故答案为:=;=。
【名师点评】此题重点考查通过单位的换算比大小和利用分数与除法间的关系计算商再比大小的知识。
22.【考点】长方体和正方体的表面积.
【答案】28.26,65.94。
【思路分析】由题意知,水池占地面积就是圆柱的底面积,涂水泥的面积是内侧面和底面,要求涂水泥的面积,可用侧面积加上底面积,根据圆柱表面积公式列式解答即可。
【解答】解:6÷2=3(米)
32×3.14=28.26(平方米)
6×3.14×2=37.68(平方米)
37.68+28.26=65.94(平方米)
所以水池占地面积28.26平方米,涂水泥的面积是65.94平方米。
故答案为:28.26,65.94。
【名师点评】此题是考查圆柱形水池内表面积的计算,要注意是内侧面积加一个底面的面积。
三.判断题
23.【考点】比例的意义和基本性质.
【答案】×
【思路分析】此题根据比例的基本性质“两内项之积等于两外项之积”即可变形得出a与b是的比。
【解答】解:2a=5b,
根据比例的基本性质可得:a:b=5:2。
故答案为:×。
【名师点评】此题考查了比例的基本性质的应用。
24.【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【答案】见试题解答内容
【思路分析】把一个圆柱削成最大的圆锥,则圆锥与原来圆柱是等底等高的,则圆锥的体积是圆柱的体积,由此即可得出消去部分的体积是圆柱体积的1.
【解答】解:削成的最大圆锥与原来圆柱等底等高,则圆锥的体积是圆柱的体积的,
所以削去部分的体积是原圆柱体积的.
故答案为:√.
【名师点评】此题考查了圆柱内削成的最大圆锥的特点以及等底等高的圆柱与圆锥的体积的倍数关系的灵活应用.
25.【考点】平行四边形的特征及性质.
【答案】√
【思路分析】平行四边形分成两个完全一样的图形,有三种分法,据下图即可正确作答.
【解答】解:将一个平行四边形分成两个完全一样的平面图形,那么这两个完全一样的平面图形可能是平行四边形,也可能是梯形,还可能是三角形;分成的每个图形的面积都是的这个平行四边形面积的一半.
所以一个平行四边形能分成两个完全一样的三角形是正确的.
故答案为:√.
【名师点评】解答此题的关键是,依据题目要求,画出正确的图,即可正确作答.
26.【考点】百分数的实际应用.
【答案】√
【思路分析】打六折,就是现价是原价的60%,所以便宜了:1﹣60%=40%,所以就是比原价便宜了40%,所以题干正确。
【解答】解:1﹣60%=40%
因此一件商品打六折,就是现价比原价便宜了40%,原题说法正确。
故答案为:√。
【名师点评】解答此题的关键是把原价看作单位“1”。
27.【考点】比的意义.
【答案】见试题解答内容
【思路分析】把一段路程的长度看作“1”,根据路程÷时间=速度,分别求出甲乙的速度,再写出相应的比,根据比的基本性质化成最简整数比.
【解答】解:(1÷10):(1÷11)
:
=11:10
甲和乙的速度比是11:10,所以本题说法错误;
故答案为:×.
【名师点评】关键是把路程的长度看作“1”,再根据路程、时间与速度之间的关系求出甲乙的速度,写出相应的比化简即可.
28.【考点】角的概念和表示.
【答案】×
【思路分析】依据角的定义就可填出正确答案.
【解答】解:角的大小和边长无关.
故答案为:×.
【名师点评】此题主要考查角的定义.
四.计算题
29.【考点】分数方程求解.
【答案】x=2;x=0.2。
【思路分析】先化简,然后根据等式的性质,方程两边同时加上0.2,然后再同时除以0.7求解;
根据比例的基本性质,把比例化成普通方程,然后再根据等式的性质,方程两边同时除以12求解。
【解答】解:
0.7x﹣0.2=1.2
0.7x﹣0.2+0.2=1.2+0.2
0.7x=1.4
x=2
12×(x+0.4)=2.4×3
12x+4.8=7.2
12x+4.8﹣4.8=7.2﹣4.8
12x=2.4
x=0.2
【名师点评】本题考查了在解方程时应根据等式的性质,即等式两边同加上、同减去、同乘上或同除以某一个数(0除外),等式的两边仍相等,同时注意“=”上下要对齐。
30.【考点】运算定律与简便运算;小数四则混合运算;分数的四则混合运算.
【答案】(1)730;
(2)6.4;
(3);
(4);
(5)2020;
(6)。
【思路分析】(1)先算除法,再算乘法,最后算减法;
(2)先算小括号里面的加法,再算中括号里面的除法,最后算括号外面的乘法;
(3)先算小括号里面的加法和减法,再算括号外面的乘法;
(4)先算小括号里面的加法,再算中括号里面的乘法,最后算括号外面的加法;
(5)根据乘法分配律进行计算;
(6)根据分数的拆项公式进行计算。
【解答】解:(1)1042﹣384÷16×13
=1042﹣24×13
=1042﹣312
=730
(2)0.8×[(1.9+1.46)÷0.42]
=0.8×[3.36÷0.42]
=0.8×8
=6.4
(3)
(4)[()]
[]
(5)20.2×83+1.7×202
=202×8.3+1.7×202
=202×(8.3+1.7)
=202×10
=2020
(6)
=(1)+()+()+……+()
=1
=1
【名师点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
五.操作题
31.【考点】作轴对称图形;作旋转一定角度后的图形;图形的放大与缩小;数对与位置.
【答案】
【思路分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(AC所在的直线)的右边画出三角形ABC顶点B的对称点,然后连接即可画出另一半使它成为轴对称图形。
(2)根据旋转的特征,三角形ABC绕点C顺时针旋转90°,点C的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据图形放大与缩小的意义,把三角形ABC的各边均放大到原来的2倍,所得到的图形就是原图形按2:1放大后的图形。
(4)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可在方格图描出所点O的位置,然后以O为圆心,以2厘米为半径画圆即可。
【解答】解:根据题意画图如下:
【名师点评】此题考查的知识点:作轴对称图形、作旋转一定度数后的图形、图形的放大与缩小、画圆、数对与位置。
六.应用题
32.【考点】按比例分配应用题.
【答案】216本。
【思路分析】用400乘(1),求出剩下的数量,再把剩下的数量按2:3,进行分配,即可解答。
【解答】解:400×(1)
=400
=360(本)
360
=360
=216(本)
答:六年级分得216本。
【名师点评】本题考查的是按比例分配应用题,掌握按比例分配的方法是解答关键。
33.【考点】简单的工程问题.
【答案】6天。
【思路分析】把工作总量看作单位“1”,则甲队的工作效率是,乙队的工作效率是(),再根据工作时间=工作总量÷工作效率和,即可计算出两队合修多少天可以完成。
【解答】解:
1
=1
=6(天)
答:两队合修6天可以完成。
【名师点评】本题解题的关键是把工作总量看作单位“1”,根据工作时间=工作总量÷工作效率和,列式计算。
34.【考点】探索某些实物体积的测量方法.
【答案】3.4立方分米。
【思路分析】根据题意可知,把石块放入容器中上升部分水的体积就等于这块石块的体积,根据圆柱的体积公式:V=πr2h,把数据代入公式求出水与石块的体积和,然后减去水的体积就是石块的体积。
【解答】解:25厘米=2.5分米
28升=28立方分米
3.14×(4÷2)2×2.5﹣28
=3.14×4×2.5﹣28
=31.4﹣28
=3.4(立方分米)
答:石块的体积是3.4立方分米。
【名师点评】此题考查的目的是理解掌握不规则物体体积的测量方法及应用,圆柱的体积公式及应用,关键是熟记公式。
35.【考点】组合图形的面积.
【答案】572。
【思路分析】如图,
设右下方两个相等的正方形边长为x,则根据题意知,右上方最大的正方形边长为x+6,根据长方形的长=长方形的长,列出方程,求出长方形的长与宽,进一步解答即可。
【解答】解:设右下方两个相等的正方形边长为x,根据图意有:
x+4+x+6=x+x+x+2
2x+10=3x+2
x=8
原长方形的长为:8+8+8+2=26
原长方形的宽为:8+6+8=22
面积为:26×22=572
答:这个长方形色块图的面积是572。
【名师点评】解决此题关键是求出长方形的长和宽,进一步用长乘宽求得面积。
36.【考点】圆柱的体积.
【答案】603。
【思路分析】根据比例尺,求出比例尺,再根据实际距离=图上距离÷比例尺,求出实际半径,然后根据圆柱的容积(体积)公式:V=πr2h,把数据代入公式解答。
【解答】解:6厘米:12分米
=6厘米:120厘米
=1:20
2
=2×20
=40(厘米)
40厘米=4分米
3.14×42×12
=3.14×16×12
=50.24×12
=602.88(立方分米)
602.88立方分米≈603升
答:它的实际容积是603升。
【名师点评】此题主要考查圆柱容积(体积)公式的灵活运用,以及比例尺的意义及应用。
37.【考点】列方程解应用题(两步需要逆思考).
【答案】(1)285;(2)3200
【思路分析】(1)根据题目信息“铁路全场约380千米,其中桥梁和隧道相当于铁路全长的75%”可知,单位“1”是铁路全长已知的,直接用铁路全长×75%就可以求出桥梁和隧道一共多长。
(2)从题目信息“平均每千米耗资约6000万元,比“天梯”青藏铁路还多。”我们知道单位“1”是青藏铁路平均每千米耗资,未知,就设它为x万元,根据它和桥梁和隧道的耗资之间的关系列出方程解答。
【解答】解:(1)380×75%=285(千米)
答:这段铁路中,桥梁和隧道一共长285千米.。
(2)设青藏铁路平均每千米耗资x万元。
(1)x=6000
x=6000
x=3200
答:青藏铁路平均每千米耗资3200万元。
【名师点评】找出题中数量之间的相等关系。
21世纪教育网(www.21cnjy.com)
同课章节目录
