28.1锐角三角函数(2)
文档属性
| 名称 | 28.1锐角三角函数(2) |  | |
| 格式 | rar | ||
| 文件大小 | 40.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-26 12:28:00 | ||
图片预览

文档简介
第二课时 第28章 锐角三角函数——余弦、正切
学习目标:理解余弦、正切的概念。
一、归纳:
1、在Rt△ABC中,∠C=90°,
(1) 锐角∠A的正弦、余弦、正切、统称为锐角∠A的三角函数。
(2) 在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c,则:
①正弦:
②余弦:
③正切:
(3) _____< sin A <_____;
____< cos A <____ (∠A锐角)
(4) 锐角三角函数值只与角的______有关,与边的长短_____。
例如,当∠A=30°时,我们有cosA=cos30°= ;
当∠A=45°时,我们有tanA=tan45°= .
例1:如图,在Rt△ABC中,∠C=90°,BC=6,sinA=,求cosA、tanB的值.
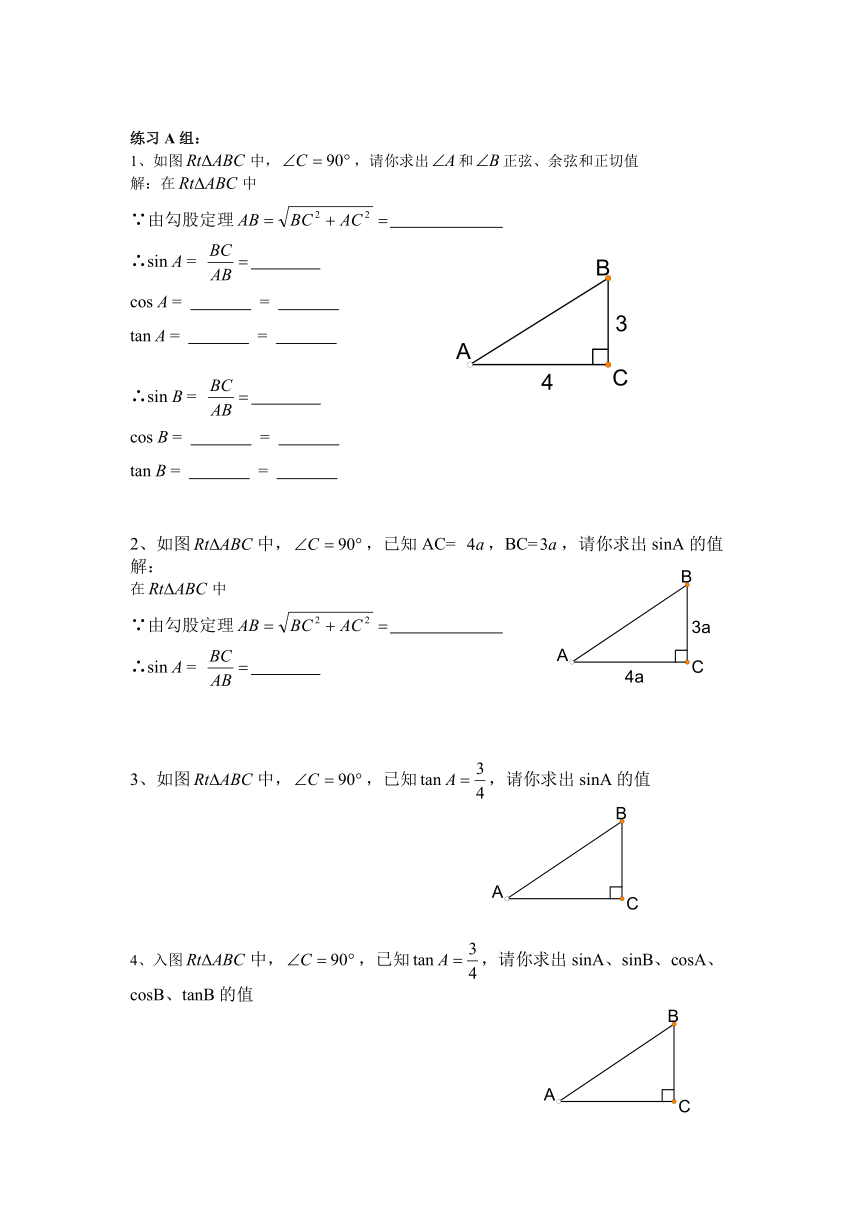
练习A组:
1、如图中,,请你求出和正弦、余弦和正切值
解:在中
∵由勾股定理
∴sin A =
cos A = =
tan A = =
∴sin B =
cos B = =
tan B = =
2、如图中,,已知AC= ,BC=,请你求出sinA的值
解:
在中
∵由勾股定理
∴sin A =
3、如图中,,已知,请你求出sinA的值
4、入图中,,已知,请你求出sinA、sinB、cosA、cosB、tanB的值
5、分别求出下列直角三角形总中两个锐角的正弦值、余弦值和正切值
6、完成下列表格:
三角函数 30° 45° 60°
sinα
cosα
tanα
B组:
本题主要考查锐解三角函数的定义,同学们只要依据的图形,不难写出,从而可判断C正确.
7、在Rt△ABC中,如果三边长度都扩大2倍,则锐角A的余切值( )
A.缩小2倍 B.扩大2倍 C.不变 D.不能确定
8、在中,∠C=90°,如果cos A=那么的值为(?)
A.?B.?C.?D.
分析 本题主要考查锐解三角函数及三角变换知识。其思路是:依据条件,可求出;再由,可求出,从而,故应选D.
9、如图:P是∠的边OA上一点,
且P点的坐标为(3,4), 则cosα=_____________
10、如图,在中,,,。请你求出图中AB和AC的长度,sinA和sinB的值。
11、在Rt△ABC中,∠C为直角,AC = 5,AB = 13,则下列正确的是( )
A.sinA= B.cotA= C.tanA= D.cosA=
12、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。
已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
五、课堂小结:
在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c,则:
①正弦:
②余弦:
③正切:
______< sin A <_____ ; _____< cos A <_____ (∠A锐角)
锐角三角函数值只与角的_______有关,与边的_______无关。
三角函数 30° 45° 60°
sinα
cosα
tanα
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,cosA,tanA也是A的函数.
学习目标:理解余弦、正切的概念。
一、归纳:
1、在Rt△ABC中,∠C=90°,
(1) 锐角∠A的正弦、余弦、正切、统称为锐角∠A的三角函数。
(2) 在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c,则:
①正弦:
②余弦:
③正切:
(3) _____< sin A <_____;
____< cos A <____ (∠A锐角)
(4) 锐角三角函数值只与角的______有关,与边的长短_____。
例如,当∠A=30°时,我们有cosA=cos30°= ;
当∠A=45°时,我们有tanA=tan45°= .
例1:如图,在Rt△ABC中,∠C=90°,BC=6,sinA=,求cosA、tanB的值.
练习A组:
1、如图中,,请你求出和正弦、余弦和正切值
解:在中
∵由勾股定理
∴sin A =
cos A = =
tan A = =
∴sin B =
cos B = =
tan B = =
2、如图中,,已知AC= ,BC=,请你求出sinA的值
解:
在中
∵由勾股定理
∴sin A =
3、如图中,,已知,请你求出sinA的值
4、入图中,,已知,请你求出sinA、sinB、cosA、cosB、tanB的值
5、分别求出下列直角三角形总中两个锐角的正弦值、余弦值和正切值
6、完成下列表格:
三角函数 30° 45° 60°
sinα
cosα
tanα
B组:
本题主要考查锐解三角函数的定义,同学们只要依据的图形,不难写出,从而可判断C正确.
7、在Rt△ABC中,如果三边长度都扩大2倍,则锐角A的余切值( )
A.缩小2倍 B.扩大2倍 C.不变 D.不能确定
8、在中,∠C=90°,如果cos A=那么的值为(?)
A.?B.?C.?D.
分析 本题主要考查锐解三角函数及三角变换知识。其思路是:依据条件,可求出;再由,可求出,从而,故应选D.
9、如图:P是∠的边OA上一点,
且P点的坐标为(3,4), 则cosα=_____________
10、如图,在中,,,。请你求出图中AB和AC的长度,sinA和sinB的值。
11、在Rt△ABC中,∠C为直角,AC = 5,AB = 13,则下列正确的是( )
A.sinA= B.cotA= C.tanA= D.cosA=
12、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。
已知AC=,BC=2,那么sin∠ACD=( )
A. B. C. D.
五、课堂小结:
在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c,则:
①正弦:
②余弦:
③正切:
______< sin A <_____ ; _____< cos A <_____ (∠A锐角)
锐角三角函数值只与角的_______有关,与边的_______无关。
三角函数 30° 45° 60°
sinα
cosα
tanα
对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,cosA,tanA也是A的函数.
