第三章 位置与坐标 质量评估(含答案)2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 第三章 位置与坐标 质量评估(含答案)2025-2026学年数学北师大版(2024)八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 222.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 00:00:00 | ||
图片预览



文档简介
第三章 位置与坐标 质量评估
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024春·山西期末]点P在第四象限内,点P到x轴的距离是6,到y轴的距离是2,则点P的坐标为( )
A.(-6,2) B.(6,-2) C.(-2,6) D.(2,-6)
2.[2024春·沈阳期中]如图所示为做课间操时,小明、小德和小红三人的相对位置,如果用(1,3)表示小明的位置,(-1,2)表示小德的位置,那么小红的位置可表示为( )
A.(2,0) B.(0,-2) C.(-2,0) D.(-2,-1)
3.[2024·沈阳期中]在平面直角坐标系中,若点A(2a-5,4-a)在x轴上,则点A的坐标为( )
A. B.(5,-1) C.(3,0) D.(0,3)
4.已知点P(-1-2a,5)关于x轴的对称点与点Q(3,b)关于y轴的对称点相同,则A(a,b)的坐标为( )
A.(1,-5) B.(1,5) C.(-1,5) D.(-1,-5)
5.如图,将长为3的长方形ABCD放在平面直角坐标系中。若点 D的坐标为(6,3),则点A的坐标为( )
A.(5,3) B.(4,3) C.(4,2) D.(3,3)
6.已知点P(-3,-3),Q(-3,4),则直线PQ( )
A.平行于x轴 B.平行于y轴
C.垂直于y轴 D.以上都不正确
7.若点M的坐标为(0,|b|+1),则下列说法中正确的是( )
A.点M在x轴正半轴上 B.点M在x轴负半轴上
C.点M在y轴正半轴上 D.点M在y轴负半轴上
8.[2024春·长沙期中]已知MN∥y轴,点M的坐标为(m-1,2m+1),点N的坐标为(2,4),则点M的坐标为( )
A.(2,7) B. C.(-1,-1) D.(2,-7)
9.如图,在平面直角坐标系中,正方形OACB的顶点O,C的坐标分别是(0,0),(2,0),则顶点B的坐标是( )
A.(1,1) B.(-1,-1) C.(1,-1) D.(-1,1)
10.在平面直角坐标系中,对于点P(a,b),我们把Q(-b+1,a+1)叫作点P的伴随点,已知A1的伴随点为A2,A2的伴随点为A3……这样依次下去,得到A1,A2,…,An。若A1的坐标为(-3,1),则A2 025的坐标为( )
A.(-3,1) B.(3,1) C.(0,-2) D.(0,4)
二、填空题(本题共5小题,每小题3分,共15分)
11.某校开展了以“纵横之间有智慧,攻防转换有乐趣”为主题的中国象棋文化节。如图是某次对弈的残局图,如果建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),那么“兵”在同一坐标系下的坐标是 。
12.在如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,2),B(5,5),C(8,0),D(2,-2),则这个四边形的面积是 。
13.对于平面直角坐标系中任意两点A(x1,y1),B(x2,y2),定义一种新运算“*”:(x1,y1)*(x2,y2)=(x1y2,x2y1)。根据这个规则,若A(x1,y1)在第三象限,B(x2,y2)在第四象限,则A*B在第 象限。
14.在平面直角坐标系中,点P(2,4)关于直线x=1的对称点的坐标是 。
15.[2024秋·苏家屯区校级期末]如图,在平面直角坐标系中,等腰直角三角形OM0M1的直角边OM0在x轴上,点M1在第一象限,且OM0=1,以点M1为直角顶点,OM1为一直角边作等腰直角三角形OM1M2,再以点M2为直角顶点,OM2为直角边作等腰直角三角形OM2M3……依此规律,点M2 025的坐标是 。
三、解答题(本题共8小题,共75分)
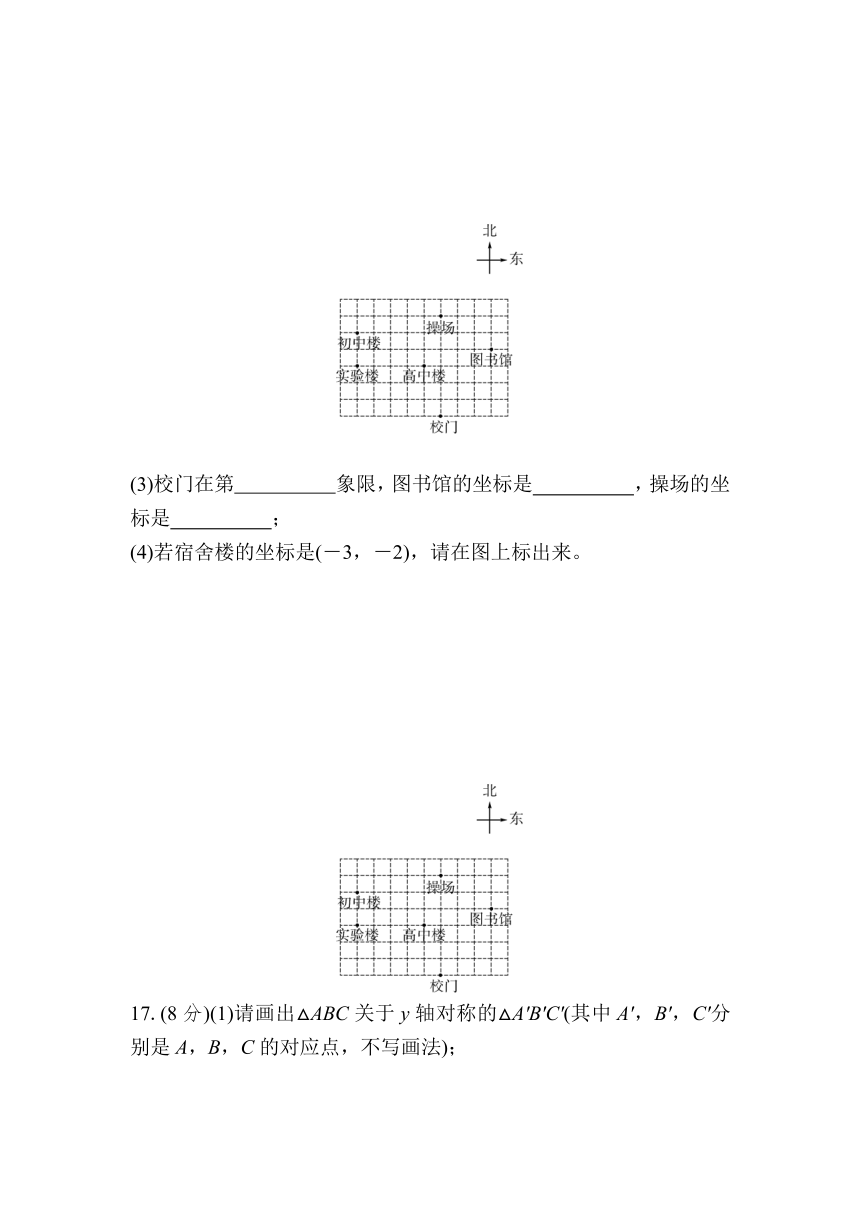
16.(8分)[2024春·宁乡市期末]如图是某校的平面示意图,若以正东为x轴正方向,正北为y轴正方向建立平面直角坐标系后,得到初中楼的坐标是(-4,2),实验楼的坐标是(-4,0)。
(1)坐标原点应为 的位置;
(2)在图中画出此平面直角坐标系;
(3)校门在第 象限,图书馆的坐标是 ,操场的坐标是 ;
(4)若宿舍楼的坐标是(-3,-2),请在图上标出来。
17.(8分)(1)请画出△ABC关于y轴对称的△A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法);
(2)直接写出A',B',C'三点的坐标。
18.(8分)[2024春·望城区期末]在平面直角坐标系中,已知点M(2-m,3m+6)。
(1)若点M在x轴上,求m的值;
(2)若点N(-4,-3),且直线MN⊥x轴,求点M的坐标。
19.(8分)已知平面直角坐标系中有一点P(m-2,2m+1),请根据题意回答下列问题:
(1)若点P在y轴上,求点P的坐标;
(2)点Q的坐标为(4,3),连接PQ,若PQ∥x轴,求PQ的长。
20.(8分)如图,在平面直角坐标系中,正方形ABCD和正方形EFGC的面积分别为64和16。
(1)请写出点A,E,F的坐标;
(2)求△BDF的面积。
21.(10分)[2024春·宁乡市期末]已知点A(0,1),B(2,0),C(4,3)。
(1)在平面直角坐标系中描出各点,画出△ABC;
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标。
22.(12分)定义:在平面直角坐标系中,已知点P1(a,b),P2(c,b),P3(c,d),这三个点中任意两点间的距离的最小值称为点P1,P2,P3的“最佳间距”。例如,如图,点P1(-1,2),P2(1,2),P3(1,3)的“最佳间距”是1。
(1)理解:点Q1(2,1),Q2(5,1),Q3(5,5)的“最佳间距”是 。
(2)探究:已知点O(0,0),A(-4,0),B(-4,y)(y≠0)。
①若点O,A,B的“最佳间距”是2,则y的值为 。
②点O,A,B的“最佳间距”最大是多少?请说明理由。
(3)迁移:当点O(0,0),E(m,0),P(m,-2m+1)的“最佳间距”取到最大值时,点P的坐标是 。
23.(13分)[2023春·茅箭区期中]【问题背景】
在平面直角坐标系中,已知点A(x1,y1),B(x2,y2),C是线段AB的中点,则点C的坐标为(,)。如A(-1,1),B(3,3),则AB的中点C的坐标为(,),即点C的坐标为(1,2)。
【解决问题】
(1)已知A(6,-2),B(-3,-3),则线段AB的中点M的坐标是 ;
(2)若点P(-3,7),线段PQ的中点坐标为(-1,5),则点Q的坐标是 ;
(3)已知三点E(4,-2),F(-3,-1),G(-1,-4),第四个点 H(x,y)与点E,F,G中的任意一个点构成的线段的中点与另外两个点构成的线段的中点重合,求点H的坐标。
参考答案
第三章质量评估
1.D 2.C 3.C 4.A 5.D 6.B 7.C 8.A 9.C 10.A 11.(-3,1) 12.31 13.四
14.(0,4) 15.(21 012,21 012)
16.(1)高中楼 (2)略 (3)四 (4,1) (1,3) (4)略
17.(1)略
(2)A'(2,3),B'(3,-1),C'(-1,-2)。
18.(1)m=-2 (2)M(-4,24)
19.(1)P(0,5) (2)PQ=5
20.(1)A(0,8),E(8,4),F(12,4)
(2)S△BDF=32
21.(1)略 (2)S△ABC=4 (3)点P的坐标为(0,5),(0,-3),(10,0)或(-6,0)。
22.(1)3 (2)①±2 ②点O,A,B的“最佳间距”最大是4。理由略。 (3)或(1,-1)
23.(1)(,-) (2)(1,3) (3)点H的坐标为(-8,-3),(6,-5)或(2,1)。
。
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.[2024春·山西期末]点P在第四象限内,点P到x轴的距离是6,到y轴的距离是2,则点P的坐标为( )
A.(-6,2) B.(6,-2) C.(-2,6) D.(2,-6)
2.[2024春·沈阳期中]如图所示为做课间操时,小明、小德和小红三人的相对位置,如果用(1,3)表示小明的位置,(-1,2)表示小德的位置,那么小红的位置可表示为( )
A.(2,0) B.(0,-2) C.(-2,0) D.(-2,-1)
3.[2024·沈阳期中]在平面直角坐标系中,若点A(2a-5,4-a)在x轴上,则点A的坐标为( )
A. B.(5,-1) C.(3,0) D.(0,3)
4.已知点P(-1-2a,5)关于x轴的对称点与点Q(3,b)关于y轴的对称点相同,则A(a,b)的坐标为( )
A.(1,-5) B.(1,5) C.(-1,5) D.(-1,-5)
5.如图,将长为3的长方形ABCD放在平面直角坐标系中。若点 D的坐标为(6,3),则点A的坐标为( )
A.(5,3) B.(4,3) C.(4,2) D.(3,3)
6.已知点P(-3,-3),Q(-3,4),则直线PQ( )
A.平行于x轴 B.平行于y轴
C.垂直于y轴 D.以上都不正确
7.若点M的坐标为(0,|b|+1),则下列说法中正确的是( )
A.点M在x轴正半轴上 B.点M在x轴负半轴上
C.点M在y轴正半轴上 D.点M在y轴负半轴上
8.[2024春·长沙期中]已知MN∥y轴,点M的坐标为(m-1,2m+1),点N的坐标为(2,4),则点M的坐标为( )
A.(2,7) B. C.(-1,-1) D.(2,-7)
9.如图,在平面直角坐标系中,正方形OACB的顶点O,C的坐标分别是(0,0),(2,0),则顶点B的坐标是( )
A.(1,1) B.(-1,-1) C.(1,-1) D.(-1,1)
10.在平面直角坐标系中,对于点P(a,b),我们把Q(-b+1,a+1)叫作点P的伴随点,已知A1的伴随点为A2,A2的伴随点为A3……这样依次下去,得到A1,A2,…,An。若A1的坐标为(-3,1),则A2 025的坐标为( )
A.(-3,1) B.(3,1) C.(0,-2) D.(0,4)
二、填空题(本题共5小题,每小题3分,共15分)
11.某校开展了以“纵横之间有智慧,攻防转换有乐趣”为主题的中国象棋文化节。如图是某次对弈的残局图,如果建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),那么“兵”在同一坐标系下的坐标是 。
12.在如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0,2),B(5,5),C(8,0),D(2,-2),则这个四边形的面积是 。
13.对于平面直角坐标系中任意两点A(x1,y1),B(x2,y2),定义一种新运算“*”:(x1,y1)*(x2,y2)=(x1y2,x2y1)。根据这个规则,若A(x1,y1)在第三象限,B(x2,y2)在第四象限,则A*B在第 象限。
14.在平面直角坐标系中,点P(2,4)关于直线x=1的对称点的坐标是 。
15.[2024秋·苏家屯区校级期末]如图,在平面直角坐标系中,等腰直角三角形OM0M1的直角边OM0在x轴上,点M1在第一象限,且OM0=1,以点M1为直角顶点,OM1为一直角边作等腰直角三角形OM1M2,再以点M2为直角顶点,OM2为直角边作等腰直角三角形OM2M3……依此规律,点M2 025的坐标是 。
三、解答题(本题共8小题,共75分)
16.(8分)[2024春·宁乡市期末]如图是某校的平面示意图,若以正东为x轴正方向,正北为y轴正方向建立平面直角坐标系后,得到初中楼的坐标是(-4,2),实验楼的坐标是(-4,0)。
(1)坐标原点应为 的位置;
(2)在图中画出此平面直角坐标系;
(3)校门在第 象限,图书馆的坐标是 ,操场的坐标是 ;
(4)若宿舍楼的坐标是(-3,-2),请在图上标出来。
17.(8分)(1)请画出△ABC关于y轴对称的△A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法);
(2)直接写出A',B',C'三点的坐标。
18.(8分)[2024春·望城区期末]在平面直角坐标系中,已知点M(2-m,3m+6)。
(1)若点M在x轴上,求m的值;
(2)若点N(-4,-3),且直线MN⊥x轴,求点M的坐标。
19.(8分)已知平面直角坐标系中有一点P(m-2,2m+1),请根据题意回答下列问题:
(1)若点P在y轴上,求点P的坐标;
(2)点Q的坐标为(4,3),连接PQ,若PQ∥x轴,求PQ的长。
20.(8分)如图,在平面直角坐标系中,正方形ABCD和正方形EFGC的面积分别为64和16。
(1)请写出点A,E,F的坐标;
(2)求△BDF的面积。
21.(10分)[2024春·宁乡市期末]已知点A(0,1),B(2,0),C(4,3)。
(1)在平面直角坐标系中描出各点,画出△ABC;
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标。
22.(12分)定义:在平面直角坐标系中,已知点P1(a,b),P2(c,b),P3(c,d),这三个点中任意两点间的距离的最小值称为点P1,P2,P3的“最佳间距”。例如,如图,点P1(-1,2),P2(1,2),P3(1,3)的“最佳间距”是1。
(1)理解:点Q1(2,1),Q2(5,1),Q3(5,5)的“最佳间距”是 。
(2)探究:已知点O(0,0),A(-4,0),B(-4,y)(y≠0)。
①若点O,A,B的“最佳间距”是2,则y的值为 。
②点O,A,B的“最佳间距”最大是多少?请说明理由。
(3)迁移:当点O(0,0),E(m,0),P(m,-2m+1)的“最佳间距”取到最大值时,点P的坐标是 。
23.(13分)[2023春·茅箭区期中]【问题背景】
在平面直角坐标系中,已知点A(x1,y1),B(x2,y2),C是线段AB的中点,则点C的坐标为(,)。如A(-1,1),B(3,3),则AB的中点C的坐标为(,),即点C的坐标为(1,2)。
【解决问题】
(1)已知A(6,-2),B(-3,-3),则线段AB的中点M的坐标是 ;
(2)若点P(-3,7),线段PQ的中点坐标为(-1,5),则点Q的坐标是 ;
(3)已知三点E(4,-2),F(-3,-1),G(-1,-4),第四个点 H(x,y)与点E,F,G中的任意一个点构成的线段的中点与另外两个点构成的线段的中点重合,求点H的坐标。
参考答案
第三章质量评估
1.D 2.C 3.C 4.A 5.D 6.B 7.C 8.A 9.C 10.A 11.(-3,1) 12.31 13.四
14.(0,4) 15.(21 012,21 012)
16.(1)高中楼 (2)略 (3)四 (4,1) (1,3) (4)略
17.(1)略
(2)A'(2,3),B'(3,-1),C'(-1,-2)。
18.(1)m=-2 (2)M(-4,24)
19.(1)P(0,5) (2)PQ=5
20.(1)A(0,8),E(8,4),F(12,4)
(2)S△BDF=32
21.(1)略 (2)S△ABC=4 (3)点P的坐标为(0,5),(0,-3),(10,0)或(-6,0)。
22.(1)3 (2)①±2 ②点O,A,B的“最佳间距”最大是4。理由略。 (3)或(1,-1)
23.(1)(,-) (2)(1,3) (3)点H的坐标为(-8,-3),(6,-5)或(2,1)。
。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
