期末质量评估(含答案) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 期末质量评估(含答案) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 305.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 21:26:48 | ||
图片预览




文档简介
期末质量评估
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.勾股数,又名毕氏三元数,下列各组数构成勾股数的是( )
A.,, B.,, C.9,40,41 D.5,15,20
2.点M(-4,-1)关于y轴对称的点的坐标为( )
A.(-4,1) B.(4,1) C.(4,-1) D.(-4,-1)
3.一组数据3,6,7,4,x的平均数是5,则这组数据的中位数是( )
A.4 B.4.5 C.5 D.6
4.已知|3x-2y-1|+=0,则x,y的值为( )
A. B. C. D.
5.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线,与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是( )
A.y=-x+4 B.y=x+4 C.y=x+8 D.y=-x+8
6.已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放。若∠1=120°,则∠2的度数为( )
A.120° B.130° C.140° D.150°
7.直线y=-ax+a与直线y=ax在同一坐标系中的大致图象可能是( )
8.我国古代数学名著《九章算术》中记载:“粟米之法:粟率五十,粝米三十。今有米在十斗桶中,不知其数。满中添粟而舂之,得米七斗。问故米几何?”意思为:50斗谷子能出30斗米,即出米率为。今有米在容量为10斗的桶中,但不知道数量是多少。向桶中加满谷子,再舂成米,共得米7斗。问原来有米多少斗?如果设原来有米x斗,向桶中加谷子y斗,那么可列方程组为( )
A. B.
C. D.
9.如图,长方体的长为2,宽为1,高为3,一只蚂蚁从点A出发,沿长方体的外表面爬到点B处觅食,则它爬行的最短路程为( )
A. B.3 C.2 D.
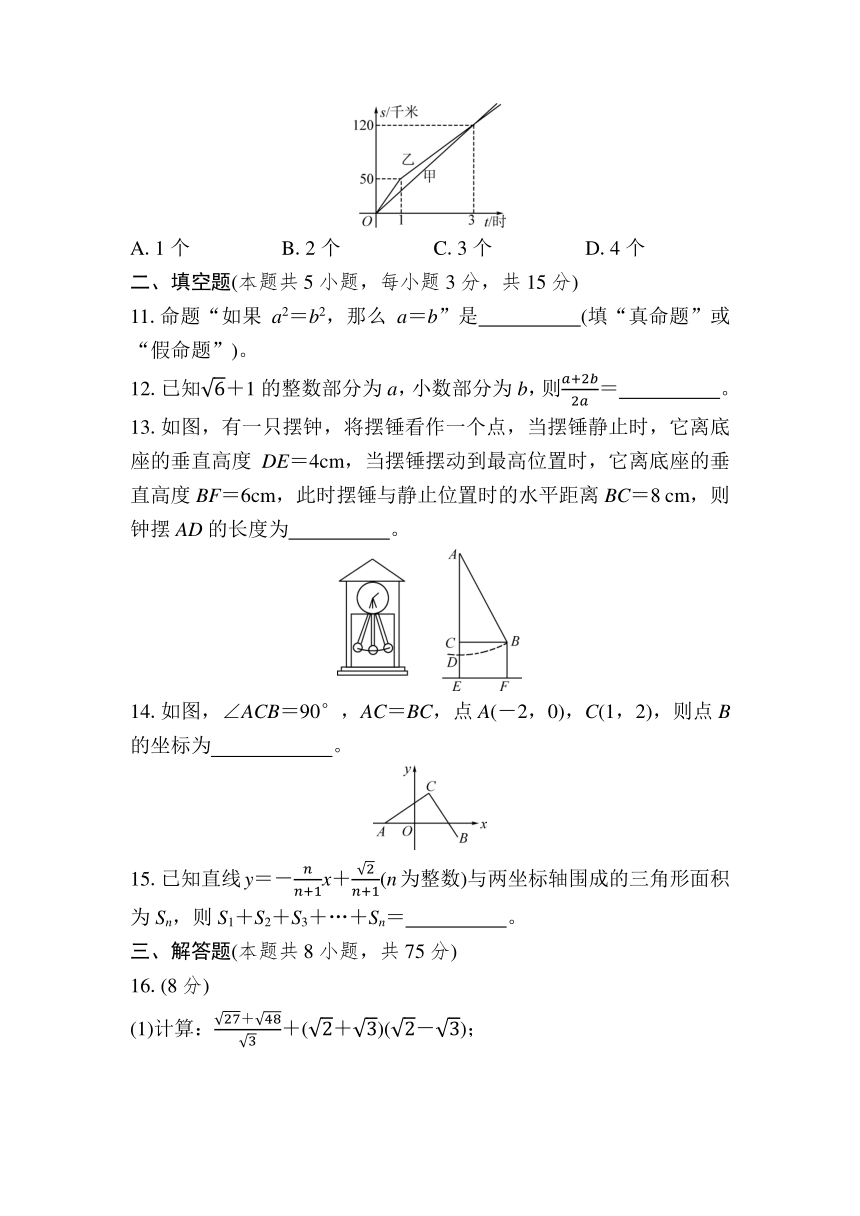
10.甲、乙两名运动员同时从A地出发前往B地,在笔直的公路上进行骑自行车训练。如图反映了甲、乙两名运动员在公路上进行训练时的行驶路程s(单位:千米)与行驶时间t(单位:时)之间的关系,下列四种说法:①甲的速度为40千米/时;②乙的速度始终为50千米/时;③行驶1小时时,乙在甲前方10千米处;④甲、乙两名运动员相距5千米时,t=0.5或t=2。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共5小题,每小题3分,共15分)
11.命题“如果a2=b2,那么a=b”是 (填“真命题”或“假命题”)。
12.已知+1的整数部分为a,小数部分为b,则= 。
13.如图,有一只摆钟,将摆锤看作一个点,当摆锤静止时,它离底座的垂直高度DE=4cm,当摆锤摆动到最高位置时,它离底座的垂直高度BF=6cm,此时摆锤与静止位置时的水平距离BC=8 cm,则钟摆AD的长度为 。
14.如图,∠ACB=90°,AC=BC,点A(-2,0),C(1,2),则点B的坐标为 。
15.已知直线y=-x+(n为整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+Sn= 。
三、解答题(本题共8小题,共75分)
16.(8分)
(1)计算:+(+)(-);
(2)解方程组:
17.(8分)如图,已知DC∥AB,E,F分别在DC,AB的延长线上,∠DCB=∠DAB,∠AGB=30°,∠AFE=60°,AE平分∠DAB。
(1)AD是否平行于BC?并说明理由。
(2)求证:AE⊥EF。
18.(8分)某科研团队研发了A,B,C三款智能机器人,为测试这三款机器人在图象识别能力和运动能力方面的综合表现,该团队对它们进行了全面测试。在图象识别能力测试中,A,B,C三款机器人的得分(满分为100分)分别为87分、85分、90分。运动能力测试由10位专业测试员根据一系列动作任务进行打分(每位测试员打分不超过10分),各位测试员打分之和作为该款智能机器人运动能力测试成绩。下面是机器人运动能力得分的统计图表:
A,B两款机器人运动
能力得分的折线图
C款机器人运动能力
得分的扇形统计图
A,B,C三款机器人运动能力测试情况统计表
机器人 测试员打分 的中位数 测试员打分的众数 运动能力测试成绩 方差
A m 9和10 85 1.85
B 8.5 8 87 s2
C 8 n p 2.01
现对三款机器人的运动能力测试数据进行详细分析,以评估哪款机器人的综合性能更优。
(1)填空:m= ,n= ;
(2)通过比较方差,判断测试员对 (填“A”“B”或“C”)款机器人运动能力测试表现评价的一致性程度更高;
(3)按图象识别能力测试成绩占40%,运动能力测试成绩占60%计算综合成绩,请你通过计算判断A,B,C三款机器人中综合成绩最高的是哪一款?
19.(8分)某汽车销售公司计划购进一批新能源汽车尝试进行销售。据了解,2辆A型汽车、3辆B型汽车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元。
(1)求A、B两种型号的汽车每辆进价分别为多少万元。
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),若该汽车销售公司销售1辆A型汽车可获利8 000元,销售1辆B型汽车可获利5 000元,则要购进A型、B型汽车各几辆,才能获得最大利润?最大利润是多少?
20.(8分)和为整数,4-1=3=2×1+1;
和为整数,9-4=5=2×2+1;
和为整数,16-9=7=2×3+1;
……
小明发现结论:若和为相邻的两个整数,且a<b,则b-a=2+1。
并给出了证明:∵和为相邻的两个整数,a<b,
∴=+1,∴b=a+2+1,
∴b-a=2+1。
请利用小明的结论和方法解决下列问题:
(1)若和为两个相邻整数,求a的值;
(2)若和为相差4的两个整数,求a的值。
21.(10分)在平面直角坐标系中,对于直线l及点P给出如下定义:过点P作y轴的垂线交直线l于点Q,若PQ≤1,则称点P为直线l的关联点,当PQ=1时,称点P为直线l的最佳关联点,当点P与点Q重合时,记PQ=0。例如,点P(1,2)是直线y=x的最佳关联点。根据阅读材料,解决下列问题。
如图,在平面直角坐标系中,已知直线l1:y=-x+3,l2:y=2x+b。
(1)已知点A(0,4),B(2,3),其中是直线l1的关联点是 ;
(2)若点D(-1,m)是直线l1的最佳关联点,求m的值;
(3)点E在x轴的正半轴上,点A(0,4),以OA、OE为边作正方形AOEF,若直线l2与正方形AOEF相交,且交点中至少有一个是直线l1的关联点,求b的取值范围。
22.(12分)(1)光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象。如图1,光线A从空气中射入水中,再从水中射入空气中,形成光线B,根据光学知识有∠1=∠2,∠3=∠4,请判断光线A与光线B是否平行,并说明理由。
图1
(2)光线照射到镜面会产生反射现象,由光学知识,入射光线与镜面的夹角与反射光线与镜面的夹角相等。如图2,有一口井,已知入射光线A与水平线OC的夹角为40°,现放置平面镜MN,可使反射光线B正好垂直照射到井底,则MN与水平线的夹角∠MOC的度数为 。
图2
(3)如图3,直线EF上有两点A,C,分别引两条射线AB,CD。已知∠BAF=110°,∠DCF=80°,射线AB绕A点以2°/秒的速度顺时针转动,同时射线CD绕点C以3°/秒的速度逆时针转动,设时间为t,在射线AB转动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t。
图3
23.(13分)[2024·余姚市期末]【定义理解】
在平面直角坐标系中,有A(m,0),B(0,n)两点,若存在点C使得∠ABC=90°,且AB=BC,则称点C为m的“等垂点”。
例如,在A(1,0),B(0,1),C(-1,0)三点中,因为∠ABC=90°,且AB=BC,所以点C为1的“等垂点”。
【探究应用】
(1)点A(2,0),B(0,2),则C(2,4) 2的“等垂点”(填“是”或“不是”)。
(2)如图1,若点A(4,0),B(0,3),若点C是4的“等垂点”,则点C的坐标为 。
图1
(3)如图2,若一次函数y=3x-5上存在5的“等垂点”,求5的“等垂点”C的坐标。
图2
【拓展提升】
(4)若在直线y=kx+b(k>0)上存在无数个5的“等垂点”,且直线y=kx+b(k>0)与x轴交于点E,与y轴交于点F,点M在线段EF上,点P在△EOF内,EP=4,OP=3,连接MP。设EM=a,直接写出△EPM的面积S关于a的函数表达式。
备用图
参考答案
期末质量评估
1.C 2.C 3.C 4.D 5.A 6.D 7.D 8.A 9.B 10.B 11.假命题 12. 13.17 cm 14.(3,-1) 15.
16.(1)原式=6。
(2)方程组的解是
17.(1)AD∥BC,理由略。 (2)略
18.(1)9 8 (2)B (3)综合成绩最高的是B款机器人。
19.(1)每辆A型汽车的进价是25万元,每辆B型汽车的进价是10万元。
(2)购进2辆A型汽车,15辆B型汽车时,才能获得最大利润,最大利润为91 000元。
20.(1)a=25 (2)a=625
21.(1)A (2)m=3或m=5 (3)2≤b≤4或-8≤b≤-4时,交点中至少有一个是直线l1的关联点。
22.(1)a∥b。理由略。 (2)65° (3)t的值为2,38,74,110或146。
23.(1)是 (2)(3,7)或(-3,-1)
(3)点C的坐标为(5,10)或C(0,-5)。
(4)△EPM的面积S关于a的函数表达式为S=a。
。
一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.勾股数,又名毕氏三元数,下列各组数构成勾股数的是( )
A.,, B.,, C.9,40,41 D.5,15,20
2.点M(-4,-1)关于y轴对称的点的坐标为( )
A.(-4,1) B.(4,1) C.(4,-1) D.(-4,-1)
3.一组数据3,6,7,4,x的平均数是5,则这组数据的中位数是( )
A.4 B.4.5 C.5 D.6
4.已知|3x-2y-1|+=0,则x,y的值为( )
A. B. C. D.
5.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线,与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是( )
A.y=-x+4 B.y=x+4 C.y=x+8 D.y=-x+8
6.已知直线l1∥l2,将含30°角的直角三角板按如图所示摆放。若∠1=120°,则∠2的度数为( )
A.120° B.130° C.140° D.150°
7.直线y=-ax+a与直线y=ax在同一坐标系中的大致图象可能是( )
8.我国古代数学名著《九章算术》中记载:“粟米之法:粟率五十,粝米三十。今有米在十斗桶中,不知其数。满中添粟而舂之,得米七斗。问故米几何?”意思为:50斗谷子能出30斗米,即出米率为。今有米在容量为10斗的桶中,但不知道数量是多少。向桶中加满谷子,再舂成米,共得米7斗。问原来有米多少斗?如果设原来有米x斗,向桶中加谷子y斗,那么可列方程组为( )
A. B.
C. D.
9.如图,长方体的长为2,宽为1,高为3,一只蚂蚁从点A出发,沿长方体的外表面爬到点B处觅食,则它爬行的最短路程为( )
A. B.3 C.2 D.
10.甲、乙两名运动员同时从A地出发前往B地,在笔直的公路上进行骑自行车训练。如图反映了甲、乙两名运动员在公路上进行训练时的行驶路程s(单位:千米)与行驶时间t(单位:时)之间的关系,下列四种说法:①甲的速度为40千米/时;②乙的速度始终为50千米/时;③行驶1小时时,乙在甲前方10千米处;④甲、乙两名运动员相距5千米时,t=0.5或t=2。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本题共5小题,每小题3分,共15分)
11.命题“如果a2=b2,那么a=b”是 (填“真命题”或“假命题”)。
12.已知+1的整数部分为a,小数部分为b,则= 。
13.如图,有一只摆钟,将摆锤看作一个点,当摆锤静止时,它离底座的垂直高度DE=4cm,当摆锤摆动到最高位置时,它离底座的垂直高度BF=6cm,此时摆锤与静止位置时的水平距离BC=8 cm,则钟摆AD的长度为 。
14.如图,∠ACB=90°,AC=BC,点A(-2,0),C(1,2),则点B的坐标为 。
15.已知直线y=-x+(n为整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+Sn= 。
三、解答题(本题共8小题,共75分)
16.(8分)
(1)计算:+(+)(-);
(2)解方程组:
17.(8分)如图,已知DC∥AB,E,F分别在DC,AB的延长线上,∠DCB=∠DAB,∠AGB=30°,∠AFE=60°,AE平分∠DAB。
(1)AD是否平行于BC?并说明理由。
(2)求证:AE⊥EF。
18.(8分)某科研团队研发了A,B,C三款智能机器人,为测试这三款机器人在图象识别能力和运动能力方面的综合表现,该团队对它们进行了全面测试。在图象识别能力测试中,A,B,C三款机器人的得分(满分为100分)分别为87分、85分、90分。运动能力测试由10位专业测试员根据一系列动作任务进行打分(每位测试员打分不超过10分),各位测试员打分之和作为该款智能机器人运动能力测试成绩。下面是机器人运动能力得分的统计图表:
A,B两款机器人运动
能力得分的折线图
C款机器人运动能力
得分的扇形统计图
A,B,C三款机器人运动能力测试情况统计表
机器人 测试员打分 的中位数 测试员打分的众数 运动能力测试成绩 方差
A m 9和10 85 1.85
B 8.5 8 87 s2
C 8 n p 2.01
现对三款机器人的运动能力测试数据进行详细分析,以评估哪款机器人的综合性能更优。
(1)填空:m= ,n= ;
(2)通过比较方差,判断测试员对 (填“A”“B”或“C”)款机器人运动能力测试表现评价的一致性程度更高;
(3)按图象识别能力测试成绩占40%,运动能力测试成绩占60%计算综合成绩,请你通过计算判断A,B,C三款机器人中综合成绩最高的是哪一款?
19.(8分)某汽车销售公司计划购进一批新能源汽车尝试进行销售。据了解,2辆A型汽车、3辆B型汽车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元。
(1)求A、B两种型号的汽车每辆进价分别为多少万元。
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),若该汽车销售公司销售1辆A型汽车可获利8 000元,销售1辆B型汽车可获利5 000元,则要购进A型、B型汽车各几辆,才能获得最大利润?最大利润是多少?
20.(8分)和为整数,4-1=3=2×1+1;
和为整数,9-4=5=2×2+1;
和为整数,16-9=7=2×3+1;
……
小明发现结论:若和为相邻的两个整数,且a<b,则b-a=2+1。
并给出了证明:∵和为相邻的两个整数,a<b,
∴=+1,∴b=a+2+1,
∴b-a=2+1。
请利用小明的结论和方法解决下列问题:
(1)若和为两个相邻整数,求a的值;
(2)若和为相差4的两个整数,求a的值。
21.(10分)在平面直角坐标系中,对于直线l及点P给出如下定义:过点P作y轴的垂线交直线l于点Q,若PQ≤1,则称点P为直线l的关联点,当PQ=1时,称点P为直线l的最佳关联点,当点P与点Q重合时,记PQ=0。例如,点P(1,2)是直线y=x的最佳关联点。根据阅读材料,解决下列问题。
如图,在平面直角坐标系中,已知直线l1:y=-x+3,l2:y=2x+b。
(1)已知点A(0,4),B(2,3),其中是直线l1的关联点是 ;
(2)若点D(-1,m)是直线l1的最佳关联点,求m的值;
(3)点E在x轴的正半轴上,点A(0,4),以OA、OE为边作正方形AOEF,若直线l2与正方形AOEF相交,且交点中至少有一个是直线l1的关联点,求b的取值范围。
22.(12分)(1)光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象。如图1,光线A从空气中射入水中,再从水中射入空气中,形成光线B,根据光学知识有∠1=∠2,∠3=∠4,请判断光线A与光线B是否平行,并说明理由。
图1
(2)光线照射到镜面会产生反射现象,由光学知识,入射光线与镜面的夹角与反射光线与镜面的夹角相等。如图2,有一口井,已知入射光线A与水平线OC的夹角为40°,现放置平面镜MN,可使反射光线B正好垂直照射到井底,则MN与水平线的夹角∠MOC的度数为 。
图2
(3)如图3,直线EF上有两点A,C,分别引两条射线AB,CD。已知∠BAF=110°,∠DCF=80°,射线AB绕A点以2°/秒的速度顺时针转动,同时射线CD绕点C以3°/秒的速度逆时针转动,设时间为t,在射线AB转动一周的时间内,是否存在某时刻,使得CD与AB平行?若存在,求出所有满足条件的时间t。
图3
23.(13分)[2024·余姚市期末]【定义理解】
在平面直角坐标系中,有A(m,0),B(0,n)两点,若存在点C使得∠ABC=90°,且AB=BC,则称点C为m的“等垂点”。
例如,在A(1,0),B(0,1),C(-1,0)三点中,因为∠ABC=90°,且AB=BC,所以点C为1的“等垂点”。
【探究应用】
(1)点A(2,0),B(0,2),则C(2,4) 2的“等垂点”(填“是”或“不是”)。
(2)如图1,若点A(4,0),B(0,3),若点C是4的“等垂点”,则点C的坐标为 。
图1
(3)如图2,若一次函数y=3x-5上存在5的“等垂点”,求5的“等垂点”C的坐标。
图2
【拓展提升】
(4)若在直线y=kx+b(k>0)上存在无数个5的“等垂点”,且直线y=kx+b(k>0)与x轴交于点E,与y轴交于点F,点M在线段EF上,点P在△EOF内,EP=4,OP=3,连接MP。设EM=a,直接写出△EPM的面积S关于a的函数表达式。
备用图
参考答案
期末质量评估
1.C 2.C 3.C 4.D 5.A 6.D 7.D 8.A 9.B 10.B 11.假命题 12. 13.17 cm 14.(3,-1) 15.
16.(1)原式=6。
(2)方程组的解是
17.(1)AD∥BC,理由略。 (2)略
18.(1)9 8 (2)B (3)综合成绩最高的是B款机器人。
19.(1)每辆A型汽车的进价是25万元,每辆B型汽车的进价是10万元。
(2)购进2辆A型汽车,15辆B型汽车时,才能获得最大利润,最大利润为91 000元。
20.(1)a=25 (2)a=625
21.(1)A (2)m=3或m=5 (3)2≤b≤4或-8≤b≤-4时,交点中至少有一个是直线l1的关联点。
22.(1)a∥b。理由略。 (2)65° (3)t的值为2,38,74,110或146。
23.(1)是 (2)(3,7)或(-3,-1)
(3)点C的坐标为(5,10)或C(0,-5)。
(4)△EPM的面积S关于a的函数表达式为S=a。
。
同课章节目录
