第14章 数据的收集与表示(单元测试.含解析)-2025-2026学年八年级上册数学华东师大版(2024)
文档属性
| 名称 | 第14章 数据的收集与表示(单元测试.含解析)-2025-2026学年八年级上册数学华东师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 724.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 06:32:02 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第14章 数据的收集与表示
一、选择题(本题共计7小题,每题3分,共计21分,)
1.(3分)如若调查你校学生学业负担是否过重,选用下列哪种方法最恰当( )
A.查阅文献资料 B.对学生问卷调查
C.对老师问卷调查 D.对校领导问卷调查
2.(3分)某班50名学生在适应性考试中,分数段在90~100分的频率为0.1,则该班在这个分数段的学生人数为( )
A.1人 B.2人 C.5人 D.10人
3.(3分)下列各组数据中,组中值不是10的是( )
A.7≤x<13 B.8≤x<12 C.3≤x<7 D.0≤x<20
4.(3分)某工厂上半年生产总值增长率的变化情况如图所示,从图看,下列结论中不正确的是( )
A.1~5月份生产总值增长率逐月减少
B.6月份生产总值的年增长率开始回升
C.这半年中每月的生产总值不断增长
D.这半年中每月的生产总值有增有减
5.(3分)某中学八年级有500名学生参加生物、地理会考,考试成绩在80分至100分之间的共有180人,则这个分数段的频率是( )
A.0.18 B.0.36 C.180 D.500
6.(3分)有一组数据,最小的为40,最大的为89,现在把它们分组,组距为10,则可分为( )
A.4组 B.5组 C.7组 D.8组
7.(3分)下表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,且九年级文艺小组活动次数与科技小组活动次数相同.
年级 课外小组活动总时间(单位:h) 文艺小组活动次数 科技小组活动次数
七年级 19 8 7
八年级 16.5 7 6
九年级 10
则九年级科技小组活动的次数是( )
A.3 B.4 C.5 D.6
二、填空题(本题共计7小题,每题3分,共计21分,)
8.(3分)据我国第6次人口普查数据公报,我国人口中0~14岁的占16.60%,15~59岁的占70.14%,60岁以上(含60岁)的占13.26%.根据上述数据绘制扇形统计图,则60岁以上(含60岁)的扇形的圆心角度数是 .(结果精确到1°)
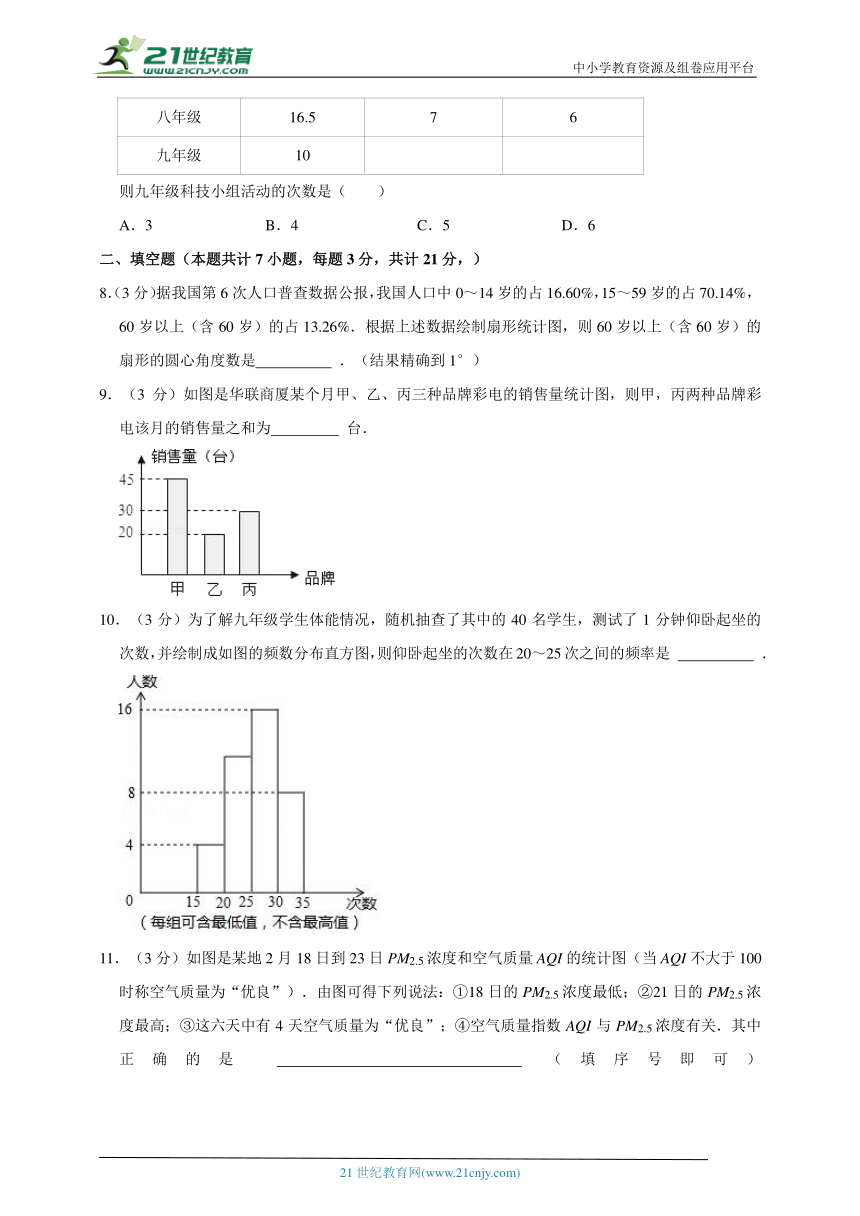
9.(3分)如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲,丙两种品牌彩电该月的销售量之和为 台.
10.(3分)为了解九年级学生体能情况,随机抽查了其中的40名学生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数分布直方图,则仰卧起坐的次数在20~25次之间的频率是 .
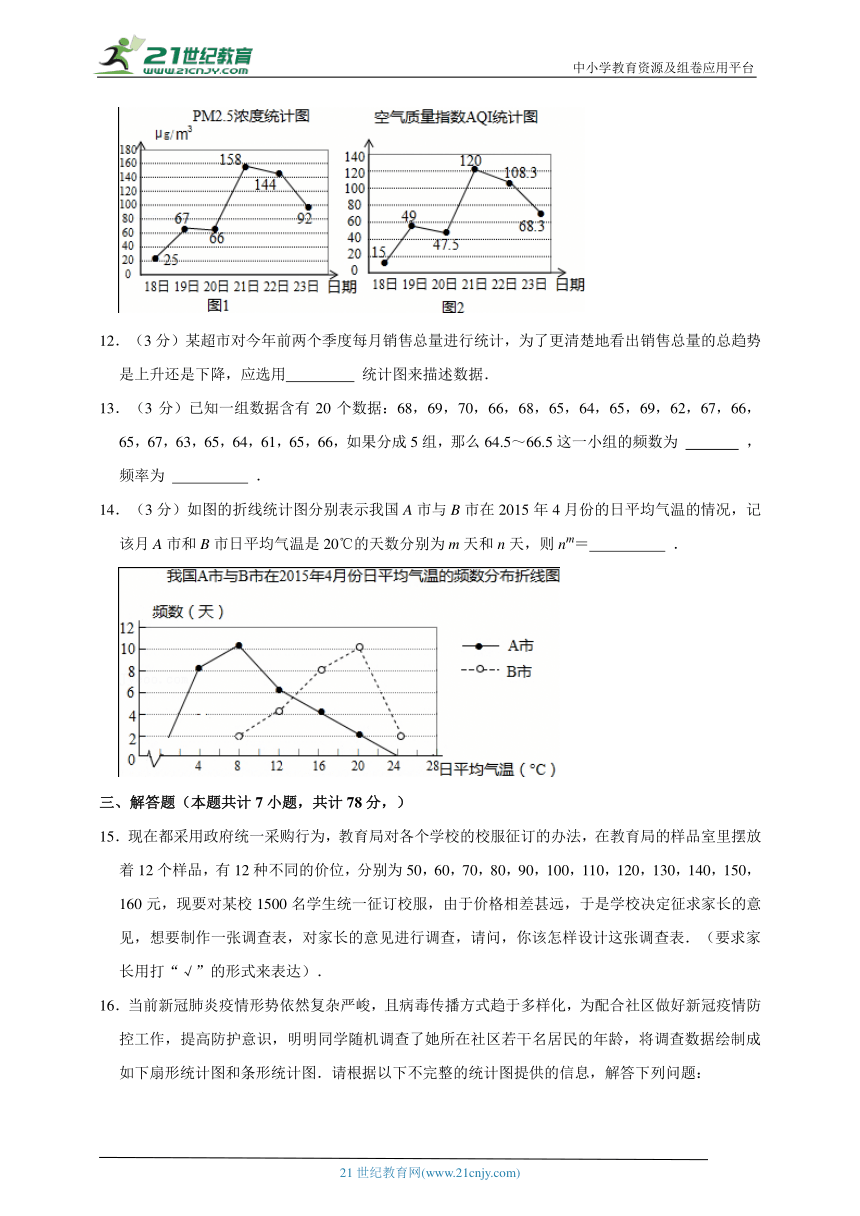
11.(3分)如图是某地2月18日到23日PM2.5浓度和空气质量AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②21日的PM2.5浓度最高;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关.其中正确的是 (填序号即可)
12.(3分)某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 统计图来描述数据.
13.(3分)已知一组数据含有20个数据:68,69,70,66,68,65,64,65,69,62,67,66,65,67,63,65,64,61,65,66,如果分成5组,那么64.5~66.5这一小组的频数为 ,频率为 .
14.(3分)如图的折线统计图分别表示我国A市与B市在2015年4月份的日平均气温的情况,记该月A市和B市日平均气温是20℃的天数分别为m天和n天,则nm= .
三、解答题(本题共计7小题,共计78分,)
15.现在都采用政府统一采购行为,教育局对各个学校的校服征订的办法,在教育局的样品室里摆放着12个样品,有12种不同的价位,分别为50,60,70,80,90,100,110,120,130,140,150,160元,现要对某校1500名学生统一征订校服,由于价格相差甚远,于是学校决定征求家长的意见,想要制作一张调查表,对家长的意见进行调查,请问,你该怎样设计这张调查表.(要求家长用打“√”的形式来表达).
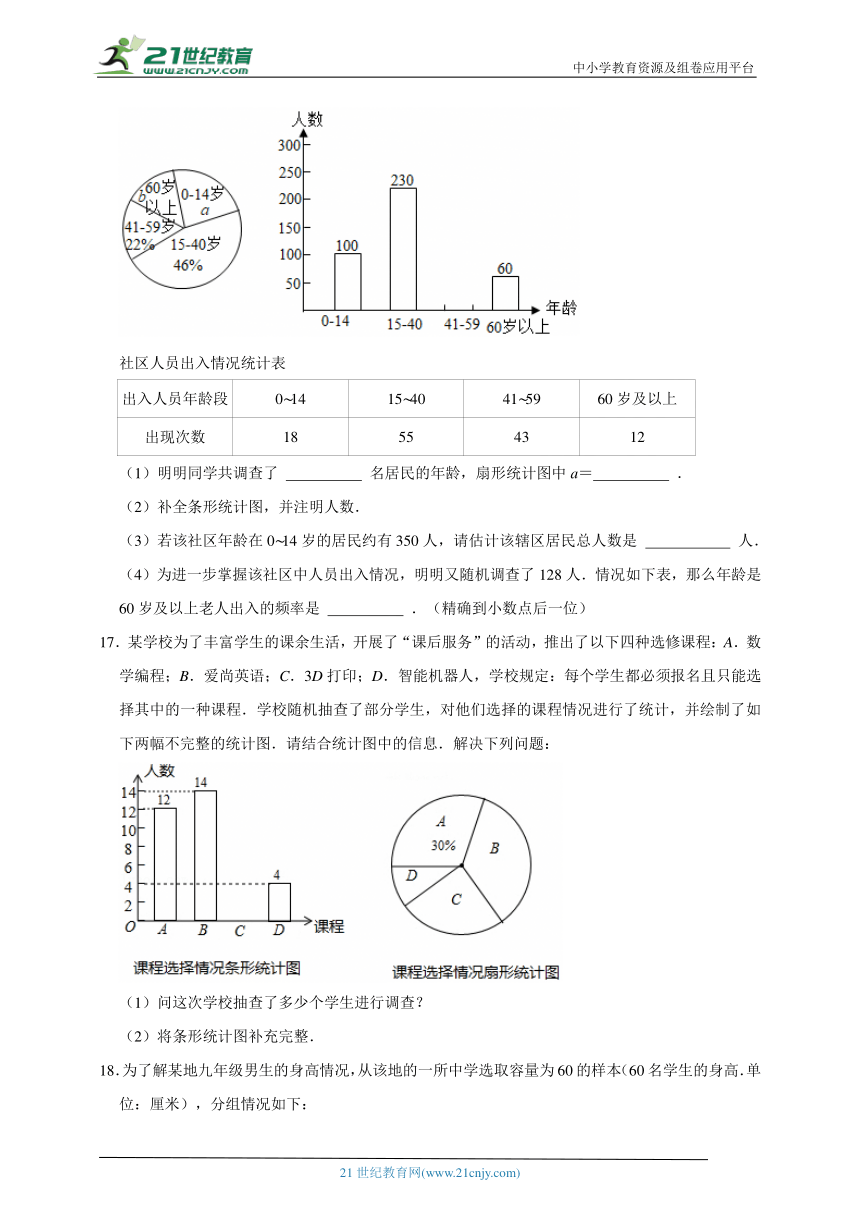
16.当前新冠肺炎疫情形势依然复杂严峻,且病毒传播方式趋于多样化,为配合社区做好新冠疫情防控工作,提高防护意识,明明同学随机调查了她所在社区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图.请根据以下不完整的统计图提供的信息,解答下列问题:
社区人员出入情况统计表
出入人员年龄段 0 14 15 40 41 59 60岁及以上
出现次数 18 55 43 12
(1)明明同学共调查了 名居民的年龄,扇形统计图中a= .
(2)补全条形统计图,并注明人数.
(3)若该社区年龄在0 14岁的居民约有350人,请估计该辖区居民总人数是 人.
(4)为进一步掌握该社区中人员出入情况,明明又随机调查了128人.情况如下表,那么年龄是60岁及以上老人出入的频率是 .(精确到小数点后一位)
17.某学校为了丰富学生的课余生活,开展了“课后服务”的活动,推出了以下四种选修课程:A.数学编程;B.爱尚英语;C.3D打印;D.智能机器人,学校规定:每个学生都必须报名且只能选择其中的一种课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息.解决下列问题:
(1)问这次学校抽查了多少个学生进行调查?
(2)将条形统计图补充完整.
18.为了解某地九年级男生的身高情况,从该地的一所中学选取容量为60的样本(60名学生的身高.单位:厘米),分组情况如下:
分组 147.5~155.5 155.5~163.5 163.5~171.5 171.5~179.5
频数 6 21 m
频率 a 0.1
求出表中a和m的值.
19.学期结束前,学校想调查学生对七年级数学实验教材的意见,特向400名学生做问卷调查,其结果如下:
意见 非常喜欢 喜欢 有一点喜欢 不喜欢
人数 200 160 32 8
(1)计算出每一种意见的人数占总调查人数的百分比;
(2)请作出反映此调查结果的扇形统计图(图中).
(3)从统计图中你能得出什么结论?说明你的理由.
20.我国五座名山的主峰的海拔高度如表所示:
山名 泰山 华山 黄山 庐山 峨眉山
海拔高度(米) 1524 1997 1873 1500 3099
(1)最矮山的海拔是 米;
(2)黄山比泰山高 米;
(3)根据表中的数据制成条形统计图.
21.省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者、节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
月均用水量x(吨) 频数(户) 频率
0<x≤4 12 a
4<x≤8 32 0.32
8<x≤12 b c
12<x≤16 20 0.2
16<x≤20 8 0.08
20<x≤24 4 0.04
(1)a= ,b= ,c= ,并将如图所示的频数分布直方图补充完整;
(2)求月均用水量超过12吨的住户占所调查总住户的百分比.
第14章 数据的收集与表示
参考答案与试题解析
一、选择题(本题共计7小题,每题3分,共计21分,)
1.(3分)如若调查你校学生学业负担是否过重,选用下列哪种方法最恰当( )
A.查阅文献资料 B.对学生问卷调查
C.对老师问卷调查 D.对校领导问卷调查
【答案】B
【分析】为了得到比较准确的结果,并且易于操作,即操作的可行性,做出判断即可.
【解答】解:为得到结果准确,并且可操作性,因此选取,对学生问卷调查,
故选:B.
【点评】考查数据数据的方法,搜集和整理数据的原则是要考虑对结果要求的准确程度和可行性.
2.(3分)某班50名学生在适应性考试中,分数段在90~100分的频率为0.1,则该班在这个分数段的学生人数为( )
A.1人 B.2人 C.5人 D.10人
【答案】C
【分析】根据频数=总数×频率,求解即可.
【解答】解:得该班在这个分数段的学生是50×0.1=5.
故选:C.
【点评】掌握频率、频数、总数三者之间的关系:频率=频数÷总数,根据条件能够对公式灵活变形.
3.(3分)下列各组数据中,组中值不是10的是( )
A.7≤x<13 B.8≤x<12 C.3≤x<7 D.0≤x<20
【答案】C
【分析】组中值就是组的两个两个分点的平均数,据此即可求得各个选项的组中值,即可作出判断.
【解答】解:A、组中值是:(7+13)=10,故选项错误;
B、组中值是:(8+12)=10,故选项错误;
C、组中值是:(3+7)=5,故选项正确;
D、组中值是(0+20)=10,故选项错误.
故选:C.
【点评】本题考查了组中值的定义,理解定义是关键.
4.(3分)某工厂上半年生产总值增长率的变化情况如图所示,从图看,下列结论中不正确的是( )
A.1~5月份生产总值增长率逐月减少
B.6月份生产总值的年增长率开始回升
C.这半年中每月的生产总值不断增长
D.这半年中每月的生产总值有增有减
【答案】D
【分析】图中数据为生产总值增长率,而不是生产总值,根据折线统计图可知增长率均为正数,所以生产总值一直在增加,只是1~5月份生产总值增长率逐月减少,6月份生产总值的年增长率开始回升,
【解答】解:每月的增长率都是正数,说明生产总值每月都增长.因而D错误.A、B、C都正确.
故选:D.
【点评】本题考查折线统计图的运用,折线统计图表示的是事物的变化情况.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
5.(3分)某中学八年级有500名学生参加生物、地理会考,考试成绩在80分至100分之间的共有180人,则这个分数段的频率是( )
A.0.18 B.0.36 C.180 D.500
【答案】B
【分析】此题只需根据频率=频数÷总数,进行计算即可.
【解答】解:根据题意,得
这个分数段的频率是180÷500=0.36.
故选:B.
【点评】掌握频率的正确计算方法:频率=频数÷总数.
6.(3分)有一组数据,最小的为40,最大的为89,现在把它们分组,组距为10,则可分为( )
A.4组 B.5组 C.7组 D.8组
【答案】B
【分析】根据组数=(最大值﹣最小值)÷组距计算,注意小数部分要进位.
【解答】解:在样本数据中最大值为89,最小值为40,它们的差是89﹣40=49,已知组距为10,那么由于4.9,故可以分成5组.
故选:B.
【点评】本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
7.(3分)下表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,且九年级文艺小组活动次数与科技小组活动次数相同.
年级 课外小组活动总时间(单位:h) 文艺小组活动次数 科技小组活动次数
七年级 19 8 7
八年级 16.5 7 6
九年级 10
则九年级科技小组活动的次数是( )
A.3 B.4 C.5 D.6
【答案】B
【分析】设文艺小组每次活动的时间为x小时,科技小组每次活动时间为y小时,根据图表七年级和八年级课外活动的总时间列方程组求解,然后求出九年级的次数.
【解答】解:方法一:设文艺小组每次活动的时间为x小时,科技小组每次活动时间为y小时,
由题意得,,
解得:,
设九年级文艺小组的活动次数为a,科技小组的活动次数为b,
则1.5a+b=10,
∵a、b为整数,且a=b,
∴a=4,b=4.
方法二:设文艺小组每次活动的时间为m小时,则科技小组每次活动时间为小时,
根据题意得7m+616.5,
解得m=1.5,
则1,
∵1.5×4+1×4=10,
∴九年级的科技活动与文艺活动的次数均为4次.
故选:B.
【点评】本题考查了统计表和二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.
二、填空题(本题共计7小题,每题3分,共计21分,)
8.(3分)据我国第6次人口普查数据公报,我国人口中0~14岁的占16.60%,15~59岁的占70.14%,60岁以上(含60岁)的占13.26%.根据上述数据绘制扇形统计图,则60岁以上(含60岁)的扇形的圆心角度数是 48° .(结果精确到1°)
【答案】见试题解答内容
【分析】利用360度乘以对应的百分比即可求得.
【解答】解:60岁以上(含60岁)的扇形的圆心角度数是:360×13.26%=47.736°≈48°.
故答案为:48°.
【点评】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°比.
9.(3分)如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲,丙两种品牌彩电该月的销售量之和为 75 台.
【答案】见试题解答内容
【分析】从图中可以看出并计算:甲,丙两种品牌彩电该月的销售量之和为45+30=75.
【解答】解:45+30=75.
【点评】从不同的统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据.
10.(3分)为了解九年级学生体能情况,随机抽查了其中的40名学生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数分布直方图,则仰卧起坐的次数在20~25次之间的频率是 0.3 .
【答案】见试题解答内容
【分析】首先利用总人数40减去其它各组的人数求得20~25次的频数,然后根据频率公式:频率,即可求解.
【解答】解:在20~25次之间的频数是:40﹣16﹣8﹣4=12,
则次数在20~25次之间的频率是:0.3.
故答案为:0.3.
【点评】本题考查了频率公式:频率,即可求解.
11.(3分)如图是某地2月18日到23日PM2.5浓度和空气质量AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②21日的PM2.5浓度最高;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关.其中正确的是 ①②③④ (填序号即可)
【答案】见试题解答内容
【分析】利用折线统计图1可判断18日对应的PM2.5浓度的值最小,则可①进行判断;根据21日对应的PM2.5浓度最高,则可对②进行判断;利用折线统计图2找出AQI不大于100的数据可对③进行判断;结合两个折线统计图,比较每天的PM2.5浓度和空气质量指数AQI可对④进行判断.
【解答】解:18日的PM2.5浓度最低,为25,所以①正确;
21日对应的PM2.5浓度最高所以②正确;
这六天中,18日、19日、20日、23日的空气质量为“优良”,所以③正确;
空气质量指数AQI与PM2.5浓度有关,PM2.5浓度越大,空气质量指数AQI越大,所以④正确.
故答案为:①②③④.
【点评】本题考查了折线统计图:折线图是用一个单位表示一定的数量,根据数量的多少描出各点,然后把各点用线段依次连接起来.以折线的上升或下降来表示统计数量增减变化.折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.
12.(3分)某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 折线 统计图来描述数据.
【答案】见试题解答内容
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目.
【解答】解:根据题意,得
要求清楚地表示销售总量的总趋势是上升还是下降,结合统计图各自的特点,应选用折线统计图.
【点评】此题考查扇形统计图、折线统计图、条形统计图各自的特点.
13.(3分)已知一组数据含有20个数据:68,69,70,66,68,65,64,65,69,62,67,66,65,67,63,65,64,61,65,66,如果分成5组,那么64.5~66.5这一小组的频数为 8 ,频率为 0.4 .
【答案】见试题解答内容
【分析】根据题意,找在64.5﹣66.5之间的数据,计算其个数;再由频率的计算方法,计算可得答案.
【解答】解:根据题意,发现数据中在64.5﹣66.5之间的有8个数据,
故64.5~66.5这一小组的频数为8,频率为0.4;
故答案为:8,0.4.
【点评】本题考查频率的计算、频数的确定方法,通过查找确定该组的频数时,要十分细心.
14.(3分)如图的折线统计图分别表示我国A市与B市在2015年4月份的日平均气温的情况,记该月A市和B市日平均气温是20℃的天数分别为m天和n天,则nm= 100 .
【答案】见试题解答内容
【分析】根据观察纵坐标,可得m、n的值,根据乘方运算,可得答案.
【解答】解:由纵坐标看出A市日平均气温是20℃的天数为2天,B市日平均气温是20℃的天数为10天,即m=2,n=10.nm=100,故答案为:100.
【点评】本题考查了折线统计图,观察统计图获得m、n的值是解题关键.
三、解答题(本题共计7小题,共计78分,)
15.现在都采用政府统一采购行为,教育局对各个学校的校服征订的办法,在教育局的样品室里摆放着12个样品,有12种不同的价位,分别为50,60,70,80,90,100,110,120,130,140,150,160元,现要对某校1500名学生统一征订校服,由于价格相差甚远,于是学校决定征求家长的意见,想要制作一张调查表,对家长的意见进行调查,请问,你该怎样设计这张调查表.(要求家长用打“√”的形式来表达).
【答案】见试题解答内容
【分析】利用已知数据范围可以分成6组,进而得出答案即可.
【解答】解:如表格所示:
价格范围 在你认为合理的价格后面打“√”,只能选一个
50~60
70~80
90~100
110~120
130~140
150~160
【点评】此题主要考查了调查收集数据的过程与方法,正确分组是解题关键.
16.当前新冠肺炎疫情形势依然复杂严峻,且病毒传播方式趋于多样化,为配合社区做好新冠疫情防控工作,提高防护意识,明明同学随机调查了她所在社区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图.请根据以下不完整的统计图提供的信息,解答下列问题:
社区人员出入情况统计表
出入人员年龄段 0 14 15 40 41 59 60岁及以上
出现次数 18 55 43 12
(1)明明同学共调查了 500 名居民的年龄,扇形统计图中a= 20% .
(2)补全条形统计图,并注明人数.
(3)若该社区年龄在0 14岁的居民约有350人,请估计该辖区居民总人数是 1750 人.
(4)为进一步掌握该社区中人员出入情况,明明又随机调查了128人.情况如下表,那么年龄是60岁及以上老人出入的频率是 0.1 .(精确到小数点后一位)
【答案】(1)500,20%.
(2)作图见解析部分.
(3)1750人.
(4)0.1.
【分析】(1)利用15﹣40的人数与百分比,求出总人数即可.再根据百分数的定义求出0﹣14的百分比a即可.
(2)求出14﹣59的人数,画出条形统计图即可.
(3)用样本估计总体的思想解决问题即可.
(4)用样本估计总体的思想解决问题即可.
【解答】解:(1)总人数500(名),a20%,
故答案为:500,20%.
(2)41﹣59的人数=500×22%=110(名),
条形图如图所示:
(3)1750(人),
故答案为:1750.
(4)0.1.
故答案为:0.1.
【点评】本题考查条形统计图,扇形统计图,样本估计总体等知识,解题的关键是掌握基本概念,属于中考常考题型.
17.某学校为了丰富学生的课余生活,开展了“课后服务”的活动,推出了以下四种选修课程:A.数学编程;B.爱尚英语;C.3D打印;D.智能机器人,学校规定:每个学生都必须报名且只能选择其中的一种课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息.解决下列问题:
(1)问这次学校抽查了多少个学生进行调查?
(2)将条形统计图补充完整.
【答案】见试题解答内容
【分析】(1)利用“A课程”的频数除以它所占的百分比得到调查的总人数;
(2)计算出“C课程”的人数后补全条形统计图即可.
【解答】解:(1)这次学校抽查的学生人数是12÷30%=40(人);
(2)C课程”的人数为40﹣12﹣14﹣4=10(人),
条形统计图补充为:
【点评】本题考查条形统计图、扇形统计图,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
18.为了解某地九年级男生的身高情况,从该地的一所中学选取容量为60的样本(60名学生的身高.单位:厘米),分组情况如下:
分组 147.5~155.5 155.5~163.5 163.5~171.5 171.5~179.5
频数 6 21 m
频率 a 0.1
求出表中a和m的值.
【答案】见试题解答内容
【分析】由从该地的一所中学选取容量为60的样本,观察表格,根据频率与频数的关系,即可求得答案.
【解答】解:∵选取容量为60的样本,
∴147.5~155.5的频率为:6÷60=0.1,155.5~163.5的频率为:21÷60=0.35,
∵171.5~179.5的频率为0.1,
∴a=1﹣0.1﹣0.35﹣0.1=0.45;
∴m=60×0.1=6.
即:a=0.45,m=6.
【点评】此题考查了频数(率)分布表.此题难度不大,注意准确认识表格是关键.
19.学期结束前,学校想调查学生对七年级数学实验教材的意见,特向400名学生做问卷调查,其结果如下:
意见 非常喜欢 喜欢 有一点喜欢 不喜欢
人数 200 160 32 8
(1)计算出每一种意见的人数占总调查人数的百分比;
(2)请作出反映此调查结果的扇形统计图(图中).
(3)从统计图中你能得出什么结论?说明你的理由.
【答案】见试题解答内容
【分析】(1)利用每种意见的人数÷总人数即可求解;
(2)利用所求的百分比,求出相应圆心角的度数,即可画图;
(3)利用统计图显示的信息,进行描述即可.
【解答】解:(1)非常喜欢:100%=50%;
喜欢:100%=40%;
有一点喜欢:100%=8%;
不喜欢:100%=2%.
(2)表示非常喜欢的圆心角=50%×360°=180度;
表示喜欢的圆心角=40%×360°=144度;
表示有一点喜欢的圆心角=8%×360°=28.8度;
表示不喜欢的圆心角=2%×360°=7.2度.
(3)从统计图中可以看出大多数同学喜欢七年级实验教材,因为在扇形统计图中喜欢的同学占绝大多数.
【点评】读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
20.我国五座名山的主峰的海拔高度如表所示:
山名 泰山 华山 黄山 庐山 峨眉山
海拔高度(米) 1524 1997 1873 1500 3099
(1)最矮山的海拔是 1500 米;
(2)黄山比泰山高 349 米;
(3)根据表中的数据制成条形统计图.
【答案】见试题解答内容
【分析】(1)观察表格中的数据,得出庐山海拔最矮,得出最矮山的海拔即可;
(2)用黄山的海拔减去泰山的海拔即可得到结果;
(3)将表格中的数据制成统计图,如图所示.
【解答】解:(1)观察表格得:最矮山的海拔是1500米;
(2)根据题意得:1873﹣1524=349(米),
则黄山比泰山高349米;
(3)如图所示:
故答案为:(1)1500;(2)349
【点评】此题考查了条形统计图,以及统计表,弄清题意是解本题的关键.
21.省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者、节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
月均用水量x(吨) 频数(户) 频率
0<x≤4 12 a
4<x≤8 32 0.32
8<x≤12 b c
12<x≤16 20 0.2
16<x≤20 8 0.08
20<x≤24 4 0.04
(1)a= 0.12 ,b= 24 ,c= 0.24 ,并将如图所示的频数分布直方图补充完整;
(2)求月均用水量超过12吨的住户占所调查总住户的百分比.
【答案】(1)0.12、24、0.24,补全图形见解答;
(2)32%.
【分析】(1)根据4<x≤8的频数和频率求出总户数,再用0<x≤4的频数乘以总数求出a,用总数减去其它月均用水量求出8<x≤12的频数,即b的值,用B的值除以总数即可求出c,从而补全统计图;
(2)把月均用水量超过12吨的住户的频率加起来即可得出答案.
【解答】解:(1)根据题意得:总户数为32÷0.32=100(户),
则a=12÷100=0.12;
b=100﹣12﹣32﹣20﹣8﹣4=24;
c=24÷100=0.24;
补全图形如下:
故答案为:0.12、24、0.24;
(2)月均用水量超过12吨的住户占所调查总住户的百分比为100%=32%.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第14章 数据的收集与表示
一、选择题(本题共计7小题,每题3分,共计21分,)
1.(3分)如若调查你校学生学业负担是否过重,选用下列哪种方法最恰当( )
A.查阅文献资料 B.对学生问卷调查
C.对老师问卷调查 D.对校领导问卷调查
2.(3分)某班50名学生在适应性考试中,分数段在90~100分的频率为0.1,则该班在这个分数段的学生人数为( )
A.1人 B.2人 C.5人 D.10人
3.(3分)下列各组数据中,组中值不是10的是( )
A.7≤x<13 B.8≤x<12 C.3≤x<7 D.0≤x<20
4.(3分)某工厂上半年生产总值增长率的变化情况如图所示,从图看,下列结论中不正确的是( )
A.1~5月份生产总值增长率逐月减少
B.6月份生产总值的年增长率开始回升
C.这半年中每月的生产总值不断增长
D.这半年中每月的生产总值有增有减
5.(3分)某中学八年级有500名学生参加生物、地理会考,考试成绩在80分至100分之间的共有180人,则这个分数段的频率是( )
A.0.18 B.0.36 C.180 D.500
6.(3分)有一组数据,最小的为40,最大的为89,现在把它们分组,组距为10,则可分为( )
A.4组 B.5组 C.7组 D.8组
7.(3分)下表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,且九年级文艺小组活动次数与科技小组活动次数相同.
年级 课外小组活动总时间(单位:h) 文艺小组活动次数 科技小组活动次数
七年级 19 8 7
八年级 16.5 7 6
九年级 10
则九年级科技小组活动的次数是( )
A.3 B.4 C.5 D.6
二、填空题(本题共计7小题,每题3分,共计21分,)
8.(3分)据我国第6次人口普查数据公报,我国人口中0~14岁的占16.60%,15~59岁的占70.14%,60岁以上(含60岁)的占13.26%.根据上述数据绘制扇形统计图,则60岁以上(含60岁)的扇形的圆心角度数是 .(结果精确到1°)
9.(3分)如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲,丙两种品牌彩电该月的销售量之和为 台.
10.(3分)为了解九年级学生体能情况,随机抽查了其中的40名学生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数分布直方图,则仰卧起坐的次数在20~25次之间的频率是 .
11.(3分)如图是某地2月18日到23日PM2.5浓度和空气质量AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②21日的PM2.5浓度最高;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关.其中正确的是 (填序号即可)
12.(3分)某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 统计图来描述数据.
13.(3分)已知一组数据含有20个数据:68,69,70,66,68,65,64,65,69,62,67,66,65,67,63,65,64,61,65,66,如果分成5组,那么64.5~66.5这一小组的频数为 ,频率为 .
14.(3分)如图的折线统计图分别表示我国A市与B市在2015年4月份的日平均气温的情况,记该月A市和B市日平均气温是20℃的天数分别为m天和n天,则nm= .
三、解答题(本题共计7小题,共计78分,)
15.现在都采用政府统一采购行为,教育局对各个学校的校服征订的办法,在教育局的样品室里摆放着12个样品,有12种不同的价位,分别为50,60,70,80,90,100,110,120,130,140,150,160元,现要对某校1500名学生统一征订校服,由于价格相差甚远,于是学校决定征求家长的意见,想要制作一张调查表,对家长的意见进行调查,请问,你该怎样设计这张调查表.(要求家长用打“√”的形式来表达).
16.当前新冠肺炎疫情形势依然复杂严峻,且病毒传播方式趋于多样化,为配合社区做好新冠疫情防控工作,提高防护意识,明明同学随机调查了她所在社区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图.请根据以下不完整的统计图提供的信息,解答下列问题:
社区人员出入情况统计表
出入人员年龄段 0 14 15 40 41 59 60岁及以上
出现次数 18 55 43 12
(1)明明同学共调查了 名居民的年龄,扇形统计图中a= .
(2)补全条形统计图,并注明人数.
(3)若该社区年龄在0 14岁的居民约有350人,请估计该辖区居民总人数是 人.
(4)为进一步掌握该社区中人员出入情况,明明又随机调查了128人.情况如下表,那么年龄是60岁及以上老人出入的频率是 .(精确到小数点后一位)
17.某学校为了丰富学生的课余生活,开展了“课后服务”的活动,推出了以下四种选修课程:A.数学编程;B.爱尚英语;C.3D打印;D.智能机器人,学校规定:每个学生都必须报名且只能选择其中的一种课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息.解决下列问题:
(1)问这次学校抽查了多少个学生进行调查?
(2)将条形统计图补充完整.
18.为了解某地九年级男生的身高情况,从该地的一所中学选取容量为60的样本(60名学生的身高.单位:厘米),分组情况如下:
分组 147.5~155.5 155.5~163.5 163.5~171.5 171.5~179.5
频数 6 21 m
频率 a 0.1
求出表中a和m的值.
19.学期结束前,学校想调查学生对七年级数学实验教材的意见,特向400名学生做问卷调查,其结果如下:
意见 非常喜欢 喜欢 有一点喜欢 不喜欢
人数 200 160 32 8
(1)计算出每一种意见的人数占总调查人数的百分比;
(2)请作出反映此调查结果的扇形统计图(图中).
(3)从统计图中你能得出什么结论?说明你的理由.
20.我国五座名山的主峰的海拔高度如表所示:
山名 泰山 华山 黄山 庐山 峨眉山
海拔高度(米) 1524 1997 1873 1500 3099
(1)最矮山的海拔是 米;
(2)黄山比泰山高 米;
(3)根据表中的数据制成条形统计图.
21.省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者、节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
月均用水量x(吨) 频数(户) 频率
0<x≤4 12 a
4<x≤8 32 0.32
8<x≤12 b c
12<x≤16 20 0.2
16<x≤20 8 0.08
20<x≤24 4 0.04
(1)a= ,b= ,c= ,并将如图所示的频数分布直方图补充完整;
(2)求月均用水量超过12吨的住户占所调查总住户的百分比.
第14章 数据的收集与表示
参考答案与试题解析
一、选择题(本题共计7小题,每题3分,共计21分,)
1.(3分)如若调查你校学生学业负担是否过重,选用下列哪种方法最恰当( )
A.查阅文献资料 B.对学生问卷调查
C.对老师问卷调查 D.对校领导问卷调查
【答案】B
【分析】为了得到比较准确的结果,并且易于操作,即操作的可行性,做出判断即可.
【解答】解:为得到结果准确,并且可操作性,因此选取,对学生问卷调查,
故选:B.
【点评】考查数据数据的方法,搜集和整理数据的原则是要考虑对结果要求的准确程度和可行性.
2.(3分)某班50名学生在适应性考试中,分数段在90~100分的频率为0.1,则该班在这个分数段的学生人数为( )
A.1人 B.2人 C.5人 D.10人
【答案】C
【分析】根据频数=总数×频率,求解即可.
【解答】解:得该班在这个分数段的学生是50×0.1=5.
故选:C.
【点评】掌握频率、频数、总数三者之间的关系:频率=频数÷总数,根据条件能够对公式灵活变形.
3.(3分)下列各组数据中,组中值不是10的是( )
A.7≤x<13 B.8≤x<12 C.3≤x<7 D.0≤x<20
【答案】C
【分析】组中值就是组的两个两个分点的平均数,据此即可求得各个选项的组中值,即可作出判断.
【解答】解:A、组中值是:(7+13)=10,故选项错误;
B、组中值是:(8+12)=10,故选项错误;
C、组中值是:(3+7)=5,故选项正确;
D、组中值是(0+20)=10,故选项错误.
故选:C.
【点评】本题考查了组中值的定义,理解定义是关键.
4.(3分)某工厂上半年生产总值增长率的变化情况如图所示,从图看,下列结论中不正确的是( )
A.1~5月份生产总值增长率逐月减少
B.6月份生产总值的年增长率开始回升
C.这半年中每月的生产总值不断增长
D.这半年中每月的生产总值有增有减
【答案】D
【分析】图中数据为生产总值增长率,而不是生产总值,根据折线统计图可知增长率均为正数,所以生产总值一直在增加,只是1~5月份生产总值增长率逐月减少,6月份生产总值的年增长率开始回升,
【解答】解:每月的增长率都是正数,说明生产总值每月都增长.因而D错误.A、B、C都正确.
故选:D.
【点评】本题考查折线统计图的运用,折线统计图表示的是事物的变化情况.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
5.(3分)某中学八年级有500名学生参加生物、地理会考,考试成绩在80分至100分之间的共有180人,则这个分数段的频率是( )
A.0.18 B.0.36 C.180 D.500
【答案】B
【分析】此题只需根据频率=频数÷总数,进行计算即可.
【解答】解:根据题意,得
这个分数段的频率是180÷500=0.36.
故选:B.
【点评】掌握频率的正确计算方法:频率=频数÷总数.
6.(3分)有一组数据,最小的为40,最大的为89,现在把它们分组,组距为10,则可分为( )
A.4组 B.5组 C.7组 D.8组
【答案】B
【分析】根据组数=(最大值﹣最小值)÷组距计算,注意小数部分要进位.
【解答】解:在样本数据中最大值为89,最小值为40,它们的差是89﹣40=49,已知组距为10,那么由于4.9,故可以分成5组.
故选:B.
【点评】本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
7.(3分)下表是某校七~九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,且九年级文艺小组活动次数与科技小组活动次数相同.
年级 课外小组活动总时间(单位:h) 文艺小组活动次数 科技小组活动次数
七年级 19 8 7
八年级 16.5 7 6
九年级 10
则九年级科技小组活动的次数是( )
A.3 B.4 C.5 D.6
【答案】B
【分析】设文艺小组每次活动的时间为x小时,科技小组每次活动时间为y小时,根据图表七年级和八年级课外活动的总时间列方程组求解,然后求出九年级的次数.
【解答】解:方法一:设文艺小组每次活动的时间为x小时,科技小组每次活动时间为y小时,
由题意得,,
解得:,
设九年级文艺小组的活动次数为a,科技小组的活动次数为b,
则1.5a+b=10,
∵a、b为整数,且a=b,
∴a=4,b=4.
方法二:设文艺小组每次活动的时间为m小时,则科技小组每次活动时间为小时,
根据题意得7m+616.5,
解得m=1.5,
则1,
∵1.5×4+1×4=10,
∴九年级的科技活动与文艺活动的次数均为4次.
故选:B.
【点评】本题考查了统计表和二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.
二、填空题(本题共计7小题,每题3分,共计21分,)
8.(3分)据我国第6次人口普查数据公报,我国人口中0~14岁的占16.60%,15~59岁的占70.14%,60岁以上(含60岁)的占13.26%.根据上述数据绘制扇形统计图,则60岁以上(含60岁)的扇形的圆心角度数是 48° .(结果精确到1°)
【答案】见试题解答内容
【分析】利用360度乘以对应的百分比即可求得.
【解答】解:60岁以上(含60岁)的扇形的圆心角度数是:360×13.26%=47.736°≈48°.
故答案为:48°.
【点评】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°比.
9.(3分)如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲,丙两种品牌彩电该月的销售量之和为 75 台.
【答案】见试题解答内容
【分析】从图中可以看出并计算:甲,丙两种品牌彩电该月的销售量之和为45+30=75.
【解答】解:45+30=75.
【点评】从不同的统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据.
10.(3分)为了解九年级学生体能情况,随机抽查了其中的40名学生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数分布直方图,则仰卧起坐的次数在20~25次之间的频率是 0.3 .
【答案】见试题解答内容
【分析】首先利用总人数40减去其它各组的人数求得20~25次的频数,然后根据频率公式:频率,即可求解.
【解答】解:在20~25次之间的频数是:40﹣16﹣8﹣4=12,
则次数在20~25次之间的频率是:0.3.
故答案为:0.3.
【点评】本题考查了频率公式:频率,即可求解.
11.(3分)如图是某地2月18日到23日PM2.5浓度和空气质量AQI的统计图(当AQI不大于100时称空气质量为“优良”).由图可得下列说法:①18日的PM2.5浓度最低;②21日的PM2.5浓度最高;③这六天中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关.其中正确的是 ①②③④ (填序号即可)
【答案】见试题解答内容
【分析】利用折线统计图1可判断18日对应的PM2.5浓度的值最小,则可①进行判断;根据21日对应的PM2.5浓度最高,则可对②进行判断;利用折线统计图2找出AQI不大于100的数据可对③进行判断;结合两个折线统计图,比较每天的PM2.5浓度和空气质量指数AQI可对④进行判断.
【解答】解:18日的PM2.5浓度最低,为25,所以①正确;
21日对应的PM2.5浓度最高所以②正确;
这六天中,18日、19日、20日、23日的空气质量为“优良”,所以③正确;
空气质量指数AQI与PM2.5浓度有关,PM2.5浓度越大,空气质量指数AQI越大,所以④正确.
故答案为:①②③④.
【点评】本题考查了折线统计图:折线图是用一个单位表示一定的数量,根据数量的多少描出各点,然后把各点用线段依次连接起来.以折线的上升或下降来表示统计数量增减变化.折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.
12.(3分)某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 折线 统计图来描述数据.
【答案】见试题解答内容
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目.
【解答】解:根据题意,得
要求清楚地表示销售总量的总趋势是上升还是下降,结合统计图各自的特点,应选用折线统计图.
【点评】此题考查扇形统计图、折线统计图、条形统计图各自的特点.
13.(3分)已知一组数据含有20个数据:68,69,70,66,68,65,64,65,69,62,67,66,65,67,63,65,64,61,65,66,如果分成5组,那么64.5~66.5这一小组的频数为 8 ,频率为 0.4 .
【答案】见试题解答内容
【分析】根据题意,找在64.5﹣66.5之间的数据,计算其个数;再由频率的计算方法,计算可得答案.
【解答】解:根据题意,发现数据中在64.5﹣66.5之间的有8个数据,
故64.5~66.5这一小组的频数为8,频率为0.4;
故答案为:8,0.4.
【点评】本题考查频率的计算、频数的确定方法,通过查找确定该组的频数时,要十分细心.
14.(3分)如图的折线统计图分别表示我国A市与B市在2015年4月份的日平均气温的情况,记该月A市和B市日平均气温是20℃的天数分别为m天和n天,则nm= 100 .
【答案】见试题解答内容
【分析】根据观察纵坐标,可得m、n的值,根据乘方运算,可得答案.
【解答】解:由纵坐标看出A市日平均气温是20℃的天数为2天,B市日平均气温是20℃的天数为10天,即m=2,n=10.nm=100,故答案为:100.
【点评】本题考查了折线统计图,观察统计图获得m、n的值是解题关键.
三、解答题(本题共计7小题,共计78分,)
15.现在都采用政府统一采购行为,教育局对各个学校的校服征订的办法,在教育局的样品室里摆放着12个样品,有12种不同的价位,分别为50,60,70,80,90,100,110,120,130,140,150,160元,现要对某校1500名学生统一征订校服,由于价格相差甚远,于是学校决定征求家长的意见,想要制作一张调查表,对家长的意见进行调查,请问,你该怎样设计这张调查表.(要求家长用打“√”的形式来表达).
【答案】见试题解答内容
【分析】利用已知数据范围可以分成6组,进而得出答案即可.
【解答】解:如表格所示:
价格范围 在你认为合理的价格后面打“√”,只能选一个
50~60
70~80
90~100
110~120
130~140
150~160
【点评】此题主要考查了调查收集数据的过程与方法,正确分组是解题关键.
16.当前新冠肺炎疫情形势依然复杂严峻,且病毒传播方式趋于多样化,为配合社区做好新冠疫情防控工作,提高防护意识,明明同学随机调查了她所在社区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图.请根据以下不完整的统计图提供的信息,解答下列问题:
社区人员出入情况统计表
出入人员年龄段 0 14 15 40 41 59 60岁及以上
出现次数 18 55 43 12
(1)明明同学共调查了 500 名居民的年龄,扇形统计图中a= 20% .
(2)补全条形统计图,并注明人数.
(3)若该社区年龄在0 14岁的居民约有350人,请估计该辖区居民总人数是 1750 人.
(4)为进一步掌握该社区中人员出入情况,明明又随机调查了128人.情况如下表,那么年龄是60岁及以上老人出入的频率是 0.1 .(精确到小数点后一位)
【答案】(1)500,20%.
(2)作图见解析部分.
(3)1750人.
(4)0.1.
【分析】(1)利用15﹣40的人数与百分比,求出总人数即可.再根据百分数的定义求出0﹣14的百分比a即可.
(2)求出14﹣59的人数,画出条形统计图即可.
(3)用样本估计总体的思想解决问题即可.
(4)用样本估计总体的思想解决问题即可.
【解答】解:(1)总人数500(名),a20%,
故答案为:500,20%.
(2)41﹣59的人数=500×22%=110(名),
条形图如图所示:
(3)1750(人),
故答案为:1750.
(4)0.1.
故答案为:0.1.
【点评】本题考查条形统计图,扇形统计图,样本估计总体等知识,解题的关键是掌握基本概念,属于中考常考题型.
17.某学校为了丰富学生的课余生活,开展了“课后服务”的活动,推出了以下四种选修课程:A.数学编程;B.爱尚英语;C.3D打印;D.智能机器人,学校规定:每个学生都必须报名且只能选择其中的一种课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息.解决下列问题:
(1)问这次学校抽查了多少个学生进行调查?
(2)将条形统计图补充完整.
【答案】见试题解答内容
【分析】(1)利用“A课程”的频数除以它所占的百分比得到调查的总人数;
(2)计算出“C课程”的人数后补全条形统计图即可.
【解答】解:(1)这次学校抽查的学生人数是12÷30%=40(人);
(2)C课程”的人数为40﹣12﹣14﹣4=10(人),
条形统计图补充为:
【点评】本题考查条形统计图、扇形统计图,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
18.为了解某地九年级男生的身高情况,从该地的一所中学选取容量为60的样本(60名学生的身高.单位:厘米),分组情况如下:
分组 147.5~155.5 155.5~163.5 163.5~171.5 171.5~179.5
频数 6 21 m
频率 a 0.1
求出表中a和m的值.
【答案】见试题解答内容
【分析】由从该地的一所中学选取容量为60的样本,观察表格,根据频率与频数的关系,即可求得答案.
【解答】解:∵选取容量为60的样本,
∴147.5~155.5的频率为:6÷60=0.1,155.5~163.5的频率为:21÷60=0.35,
∵171.5~179.5的频率为0.1,
∴a=1﹣0.1﹣0.35﹣0.1=0.45;
∴m=60×0.1=6.
即:a=0.45,m=6.
【点评】此题考查了频数(率)分布表.此题难度不大,注意准确认识表格是关键.
19.学期结束前,学校想调查学生对七年级数学实验教材的意见,特向400名学生做问卷调查,其结果如下:
意见 非常喜欢 喜欢 有一点喜欢 不喜欢
人数 200 160 32 8
(1)计算出每一种意见的人数占总调查人数的百分比;
(2)请作出反映此调查结果的扇形统计图(图中).
(3)从统计图中你能得出什么结论?说明你的理由.
【答案】见试题解答内容
【分析】(1)利用每种意见的人数÷总人数即可求解;
(2)利用所求的百分比,求出相应圆心角的度数,即可画图;
(3)利用统计图显示的信息,进行描述即可.
【解答】解:(1)非常喜欢:100%=50%;
喜欢:100%=40%;
有一点喜欢:100%=8%;
不喜欢:100%=2%.
(2)表示非常喜欢的圆心角=50%×360°=180度;
表示喜欢的圆心角=40%×360°=144度;
表示有一点喜欢的圆心角=8%×360°=28.8度;
表示不喜欢的圆心角=2%×360°=7.2度.
(3)从统计图中可以看出大多数同学喜欢七年级实验教材,因为在扇形统计图中喜欢的同学占绝大多数.
【点评】读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
20.我国五座名山的主峰的海拔高度如表所示:
山名 泰山 华山 黄山 庐山 峨眉山
海拔高度(米) 1524 1997 1873 1500 3099
(1)最矮山的海拔是 1500 米;
(2)黄山比泰山高 349 米;
(3)根据表中的数据制成条形统计图.
【答案】见试题解答内容
【分析】(1)观察表格中的数据,得出庐山海拔最矮,得出最矮山的海拔即可;
(2)用黄山的海拔减去泰山的海拔即可得到结果;
(3)将表格中的数据制成统计图,如图所示.
【解答】解:(1)观察表格得:最矮山的海拔是1500米;
(2)根据题意得:1873﹣1524=349(米),
则黄山比泰山高349米;
(3)如图所示:
故答案为:(1)1500;(2)349
【点评】此题考查了条形统计图,以及统计表,弄清题意是解本题的关键.
21.省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者、节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
月均用水量x(吨) 频数(户) 频率
0<x≤4 12 a
4<x≤8 32 0.32
8<x≤12 b c
12<x≤16 20 0.2
16<x≤20 8 0.08
20<x≤24 4 0.04
(1)a= 0.12 ,b= 24 ,c= 0.24 ,并将如图所示的频数分布直方图补充完整;
(2)求月均用水量超过12吨的住户占所调查总住户的百分比.
【答案】(1)0.12、24、0.24,补全图形见解答;
(2)32%.
【分析】(1)根据4<x≤8的频数和频率求出总户数,再用0<x≤4的频数乘以总数求出a,用总数减去其它月均用水量求出8<x≤12的频数,即b的值,用B的值除以总数即可求出c,从而补全统计图;
(2)把月均用水量超过12吨的住户的频率加起来即可得出答案.
【解答】解:(1)根据题意得:总户数为32÷0.32=100(户),
则a=12÷100=0.12;
b=100﹣12﹣32﹣20﹣8﹣4=24;
c=24÷100=0.24;
补全图形如下:
故答案为:0.12、24、0.24;
(2)月均用水量超过12吨的住户占所调查总住户的百分比为100%=32%.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
