1.4 用 一元二次方程解决问题 同步练习 (含答案)2025-2026学年苏科版九年级数学上册
文档属性
| 名称 | 1.4 用 一元二次方程解决问题 同步练习 (含答案)2025-2026学年苏科版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 714.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 10:24:45 | ||
图片预览




文档简介
1.4 用 一元二次方程解决问题 同步练习
(考试时间为90分钟,满分为100分)
一、选择题:本题共10小题,每小题2分,共20分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程是一元高次方程的是( )
A.x4+1=0 B.x2﹣3x﹣1=0
C. D.x+3=0
2.下列二项方程中,有两个实数根的是( )
A.x5+1=0 B.x4﹣1=0 C.x3﹣1=0 D.x2+1=0
3.一次会议上,每两个参加会议的人都相互握一次手,有人统计一共握了66次手,设到会的人数为x人,则根据题意列方程为( )
A. B.x(x﹣1)=66
C. D.x(x+1)=66
4.“读万卷书,行万里路.”某校为了丰富学生的阅历知识,坚持开展课外阅读活动,学生人均阅读量从七年级的每年64万字增加到九年级的每年144万字.设该校七至九年级人均阅读量年均增长率为x,则可列方程为( )
A.64(1+x)2=144 B.64(1+x%)2=144
C.64(1+2x)=144 D.64+64(1+x)+64(1+x)2=144
5.如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644平方米,则道路的宽应为多少米?设道路的宽为x米,则可列方程为( )
A.100×80﹣100x﹣80x=7644 B.(100﹣x)(80﹣x)+x2=7644
C.(100﹣x)(80﹣x)=7644 D.100x+80x=356
第5题 第8题 第9题 第10题
6.《田亩比类乘除捷法》是我国古代数学家杨辉的著作.其中有一个数学问题:“直田积八百九十一步,只云长阔共六十步,问长多阔几何?”译文:“一块矩形田地的面积为891平方步,只知道它的长与宽共60步,问它的长比宽多多少步?”则长比宽多( )
A.3步 B.6步 C.9步 D.12步
7.甲流病毒是一种传染性极强的急性呼吸道传染病,感染者的临床以发热、乏力、干咳为主要表现.在“甲流”初期,有1人感染了“甲流病毒”,如若得不到有效控制,经过两轮传染后共有225人感染了“甲流病毒”,设每轮传染中平均一个人传染了x个人,则根据题意列出方程是( )
A.x+x(1+x)=225 B.1+x+x2=225
C.1+x+x(1+x)=225 D.x(1+x)=225
8.《九章算术》中有一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:如图,一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?若设折断处离地面x尺,则下面所列方程正确的是( )
A.x2+32=(1﹣x)2 B.x2+(1﹣x)2=32
C.x2+(10﹣x)2=32 D.x2+32=(10﹣x)2
9.如图,已知长方形铁皮的长为10cm,宽为8cm,分别在它的四个角上剪去边长为xcm的正方形,做成底面积为24cm2的无盖长方体盒子,则可列方程为( )
A.(10﹣2x)(8﹣2x)=24 B.(10﹣x)(8﹣x)=24
C.(10﹣x)(8﹣2x)=24 D.(10﹣2x)(8﹣x)=24
10.如图所示,点阵M的层数用n表示,点数总和用S表示,当S=66时,则n的值为( )
A.10 B.11 C.12 D.13
二、填空题:本题共8小题,每小题2分,共16分。
11.已知关于x的方程,则x= .
12.方程的解是 .
13.无理方程的解是 .
14.某云平台的网络安全事件中,最初有4台服务器遭受攻击并感染病毒.两轮传播后共有196台服务器被控制,则每轮中平均每台服务器传播设备的台数为 .
15.某商场将进货价为55元的某种服装以75元售出,平均每天可售30件,为了尽快减少库存,商场决定采取适当的降价措施,调查发现:每件降价1元,则每天可多售5件,如果每天要盈利800元,每件应降价 元.
16.如图,某牧场准备利用现成的一堵“7”字形的墙面粗线表示墙面(粗线A﹣B﹣C表示墙面)建饲养场.已知AB⊥BC,AB=3米,BC=9米,现计划用总长为38米的篱笆围建一个“日”字形的饲养场BDEF(细线表示篱笆,饲养场中间用篱笆GH隔开),并在每个区域开一个宽2米的门,点F在线段BC的延长线上.设EF的长为x米,若要求所围成的饲养场BDEF面积为84平方米,则可列方程 (不用化简).
第16题 第17题 第18题
17.如图,在△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,以2cm/s的速度沿CA方向运动;同时动点Q从点B出发,以1cm/s的速度沿BC方向运动.则运动 秒后P、Q两点相距25cm.
18.在2024年12月的日历表上用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为513,则这个最小数为 .
三、解答题:本题共6小题,共64分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分)如图,利用一面墙(墙的长度不限),用20m长的篱笆围成一个矩形场地ABCD.
(1)若矩形场地的面积为48m2,求AB的长;
(2)该矩形场地的面积能否为60m2?若能,求出AB的长;若不能,请说明理由.
20.本小题分)随着旅游旺季的到来,烟台某景区游客人数逐月增加,3月份游客人数为1.6万人,5月份游客人数为2.5万人.
(1)求这两个月该景区游客人数的月平均增长率;
(2)预计6月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区6月1日至6月20日已接待游客2.125万人,则6月份后10天日均接待游客人数最多是多少万人?
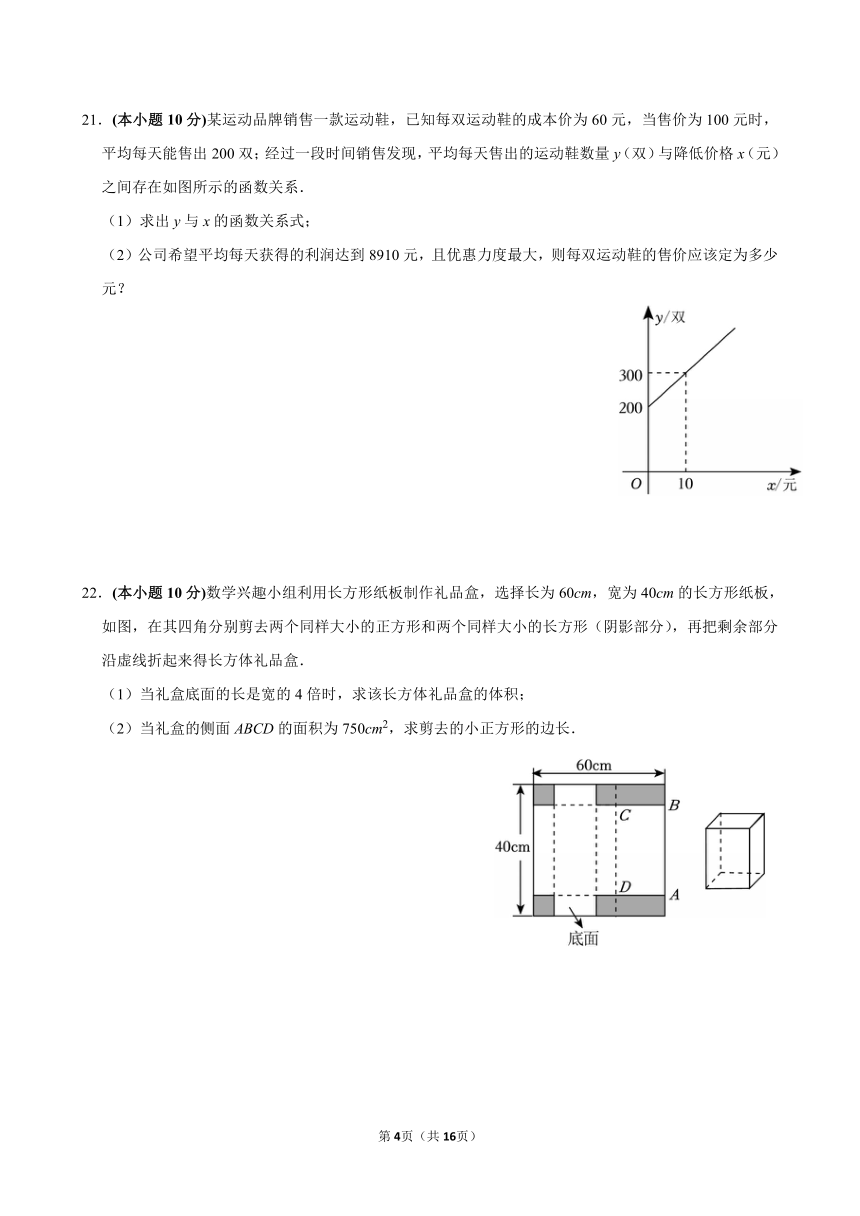
21.本小题分)某运动品牌销售一款运动鞋,已知每双运动鞋的成本价为60元,当售价为100元时,平均每天能售出200双;经过一段时间销售发现,平均每天售出的运动鞋数量y(双)与降低价格x(元)之间存在如图所示的函数关系.
(1)求出y与x的函数关系式;
(2)公司希望平均每天获得的利润达到8910元,且优惠力度最大,则每双运动鞋的售价应该定为多少元?
22.本小题分)数学兴趣小组利用长方形纸板制作礼品盒,选择长为60cm,宽为40cm的长方形纸板,如图,在其四角分别剪去两个同样大小的正方形和两个同样大小的长方形(阴影部分),再把剩余部分沿虚线折起来得长方体礼品盒.
(1)当礼盒底面的长是宽的4倍时,求该长方体礼品盒的体积;
(2)当礼盒的侧面ABCD的面积为750cm2,求剪去的小正方形的边长.
23.本小题2分)在日历上,我们可以发现其中某些数满足一定的规律,如图是2024年10月份的日历.我们任意选择其中所示的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:9×11﹣3×17=48,13×15﹣7×21=48.不难发现,结果都是48.
(1)请证明发现的规律;
(2)若用一个如图所示菱形框,再框出5个数字,其中最小数与最大数的积为435,求出这5个数中的最大数.
24.本小题分)【综合与实践】
学校劳动实践基地的开发能让学生体验劳动的艰辛,品味获得劳动成果的喜悦,同时满足学生劳动教育实践需要.如图是某校劳动实践基地的示意图,该基地为两边靠墙的矩形ABCD,面积为360平方米,墙AB的长为15米.
【实践应用】
(1)据学校管理人员介绍,该基地2023年的面积只有250平方米,连续两年扩建,并且两年的增长率相同,请求出这个增长率;
(2)如图所示,学校打算在基地内用总长度为33米的栅栏围成两面靠墙的三个大小相同的矩形空地用来养殖小动物,总面积为72平方米,求矩形空地的宽EF为多少米?
答案与解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B A A C B C D A B
一.选择题(共10小题)
1.下列方程是一元高次方程的是( )
A.x4+1=0 B.x2﹣3x﹣1=0
C. D.x+3=0
【解答】解:这四个方程都只含一个未知数,
因为B、D中未知数的项的次数小于等于2,
所以B、D选项不符合题意,
C中分母中含有未知数,是分式方程,C选项不符合题意;
A符合一元高次方程定义:只含一个未知数,未知项的最高次数大于等于3的整式方程,A选项符合题意.
故选:A.
2.下列二项方程中,有两个实数根的是( )
A.x5+1=0 B.x4﹣1=0 C.x3﹣1=0 D.x2+1=0
【解答】解:x5+1=0的实数根为x=﹣1,故A不符合题意;
x4﹣1=0的实数根为x=±1,故B符合题意;
x3﹣1=0的实数根为x=1,故C不符合题意;
x2+1=0无实数根,故D不符合题意;
故选:B.
3.一次会议上,每两个参加会议的人都相互握一次手,有人统计一共握了66次手,设到会的人数为x人,则根据题意列方程为( )
A. B.x(x﹣1)=66
C. D.x(x+1)=66
【解答】解:依题意得x(x﹣1)=66.
故选:A.
4.“读万卷书,行万里路.”某校为了丰富学生的阅历知识,坚持开展课外阅读活动,学生人均阅读量从七年级的每年64万字增加到九年级的每年144万字.设该校七至九年级人均阅读量年均增长率为x,则可列方程为( )
A.64(1+x)2=144
B.64(1+x%)2=144
C.64(1+2x)=144
D.64+64(1+x)+64(1+x)2=144
【解答】解:根据题意得:64(1+x)2=144.
故选:A.
5.如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644平方米,则道路的宽应为多少米?设道路的宽为x米,则可列方程为( )
A.100×80﹣100x﹣80x=7644
B.(100﹣x)(80﹣x)+x2=7644
C.(100﹣x)(80﹣x)=7644
D.100x+80x=356
【解答】解:设道路的宽应为x米,由题意有
(100﹣x)(80﹣x)=7644,
故选:C.
6.《田亩比类乘除捷法》是我国古代数学家杨辉的著作.其中有一个数学问题:“直田积八百九十一步,只云长阔共六十步,问长多阔几何?”译文:“一块矩形田地的面积为891平方步,只知道它的长与宽共60步,问它的长比宽多多少步?”则长比宽多( )
A.3步 B.6步 C.9步 D.12步
【解答】解:设矩形田地的长为x步,则宽为(60﹣x)步,
依题意得:x(60﹣x)=891,
整理得:x2﹣60x+891=0,
解得x1=33,x2=27.
当x=33时,60﹣x=60﹣33=27<33,符合题意,此时x﹣(60﹣x)=33﹣27=6;
当x=27时,60﹣x=60﹣27=33>27,不符合题意,舍去.
∴长比宽多6步.
综上所述,只有选项B正确,符合题意,
故选:B.
7.甲流病毒是一种传染性极强的急性呼吸道传染病,感染者的临床以发热、乏力、干咳为主要表现.在“甲流”初期,有1人感染了“甲流病毒”,如若得不到有效控制,经过两轮传染后共有225人感染了“甲流病毒”,设每轮传染中平均一个人传染了x个人,则根据题意列出方程是( )
A.x+x(1+x)=225 B.1+x+x2=225
C.1+x+x(1+x)=225 D.x(1+x)=225
【解答】解:∵每轮传染中平均一个人传染了x个人,
∴第一轮传染中有x人被感染,第二轮传染中有x(1+x)人被感染.
根据题意得:1+x+x(1+x)=225.
故选:C.
8.《九章算术》中有一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:如图,一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?若设折断处离地面x尺,则下面所列方程正确的是( )
A.x2+32=(1﹣x)2 B.x2+(1﹣x)2=32
C.x2+(10﹣x)2=32 D.x2+32=(10﹣x)2
【解答】解:根据题意可得:x2+32=(10﹣x)2,
故选:D.
9.如图,已知长方形铁皮的长为10cm,宽为8cm,分别在它的四个角上剪去边长为xcm的正方形,做成底面积为24cm2的无盖长方体盒子,则可列方程为( )
A.(10﹣2x)(8﹣2x)=24 B.(10﹣x)(8﹣x)=24
C.(10﹣x)(8﹣2x)=24 D.(10﹣2x)(8﹣x)=24
【解答】解:根据(长方形的长﹣2x)(长方形的宽﹣2x)=24cm2可得:
(10﹣2x)(8﹣2x)=24,
故选:A.
10.如图所示,点阵M的层数用n表示,点数总和用S表示,当S=66时,则n的值为( )
A.10 B.11 C.12 D.13
【解答】解:根据题意得:Sn(n+1).
∵S=66,
∴n(n+1)=66,
解得:n1=11,n2=﹣12(舍去).
故选:B.
二.填空题(共8小题)
11.已知关于x的方程,则x= 2 .
【解答】解:两边平方得:8﹣2x=x2,
变形得:x2+2x﹣8=0,
解得x1=﹣4,x2=2,
经检验,x=﹣4为原方程的增根,x=2是原方程的解,
∴原方程的解为x=2,
故答案为:2.
12.方程的解是 x=3 .
【解答】解:∵,
∴或.
∴x=﹣2或x=3.
∵2+x≥0且x﹣3≥0,
∴x≥3.
故原方程的解为:x=3.
故答案为:x=3.
13.无理方程的解是 x=1 .
【解答】解:原方程两边同时平方得:x2﹣4x+3=1﹣x,
整理得:x2﹣3x+2=0,
解得:x=1或x=2,
经检验,x=1是原方程的解,x=2时,1﹣x<0,应舍去,
故答案为:x=1.
14.某云平台的网络安全事件中,最初有4台服务器遭受攻击并感染病毒.两轮传播后共有196台服务器被控制,则每轮中平均每台服务器传播设备的台数为 6 .
【解答】解:设每轮中平均每台服务器传播设备的台数为x,根据题意可得:
4+4x+x(4+4x)=196,
解得x1=6,x2=﹣8(舍),
故答案为:6.
15.某商场将进货价为55元的某种服装以75元售出,平均每天可售30件,为了尽快减少库存,商场决定采取适当的降价措施,调查发现:每件降价1元,则每天可多售5件,如果每天要盈利800元,每件应降价 10 元.
【解答】解:设每件应降价x元,则每件的盈利为(75﹣x﹣55)元,每天可售出(30+5x)件,
根据题意得:(75﹣x﹣55)(30+5x)=800,
整理得:x2﹣14x+40=0,
解得:x1=10,x2=4(不符合题意,舍去),
即每件应降价10元,
故答案为:10.
16.如图,某牧场准备利用现成的一堵“7”字形的墙面粗线表示墙面(粗线A﹣B﹣C表示墙面)建饲养场.已知AB⊥BC,AB=3米,BC=9米,现计划用总长为38米的篱笆围建一个“日”字形的饲养场BDEF(细线表示篱笆,饲养场中间用篱笆GH隔开),并在每个区域开一个宽2米的门,点F在线段BC的延长线上.设EF的长为x米,若要求所围成的饲养场BDEF面积为84平方米,则可列方程 x=84 (不用化简).
【解答】解:设EF的长为x米,则DE(米),
依题意得: x=84,
故答案为: x=84.
17.如图,在△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,以2cm/s的速度沿CA方向运动;同时动点Q从点B出发,以1cm/s的速度沿BC方向运动.则运动 10 秒后P、Q两点相距25cm.
【解答】解:设运动x秒后P、Q两点相距25cm,
则CP=2x cm,CQ=(25﹣x)cm,
由题意得:(2x)2+(25﹣x)2=252,
整理得:x2﹣10x=0,
解得:x1=10,x2=0(不合题意,舍去),
故答案为:10.
18.在2024年12月的日历表上用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为513,则这个最小数为 19 .
【解答】解:设这个最小数为x,则另外三个数分别为x+1,x+7,x+8,
根据题意得:x(x+8)=513,
整理得:x2+8x﹣513=0,
解得:x1=19,x2=﹣27(不符合题意,舍去),
∴这个最小数为19.
故答案为:19.
三.解答题(共6小题)
19.如图,利用一面墙(墙的长度不限),用20m长的篱笆围成一个矩形场地ABCD.
(1)若矩形场地的面积为48m2,求AB的长;
(2)该矩形场地的面积能否为60m2?若能,求出AB的长;若不能,请说明理由.
【解答】解:(1)设AB=x m,则BC=(20﹣2x)m,
根据题意得:x(20﹣2x)=48,
整理得:x2﹣10x+24=0,
解得:x1=4,x2=6.
答:AB的长为4或6m;
(2)该矩形场地的面积不能为60m2,理由如下:
假设该矩形场地的面积能为60m2,设AB=y m,则BC=(20﹣2y)m,
根据题意得:y(20﹣2y)=60,
整理得:y2﹣10y+30=0,
∵Δ=(﹣10)2﹣4×1×30=﹣20<0,
∴原方程没有实数根,
∴假设不成立,即该矩形场地的面积不能为60m2.
20.随着旅游旺季的到来,烟台某景区游客人数逐月增加,3月份游客人数为1.6万人,5月份游客人数为2.5万人.
(1)求这两个月该景区游客人数的月平均增长率;
(2)预计6月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区6月1日至6月20日已接待游客2.125万人,则6月份后10天日均接待游客人数最多是多少万人?
【解答】解:(1)设这两个月中该景区游客人数的月平均增长率为x,
根据题意得:1.6(1+x)2=2.5,
解得:x1=0.25=25%,x2=﹣2.25(不符合题意,舍去),
答:这两个月中该景区游客人数的月平均增长率为25%;
(2)设6月份后10天日均接待游客人数是y万人,
根据题意得:2.125+10y≤2.5×(1+25%),
解得:y≤0.1,
答:6月份后10天日均接待游客人数最多是0.1万人.
21.某运动品牌销售一款运动鞋,已知每双运动鞋的成本价为60元,当售价为100元时,平均每天能售出200双;经过一段时间销售发现,平均每天售出的运动鞋数量y(双)与降低价格x(元)之间存在如图所示的函数关系.
(1)求出y与x的函数关系式;
(2)公司希望平均每天获得的利润达到8910元,且优惠力度最大,则每双运动鞋的售价应该定为多少元?
【解答】解:(1)设y与x的函数关系式为y=kx+b(k≠0),
将(0,200),(10,300)代入y=kx+b得:
,
解得,
∴y与x的函数关系式为y=10x+200;
(2)根据题意得:(100﹣60﹣x)(10x+200)=8910,
整理得:x2﹣20x+91=0,
解得x1=7,x2=13,
又∵要求优惠力度最大,
∴x=13,
∴100﹣x=100﹣13=87.
答:每双运动鞋的售价应该定为87元.
22.数学兴趣小组利用长方形纸板制作礼品盒,选择长为60cm,宽为40cm的长方形纸板,如图,在其四角分别剪去两个同样大小的正方形和两个同样大小的长方形(阴影部分),再把剩余部分沿虚线折起来得长方体礼品盒.
(1)当礼盒底面的长是宽的4倍时,求该长方体礼品盒的体积;
(2)当礼盒的侧面ABCD的面积为750cm2,求剪去的小正方形的边长.
【解答】解:(1)设小正方形的边长为x,则礼盒底面的长是,宽为x,
由题意得30﹣x=4x,
解得x=6,
∴长为24,宽为6,高为40﹣2×6=28,
∴体积为:24×6×28=4032(cm3);
(2)设小正方形的边长为m,根据题意可得一元二次方程为:
(30﹣m)(40﹣2m)=750,
整理得m2﹣50m+225=0,
解得m=5或m=45(舍),
∴剪去的小正方形的边长为5cm.
23.在日历上,我们可以发现其中某些数满足一定的规律,如图是2024年10月份的日历.我们任意选择其中所示的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:9×11﹣3×17=48,13×15﹣7×21=48.不难发现,结果都是48.
(1)请证明发现的规律;
(2)若用一个如图所示菱形框,再框出5个数字,其中最小数与最大数的积为435,求出这5个数中的最大数.
【解答】(1)证明:设中间的数为a,则另外4个数分别为(a﹣7),(a﹣1),(a+1),(a+7),
∴(a﹣1)(a+1)﹣(a﹣7)(a+7),
=a2﹣1﹣(a2﹣49),
=48.
(2)解:设这5个数中的最大数为x,则最小数为(x﹣14),
依题意得:x(x﹣14)=435,
解得:x1=29,x2=﹣15(不合题意,舍去).
答:这5个数中的最大数为29.
24.【综合与实践】
学校劳动实践基地的开发能让学生体验劳动的艰辛,品味获得劳动成果的喜悦,同时满足学生劳动教育实践需要.如图是某校劳动实践基地的示意图,该基地为两边靠墙的矩形ABCD,面积为360平方米,墙AB的长为15米.
【实践应用】
(1)据学校管理人员介绍,该基地2023年的面积只有250平方米,连续两年扩建,并且两年的增长率相同,请求出这个增长率;
(2)如图所示,学校打算在基地内用总长度为33米的栅栏围成两面靠墙的三个大小相同的矩形空地用来养殖小动物,总面积为72平方米,求矩形空地的宽EF为多少米?
【解答】解:(1)设这个增长率为x,由题意列一元二次方程得:
250(1+x)2=360,
整理得,250x2+500x+140=0,
解得x1=﹣2.2(不合题意舍去),x2=0.2=20%,
答:这个增长率为20%;
(2)∵矩形ABCD,面积为360平方米,墙AB的长为15米,
∴AD=360÷15=24,
设矩形空地的宽EF为y米,则FG的长为(33﹣3y)米,
由题意列一元二次方程得:y(33﹣3y)=72,
整理得:y2+11y+24=0,
解得y1=3,y2=8,
当y=3时,FG的长为:33﹣3×3=24>15,不合题意,舍去;
当y=8时,BC的长为:33﹣3×8=9<15,符合题意.
∴EF=8米.
答:场地的宽EF为8米.
第1页(共1页)
(考试时间为90分钟,满分为100分)
一、选择题:本题共10小题,每小题2分,共20分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程是一元高次方程的是( )
A.x4+1=0 B.x2﹣3x﹣1=0
C. D.x+3=0
2.下列二项方程中,有两个实数根的是( )
A.x5+1=0 B.x4﹣1=0 C.x3﹣1=0 D.x2+1=0
3.一次会议上,每两个参加会议的人都相互握一次手,有人统计一共握了66次手,设到会的人数为x人,则根据题意列方程为( )
A. B.x(x﹣1)=66
C. D.x(x+1)=66
4.“读万卷书,行万里路.”某校为了丰富学生的阅历知识,坚持开展课外阅读活动,学生人均阅读量从七年级的每年64万字增加到九年级的每年144万字.设该校七至九年级人均阅读量年均增长率为x,则可列方程为( )
A.64(1+x)2=144 B.64(1+x%)2=144
C.64(1+2x)=144 D.64+64(1+x)+64(1+x)2=144
5.如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644平方米,则道路的宽应为多少米?设道路的宽为x米,则可列方程为( )
A.100×80﹣100x﹣80x=7644 B.(100﹣x)(80﹣x)+x2=7644
C.(100﹣x)(80﹣x)=7644 D.100x+80x=356
第5题 第8题 第9题 第10题
6.《田亩比类乘除捷法》是我国古代数学家杨辉的著作.其中有一个数学问题:“直田积八百九十一步,只云长阔共六十步,问长多阔几何?”译文:“一块矩形田地的面积为891平方步,只知道它的长与宽共60步,问它的长比宽多多少步?”则长比宽多( )
A.3步 B.6步 C.9步 D.12步
7.甲流病毒是一种传染性极强的急性呼吸道传染病,感染者的临床以发热、乏力、干咳为主要表现.在“甲流”初期,有1人感染了“甲流病毒”,如若得不到有效控制,经过两轮传染后共有225人感染了“甲流病毒”,设每轮传染中平均一个人传染了x个人,则根据题意列出方程是( )
A.x+x(1+x)=225 B.1+x+x2=225
C.1+x+x(1+x)=225 D.x(1+x)=225
8.《九章算术》中有一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:如图,一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?若设折断处离地面x尺,则下面所列方程正确的是( )
A.x2+32=(1﹣x)2 B.x2+(1﹣x)2=32
C.x2+(10﹣x)2=32 D.x2+32=(10﹣x)2
9.如图,已知长方形铁皮的长为10cm,宽为8cm,分别在它的四个角上剪去边长为xcm的正方形,做成底面积为24cm2的无盖长方体盒子,则可列方程为( )
A.(10﹣2x)(8﹣2x)=24 B.(10﹣x)(8﹣x)=24
C.(10﹣x)(8﹣2x)=24 D.(10﹣2x)(8﹣x)=24
10.如图所示,点阵M的层数用n表示,点数总和用S表示,当S=66时,则n的值为( )
A.10 B.11 C.12 D.13
二、填空题:本题共8小题,每小题2分,共16分。
11.已知关于x的方程,则x= .
12.方程的解是 .
13.无理方程的解是 .
14.某云平台的网络安全事件中,最初有4台服务器遭受攻击并感染病毒.两轮传播后共有196台服务器被控制,则每轮中平均每台服务器传播设备的台数为 .
15.某商场将进货价为55元的某种服装以75元售出,平均每天可售30件,为了尽快减少库存,商场决定采取适当的降价措施,调查发现:每件降价1元,则每天可多售5件,如果每天要盈利800元,每件应降价 元.
16.如图,某牧场准备利用现成的一堵“7”字形的墙面粗线表示墙面(粗线A﹣B﹣C表示墙面)建饲养场.已知AB⊥BC,AB=3米,BC=9米,现计划用总长为38米的篱笆围建一个“日”字形的饲养场BDEF(细线表示篱笆,饲养场中间用篱笆GH隔开),并在每个区域开一个宽2米的门,点F在线段BC的延长线上.设EF的长为x米,若要求所围成的饲养场BDEF面积为84平方米,则可列方程 (不用化简).
第16题 第17题 第18题
17.如图,在△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,以2cm/s的速度沿CA方向运动;同时动点Q从点B出发,以1cm/s的速度沿BC方向运动.则运动 秒后P、Q两点相距25cm.
18.在2024年12月的日历表上用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为513,则这个最小数为 .
三、解答题:本题共6小题,共64分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分)如图,利用一面墙(墙的长度不限),用20m长的篱笆围成一个矩形场地ABCD.
(1)若矩形场地的面积为48m2,求AB的长;
(2)该矩形场地的面积能否为60m2?若能,求出AB的长;若不能,请说明理由.
20.本小题分)随着旅游旺季的到来,烟台某景区游客人数逐月增加,3月份游客人数为1.6万人,5月份游客人数为2.5万人.
(1)求这两个月该景区游客人数的月平均增长率;
(2)预计6月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区6月1日至6月20日已接待游客2.125万人,则6月份后10天日均接待游客人数最多是多少万人?
21.本小题分)某运动品牌销售一款运动鞋,已知每双运动鞋的成本价为60元,当售价为100元时,平均每天能售出200双;经过一段时间销售发现,平均每天售出的运动鞋数量y(双)与降低价格x(元)之间存在如图所示的函数关系.
(1)求出y与x的函数关系式;
(2)公司希望平均每天获得的利润达到8910元,且优惠力度最大,则每双运动鞋的售价应该定为多少元?
22.本小题分)数学兴趣小组利用长方形纸板制作礼品盒,选择长为60cm,宽为40cm的长方形纸板,如图,在其四角分别剪去两个同样大小的正方形和两个同样大小的长方形(阴影部分),再把剩余部分沿虚线折起来得长方体礼品盒.
(1)当礼盒底面的长是宽的4倍时,求该长方体礼品盒的体积;
(2)当礼盒的侧面ABCD的面积为750cm2,求剪去的小正方形的边长.
23.本小题2分)在日历上,我们可以发现其中某些数满足一定的规律,如图是2024年10月份的日历.我们任意选择其中所示的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:9×11﹣3×17=48,13×15﹣7×21=48.不难发现,结果都是48.
(1)请证明发现的规律;
(2)若用一个如图所示菱形框,再框出5个数字,其中最小数与最大数的积为435,求出这5个数中的最大数.
24.本小题分)【综合与实践】
学校劳动实践基地的开发能让学生体验劳动的艰辛,品味获得劳动成果的喜悦,同时满足学生劳动教育实践需要.如图是某校劳动实践基地的示意图,该基地为两边靠墙的矩形ABCD,面积为360平方米,墙AB的长为15米.
【实践应用】
(1)据学校管理人员介绍,该基地2023年的面积只有250平方米,连续两年扩建,并且两年的增长率相同,请求出这个增长率;
(2)如图所示,学校打算在基地内用总长度为33米的栅栏围成两面靠墙的三个大小相同的矩形空地用来养殖小动物,总面积为72平方米,求矩形空地的宽EF为多少米?
答案与解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B A A C B C D A B
一.选择题(共10小题)
1.下列方程是一元高次方程的是( )
A.x4+1=0 B.x2﹣3x﹣1=0
C. D.x+3=0
【解答】解:这四个方程都只含一个未知数,
因为B、D中未知数的项的次数小于等于2,
所以B、D选项不符合题意,
C中分母中含有未知数,是分式方程,C选项不符合题意;
A符合一元高次方程定义:只含一个未知数,未知项的最高次数大于等于3的整式方程,A选项符合题意.
故选:A.
2.下列二项方程中,有两个实数根的是( )
A.x5+1=0 B.x4﹣1=0 C.x3﹣1=0 D.x2+1=0
【解答】解:x5+1=0的实数根为x=﹣1,故A不符合题意;
x4﹣1=0的实数根为x=±1,故B符合题意;
x3﹣1=0的实数根为x=1,故C不符合题意;
x2+1=0无实数根,故D不符合题意;
故选:B.
3.一次会议上,每两个参加会议的人都相互握一次手,有人统计一共握了66次手,设到会的人数为x人,则根据题意列方程为( )
A. B.x(x﹣1)=66
C. D.x(x+1)=66
【解答】解:依题意得x(x﹣1)=66.
故选:A.
4.“读万卷书,行万里路.”某校为了丰富学生的阅历知识,坚持开展课外阅读活动,学生人均阅读量从七年级的每年64万字增加到九年级的每年144万字.设该校七至九年级人均阅读量年均增长率为x,则可列方程为( )
A.64(1+x)2=144
B.64(1+x%)2=144
C.64(1+2x)=144
D.64+64(1+x)+64(1+x)2=144
【解答】解:根据题意得:64(1+x)2=144.
故选:A.
5.如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644平方米,则道路的宽应为多少米?设道路的宽为x米,则可列方程为( )
A.100×80﹣100x﹣80x=7644
B.(100﹣x)(80﹣x)+x2=7644
C.(100﹣x)(80﹣x)=7644
D.100x+80x=356
【解答】解:设道路的宽应为x米,由题意有
(100﹣x)(80﹣x)=7644,
故选:C.
6.《田亩比类乘除捷法》是我国古代数学家杨辉的著作.其中有一个数学问题:“直田积八百九十一步,只云长阔共六十步,问长多阔几何?”译文:“一块矩形田地的面积为891平方步,只知道它的长与宽共60步,问它的长比宽多多少步?”则长比宽多( )
A.3步 B.6步 C.9步 D.12步
【解答】解:设矩形田地的长为x步,则宽为(60﹣x)步,
依题意得:x(60﹣x)=891,
整理得:x2﹣60x+891=0,
解得x1=33,x2=27.
当x=33时,60﹣x=60﹣33=27<33,符合题意,此时x﹣(60﹣x)=33﹣27=6;
当x=27时,60﹣x=60﹣27=33>27,不符合题意,舍去.
∴长比宽多6步.
综上所述,只有选项B正确,符合题意,
故选:B.
7.甲流病毒是一种传染性极强的急性呼吸道传染病,感染者的临床以发热、乏力、干咳为主要表现.在“甲流”初期,有1人感染了“甲流病毒”,如若得不到有效控制,经过两轮传染后共有225人感染了“甲流病毒”,设每轮传染中平均一个人传染了x个人,则根据题意列出方程是( )
A.x+x(1+x)=225 B.1+x+x2=225
C.1+x+x(1+x)=225 D.x(1+x)=225
【解答】解:∵每轮传染中平均一个人传染了x个人,
∴第一轮传染中有x人被感染,第二轮传染中有x(1+x)人被感染.
根据题意得:1+x+x(1+x)=225.
故选:C.
8.《九章算术》中有一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:如图,一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?若设折断处离地面x尺,则下面所列方程正确的是( )
A.x2+32=(1﹣x)2 B.x2+(1﹣x)2=32
C.x2+(10﹣x)2=32 D.x2+32=(10﹣x)2
【解答】解:根据题意可得:x2+32=(10﹣x)2,
故选:D.
9.如图,已知长方形铁皮的长为10cm,宽为8cm,分别在它的四个角上剪去边长为xcm的正方形,做成底面积为24cm2的无盖长方体盒子,则可列方程为( )
A.(10﹣2x)(8﹣2x)=24 B.(10﹣x)(8﹣x)=24
C.(10﹣x)(8﹣2x)=24 D.(10﹣2x)(8﹣x)=24
【解答】解:根据(长方形的长﹣2x)(长方形的宽﹣2x)=24cm2可得:
(10﹣2x)(8﹣2x)=24,
故选:A.
10.如图所示,点阵M的层数用n表示,点数总和用S表示,当S=66时,则n的值为( )
A.10 B.11 C.12 D.13
【解答】解:根据题意得:Sn(n+1).
∵S=66,
∴n(n+1)=66,
解得:n1=11,n2=﹣12(舍去).
故选:B.
二.填空题(共8小题)
11.已知关于x的方程,则x= 2 .
【解答】解:两边平方得:8﹣2x=x2,
变形得:x2+2x﹣8=0,
解得x1=﹣4,x2=2,
经检验,x=﹣4为原方程的增根,x=2是原方程的解,
∴原方程的解为x=2,
故答案为:2.
12.方程的解是 x=3 .
【解答】解:∵,
∴或.
∴x=﹣2或x=3.
∵2+x≥0且x﹣3≥0,
∴x≥3.
故原方程的解为:x=3.
故答案为:x=3.
13.无理方程的解是 x=1 .
【解答】解:原方程两边同时平方得:x2﹣4x+3=1﹣x,
整理得:x2﹣3x+2=0,
解得:x=1或x=2,
经检验,x=1是原方程的解,x=2时,1﹣x<0,应舍去,
故答案为:x=1.
14.某云平台的网络安全事件中,最初有4台服务器遭受攻击并感染病毒.两轮传播后共有196台服务器被控制,则每轮中平均每台服务器传播设备的台数为 6 .
【解答】解:设每轮中平均每台服务器传播设备的台数为x,根据题意可得:
4+4x+x(4+4x)=196,
解得x1=6,x2=﹣8(舍),
故答案为:6.
15.某商场将进货价为55元的某种服装以75元售出,平均每天可售30件,为了尽快减少库存,商场决定采取适当的降价措施,调查发现:每件降价1元,则每天可多售5件,如果每天要盈利800元,每件应降价 10 元.
【解答】解:设每件应降价x元,则每件的盈利为(75﹣x﹣55)元,每天可售出(30+5x)件,
根据题意得:(75﹣x﹣55)(30+5x)=800,
整理得:x2﹣14x+40=0,
解得:x1=10,x2=4(不符合题意,舍去),
即每件应降价10元,
故答案为:10.
16.如图,某牧场准备利用现成的一堵“7”字形的墙面粗线表示墙面(粗线A﹣B﹣C表示墙面)建饲养场.已知AB⊥BC,AB=3米,BC=9米,现计划用总长为38米的篱笆围建一个“日”字形的饲养场BDEF(细线表示篱笆,饲养场中间用篱笆GH隔开),并在每个区域开一个宽2米的门,点F在线段BC的延长线上.设EF的长为x米,若要求所围成的饲养场BDEF面积为84平方米,则可列方程 x=84 (不用化简).
【解答】解:设EF的长为x米,则DE(米),
依题意得: x=84,
故答案为: x=84.
17.如图,在△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,以2cm/s的速度沿CA方向运动;同时动点Q从点B出发,以1cm/s的速度沿BC方向运动.则运动 10 秒后P、Q两点相距25cm.
【解答】解:设运动x秒后P、Q两点相距25cm,
则CP=2x cm,CQ=(25﹣x)cm,
由题意得:(2x)2+(25﹣x)2=252,
整理得:x2﹣10x=0,
解得:x1=10,x2=0(不合题意,舍去),
故答案为:10.
18.在2024年12月的日历表上用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为513,则这个最小数为 19 .
【解答】解:设这个最小数为x,则另外三个数分别为x+1,x+7,x+8,
根据题意得:x(x+8)=513,
整理得:x2+8x﹣513=0,
解得:x1=19,x2=﹣27(不符合题意,舍去),
∴这个最小数为19.
故答案为:19.
三.解答题(共6小题)
19.如图,利用一面墙(墙的长度不限),用20m长的篱笆围成一个矩形场地ABCD.
(1)若矩形场地的面积为48m2,求AB的长;
(2)该矩形场地的面积能否为60m2?若能,求出AB的长;若不能,请说明理由.
【解答】解:(1)设AB=x m,则BC=(20﹣2x)m,
根据题意得:x(20﹣2x)=48,
整理得:x2﹣10x+24=0,
解得:x1=4,x2=6.
答:AB的长为4或6m;
(2)该矩形场地的面积不能为60m2,理由如下:
假设该矩形场地的面积能为60m2,设AB=y m,则BC=(20﹣2y)m,
根据题意得:y(20﹣2y)=60,
整理得:y2﹣10y+30=0,
∵Δ=(﹣10)2﹣4×1×30=﹣20<0,
∴原方程没有实数根,
∴假设不成立,即该矩形场地的面积不能为60m2.
20.随着旅游旺季的到来,烟台某景区游客人数逐月增加,3月份游客人数为1.6万人,5月份游客人数为2.5万人.
(1)求这两个月该景区游客人数的月平均增长率;
(2)预计6月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区6月1日至6月20日已接待游客2.125万人,则6月份后10天日均接待游客人数最多是多少万人?
【解答】解:(1)设这两个月中该景区游客人数的月平均增长率为x,
根据题意得:1.6(1+x)2=2.5,
解得:x1=0.25=25%,x2=﹣2.25(不符合题意,舍去),
答:这两个月中该景区游客人数的月平均增长率为25%;
(2)设6月份后10天日均接待游客人数是y万人,
根据题意得:2.125+10y≤2.5×(1+25%),
解得:y≤0.1,
答:6月份后10天日均接待游客人数最多是0.1万人.
21.某运动品牌销售一款运动鞋,已知每双运动鞋的成本价为60元,当售价为100元时,平均每天能售出200双;经过一段时间销售发现,平均每天售出的运动鞋数量y(双)与降低价格x(元)之间存在如图所示的函数关系.
(1)求出y与x的函数关系式;
(2)公司希望平均每天获得的利润达到8910元,且优惠力度最大,则每双运动鞋的售价应该定为多少元?
【解答】解:(1)设y与x的函数关系式为y=kx+b(k≠0),
将(0,200),(10,300)代入y=kx+b得:
,
解得,
∴y与x的函数关系式为y=10x+200;
(2)根据题意得:(100﹣60﹣x)(10x+200)=8910,
整理得:x2﹣20x+91=0,
解得x1=7,x2=13,
又∵要求优惠力度最大,
∴x=13,
∴100﹣x=100﹣13=87.
答:每双运动鞋的售价应该定为87元.
22.数学兴趣小组利用长方形纸板制作礼品盒,选择长为60cm,宽为40cm的长方形纸板,如图,在其四角分别剪去两个同样大小的正方形和两个同样大小的长方形(阴影部分),再把剩余部分沿虚线折起来得长方体礼品盒.
(1)当礼盒底面的长是宽的4倍时,求该长方体礼品盒的体积;
(2)当礼盒的侧面ABCD的面积为750cm2,求剪去的小正方形的边长.
【解答】解:(1)设小正方形的边长为x,则礼盒底面的长是,宽为x,
由题意得30﹣x=4x,
解得x=6,
∴长为24,宽为6,高为40﹣2×6=28,
∴体积为:24×6×28=4032(cm3);
(2)设小正方形的边长为m,根据题意可得一元二次方程为:
(30﹣m)(40﹣2m)=750,
整理得m2﹣50m+225=0,
解得m=5或m=45(舍),
∴剪去的小正方形的边长为5cm.
23.在日历上,我们可以发现其中某些数满足一定的规律,如图是2024年10月份的日历.我们任意选择其中所示的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:9×11﹣3×17=48,13×15﹣7×21=48.不难发现,结果都是48.
(1)请证明发现的规律;
(2)若用一个如图所示菱形框,再框出5个数字,其中最小数与最大数的积为435,求出这5个数中的最大数.
【解答】(1)证明:设中间的数为a,则另外4个数分别为(a﹣7),(a﹣1),(a+1),(a+7),
∴(a﹣1)(a+1)﹣(a﹣7)(a+7),
=a2﹣1﹣(a2﹣49),
=48.
(2)解:设这5个数中的最大数为x,则最小数为(x﹣14),
依题意得:x(x﹣14)=435,
解得:x1=29,x2=﹣15(不合题意,舍去).
答:这5个数中的最大数为29.
24.【综合与实践】
学校劳动实践基地的开发能让学生体验劳动的艰辛,品味获得劳动成果的喜悦,同时满足学生劳动教育实践需要.如图是某校劳动实践基地的示意图,该基地为两边靠墙的矩形ABCD,面积为360平方米,墙AB的长为15米.
【实践应用】
(1)据学校管理人员介绍,该基地2023年的面积只有250平方米,连续两年扩建,并且两年的增长率相同,请求出这个增长率;
(2)如图所示,学校打算在基地内用总长度为33米的栅栏围成两面靠墙的三个大小相同的矩形空地用来养殖小动物,总面积为72平方米,求矩形空地的宽EF为多少米?
【解答】解:(1)设这个增长率为x,由题意列一元二次方程得:
250(1+x)2=360,
整理得,250x2+500x+140=0,
解得x1=﹣2.2(不合题意舍去),x2=0.2=20%,
答:这个增长率为20%;
(2)∵矩形ABCD,面积为360平方米,墙AB的长为15米,
∴AD=360÷15=24,
设矩形空地的宽EF为y米,则FG的长为(33﹣3y)米,
由题意列一元二次方程得:y(33﹣3y)=72,
整理得:y2+11y+24=0,
解得y1=3,y2=8,
当y=3时,FG的长为:33﹣3×3=24>15,不合题意,舍去;
当y=8时,BC的长为:33﹣3×8=9<15,符合题意.
∴EF=8米.
答:场地的宽EF为8米.
第1页(共1页)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
