第3章 代数式(新课预习.含解析)-2025-2026学年七年级上册数学人教版(2024)
文档属性
| 名称 | 第3章 代数式(新课预习.含解析)-2025-2026学年七年级上册数学人教版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 581.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 15:39:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第3章 代数式
一.选择题(共10小题)
1.(2024 威县校级模拟)x表示一个两位数,把6写到x的右边组成一个三位数,则表示这个三位数的式子是( )
A.6x B.10x+6 C.100x+6 D.600+x
2.(2023秋 五峰县期末)如图,池塘边有一块长为a,宽为b的长方形土地,现将其余三面都留出宽是2的小路,中间余下的长方形部分做菜地,则菜地的周长为( )
A.a+2b﹣4 B.a+2b C.2a+2b﹣8 D.2a+2b﹣12
3.(2024秋 安宁区校级期末)下列选项中的量不能用“0.9a”表示的是( )
A.边长为a,且这条边上的高为0.9的三角形的面积
B.原价为a元/千克的商品打九折后的售价
C.以0.9千米/小时的速度匀速行驶a小时所经过的路程
D.一本书共a页,看了整本书的后剩下的页数
4.(2024春 南岗区校级月考)某轮船顺水航行的速度为x km/h,水速为y km/h,则该轮船逆水航行速度为( )km/h.
A.x﹣y B.x+y C.2x﹣y D.x﹣2y
5.(2023秋 沙市区期末)某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶.如果以每包元的价格全部卖出这种茶叶,那么这家商店( )
A.盈利了 B.亏损了
C.不盈不亏 D.盈亏不能确定
6.(2024秋 江北区校级期中)某重点中学初一(2)班有48名同学,开学之际,要将一批作业练习本分发给全班同学,如果每人分a本,则剩余3本,那么这批作业练习本共( )本.
A.48a﹣3 B.48a+3 C.144﹣a D.144+a
7.(2024秋 合江县期中)某电子产品原价为m,9月迎来开学季,商家开展“教育优惠”活动,现售价为0.8m﹣100则下列说法中,符合题意的是( )
A.原价减100元后再打8折
B.原价打8折后再减100元
C.原价打2折后再减100元
D.原价减100元后再打2折
8.(2023秋 乌鲁木齐期末)为了进一步推进“双减”政策,提升学校课后服务水平,我校开展了选修课程,每位学生可以选择一个选修课程参加,已知参加“学科类选修课程”的有m人,参加“音体美选修课程”的人数比参加“学科类选修课程”的人数多6人,参加“科技类选修课程”的人数比参加“音体美选修课程”人数的多2人,则参加三类选修课程的总人数为( )
A.m+6 B. C. D.
9.(2024 青岛开学)下列选项中,能用代数式2a+6表示的是( )
A.三角形的周长 B.长方形的周长
C.梯形的面积 D.长方体的体积
10.(2023秋 襄城县期末)用字母表示的代数式是具有一定意义的,下列赋予4a实际意义的例子中错误的是( )
A.若水果的价格是4元/千克,则4a表示买a千克该水果的金额
B.若一个两位数的十位数字是4,个位数字a,则4a表示这个两位数
C.汽车行驶速度是a千米/小时,则4a表示这辆汽车行驶4小时的路程
D.若a表示一个正方形的边长,则4a表示这个正方形的周长
二.填空题(共5小题)
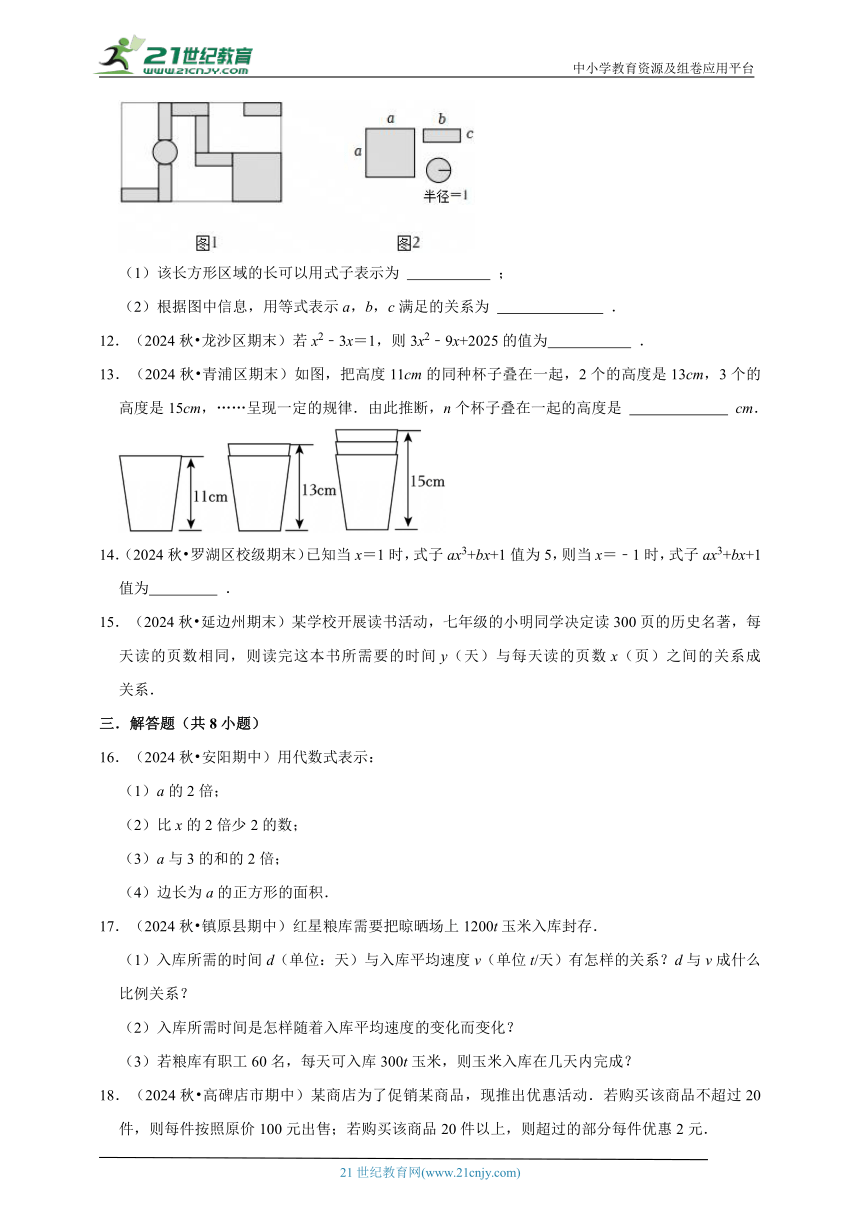
11.(2024秋 黄陂区期末)如图1.在一块长方形区域中布置了图中阴影部分所示的展区,其中的展台有三种不同的形状,其规格如图2所示.
(1)该长方形区域的长可以用式子表示为 ;
(2)根据图中信息,用等式表示a,b,c满足的关系为 .
12.(2024秋 龙沙区期末)若x2﹣3x=1,则3x2﹣9x+2025的值为 .
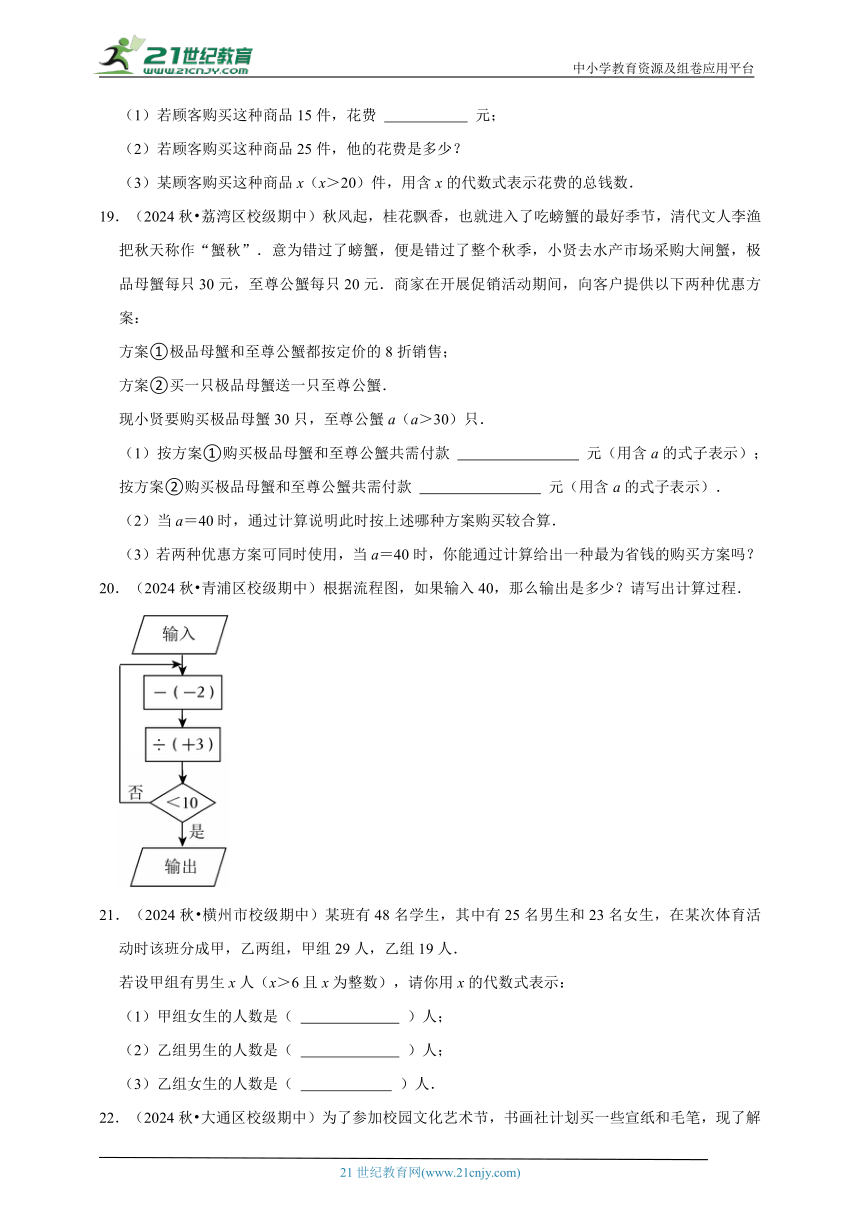
13.(2024秋 青浦区期末)如图,把高度11cm的同种杯子叠在一起,2个的高度是13cm,3个的高度是15cm,……呈现一定的规律.由此推断,n个杯子叠在一起的高度是 cm.
14.(2024秋 罗湖区校级期末)已知当x=1时,式子ax3+bx+1值为5,则当x=﹣1时,式子ax3+bx+1值为 .
15.(2024秋 延边州期末)某学校开展读书活动,七年级的小明同学决定读300页的历史名著,每天读的页数相同,则读完这本书所需要的时间y(天)与每天读的页数x(页)之间的关系成 关系.
三.解答题(共8小题)
16.(2024秋 安阳期中)用代数式表示:
(1)a的2倍;
(2)比x的2倍少2的数;
(3)a与3的和的2倍;
(4)边长为a的正方形的面积.
17.(2024秋 镇原县期中)红星粮库需要把晾晒场上1200t玉米入库封存.
(1)入库所需的时间d(单位:天)与入库平均速度v(单位t/天)有怎样的关系?d与v成什么比例关系?
(2)入库所需时间是怎样随着入库平均速度的变化而变化?
(3)若粮库有职工60名,每天可入库300t玉米,则玉米入库在几天内完成?
18.(2024秋 高碑店市期中)某商店为了促销某商品,现推出优惠活动.若购买该商品不超过20件,则每件按照原价100元出售;若购买该商品20件以上,则超过的部分每件优惠2元.
(1)若顾客购买这种商品15件,花费 元;
(2)若顾客购买这种商品25件,他的花费是多少?
(3)某顾客购买这种商品x(x>20)件,用含x的代数式表示花费的总钱数.
19.(2024秋 荔湾区校级期中)秋风起,桂花飘香,也就进入了吃螃蟹的最好季节,清代文人李渔把秋天称作“蟹秋”.意为错过了螃蟹,便是错过了整个秋季,小贤去水产市场采购大闸蟹,极品母蟹每只30元,至尊公蟹每只20元.商家在开展促销活动期间,向客户提供以下两种优惠方案:
方案①极品母蟹和至尊公蟹都按定价的8折销售;
方案②买一只极品母蟹送一只至尊公蟹.
现小贤要购买极品母蟹30只,至尊公蟹a(a>30)只.
(1)按方案①购买极品母蟹和至尊公蟹共需付款 元(用含a的式子表示);按方案②购买极品母蟹和至尊公蟹共需付款 元(用含a的式子表示).
(2)当a=40时,通过计算说明此时按上述哪种方案购买较合算.
(3)若两种优惠方案可同时使用,当a=40时,你能通过计算给出一种最为省钱的购买方案吗?
20.(2024秋 青浦区校级期中)根据流程图,如果输入40,那么输出是多少?请写出计算过程.
21.(2024秋 横州市校级期中)某班有48名学生,其中有25名男生和23名女生,在某次体育活动时该班分成甲,乙两组,甲组29人,乙组19人.
若设甲组有男生x人(x>6且x为整数),请你用x的代数式表示:
(1)甲组女生的人数是( )人;
(2)乙组男生的人数是( )人;
(3)乙组女生的人数是( )人.
22.(2024秋 大通区校级期中)为了参加校园文化艺术节,书画社计划买一些宣纸和毛笔,现了解情况如下:甲、乙两家文具商店出售同样的毛笔和宣纸,毛笔每支20元,宣纸每张4元.甲商店的优惠办法是:买1支毛笔送1张宣纸;乙商店的优惠办法是:全部商品按定价的9折出售.书画社想购买毛笔10支,宣纸x张(x>10).
(1)若到甲商店购买,应付 元;若到乙商店购买,应付 元(用含x的代数式表示);
(2)若x=30时,去哪家商店购买较合算?请计算说明;
(3)若x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付多少元?
23.(2024秋 崇阳县校级期中)如图所示,在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r m,广场的长为a m,宽为b m.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为400m,宽为200m,圆形花坛的半径为15m,求广场空地的面积.(计算结果保留π)
第3章 代数式
参考答案与试题解析
一.选择题(共10小题)
1.(2024 威县校级模拟)x表示一个两位数,把6写到x的右边组成一个三位数,则表示这个三位数的式子是( )
A.6x B.10x+6 C.100x+6 D.600+x
【考点】列代数式.
【专题】计算题;运算能力.
【答案】B
【分析】x原来的最高位是十位,现在扩大了10倍,而6写到x的右边组成一个三位数,6成为三位数的个位,即可得出结果.
【解答】解:根据题意可知,x表示一个两位数,把6写到x的右边组成一个三位数,
∴相当于将x扩大了10倍,
∴表示这个三位数的式子是10x+6,
故答案为:B.
【点评】本题考查的是列代数式,根据题意正确列出代数式是解题的关键.
2.(2023秋 五峰县期末)如图,池塘边有一块长为a,宽为b的长方形土地,现将其余三面都留出宽是2的小路,中间余下的长方形部分做菜地,则菜地的周长为( )
A.a+2b﹣4 B.a+2b C.2a+2b﹣8 D.2a+2b﹣12
【考点】列代数式.
【专题】整式;运算能力.
【答案】D
【分析】先根据所给的图形,得出菜地的长和宽,再根据长方形周长公式求解即可.
【解答】解:由图可以看出:菜地的长为a﹣4,宽为b﹣2,
菜地的周长C=2(a﹣4)+2(b﹣2)=2(a+b﹣6)=2a+2b﹣12.
故选:D.
【点评】本题主要考查列代数式.从生活实际中出发,以数学知识解决生活实际中的问题,同时也考查了长方形周长的计算.
3.(2024秋 安宁区校级期末)下列选项中的量不能用“0.9a”表示的是( )
A.边长为a,且这条边上的高为0.9的三角形的面积
B.原价为a元/千克的商品打九折后的售价
C.以0.9千米/小时的速度匀速行驶a小时所经过的路程
D.一本书共a页,看了整本书的后剩下的页数
【考点】列代数式.
【专题】整式;符号意识.
【答案】A
【分析】选项A根据三角形的面积公式解答即可;选项B根据“售价=原价×折数”判断即可;选项C根据“路程=速度×时间”判断即可;选项D根据“剩下的页数=全数的页数﹣已看的页数”判断即可.
【解答】解:A.边长为a,且这条边上的高为0.9的三角形的面积为0.9a=0.45a,故本选项符合题意;
B.原价为a元/千克的商品打九折后的售价为0.9a元/千克,故本选项不符合题意;
C.以0.9千米/小时的速度匀速行驶a小时所经过的路程为0.9a千米,故本选项不符合题意;
D.一本书共a页,看了整本书的后剩下的页数为0.9a页,故本选项不符合题意.
故选:A.
【点评】本题考查了列代数式,理清各个选项中的数量关系是解答本题的关键.
4.(2024春 南岗区校级月考)某轮船顺水航行的速度为x km/h,水速为y km/h,则该轮船逆水航行速度为( )km/h.
A.x﹣y B.x+y C.2x﹣y D.x﹣2y
【考点】列代数式.
【专题】计算题;推理能力.
【答案】D
【分析】根据轮船顺水航行的速度及水速,求出轮船在静水中的航速,再用轮船在静水中的航速减去水速即为轮船逆水航行的速度.
【解答】解:因为轮船在静水中的航速为(x﹣y) km/h,水速为y km/h,
所以轮船在逆水中的航速为(x﹣2y )km/h.
故选:D.
【点评】本题考查了根据实际问题列代数式,解题的关键是求出轮船在静水中的航速.
5.(2023秋 沙市区期末)某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶.如果以每包元的价格全部卖出这种茶叶,那么这家商店( )
A.盈利了 B.亏损了
C.不盈不亏 D.盈亏不能确定
【考点】列代数式.
【专题】整式;应用意识.
【答案】A
【分析】先根据题意列出进货的成本与销售额,再作差比较即可.
【解答】解:由题意得,进货成本=40m+60n,销售额,
故50(m+n)﹣(40m+60n)
=50m+50n﹣40m﹣60n
=10(m﹣n),
∵m>n,
∴10(m﹣n)>0,
∴这家商店盈利.
故选:A.
【点评】本题考查列代数式,熟知整式的加减实质上就是合并同类项是解答此题的关键.
6.(2024秋 江北区校级期中)某重点中学初一(2)班有48名同学,开学之际,要将一批作业练习本分发给全班同学,如果每人分a本,则剩余3本,那么这批作业练习本共( )本.
A.48a﹣3 B.48a+3 C.144﹣a D.144+a
【考点】列代数式.
【专题】整式;运算能力.
【答案】B
【分析】根据初一(2)班有48名同学,开学之际,要将一批作业练习本分发给全班同学,每人分a本,则剩余3本,可以用a的代数式表示出这批作业练习本的总本数.
【解答】解:由题意可得,
这批作业本共(48a+3)本,
故选:B.
【点评】本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.
7.(2024秋 合江县期中)某电子产品原价为m,9月迎来开学季,商家开展“教育优惠”活动,现售价为0.8m﹣100则下列说法中,符合题意的是( )
A.原价减100元后再打8折
B.原价打8折后再减100元
C.原价打2折后再减100元
D.原价减100元后再打2折
【考点】代数式.
【专题】整式;符号意识.
【答案】B
【分析】0.8m即在原价的基础上打8折,﹣100即降价100元,据此求解即可.
【解答】解:0.8m﹣100表示的是原价先打8折,再降价100元,
故选:B.
【点评】本题主要考查了代数式的意义,正确理解题意是解题的关键.
8.(2023秋 乌鲁木齐期末)为了进一步推进“双减”政策,提升学校课后服务水平,我校开展了选修课程,每位学生可以选择一个选修课程参加,已知参加“学科类选修课程”的有m人,参加“音体美选修课程”的人数比参加“学科类选修课程”的人数多6人,参加“科技类选修课程”的人数比参加“音体美选修课程”人数的多2人,则参加三类选修课程的总人数为( )
A.m+6 B. C. D.
【考点】列代数式.
【专题】整式;运算能力.
【答案】B
【分析】根据题意可知,参加三类选修课程的总人数m+(m+6),进一步化简即可.
【解答】解:根据题意可知,参加三类选修课程的总人数m+(m+6)
=m+m+6m+3+2
m+11,
故选:B.
【点评】本题考查了列代数式,合并同类项,根据题意列出代数式是解题的关键.
9.(2024 青岛开学)下列选项中,能用代数式2a+6表示的是( )
A.三角形的周长 B.长方形的周长
C.梯形的面积 D.长方体的体积
【考点】代数式.
【专题】整式;运算能力.
【答案】B
【分析】根据图形列出代数式,即可求解.
【解答】解:A、三角形的周长为2+6+a=8+a,与题干不符,不符合题意;
B.长方形的周长为2(a+3)=2a+6,与题干不符,符合题意;
C.梯形的面积为,与题干不符,不符合题意;
D.长方体的体积为2×6×a=12a,与题干不符,不符合题意.
故选:B.
【点评】本题考查了代数式,掌握求代数式的方法是关键.
10.(2023秋 襄城县期末)用字母表示的代数式是具有一定意义的,下列赋予4a实际意义的例子中错误的是( )
A.若水果的价格是4元/千克,则4a表示买a千克该水果的金额
B.若一个两位数的十位数字是4,个位数字a,则4a表示这个两位数
C.汽车行驶速度是a千米/小时,则4a表示这辆汽车行驶4小时的路程
D.若a表示一个正方形的边长,则4a表示这个正方形的周长
【考点】代数式.
【专题】数与式;运算能力.
【答案】B
【分析】根据代数式表示的实际意义的方法分别判断每个选项,只有B选项中,若一个两位数的十位数字是4,个位数字a,则4×10+a表示这个两位数,从而得出答案.
【解答】解:根据题目:
A若水果的价格是4元/千克,则4a表示买a千克该水果的金额,此说法正确,故不符合题意;
B若一个两位数的十位数字是4,个位数字a,则4×10+a表示这个两位数,选项中说法不正确,故符合题意;
C汽车行驶速度是a千米/小时,则4a表示这辆汽车行驶4小时的路程,此说法正确,故不符合题意;
D若a表示一个正方形的边长,则4a表示这个正方形的周长,此说法正确,故不符合题意.
故选:B.
【点评】本题考查了代数式,掌握代数式的书写规范和实际问题中数量间的关系是解答本题的关键.
二.填空题(共5小题)
11.(2024秋 黄陂区期末)如图1.在一块长方形区域中布置了图中阴影部分所示的展区,其中的展台有三种不同的形状,其规格如图2所示.
(1)该长方形区域的长可以用式子表示为 a+3b ;
(2)根据图中信息,用等式表示a,b,c满足的关系为 a﹣b+c=2 .
【考点】列代数式.
【专题】整式;应用意识.
【答案】(1)a+3b;
(2)a﹣b+c=2.
【分析】(1)根据图中关系列出代数式即可;
(2)根据宽相等得出等量关系式即可.
【解答】解:(1)由图知,该长方形区域的长为a+3b,
故答案为:a+3b;
(2)由图知该长方形区域的宽为a+b+c或2b+2,
∴a+b+c=2b+2,
故答案为:a﹣b+c=2.
【点评】本题主要考查列代数式的知识,根据图中熟练关系列出代数式是解题的关键.
12.(2024秋 龙沙区期末)若x2﹣3x=1,则3x2﹣9x+2025的值为 2028 .
【考点】代数式求值.
【专题】整式;运算能力.
【答案】2028.
【分析】将原式变形后代入数值计算即可.
【解答】解:∵x2﹣3x=1,
∴3x2﹣9x+2025
=3(x2﹣3x)+2025
=3×1+2025
=2028,
故答案为:2028.
【点评】本题考查代数式求值,将原式进行正确的变形是解题的关键.
13.(2024秋 青浦区期末)如图,把高度11cm的同种杯子叠在一起,2个的高度是13cm,3个的高度是15cm,……呈现一定的规律.由此推断,n个杯子叠在一起的高度是 (9+2n) cm.
【考点】列代数式.
【专题】整式;几何直观;运算能力.
【答案】(9+2n).
【分析】根据图形,可以列出算式11+(13﹣11)×(n﹣1),然后计算即可.
【解答】解:由题意可得,
n个杯子叠在一起的高度是:11+(13﹣11)×(n﹣1)
=11+2(n﹣1)
=11+2n﹣2
=(9+2n)cm,
故答案为:(9+2n).
【点评】本题考查列代数式,解答本题的关键是明确题意,列出相应的算式.
14.(2024秋 罗湖区校级期末)已知当x=1时,式子ax3+bx+1值为5,则当x=﹣1时,式子ax3+bx+1值为 ﹣3 .
【考点】代数式求值.
【专题】整式.
【答案】见试题解答内容
【分析】把x=1时,代入式子ax3+bx+1,求出a+b=4,即可求解.
【解答】解:把x=1时,代入式子ax3+bx+1,
即:a+b+1=5,
把x=﹣1时,代入式子ax3+bx+1
则:ax3+bx+1
=﹣(a+b)+1=﹣3.
【点评】本题考查的是代数式求值,把给定的x值代入即可.
15.(2024秋 延边州期末)某学校开展读书活动,七年级的小明同学决定读300页的历史名著,每天读的页数相同,则读完这本书所需要的时间y(天)与每天读的页数x(页)之间的关系成 反比例 关系.
【考点】反比例.
【专题】分式;运算能力.
【答案】反比例.
【分析】根据等量关系:读书时间=读书总量÷每天读书量,即可得到答案.
【解答】解:根据题意可知,,
∴y与x之间的关系成反比例关系.
故答案为:反比例.
【点评】本题考查了反比例,掌握反比例的定义是关键.
三.解答题(共8小题)
16.(2024秋 安阳期中)用代数式表示:
(1)a的2倍;
(2)比x的2倍少2的数;
(3)a与3的和的2倍;
(4)边长为a的正方形的面积.
【考点】列代数式.
【专题】整式;应用意识.
【答案】(1)2a;
(2)2x﹣2;
(3)2(a+3);
(4)a2.
【分析】(1)根据题意,列出代数式,即可;
(2)根据题意,列出代数式,即可;
(3)根据题意,列出代数式,即可;
(4)根据题意,列出代数式,即可.
【解答】解:(1)a的2倍为:2a;
(2)比x的2倍少2的数为:2x﹣2;
(3)a与3的和的2倍为:2(a+3);
(4)边长为a的正方形的面积为:a2.
【点评】本题考查列代数式,正确读懂题意是解题关键.
17.(2024秋 镇原县期中)红星粮库需要把晾晒场上1200t玉米入库封存.
(1)入库所需的时间d(单位:天)与入库平均速度v(单位t/天)有怎样的关系?d与v成什么比例关系?
(2)入库所需时间是怎样随着入库平均速度的变化而变化?
(3)若粮库有职工60名,每天可入库300t玉米,则玉米入库在几天内完成?
【考点】代数式求值;列代数式.
【专题】整式;运算能力.
【答案】(1),d与v成反比关系;
(2)入库所需时间随入库平均速度的变大而变小;
(3)4天内完成.
【分析】(1)由题意直接列出代数式即可,根据当分子一定时,分母越大,分数值越小即可得出d与v成反比关系;
(2)结合d与v成反比关系,可知入库所需时间随入库平均速度的变大而变小;
(3)将v=300t,代入(1)所列代数式求值即可.
【解答】解:(1)由题意可知,
当分子一定时,v越大,d越小,
所以d与v成反比关系;
(2)入库所需时间随入库平均速度的变大而变小;
(3)由题意可知v=300t,
所以(天),
所以玉米入库在4天内完成.
【点评】本题考查列代数式,代数式求值,理解题意正确列出代数式是解题关键.
18.(2024秋 高碑店市期中)某商店为了促销某商品,现推出优惠活动.若购买该商品不超过20件,则每件按照原价100元出售;若购买该商品20件以上,则超过的部分每件优惠2元.
(1)若顾客购买这种商品15件,花费 1500 元;
(2)若顾客购买这种商品25件,他的花费是多少?
(3)某顾客购买这种商品x(x>20)件,用含x的代数式表示花费的总钱数.
【考点】列代数式.
【专题】整式;运算能力.
【答案】(1)1500;
(2)若顾客购买这种商品25件,他的花费是2490元;
(3)花费的总钱数为(98x+40)元.
【分析】(1)根据购买该商品不超过20件,则每件按照原价100元出售,列出算式进行计算即可;
(2)根据购买该商品20件以上,则超过的部分每件优惠2元,列出算式进行计算即可;
(3)根据购买这种商品x(x>20)件,购买该商品20件以上,则超过的部分每件优惠2元,列出算式进行计算即可.
【解答】解:(1)购买这种商品15件,花费为:100×15=1500(元).
故答案为:1500;
(2)20×100+98×5=2490(元).
答:花费是2490元.
(3)100×20+98(x﹣20)=98x+40.
答:花费的总钱数为(98x+40)元.
【点评】本题主要考查了有理数混合运算的应用,列代数式,解题的关键是理解题意,根据题意列出算式.
19.(2024秋 荔湾区校级期中)秋风起,桂花飘香,也就进入了吃螃蟹的最好季节,清代文人李渔把秋天称作“蟹秋”.意为错过了螃蟹,便是错过了整个秋季,小贤去水产市场采购大闸蟹,极品母蟹每只30元,至尊公蟹每只20元.商家在开展促销活动期间,向客户提供以下两种优惠方案:
方案①极品母蟹和至尊公蟹都按定价的8折销售;
方案②买一只极品母蟹送一只至尊公蟹.
现小贤要购买极品母蟹30只,至尊公蟹a(a>30)只.
(1)按方案①购买极品母蟹和至尊公蟹共需付款 (720+16a) 元(用含a的式子表示);按方案②购买极品母蟹和至尊公蟹共需付款 (300+20a) 元(用含a的式子表示).
(2)当a=40时,通过计算说明此时按上述哪种方案购买较合算.
(3)若两种优惠方案可同时使用,当a=40时,你能通过计算给出一种最为省钱的购买方案吗?
【考点】列代数式;代数式求值.
【专题】整式;运算能力.
【答案】见试题解答内容
【分析】(1)分别按照方案①和方案②的优惠方案,进行计算即可解答;
(2)把a=40代入(1)中的结论,进行计算即可解答;
(3)两种优惠方案可同时使用,可先按方案②购买30极品母蟹,再送30只至尊公蟹,然后按方案①购买10只至尊公蟹,最后进行计算比较即可解答.
【解答】解:(1)由题意得:
按方案①购买极品母蟹和至尊公蟹共需付款
=0.8×(30×30+20a)
=0.8×(900+20a)
=(720+16a)元,
按方案②购买极品母蟹和至尊公蟹共需付款
=30×30+20(a﹣30)
=900+20a﹣600
=(300+20a)元,
∴按方案①购买极品母蟹和至尊公蟹共需付款(720+16a)元;按方案②购买极品母蟹和至尊公蟹共需付款(300+20a)元,
故答案为:(720+16a),(300+20a);
(2)当a=40时,
按方案①购买极品母蟹和至尊公蟹共需付款
=720+16×40
=720+640
=1360(元),
按方案②购买极品母蟹和至尊公蟹共需付款
=300+20×40
=300+800
=1100(元),
∵1100<1360,
∴按方案②购买较为合算;
(3)若两种优惠方案可同时使用,则可先按方案②购买30极品母蟹,再送30只至尊公蟹,然后按方案①购买10只至尊公蟹,
理由:30×30+(40﹣30)×20×0.8
=900+10×20×0.8
=900+160
=1060(元),
∵1060<1100<1360,
∴最为省钱的购买方案是:先按方案②购买30极品母蟹,再送30只至尊公蟹,然后按方案①购买10只至尊公蟹.
【点评】本题考查了列代数式,代数式求值,准确熟练地进行计算是解题的关键.
20.(2024秋 青浦区校级期中)根据流程图,如果输入40,那么输出是多少?请写出计算过程.
【考点】代数式求值;有理数的混合运算.
【专题】实数;运算能力.
【答案】输出的是5.
【分析】将40输入后按照运算程序进行计算、求解.
【解答】解:输出的是5,
当输入40时,
40﹣(﹣2)=42,42÷(+3)=14,14>10;
再输入14时,
14﹣(﹣2)=16,16÷(+3)=5,510,
∴输出的是5.
【点评】此题考查了有理数的计算能力,关键是能准确理解并运用该运算程序进行计算.
21.(2024秋 横州市校级期中)某班有48名学生,其中有25名男生和23名女生,在某次体育活动时该班分成甲,乙两组,甲组29人,乙组19人.
若设甲组有男生x人(x>6且x为整数),请你用x的代数式表示:
(1)甲组女生的人数是( (29﹣x) )人;
(2)乙组男生的人数是( (25﹣x) )人;
(3)乙组女生的人数是( (x﹣6) )人.
【考点】列代数式.
【专题】整式;应用意识.
【答案】(1)(29﹣x);
(2)(25﹣x);
(3)(x﹣6).
【分析】(1)用甲组总人数减去甲组有男生人数即可得出答案;
(2)用男生总人数减去甲组男生人数即可得答案;
(3)用乙组总人数减去(2)中所求男生人数即可得答案.
【解答】解:(1)由题意可得:甲组女生的人数是(29﹣x)人.
故答案为:(29﹣x).
(2)∵共有25名男生,甲组有男生x人,
∴乙组男生的人数是(25﹣x)人.
故答案为:(25﹣x).
(3)∵乙组有19人,由(2)可知乙组男生的人数是(25﹣x)人,
∴乙组女生的人数是19﹣(25﹣x)=(x﹣6)人.
故答案为:(x﹣6).
【点评】本题主要考查列代数式,仔细审题,根据题意找到正确的等量关系是解答本题的关键.
22.(2024秋 大通区校级期中)为了参加校园文化艺术节,书画社计划买一些宣纸和毛笔,现了解情况如下:甲、乙两家文具商店出售同样的毛笔和宣纸,毛笔每支20元,宣纸每张4元.甲商店的优惠办法是:买1支毛笔送1张宣纸;乙商店的优惠办法是:全部商品按定价的9折出售.书画社想购买毛笔10支,宣纸x张(x>10).
(1)若到甲商店购买,应付 (4x+160) 元;若到乙商店购买,应付 (3.6x+180) 元(用含x的代数式表示);
(2)若x=30时,去哪家商店购买较合算?请计算说明;
(3)若x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付多少元?
【考点】代数式求值;列代数式.
【专题】整式;运算能力.
【答案】见试题解答内容
【分析】(1)到甲商店购买的费用:10支毛笔的费用+(x﹣10)张宣纸的费用;到乙商店购买的费用:(10支毛笔的费用+x张宣纸的费用)×90%,把相关数值代入求解即可;
(2)把x=30代入(1)得到的式子进行计算,然后比较结果即可;
(3)先到甲商店购买10支毛笔,送10张宣纸,再到乙商店购买20张宣纸即可.
【解答】解:(1)到甲商店购买的费用:20×10+4(x﹣10)=(4x+160)元;
到乙商店购买的费用:(20×10+4x)×90%=(3.6x+180)元;
故答案为:(4x+160),(3.6x+180);
(2)若x=30时,到甲商店购买较为合算.
当x=30时,
到甲商店购买的费用:4×30+160=280(元);
到乙商店购买的费用:3.6×30+180=288(元);
∵280<288,
∴到甲商店购买较为合算;
(3)当x=30时,
先到甲商店购买10支毛笔,送10张宣纸,再到乙商店购买30﹣10=20张宣纸,
则费用为:10×20+20×4×90%=272(元).
【点评】本题考查了列代数式的知识,代数式求值及有理数四则运算的实际应用,解决问题的关键是读懂题意,找到所求的量的等量关系.
23.(2024秋 崇阳县校级期中)如图所示,在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r m,广场的长为a m,宽为b m.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为400m,宽为200m,圆形花坛的半径为15m,求广场空地的面积.(计算结果保留π)
【考点】列代数式.
【专题】整式;运算能力.
【答案】(1)(ab﹣πr2)m2;(2)(80000﹣225π)m2.
【分析】(1)根据题意广场空的面积等于长方形的面积减去一个圆的面积,据此列出代数式即可;
(2)根据题意,将已知数据代入(1)中代数式求值即可.
【解答】解:(1)依题意,圆形的半径为r m,广场长为a m,宽为b m,
则广场空地的面积为(ab﹣πr2)m2.
(2)∵广场的长为400m,宽为200m,圆形花坛的半径为15m.
∴(ab﹣πr2)m2=(400×200﹣152π)m2=(80000﹣225π)m2.
【点评】本题考查了列代数式,根据字母的值求代数式的值,理解题意,列出代数式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第3章 代数式
一.选择题(共10小题)
1.(2024 威县校级模拟)x表示一个两位数,把6写到x的右边组成一个三位数,则表示这个三位数的式子是( )
A.6x B.10x+6 C.100x+6 D.600+x
2.(2023秋 五峰县期末)如图,池塘边有一块长为a,宽为b的长方形土地,现将其余三面都留出宽是2的小路,中间余下的长方形部分做菜地,则菜地的周长为( )
A.a+2b﹣4 B.a+2b C.2a+2b﹣8 D.2a+2b﹣12
3.(2024秋 安宁区校级期末)下列选项中的量不能用“0.9a”表示的是( )
A.边长为a,且这条边上的高为0.9的三角形的面积
B.原价为a元/千克的商品打九折后的售价
C.以0.9千米/小时的速度匀速行驶a小时所经过的路程
D.一本书共a页,看了整本书的后剩下的页数
4.(2024春 南岗区校级月考)某轮船顺水航行的速度为x km/h,水速为y km/h,则该轮船逆水航行速度为( )km/h.
A.x﹣y B.x+y C.2x﹣y D.x﹣2y
5.(2023秋 沙市区期末)某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶.如果以每包元的价格全部卖出这种茶叶,那么这家商店( )
A.盈利了 B.亏损了
C.不盈不亏 D.盈亏不能确定
6.(2024秋 江北区校级期中)某重点中学初一(2)班有48名同学,开学之际,要将一批作业练习本分发给全班同学,如果每人分a本,则剩余3本,那么这批作业练习本共( )本.
A.48a﹣3 B.48a+3 C.144﹣a D.144+a
7.(2024秋 合江县期中)某电子产品原价为m,9月迎来开学季,商家开展“教育优惠”活动,现售价为0.8m﹣100则下列说法中,符合题意的是( )
A.原价减100元后再打8折
B.原价打8折后再减100元
C.原价打2折后再减100元
D.原价减100元后再打2折
8.(2023秋 乌鲁木齐期末)为了进一步推进“双减”政策,提升学校课后服务水平,我校开展了选修课程,每位学生可以选择一个选修课程参加,已知参加“学科类选修课程”的有m人,参加“音体美选修课程”的人数比参加“学科类选修课程”的人数多6人,参加“科技类选修课程”的人数比参加“音体美选修课程”人数的多2人,则参加三类选修课程的总人数为( )
A.m+6 B. C. D.
9.(2024 青岛开学)下列选项中,能用代数式2a+6表示的是( )
A.三角形的周长 B.长方形的周长
C.梯形的面积 D.长方体的体积
10.(2023秋 襄城县期末)用字母表示的代数式是具有一定意义的,下列赋予4a实际意义的例子中错误的是( )
A.若水果的价格是4元/千克,则4a表示买a千克该水果的金额
B.若一个两位数的十位数字是4,个位数字a,则4a表示这个两位数
C.汽车行驶速度是a千米/小时,则4a表示这辆汽车行驶4小时的路程
D.若a表示一个正方形的边长,则4a表示这个正方形的周长
二.填空题(共5小题)
11.(2024秋 黄陂区期末)如图1.在一块长方形区域中布置了图中阴影部分所示的展区,其中的展台有三种不同的形状,其规格如图2所示.
(1)该长方形区域的长可以用式子表示为 ;
(2)根据图中信息,用等式表示a,b,c满足的关系为 .
12.(2024秋 龙沙区期末)若x2﹣3x=1,则3x2﹣9x+2025的值为 .
13.(2024秋 青浦区期末)如图,把高度11cm的同种杯子叠在一起,2个的高度是13cm,3个的高度是15cm,……呈现一定的规律.由此推断,n个杯子叠在一起的高度是 cm.
14.(2024秋 罗湖区校级期末)已知当x=1时,式子ax3+bx+1值为5,则当x=﹣1时,式子ax3+bx+1值为 .
15.(2024秋 延边州期末)某学校开展读书活动,七年级的小明同学决定读300页的历史名著,每天读的页数相同,则读完这本书所需要的时间y(天)与每天读的页数x(页)之间的关系成 关系.
三.解答题(共8小题)
16.(2024秋 安阳期中)用代数式表示:
(1)a的2倍;
(2)比x的2倍少2的数;
(3)a与3的和的2倍;
(4)边长为a的正方形的面积.
17.(2024秋 镇原县期中)红星粮库需要把晾晒场上1200t玉米入库封存.
(1)入库所需的时间d(单位:天)与入库平均速度v(单位t/天)有怎样的关系?d与v成什么比例关系?
(2)入库所需时间是怎样随着入库平均速度的变化而变化?
(3)若粮库有职工60名,每天可入库300t玉米,则玉米入库在几天内完成?
18.(2024秋 高碑店市期中)某商店为了促销某商品,现推出优惠活动.若购买该商品不超过20件,则每件按照原价100元出售;若购买该商品20件以上,则超过的部分每件优惠2元.
(1)若顾客购买这种商品15件,花费 元;
(2)若顾客购买这种商品25件,他的花费是多少?
(3)某顾客购买这种商品x(x>20)件,用含x的代数式表示花费的总钱数.
19.(2024秋 荔湾区校级期中)秋风起,桂花飘香,也就进入了吃螃蟹的最好季节,清代文人李渔把秋天称作“蟹秋”.意为错过了螃蟹,便是错过了整个秋季,小贤去水产市场采购大闸蟹,极品母蟹每只30元,至尊公蟹每只20元.商家在开展促销活动期间,向客户提供以下两种优惠方案:
方案①极品母蟹和至尊公蟹都按定价的8折销售;
方案②买一只极品母蟹送一只至尊公蟹.
现小贤要购买极品母蟹30只,至尊公蟹a(a>30)只.
(1)按方案①购买极品母蟹和至尊公蟹共需付款 元(用含a的式子表示);按方案②购买极品母蟹和至尊公蟹共需付款 元(用含a的式子表示).
(2)当a=40时,通过计算说明此时按上述哪种方案购买较合算.
(3)若两种优惠方案可同时使用,当a=40时,你能通过计算给出一种最为省钱的购买方案吗?
20.(2024秋 青浦区校级期中)根据流程图,如果输入40,那么输出是多少?请写出计算过程.
21.(2024秋 横州市校级期中)某班有48名学生,其中有25名男生和23名女生,在某次体育活动时该班分成甲,乙两组,甲组29人,乙组19人.
若设甲组有男生x人(x>6且x为整数),请你用x的代数式表示:
(1)甲组女生的人数是( )人;
(2)乙组男生的人数是( )人;
(3)乙组女生的人数是( )人.
22.(2024秋 大通区校级期中)为了参加校园文化艺术节,书画社计划买一些宣纸和毛笔,现了解情况如下:甲、乙两家文具商店出售同样的毛笔和宣纸,毛笔每支20元,宣纸每张4元.甲商店的优惠办法是:买1支毛笔送1张宣纸;乙商店的优惠办法是:全部商品按定价的9折出售.书画社想购买毛笔10支,宣纸x张(x>10).
(1)若到甲商店购买,应付 元;若到乙商店购买,应付 元(用含x的代数式表示);
(2)若x=30时,去哪家商店购买较合算?请计算说明;
(3)若x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付多少元?
23.(2024秋 崇阳县校级期中)如图所示,在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r m,广场的长为a m,宽为b m.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为400m,宽为200m,圆形花坛的半径为15m,求广场空地的面积.(计算结果保留π)
第3章 代数式
参考答案与试题解析
一.选择题(共10小题)
1.(2024 威县校级模拟)x表示一个两位数,把6写到x的右边组成一个三位数,则表示这个三位数的式子是( )
A.6x B.10x+6 C.100x+6 D.600+x
【考点】列代数式.
【专题】计算题;运算能力.
【答案】B
【分析】x原来的最高位是十位,现在扩大了10倍,而6写到x的右边组成一个三位数,6成为三位数的个位,即可得出结果.
【解答】解:根据题意可知,x表示一个两位数,把6写到x的右边组成一个三位数,
∴相当于将x扩大了10倍,
∴表示这个三位数的式子是10x+6,
故答案为:B.
【点评】本题考查的是列代数式,根据题意正确列出代数式是解题的关键.
2.(2023秋 五峰县期末)如图,池塘边有一块长为a,宽为b的长方形土地,现将其余三面都留出宽是2的小路,中间余下的长方形部分做菜地,则菜地的周长为( )
A.a+2b﹣4 B.a+2b C.2a+2b﹣8 D.2a+2b﹣12
【考点】列代数式.
【专题】整式;运算能力.
【答案】D
【分析】先根据所给的图形,得出菜地的长和宽,再根据长方形周长公式求解即可.
【解答】解:由图可以看出:菜地的长为a﹣4,宽为b﹣2,
菜地的周长C=2(a﹣4)+2(b﹣2)=2(a+b﹣6)=2a+2b﹣12.
故选:D.
【点评】本题主要考查列代数式.从生活实际中出发,以数学知识解决生活实际中的问题,同时也考查了长方形周长的计算.
3.(2024秋 安宁区校级期末)下列选项中的量不能用“0.9a”表示的是( )
A.边长为a,且这条边上的高为0.9的三角形的面积
B.原价为a元/千克的商品打九折后的售价
C.以0.9千米/小时的速度匀速行驶a小时所经过的路程
D.一本书共a页,看了整本书的后剩下的页数
【考点】列代数式.
【专题】整式;符号意识.
【答案】A
【分析】选项A根据三角形的面积公式解答即可;选项B根据“售价=原价×折数”判断即可;选项C根据“路程=速度×时间”判断即可;选项D根据“剩下的页数=全数的页数﹣已看的页数”判断即可.
【解答】解:A.边长为a,且这条边上的高为0.9的三角形的面积为0.9a=0.45a,故本选项符合题意;
B.原价为a元/千克的商品打九折后的售价为0.9a元/千克,故本选项不符合题意;
C.以0.9千米/小时的速度匀速行驶a小时所经过的路程为0.9a千米,故本选项不符合题意;
D.一本书共a页,看了整本书的后剩下的页数为0.9a页,故本选项不符合题意.
故选:A.
【点评】本题考查了列代数式,理清各个选项中的数量关系是解答本题的关键.
4.(2024春 南岗区校级月考)某轮船顺水航行的速度为x km/h,水速为y km/h,则该轮船逆水航行速度为( )km/h.
A.x﹣y B.x+y C.2x﹣y D.x﹣2y
【考点】列代数式.
【专题】计算题;推理能力.
【答案】D
【分析】根据轮船顺水航行的速度及水速,求出轮船在静水中的航速,再用轮船在静水中的航速减去水速即为轮船逆水航行的速度.
【解答】解:因为轮船在静水中的航速为(x﹣y) km/h,水速为y km/h,
所以轮船在逆水中的航速为(x﹣2y )km/h.
故选:D.
【点评】本题考查了根据实际问题列代数式,解题的关键是求出轮船在静水中的航速.
5.(2023秋 沙市区期末)某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶.如果以每包元的价格全部卖出这种茶叶,那么这家商店( )
A.盈利了 B.亏损了
C.不盈不亏 D.盈亏不能确定
【考点】列代数式.
【专题】整式;应用意识.
【答案】A
【分析】先根据题意列出进货的成本与销售额,再作差比较即可.
【解答】解:由题意得,进货成本=40m+60n,销售额,
故50(m+n)﹣(40m+60n)
=50m+50n﹣40m﹣60n
=10(m﹣n),
∵m>n,
∴10(m﹣n)>0,
∴这家商店盈利.
故选:A.
【点评】本题考查列代数式,熟知整式的加减实质上就是合并同类项是解答此题的关键.
6.(2024秋 江北区校级期中)某重点中学初一(2)班有48名同学,开学之际,要将一批作业练习本分发给全班同学,如果每人分a本,则剩余3本,那么这批作业练习本共( )本.
A.48a﹣3 B.48a+3 C.144﹣a D.144+a
【考点】列代数式.
【专题】整式;运算能力.
【答案】B
【分析】根据初一(2)班有48名同学,开学之际,要将一批作业练习本分发给全班同学,每人分a本,则剩余3本,可以用a的代数式表示出这批作业练习本的总本数.
【解答】解:由题意可得,
这批作业本共(48a+3)本,
故选:B.
【点评】本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.
7.(2024秋 合江县期中)某电子产品原价为m,9月迎来开学季,商家开展“教育优惠”活动,现售价为0.8m﹣100则下列说法中,符合题意的是( )
A.原价减100元后再打8折
B.原价打8折后再减100元
C.原价打2折后再减100元
D.原价减100元后再打2折
【考点】代数式.
【专题】整式;符号意识.
【答案】B
【分析】0.8m即在原价的基础上打8折,﹣100即降价100元,据此求解即可.
【解答】解:0.8m﹣100表示的是原价先打8折,再降价100元,
故选:B.
【点评】本题主要考查了代数式的意义,正确理解题意是解题的关键.
8.(2023秋 乌鲁木齐期末)为了进一步推进“双减”政策,提升学校课后服务水平,我校开展了选修课程,每位学生可以选择一个选修课程参加,已知参加“学科类选修课程”的有m人,参加“音体美选修课程”的人数比参加“学科类选修课程”的人数多6人,参加“科技类选修课程”的人数比参加“音体美选修课程”人数的多2人,则参加三类选修课程的总人数为( )
A.m+6 B. C. D.
【考点】列代数式.
【专题】整式;运算能力.
【答案】B
【分析】根据题意可知,参加三类选修课程的总人数m+(m+6),进一步化简即可.
【解答】解:根据题意可知,参加三类选修课程的总人数m+(m+6)
=m+m+6m+3+2
m+11,
故选:B.
【点评】本题考查了列代数式,合并同类项,根据题意列出代数式是解题的关键.
9.(2024 青岛开学)下列选项中,能用代数式2a+6表示的是( )
A.三角形的周长 B.长方形的周长
C.梯形的面积 D.长方体的体积
【考点】代数式.
【专题】整式;运算能力.
【答案】B
【分析】根据图形列出代数式,即可求解.
【解答】解:A、三角形的周长为2+6+a=8+a,与题干不符,不符合题意;
B.长方形的周长为2(a+3)=2a+6,与题干不符,符合题意;
C.梯形的面积为,与题干不符,不符合题意;
D.长方体的体积为2×6×a=12a,与题干不符,不符合题意.
故选:B.
【点评】本题考查了代数式,掌握求代数式的方法是关键.
10.(2023秋 襄城县期末)用字母表示的代数式是具有一定意义的,下列赋予4a实际意义的例子中错误的是( )
A.若水果的价格是4元/千克,则4a表示买a千克该水果的金额
B.若一个两位数的十位数字是4,个位数字a,则4a表示这个两位数
C.汽车行驶速度是a千米/小时,则4a表示这辆汽车行驶4小时的路程
D.若a表示一个正方形的边长,则4a表示这个正方形的周长
【考点】代数式.
【专题】数与式;运算能力.
【答案】B
【分析】根据代数式表示的实际意义的方法分别判断每个选项,只有B选项中,若一个两位数的十位数字是4,个位数字a,则4×10+a表示这个两位数,从而得出答案.
【解答】解:根据题目:
A若水果的价格是4元/千克,则4a表示买a千克该水果的金额,此说法正确,故不符合题意;
B若一个两位数的十位数字是4,个位数字a,则4×10+a表示这个两位数,选项中说法不正确,故符合题意;
C汽车行驶速度是a千米/小时,则4a表示这辆汽车行驶4小时的路程,此说法正确,故不符合题意;
D若a表示一个正方形的边长,则4a表示这个正方形的周长,此说法正确,故不符合题意.
故选:B.
【点评】本题考查了代数式,掌握代数式的书写规范和实际问题中数量间的关系是解答本题的关键.
二.填空题(共5小题)
11.(2024秋 黄陂区期末)如图1.在一块长方形区域中布置了图中阴影部分所示的展区,其中的展台有三种不同的形状,其规格如图2所示.
(1)该长方形区域的长可以用式子表示为 a+3b ;
(2)根据图中信息,用等式表示a,b,c满足的关系为 a﹣b+c=2 .
【考点】列代数式.
【专题】整式;应用意识.
【答案】(1)a+3b;
(2)a﹣b+c=2.
【分析】(1)根据图中关系列出代数式即可;
(2)根据宽相等得出等量关系式即可.
【解答】解:(1)由图知,该长方形区域的长为a+3b,
故答案为:a+3b;
(2)由图知该长方形区域的宽为a+b+c或2b+2,
∴a+b+c=2b+2,
故答案为:a﹣b+c=2.
【点评】本题主要考查列代数式的知识,根据图中熟练关系列出代数式是解题的关键.
12.(2024秋 龙沙区期末)若x2﹣3x=1,则3x2﹣9x+2025的值为 2028 .
【考点】代数式求值.
【专题】整式;运算能力.
【答案】2028.
【分析】将原式变形后代入数值计算即可.
【解答】解:∵x2﹣3x=1,
∴3x2﹣9x+2025
=3(x2﹣3x)+2025
=3×1+2025
=2028,
故答案为:2028.
【点评】本题考查代数式求值,将原式进行正确的变形是解题的关键.
13.(2024秋 青浦区期末)如图,把高度11cm的同种杯子叠在一起,2个的高度是13cm,3个的高度是15cm,……呈现一定的规律.由此推断,n个杯子叠在一起的高度是 (9+2n) cm.
【考点】列代数式.
【专题】整式;几何直观;运算能力.
【答案】(9+2n).
【分析】根据图形,可以列出算式11+(13﹣11)×(n﹣1),然后计算即可.
【解答】解:由题意可得,
n个杯子叠在一起的高度是:11+(13﹣11)×(n﹣1)
=11+2(n﹣1)
=11+2n﹣2
=(9+2n)cm,
故答案为:(9+2n).
【点评】本题考查列代数式,解答本题的关键是明确题意,列出相应的算式.
14.(2024秋 罗湖区校级期末)已知当x=1时,式子ax3+bx+1值为5,则当x=﹣1时,式子ax3+bx+1值为 ﹣3 .
【考点】代数式求值.
【专题】整式.
【答案】见试题解答内容
【分析】把x=1时,代入式子ax3+bx+1,求出a+b=4,即可求解.
【解答】解:把x=1时,代入式子ax3+bx+1,
即:a+b+1=5,
把x=﹣1时,代入式子ax3+bx+1
则:ax3+bx+1
=﹣(a+b)+1=﹣3.
【点评】本题考查的是代数式求值,把给定的x值代入即可.
15.(2024秋 延边州期末)某学校开展读书活动,七年级的小明同学决定读300页的历史名著,每天读的页数相同,则读完这本书所需要的时间y(天)与每天读的页数x(页)之间的关系成 反比例 关系.
【考点】反比例.
【专题】分式;运算能力.
【答案】反比例.
【分析】根据等量关系:读书时间=读书总量÷每天读书量,即可得到答案.
【解答】解:根据题意可知,,
∴y与x之间的关系成反比例关系.
故答案为:反比例.
【点评】本题考查了反比例,掌握反比例的定义是关键.
三.解答题(共8小题)
16.(2024秋 安阳期中)用代数式表示:
(1)a的2倍;
(2)比x的2倍少2的数;
(3)a与3的和的2倍;
(4)边长为a的正方形的面积.
【考点】列代数式.
【专题】整式;应用意识.
【答案】(1)2a;
(2)2x﹣2;
(3)2(a+3);
(4)a2.
【分析】(1)根据题意,列出代数式,即可;
(2)根据题意,列出代数式,即可;
(3)根据题意,列出代数式,即可;
(4)根据题意,列出代数式,即可.
【解答】解:(1)a的2倍为:2a;
(2)比x的2倍少2的数为:2x﹣2;
(3)a与3的和的2倍为:2(a+3);
(4)边长为a的正方形的面积为:a2.
【点评】本题考查列代数式,正确读懂题意是解题关键.
17.(2024秋 镇原县期中)红星粮库需要把晾晒场上1200t玉米入库封存.
(1)入库所需的时间d(单位:天)与入库平均速度v(单位t/天)有怎样的关系?d与v成什么比例关系?
(2)入库所需时间是怎样随着入库平均速度的变化而变化?
(3)若粮库有职工60名,每天可入库300t玉米,则玉米入库在几天内完成?
【考点】代数式求值;列代数式.
【专题】整式;运算能力.
【答案】(1),d与v成反比关系;
(2)入库所需时间随入库平均速度的变大而变小;
(3)4天内完成.
【分析】(1)由题意直接列出代数式即可,根据当分子一定时,分母越大,分数值越小即可得出d与v成反比关系;
(2)结合d与v成反比关系,可知入库所需时间随入库平均速度的变大而变小;
(3)将v=300t,代入(1)所列代数式求值即可.
【解答】解:(1)由题意可知,
当分子一定时,v越大,d越小,
所以d与v成反比关系;
(2)入库所需时间随入库平均速度的变大而变小;
(3)由题意可知v=300t,
所以(天),
所以玉米入库在4天内完成.
【点评】本题考查列代数式,代数式求值,理解题意正确列出代数式是解题关键.
18.(2024秋 高碑店市期中)某商店为了促销某商品,现推出优惠活动.若购买该商品不超过20件,则每件按照原价100元出售;若购买该商品20件以上,则超过的部分每件优惠2元.
(1)若顾客购买这种商品15件,花费 1500 元;
(2)若顾客购买这种商品25件,他的花费是多少?
(3)某顾客购买这种商品x(x>20)件,用含x的代数式表示花费的总钱数.
【考点】列代数式.
【专题】整式;运算能力.
【答案】(1)1500;
(2)若顾客购买这种商品25件,他的花费是2490元;
(3)花费的总钱数为(98x+40)元.
【分析】(1)根据购买该商品不超过20件,则每件按照原价100元出售,列出算式进行计算即可;
(2)根据购买该商品20件以上,则超过的部分每件优惠2元,列出算式进行计算即可;
(3)根据购买这种商品x(x>20)件,购买该商品20件以上,则超过的部分每件优惠2元,列出算式进行计算即可.
【解答】解:(1)购买这种商品15件,花费为:100×15=1500(元).
故答案为:1500;
(2)20×100+98×5=2490(元).
答:花费是2490元.
(3)100×20+98(x﹣20)=98x+40.
答:花费的总钱数为(98x+40)元.
【点评】本题主要考查了有理数混合运算的应用,列代数式,解题的关键是理解题意,根据题意列出算式.
19.(2024秋 荔湾区校级期中)秋风起,桂花飘香,也就进入了吃螃蟹的最好季节,清代文人李渔把秋天称作“蟹秋”.意为错过了螃蟹,便是错过了整个秋季,小贤去水产市场采购大闸蟹,极品母蟹每只30元,至尊公蟹每只20元.商家在开展促销活动期间,向客户提供以下两种优惠方案:
方案①极品母蟹和至尊公蟹都按定价的8折销售;
方案②买一只极品母蟹送一只至尊公蟹.
现小贤要购买极品母蟹30只,至尊公蟹a(a>30)只.
(1)按方案①购买极品母蟹和至尊公蟹共需付款 (720+16a) 元(用含a的式子表示);按方案②购买极品母蟹和至尊公蟹共需付款 (300+20a) 元(用含a的式子表示).
(2)当a=40时,通过计算说明此时按上述哪种方案购买较合算.
(3)若两种优惠方案可同时使用,当a=40时,你能通过计算给出一种最为省钱的购买方案吗?
【考点】列代数式;代数式求值.
【专题】整式;运算能力.
【答案】见试题解答内容
【分析】(1)分别按照方案①和方案②的优惠方案,进行计算即可解答;
(2)把a=40代入(1)中的结论,进行计算即可解答;
(3)两种优惠方案可同时使用,可先按方案②购买30极品母蟹,再送30只至尊公蟹,然后按方案①购买10只至尊公蟹,最后进行计算比较即可解答.
【解答】解:(1)由题意得:
按方案①购买极品母蟹和至尊公蟹共需付款
=0.8×(30×30+20a)
=0.8×(900+20a)
=(720+16a)元,
按方案②购买极品母蟹和至尊公蟹共需付款
=30×30+20(a﹣30)
=900+20a﹣600
=(300+20a)元,
∴按方案①购买极品母蟹和至尊公蟹共需付款(720+16a)元;按方案②购买极品母蟹和至尊公蟹共需付款(300+20a)元,
故答案为:(720+16a),(300+20a);
(2)当a=40时,
按方案①购买极品母蟹和至尊公蟹共需付款
=720+16×40
=720+640
=1360(元),
按方案②购买极品母蟹和至尊公蟹共需付款
=300+20×40
=300+800
=1100(元),
∵1100<1360,
∴按方案②购买较为合算;
(3)若两种优惠方案可同时使用,则可先按方案②购买30极品母蟹,再送30只至尊公蟹,然后按方案①购买10只至尊公蟹,
理由:30×30+(40﹣30)×20×0.8
=900+10×20×0.8
=900+160
=1060(元),
∵1060<1100<1360,
∴最为省钱的购买方案是:先按方案②购买30极品母蟹,再送30只至尊公蟹,然后按方案①购买10只至尊公蟹.
【点评】本题考查了列代数式,代数式求值,准确熟练地进行计算是解题的关键.
20.(2024秋 青浦区校级期中)根据流程图,如果输入40,那么输出是多少?请写出计算过程.
【考点】代数式求值;有理数的混合运算.
【专题】实数;运算能力.
【答案】输出的是5.
【分析】将40输入后按照运算程序进行计算、求解.
【解答】解:输出的是5,
当输入40时,
40﹣(﹣2)=42,42÷(+3)=14,14>10;
再输入14时,
14﹣(﹣2)=16,16÷(+3)=5,510,
∴输出的是5.
【点评】此题考查了有理数的计算能力,关键是能准确理解并运用该运算程序进行计算.
21.(2024秋 横州市校级期中)某班有48名学生,其中有25名男生和23名女生,在某次体育活动时该班分成甲,乙两组,甲组29人,乙组19人.
若设甲组有男生x人(x>6且x为整数),请你用x的代数式表示:
(1)甲组女生的人数是( (29﹣x) )人;
(2)乙组男生的人数是( (25﹣x) )人;
(3)乙组女生的人数是( (x﹣6) )人.
【考点】列代数式.
【专题】整式;应用意识.
【答案】(1)(29﹣x);
(2)(25﹣x);
(3)(x﹣6).
【分析】(1)用甲组总人数减去甲组有男生人数即可得出答案;
(2)用男生总人数减去甲组男生人数即可得答案;
(3)用乙组总人数减去(2)中所求男生人数即可得答案.
【解答】解:(1)由题意可得:甲组女生的人数是(29﹣x)人.
故答案为:(29﹣x).
(2)∵共有25名男生,甲组有男生x人,
∴乙组男生的人数是(25﹣x)人.
故答案为:(25﹣x).
(3)∵乙组有19人,由(2)可知乙组男生的人数是(25﹣x)人,
∴乙组女生的人数是19﹣(25﹣x)=(x﹣6)人.
故答案为:(x﹣6).
【点评】本题主要考查列代数式,仔细审题,根据题意找到正确的等量关系是解答本题的关键.
22.(2024秋 大通区校级期中)为了参加校园文化艺术节,书画社计划买一些宣纸和毛笔,现了解情况如下:甲、乙两家文具商店出售同样的毛笔和宣纸,毛笔每支20元,宣纸每张4元.甲商店的优惠办法是:买1支毛笔送1张宣纸;乙商店的优惠办法是:全部商品按定价的9折出售.书画社想购买毛笔10支,宣纸x张(x>10).
(1)若到甲商店购买,应付 (4x+160) 元;若到乙商店购买,应付 (3.6x+180) 元(用含x的代数式表示);
(2)若x=30时,去哪家商店购买较合算?请计算说明;
(3)若x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付多少元?
【考点】代数式求值;列代数式.
【专题】整式;运算能力.
【答案】见试题解答内容
【分析】(1)到甲商店购买的费用:10支毛笔的费用+(x﹣10)张宣纸的费用;到乙商店购买的费用:(10支毛笔的费用+x张宣纸的费用)×90%,把相关数值代入求解即可;
(2)把x=30代入(1)得到的式子进行计算,然后比较结果即可;
(3)先到甲商店购买10支毛笔,送10张宣纸,再到乙商店购买20张宣纸即可.
【解答】解:(1)到甲商店购买的费用:20×10+4(x﹣10)=(4x+160)元;
到乙商店购买的费用:(20×10+4x)×90%=(3.6x+180)元;
故答案为:(4x+160),(3.6x+180);
(2)若x=30时,到甲商店购买较为合算.
当x=30时,
到甲商店购买的费用:4×30+160=280(元);
到乙商店购买的费用:3.6×30+180=288(元);
∵280<288,
∴到甲商店购买较为合算;
(3)当x=30时,
先到甲商店购买10支毛笔,送10张宣纸,再到乙商店购买30﹣10=20张宣纸,
则费用为:10×20+20×4×90%=272(元).
【点评】本题考查了列代数式的知识,代数式求值及有理数四则运算的实际应用,解决问题的关键是读懂题意,找到所求的量的等量关系.
23.(2024秋 崇阳县校级期中)如图所示,在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r m,广场的长为a m,宽为b m.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为400m,宽为200m,圆形花坛的半径为15m,求广场空地的面积.(计算结果保留π)
【考点】列代数式.
【专题】整式;运算能力.
【答案】(1)(ab﹣πr2)m2;(2)(80000﹣225π)m2.
【分析】(1)根据题意广场空的面积等于长方形的面积减去一个圆的面积,据此列出代数式即可;
(2)根据题意,将已知数据代入(1)中代数式求值即可.
【解答】解:(1)依题意,圆形的半径为r m,广场长为a m,宽为b m,
则广场空地的面积为(ab﹣πr2)m2.
(2)∵广场的长为400m,宽为200m,圆形花坛的半径为15m.
∴(ab﹣πr2)m2=(400×200﹣152π)m2=(80000﹣225π)m2.
【点评】本题考查了列代数式,根据字母的值求代数式的值,理解题意,列出代数式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
