4.6 利用相似三角形测高(新课预习.含解析)-2025-2026学年九年级上册数学
文档属性
| 名称 | 4.6 利用相似三角形测高(新课预习.含解析)-2025-2026学年九年级上册数学 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 15:48:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
4.6 利用相似三角形测高
一.选择题(共7小题)
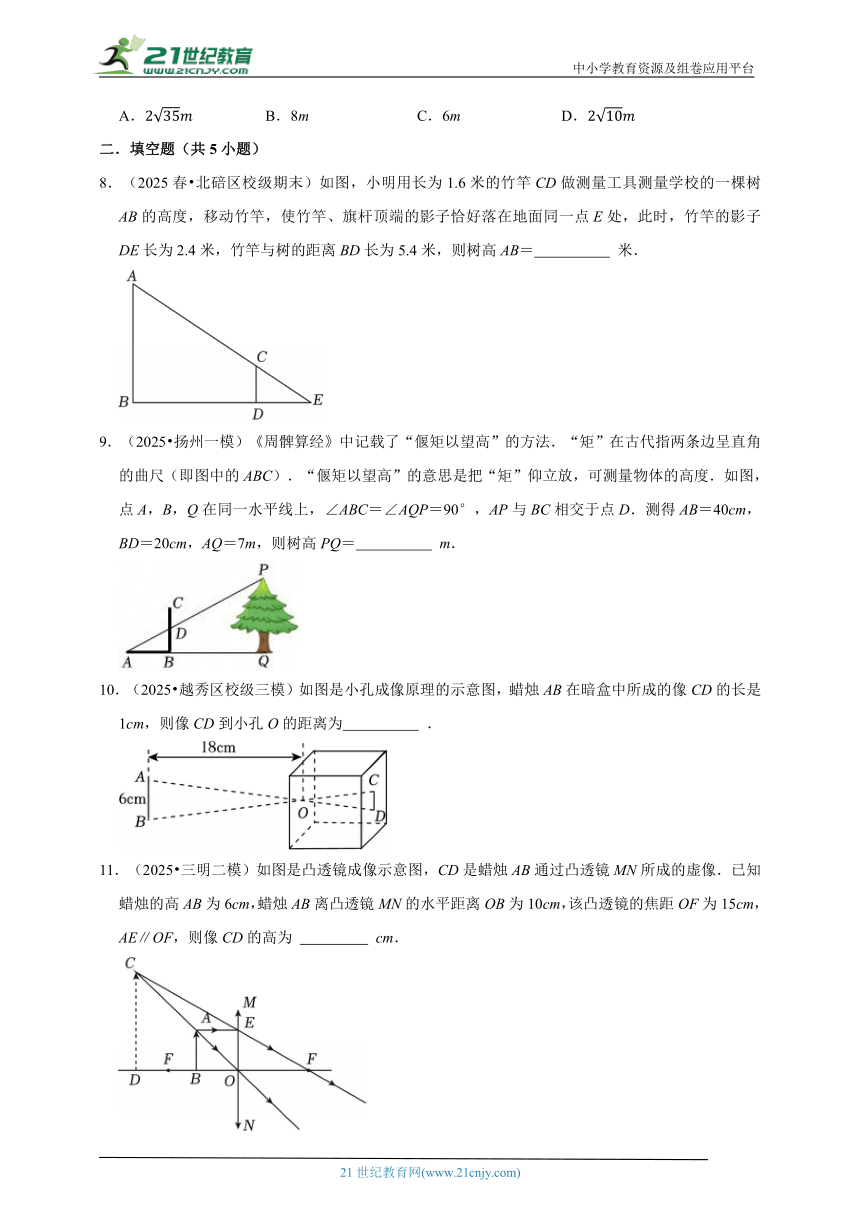
1.(2025春 高青县期末)如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1m,BC=9m,则建筑物CD的高是( )
A.13.5m B.15m C.16.5m D.18m
2.(2025春 历下区期中)如图1是装满了液体的高脚杯(数据如图所示),图2是用去部分液体后的高脚杯(数据如图所示),则图2中液面AB的宽度为( )
A.1cm B.2cm C.3cm D.4cm
3.(2025 开福区校级三模)如图,点B,C,D,E处的读数分别为15,12,0,1,若直尺宽BD=1cm,则AB的长为( )
A.1.5cm B.1cm C.0.5cm D.
4.(2025 西湖区校级三模)如图,小明为了测量河宽AB,先在BA延长线上取一点D,再在同岸取一点C,使CD⊥AB,测得∠CAD=60°,∠BCA=30°,CD=12m,那么河宽AB为( )
A.8m B.12m C.6m D.24m
5.(2025 上城区校级一模)小明用两根小木棍AC,BD自制成一个如图所示的“X形”测量工具,AC与BD交于点O,OA=OB,OC=OD,OB=3OD.现将其放进一个锥形瓶,经测量,CD=3cm,则该锥形瓶底部的内径AB的长为( )
A.6cm B.9cm C.12cm D.15cm
6.(2025 罗湖区校级模拟)如图,一块材料的形状是锐角三角形ABC,边BC长12cm,BC边上的高AD为10cm,把它加工成正方形零件,使正方形的一边GH在BC上,其余两个顶点E、F分别在AB、AC上,则这个正方形零件的边长是( )
A.cm B.5cm C.6cm D.7cm
7.(2025春 萧山区月考)如图,小明在A时测得某树的影长为10m,在B时又测得该树的影长为4m,若两次日照的光线互相垂直,则树的高度为( )
A. B.8m C.6m D.
二.填空题(共5小题)
8.(2025春 北碚区校级期末)如图,小明用长为1.6米的竹竿CD做测量工具测量学校的一棵树AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面同一点E处,此时,竹竿的影子DE长为2.4米,竹竿与树的距离BD长为5.4米,则树高AB= 米.
9.(2025 扬州一模)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A,B,Q在同一水平线上,∠ABC=∠AQP=90°,AP与BC相交于点D.测得AB=40cm,BD=20cm,AQ=7m,则树高PQ= m.
10.(2025 越秀区校级三模)如图是小孔成像原理的示意图,蜡烛AB在暗盒中所成的像CD的长是1cm,则像CD到小孔O的距离为 .
11.(2025 三明二模)如图是凸透镜成像示意图,CD是蜡烛AB通过凸透镜MN所成的虚像.已知蜡烛的高AB为6cm,蜡烛AB离凸透镜MN的水平距离OB为10cm,该凸透镜的焦距OF为15cm,AE∥OF,则像CD的高为 cm.
12.(2025 立山区三模)如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=2米,AE=0.8米,EC=2.4米,那么CD的长为 米.
三.解答题(共3小题)
13.(2025 陈仓区校级模拟)小凌和数学小组的同学在老师的指导下,利用课余时间进行测量华清池《长恨歌》群雕最高点到地面距离PQ的活动.如图,小凌在B处竖立一根竖杆AB,在点A处架设一根横杆CD,杆CD可以绕着点A在平面内旋转.在工作人员的帮助下小凌测得PQ与AB之间的距离QB为29.4m,小凌绕点A转动杆CD,通过观测发现当点D恰好位于点D'时(此时点C位于点C′),雕塑的顶端P在D'C'的延长线上.测得AB=2.5m,点D'到CD的距离为2m,点D'到AB的距离为4.2m.PQ⊥QB,AB⊥QB,CD∥QB,图中所有点均在同一平面内,请你求出《长恨歌》群雕最高点到地面的距离PQ.
14.(2025 花都区二模)九年级数学项目式学习小组通过学习知道太阳光是平行光,可以借助太阳光线构成两个相似三角形,来计算出一些没办法直接测量的物体的高度.学习小组利用可伸缩的标杆和卷尺展开了测量物体高度的学习.
(1)如图,若垂直于地面的标杆OP=2米,它的影长OG=1米,同一时刻,旗杆的影长HN=6米,则旗杆MN的高度为 米;
(2)如图,学习小组计划测量运动场围墙外的电线杆AB的高度,但受围墙的阻碍,没办法直接测量电线杆的影长.同学们进行了如下操作:①在某一时刻,垂直于地面的2米标杆OC的端点C的影子恰好与电线杆AB的端点A的影子重合于点E,测得OE=2.2米;②把标杆缩短为1.2米,记作OD,过了一段时间,标杆OD的端点D的影子恰好与电线杆AB的端点A的影子重合于点F,测得OF=1.2米.请求出电线杆AB的高度.
15.(2025 河南)焦裕禄纪念园是全国重点革命烈士纪念建筑物保护单位,革命烈士纪念碑位于纪念园南部的中心.某综合与实践小组开展测量纪念碑高度的活动,记录如下.
活动主题 测量纪念碑的高度
实物图和测量示意图
测量说明 如图,纪念碑AB位于有台阶的平台BC上,太阳光下,其顶端A的影子落在点D处,同一时刻,竖直放置的标杆DE顶端E的影子落在点F处,位于点M处的观测者眼睛所在位置为点N,点N,E,A在一条直线上,纪念碑底部点B在观测者的水平视线上.
测量数据 DE=2.1m,DF=2.1m,DM=1m,MN=1.2m.
备注 点F,M,D,C在同一水平线上.
根据以上信息,解决下列问题.
(1)由标杆的影子DF的长和标杆DE的长相等,可得CD=CA,请说明理由.
(2)求纪念碑AB的高度.
(3)小红通过间接测量得到CD的长,进而求出纪念碑AB的高度约为18.5m.查阅资料得知,纪念碑的实际高度为19.64m.请判断小红的结果和(2)中的结果哪个误差较大?并分析误差较大的可能原因(写出一条即可).
4.6 利用相似三角形测高
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 高青县期末)如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1m,BC=9m,则建筑物CD的高是( )
A.13.5m B.15m C.16.5m D.18m
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】B
【分析】根据题意可得:EB⊥AC,CD⊥AC,从而利用垂直定义可得:∠ABE=∠ACD=90°,然后证明A字模型△ABE∽△ACD,从而利用相似三角形的性质进行计算,即可解答.
【解答】解:由题意得:EB⊥AC,CD⊥AC,
∴∠ABE=∠ACD=90°,
∵∠A=∠A,
∴△ABE∽△ACD,
∴,
∴,
解得:CD=15,
∴建筑物CD的高是15m,
故选:B.
【点评】本题考查了相似三角形的应用,熟练掌握A字模型相似三角形是解题的关键.
2.(2025春 历下区期中)如图1是装满了液体的高脚杯(数据如图所示),图2是用去部分液体后的高脚杯(数据如图所示),则图2中液面AB的宽度为( )
A.1cm B.2cm C.3cm D.4cm
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】C
【分析】根据题意可得:AB∥CD,从而可得∠OAB=∠OCD,∠OBA=∠ODC,然后证明△OAB∽△OCD,从而利用相似三角形的性质进行计算,即可解答.
【解答】解:如图:
由题意得:AB∥CD,
∴∠OAB=∠OCD,∠OBA=∠ODC,
∴△OAB∽△OCD,
∴,
∴,
解得:AB=3,
∴图2中液面AB的宽度为3cm,
故选:C.
【点评】本题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解题的关键.
3.(2025 开福区校级三模)如图,点B,C,D,E处的读数分别为15,12,0,1,若直尺宽BD=1cm,则AB的长为( )
A.1.5cm B.1cm C.0.5cm D.
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】A
【分析】证明△ADE∽△ABC,根据相似三角形的性质列出比例式,把已知数据代入计算即可.
【解答】解:点B,C,D,E处的读数分别为15,12,0,1,
∴BC=3,DE=1,
∵DE∥BC,
∴∠ADE=∠ABC,
∵∠A=∠A,
∴△ADE∽△ABC,
∴,
即,解得,
∴AB=AD+BD=1.5.
故选:A.
【点评】本题考查的是相似三角形的应用,掌握相似三角形的判定和性质是解题的关键.
4.(2025 西湖区校级三模)如图,小明为了测量河宽AB,先在BA延长线上取一点D,再在同岸取一点C,使CD⊥AB,测得∠CAD=60°,∠BCA=30°,CD=12m,那么河宽AB为( )
A.8m B.12m C.6m D.24m
【考点】相似三角形的应用.
【专题】等腰三角形与直角三角形;图形的相似;运算能力;推理能力.
【答案】A
【分析】证得ADAC=AB,再证得△ADC∽△CDB,根据相似三角形的性质即可求出AB.
【解答】解:∵∠CAD=60°,∠BCA=30°,
∴∠B=∠CAD﹣∠BCA=30°=∠BCA,
∴AB=AC,
Rt△ACD中,
∵∠CAD=60°,CD=12m,
∴∠ACD=30°,
∴ADACAB,∠ACD=∠B,
∵∠ADC=∠CDB,
∴△ADC∽△CDB,
∴,
∴,
解得AB=8m.
故选:A.
【点评】本题主要考查了等腰三角形的判定,含30°的直角三角形的性质,相似三角形的性质和判定,证得△ADC∽△CDB是解决问题的关键.
5.(2025 上城区校级一模)小明用两根小木棍AC,BD自制成一个如图所示的“X形”测量工具,AC与BD交于点O,OA=OB,OC=OD,OB=3OD.现将其放进一个锥形瓶,经测量,CD=3cm,则该锥形瓶底部的内径AB的长为( )
A.6cm B.9cm C.12cm D.15cm
【考点】相似三角形的应用.
【专题】三角形.
【答案】B
【分析】证明两个三角形相似,即可求出AB的长度.
【解答】解:∵OA=OB,OC=OD,
∴△AOB和△DOC都是等腰三角形,
∵∠DOC=∠BOA,
∴△AOB∽△DOC,
∵OB=3OD,
∴,
∴3,
∴AB=9,
故选:B.
【点评】本题主要考查了相似三角形的应用,正确找出相似三角形是解题的关键.
6.(2025 罗湖区校级模拟)如图,一块材料的形状是锐角三角形ABC,边BC长12cm,BC边上的高AD为10cm,把它加工成正方形零件,使正方形的一边GH在BC上,其余两个顶点E、F分别在AB、AC上,则这个正方形零件的边长是( )
A.cm B.5cm C.6cm D.7cm
【考点】相似三角形的应用.
【专题】推理能力.
【答案】A
【分析】证明△AEF∽△ABC,则,设正方形零件EFHG的边长为x,则AK=10﹣x,根据相似三角形的性质得到,解方程即可.
【解答】解:∵四边形EFHG是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
又∵AD⊥BC,
∴,
设正方形零件EFHG的边长为x cm,则AK=(10﹣x)cm,
∴,
解得:,
即这个正方形零件的边长为.
故选:A.
【点评】本题主要考查相似三角形的应用,掌握相似三角形的性质是解题的关键.
7.(2025春 萧山区月考)如图,小明在A时测得某树的影长为10m,在B时又测得该树的影长为4m,若两次日照的光线互相垂直,则树的高度为( )
A. B.8m C.6m D.
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】D
【分析】根据题意可得:EF=4m,DF=10m,CF⊥DE,从而可得∠CFE=∠CFD=90°,进而可得∠ECF+∠CEF=90°,再根据垂直定义可得:∠ECD=90°,从而可得∠ECF+∠DCF=90°,进而可得∠CEF=∠DCF,然后证明△CFE∽△DFC,从而利用相似三角形的性质进行计算,即可解答.
【解答】解:如图:
由题意得:EF=4m,DF=10m,CF⊥DE,
∴∠CFE=∠CFD=90°,
∴∠ECF+∠CEF=90°,
∵AD⊥BE,
∴∠ECD=90°,
∴∠ECF+∠DCF=90°,
∴∠CEF=∠DCF,
∴△CFE∽△DFC,
∴,
∴CF2=DF EF=10×4=40,
∴CF=2或CF=﹣2(舍去),
∴树的高度为2米,
故选:D.
【点评】本题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解题的关键.
二.填空题(共5小题)
8.(2025春 北碚区校级期末)如图,小明用长为1.6米的竹竿CD做测量工具测量学校的一棵树AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面同一点E处,此时,竹竿的影子DE长为2.4米,竹竿与树的距离BD长为5.4米,则树高AB= 5.2 米.
【考点】相似三角形的应用.
【专题】图形的相似;推理能力.
【答案】5.2.
【分析】根据题意判定三角形相似,由相似三角形的性质列比例关系,代入数据计算即可.
【解答】解:根据题意可知,AB⊥BE,CD⊥BE,
∴CD∥AB,
∴△ECD∽△EAB,
∴,
设树高AB=x米,
∴,
∴x=5.2,
∴树高AB=5.2米,
故答案为:5.2.
【点评】本题考查相似三角形的应用,相似三角形的判定和性质,解题的关键是熟练掌握相似三角形的判定和性质.
9.(2025 扬州一模)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A,B,Q在同一水平线上,∠ABC=∠AQP=90°,AP与BC相交于点D.测得AB=40cm,BD=20cm,AQ=7m,则树高PQ= 3.5 m.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】3.5.
【分析】证明△ABD∽△AQP,利用相似三角形的性质列比例求解即可.
【解答】解:∵点A,B,Q在同一水平线上,∠ABC=∠AQP=90°,∠A=∠A,
∴△ABD∽△AQP,
∴,
∵AB=40cm,BD=20cm,AQ=7m=700cm,
∴,
解得PQ=350,
∴PQ=350cm=3.5m,
故答案为:3.5.
【点评】本题考查相似三角形的应用,解答本题的关键是熟练掌握相似三角形的性质.
10.(2025 越秀区校级三模)如图是小孔成像原理的示意图,蜡烛AB在暗盒中所成的像CD的长是1cm,则像CD到小孔O的距离为 3cm .
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】3cm.
【分析】过点O作OE⊥AB,垂足为E,延长EO交CD于点F,则OF⊥CD,然后证明8字模型△ABO∽△DCO,从而利用相似三角形的性质进行计算即可解答.
【解答】解:过点O作OE⊥AB,垂足为E,延长EO交CD于点F,则OF⊥CD,
由题意得:AB∥CD,
∴∠OAB=∠ODC,∠ABO=∠OCD,
∴△ABO∽△DCO,
∴,
∴,
解得:FO=3,
∴像CD到小孔O的距离为3cm,
故答案为:3cm.
【点评】本题考查了相似三角形的应用,准确熟练地进行计算是解题的关键.
11.(2025 三明二模)如图是凸透镜成像示意图,CD是蜡烛AB通过凸透镜MN所成的虚像.已知蜡烛的高AB为6cm,蜡烛AB离凸透镜MN的水平距离OB为10cm,该凸透镜的焦距OF为15cm,AE∥OF,则像CD的高为 18 cm.
【考点】相似三角形的应用.
【专题】图形的相似.
【答案】18.
【分析】先证△CAE∽△COF得出,再证△OAB∽△OCD,根据相似三角形的对应边成比例得出即可求出CD的长.
【解答】解:由题意得,AB∥MN,AE∥OF,AB∥CD,蜡烛AB离凸透镜MN的水平距离OB为10cm,
∴四边形ABOE是平行四边形,
∴AE=OB=10cm,
∵AE∥OF,蜡烛的高AB为6cm,该凸透镜的焦距OF为15cm,
∴△CAE∽△COF,
∴,
∴,
∵AB∥CD,
∴△OAB∽△OCD,
∴,
∴,
∴CD=18,
故答案为:18.
【点评】本题考查了相似三角形的应用,熟练掌握相似三角形的判定和性质是解题的关键.
12.(2025 立山区三模)如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=2米,AE=0.8米,EC=2.4米,那么CD的长为 6 米.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】6.
【分析】由题意知:△ABE∽△CDE,得出对应边成比例即可得出CD.
【解答】解:由题意知:AB∥CD,
∴∠BAE=∠C,∠B=∠CDE,
∴△ABE∽△CDE,
∴,
∴,
∴CD=6米,
经检验,CD=6是所列方程的解,
故答案为:6.
【点评】本题考查了相似三角形的应用,正确找出相似的三角形是解题的关键.
三.解答题(共3小题)
13.(2025 陈仓区校级模拟)小凌和数学小组的同学在老师的指导下,利用课余时间进行测量华清池《长恨歌》群雕最高点到地面距离PQ的活动.如图,小凌在B处竖立一根竖杆AB,在点A处架设一根横杆CD,杆CD可以绕着点A在平面内旋转.在工作人员的帮助下小凌测得PQ与AB之间的距离QB为29.4m,小凌绕点A转动杆CD,通过观测发现当点D恰好位于点D'时(此时点C位于点C′),雕塑的顶端P在D'C'的延长线上.测得AB=2.5m,点D'到CD的距离为2m,点D'到AB的距离为4.2m.PQ⊥QB,AB⊥QB,CD∥QB,图中所有点均在同一平面内,请你求出《长恨歌》群雕最高点到地面的距离PQ.
【考点】相似三角形的应用;点到直线的距离;平行线的性质.
【专题】线段、角、相交线与平行线;图形的相似;运算能力;推理能力.
【答案】16.5m.
【分析】延长DC交PQ于点M,过点D′作D′N⊥AB于N,则四边形AMQB是矩形,AN=2m,D′N=4.2m,AM=QB=29.4m,MQ=AB=2.5m,判定△AND′∽△PMA,推出PM:AN=MA:ND′,求出PM=14m,于是得到PQ=PM+MQ=16.5m.
【解答】解:延长DC交PQ于点M,过点D′作D′N⊥AB于N,则四边形AMQB是矩形,AN=2m,D′N=4.2m,AM=QB=29.4m,MQ=AB=2.5m,
∵AB∥PQ,
∴∠NAD′=∠P,
∵∠AND′=∠PMA=90°,
∴△AND′∽△PMA,
∴PM:AN=MA:ND′,
∴PM:2=29.4:4.2,
∴PM=14m,
∴PQ=PM+MQ=16.5m,
∴《长恨歌》群雕最高点到地面距离PQ的长为16.5m.
【点评】本题考查相似三角形的应用,关键是判定△AND′∽△PMA,推出PM:AN=MA:ND′.
14.(2025 花都区二模)九年级数学项目式学习小组通过学习知道太阳光是平行光,可以借助太阳光线构成两个相似三角形,来计算出一些没办法直接测量的物体的高度.学习小组利用可伸缩的标杆和卷尺展开了测量物体高度的学习.
(1)如图,若垂直于地面的标杆OP=2米,它的影长OG=1米,同一时刻,旗杆的影长HN=6米,则旗杆MN的高度为 12 米;
(2)如图,学习小组计划测量运动场围墙外的电线杆AB的高度,但受围墙的阻碍,没办法直接测量电线杆的影长.同学们进行了如下操作:①在某一时刻,垂直于地面的2米标杆OC的端点C的影子恰好与电线杆AB的端点A的影子重合于点E,测得OE=2.2米;②把标杆缩短为1.2米,记作OD,过了一段时间,标杆OD的端点D的影子恰好与电线杆AB的端点A的影子重合于点F,测得OF=1.2米.请求出电线杆AB的高度.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】(1)12;
(2)电线杆AB的高度为10米.
【分析】(1)在同一时刻,物体的实际高度和影长成比例,据此列方程即可解答;
(2)根据相似三角形的判定和性质定理即可得到结论.
【解答】解:(1)根据题意得,,
∴,
∴MN=12,
答:旗杆MN的高度为12米;
故答案为:12;
(2)设OB=m米,AB=n米,
由题意得,△OCE∽△BAE,△ODF∽△BAF,
∴,,
∴,,
解得AB=10,
答:电线杆AB的高度为10米.
【点评】本题考查了相似三角形的应用,熟练掌握相似三角形的判定和性质是解题的关键.
15.(2025 河南)焦裕禄纪念园是全国重点革命烈士纪念建筑物保护单位,革命烈士纪念碑位于纪念园南部的中心.某综合与实践小组开展测量纪念碑高度的活动,记录如下.
活动主题 测量纪念碑的高度
实物图和测量示意图
测量说明 如图,纪念碑AB位于有台阶的平台BC上,太阳光下,其顶端A的影子落在点D处,同一时刻,竖直放置的标杆DE顶端E的影子落在点F处,位于点M处的观测者眼睛所在位置为点N,点N,E,A在一条直线上,纪念碑底部点B在观测者的水平视线上.
测量数据 DE=2.1m,DF=2.1m,DM=1m,MN=1.2m.
备注 点F,M,D,C在同一水平线上.
根据以上信息,解决下列问题.
(1)由标杆的影子DF的长和标杆DE的长相等,可得CD=CA,请说明理由.
(2)求纪念碑AB的高度.
(3)小红通过间接测量得到CD的长,进而求出纪念碑AB的高度约为18.5m.查阅资料得知,纪念碑的实际高度为19.64m.请判断小红的结果和(2)中的结果哪个误差较大?并分析误差较大的可能原因(写出一条即可).
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】(1)见解析;
(2)纪念碑AB的高度为19.8m.
(3)小红的结果误差较大,理由见解析.
【分析】(1)根据平行投影的性质可得,即可证明结论;
(2)令BN与DE的交点为H,则四边形BCDH和MNHD是矩形,设AB=x m,证明△NEH﹣△NAB得到,求出x的值即可;
(3)比较纪念碑的实际高度与小红和(2)中的结果,得到误差较大的一方,再分析可能的原因即可.
【解答】解:(1)∵太阳光下,其顶端A的影子落在点D处,同一时刻,竖直放置的标杆DE顶端E的影子落在点F处,
∴,
∵标杆的影子DF的长和标杆DE的长相等,
即DE=DF,
∴CD=CA;
(2)如图,令BN与DE的交点为H,
则四边形BCDH和MNHD是矩形,
∵DE=2.1m,DF=2.1m,DM=1m,MN=1.2m,
∴CD=BH,BC=DH=MN=1.2m,NH=DM=1m,
∴EH=DE﹣DH=0.9m,
设AB=x m,则AC=AB+BC=(1.2+x)m,
∴BH=CD=(1.2+x)m,
∴NB=BH+NH=(2.2+x),
∵EH∥AB,
∴△NEH∽△NAB,
∴,
∴,
解得:x=19.8,
答:纪念碑AB的高度为19.8m.
(3)纪念碑的实际高度为19.64m,小红求出纪念碑AB的高度约为18.5m,(2)中纪念碑AB的高度为19.8m,
则小红的结果误差较大,
理由是:纪念碑AB位于有台阶的平台BC上,点C的位置无法正确定位,使得CD的长存在误差,影响计算结果.
【点评】本题考查了相似三角形的应用,平行投影,矩形的判定和性质,掌握相似三角形的判定和性质是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.6 利用相似三角形测高
一.选择题(共7小题)
1.(2025春 高青县期末)如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1m,BC=9m,则建筑物CD的高是( )
A.13.5m B.15m C.16.5m D.18m
2.(2025春 历下区期中)如图1是装满了液体的高脚杯(数据如图所示),图2是用去部分液体后的高脚杯(数据如图所示),则图2中液面AB的宽度为( )
A.1cm B.2cm C.3cm D.4cm
3.(2025 开福区校级三模)如图,点B,C,D,E处的读数分别为15,12,0,1,若直尺宽BD=1cm,则AB的长为( )
A.1.5cm B.1cm C.0.5cm D.
4.(2025 西湖区校级三模)如图,小明为了测量河宽AB,先在BA延长线上取一点D,再在同岸取一点C,使CD⊥AB,测得∠CAD=60°,∠BCA=30°,CD=12m,那么河宽AB为( )
A.8m B.12m C.6m D.24m
5.(2025 上城区校级一模)小明用两根小木棍AC,BD自制成一个如图所示的“X形”测量工具,AC与BD交于点O,OA=OB,OC=OD,OB=3OD.现将其放进一个锥形瓶,经测量,CD=3cm,则该锥形瓶底部的内径AB的长为( )
A.6cm B.9cm C.12cm D.15cm
6.(2025 罗湖区校级模拟)如图,一块材料的形状是锐角三角形ABC,边BC长12cm,BC边上的高AD为10cm,把它加工成正方形零件,使正方形的一边GH在BC上,其余两个顶点E、F分别在AB、AC上,则这个正方形零件的边长是( )
A.cm B.5cm C.6cm D.7cm
7.(2025春 萧山区月考)如图,小明在A时测得某树的影长为10m,在B时又测得该树的影长为4m,若两次日照的光线互相垂直,则树的高度为( )
A. B.8m C.6m D.
二.填空题(共5小题)
8.(2025春 北碚区校级期末)如图,小明用长为1.6米的竹竿CD做测量工具测量学校的一棵树AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面同一点E处,此时,竹竿的影子DE长为2.4米,竹竿与树的距离BD长为5.4米,则树高AB= 米.
9.(2025 扬州一模)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A,B,Q在同一水平线上,∠ABC=∠AQP=90°,AP与BC相交于点D.测得AB=40cm,BD=20cm,AQ=7m,则树高PQ= m.
10.(2025 越秀区校级三模)如图是小孔成像原理的示意图,蜡烛AB在暗盒中所成的像CD的长是1cm,则像CD到小孔O的距离为 .
11.(2025 三明二模)如图是凸透镜成像示意图,CD是蜡烛AB通过凸透镜MN所成的虚像.已知蜡烛的高AB为6cm,蜡烛AB离凸透镜MN的水平距离OB为10cm,该凸透镜的焦距OF为15cm,AE∥OF,则像CD的高为 cm.
12.(2025 立山区三模)如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=2米,AE=0.8米,EC=2.4米,那么CD的长为 米.
三.解答题(共3小题)
13.(2025 陈仓区校级模拟)小凌和数学小组的同学在老师的指导下,利用课余时间进行测量华清池《长恨歌》群雕最高点到地面距离PQ的活动.如图,小凌在B处竖立一根竖杆AB,在点A处架设一根横杆CD,杆CD可以绕着点A在平面内旋转.在工作人员的帮助下小凌测得PQ与AB之间的距离QB为29.4m,小凌绕点A转动杆CD,通过观测发现当点D恰好位于点D'时(此时点C位于点C′),雕塑的顶端P在D'C'的延长线上.测得AB=2.5m,点D'到CD的距离为2m,点D'到AB的距离为4.2m.PQ⊥QB,AB⊥QB,CD∥QB,图中所有点均在同一平面内,请你求出《长恨歌》群雕最高点到地面的距离PQ.
14.(2025 花都区二模)九年级数学项目式学习小组通过学习知道太阳光是平行光,可以借助太阳光线构成两个相似三角形,来计算出一些没办法直接测量的物体的高度.学习小组利用可伸缩的标杆和卷尺展开了测量物体高度的学习.
(1)如图,若垂直于地面的标杆OP=2米,它的影长OG=1米,同一时刻,旗杆的影长HN=6米,则旗杆MN的高度为 米;
(2)如图,学习小组计划测量运动场围墙外的电线杆AB的高度,但受围墙的阻碍,没办法直接测量电线杆的影长.同学们进行了如下操作:①在某一时刻,垂直于地面的2米标杆OC的端点C的影子恰好与电线杆AB的端点A的影子重合于点E,测得OE=2.2米;②把标杆缩短为1.2米,记作OD,过了一段时间,标杆OD的端点D的影子恰好与电线杆AB的端点A的影子重合于点F,测得OF=1.2米.请求出电线杆AB的高度.
15.(2025 河南)焦裕禄纪念园是全国重点革命烈士纪念建筑物保护单位,革命烈士纪念碑位于纪念园南部的中心.某综合与实践小组开展测量纪念碑高度的活动,记录如下.
活动主题 测量纪念碑的高度
实物图和测量示意图
测量说明 如图,纪念碑AB位于有台阶的平台BC上,太阳光下,其顶端A的影子落在点D处,同一时刻,竖直放置的标杆DE顶端E的影子落在点F处,位于点M处的观测者眼睛所在位置为点N,点N,E,A在一条直线上,纪念碑底部点B在观测者的水平视线上.
测量数据 DE=2.1m,DF=2.1m,DM=1m,MN=1.2m.
备注 点F,M,D,C在同一水平线上.
根据以上信息,解决下列问题.
(1)由标杆的影子DF的长和标杆DE的长相等,可得CD=CA,请说明理由.
(2)求纪念碑AB的高度.
(3)小红通过间接测量得到CD的长,进而求出纪念碑AB的高度约为18.5m.查阅资料得知,纪念碑的实际高度为19.64m.请判断小红的结果和(2)中的结果哪个误差较大?并分析误差较大的可能原因(写出一条即可).
4.6 利用相似三角形测高
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 高青县期末)如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1m,BC=9m,则建筑物CD的高是( )
A.13.5m B.15m C.16.5m D.18m
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】B
【分析】根据题意可得:EB⊥AC,CD⊥AC,从而利用垂直定义可得:∠ABE=∠ACD=90°,然后证明A字模型△ABE∽△ACD,从而利用相似三角形的性质进行计算,即可解答.
【解答】解:由题意得:EB⊥AC,CD⊥AC,
∴∠ABE=∠ACD=90°,
∵∠A=∠A,
∴△ABE∽△ACD,
∴,
∴,
解得:CD=15,
∴建筑物CD的高是15m,
故选:B.
【点评】本题考查了相似三角形的应用,熟练掌握A字模型相似三角形是解题的关键.
2.(2025春 历下区期中)如图1是装满了液体的高脚杯(数据如图所示),图2是用去部分液体后的高脚杯(数据如图所示),则图2中液面AB的宽度为( )
A.1cm B.2cm C.3cm D.4cm
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】C
【分析】根据题意可得:AB∥CD,从而可得∠OAB=∠OCD,∠OBA=∠ODC,然后证明△OAB∽△OCD,从而利用相似三角形的性质进行计算,即可解答.
【解答】解:如图:
由题意得:AB∥CD,
∴∠OAB=∠OCD,∠OBA=∠ODC,
∴△OAB∽△OCD,
∴,
∴,
解得:AB=3,
∴图2中液面AB的宽度为3cm,
故选:C.
【点评】本题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解题的关键.
3.(2025 开福区校级三模)如图,点B,C,D,E处的读数分别为15,12,0,1,若直尺宽BD=1cm,则AB的长为( )
A.1.5cm B.1cm C.0.5cm D.
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】A
【分析】证明△ADE∽△ABC,根据相似三角形的性质列出比例式,把已知数据代入计算即可.
【解答】解:点B,C,D,E处的读数分别为15,12,0,1,
∴BC=3,DE=1,
∵DE∥BC,
∴∠ADE=∠ABC,
∵∠A=∠A,
∴△ADE∽△ABC,
∴,
即,解得,
∴AB=AD+BD=1.5.
故选:A.
【点评】本题考查的是相似三角形的应用,掌握相似三角形的判定和性质是解题的关键.
4.(2025 西湖区校级三模)如图,小明为了测量河宽AB,先在BA延长线上取一点D,再在同岸取一点C,使CD⊥AB,测得∠CAD=60°,∠BCA=30°,CD=12m,那么河宽AB为( )
A.8m B.12m C.6m D.24m
【考点】相似三角形的应用.
【专题】等腰三角形与直角三角形;图形的相似;运算能力;推理能力.
【答案】A
【分析】证得ADAC=AB,再证得△ADC∽△CDB,根据相似三角形的性质即可求出AB.
【解答】解:∵∠CAD=60°,∠BCA=30°,
∴∠B=∠CAD﹣∠BCA=30°=∠BCA,
∴AB=AC,
Rt△ACD中,
∵∠CAD=60°,CD=12m,
∴∠ACD=30°,
∴ADACAB,∠ACD=∠B,
∵∠ADC=∠CDB,
∴△ADC∽△CDB,
∴,
∴,
解得AB=8m.
故选:A.
【点评】本题主要考查了等腰三角形的判定,含30°的直角三角形的性质,相似三角形的性质和判定,证得△ADC∽△CDB是解决问题的关键.
5.(2025 上城区校级一模)小明用两根小木棍AC,BD自制成一个如图所示的“X形”测量工具,AC与BD交于点O,OA=OB,OC=OD,OB=3OD.现将其放进一个锥形瓶,经测量,CD=3cm,则该锥形瓶底部的内径AB的长为( )
A.6cm B.9cm C.12cm D.15cm
【考点】相似三角形的应用.
【专题】三角形.
【答案】B
【分析】证明两个三角形相似,即可求出AB的长度.
【解答】解:∵OA=OB,OC=OD,
∴△AOB和△DOC都是等腰三角形,
∵∠DOC=∠BOA,
∴△AOB∽△DOC,
∵OB=3OD,
∴,
∴3,
∴AB=9,
故选:B.
【点评】本题主要考查了相似三角形的应用,正确找出相似三角形是解题的关键.
6.(2025 罗湖区校级模拟)如图,一块材料的形状是锐角三角形ABC,边BC长12cm,BC边上的高AD为10cm,把它加工成正方形零件,使正方形的一边GH在BC上,其余两个顶点E、F分别在AB、AC上,则这个正方形零件的边长是( )
A.cm B.5cm C.6cm D.7cm
【考点】相似三角形的应用.
【专题】推理能力.
【答案】A
【分析】证明△AEF∽△ABC,则,设正方形零件EFHG的边长为x,则AK=10﹣x,根据相似三角形的性质得到,解方程即可.
【解答】解:∵四边形EFHG是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
又∵AD⊥BC,
∴,
设正方形零件EFHG的边长为x cm,则AK=(10﹣x)cm,
∴,
解得:,
即这个正方形零件的边长为.
故选:A.
【点评】本题主要考查相似三角形的应用,掌握相似三角形的性质是解题的关键.
7.(2025春 萧山区月考)如图,小明在A时测得某树的影长为10m,在B时又测得该树的影长为4m,若两次日照的光线互相垂直,则树的高度为( )
A. B.8m C.6m D.
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】D
【分析】根据题意可得:EF=4m,DF=10m,CF⊥DE,从而可得∠CFE=∠CFD=90°,进而可得∠ECF+∠CEF=90°,再根据垂直定义可得:∠ECD=90°,从而可得∠ECF+∠DCF=90°,进而可得∠CEF=∠DCF,然后证明△CFE∽△DFC,从而利用相似三角形的性质进行计算,即可解答.
【解答】解:如图:
由题意得:EF=4m,DF=10m,CF⊥DE,
∴∠CFE=∠CFD=90°,
∴∠ECF+∠CEF=90°,
∵AD⊥BE,
∴∠ECD=90°,
∴∠ECF+∠DCF=90°,
∴∠CEF=∠DCF,
∴△CFE∽△DFC,
∴,
∴CF2=DF EF=10×4=40,
∴CF=2或CF=﹣2(舍去),
∴树的高度为2米,
故选:D.
【点评】本题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解题的关键.
二.填空题(共5小题)
8.(2025春 北碚区校级期末)如图,小明用长为1.6米的竹竿CD做测量工具测量学校的一棵树AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面同一点E处,此时,竹竿的影子DE长为2.4米,竹竿与树的距离BD长为5.4米,则树高AB= 5.2 米.
【考点】相似三角形的应用.
【专题】图形的相似;推理能力.
【答案】5.2.
【分析】根据题意判定三角形相似,由相似三角形的性质列比例关系,代入数据计算即可.
【解答】解:根据题意可知,AB⊥BE,CD⊥BE,
∴CD∥AB,
∴△ECD∽△EAB,
∴,
设树高AB=x米,
∴,
∴x=5.2,
∴树高AB=5.2米,
故答案为:5.2.
【点评】本题考查相似三角形的应用,相似三角形的判定和性质,解题的关键是熟练掌握相似三角形的判定和性质.
9.(2025 扬州一模)《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的ABC).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度.如图,点A,B,Q在同一水平线上,∠ABC=∠AQP=90°,AP与BC相交于点D.测得AB=40cm,BD=20cm,AQ=7m,则树高PQ= 3.5 m.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】3.5.
【分析】证明△ABD∽△AQP,利用相似三角形的性质列比例求解即可.
【解答】解:∵点A,B,Q在同一水平线上,∠ABC=∠AQP=90°,∠A=∠A,
∴△ABD∽△AQP,
∴,
∵AB=40cm,BD=20cm,AQ=7m=700cm,
∴,
解得PQ=350,
∴PQ=350cm=3.5m,
故答案为:3.5.
【点评】本题考查相似三角形的应用,解答本题的关键是熟练掌握相似三角形的性质.
10.(2025 越秀区校级三模)如图是小孔成像原理的示意图,蜡烛AB在暗盒中所成的像CD的长是1cm,则像CD到小孔O的距离为 3cm .
【考点】相似三角形的应用.
【专题】图形的相似;运算能力.
【答案】3cm.
【分析】过点O作OE⊥AB,垂足为E,延长EO交CD于点F,则OF⊥CD,然后证明8字模型△ABO∽△DCO,从而利用相似三角形的性质进行计算即可解答.
【解答】解:过点O作OE⊥AB,垂足为E,延长EO交CD于点F,则OF⊥CD,
由题意得:AB∥CD,
∴∠OAB=∠ODC,∠ABO=∠OCD,
∴△ABO∽△DCO,
∴,
∴,
解得:FO=3,
∴像CD到小孔O的距离为3cm,
故答案为:3cm.
【点评】本题考查了相似三角形的应用,准确熟练地进行计算是解题的关键.
11.(2025 三明二模)如图是凸透镜成像示意图,CD是蜡烛AB通过凸透镜MN所成的虚像.已知蜡烛的高AB为6cm,蜡烛AB离凸透镜MN的水平距离OB为10cm,该凸透镜的焦距OF为15cm,AE∥OF,则像CD的高为 18 cm.
【考点】相似三角形的应用.
【专题】图形的相似.
【答案】18.
【分析】先证△CAE∽△COF得出,再证△OAB∽△OCD,根据相似三角形的对应边成比例得出即可求出CD的长.
【解答】解:由题意得,AB∥MN,AE∥OF,AB∥CD,蜡烛AB离凸透镜MN的水平距离OB为10cm,
∴四边形ABOE是平行四边形,
∴AE=OB=10cm,
∵AE∥OF,蜡烛的高AB为6cm,该凸透镜的焦距OF为15cm,
∴△CAE∽△COF,
∴,
∴,
∵AB∥CD,
∴△OAB∽△OCD,
∴,
∴,
∴CD=18,
故答案为:18.
【点评】本题考查了相似三角形的应用,熟练掌握相似三角形的判定和性质是解题的关键.
12.(2025 立山区三模)如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=2米,AE=0.8米,EC=2.4米,那么CD的长为 6 米.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】6.
【分析】由题意知:△ABE∽△CDE,得出对应边成比例即可得出CD.
【解答】解:由题意知:AB∥CD,
∴∠BAE=∠C,∠B=∠CDE,
∴△ABE∽△CDE,
∴,
∴,
∴CD=6米,
经检验,CD=6是所列方程的解,
故答案为:6.
【点评】本题考查了相似三角形的应用,正确找出相似的三角形是解题的关键.
三.解答题(共3小题)
13.(2025 陈仓区校级模拟)小凌和数学小组的同学在老师的指导下,利用课余时间进行测量华清池《长恨歌》群雕最高点到地面距离PQ的活动.如图,小凌在B处竖立一根竖杆AB,在点A处架设一根横杆CD,杆CD可以绕着点A在平面内旋转.在工作人员的帮助下小凌测得PQ与AB之间的距离QB为29.4m,小凌绕点A转动杆CD,通过观测发现当点D恰好位于点D'时(此时点C位于点C′),雕塑的顶端P在D'C'的延长线上.测得AB=2.5m,点D'到CD的距离为2m,点D'到AB的距离为4.2m.PQ⊥QB,AB⊥QB,CD∥QB,图中所有点均在同一平面内,请你求出《长恨歌》群雕最高点到地面的距离PQ.
【考点】相似三角形的应用;点到直线的距离;平行线的性质.
【专题】线段、角、相交线与平行线;图形的相似;运算能力;推理能力.
【答案】16.5m.
【分析】延长DC交PQ于点M,过点D′作D′N⊥AB于N,则四边形AMQB是矩形,AN=2m,D′N=4.2m,AM=QB=29.4m,MQ=AB=2.5m,判定△AND′∽△PMA,推出PM:AN=MA:ND′,求出PM=14m,于是得到PQ=PM+MQ=16.5m.
【解答】解:延长DC交PQ于点M,过点D′作D′N⊥AB于N,则四边形AMQB是矩形,AN=2m,D′N=4.2m,AM=QB=29.4m,MQ=AB=2.5m,
∵AB∥PQ,
∴∠NAD′=∠P,
∵∠AND′=∠PMA=90°,
∴△AND′∽△PMA,
∴PM:AN=MA:ND′,
∴PM:2=29.4:4.2,
∴PM=14m,
∴PQ=PM+MQ=16.5m,
∴《长恨歌》群雕最高点到地面距离PQ的长为16.5m.
【点评】本题考查相似三角形的应用,关键是判定△AND′∽△PMA,推出PM:AN=MA:ND′.
14.(2025 花都区二模)九年级数学项目式学习小组通过学习知道太阳光是平行光,可以借助太阳光线构成两个相似三角形,来计算出一些没办法直接测量的物体的高度.学习小组利用可伸缩的标杆和卷尺展开了测量物体高度的学习.
(1)如图,若垂直于地面的标杆OP=2米,它的影长OG=1米,同一时刻,旗杆的影长HN=6米,则旗杆MN的高度为 12 米;
(2)如图,学习小组计划测量运动场围墙外的电线杆AB的高度,但受围墙的阻碍,没办法直接测量电线杆的影长.同学们进行了如下操作:①在某一时刻,垂直于地面的2米标杆OC的端点C的影子恰好与电线杆AB的端点A的影子重合于点E,测得OE=2.2米;②把标杆缩短为1.2米,记作OD,过了一段时间,标杆OD的端点D的影子恰好与电线杆AB的端点A的影子重合于点F,测得OF=1.2米.请求出电线杆AB的高度.
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】(1)12;
(2)电线杆AB的高度为10米.
【分析】(1)在同一时刻,物体的实际高度和影长成比例,据此列方程即可解答;
(2)根据相似三角形的判定和性质定理即可得到结论.
【解答】解:(1)根据题意得,,
∴,
∴MN=12,
答:旗杆MN的高度为12米;
故答案为:12;
(2)设OB=m米,AB=n米,
由题意得,△OCE∽△BAE,△ODF∽△BAF,
∴,,
∴,,
解得AB=10,
答:电线杆AB的高度为10米.
【点评】本题考查了相似三角形的应用,熟练掌握相似三角形的判定和性质是解题的关键.
15.(2025 河南)焦裕禄纪念园是全国重点革命烈士纪念建筑物保护单位,革命烈士纪念碑位于纪念园南部的中心.某综合与实践小组开展测量纪念碑高度的活动,记录如下.
活动主题 测量纪念碑的高度
实物图和测量示意图
测量说明 如图,纪念碑AB位于有台阶的平台BC上,太阳光下,其顶端A的影子落在点D处,同一时刻,竖直放置的标杆DE顶端E的影子落在点F处,位于点M处的观测者眼睛所在位置为点N,点N,E,A在一条直线上,纪念碑底部点B在观测者的水平视线上.
测量数据 DE=2.1m,DF=2.1m,DM=1m,MN=1.2m.
备注 点F,M,D,C在同一水平线上.
根据以上信息,解决下列问题.
(1)由标杆的影子DF的长和标杆DE的长相等,可得CD=CA,请说明理由.
(2)求纪念碑AB的高度.
(3)小红通过间接测量得到CD的长,进而求出纪念碑AB的高度约为18.5m.查阅资料得知,纪念碑的实际高度为19.64m.请判断小红的结果和(2)中的结果哪个误差较大?并分析误差较大的可能原因(写出一条即可).
【考点】相似三角形的应用.
【专题】图形的相似;应用意识.
【答案】(1)见解析;
(2)纪念碑AB的高度为19.8m.
(3)小红的结果误差较大,理由见解析.
【分析】(1)根据平行投影的性质可得,即可证明结论;
(2)令BN与DE的交点为H,则四边形BCDH和MNHD是矩形,设AB=x m,证明△NEH﹣△NAB得到,求出x的值即可;
(3)比较纪念碑的实际高度与小红和(2)中的结果,得到误差较大的一方,再分析可能的原因即可.
【解答】解:(1)∵太阳光下,其顶端A的影子落在点D处,同一时刻,竖直放置的标杆DE顶端E的影子落在点F处,
∴,
∵标杆的影子DF的长和标杆DE的长相等,
即DE=DF,
∴CD=CA;
(2)如图,令BN与DE的交点为H,
则四边形BCDH和MNHD是矩形,
∵DE=2.1m,DF=2.1m,DM=1m,MN=1.2m,
∴CD=BH,BC=DH=MN=1.2m,NH=DM=1m,
∴EH=DE﹣DH=0.9m,
设AB=x m,则AC=AB+BC=(1.2+x)m,
∴BH=CD=(1.2+x)m,
∴NB=BH+NH=(2.2+x),
∵EH∥AB,
∴△NEH∽△NAB,
∴,
∴,
解得:x=19.8,
答:纪念碑AB的高度为19.8m.
(3)纪念碑的实际高度为19.64m,小红求出纪念碑AB的高度约为18.5m,(2)中纪念碑AB的高度为19.8m,
则小红的结果误差较大,
理由是:纪念碑AB位于有台阶的平台BC上,点C的位置无法正确定位,使得CD的长存在误差,影响计算结果.
【点评】本题考查了相似三角形的应用,平行投影,矩形的判定和性质,掌握相似三角形的判定和性质是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
