5.1 投影(新课预习.含解析)-2025-2026学年九年级上册数学北师大版
文档属性
| 名称 | 5.1 投影(新课预习.含解析)-2025-2026学年九年级上册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-08 06:43:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.1 投影
一.选择题(共7小题)
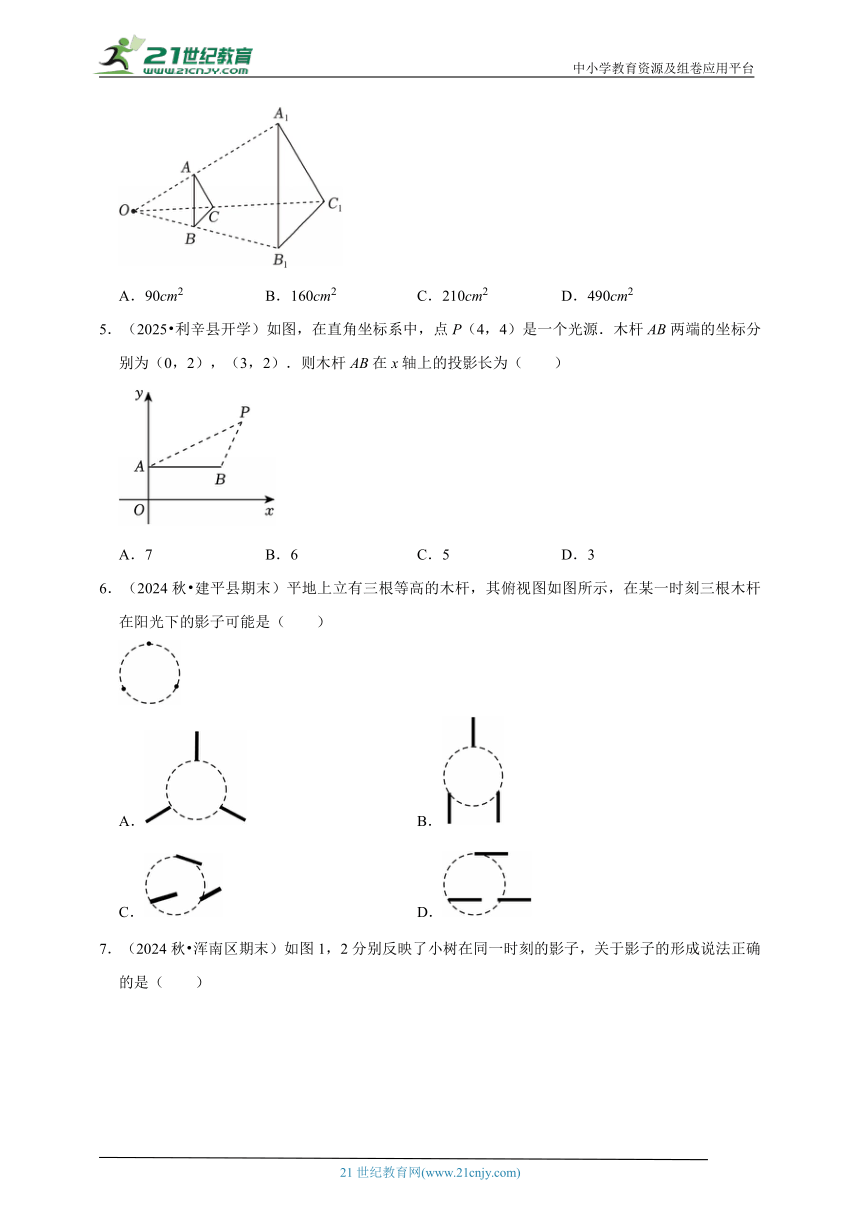
1.(2025 孝南区校级三模)如图,在平面直角坐标系中,点A(1,4),是一个光源.木杆BC两端的坐标分别为(﹣1,2),(2,2).则木杆BC在x轴上的投影长为( )
A.3 B.4 C.6 D.12
2.(2025 鹿城区校级三模)下列投影中,属于平行投影的是( )
A. B.
C. D.
3.(2025 高州市模拟)圭表是古代汉族科学家发明的度量日影长度以定节令的一种天文仪器,由”圭”和”表”两个部件组成.当太阳照着表的时候,圭上出现了表的影子,根据影子的方向和长度,就能读出时间.则表在圭面上形成的投影是( )
A.中心投影
B.平行投影
C.既是平行投影又是中心投影
D.不能确定
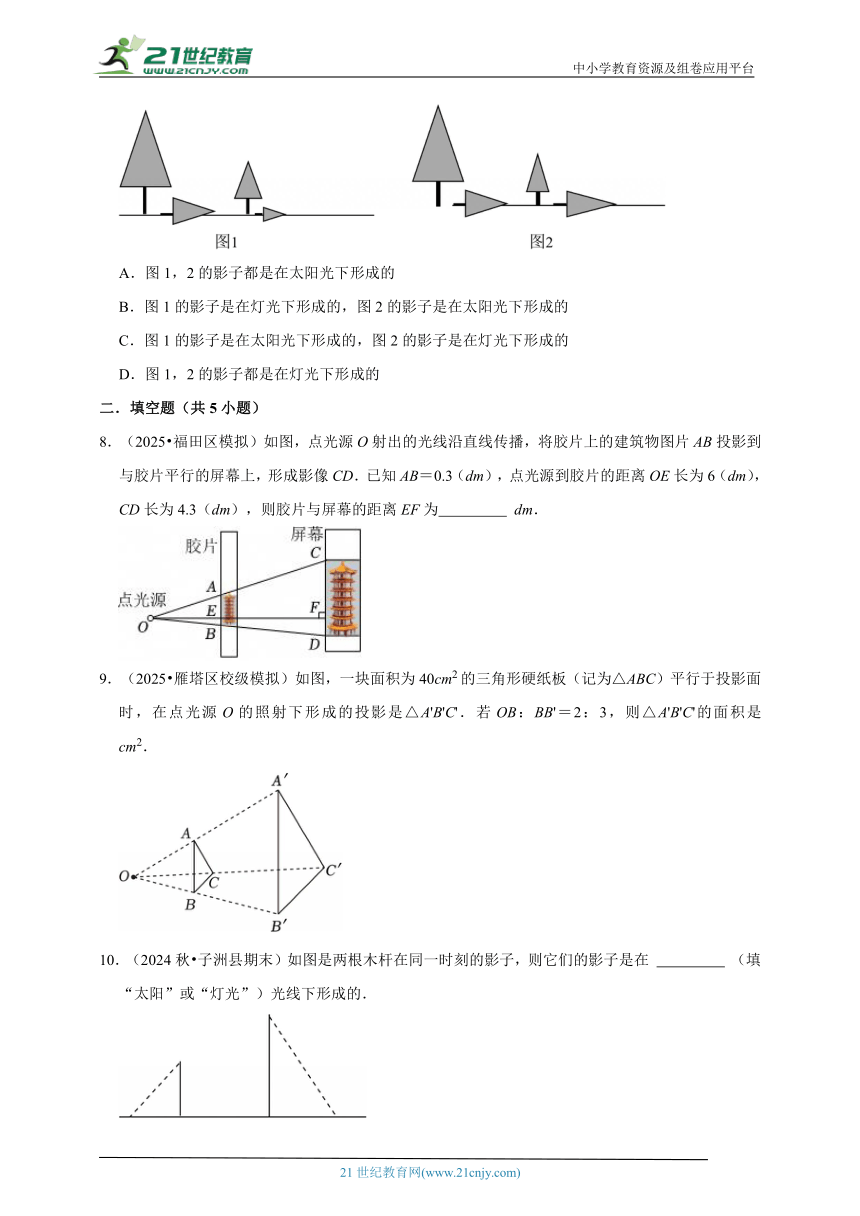
4.(2025 惠东县模拟)如图,一块面积为90cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1,若OB:BB1=3:4,则△A1B1C1的面积是( )
A.90cm2 B.160cm2 C.210cm2 D.490cm2
5.(2025 利辛县开学)如图,在直角坐标系中,点P(4,4)是一个光源.木杆AB两端的坐标分别为(0,2),(3,2).则木杆AB在x轴上的投影长为( )
A.7 B.6 C.5 D.3
6.(2024秋 建平县期末)平地上立有三根等高的木杆,其俯视图如图所示,在某一时刻三根木杆在阳光下的影子可能是( )
A. B.
C. D.
7.(2024秋 浑南区期末)如图1,2分别反映了小树在同一时刻的影子,关于影子的形成说法正确的是( )
A.图1,2的影子都是在太阳光下形成的
B.图1的影子是在灯光下形成的,图2的影子是在太阳光下形成的
C.图1的影子是在太阳光下形成的,图2的影子是在灯光下形成的
D.图1,2的影子都是在灯光下形成的
二.填空题(共5小题)
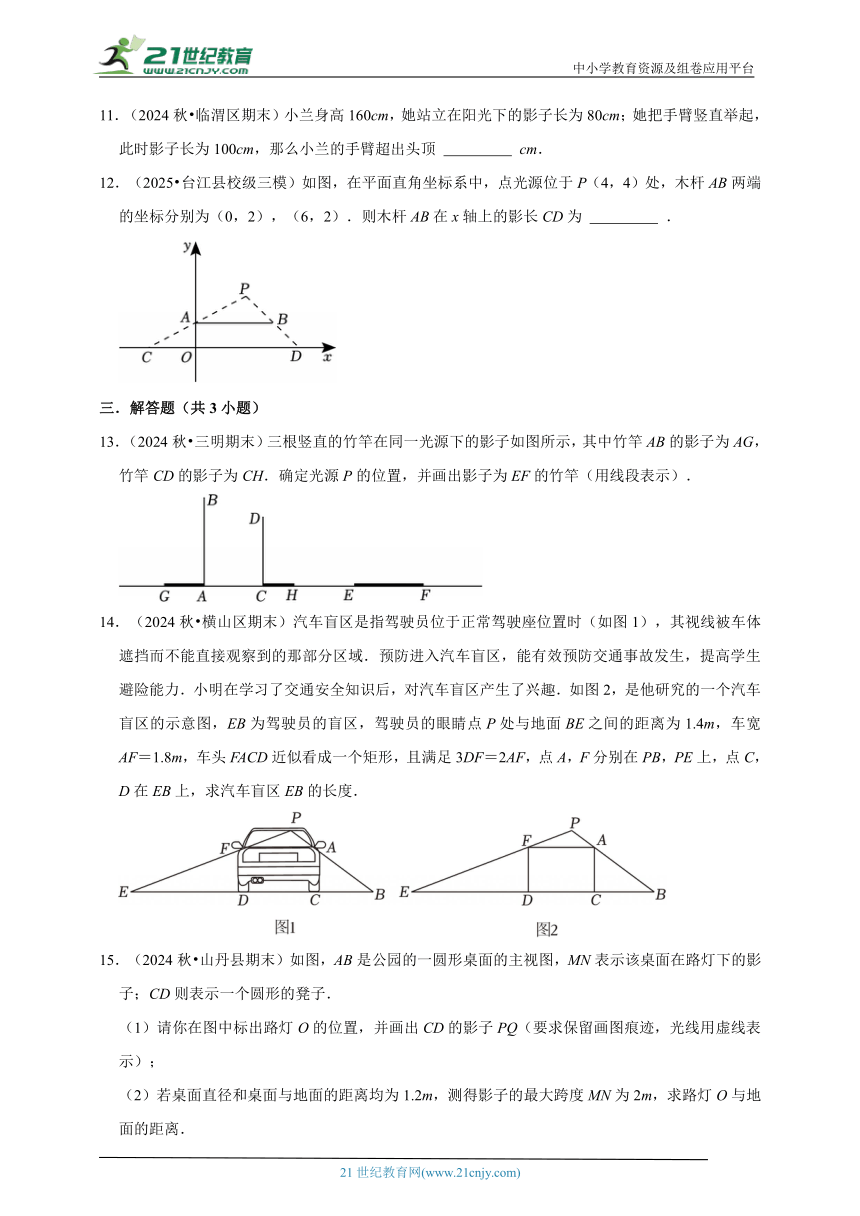
8.(2025 福田区模拟)如图,点光源O射出的光线沿直线传播,将胶片上的建筑物图片AB投影到与胶片平行的屏幕上,形成影像CD.已知AB=0.3(dm),点光源到胶片的距离OE长为6(dm),CD长为4.3(dm),则胶片与屏幕的距离EF为 dm.
9.(2025 雁塔区校级模拟)如图,一块面积为40cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A'B'C'.若OB:BB'=2:3,则△A'B'C'的面积是 cm2.
10.(2024秋 子洲县期末)如图是两根木杆在同一时刻的影子,则它们的影子是在 (填“太阳”或“灯光”)光线下形成的.
11.(2024秋 临渭区期末)小兰身高160cm,她站立在阳光下的影子长为80cm;她把手臂竖直举起,此时影子长为100cm,那么小兰的手臂超出头顶 cm.
12.(2025 台江县校级三模)如图,在平面直角坐标系中,点光源位于P(4,4)处,木杆AB两端的坐标分别为(0,2),(6,2).则木杆AB在x轴上的影长CD为 .
三.解答题(共3小题)
13.(2024秋 三明期末)三根竖直的竹竿在同一光源下的影子如图所示,其中竹竿AB的影子为AG,竹竿CD的影子为CH.确定光源P的位置,并画出影子为EF的竹竿(用线段表示).
14.(2024秋 横山区期末)汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图2,是他研究的一个汽车盲区的示意图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE之间的距离为1.4m,车宽AF=1.8m,车头FACD近似看成一个矩形,且满足3DF=2AF,点A,F分别在PB,PE上,点C,D在EB上,求汽车盲区EB的长度.
15.(2024秋 山丹县期末)如图,AB是公园的一圆形桌面的主视图,MN表示该桌面在路灯下的影子;CD则表示一个圆形的凳子.
(1)请你在图中标出路灯O的位置,并画出CD的影子PQ(要求保留画图痕迹,光线用虚线表示);
(2)若桌面直径和桌面与地面的距离均为1.2m,测得影子的最大跨度MN为2m,求路灯O与地面的距离.
5.1 投影
参考答案与试题解析
一.选择题(共7小题)
1.(2025 孝南区校级三模)如图,在平面直角坐标系中,点A(1,4),是一个光源.木杆BC两端的坐标分别为(﹣1,2),(2,2).则木杆BC在x轴上的投影长为( )
A.3 B.4 C.6 D.12
【考点】平行投影;坐标确定位置.
【专题】投影与视图;推理能力.
【答案】C
【分析】利用平行投影,转化为相似三角形,将点的坐标转化为线段的长,根据相似三角形的性质得出答案即可.
【解答】解:如图,设AB交x轴于点D,AC交x轴于点E,作AN⊥x轴于点N,交BC于点M,
∵木杆BC两端的坐标分别为(﹣1,2),(2,2),
∴BC∥DE,
∴△ABC∽△ADE,
∴,
即,
解得DE=6,
∴木杆BC在x轴上的投影长为6.
故选:C.
【点评】本题考查中心投影,构造相似三角形,利用相似三角形的性质求解是解决此类问题的基本方法.
2.(2025 鹿城区校级三模)下列投影中,属于平行投影的是( )
A. B.
C. D.
【考点】平行投影.
【专题】投影与视图;几何直观.
【答案】D
【分析】定义:在一束平行光线照射下形成的投影叫做平行投影.特征:平行投影的投影线是平行的.根据平行投影的定义逐项判断即可.
【解答】解:根据定义:在一束平行光线照射下形成的投影叫做平行投影.特征:平行投影的投影线是平行的判断如下:
A.如图,
属于中心投影,故不符合题意;
B.如图,
属于中心投影,故不符合题意;
C.如图,
属于中心投影,故不符合题意;
D.如图,
属于平行投影,故符合题意;
故选:D.
【点评】本题考查了平行投影的知识,正确记忆相关知识点是解题关键.
3.(2025 高州市模拟)圭表是古代汉族科学家发明的度量日影长度以定节令的一种天文仪器,由”圭”和”表”两个部件组成.当太阳照着表的时候,圭上出现了表的影子,根据影子的方向和长度,就能读出时间.则表在圭面上形成的投影是( )
A.中心投影
B.平行投影
C.既是平行投影又是中心投影
D.不能确定
【考点】中心投影;平行投影.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据中心投影和平行投影的定义,结合光的照射方式判断即可.
【解答】解:表在圭面上形成的投影是平行投影.
故选:B.
【点评】本题考查了平行投影,平行线的判定,正确分析光的照射方式是解答本题的关键.中心投影的定义:光由一点向外散射形成的投影;平行投影的定义:光源以平行的方式照射到物体上形成的投影.
4.(2025 惠东县模拟)如图,一块面积为90cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1,若OB:BB1=3:4,则△A1B1C1的面积是( )
A.90cm2 B.160cm2 C.210cm2 D.490cm2
【考点】中心投影;三角形的面积.
【专题】图形的相似;运算能力.
【答案】D
【分析】△ABC与△A1B1C1是位似图形,求出位似比,再根据面积比等于位似比的平方即可求解.
【解答】解:由平行投影可知△ABC与△A1B1C1是位似图形,
∵OB:BB1=3:4,
∴OB:OB1=3:7,
∴△ABC与△A1B1C1的位似比为3:7,
∴,
△A1B1C1的面积是90490(cm2),
故选:D.
【点评】本题考查中心投影,掌握位似的性质是解题的关键.
5.(2025 利辛县开学)如图,在直角坐标系中,点P(4,4)是一个光源.木杆AB两端的坐标分别为(0,2),(3,2).则木杆AB在x轴上的投影长为( )
A.7 B.6 C.5 D.3
【考点】中心投影;相似三角形的性质.
【专题】三角形;图形的相似;投影与视图;运算能力;推理能力.
【答案】B
【分析】延长PA、PB交x轴于A′、B′,作PE⊥x轴于E,交AB于D,由题意得P(4,4),A(0,2),B(3,2),则PD=2,PE=4,AB=3,根据AB∥A′B′,推出△PAB∽△PA′B′,得到相似比,求出A'B'的值即可.
【解答】解:延长PA、PB交x轴于A′、B′,作PE⊥x轴于E,交AB于D,
∵P(4,4),A(0,2),B(3,2),
∴PD=2,PE=4,AB=3,
∵AB∥A′B′,
∴△PAB∽△PA′B′,
∴,即,
∴A'B'=6.
故选:B.
【点评】本题考查了中心投影,相似三角形的性质,正确理中心投影的原理是题的关键.
6.(2024秋 建平县期末)平地上立有三根等高的木杆,其俯视图如图所示,在某一时刻三根木杆在阳光下的影子可能是( )
A. B.
C. D.
【考点】平行投影.
【专题】投影与视图;几何直观.
【答案】D
【分析】根据平行投影的定义判断即可.
【解答】解:根据平行投影的定义可知,在某一时刻三根木杆在阳光下的影子可能是:
故选:D.
【点评】本题考查平行投影,解题的关键是理解平行投影的定义,属于中考常考题型.
7.(2024秋 浑南区期末)如图1,2分别反映了小树在同一时刻的影子,关于影子的形成说法正确的是( )
A.图1,2的影子都是在太阳光下形成的
B.图1的影子是在灯光下形成的,图2的影子是在太阳光下形成的
C.图1的影子是在太阳光下形成的,图2的影子是在灯光下形成的
D.图1,2的影子都是在灯光下形成的
【考点】中心投影;平行投影.
【专题】投影与视图;几何直观.
【答案】C
【分析】利用中心投影和平行投影解答.
【解答】解:图1可看成是平行投影形成的,图2是中心投影形成的,
所以图1的影子是在太阳光下形成的,图2的影子是在灯光下形成的.
故选:C.
【点评】本题考查了平行投影,中心投影,解题的关键是掌握平行投影,中心投影的定义.
二.填空题(共5小题)
8.(2025 福田区模拟)如图,点光源O射出的光线沿直线传播,将胶片上的建筑物图片AB投影到与胶片平行的屏幕上,形成影像CD.已知AB=0.3(dm),点光源到胶片的距离OE长为6(dm),CD长为4.3(dm),则胶片与屏幕的距离EF为 80 dm.
【考点】中心投影.
【专题】平移、旋转与对称;运算能力.
【答案】80.
【分析】证明△OAB∽△OCD,推出,构建方程求出EF即可.
【解答】解:∵AB∥CD,
∴△OAB∽△OCD,
∵OF⊥CD,
∴OF⊥AB,
∴,
∴,
∴EF=80(dm),
故答案为:80.
【点评】本题考查中心投影,相似三角形的判定和性质等知识,解题的关键是学会利用相似三角形的性质解决问题.
9.(2025 雁塔区校级模拟)如图,一块面积为40cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A'B'C'.若OB:BB'=2:3,则△A'B'C'的面积是 250 cm2.
【考点】中心投影.
【专题】投影与视图;运算能力.
【答案】250.
【分析】△ABC与△A'B'C'是位似图形,求出位似比,再根据面积比等于位似比的平方即可求解.
【解答】解:∵OB:BB'=2:3,
∴OB:OB'=2:5,
∴△ABC与△A'B'C'的位似比为2:5,
∴,
∴250(cm2).
故答案为:250.
【点评】本题考查平行投影,熟练掌握该知识点是关键.
10.(2024秋 子洲县期末)如图是两根木杆在同一时刻的影子,则它们的影子是在 灯光 (填“太阳”或“灯光”)光线下形成的.
【考点】中心投影;平行投影.
【专题】投影与视图;推理能力.
【答案】灯光.
【分析】根据光线的平行和相交即可判断是平行投影和中心投影.
【解答】解:因为影子的顶点和木杆的顶点的连线不平行,
所以它们的光线应该是点光源.它们是灯光下的投影.
故答案为:灯光.
【点评】本题考查了中心投影和平行投影,熟知以上知识是解题的关键.
11.(2024秋 临渭区期末)小兰身高160cm,她站立在阳光下的影子长为80cm;她把手臂竖直举起,此时影子长为100cm,那么小兰的手臂超出头顶 40 cm.
【考点】平行投影.
【专题】投影与视图;应用意识.
【答案】见试题解答内容
【分析】根据在同一时物体的高度和影长成正比,设出手臂竖直举起时总高度x,即可列方程解出x的值,再减去身高即可得出小刚举起的手臂超出头顶的高度.
【解答】解:设手臂竖直举起时总高度x cm,则,
解得x=200,
200﹣160=40(cm),
故小兰的手臂超出头顶40cm,
故答案为:40
【点评】本题考查的是相似三角形的应用,熟知同一时刻物体的高度和影长成正比是解答此题的关键.
12.(2025 台江县校级三模)如图,在平面直角坐标系中,点光源位于P(4,4)处,木杆AB两端的坐标分别为(0,2),(6,2).则木杆AB在x轴上的影长CD为 12 .
【考点】中心投影;坐标确定位置.
【专题】投影与视图;推理能力.
【答案】见试题解答内容
【分析】利用中心投影,作PE⊥x轴于E,交AB于M,如图,证明△PAB∽△CPD,然后利用相似比可求出CD的长.
【解答】解:过P作PE⊥x轴于E,交AB于M,如图,
∵P(4,4),A(0,2),B(6,2).
∴PM=2,PE=4,AB=6,
∵AB∥CD,
∴.
∴,
∴CD=12,
故答案为:12.
【点评】本题考查了中心投影:中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.
三.解答题(共3小题)
13.(2024秋 三明期末)三根竖直的竹竿在同一光源下的影子如图所示,其中竹竿AB的影子为AG,竹竿CD的影子为CH.确定光源P的位置,并画出影子为EF的竹竿(用线段表示).
【考点】中心投影.
【专题】投影与视图;运算能力.
【答案】见解析.
【分析】首先作出光源点O,连接OF,过点E作EK⊥EF交OF于点K,线段EK即为所求.
【解答】解:如图,线段EK即为所求.
【点评】本题考查中心投影,解题的关键是理解题意,正确画出图形.
14.(2024秋 横山区期末)汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图2,是他研究的一个汽车盲区的示意图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE之间的距离为1.4m,车宽AF=1.8m,车头FACD近似看成一个矩形,且满足3DF=2AF,点A,F分别在PB,PE上,点C,D在EB上,求汽车盲区EB的长度.
【考点】视点、视角和盲区;矩形的性质;相似三角形的判定与性质.
【专题】几何图形;运算能力.
【答案】12.6m.
【分析】过点P作PN⊥EB于点N,交AF于点M.理由相似三角形的性质求解.
【解答】解:如图2,过点P作PN⊥EB于点N,交AF于点M.
∵3DF=2AF,AF=1.8m,
∴DF=1.2m,
∵∠FDC=90°,AF∥CD,
∴DF⊥DC
∵MN⊥DC,
∴DF=MN=1.2m,
∵PN=1.4m,
∴PM=PN﹣MN=1.4﹣1.2=0.2m
∵AF∥EB,
∴∠PFA=∠E,∠PAF=∠B,
∴△PAF∽△PBE,
根据相似三角形的性质可得:
,
∴,
∴EB=12.6m
答:汽车盲区EB的长度为12.6m.
【点评】本题考查视点、视角和盲区,相似三角形的判定和性质,矩形的性质等知识,解题的关键是学会添加常用辅助线,利用相似三角形的性质解决问题.
15.(2024秋 山丹县期末)如图,AB是公园的一圆形桌面的主视图,MN表示该桌面在路灯下的影子;CD则表示一个圆形的凳子.
(1)请你在图中标出路灯O的位置,并画出CD的影子PQ(要求保留画图痕迹,光线用虚线表示);
(2)若桌面直径和桌面与地面的距离均为1.2m,测得影子的最大跨度MN为2m,求路灯O与地面的距离.
【考点】中心投影.
【专题】计算题.
【答案】见试题解答内容
【分析】(1)延长MA、NB,它们的交点即为路灯O的位置,然后再连接OC、OD,并延长交地面于P、Q点,则PQ为CD的影子;
(2)作OF⊥MN交AB于E,如图,AB=1.2m,EF=1.2m,MN=2m,证明△OAB∽△OMN,利用相似比计算出OF即可得到路灯O与地面的距离.
【解答】解:(1)如图,延长MA、NB,它们的交点为O点,再连接OC、OD,并延长交地面于P、Q点,则PQ为CD的影子,所以点O和PQ为所作;
(2)作OF⊥MN交AB于E,如图,AB=1.2m,EF=1.2m,MN=2m,
∵AB∥MN,
∴△OAB∽△OMN,
∴AB:MN=OE:OF,即1.2:2=(OF﹣1.2):OF,解得OF=3(m).
答:路灯O与地面的距离为3m.
【点评】本题考查了中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.也考查了相似三角形的判定与性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1 投影
一.选择题(共7小题)
1.(2025 孝南区校级三模)如图,在平面直角坐标系中,点A(1,4),是一个光源.木杆BC两端的坐标分别为(﹣1,2),(2,2).则木杆BC在x轴上的投影长为( )
A.3 B.4 C.6 D.12
2.(2025 鹿城区校级三模)下列投影中,属于平行投影的是( )
A. B.
C. D.
3.(2025 高州市模拟)圭表是古代汉族科学家发明的度量日影长度以定节令的一种天文仪器,由”圭”和”表”两个部件组成.当太阳照着表的时候,圭上出现了表的影子,根据影子的方向和长度,就能读出时间.则表在圭面上形成的投影是( )
A.中心投影
B.平行投影
C.既是平行投影又是中心投影
D.不能确定
4.(2025 惠东县模拟)如图,一块面积为90cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1,若OB:BB1=3:4,则△A1B1C1的面积是( )
A.90cm2 B.160cm2 C.210cm2 D.490cm2
5.(2025 利辛县开学)如图,在直角坐标系中,点P(4,4)是一个光源.木杆AB两端的坐标分别为(0,2),(3,2).则木杆AB在x轴上的投影长为( )
A.7 B.6 C.5 D.3
6.(2024秋 建平县期末)平地上立有三根等高的木杆,其俯视图如图所示,在某一时刻三根木杆在阳光下的影子可能是( )
A. B.
C. D.
7.(2024秋 浑南区期末)如图1,2分别反映了小树在同一时刻的影子,关于影子的形成说法正确的是( )
A.图1,2的影子都是在太阳光下形成的
B.图1的影子是在灯光下形成的,图2的影子是在太阳光下形成的
C.图1的影子是在太阳光下形成的,图2的影子是在灯光下形成的
D.图1,2的影子都是在灯光下形成的
二.填空题(共5小题)
8.(2025 福田区模拟)如图,点光源O射出的光线沿直线传播,将胶片上的建筑物图片AB投影到与胶片平行的屏幕上,形成影像CD.已知AB=0.3(dm),点光源到胶片的距离OE长为6(dm),CD长为4.3(dm),则胶片与屏幕的距离EF为 dm.
9.(2025 雁塔区校级模拟)如图,一块面积为40cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A'B'C'.若OB:BB'=2:3,则△A'B'C'的面积是 cm2.
10.(2024秋 子洲县期末)如图是两根木杆在同一时刻的影子,则它们的影子是在 (填“太阳”或“灯光”)光线下形成的.
11.(2024秋 临渭区期末)小兰身高160cm,她站立在阳光下的影子长为80cm;她把手臂竖直举起,此时影子长为100cm,那么小兰的手臂超出头顶 cm.
12.(2025 台江县校级三模)如图,在平面直角坐标系中,点光源位于P(4,4)处,木杆AB两端的坐标分别为(0,2),(6,2).则木杆AB在x轴上的影长CD为 .
三.解答题(共3小题)
13.(2024秋 三明期末)三根竖直的竹竿在同一光源下的影子如图所示,其中竹竿AB的影子为AG,竹竿CD的影子为CH.确定光源P的位置,并画出影子为EF的竹竿(用线段表示).
14.(2024秋 横山区期末)汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图2,是他研究的一个汽车盲区的示意图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE之间的距离为1.4m,车宽AF=1.8m,车头FACD近似看成一个矩形,且满足3DF=2AF,点A,F分别在PB,PE上,点C,D在EB上,求汽车盲区EB的长度.
15.(2024秋 山丹县期末)如图,AB是公园的一圆形桌面的主视图,MN表示该桌面在路灯下的影子;CD则表示一个圆形的凳子.
(1)请你在图中标出路灯O的位置,并画出CD的影子PQ(要求保留画图痕迹,光线用虚线表示);
(2)若桌面直径和桌面与地面的距离均为1.2m,测得影子的最大跨度MN为2m,求路灯O与地面的距离.
5.1 投影
参考答案与试题解析
一.选择题(共7小题)
1.(2025 孝南区校级三模)如图,在平面直角坐标系中,点A(1,4),是一个光源.木杆BC两端的坐标分别为(﹣1,2),(2,2).则木杆BC在x轴上的投影长为( )
A.3 B.4 C.6 D.12
【考点】平行投影;坐标确定位置.
【专题】投影与视图;推理能力.
【答案】C
【分析】利用平行投影,转化为相似三角形,将点的坐标转化为线段的长,根据相似三角形的性质得出答案即可.
【解答】解:如图,设AB交x轴于点D,AC交x轴于点E,作AN⊥x轴于点N,交BC于点M,
∵木杆BC两端的坐标分别为(﹣1,2),(2,2),
∴BC∥DE,
∴△ABC∽△ADE,
∴,
即,
解得DE=6,
∴木杆BC在x轴上的投影长为6.
故选:C.
【点评】本题考查中心投影,构造相似三角形,利用相似三角形的性质求解是解决此类问题的基本方法.
2.(2025 鹿城区校级三模)下列投影中,属于平行投影的是( )
A. B.
C. D.
【考点】平行投影.
【专题】投影与视图;几何直观.
【答案】D
【分析】定义:在一束平行光线照射下形成的投影叫做平行投影.特征:平行投影的投影线是平行的.根据平行投影的定义逐项判断即可.
【解答】解:根据定义:在一束平行光线照射下形成的投影叫做平行投影.特征:平行投影的投影线是平行的判断如下:
A.如图,
属于中心投影,故不符合题意;
B.如图,
属于中心投影,故不符合题意;
C.如图,
属于中心投影,故不符合题意;
D.如图,
属于平行投影,故符合题意;
故选:D.
【点评】本题考查了平行投影的知识,正确记忆相关知识点是解题关键.
3.(2025 高州市模拟)圭表是古代汉族科学家发明的度量日影长度以定节令的一种天文仪器,由”圭”和”表”两个部件组成.当太阳照着表的时候,圭上出现了表的影子,根据影子的方向和长度,就能读出时间.则表在圭面上形成的投影是( )
A.中心投影
B.平行投影
C.既是平行投影又是中心投影
D.不能确定
【考点】中心投影;平行投影.
【专题】投影与视图;空间观念.
【答案】B
【分析】根据中心投影和平行投影的定义,结合光的照射方式判断即可.
【解答】解:表在圭面上形成的投影是平行投影.
故选:B.
【点评】本题考查了平行投影,平行线的判定,正确分析光的照射方式是解答本题的关键.中心投影的定义:光由一点向外散射形成的投影;平行投影的定义:光源以平行的方式照射到物体上形成的投影.
4.(2025 惠东县模拟)如图,一块面积为90cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1,若OB:BB1=3:4,则△A1B1C1的面积是( )
A.90cm2 B.160cm2 C.210cm2 D.490cm2
【考点】中心投影;三角形的面积.
【专题】图形的相似;运算能力.
【答案】D
【分析】△ABC与△A1B1C1是位似图形,求出位似比,再根据面积比等于位似比的平方即可求解.
【解答】解:由平行投影可知△ABC与△A1B1C1是位似图形,
∵OB:BB1=3:4,
∴OB:OB1=3:7,
∴△ABC与△A1B1C1的位似比为3:7,
∴,
△A1B1C1的面积是90490(cm2),
故选:D.
【点评】本题考查中心投影,掌握位似的性质是解题的关键.
5.(2025 利辛县开学)如图,在直角坐标系中,点P(4,4)是一个光源.木杆AB两端的坐标分别为(0,2),(3,2).则木杆AB在x轴上的投影长为( )
A.7 B.6 C.5 D.3
【考点】中心投影;相似三角形的性质.
【专题】三角形;图形的相似;投影与视图;运算能力;推理能力.
【答案】B
【分析】延长PA、PB交x轴于A′、B′,作PE⊥x轴于E,交AB于D,由题意得P(4,4),A(0,2),B(3,2),则PD=2,PE=4,AB=3,根据AB∥A′B′,推出△PAB∽△PA′B′,得到相似比,求出A'B'的值即可.
【解答】解:延长PA、PB交x轴于A′、B′,作PE⊥x轴于E,交AB于D,
∵P(4,4),A(0,2),B(3,2),
∴PD=2,PE=4,AB=3,
∵AB∥A′B′,
∴△PAB∽△PA′B′,
∴,即,
∴A'B'=6.
故选:B.
【点评】本题考查了中心投影,相似三角形的性质,正确理中心投影的原理是题的关键.
6.(2024秋 建平县期末)平地上立有三根等高的木杆,其俯视图如图所示,在某一时刻三根木杆在阳光下的影子可能是( )
A. B.
C. D.
【考点】平行投影.
【专题】投影与视图;几何直观.
【答案】D
【分析】根据平行投影的定义判断即可.
【解答】解:根据平行投影的定义可知,在某一时刻三根木杆在阳光下的影子可能是:
故选:D.
【点评】本题考查平行投影,解题的关键是理解平行投影的定义,属于中考常考题型.
7.(2024秋 浑南区期末)如图1,2分别反映了小树在同一时刻的影子,关于影子的形成说法正确的是( )
A.图1,2的影子都是在太阳光下形成的
B.图1的影子是在灯光下形成的,图2的影子是在太阳光下形成的
C.图1的影子是在太阳光下形成的,图2的影子是在灯光下形成的
D.图1,2的影子都是在灯光下形成的
【考点】中心投影;平行投影.
【专题】投影与视图;几何直观.
【答案】C
【分析】利用中心投影和平行投影解答.
【解答】解:图1可看成是平行投影形成的,图2是中心投影形成的,
所以图1的影子是在太阳光下形成的,图2的影子是在灯光下形成的.
故选:C.
【点评】本题考查了平行投影,中心投影,解题的关键是掌握平行投影,中心投影的定义.
二.填空题(共5小题)
8.(2025 福田区模拟)如图,点光源O射出的光线沿直线传播,将胶片上的建筑物图片AB投影到与胶片平行的屏幕上,形成影像CD.已知AB=0.3(dm),点光源到胶片的距离OE长为6(dm),CD长为4.3(dm),则胶片与屏幕的距离EF为 80 dm.
【考点】中心投影.
【专题】平移、旋转与对称;运算能力.
【答案】80.
【分析】证明△OAB∽△OCD,推出,构建方程求出EF即可.
【解答】解:∵AB∥CD,
∴△OAB∽△OCD,
∵OF⊥CD,
∴OF⊥AB,
∴,
∴,
∴EF=80(dm),
故答案为:80.
【点评】本题考查中心投影,相似三角形的判定和性质等知识,解题的关键是学会利用相似三角形的性质解决问题.
9.(2025 雁塔区校级模拟)如图,一块面积为40cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A'B'C'.若OB:BB'=2:3,则△A'B'C'的面积是 250 cm2.
【考点】中心投影.
【专题】投影与视图;运算能力.
【答案】250.
【分析】△ABC与△A'B'C'是位似图形,求出位似比,再根据面积比等于位似比的平方即可求解.
【解答】解:∵OB:BB'=2:3,
∴OB:OB'=2:5,
∴△ABC与△A'B'C'的位似比为2:5,
∴,
∴250(cm2).
故答案为:250.
【点评】本题考查平行投影,熟练掌握该知识点是关键.
10.(2024秋 子洲县期末)如图是两根木杆在同一时刻的影子,则它们的影子是在 灯光 (填“太阳”或“灯光”)光线下形成的.
【考点】中心投影;平行投影.
【专题】投影与视图;推理能力.
【答案】灯光.
【分析】根据光线的平行和相交即可判断是平行投影和中心投影.
【解答】解:因为影子的顶点和木杆的顶点的连线不平行,
所以它们的光线应该是点光源.它们是灯光下的投影.
故答案为:灯光.
【点评】本题考查了中心投影和平行投影,熟知以上知识是解题的关键.
11.(2024秋 临渭区期末)小兰身高160cm,她站立在阳光下的影子长为80cm;她把手臂竖直举起,此时影子长为100cm,那么小兰的手臂超出头顶 40 cm.
【考点】平行投影.
【专题】投影与视图;应用意识.
【答案】见试题解答内容
【分析】根据在同一时物体的高度和影长成正比,设出手臂竖直举起时总高度x,即可列方程解出x的值,再减去身高即可得出小刚举起的手臂超出头顶的高度.
【解答】解:设手臂竖直举起时总高度x cm,则,
解得x=200,
200﹣160=40(cm),
故小兰的手臂超出头顶40cm,
故答案为:40
【点评】本题考查的是相似三角形的应用,熟知同一时刻物体的高度和影长成正比是解答此题的关键.
12.(2025 台江县校级三模)如图,在平面直角坐标系中,点光源位于P(4,4)处,木杆AB两端的坐标分别为(0,2),(6,2).则木杆AB在x轴上的影长CD为 12 .
【考点】中心投影;坐标确定位置.
【专题】投影与视图;推理能力.
【答案】见试题解答内容
【分析】利用中心投影,作PE⊥x轴于E,交AB于M,如图,证明△PAB∽△CPD,然后利用相似比可求出CD的长.
【解答】解:过P作PE⊥x轴于E,交AB于M,如图,
∵P(4,4),A(0,2),B(6,2).
∴PM=2,PE=4,AB=6,
∵AB∥CD,
∴.
∴,
∴CD=12,
故答案为:12.
【点评】本题考查了中心投影:中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.
三.解答题(共3小题)
13.(2024秋 三明期末)三根竖直的竹竿在同一光源下的影子如图所示,其中竹竿AB的影子为AG,竹竿CD的影子为CH.确定光源P的位置,并画出影子为EF的竹竿(用线段表示).
【考点】中心投影.
【专题】投影与视图;运算能力.
【答案】见解析.
【分析】首先作出光源点O,连接OF,过点E作EK⊥EF交OF于点K,线段EK即为所求.
【解答】解:如图,线段EK即为所求.
【点评】本题考查中心投影,解题的关键是理解题意,正确画出图形.
14.(2024秋 横山区期末)汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图2,是他研究的一个汽车盲区的示意图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE之间的距离为1.4m,车宽AF=1.8m,车头FACD近似看成一个矩形,且满足3DF=2AF,点A,F分别在PB,PE上,点C,D在EB上,求汽车盲区EB的长度.
【考点】视点、视角和盲区;矩形的性质;相似三角形的判定与性质.
【专题】几何图形;运算能力.
【答案】12.6m.
【分析】过点P作PN⊥EB于点N,交AF于点M.理由相似三角形的性质求解.
【解答】解:如图2,过点P作PN⊥EB于点N,交AF于点M.
∵3DF=2AF,AF=1.8m,
∴DF=1.2m,
∵∠FDC=90°,AF∥CD,
∴DF⊥DC
∵MN⊥DC,
∴DF=MN=1.2m,
∵PN=1.4m,
∴PM=PN﹣MN=1.4﹣1.2=0.2m
∵AF∥EB,
∴∠PFA=∠E,∠PAF=∠B,
∴△PAF∽△PBE,
根据相似三角形的性质可得:
,
∴,
∴EB=12.6m
答:汽车盲区EB的长度为12.6m.
【点评】本题考查视点、视角和盲区,相似三角形的判定和性质,矩形的性质等知识,解题的关键是学会添加常用辅助线,利用相似三角形的性质解决问题.
15.(2024秋 山丹县期末)如图,AB是公园的一圆形桌面的主视图,MN表示该桌面在路灯下的影子;CD则表示一个圆形的凳子.
(1)请你在图中标出路灯O的位置,并画出CD的影子PQ(要求保留画图痕迹,光线用虚线表示);
(2)若桌面直径和桌面与地面的距离均为1.2m,测得影子的最大跨度MN为2m,求路灯O与地面的距离.
【考点】中心投影.
【专题】计算题.
【答案】见试题解答内容
【分析】(1)延长MA、NB,它们的交点即为路灯O的位置,然后再连接OC、OD,并延长交地面于P、Q点,则PQ为CD的影子;
(2)作OF⊥MN交AB于E,如图,AB=1.2m,EF=1.2m,MN=2m,证明△OAB∽△OMN,利用相似比计算出OF即可得到路灯O与地面的距离.
【解答】解:(1)如图,延长MA、NB,它们的交点为O点,再连接OC、OD,并延长交地面于P、Q点,则PQ为CD的影子,所以点O和PQ为所作;
(2)作OF⊥MN交AB于E,如图,AB=1.2m,EF=1.2m,MN=2m,
∵AB∥MN,
∴△OAB∽△OMN,
∴AB:MN=OE:OF,即1.2:2=(OF﹣1.2):OF,解得OF=3(m).
答:路灯O与地面的距离为3m.
【点评】本题考查了中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.如物体在灯光的照射下形成的影子就是中心投影.中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.也考查了相似三角形的判定与性质.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
