6.3 反比例函数的应用(新课预习.含解析)-2025-2026学年九年级上册数学北师大版
文档属性
| 名称 | 6.3 反比例函数的应用(新课预习.含解析)-2025-2026学年九年级上册数学北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1018.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 15:46:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.3反比例函数的应用
一.选择题(共7小题)
1.(2025春 合肥期末)有一并联电路,两电阻阻值分别为R1,R2,总电阻为R,三者的关系为:.若已知R、R1,则R2为( )
A. B. C. D.
2.(2025 长春)在功W(J)一定的条件下,功率P(W)与做功时间t(s)成反比例,P(W)与t(s)之间的函数关系如图所示.当25≤t≤40时,P的值可以为( )
A.24 B.27 C.45 D.50
3.(2025春 莱西市期末)机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数,其图象如图所示.下列说法错误的是( )
A.函数表达式为
B.已知机器狗无载重时的最快移动速度为9m/s,则机器狗的质量为40kg
C.机器狗的质量越大,其移动速度越快
D.要使机器狗的最快移动速度v不低于5m/s,其载重后总质量不能大于72kg
4.(2025 南山区校级模拟)物理兴趣小组在实验室研究电学时设计了一个电路,其电路图如图1所示.经测试,发现电流I(A)随着电阻R(Ω)的变化而变化,并结合数据描点,连线,画成图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最大电流是36A B.最大电流是27A
C.最小电流是36A D.最小电流是27A
5.(2025春 上杭县期中)生活用电器中额定电压U(单位:v),额定功率P(单位:w),电阻R(单位:Ω)之间有如下数量关系:R,如图,该用电器的额定电压的标识已经模糊不清,若已知电阻R=3.2Ω,则它的额定电压U应为( )
A.±16 B.±4 C.4 D.16
6.(2025春 丰台区期末)下列变量之间关系中,一个变量是另一个变量的正比例函数的是( )
A.正方形的面积S随着边长x的变化而变化
B.圆的周长C随着半径r的变化而变化
C.面积为20的三角形的一边a,随着这边上的高h的变化而变化
D.矩形的一边长为a,比它的邻边短2,矩形的周长l随着边长a的变化而变化
7.(2025春 宝应县期末)在温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,加压后气体对气缸壁所产生的压强P(kPa)与气缸内气体的体积V(ml)成反比例,P关于V的函数图象如图所示.当压强( )时,气体体积压缩了40ml.
A.100kPa加到125kPa B.75kPa加到100kPa
C.50kPa加到75kPa D.25kPa加到50kPa
二.填空题(共5小题)
8.(2025春 舟山期末)已知在温度不变的条件下,汽缸内气体的体积V(mL)和气体对气缸壁所产生的压强p(kPa)成反比例关系,当V=80时,p=75,则当V=120时,p= .
9.(2025春 海州区期末)物理学中电磁波的波长λ(m)会随着电磁波的频率f(MHz)的变化而变化.已知波长λ与频率f是反比例函数关系,如表是它们的部分对应值.若f=75MHz,则电磁波的波长λ= m.
频率f/MHz 10 15 50
波长λ/m 30 20 6
10.(2025 雨花区校级三模)在二胡演奏中,当弦的张力、线密度等条件不变时,弦的振动频率f(赫兹)与振动弦长l(米)近似成反比例关系,即(k为常数,k≠0).若振动弦长l为0.6米时,测得振动频率f为200赫兹,则k的值为 .
11.(2025春 上城区期末)如图,根据杠杆平衡原理设计的装置,在左边固定的A盘中放置一个质量固定的重物,在右边可左右移动的B盘中放置一定质量的砝码,使仪器水平平衡,改变B盘与点O之间的距离x(cm),记录相应的B盘中的砝码质量y(g),得到如下表格,
B盘与点O的距离x(cm) 10 15 20 25 30
B盘中的砝码质量y(g) 30 20 15 12 10
当砝码的质量为24g时,则B盘与O点之间的距离为 cm.
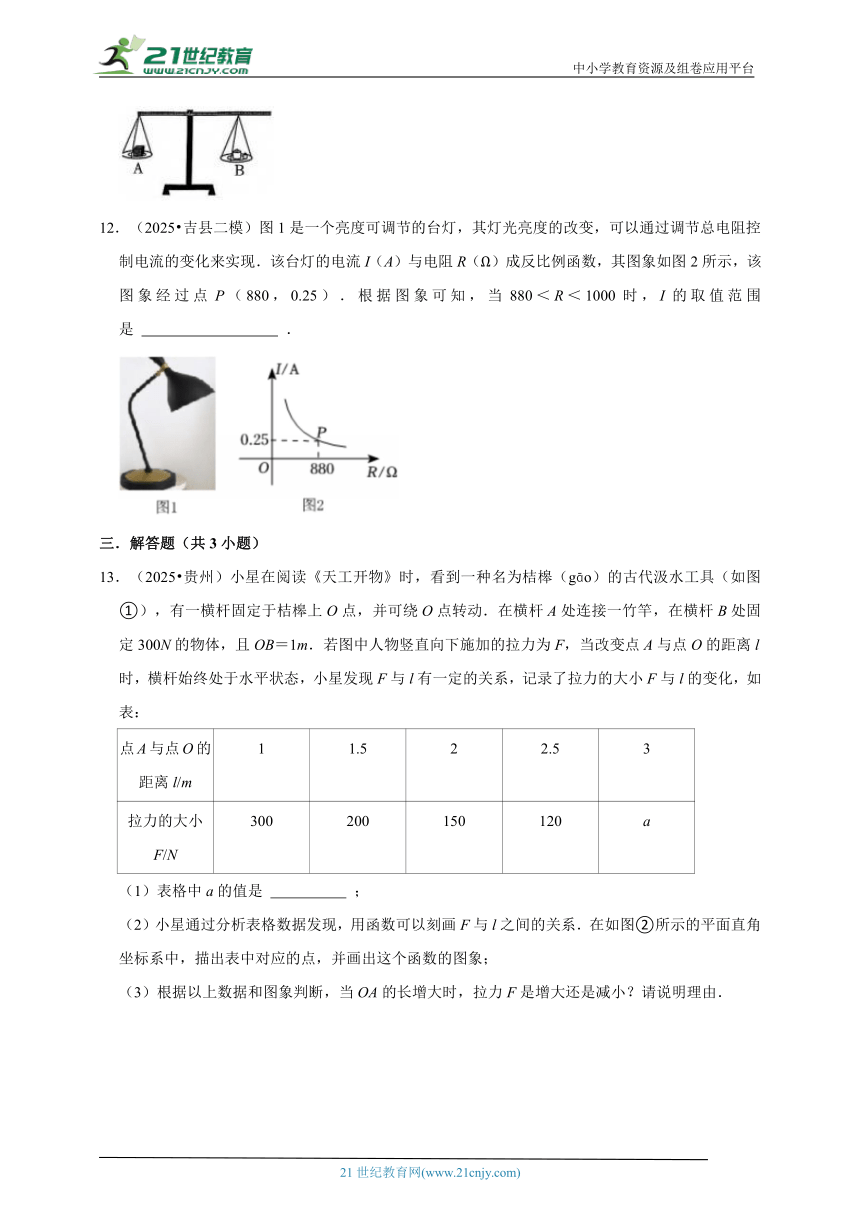
12.(2025 吉县二模)图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.该台灯的电流I(A)与电阻R(Ω)成反比例函数,其图象如图2所示,该图象经过点P(880,0.25).根据图象可知,当880<R<1000时,I的取值范围是 .
三.解答题(共3小题)
13.(2025 贵州)小星在阅读《天工开物》时,看到一种名为桔槔(gāo)的古代汲水工具(如图①),有一横杆固定于桔槔上O点,并可绕O点转动.在横杆A处连接一竹竿,在横杆B处固定300N的物体,且OB=1m.若图中人物竖直向下施加的拉力为F,当改变点A与点O的距离l时,横杆始终处于水平状态,小星发现F与l有一定的关系,记录了拉力的大小F与l的变化,如表:
点A与点O的距离l/m 1 1.5 2 2.5 3
拉力的大小F/N 300 200 150 120 a
(1)表格中a的值是 ;
(2)小星通过分析表格数据发现,用函数可以刻画F与l之间的关系.在如图②所示的平面直角坐标系中,描出表中对应的点,并画出这个函数的图象;
(3)根据以上数据和图象判断,当OA的长增大时,拉力F是增大还是减小?请说明理由.
14.(2025春 宿豫区期末)如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数的图象交于点B(3,n),点P(n+2,2)是反比例函数图象上的一点.
(1)求m的值;
(2)根据图象,直接写出当反比例函数值小于或等于直线BP的函数值时,自变量x的取值范围;
(3)连接OB,若OB与x轴正方向夹角∠BOC=2∠BAO,求一次函数y=kx+b的表达式.
15.(2025 东莞市三模)如图为某公园“水上滑梯”的侧面图,其中BC段可看成是一段双曲线,矩形AOEB为向上攀爬的梯子,OA=6米,AB=2米.以点O为原点,水面所在直线为x轴建立如图的直角坐标系,其中点E在x轴上.
(1)求BC段滑梯所在的双曲线的解析式(不需写出x的取值范围);
(2)出口C点距离水面的距离为1.5米,求B,C之间的水平距离;
(3)若要在滑梯BC上的Q点处设置一个安全警示牌,要求安全警示牌到BE的距离不超过2米,求点Q到水面的距离至少多少米?
6.3反比例函数的应用
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 合肥期末)有一并联电路,两电阻阻值分别为R1,R2,总电阻为R,三者的关系为:.若已知R、R1,则R2为( )
A. B. C. D.
【考点】反比例函数的应用;分式的加减法.
【专题】分式;运算能力.
【答案】D
【分析】利用,求出,再求出倒数即可得出结论.
【解答】解:由条件可知,
∴;
故选:D.
【点评】本题考查异分母的分式的加减运算.熟练掌握运算法则是关键.
2.(2025 长春)在功W(J)一定的条件下,功率P(W)与做功时间t(s)成反比例,P(W)与t(s)之间的函数关系如图所示.当25≤t≤40时,P的值可以为( )
A.24 B.27 C.45 D.50
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】C
【分析】先根据待定系数法求出反比例函数解析式,再求出当t=25和t=40时的函数值,根据反比例函数的性质即可得到答案.
【解答】解:设功率P(单位:w)与做功的时间t(单位:s)的函数解析式为P(k≠0),
把t=60,P=20代入解析式得:20,
解得:k=1200,
∴功率P(单位:w)与做功的时间t(单位:s)的函数解析式为P;
∵反比例函数的图象在第一象限内,P随t的增大而减小,
∴当t≥25时,P48,
当t≤40时,P30,
∴30≤t≤48,
故选:C.
【点评】本题考查反比例函数的应用,关键是用待定系数法求函数解析式.
3.(2025春 莱西市期末)机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数,其图象如图所示.下列说法错误的是( )
A.函数表达式为
B.已知机器狗无载重时的最快移动速度为9m/s,则机器狗的质量为40kg
C.机器狗的质量越大,其移动速度越快
D.要使机器狗的最快移动速度v不低于5m/s,其载重后总质量不能大于72kg
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】C
【分析】利用待定系数法求出反比例函数解析式,根据解析式和反比例函数的性质求解即可.
【解答】解:最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数,设反比例函数解析式为v,
∵反比例函数的图象经过点(60,6),
∴6,
解得:k=360,
∴反比例函数解析式为v(m>0),故选项A不符合题意;
当v=9m/s时,得:9,
解得:m=40,
经检验,m=40是原方程的解,故选项B不符合题意;
∵反比例函数的图象在第一象限内,P随t的增大而减小,
即机器狗的质量越大,其移动速度越慢,故选项C符合题意;
当v≥5m/s,5,
解得m≤72kg,故选项D不符合题意.
故选:C.
【点评】本题考查了反比例函数的应用,待定系数法求反比例函数解析式是解题的关键.
4.(2025 南山区校级模拟)物理兴趣小组在实验室研究电学时设计了一个电路,其电路图如图1所示.经测试,发现电流I(A)随着电阻R(Ω)的变化而变化,并结合数据描点,连线,画成图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最大电流是36A B.最大电流是27A
C.最小电流是36A D.最小电流是27A
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】A
【分析】可设,由于点(4,9)代入这个函数解析式,则可求得k的值,然后代入R=1求得I的值即可.
【解答】解:根据电压=电流×电阻,设,
将点(4,9)代入得,解得U=36,
∴;
若该电路的最小电阻值为1Ω,该电路能通过的最大电流是,
故选:A.
【点评】本题考查了反比例函数的解析式,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
5.(2025春 上杭县期中)生活用电器中额定电压U(单位:v),额定功率P(单位:w),电阻R(单位:Ω)之间有如下数量关系:R,如图,该用电器的额定电压的标识已经模糊不清,若已知电阻R=3.2Ω,则它的额定电压U应为( )
A.±16 B.±4 C.4 D.16
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】C
【分析】根据反比例函数解析式,把P,R的值待入解析式即可.
【解答】解:由题意知,R=3.2Ω,P=5W,R,
∴U2=PR=5×3.2=16,
∴U=4(负值舍去),
故选:C.
【点评】本题考查反比例函数的应用,关键是确定出P,R的值.
6.(2025春 丰台区期末)下列变量之间关系中,一个变量是另一个变量的正比例函数的是( )
A.正方形的面积S随着边长x的变化而变化
B.圆的周长C随着半径r的变化而变化
C.面积为20的三角形的一边a,随着这边上的高h的变化而变化
D.矩形的一边长为a,比它的邻边短2,矩形的周长l随着边长a的变化而变化
【考点】反比例函数的应用.
【专题】一次函数及其应用;推理能力.
【答案】B
【分析】先依据题意列出函数关系式,然后依据函数关系式进行判断即可.
【解答】解:A、S=x2是二次函数,故此选项不符合题意;
B、C=4x是正比例函数,故此选项符合题意;
C、∵ah=20,
∴a,是反比例函数,故此选项不符合题意;
D、∵矩形的一边长为a,则它的邻边为a+2,
∴矩形的周长l=2(a+a+2)=4a+4,是一次函数,故此选项不符合题意.
故选:B.
【点评】本题主要考查的是正比例函数的定义,熟练掌握正比例函数的定义是解题的关键.正比例函数的定义:一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数.
7.(2025春 宝应县期末)在温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,加压后气体对气缸壁所产生的压强P(kPa)与气缸内气体的体积V(ml)成反比例,P关于V的函数图象如图所示.当压强( )时,气体体积压缩了40ml.
A.100kPa加到125kPa B.75kPa加到100kPa
C.50kPa加到75kPa D.25kPa加到50kPa
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】C
【分析】利用待定系数法求出P关于V的函数关系式,将V表示为P的函数,设当P=P1时,V=V1,当P=P2时,V=V2,将它们分别代入V关于P的函数关系式,当V1﹣V2=40时得到关于P1和P2的数量关系式,将各个选项中的值作为P1和P2分别代入这个等式,能使等式成立的就为正确答案.
【解答】解:设P关于V的函数关系式为P(k为常数,且k≠0),
将坐标(100,60)代入P,
得60,
解得k=6000,
∴P关于V的函数关系式为P,
∴V,
设当P=P1时,V=V1,当P=P2时,V=V2,
则V1,V2,
V1﹣V2=6000()=40,
∴,
当P1=100,P2=125时,,
∴A不符合题意;
当P1=75,P2=100时,,
∴B不符合题意;
当P1=50,P2=75时,,
∴C符合题意;
当P1=25,P2=50时,,
∴D不符合题意.
故选:C.
【点评】本题考查反比例函数的应用,掌握待定系数法求反比例函数的关系式是解题的关键.
二.填空题(共5小题)
8.(2025春 舟山期末)已知在温度不变的条件下,汽缸内气体的体积V(mL)和气体对气缸壁所产生的压强p(kPa)成反比例关系,当V=80时,p=75,则当V=120时,p= 50kPa .
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】50kPa.
【分析】运用待定系数法求出反比例函数的解析式,把V=120代入即可得出答案.
【解答】解:设这个反比例函数的解析式为V,
∵V=80时,p=75,
∴k=PV=75×80=6000,
∴V,
当V=120时,p50(kPa).
故答案为:50kPa.
【点评】本题考查了反比例函数的实际应用,读懂题意,得出反比例函数的解析式是解本题的关键.
9.(2025春 海州区期末)物理学中电磁波的波长λ(m)会随着电磁波的频率f(MHz)的变化而变化.已知波长λ与频率f是反比例函数关系,如表是它们的部分对应值.若f=75MHz,则电磁波的波长λ= 4 m.
频率f/MHz 10 15 50
波长λ/m 30 20 6
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】4.
【分析】根据反比例函数的两个变量之积为常数求出波长λ与频率f之间的函数关系式,当f=75时,求出对应λ的值即可.
【解答】解:由表格可知,λf=300,
∴波长λ与频率f之间的函数关系式为λ,
当f=75时,λ4.
故答案为:4.
【点评】本题考查反比例函数的应用,根据反比例函数的两个变量之积为常数求出波长λ与频率f之间的函数关系式是解题的关键.
10.(2025 雨花区校级三模)在二胡演奏中,当弦的张力、线密度等条件不变时,弦的振动频率f(赫兹)与振动弦长l(米)近似成反比例关系,即(k为常数,k≠0).若振动弦长l为0.6米时,测得振动频率f为200赫兹,则k的值为 120 .
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】120.
【分析】将l=0.6,f=200代入f,得到关于k的方程并求解即可.
【解答】解:将l=0.6,f=200代入f,
得200,
解得k=120.
故答案为:120.
【点评】本题考查反比例函数的应用,掌握用代入自变量与函数值的方法计算比例系数是解题的关键.
11.(2025春 上城区期末)如图,根据杠杆平衡原理设计的装置,在左边固定的A盘中放置一个质量固定的重物,在右边可左右移动的B盘中放置一定质量的砝码,使仪器水平平衡,改变B盘与点O之间的距离x(cm),记录相应的B盘中的砝码质量y(g),得到如下表格,
B盘与点O的距离x(cm) 10 15 20 25 30
B盘中的砝码质量y(g) 30 20 15 12 10
当砝码的质量为24g时,则B盘与O点之间的距离为 12.5 cm.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】12.5.
【分析】根据表格中变量的变化规律写出y与x的函数关系式,当y=24时,求出对应x的值即可.
【解答】解:根据表格,得xy=300,
∴y与x的函数关系式为y,
当y=24时,得24,
解得x=12.5,
∴B盘与O点之间的距离为12.5cm.
故答案为:12.5.
【点评】本题考查反比例函数的应用,根据变量的变化规律写出y与x的函数关系式是解题的关键.
12.(2025 吉县二模)图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.该台灯的电流I(A)与电阻R(Ω)成反比例函数,其图象如图2所示,该图象经过点P(880,0.25).根据图象可知,当880<R<1000时,I的取值范围是 0.22<I<0.25 .
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】0.22<I<0.25.
【分析】先由待定系数法求出反比例函数的解析式,然后分别求出R=880和R=1000时对应的I,最后观察图象即可求解.
【解答】解:设I与R的函数关系式是,
∵图象经过点P(880,0.25),
∴,
∴U=220,
∴,
当R=880时,;
当R=1000时,,
∴当880<R<1000时,I的取值范围是0.22<I<0.25.
故答案为:0.22<I<0.25.
【点评】本题主要考查了反比例函数的应用,由待定系数法求出反比例函数的解析式是解决问题的关键.
三.解答题(共3小题)
13.(2025 贵州)小星在阅读《天工开物》时,看到一种名为桔槔(gāo)的古代汲水工具(如图①),有一横杆固定于桔槔上O点,并可绕O点转动.在横杆A处连接一竹竿,在横杆B处固定300N的物体,且OB=1m.若图中人物竖直向下施加的拉力为F,当改变点A与点O的距离l时,横杆始终处于水平状态,小星发现F与l有一定的关系,记录了拉力的大小F与l的变化,如表:
点A与点O的距离l/m 1 1.5 2 2.5 3
拉力的大小F/N 300 200 150 120 a
(1)表格中a的值是 100 ;
(2)小星通过分析表格数据发现,用函数可以刻画F与l之间的关系.在如图②所示的平面直角坐标系中,描出表中对应的点,并画出这个函数的图象;
(3)根据以上数据和图象判断,当OA的长增大时,拉力F是增大还是减小?请说明理由.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】(1)100;
(2)见解析;
(3)当OA的长增大时,拉力F是增大还是减小,理由见解析.
【分析】(1)根据表中数据,可发现l与F的乘积为定值300,即可得到答案;
(2)将表格中的数值在平面直角坐标系中描出各点,将所描出的点用平滑的曲线连接起来就得到这个函数的图象;
(3)根据反比例函数的性质即可得到答案.
【解答】解:(1)根据表中数据,可发现l与F的乘积为定值300,
∴3a﹣300,
∴a=100,
故答案为:100;
(2)画出F与l的函数图象如图所示:
(3)当OA的长增大时,拉力F是增大还是减小,理由如下:
∵F、l都是正数,
∴这条曲线是反比例函数的一支,
∵FL=300,
∴其函数表达式为F,
∵k>0,
∴在第一象限内,F素l的增大而减小,
即当OA的长增大时,拉力F是减小.
【点评】本题考查了反比例函数的应用,解答本题的关键是仔细观察表格,得出F与L的积为定值,从而得出函数关系式.
14.(2025春 宿豫区期末)如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数的图象交于点B(3,n),点P(n+2,2)是反比例函数图象上的一点.
(1)求m的值;
(2)根据图象,直接写出当反比例函数值小于或等于直线BP的函数值时,自变量x的取值范围;
(3)连接OB,若OB与x轴正方向夹角∠BOC=2∠BAO,求一次函数y=kx+b的表达式.
【考点】反比例函数综合题.
【专题】代数几何综合题;反比例函数及其应用;等腰三角形与直角三角形;运算能力.
【答案】(1)m的值为12;
(2)3<x<6;
(3)一次函数的表达式为yx.
【分析】(1)把B、P的坐标代入反比例函数解析式中,即可求得m,n的值;
(2)观察图象即可得出答案;
(3)由题意可推出∠BAO=∠ABO,则OA=OB,求得A(﹣5,0),再运用待定系数法即可求得答案.
【解答】解:(1)∵反比例函数y(x>0)的图象经过B(3,n),P(n+2,2)两点,
∴m=3n=2(n+2),
解得:m=12,n=4,
∴m的值为12;
(2)∵B(3,4),P(6,2),
∴观察图象可得,当反比例函数值小于或等于直线BP的函数值时,3<x<6;
(3)如图,
∵∠BOC=∠BAO+∠ABO,∠BOC=2∠BAO,
∴∠BAO=∠ABO,
∴OA=OB,
∵B(3,4),
∴OB5,
∴OA=5,
∵点A在x轴负半轴上,
∴A(﹣5,0),
把A(﹣5,0),B(3,4)代入y=kx+b,得,
解得:,
∴一次函数的表达式为yx.
【点评】本题是反比例函数综合题,考查了待定系数法,反比例函数的图象和性质,等腰三角形的判定等,本题考查知识点较多,综合性较强,但难度不大.
15.(2025 东莞市三模)如图为某公园“水上滑梯”的侧面图,其中BC段可看成是一段双曲线,矩形AOEB为向上攀爬的梯子,OA=6米,AB=2米.以点O为原点,水面所在直线为x轴建立如图的直角坐标系,其中点E在x轴上.
(1)求BC段滑梯所在的双曲线的解析式(不需写出x的取值范围);
(2)出口C点距离水面的距离为1.5米,求B,C之间的水平距离;
(3)若要在滑梯BC上的Q点处设置一个安全警示牌,要求安全警示牌到BE的距离不超过2米,求点Q到水面的距离至少多少米?
【考点】反比例函数的应用;平面展开﹣最短路径问题.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】(1)y;
(2)6米;
(3)3米.
【分析】(1)利用待定系数法计算即可;
(2)设点C的坐标为(m,1.5)并代入y与x的函数关系式,求出m的值再减去AB的长即可;
(3)设点Q的坐标为(a,b)并代入y与x的函数关系式,将a用b表示出来,根据a﹣2≤2列关于b的不等式并求其解集,从而得到b的最小值即可.
【解答】解:(1)∵OA=6米,AB=2米,
∴点B的坐标为(2,6),
设BC段滑梯所在的双曲线的解析式为y(k为常数,且k≠0),
将坐标B(2,6)代入y,
得6,
解得k=12,
∴BC段滑梯所在的双曲线的解析式为y.
(2)设点C的坐标为(m,1.5),
将C(m,1.5)代入y,
得1.5,
解得m=8,
8﹣2=6(米),
∴B,C之间的水平距离为6米.
(3)设点Q的坐标为(a,b),
将Q(a,b)代入y,
得b,
∴a,
根据题意,得2≤2,
解得b≥3,
∴点Q到水面的距离至少3米.
【点评】本题考查反比例函数的应用,掌握待定系数法求反比例函数的关系式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.3反比例函数的应用
一.选择题(共7小题)
1.(2025春 合肥期末)有一并联电路,两电阻阻值分别为R1,R2,总电阻为R,三者的关系为:.若已知R、R1,则R2为( )
A. B. C. D.
2.(2025 长春)在功W(J)一定的条件下,功率P(W)与做功时间t(s)成反比例,P(W)与t(s)之间的函数关系如图所示.当25≤t≤40时,P的值可以为( )
A.24 B.27 C.45 D.50
3.(2025春 莱西市期末)机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数,其图象如图所示.下列说法错误的是( )
A.函数表达式为
B.已知机器狗无载重时的最快移动速度为9m/s,则机器狗的质量为40kg
C.机器狗的质量越大,其移动速度越快
D.要使机器狗的最快移动速度v不低于5m/s,其载重后总质量不能大于72kg
4.(2025 南山区校级模拟)物理兴趣小组在实验室研究电学时设计了一个电路,其电路图如图1所示.经测试,发现电流I(A)随着电阻R(Ω)的变化而变化,并结合数据描点,连线,画成图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最大电流是36A B.最大电流是27A
C.最小电流是36A D.最小电流是27A
5.(2025春 上杭县期中)生活用电器中额定电压U(单位:v),额定功率P(单位:w),电阻R(单位:Ω)之间有如下数量关系:R,如图,该用电器的额定电压的标识已经模糊不清,若已知电阻R=3.2Ω,则它的额定电压U应为( )
A.±16 B.±4 C.4 D.16
6.(2025春 丰台区期末)下列变量之间关系中,一个变量是另一个变量的正比例函数的是( )
A.正方形的面积S随着边长x的变化而变化
B.圆的周长C随着半径r的变化而变化
C.面积为20的三角形的一边a,随着这边上的高h的变化而变化
D.矩形的一边长为a,比它的邻边短2,矩形的周长l随着边长a的变化而变化
7.(2025春 宝应县期末)在温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,加压后气体对气缸壁所产生的压强P(kPa)与气缸内气体的体积V(ml)成反比例,P关于V的函数图象如图所示.当压强( )时,气体体积压缩了40ml.
A.100kPa加到125kPa B.75kPa加到100kPa
C.50kPa加到75kPa D.25kPa加到50kPa
二.填空题(共5小题)
8.(2025春 舟山期末)已知在温度不变的条件下,汽缸内气体的体积V(mL)和气体对气缸壁所产生的压强p(kPa)成反比例关系,当V=80时,p=75,则当V=120时,p= .
9.(2025春 海州区期末)物理学中电磁波的波长λ(m)会随着电磁波的频率f(MHz)的变化而变化.已知波长λ与频率f是反比例函数关系,如表是它们的部分对应值.若f=75MHz,则电磁波的波长λ= m.
频率f/MHz 10 15 50
波长λ/m 30 20 6
10.(2025 雨花区校级三模)在二胡演奏中,当弦的张力、线密度等条件不变时,弦的振动频率f(赫兹)与振动弦长l(米)近似成反比例关系,即(k为常数,k≠0).若振动弦长l为0.6米时,测得振动频率f为200赫兹,则k的值为 .
11.(2025春 上城区期末)如图,根据杠杆平衡原理设计的装置,在左边固定的A盘中放置一个质量固定的重物,在右边可左右移动的B盘中放置一定质量的砝码,使仪器水平平衡,改变B盘与点O之间的距离x(cm),记录相应的B盘中的砝码质量y(g),得到如下表格,
B盘与点O的距离x(cm) 10 15 20 25 30
B盘中的砝码质量y(g) 30 20 15 12 10
当砝码的质量为24g时,则B盘与O点之间的距离为 cm.
12.(2025 吉县二模)图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.该台灯的电流I(A)与电阻R(Ω)成反比例函数,其图象如图2所示,该图象经过点P(880,0.25).根据图象可知,当880<R<1000时,I的取值范围是 .
三.解答题(共3小题)
13.(2025 贵州)小星在阅读《天工开物》时,看到一种名为桔槔(gāo)的古代汲水工具(如图①),有一横杆固定于桔槔上O点,并可绕O点转动.在横杆A处连接一竹竿,在横杆B处固定300N的物体,且OB=1m.若图中人物竖直向下施加的拉力为F,当改变点A与点O的距离l时,横杆始终处于水平状态,小星发现F与l有一定的关系,记录了拉力的大小F与l的变化,如表:
点A与点O的距离l/m 1 1.5 2 2.5 3
拉力的大小F/N 300 200 150 120 a
(1)表格中a的值是 ;
(2)小星通过分析表格数据发现,用函数可以刻画F与l之间的关系.在如图②所示的平面直角坐标系中,描出表中对应的点,并画出这个函数的图象;
(3)根据以上数据和图象判断,当OA的长增大时,拉力F是增大还是减小?请说明理由.
14.(2025春 宿豫区期末)如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数的图象交于点B(3,n),点P(n+2,2)是反比例函数图象上的一点.
(1)求m的值;
(2)根据图象,直接写出当反比例函数值小于或等于直线BP的函数值时,自变量x的取值范围;
(3)连接OB,若OB与x轴正方向夹角∠BOC=2∠BAO,求一次函数y=kx+b的表达式.
15.(2025 东莞市三模)如图为某公园“水上滑梯”的侧面图,其中BC段可看成是一段双曲线,矩形AOEB为向上攀爬的梯子,OA=6米,AB=2米.以点O为原点,水面所在直线为x轴建立如图的直角坐标系,其中点E在x轴上.
(1)求BC段滑梯所在的双曲线的解析式(不需写出x的取值范围);
(2)出口C点距离水面的距离为1.5米,求B,C之间的水平距离;
(3)若要在滑梯BC上的Q点处设置一个安全警示牌,要求安全警示牌到BE的距离不超过2米,求点Q到水面的距离至少多少米?
6.3反比例函数的应用
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 合肥期末)有一并联电路,两电阻阻值分别为R1,R2,总电阻为R,三者的关系为:.若已知R、R1,则R2为( )
A. B. C. D.
【考点】反比例函数的应用;分式的加减法.
【专题】分式;运算能力.
【答案】D
【分析】利用,求出,再求出倒数即可得出结论.
【解答】解:由条件可知,
∴;
故选:D.
【点评】本题考查异分母的分式的加减运算.熟练掌握运算法则是关键.
2.(2025 长春)在功W(J)一定的条件下,功率P(W)与做功时间t(s)成反比例,P(W)与t(s)之间的函数关系如图所示.当25≤t≤40时,P的值可以为( )
A.24 B.27 C.45 D.50
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】C
【分析】先根据待定系数法求出反比例函数解析式,再求出当t=25和t=40时的函数值,根据反比例函数的性质即可得到答案.
【解答】解:设功率P(单位:w)与做功的时间t(单位:s)的函数解析式为P(k≠0),
把t=60,P=20代入解析式得:20,
解得:k=1200,
∴功率P(单位:w)与做功的时间t(单位:s)的函数解析式为P;
∵反比例函数的图象在第一象限内,P随t的增大而减小,
∴当t≥25时,P48,
当t≤40时,P30,
∴30≤t≤48,
故选:C.
【点评】本题考查反比例函数的应用,关键是用待定系数法求函数解析式.
3.(2025春 莱西市期末)机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数,其图象如图所示.下列说法错误的是( )
A.函数表达式为
B.已知机器狗无载重时的最快移动速度为9m/s,则机器狗的质量为40kg
C.机器狗的质量越大,其移动速度越快
D.要使机器狗的最快移动速度v不低于5m/s,其载重后总质量不能大于72kg
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】C
【分析】利用待定系数法求出反比例函数解析式,根据解析式和反比例函数的性质求解即可.
【解答】解:最快移动速度v(m/s)是载重后总质量m(kg)的反比例函数,设反比例函数解析式为v,
∵反比例函数的图象经过点(60,6),
∴6,
解得:k=360,
∴反比例函数解析式为v(m>0),故选项A不符合题意;
当v=9m/s时,得:9,
解得:m=40,
经检验,m=40是原方程的解,故选项B不符合题意;
∵反比例函数的图象在第一象限内,P随t的增大而减小,
即机器狗的质量越大,其移动速度越慢,故选项C符合题意;
当v≥5m/s,5,
解得m≤72kg,故选项D不符合题意.
故选:C.
【点评】本题考查了反比例函数的应用,待定系数法求反比例函数解析式是解题的关键.
4.(2025 南山区校级模拟)物理兴趣小组在实验室研究电学时设计了一个电路,其电路图如图1所示.经测试,发现电流I(A)随着电阻R(Ω)的变化而变化,并结合数据描点,连线,画成图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最大电流是36A B.最大电流是27A
C.最小电流是36A D.最小电流是27A
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】A
【分析】可设,由于点(4,9)代入这个函数解析式,则可求得k的值,然后代入R=1求得I的值即可.
【解答】解:根据电压=电流×电阻,设,
将点(4,9)代入得,解得U=36,
∴;
若该电路的最小电阻值为1Ω,该电路能通过的最大电流是,
故选:A.
【点评】本题考查了反比例函数的解析式,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
5.(2025春 上杭县期中)生活用电器中额定电压U(单位:v),额定功率P(单位:w),电阻R(单位:Ω)之间有如下数量关系:R,如图,该用电器的额定电压的标识已经模糊不清,若已知电阻R=3.2Ω,则它的额定电压U应为( )
A.±16 B.±4 C.4 D.16
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】C
【分析】根据反比例函数解析式,把P,R的值待入解析式即可.
【解答】解:由题意知,R=3.2Ω,P=5W,R,
∴U2=PR=5×3.2=16,
∴U=4(负值舍去),
故选:C.
【点评】本题考查反比例函数的应用,关键是确定出P,R的值.
6.(2025春 丰台区期末)下列变量之间关系中,一个变量是另一个变量的正比例函数的是( )
A.正方形的面积S随着边长x的变化而变化
B.圆的周长C随着半径r的变化而变化
C.面积为20的三角形的一边a,随着这边上的高h的变化而变化
D.矩形的一边长为a,比它的邻边短2,矩形的周长l随着边长a的变化而变化
【考点】反比例函数的应用.
【专题】一次函数及其应用;推理能力.
【答案】B
【分析】先依据题意列出函数关系式,然后依据函数关系式进行判断即可.
【解答】解:A、S=x2是二次函数,故此选项不符合题意;
B、C=4x是正比例函数,故此选项符合题意;
C、∵ah=20,
∴a,是反比例函数,故此选项不符合题意;
D、∵矩形的一边长为a,则它的邻边为a+2,
∴矩形的周长l=2(a+a+2)=4a+4,是一次函数,故此选项不符合题意.
故选:B.
【点评】本题主要考查的是正比例函数的定义,熟练掌握正比例函数的定义是解题的关键.正比例函数的定义:一般地,形如y=kx(k是常数,k≠0)的函数叫做正比例函数,其中k叫做比例系数.
7.(2025春 宝应县期末)在温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,加压后气体对气缸壁所产生的压强P(kPa)与气缸内气体的体积V(ml)成反比例,P关于V的函数图象如图所示.当压强( )时,气体体积压缩了40ml.
A.100kPa加到125kPa B.75kPa加到100kPa
C.50kPa加到75kPa D.25kPa加到50kPa
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】C
【分析】利用待定系数法求出P关于V的函数关系式,将V表示为P的函数,设当P=P1时,V=V1,当P=P2时,V=V2,将它们分别代入V关于P的函数关系式,当V1﹣V2=40时得到关于P1和P2的数量关系式,将各个选项中的值作为P1和P2分别代入这个等式,能使等式成立的就为正确答案.
【解答】解:设P关于V的函数关系式为P(k为常数,且k≠0),
将坐标(100,60)代入P,
得60,
解得k=6000,
∴P关于V的函数关系式为P,
∴V,
设当P=P1时,V=V1,当P=P2时,V=V2,
则V1,V2,
V1﹣V2=6000()=40,
∴,
当P1=100,P2=125时,,
∴A不符合题意;
当P1=75,P2=100时,,
∴B不符合题意;
当P1=50,P2=75时,,
∴C符合题意;
当P1=25,P2=50时,,
∴D不符合题意.
故选:C.
【点评】本题考查反比例函数的应用,掌握待定系数法求反比例函数的关系式是解题的关键.
二.填空题(共5小题)
8.(2025春 舟山期末)已知在温度不变的条件下,汽缸内气体的体积V(mL)和气体对气缸壁所产生的压强p(kPa)成反比例关系,当V=80时,p=75,则当V=120时,p= 50kPa .
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】50kPa.
【分析】运用待定系数法求出反比例函数的解析式,把V=120代入即可得出答案.
【解答】解:设这个反比例函数的解析式为V,
∵V=80时,p=75,
∴k=PV=75×80=6000,
∴V,
当V=120时,p50(kPa).
故答案为:50kPa.
【点评】本题考查了反比例函数的实际应用,读懂题意,得出反比例函数的解析式是解本题的关键.
9.(2025春 海州区期末)物理学中电磁波的波长λ(m)会随着电磁波的频率f(MHz)的变化而变化.已知波长λ与频率f是反比例函数关系,如表是它们的部分对应值.若f=75MHz,则电磁波的波长λ= 4 m.
频率f/MHz 10 15 50
波长λ/m 30 20 6
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】4.
【分析】根据反比例函数的两个变量之积为常数求出波长λ与频率f之间的函数关系式,当f=75时,求出对应λ的值即可.
【解答】解:由表格可知,λf=300,
∴波长λ与频率f之间的函数关系式为λ,
当f=75时,λ4.
故答案为:4.
【点评】本题考查反比例函数的应用,根据反比例函数的两个变量之积为常数求出波长λ与频率f之间的函数关系式是解题的关键.
10.(2025 雨花区校级三模)在二胡演奏中,当弦的张力、线密度等条件不变时,弦的振动频率f(赫兹)与振动弦长l(米)近似成反比例关系,即(k为常数,k≠0).若振动弦长l为0.6米时,测得振动频率f为200赫兹,则k的值为 120 .
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】120.
【分析】将l=0.6,f=200代入f,得到关于k的方程并求解即可.
【解答】解:将l=0.6,f=200代入f,
得200,
解得k=120.
故答案为:120.
【点评】本题考查反比例函数的应用,掌握用代入自变量与函数值的方法计算比例系数是解题的关键.
11.(2025春 上城区期末)如图,根据杠杆平衡原理设计的装置,在左边固定的A盘中放置一个质量固定的重物,在右边可左右移动的B盘中放置一定质量的砝码,使仪器水平平衡,改变B盘与点O之间的距离x(cm),记录相应的B盘中的砝码质量y(g),得到如下表格,
B盘与点O的距离x(cm) 10 15 20 25 30
B盘中的砝码质量y(g) 30 20 15 12 10
当砝码的质量为24g时,则B盘与O点之间的距离为 12.5 cm.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】12.5.
【分析】根据表格中变量的变化规律写出y与x的函数关系式,当y=24时,求出对应x的值即可.
【解答】解:根据表格,得xy=300,
∴y与x的函数关系式为y,
当y=24时,得24,
解得x=12.5,
∴B盘与O点之间的距离为12.5cm.
故答案为:12.5.
【点评】本题考查反比例函数的应用,根据变量的变化规律写出y与x的函数关系式是解题的关键.
12.(2025 吉县二模)图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.该台灯的电流I(A)与电阻R(Ω)成反比例函数,其图象如图2所示,该图象经过点P(880,0.25).根据图象可知,当880<R<1000时,I的取值范围是 0.22<I<0.25 .
【考点】反比例函数的应用.
【专题】反比例函数及其应用;运算能力.
【答案】0.22<I<0.25.
【分析】先由待定系数法求出反比例函数的解析式,然后分别求出R=880和R=1000时对应的I,最后观察图象即可求解.
【解答】解:设I与R的函数关系式是,
∵图象经过点P(880,0.25),
∴,
∴U=220,
∴,
当R=880时,;
当R=1000时,,
∴当880<R<1000时,I的取值范围是0.22<I<0.25.
故答案为:0.22<I<0.25.
【点评】本题主要考查了反比例函数的应用,由待定系数法求出反比例函数的解析式是解决问题的关键.
三.解答题(共3小题)
13.(2025 贵州)小星在阅读《天工开物》时,看到一种名为桔槔(gāo)的古代汲水工具(如图①),有一横杆固定于桔槔上O点,并可绕O点转动.在横杆A处连接一竹竿,在横杆B处固定300N的物体,且OB=1m.若图中人物竖直向下施加的拉力为F,当改变点A与点O的距离l时,横杆始终处于水平状态,小星发现F与l有一定的关系,记录了拉力的大小F与l的变化,如表:
点A与点O的距离l/m 1 1.5 2 2.5 3
拉力的大小F/N 300 200 150 120 a
(1)表格中a的值是 100 ;
(2)小星通过分析表格数据发现,用函数可以刻画F与l之间的关系.在如图②所示的平面直角坐标系中,描出表中对应的点,并画出这个函数的图象;
(3)根据以上数据和图象判断,当OA的长增大时,拉力F是增大还是减小?请说明理由.
【考点】反比例函数的应用.
【专题】反比例函数及其应用;应用意识.
【答案】(1)100;
(2)见解析;
(3)当OA的长增大时,拉力F是增大还是减小,理由见解析.
【分析】(1)根据表中数据,可发现l与F的乘积为定值300,即可得到答案;
(2)将表格中的数值在平面直角坐标系中描出各点,将所描出的点用平滑的曲线连接起来就得到这个函数的图象;
(3)根据反比例函数的性质即可得到答案.
【解答】解:(1)根据表中数据,可发现l与F的乘积为定值300,
∴3a﹣300,
∴a=100,
故答案为:100;
(2)画出F与l的函数图象如图所示:
(3)当OA的长增大时,拉力F是增大还是减小,理由如下:
∵F、l都是正数,
∴这条曲线是反比例函数的一支,
∵FL=300,
∴其函数表达式为F,
∵k>0,
∴在第一象限内,F素l的增大而减小,
即当OA的长增大时,拉力F是减小.
【点评】本题考查了反比例函数的应用,解答本题的关键是仔细观察表格,得出F与L的积为定值,从而得出函数关系式.
14.(2025春 宿豫区期末)如图所示,一次函数y=kx+b的图象与x轴交于点A,与反比例函数的图象交于点B(3,n),点P(n+2,2)是反比例函数图象上的一点.
(1)求m的值;
(2)根据图象,直接写出当反比例函数值小于或等于直线BP的函数值时,自变量x的取值范围;
(3)连接OB,若OB与x轴正方向夹角∠BOC=2∠BAO,求一次函数y=kx+b的表达式.
【考点】反比例函数综合题.
【专题】代数几何综合题;反比例函数及其应用;等腰三角形与直角三角形;运算能力.
【答案】(1)m的值为12;
(2)3<x<6;
(3)一次函数的表达式为yx.
【分析】(1)把B、P的坐标代入反比例函数解析式中,即可求得m,n的值;
(2)观察图象即可得出答案;
(3)由题意可推出∠BAO=∠ABO,则OA=OB,求得A(﹣5,0),再运用待定系数法即可求得答案.
【解答】解:(1)∵反比例函数y(x>0)的图象经过B(3,n),P(n+2,2)两点,
∴m=3n=2(n+2),
解得:m=12,n=4,
∴m的值为12;
(2)∵B(3,4),P(6,2),
∴观察图象可得,当反比例函数值小于或等于直线BP的函数值时,3<x<6;
(3)如图,
∵∠BOC=∠BAO+∠ABO,∠BOC=2∠BAO,
∴∠BAO=∠ABO,
∴OA=OB,
∵B(3,4),
∴OB5,
∴OA=5,
∵点A在x轴负半轴上,
∴A(﹣5,0),
把A(﹣5,0),B(3,4)代入y=kx+b,得,
解得:,
∴一次函数的表达式为yx.
【点评】本题是反比例函数综合题,考查了待定系数法,反比例函数的图象和性质,等腰三角形的判定等,本题考查知识点较多,综合性较强,但难度不大.
15.(2025 东莞市三模)如图为某公园“水上滑梯”的侧面图,其中BC段可看成是一段双曲线,矩形AOEB为向上攀爬的梯子,OA=6米,AB=2米.以点O为原点,水面所在直线为x轴建立如图的直角坐标系,其中点E在x轴上.
(1)求BC段滑梯所在的双曲线的解析式(不需写出x的取值范围);
(2)出口C点距离水面的距离为1.5米,求B,C之间的水平距离;
(3)若要在滑梯BC上的Q点处设置一个安全警示牌,要求安全警示牌到BE的距离不超过2米,求点Q到水面的距离至少多少米?
【考点】反比例函数的应用;平面展开﹣最短路径问题.
【专题】反比例函数及其应用;运算能力;应用意识.
【答案】(1)y;
(2)6米;
(3)3米.
【分析】(1)利用待定系数法计算即可;
(2)设点C的坐标为(m,1.5)并代入y与x的函数关系式,求出m的值再减去AB的长即可;
(3)设点Q的坐标为(a,b)并代入y与x的函数关系式,将a用b表示出来,根据a﹣2≤2列关于b的不等式并求其解集,从而得到b的最小值即可.
【解答】解:(1)∵OA=6米,AB=2米,
∴点B的坐标为(2,6),
设BC段滑梯所在的双曲线的解析式为y(k为常数,且k≠0),
将坐标B(2,6)代入y,
得6,
解得k=12,
∴BC段滑梯所在的双曲线的解析式为y.
(2)设点C的坐标为(m,1.5),
将C(m,1.5)代入y,
得1.5,
解得m=8,
8﹣2=6(米),
∴B,C之间的水平距离为6米.
(3)设点Q的坐标为(a,b),
将Q(a,b)代入y,
得b,
∴a,
根据题意,得2≤2,
解得b≥3,
∴点Q到水面的距离至少3米.
【点评】本题考查反比例函数的应用,掌握待定系数法求反比例函数的关系式是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
