人教版高中数学必修1 《对数函数图像与性质》复习课课件(共25张) (共25张PPT)
文档属性
| 名称 | 人教版高中数学必修1 《对数函数图像与性质》复习课课件(共25张) (共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 510.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-22 11:55:02 | ||
图片预览







文档简介
课件25张PPT。对数函数的图象和性质欢 迎 指 导教学目标:
1.会画有关对数函数的图象,并能解决相应问题。
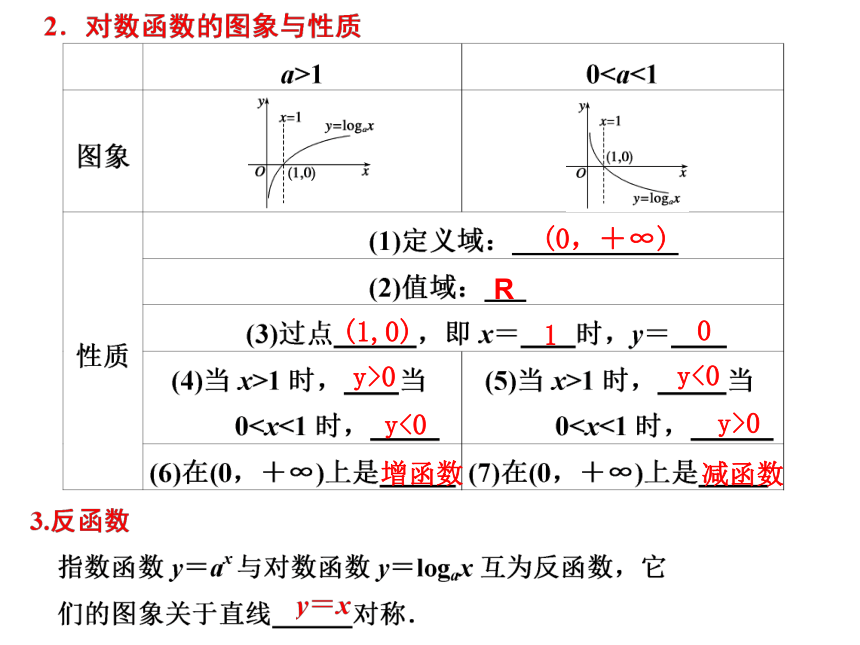
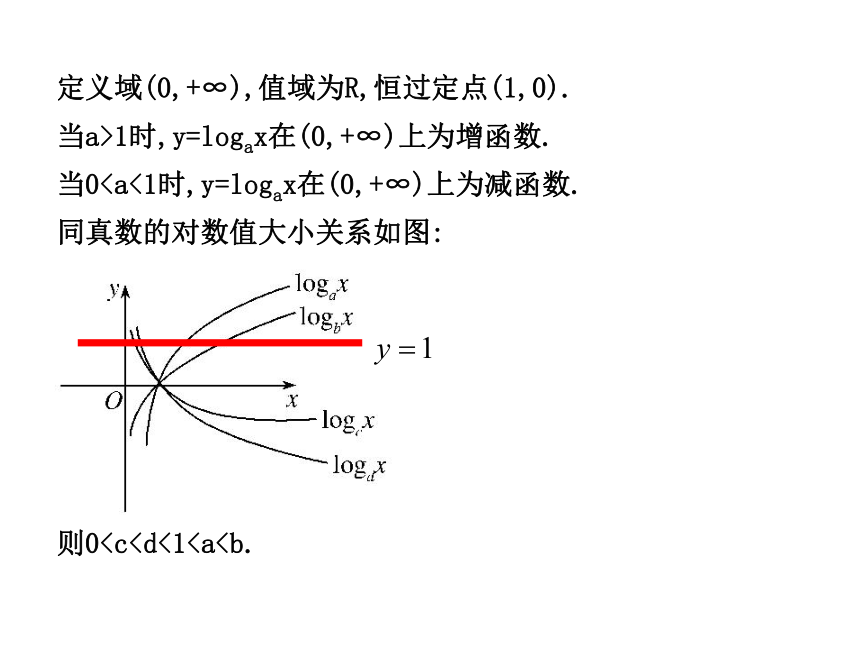
2.掌握对数函数的性质,会解有关定义域、值域、单调性、奇偶性等综合问题。(0,+∞) R(1,0) 1 0 y>0 y<0 y<0 y>0 增函数 减函数 定义域(0,+∞),值域为R,恒过定点(1,0). 当a>1时,y=logax在(0,+∞)上为增函数. 当0f(a+1)
C.f(b-2)解析:由f(x)=loga|x-b|在(0,+∞)上单调递增,
且f(x)为偶函数,∴b=0,a>1,故f(b-2)=f(2),又a>1,
∴a+1>2,由f(x)在(0,+∞)上单调递增知f(a+1)>f(2),
即f(a+1)>f(b-2),答案为C.c题型二 对数函数的性质
例2(1)若f(x)的定义域为R,求实数a的取值范围;
(2)若f(x)的值域为R,求实数a的取值范围;
(3)若函数f(x)在[-1,+∞)内有意义,求实数a的值; (4)若函数f(x)的定义域为(-∞,1)∪(3,+∞),求实数a的值;
(5)若函数f(x)的值域为(-∞,-1],求实数a的值;
(6)若函数f(x)在(-∞,1]内为增函数,求实数a的取值范围.(4)由题意得x2-2ax+3>0的解集为(-∞,1)∪(3,+∞),
即x2-2ax+3=0有两根1,3,
由题意得1+3=2a,得a=2
∴当a=2时,函数f(x)的定义域为(-∞,1)∪(3,+∞).点评:
研究形如y=logaf(x)的函数的单调性时,必须保证函数的定义域,同时要注意复合函数的单调性.小结一:知识总结小结二:数学思想与方法(定义域是函数的命,若丢了函数的命,就会丢了自己的命)数形结合思想、转化划归思想
换元法、类比法课时作业
1.为了得到 的图象只需把函数y=lgx的图象上点 ( ) A.向左平移3个单位长度,再向上平移1个单位长度 B.向右平移3个单位长度,再向上平移1个单位长度 C.向左平移3个单位长度,再向下平移1个单位长度 D.向右平移3个单位长度,再向下平移1个单位长度
3.已知函数f(x)=lg(ax2+2ax+1)的定义域为R,则实数a∈________.5.设f(x)=lg( +a)是奇函数,则使f(x)<0的x的取值范围是6.记函数(1)求A∩B和A∪B; (2)若C={x|4x+p<0},C?A,求实数p的取值范围.________________________1.为了得到 的图象只需把函数y=lgx的图象上点 ( ) A.向左平移3个单位长度,再向上平移1个单位长度 B.向右平移3个单位长度,再向上平移1个单位长度 C.向左平移3个单位长度,再向下平移1个单位长度 D.向右平移3个单位长度,再向下平移1个单位长度答案:D答案:A解析:由复合函数的单调性可知.3.已知函数f(x)=lg(ax2+2ax+1)的定义域为R,则实数a∈ ________.答案:[0,1)答案:05.设f(x)=lg( +a)是奇函数,则使f(x)<0的x的取值范围是 ( ) A.(-1,0) B.(0,1) C.(-∞,0) D.(-∞,0)∪(1,+∞)答案:A(1)求A∩B和A∪B; (2)若C={x|4x+p<0},C?A,求实数p的取值范围.
1.会画有关对数函数的图象,并能解决相应问题。
2.掌握对数函数的性质,会解有关定义域、值域、单调性、奇偶性等综合问题。(0,+∞) R(1,0) 1 0 y>0 y<0 y<0 y>0 增函数 减函数 定义域(0,+∞),值域为R,恒过定点(1,0). 当a>1时,y=logax在(0,+∞)上为增函数. 当0
换元法、类比法课时作业
1.为了得到 的图象只需把函数y=lgx的图象上点 ( ) A.向左平移3个单位长度,再向上平移1个单位长度 B.向右平移3个单位长度,再向上平移1个单位长度 C.向左平移3个单位长度,再向下平移1个单位长度 D.向右平移3个单位长度,再向下平移1个单位长度
3.已知函数f(x)=lg(ax2+2ax+1)的定义域为R,则实数a∈________.5.设f(x)=lg( +a)是奇函数,则使f(x)<0的x的取值范围是6.记函数(1)求A∩B和A∪B; (2)若C={x|4x+p<0},C?A,求实数p的取值范围.________________________1.为了得到 的图象只需把函数y=lgx的图象上点 ( ) A.向左平移3个单位长度,再向上平移1个单位长度 B.向右平移3个单位长度,再向上平移1个单位长度 C.向左平移3个单位长度,再向下平移1个单位长度 D.向右平移3个单位长度,再向下平移1个单位长度答案:D答案:A解析:由复合函数的单调性可知.3.已知函数f(x)=lg(ax2+2ax+1)的定义域为R,则实数a∈ ________.答案:[0,1)答案:05.设f(x)=lg( +a)是奇函数,则使f(x)<0的x的取值范围是 ( ) A.(-1,0) B.(0,1) C.(-∞,0) D.(-∞,0)∪(1,+∞)答案:A(1)求A∩B和A∪B; (2)若C={x|4x+p<0},C?A,求实数p的取值范围.
