2026年中考数学一轮复习 锐角三角函数(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 锐角三角函数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 23:38:32 | ||
图片预览


文档简介
中考数学一轮复习 锐角三角函数
一.选择题(共10小题)
1.(2025 梅县区一模)在中,,,,则的度数为
A. B. C. D.
2.(2025 绥化模拟)在△中,,设,,所对的边分别为,,,则
A. B. C. D.
3.(2025 义乌市模拟)若是锐角,且,则
A. B. C. D.
4.(2025 邵阳模拟)放在正方形网格纸的位置如图,则的值为
A. B. C. D.
5.(2025 道里区模拟)如图,某数学兴趣小组测量一棵树的高度,在点处测得树顶的仰角为,在点处测得树顶的仰角为,且、、三点在同一直线上,若米,则这棵树的高度是
A.米 B.米 C.米 D.米
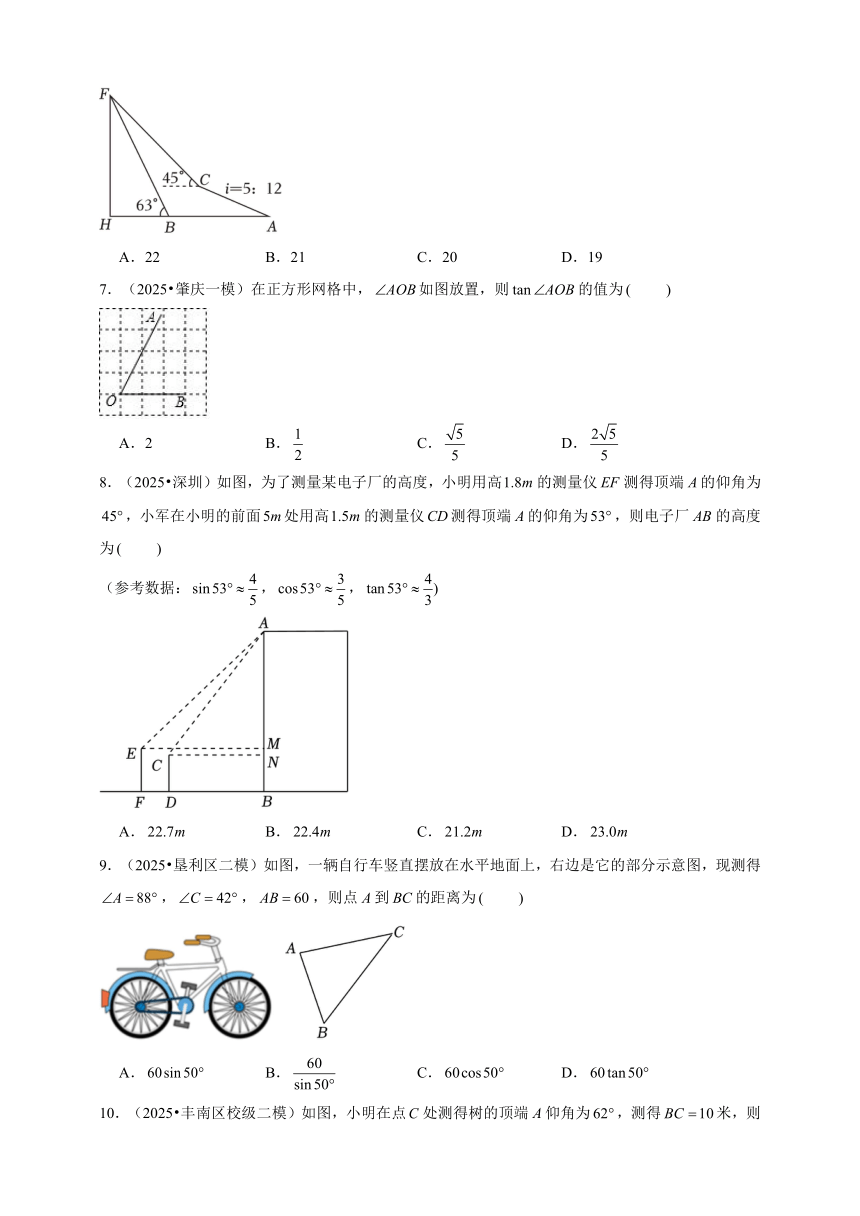
6.(2025 海珠区一模)如图,小乐和小静一起从点出发去拍摄木棉树.小乐沿着水平面步行到达点时拍到树顶点,仰角为;小静沿着坡度的斜坡步行到达点时拍到树顶点,仰角为,那么这棵木棉树的高度约 .(结果精确到(参考数据:,,
A.22 B.21 C.20 D.19
7.(2025 肇庆一模)在正方形网格中,如图放置,则的值为
A.2 B. C. D.
8.(2025 深圳)如图,为了测量某电子厂的高度,小明用高的测量仪测得顶端的仰角为,小军在小明的前面处用高的测量仪测得顶端的仰角为,则电子厂的高度为
(参考数据:,,
A. B. C. D.
9.(2025 垦利区二模)如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得,,,则点到的距离为
A. B. C. D.
10.(2025 丰南区校级二模)如图,小明在点处测得树的顶端仰角为,测得米,则树的高(单位:米)为
A. B. C. D.
二.填空题(共10小题)
11.(2025 新泰市三模)如图所示,某数学兴趣小组利用无人机测大楼的高度,无人机在空中点处,测得点距地面上点100米,点处俯角为,楼顶点处的俯角为,已知点与大楼的距离为80米(点,,,在同一平面内),则大楼的高度 米.(结果精确到0.1米,参考数据:.
12.(2025 东营区模拟)如图,已知公路上,两点之间的距离为20米,点在的南偏西的方向上,在的南偏西方向上,则点到公路的距离为 米.
13.(2025 江西)将图1所示的七巧板,拼成图2所示的四边形,连接,则 .
14.(2025 凉州区一模)已知为锐角.若,则 .
15.(2025 长沙一模)如图,是操场上直立的一根旗杆,旗杆上有一点,用测角仪(测角仪的高度忽略不计)测得地面上的点到点的仰角,到点的仰角,若米,则旗杆的高度 米.
16.(2025 揭东区一模)如图,是放置在正方形网格中的一个角,则的值是 .
17.(2025 旺苍县三模)如图,,,,均为网格图中的格点,线段与相交于点,则的正切值为 .
18.(2025 徐汇区三模)一斜坡的坡角为,坡长比坡高多100米,那么斜坡的高为 (用的锐角三角比表示).
19.(2025 中山市一模)一个斜坡的坡度,若某人沿斜坡直线前进,则垂直高度上升了 .
20.(2025 广西模拟)图1为手机支架实物图,图2为它的侧面示意图,“型”托架用于放置手机,支架两端分别与托架和底座(其厚度忽略不计)相连,支架端可调节旋转角度,已知,,支架调整到图2位置时,,.因实际需要,现将支架端角度调整为,如图3所示,则点的位置较原来的位置上升高度为 .
三.解答题(共5小题)
21.(2025 惠州二模)热气球的探测器显示,从热气球看一栋楼顶部的仰角是,看这栋楼底的俯角为,热气球与楼的水平距离为120米,这栋楼有多高?
22.(2025 澄迈县模拟)如图,为了测量某建筑物的高度,小颖采用了如下的方法:先从与建筑物底端在同一水平线上的点出发,沿斜坡行走130米至坡顶处,再从处沿水平方向继续前行若干米后至点处,在点测得该建筑物顶端的仰角为,建筑物底端的俯角为,点、、、、在同一平面内,斜坡的坡度.根据小颖的测量数据,求建筑物的高度.(参考数据:
23.(2025 重庆模拟)某动物园熊猫基地新诞生了一只小熊猫,吸引了大批游客前往观看.由于、之间的道路正在进行维护,暂时不能通行,游客由入口进入园区之后可步行到达点,然后可以选择乘坐空中缆车从,也可选择乘坐观光车从.已知点在点的北偏东方向上,点在点的正东方向,点在点的正东方向300米处,点在点的北偏东方向上,且米.(参考数据:,,
(1)求的长度(精确到个位);
(2)已知空中缆车的速度是每分钟200米,观光车的速度是每分钟320米,若游客想尽快到达熊猫基地,应选择乘坐空中缆车还是观光车?
24.(2025 泰兴市三模)如图1是一款多功能可调节的桌面手机、平板支架.点、、处均可旋转,处可摆放平板或者手机.其中,,.研究表明,当手机与桌面的夹角为时,更符合人体工学设计,也是多数人操作手机最舒适的角度.
(1)如图2,当和桌面垂直且时,可将绕点旋转一定的角度,就能达到最舒适的观影状态,求此时的度数;
(2)在(1)的条件下求点到的距离(结果保留整数).(参考数据:,,.
25.(2025 淮安)拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形,的长度为,两节可调节的拉杆长度相等,且与在同一条直线上.如图1,当拉杆伸出一节时,与地面夹角;如图2,当拉杆伸出两节、时,与地面夹角,两种情况下拉杆把手点距离地面高度相同.求每节拉杆的长度.
(参考数据:,,,
中考数学一轮复习 锐角三角函数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 梅县区一模)在中,,,,则的度数为
A. B. C. D.
【答案】
【考点】特殊角的三角函数值
【专题】解直角三角形及其应用
【分析】直接利用已知画出直角三角形,再利用锐角三角函数关系得出答案.
【解答】解:,,,
,
.
故选:.
【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
2.(2025 绥化模拟)在△中,,设,,所对的边分别为,,,则
A. B. C. D.
【答案】
【考点】锐角三角函数的定义
【专题】运算能力;解直角三角形及其应用
【分析】根据正弦、正切的定义计算,判断即可.
【解答】解:、,
则,本选项说法错误;
、,本选项说法正确;
、,
则,本选项说法错误;
、,本选项说法错误;
故选:.
【点评】本题考查的是锐角三角函数的定义,掌握正弦、正切的定义是解题的关键.
3.(2025 义乌市模拟)若是锐角,且,则
A. B. C. D.
【答案】
【考点】锐角三角函数的增减性
【专题】等腰三角形与直角三角形;数感
【分析】正弦值随着角度的增大(或减小)而增大(或减小),据此可得结论.
【解答】解:是锐角,且,
,
故选:.
【点评】本题主要考查了锐角三角函数的增减性,正弦值随着角度的增大(或减小)而增大(或减小).
4.(2025 邵阳模拟)放在正方形网格纸的位置如图,则的值为
A. B. C. D.
【答案】
【考点】勾股定理;勾股定理的逆定理;锐角三角函数的定义
【分析】连接,再利用勾股定理分别计算出、、的长,然后再根据勾股定理逆定理证明,再利用三角函数定义可得答案.
【解答】解:连接,如图:
,,,
,
.
故选:.
【点评】此题主要考查了勾股定理,勾股定理逆定理,以及锐角三角函数定义,关键是证明.
5.(2025 道里区模拟)如图,某数学兴趣小组测量一棵树的高度,在点处测得树顶的仰角为,在点处测得树顶的仰角为,且、、三点在同一直线上,若米,则这棵树的高度是
A.米 B.米 C.米 D.米
【答案】
【考点】解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;运算能力;推理能力
【分析】根据题意可得:,设米,然后在中,利用锐角三角函数的定义求出的长,再在中,利用锐角三角函数的定义求出的长,然后根据,列出关于的方程,进行计算即可解答.
【解答】解:由题意得:,
设米,
在中,,
(米,
在中,,,
(米,
,
,
解得,
(米,
这棵树的高度约为米.
故选:.
【点评】本题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
6.(2025 海珠区一模)如图,小乐和小静一起从点出发去拍摄木棉树.小乐沿着水平面步行到达点时拍到树顶点,仰角为;小静沿着坡度的斜坡步行到达点时拍到树顶点,仰角为,那么这棵木棉树的高度约 .(结果精确到(参考数据:,,
A.22 B.21 C.20 D.19
【答案】
【考点】解直角三角形的应用坡度坡角问题;解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;运算能力
【分析】过点作,垂足为,过点作,垂足为,根据题意可得:,,米,再根据已知可设米,则米,然后在△中,利用勾股定理进行计算可得米,米,最后设米,则米,分别在△和△中,利用锐角三角函数的定义求出和的长,从而列出关于的方程进行计算,即可解答.
【解答】解:过点作,垂足为,过点作,垂足为,
由题意得:,,米,
斜坡的坡度,
,
设米,则米,
在△中,(米,
米,
,
解得:,
米,米,
设米,
米,
在△中,,
米,
在△中,,
米,
,
,
解得:,
(米,
这棵木棉树的高度约为20米,
故选:.
【点评】本题考查了解直角三角形的应用仰角俯角问题,坡度坡角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
7.(2025 肇庆一模)在正方形网格中,如图放置,则的值为
A.2 B. C. D.
【答案】
【考点】锐角三角函数的定义
【专题】等腰三角形与直角三角形
【分析】根据图形找出角的两边经过的格点以及点组成的直角三角形,然后根据锐角的正切等于对边比邻边解答.
【解答】解:如图,.
故选.
【点评】本题考查了锐角三角函数的定义,熟练掌握网格结构找出直角三角形是解题的关键.
8.(2025 深圳)如图,为了测量某电子厂的高度,小明用高的测量仪测得顶端的仰角为,小军在小明的前面处用高的测量仪测得顶端的仰角为,则电子厂的高度为
(参考数据:,,
A. B. C. D.
【答案】
【考点】解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;运算能力
【分析】根据题意可得:,,,,,,,然后设 ,则,分别在△和△中,利用锐角三角函数的定义求出和的长,从而列出关于的方程,进行计算即可解答.
【解答】解:由题意得:,,,,,,,
设 ,
,
在△中,,
,
在△中,,
,
,
,
解得:,
,
,
电子厂的高度约为,
故选:.
【点评】本题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
9.(2025 垦利区二模)如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得,,,则点到的距离为
A. B. C. D.
【答案】
【考点】解直角三角形的应用
【专题】解直角三角形及其应用;应用意识
【分析】先求出,再用三角函数定义,求出,即可得出答案.
【解答】解:过点作于点,如图所示:
,,
,
在中,,
点到的距离为,故正确.
故选:.
【点评】本题主要考查了三角形内角和定理的应用,三角函数的应用,点到直线的距离,解题的关键是熟练掌握三角函数的定义.
10.(2025 丰南区校级二模)如图,小明在点处测得树的顶端仰角为,测得米,则树的高(单位:米)为
A. B. C. D.
【答案】
【考点】解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;运算能力
【分析】根据题意可得:,,然后在中,利用锐角三角函数的定义进行计算即可解答.
【解答】解:由题意得:
,,
在中,米,
(米,
故选:.
【点评】本题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
二.填空题(共10小题)
11.(2025 新泰市三模)如图所示,某数学兴趣小组利用无人机测大楼的高度,无人机在空中点处,测得点距地面上点100米,点处俯角为,楼顶点处的俯角为,已知点与大楼的距离为80米(点,,,在同一平面内),则大楼的高度 69.3 米.(结果精确到0.1米,参考数据:.
【答案】69.3.
【考点】解直角三角形的应用仰角俯角问题
【专题】应用意识;解直角三角形及其应用
【分析】过作于,过作于,而,则四边形是矩形,先解,求出,,得到的长度,再解,得到的长即可解决问题.
【解答】解:如图所示:
过作于,过作于,而,
则四边形是矩形,
,,
由题意可得:米,,,米,
(米,(米,
(米,
(米,
(米,
大楼的高度约为69.3米.
故答案为:69.3.
【点评】本题考查的是解直角三角形的应用仰角俯角问题,矩形的判定与性质,理解仰角与俯角的含义是解本题的关键.
12.(2025 东营区模拟)如图,已知公路上,两点之间的距离为20米,点在的南偏西的方向上,在的南偏西方向上,则点到公路的距离为 米.
【答案】.
【考点】解直角三角形的应用方向角问题
【专题】运算能力;推理能力;应用意识;等腰三角形与直角三角形;解直角三角形及其应用
【分析】过点作公路于点,证,得米,再在中,根据计算求得的长即可.
【解答】解:如图,过点作公路于点,
则,,,米,
,,
,
米,
在中,,
(米,
故答案为:.
【点评】本题主要考查了解直角三角形的应用、等腰三角形的判定等知识,正确作出辅助线构造直角三角形是解决问题的关键.
13.(2025 江西)将图1所示的七巧板,拼成图2所示的四边形,连接,则 .
【答案】.
【考点】七巧板;平行四边形的判定与性质;解直角三角形
【专题】解直角三角形及其应用;运算能力
【分析】根据所给拼图,得出四边形是平行四边形,根据平行四边形的性质及正切的定义即可解决问题.
【解答】解:令与的交点为,
,
,
又,
四边形是平行四边形,
与互相平分,
.
,
.
在中,
.
故答案为:.
【点评】本题考查解直角三角形、七巧板及平行四边形的判定与性质,能根据所拼图形得出四边形是平行四边形及熟知正切的定义是解题的关键.
14.(2025 凉州区一模)已知为锐角.若,则 60 .
【答案】60.
【考点】特殊角的三角函数值
【专题】等腰三角形与直角三角形;运算能力
【分析】根据特殊角的三角函数值计算.
【解答】解:,
.
故答案为:60.
【点评】本题考查特殊角三角函数值,熟记各特殊角三角函数值是解题的关键.
15.(2025 长沙一模)如图,是操场上直立的一根旗杆,旗杆上有一点,用测角仪(测角仪的高度忽略不计)测得地面上的点到点的仰角,到点的仰角,若米,则旗杆的高度 米.
【答案】.
【考点】解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;运算能力
【分析】在中,根据,求出米,在中,根据即可求出的高度.
【解答】解:在中,
,
米,
在中,
,
(米.
故答案为:.
【点评】本题考查了解直角三角形的应用,解题的关键是根据仰角构造直角三角形,解直角三角形,难度一般.
16.(2025 揭东区一模)如图,是放置在正方形网格中的一个角,则的值是 .
【考点】三角形的面积;勾股定理;锐角三角函数的定义
【分析】首先连接,由勾股定理易求得,,,然后由勾股定理的逆定理,可证得是等腰直角三角形,继而可求得的值.
【解答】解:连接,
,,,
,,
是等腰直角三角形,即,
,
.
故答案为:.
【点评】此题考查了锐角三角函数的定义、勾股定理以及勾股定理的逆定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.
17.(2025 旺苍县三模)如图,,,,均为网格图中的格点,线段与相交于点,则的正切值为 3 .
【答案】3.
【考点】解直角三角形
【专题】解直角三角形及其应用;运算能力
【分析】连接,,根据题意可得,从而可得,然后利用勾股定理的逆定理证明是直角三角形,最后根据锐角三角函数的定义,进行计算即可解答.
【解答】解:连接,,
由题意得:
,
,
由题意得:
,
,
,
,
是直角三角形,
,
的正切值为:3,
故答案为:3.
【点评】本题考查了解直角三角形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
18.(2025 徐汇区三模)一斜坡的坡角为,坡长比坡高多100米,那么斜坡的高为 米 (用的锐角三角比表示).
【考点】解直角三角形的应用坡度坡角问题
【专题】解直角三角形及其应用;应用意识
【分析】设斜坡的高为米,根据正弦的定义用表示出,根据题意列出方程,解方程得到答案.
【解答】解:设斜坡的高为米,
在△中,,
,
米,
由题意得:,
解得:,
故答案为:米.
【点评】本题考查的是解直角三角形的应用坡度坡角问题,熟记锐角三角函数的定义是解题的关键.
19.(2025 中山市一模)一个斜坡的坡度,若某人沿斜坡直线前进,则垂直高度上升了 .
【考点】:解直角三角形的应用坡度坡角问题
【分析】根据题意作出图形,由坡度定义可得位置升高的高度即为坡角所对的直角边.根据题意可得,,可解出直角边,即得到位置升高的高度.
【解答】解:由题意得,,
,
,
.
故答案为:.
【点评】本题主要考查坡度的定义以及解直角三角形的应用,注意画出示意图会使问题具体化.
20.(2025 广西模拟)图1为手机支架实物图,图2为它的侧面示意图,“型”托架用于放置手机,支架两端分别与托架和底座(其厚度忽略不计)相连,支架端可调节旋转角度,已知,,支架调整到图2位置时,,.因实际需要,现将支架端角度调整为,如图3所示,则点的位置较原来的位置上升高度为 .
【答案】.
【考点】解直角三角形的应用
【分析】如图2,过点作交于点,过点作交于点,过点作于点,如图3,延长交于点,在和中分别算出和,求出点到的距离,再在中,算出,,再作差即可求得.
【解答】解:如图2,过点作交于点,过点作交于点,过点作于点,如图3,延长交于点
旋转前如图
,,,
,
,,
,,
,
在和中,
,
,
故点到的距离为:,
旋转后如图
,
,
,
,
在中,
,
故,
点的位置较原来的位置上升高度为:,
故答案为:.
【点评】本题主要考查解直角三角形的实际应用,解答本题的关键是作出辅助线,构造直角三角形.
三.解答题(共5小题)
21.(2025 惠州二模)热气球的探测器显示,从热气球看一栋楼顶部的仰角是,看这栋楼底的俯角为,热气球与楼的水平距离为120米,这栋楼有多高?
【答案】这栋楼的高度约为米.
【考点】解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;应用意识
【分析】在直角三角形中和直角三角形中,根据锐角三角函数中的正切可以分别求得和的长,从而可以求得的长,本题得以解决.
【解答】解:如图,
由题意可得,
,,米,,
在中,,米,
(米,
在中,,米,
(米,
(米,
即这栋楼的高度约为米.
【点评】本题考查解直角三角形的应用仰角俯角问题,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
22.(2025 澄迈县模拟)如图,为了测量某建筑物的高度,小颖采用了如下的方法:先从与建筑物底端在同一水平线上的点出发,沿斜坡行走130米至坡顶处,再从处沿水平方向继续前行若干米后至点处,在点测得该建筑物顶端的仰角为,建筑物底端的俯角为,点、、、、在同一平面内,斜坡的坡度.根据小颖的测量数据,求建筑物的高度.(参考数据:
【答案】米.
【考点】解直角三角形的应用坡度坡角问题;解直角三角形的应用仰角俯角问题
【专题】等腰三角形与直角三角形;解直角三角形及其应用;运算能力;推理能力;应用意识
【分析】过作于,延长交于.则四边形是矩形,得,在中求出,再解直角三角形求出、的长,即可解决问题.
【解答】解:如图,过作于,延长交于.
则四边形是矩形,
,
在中,米,,
(米,
(米,
在中,,
是等腰直角三角形,
(米,
在中,,,
(米,
(米.
答:建筑物的高度为米.
【点评】本题考查了解直角三角形的应用—仰角俯角问题、坡度坡角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
23.(2025 重庆模拟)某动物园熊猫基地新诞生了一只小熊猫,吸引了大批游客前往观看.由于、之间的道路正在进行维护,暂时不能通行,游客由入口进入园区之后可步行到达点,然后可以选择乘坐空中缆车从,也可选择乘坐观光车从.已知点在点的北偏东方向上,点在点的正东方向,点在点的正东方向300米处,点在点的北偏东方向上,且米.(参考数据:,,
(1)求的长度(精确到个位);
(2)已知空中缆车的速度是每分钟200米,观光车的速度是每分钟320米,若游客想尽快到达熊猫基地,应选择乘坐空中缆车还是观光车?
【考点】勾股定理的应用;解直角三角形的应用方向角问题
【专题】解直角三角形及其应用;运算能力
【分析】(1)作于,于,推出四边形是矩形,得到,,求出(米,由锐角的正切定义求出的长,由是等腰直角三角形,得到,求出的长,即可解决问题;
(2)分别求出乘坐空中缆车,观光车所用的时间,即可判断.
【解答】解:(1)作于,于,
,
四边形是矩形,
,,
,
(米,
,
(米,
,
是等腰直角三角形,
(米,
(米,
(米;
(2)由勾股定理得到(米,
(米,
乘坐观光车的时间是(分钟),乘坐空中缆车的时间是(分钟),
应选择乘坐观光车.
【点评】本题考查解直角三角形的应用—方向角问题,勾股定理,关键是通过作辅助线构造直角三角形,应用三角函数定义来解决问题.
24.(2025 泰兴市三模)如图1是一款多功能可调节的桌面手机、平板支架.点、、处均可旋转,处可摆放平板或者手机.其中,,.研究表明,当手机与桌面的夹角为时,更符合人体工学设计,也是多数人操作手机最舒适的角度.
(1)如图2,当和桌面垂直且时,可将绕点旋转一定的角度,就能达到最舒适的观影状态,求此时的度数;
(2)在(1)的条件下求点到的距离(结果保留整数).(参考数据:,,.
【答案】(1)此时的度数为;
(2)点到的距离约为.
【考点】多边形内角与外角;解直角三角形的应用
【专题】解直角三角形及其应用;运算能力
【分析】(1)过点作于,根据题意可得:,,再根据垂直定义可得,然后利用四边形内角和定理进行计算,即可解答;
(2)过点作于,过点作于,根据垂直定义可得,再根据题意可得:,然后利用直角三角形的两个锐角互余可得,从而可得,进而可得,最后分别在和中,利用锐角三角函数的定义求出和的长,从而利用线段的和差关系进行计算即可解答.
【解答】解:(1)过点作于,
由题意得:,,
,
,
,
此时的度数为;
(2)过点作于,过点作于,
,
由题意得:,
,
,
,
,
,
在中,,
,
在中,,
,
,
答:点到的距离约为.
【点评】本题考查了解直角三角形的应用,多边形的内角与外角,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
25.(2025 淮安)拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形,的长度为,两节可调节的拉杆长度相等,且与在同一条直线上.如图1,当拉杆伸出一节时,与地面夹角;如图2,当拉杆伸出两节、时,与地面夹角,两种情况下拉杆把手点距离地面高度相同.求每节拉杆的长度.
(参考数据:,,,
【答案】每节拉杆的长度为.
【考点】解直角三角形的应用坡度坡角问题
【专题】运算能力;等腰三角形与直角三角形
【分析】根据题意,设设 ,分两种情况计算出和的长,利用建立方程,求出值即可.
【解答】解:如图1,作,垂足为,设 ,则,
,
,
如图2,作,垂足为,则,
,
,
,
,
解得:.
答:每节拉杆的长度为.
【点评】本题考查了解直角三角形的应用坡度坡角,熟练掌握解直角三角形是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
一.选择题(共10小题)
1.(2025 梅县区一模)在中,,,,则的度数为
A. B. C. D.
2.(2025 绥化模拟)在△中,,设,,所对的边分别为,,,则
A. B. C. D.
3.(2025 义乌市模拟)若是锐角,且,则
A. B. C. D.
4.(2025 邵阳模拟)放在正方形网格纸的位置如图,则的值为
A. B. C. D.
5.(2025 道里区模拟)如图,某数学兴趣小组测量一棵树的高度,在点处测得树顶的仰角为,在点处测得树顶的仰角为,且、、三点在同一直线上,若米,则这棵树的高度是
A.米 B.米 C.米 D.米
6.(2025 海珠区一模)如图,小乐和小静一起从点出发去拍摄木棉树.小乐沿着水平面步行到达点时拍到树顶点,仰角为;小静沿着坡度的斜坡步行到达点时拍到树顶点,仰角为,那么这棵木棉树的高度约 .(结果精确到(参考数据:,,
A.22 B.21 C.20 D.19
7.(2025 肇庆一模)在正方形网格中,如图放置,则的值为
A.2 B. C. D.
8.(2025 深圳)如图,为了测量某电子厂的高度,小明用高的测量仪测得顶端的仰角为,小军在小明的前面处用高的测量仪测得顶端的仰角为,则电子厂的高度为
(参考数据:,,
A. B. C. D.
9.(2025 垦利区二模)如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得,,,则点到的距离为
A. B. C. D.
10.(2025 丰南区校级二模)如图,小明在点处测得树的顶端仰角为,测得米,则树的高(单位:米)为
A. B. C. D.
二.填空题(共10小题)
11.(2025 新泰市三模)如图所示,某数学兴趣小组利用无人机测大楼的高度,无人机在空中点处,测得点距地面上点100米,点处俯角为,楼顶点处的俯角为,已知点与大楼的距离为80米(点,,,在同一平面内),则大楼的高度 米.(结果精确到0.1米,参考数据:.
12.(2025 东营区模拟)如图,已知公路上,两点之间的距离为20米,点在的南偏西的方向上,在的南偏西方向上,则点到公路的距离为 米.
13.(2025 江西)将图1所示的七巧板,拼成图2所示的四边形,连接,则 .
14.(2025 凉州区一模)已知为锐角.若,则 .
15.(2025 长沙一模)如图,是操场上直立的一根旗杆,旗杆上有一点,用测角仪(测角仪的高度忽略不计)测得地面上的点到点的仰角,到点的仰角,若米,则旗杆的高度 米.
16.(2025 揭东区一模)如图,是放置在正方形网格中的一个角,则的值是 .
17.(2025 旺苍县三模)如图,,,,均为网格图中的格点,线段与相交于点,则的正切值为 .
18.(2025 徐汇区三模)一斜坡的坡角为,坡长比坡高多100米,那么斜坡的高为 (用的锐角三角比表示).
19.(2025 中山市一模)一个斜坡的坡度,若某人沿斜坡直线前进,则垂直高度上升了 .
20.(2025 广西模拟)图1为手机支架实物图,图2为它的侧面示意图,“型”托架用于放置手机,支架两端分别与托架和底座(其厚度忽略不计)相连,支架端可调节旋转角度,已知,,支架调整到图2位置时,,.因实际需要,现将支架端角度调整为,如图3所示,则点的位置较原来的位置上升高度为 .
三.解答题(共5小题)
21.(2025 惠州二模)热气球的探测器显示,从热气球看一栋楼顶部的仰角是,看这栋楼底的俯角为,热气球与楼的水平距离为120米,这栋楼有多高?
22.(2025 澄迈县模拟)如图,为了测量某建筑物的高度,小颖采用了如下的方法:先从与建筑物底端在同一水平线上的点出发,沿斜坡行走130米至坡顶处,再从处沿水平方向继续前行若干米后至点处,在点测得该建筑物顶端的仰角为,建筑物底端的俯角为,点、、、、在同一平面内,斜坡的坡度.根据小颖的测量数据,求建筑物的高度.(参考数据:
23.(2025 重庆模拟)某动物园熊猫基地新诞生了一只小熊猫,吸引了大批游客前往观看.由于、之间的道路正在进行维护,暂时不能通行,游客由入口进入园区之后可步行到达点,然后可以选择乘坐空中缆车从,也可选择乘坐观光车从.已知点在点的北偏东方向上,点在点的正东方向,点在点的正东方向300米处,点在点的北偏东方向上,且米.(参考数据:,,
(1)求的长度(精确到个位);
(2)已知空中缆车的速度是每分钟200米,观光车的速度是每分钟320米,若游客想尽快到达熊猫基地,应选择乘坐空中缆车还是观光车?
24.(2025 泰兴市三模)如图1是一款多功能可调节的桌面手机、平板支架.点、、处均可旋转,处可摆放平板或者手机.其中,,.研究表明,当手机与桌面的夹角为时,更符合人体工学设计,也是多数人操作手机最舒适的角度.
(1)如图2,当和桌面垂直且时,可将绕点旋转一定的角度,就能达到最舒适的观影状态,求此时的度数;
(2)在(1)的条件下求点到的距离(结果保留整数).(参考数据:,,.
25.(2025 淮安)拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形,的长度为,两节可调节的拉杆长度相等,且与在同一条直线上.如图1,当拉杆伸出一节时,与地面夹角;如图2,当拉杆伸出两节、时,与地面夹角,两种情况下拉杆把手点距离地面高度相同.求每节拉杆的长度.
(参考数据:,,,
中考数学一轮复习 锐角三角函数
参考答案与试题解析
一.选择题(共10小题)
1.(2025 梅县区一模)在中,,,,则的度数为
A. B. C. D.
【答案】
【考点】特殊角的三角函数值
【专题】解直角三角形及其应用
【分析】直接利用已知画出直角三角形,再利用锐角三角函数关系得出答案.
【解答】解:,,,
,
.
故选:.
【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.
2.(2025 绥化模拟)在△中,,设,,所对的边分别为,,,则
A. B. C. D.
【答案】
【考点】锐角三角函数的定义
【专题】运算能力;解直角三角形及其应用
【分析】根据正弦、正切的定义计算,判断即可.
【解答】解:、,
则,本选项说法错误;
、,本选项说法正确;
、,
则,本选项说法错误;
、,本选项说法错误;
故选:.
【点评】本题考查的是锐角三角函数的定义,掌握正弦、正切的定义是解题的关键.
3.(2025 义乌市模拟)若是锐角,且,则
A. B. C. D.
【答案】
【考点】锐角三角函数的增减性
【专题】等腰三角形与直角三角形;数感
【分析】正弦值随着角度的增大(或减小)而增大(或减小),据此可得结论.
【解答】解:是锐角,且,
,
故选:.
【点评】本题主要考查了锐角三角函数的增减性,正弦值随着角度的增大(或减小)而增大(或减小).
4.(2025 邵阳模拟)放在正方形网格纸的位置如图,则的值为
A. B. C. D.
【答案】
【考点】勾股定理;勾股定理的逆定理;锐角三角函数的定义
【分析】连接,再利用勾股定理分别计算出、、的长,然后再根据勾股定理逆定理证明,再利用三角函数定义可得答案.
【解答】解:连接,如图:
,,,
,
.
故选:.
【点评】此题主要考查了勾股定理,勾股定理逆定理,以及锐角三角函数定义,关键是证明.
5.(2025 道里区模拟)如图,某数学兴趣小组测量一棵树的高度,在点处测得树顶的仰角为,在点处测得树顶的仰角为,且、、三点在同一直线上,若米,则这棵树的高度是
A.米 B.米 C.米 D.米
【答案】
【考点】解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;运算能力;推理能力
【分析】根据题意可得:,设米,然后在中,利用锐角三角函数的定义求出的长,再在中,利用锐角三角函数的定义求出的长,然后根据,列出关于的方程,进行计算即可解答.
【解答】解:由题意得:,
设米,
在中,,
(米,
在中,,,
(米,
,
,
解得,
(米,
这棵树的高度约为米.
故选:.
【点评】本题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
6.(2025 海珠区一模)如图,小乐和小静一起从点出发去拍摄木棉树.小乐沿着水平面步行到达点时拍到树顶点,仰角为;小静沿着坡度的斜坡步行到达点时拍到树顶点,仰角为,那么这棵木棉树的高度约 .(结果精确到(参考数据:,,
A.22 B.21 C.20 D.19
【答案】
【考点】解直角三角形的应用坡度坡角问题;解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;运算能力
【分析】过点作,垂足为,过点作,垂足为,根据题意可得:,,米,再根据已知可设米,则米,然后在△中,利用勾股定理进行计算可得米,米,最后设米,则米,分别在△和△中,利用锐角三角函数的定义求出和的长,从而列出关于的方程进行计算,即可解答.
【解答】解:过点作,垂足为,过点作,垂足为,
由题意得:,,米,
斜坡的坡度,
,
设米,则米,
在△中,(米,
米,
,
解得:,
米,米,
设米,
米,
在△中,,
米,
在△中,,
米,
,
,
解得:,
(米,
这棵木棉树的高度约为20米,
故选:.
【点评】本题考查了解直角三角形的应用仰角俯角问题,坡度坡角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
7.(2025 肇庆一模)在正方形网格中,如图放置,则的值为
A.2 B. C. D.
【答案】
【考点】锐角三角函数的定义
【专题】等腰三角形与直角三角形
【分析】根据图形找出角的两边经过的格点以及点组成的直角三角形,然后根据锐角的正切等于对边比邻边解答.
【解答】解:如图,.
故选.
【点评】本题考查了锐角三角函数的定义,熟练掌握网格结构找出直角三角形是解题的关键.
8.(2025 深圳)如图,为了测量某电子厂的高度,小明用高的测量仪测得顶端的仰角为,小军在小明的前面处用高的测量仪测得顶端的仰角为,则电子厂的高度为
(参考数据:,,
A. B. C. D.
【答案】
【考点】解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;运算能力
【分析】根据题意可得:,,,,,,,然后设 ,则,分别在△和△中,利用锐角三角函数的定义求出和的长,从而列出关于的方程,进行计算即可解答.
【解答】解:由题意得:,,,,,,,
设 ,
,
在△中,,
,
在△中,,
,
,
,
解得:,
,
,
电子厂的高度约为,
故选:.
【点评】本题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
9.(2025 垦利区二模)如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得,,,则点到的距离为
A. B. C. D.
【答案】
【考点】解直角三角形的应用
【专题】解直角三角形及其应用;应用意识
【分析】先求出,再用三角函数定义,求出,即可得出答案.
【解答】解:过点作于点,如图所示:
,,
,
在中,,
点到的距离为,故正确.
故选:.
【点评】本题主要考查了三角形内角和定理的应用,三角函数的应用,点到直线的距离,解题的关键是熟练掌握三角函数的定义.
10.(2025 丰南区校级二模)如图,小明在点处测得树的顶端仰角为,测得米,则树的高(单位:米)为
A. B. C. D.
【答案】
【考点】解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;运算能力
【分析】根据题意可得:,,然后在中,利用锐角三角函数的定义进行计算即可解答.
【解答】解:由题意得:
,,
在中,米,
(米,
故选:.
【点评】本题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解题的关键.
二.填空题(共10小题)
11.(2025 新泰市三模)如图所示,某数学兴趣小组利用无人机测大楼的高度,无人机在空中点处,测得点距地面上点100米,点处俯角为,楼顶点处的俯角为,已知点与大楼的距离为80米(点,,,在同一平面内),则大楼的高度 69.3 米.(结果精确到0.1米,参考数据:.
【答案】69.3.
【考点】解直角三角形的应用仰角俯角问题
【专题】应用意识;解直角三角形及其应用
【分析】过作于,过作于,而,则四边形是矩形,先解,求出,,得到的长度,再解,得到的长即可解决问题.
【解答】解:如图所示:
过作于,过作于,而,
则四边形是矩形,
,,
由题意可得:米,,,米,
(米,(米,
(米,
(米,
(米,
大楼的高度约为69.3米.
故答案为:69.3.
【点评】本题考查的是解直角三角形的应用仰角俯角问题,矩形的判定与性质,理解仰角与俯角的含义是解本题的关键.
12.(2025 东营区模拟)如图,已知公路上,两点之间的距离为20米,点在的南偏西的方向上,在的南偏西方向上,则点到公路的距离为 米.
【答案】.
【考点】解直角三角形的应用方向角问题
【专题】运算能力;推理能力;应用意识;等腰三角形与直角三角形;解直角三角形及其应用
【分析】过点作公路于点,证,得米,再在中,根据计算求得的长即可.
【解答】解:如图,过点作公路于点,
则,,,米,
,,
,
米,
在中,,
(米,
故答案为:.
【点评】本题主要考查了解直角三角形的应用、等腰三角形的判定等知识,正确作出辅助线构造直角三角形是解决问题的关键.
13.(2025 江西)将图1所示的七巧板,拼成图2所示的四边形,连接,则 .
【答案】.
【考点】七巧板;平行四边形的判定与性质;解直角三角形
【专题】解直角三角形及其应用;运算能力
【分析】根据所给拼图,得出四边形是平行四边形,根据平行四边形的性质及正切的定义即可解决问题.
【解答】解:令与的交点为,
,
,
又,
四边形是平行四边形,
与互相平分,
.
,
.
在中,
.
故答案为:.
【点评】本题考查解直角三角形、七巧板及平行四边形的判定与性质,能根据所拼图形得出四边形是平行四边形及熟知正切的定义是解题的关键.
14.(2025 凉州区一模)已知为锐角.若,则 60 .
【答案】60.
【考点】特殊角的三角函数值
【专题】等腰三角形与直角三角形;运算能力
【分析】根据特殊角的三角函数值计算.
【解答】解:,
.
故答案为:60.
【点评】本题考查特殊角三角函数值,熟记各特殊角三角函数值是解题的关键.
15.(2025 长沙一模)如图,是操场上直立的一根旗杆,旗杆上有一点,用测角仪(测角仪的高度忽略不计)测得地面上的点到点的仰角,到点的仰角,若米,则旗杆的高度 米.
【答案】.
【考点】解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;运算能力
【分析】在中,根据,求出米,在中,根据即可求出的高度.
【解答】解:在中,
,
米,
在中,
,
(米.
故答案为:.
【点评】本题考查了解直角三角形的应用,解题的关键是根据仰角构造直角三角形,解直角三角形,难度一般.
16.(2025 揭东区一模)如图,是放置在正方形网格中的一个角,则的值是 .
【考点】三角形的面积;勾股定理;锐角三角函数的定义
【分析】首先连接,由勾股定理易求得,,,然后由勾股定理的逆定理,可证得是等腰直角三角形,继而可求得的值.
【解答】解:连接,
,,,
,,
是等腰直角三角形,即,
,
.
故答案为:.
【点评】此题考查了锐角三角函数的定义、勾股定理以及勾股定理的逆定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.
17.(2025 旺苍县三模)如图,,,,均为网格图中的格点,线段与相交于点,则的正切值为 3 .
【答案】3.
【考点】解直角三角形
【专题】解直角三角形及其应用;运算能力
【分析】连接,,根据题意可得,从而可得,然后利用勾股定理的逆定理证明是直角三角形,最后根据锐角三角函数的定义,进行计算即可解答.
【解答】解:连接,,
由题意得:
,
,
由题意得:
,
,
,
,
是直角三角形,
,
的正切值为:3,
故答案为:3.
【点评】本题考查了解直角三角形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
18.(2025 徐汇区三模)一斜坡的坡角为,坡长比坡高多100米,那么斜坡的高为 米 (用的锐角三角比表示).
【考点】解直角三角形的应用坡度坡角问题
【专题】解直角三角形及其应用;应用意识
【分析】设斜坡的高为米,根据正弦的定义用表示出,根据题意列出方程,解方程得到答案.
【解答】解:设斜坡的高为米,
在△中,,
,
米,
由题意得:,
解得:,
故答案为:米.
【点评】本题考查的是解直角三角形的应用坡度坡角问题,熟记锐角三角函数的定义是解题的关键.
19.(2025 中山市一模)一个斜坡的坡度,若某人沿斜坡直线前进,则垂直高度上升了 .
【考点】:解直角三角形的应用坡度坡角问题
【分析】根据题意作出图形,由坡度定义可得位置升高的高度即为坡角所对的直角边.根据题意可得,,可解出直角边,即得到位置升高的高度.
【解答】解:由题意得,,
,
,
.
故答案为:.
【点评】本题主要考查坡度的定义以及解直角三角形的应用,注意画出示意图会使问题具体化.
20.(2025 广西模拟)图1为手机支架实物图,图2为它的侧面示意图,“型”托架用于放置手机,支架两端分别与托架和底座(其厚度忽略不计)相连,支架端可调节旋转角度,已知,,支架调整到图2位置时,,.因实际需要,现将支架端角度调整为,如图3所示,则点的位置较原来的位置上升高度为 .
【答案】.
【考点】解直角三角形的应用
【分析】如图2,过点作交于点,过点作交于点,过点作于点,如图3,延长交于点,在和中分别算出和,求出点到的距离,再在中,算出,,再作差即可求得.
【解答】解:如图2,过点作交于点,过点作交于点,过点作于点,如图3,延长交于点
旋转前如图
,,,
,
,,
,,
,
在和中,
,
,
故点到的距离为:,
旋转后如图
,
,
,
,
在中,
,
故,
点的位置较原来的位置上升高度为:,
故答案为:.
【点评】本题主要考查解直角三角形的实际应用,解答本题的关键是作出辅助线,构造直角三角形.
三.解答题(共5小题)
21.(2025 惠州二模)热气球的探测器显示,从热气球看一栋楼顶部的仰角是,看这栋楼底的俯角为,热气球与楼的水平距离为120米,这栋楼有多高?
【答案】这栋楼的高度约为米.
【考点】解直角三角形的应用仰角俯角问题
【专题】解直角三角形及其应用;应用意识
【分析】在直角三角形中和直角三角形中,根据锐角三角函数中的正切可以分别求得和的长,从而可以求得的长,本题得以解决.
【解答】解:如图,
由题意可得,
,,米,,
在中,,米,
(米,
在中,,米,
(米,
(米,
即这栋楼的高度约为米.
【点评】本题考查解直角三角形的应用仰角俯角问题,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
22.(2025 澄迈县模拟)如图,为了测量某建筑物的高度,小颖采用了如下的方法:先从与建筑物底端在同一水平线上的点出发,沿斜坡行走130米至坡顶处,再从处沿水平方向继续前行若干米后至点处,在点测得该建筑物顶端的仰角为,建筑物底端的俯角为,点、、、、在同一平面内,斜坡的坡度.根据小颖的测量数据,求建筑物的高度.(参考数据:
【答案】米.
【考点】解直角三角形的应用坡度坡角问题;解直角三角形的应用仰角俯角问题
【专题】等腰三角形与直角三角形;解直角三角形及其应用;运算能力;推理能力;应用意识
【分析】过作于,延长交于.则四边形是矩形,得,在中求出,再解直角三角形求出、的长,即可解决问题.
【解答】解:如图,过作于,延长交于.
则四边形是矩形,
,
在中,米,,
(米,
(米,
在中,,
是等腰直角三角形,
(米,
在中,,,
(米,
(米.
答:建筑物的高度为米.
【点评】本题考查了解直角三角形的应用—仰角俯角问题、坡度坡角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
23.(2025 重庆模拟)某动物园熊猫基地新诞生了一只小熊猫,吸引了大批游客前往观看.由于、之间的道路正在进行维护,暂时不能通行,游客由入口进入园区之后可步行到达点,然后可以选择乘坐空中缆车从,也可选择乘坐观光车从.已知点在点的北偏东方向上,点在点的正东方向,点在点的正东方向300米处,点在点的北偏东方向上,且米.(参考数据:,,
(1)求的长度(精确到个位);
(2)已知空中缆车的速度是每分钟200米,观光车的速度是每分钟320米,若游客想尽快到达熊猫基地,应选择乘坐空中缆车还是观光车?
【考点】勾股定理的应用;解直角三角形的应用方向角问题
【专题】解直角三角形及其应用;运算能力
【分析】(1)作于,于,推出四边形是矩形,得到,,求出(米,由锐角的正切定义求出的长,由是等腰直角三角形,得到,求出的长,即可解决问题;
(2)分别求出乘坐空中缆车,观光车所用的时间,即可判断.
【解答】解:(1)作于,于,
,
四边形是矩形,
,,
,
(米,
,
(米,
,
是等腰直角三角形,
(米,
(米,
(米;
(2)由勾股定理得到(米,
(米,
乘坐观光车的时间是(分钟),乘坐空中缆车的时间是(分钟),
应选择乘坐观光车.
【点评】本题考查解直角三角形的应用—方向角问题,勾股定理,关键是通过作辅助线构造直角三角形,应用三角函数定义来解决问题.
24.(2025 泰兴市三模)如图1是一款多功能可调节的桌面手机、平板支架.点、、处均可旋转,处可摆放平板或者手机.其中,,.研究表明,当手机与桌面的夹角为时,更符合人体工学设计,也是多数人操作手机最舒适的角度.
(1)如图2,当和桌面垂直且时,可将绕点旋转一定的角度,就能达到最舒适的观影状态,求此时的度数;
(2)在(1)的条件下求点到的距离(结果保留整数).(参考数据:,,.
【答案】(1)此时的度数为;
(2)点到的距离约为.
【考点】多边形内角与外角;解直角三角形的应用
【专题】解直角三角形及其应用;运算能力
【分析】(1)过点作于,根据题意可得:,,再根据垂直定义可得,然后利用四边形内角和定理进行计算,即可解答;
(2)过点作于,过点作于,根据垂直定义可得,再根据题意可得:,然后利用直角三角形的两个锐角互余可得,从而可得,进而可得,最后分别在和中,利用锐角三角函数的定义求出和的长,从而利用线段的和差关系进行计算即可解答.
【解答】解:(1)过点作于,
由题意得:,,
,
,
,
此时的度数为;
(2)过点作于,过点作于,
,
由题意得:,
,
,
,
,
,
在中,,
,
在中,,
,
,
答:点到的距离约为.
【点评】本题考查了解直角三角形的应用,多边形的内角与外角,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
25.(2025 淮安)拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形,的长度为,两节可调节的拉杆长度相等,且与在同一条直线上.如图1,当拉杆伸出一节时,与地面夹角;如图2,当拉杆伸出两节、时,与地面夹角,两种情况下拉杆把手点距离地面高度相同.求每节拉杆的长度.
(参考数据:,,,
【答案】每节拉杆的长度为.
【考点】解直角三角形的应用坡度坡角问题
【专题】运算能力;等腰三角形与直角三角形
【分析】根据题意,设设 ,分两种情况计算出和的长,利用建立方程,求出值即可.
【解答】解:如图1,作,垂足为,设 ,则,
,
,
如图2,作,垂足为,则,
,
,
,
,
解得:.
答:每节拉杆的长度为.
【点评】本题考查了解直角三角形的应用坡度坡角,熟练掌握解直角三角形是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
