第1章《三角形》章节测试卷(含答案)苏科版八年级数学上册
文档属性
| 名称 | 第1章《三角形》章节测试卷(含答案)苏科版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 836.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-05 23:59:02 | ||
图片预览




文档简介
第1章《三角形》章节测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.如图,小深在池塘一侧选取了点,测得,,那么池塘两岸,间的距离可能是( ).
A.9 B.8 C.5 D.2
2.如图,已知,补充下列条件中的一个后,仍不能判定的是( )
A. B. C. D.
3.如图,以△ABC的一边为公共边,向外作与△ABC全等的三角形,可以作( )个
A.3 B.4 C.6 D.9
4.如图,在中,,,平分,点P为线段AD上一点,过点P作交的延长线于点E,则的度数为( )
A. B. C. D.
5.如图,正方形的边长为1,、上各有一点P、Q,如果的周长为2,则的度数为( )
A. B. C. D.
6.如图,是边长为3的等边三角形,点Q是边上一点,于点D,点E为边延长线上一点,且满足,连接交于点F,则的长为( )
A. B. C.1 D.
7.如图,在四边形中,是的平分线,且.若,则四边形的周长为( )
A. B. C. D.
8.如图,D、E分别是边上的点,,,设的面积为,的面积为,若,则( )
A.3 B.2 C. D.4
9.一副三角尺如图放置,为中点,将绕点旋转,边分别与边分别交于点,若,则阴影部分面积为( )
A. B. C. D.
10.如图,点为线段上一动点(不与点、重合),在同侧分别作等边和等边,与交于点,与交于点,与交于点,连接、,以下结论:①;②为等边三角形;③;④平分;正确的有( )个
A.1 B.2 C.3 D.4
二.填空题(共6小题,满分18分,每小题3分)
11.如图,是的边上的中线,是的边上的中线,是的边上的中线,连接,.若的面积是,则阴影部分的面积是 .
12.如图所示,线段,射线于点A,点C是射线上一动点,分别以为直角边作等腰直角三角形,得与中,连接交射线于点M,则的长为 .
13.如图,于点,射线于点B,一动点E从A点出发以2个单位/秒的速度沿射线运动,点D为射线上一动点,随着E点运动而运动,且始终保持,若点E经过t秒与全等,则t的值为 秒.
14.如图,在中,,,D为线段上一动点不与点B,C重合,连接,作,交线段于
(1)当D为中点时, °;
(2)当时, °
15.如图,在等腰三角形中,,点,在等腰三角形的内部,连接,使,且平分.若,则 .
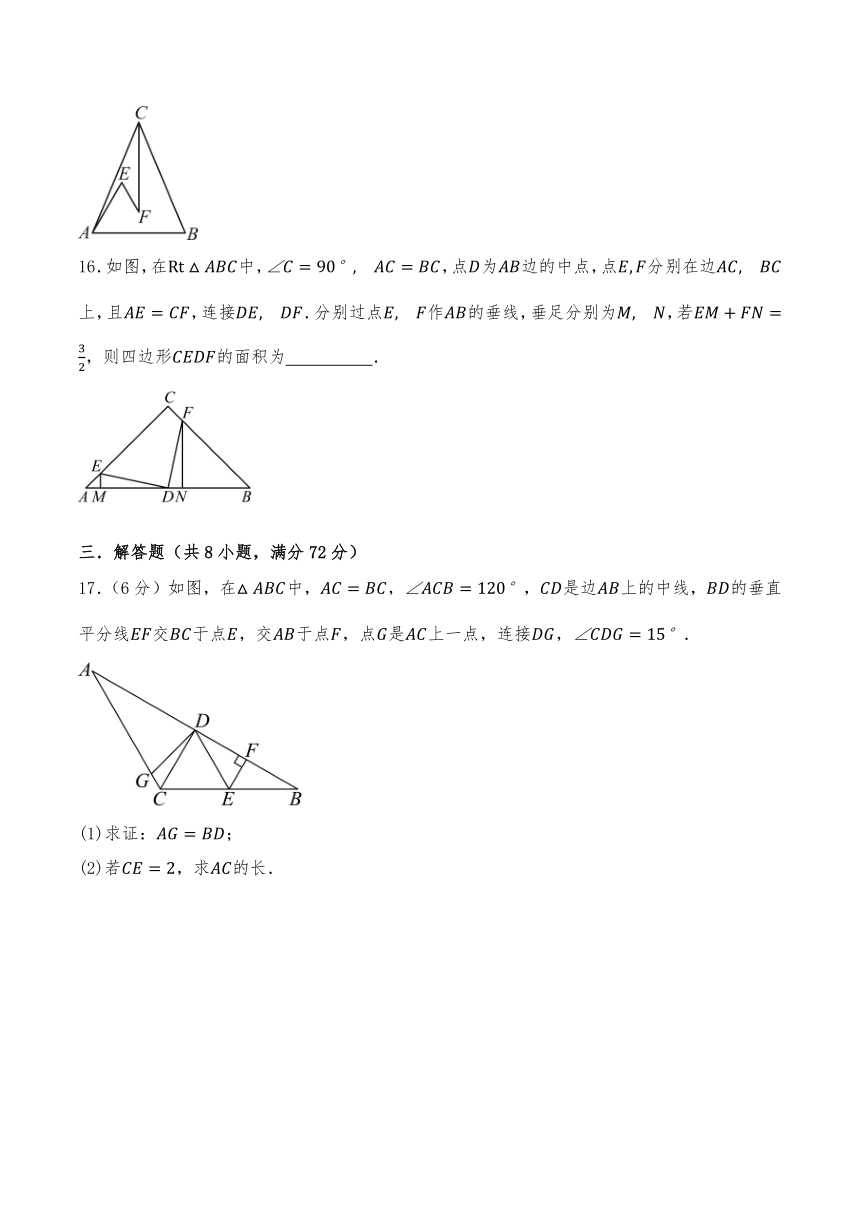
16.如图,在中,,点为边的中点,点分别在边上,且,连接.分别过点作的垂线,垂足分别为,若,则四边形的面积为 .
三.解答题(共8小题,满分72分)
17.(6分)如图,在中,,,是边上的中线,的垂直平分线交于点,交于点,点是上一点,连接,.
(1)求证:;
(2)若,求的长.
18.(6分)把三角形纸片沿折叠.
(1)如图1,点落在四边形内部点A处时,与之间有一种数量关系始终保持不变,写出这种关系并证明;
(2)如图2,点落在四边形外部点A处时,直接写出与之间的数量关系.
19.(8分)如图,为的中线,为的中线.
(1)已知,的周长为,求的周长;
(2)在中作边上的高;
(3)若的面积为40,,则点到边的距离为多少?
20.(8分)如图,等边三角形纸片中,点在边(不包含端点,)上运动,连接,将对折,点落在直线上的点处,得到折痕;将对折,点落在直线上的点处,得到折痕.
(1)若,求的度数;
(2)试问:的大小是否会随着点的运动而变化?若不变,求出的度数;若变化,请说明理由.
21.(10分)如图,四边形中,,平分,,交于点.
(1)如图1,若,
①求证:;
②作平分,如图2,求证:.
(2)如图3,作平分,在锐角内部作射线,交于,若的大小为,试说明:平分.
22.(10分)【特例感知】
如图1,在中,,求边上的中线的取值范围.
(1)中线的取值范围是______.
【类比迁移】
(2)如图2,在四边形中,为的中点,点在上,,,求证:平分.
【拓展应用】
(3)如图3,在中,是边上的中线,E是上一点,连接并延长交于点F,,求证:.
23.(12分)【问题处理】
(1)如图1,为等腰三角形,,为边上的一点,连接,以为边作,.过点作交于,若,求证:.
【拓展提升】
(2)如图2,某家具厂制作等边三角形木质装饰框架,边上有一个预先开槽的固定节点(用于拼接),工人在边安装滑动定位块,并以为边加工等边三角形木片,最后连接加固.为计算木料长度,现需探究(定位块到端点的距离)、(固定节点到端点的距离)、(加固边)的数量关系,请你帮助工匠找出,,之间的数量关系,并说明理由.
24.(12分)(24-25七年级下·河南郑州·期中)【材料阅读】小芳在学习完全等三角形后,她尝试用三种不同方式摆放一副三角板.如图:在中,,;在中,,,并提出了相应的问题.
【发现】如图1,将两个三角板互不重叠地摆放在一起,当顶点摆放在线段上时,过点作,垂足为,过点作,垂足为.
(1)图1中,,,求的长.请补充小芳的过程.
,
,
∵,,
,,
,
,
……
(补充小芳的过程)
(2)【类比】如图2,将两个三角板叠放在一起,当顶点在线段上且顶点在线段上时,过点作,垂足为,猜想,,之间的数量关系,并说明理由.
(3)【拓展】如图3,将两个三角板叠放在一起,当顶点在线段上且顶点在线段上时,若,,连接,请直接写出的面积.
参考答案
一.选择题
1.C
【分析】本题考查了三角形的三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边的知识,掌握以上知识是解答本题的关键;
本题根据三角形的三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边的知识,进行作答,即可求解;
【详解】解:根据三角形的三边关系可得:,
即,
逐一核对选项,只有选项C符合,
故选:C
2.B
【分析】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.由全等三角形的判定方法:、、、、,逐一选项分析即可.
【详解】解:A、由能判定,本选项不符合题意;
B、和分别是、的对角,不能判定,本选项符合题意;
C、由能判定,本选项不符合题意;
D、由能判定,本选项不符合题意;
故选B.
3.C
【分析】根据三条边分别对应相等的两个三角形全等,据此进行作图即可得到答案.
【详解】解:根据题意可以作出的三角形如下图所示:
△BAE ≌△ABC △DCB ≌△ABC △CFA ≌△ABC
△ABG ≌△ABC △IBC ≌△ABC △AHC ≌△ABC
故选C.
4.B
【分析】本题主要考查了三角形内角和定理,角平分线的定义,解答的关键是结合图形分析清楚角与角之间的关系.
先根据三角形的内角和定理求得的度数,再根据角平分线的定义求得的度数,从而根据三角形外角的性质即可求出度数,进一步求得的度数.
【详解】解:∵,,
∴,
∵平分,
∴,
∴,
∵,
∴.
故选:B.
5.B
【分析】本题考查了全等三角形的判定与性质,正方形的性质,首先从的周长入手求出,延长至,使,连接,然后利用全等来解.
【详解】解:如图所示,延长至,使,连接,
的周长为2,即,
∵正方形的边长是1,
∴,,,
,
,
在和中,
,
∴,
,,
∴,
,
,
∴,
在与中,,,,
∴,
.
故选:B.
6.A
【分析】本题考查了等边三角形的性质、全等三角形的性质与判定,熟练掌握以上知识点,添加适当的辅助线构造全等三角形是解题的关键.作交的延长线于点,利用全等三角形判定证出,得到,,再证出,得到,再利用线段和差即可求出的长.
【详解】解:作交的延长线于点,
是边长为3的等边三角形,
,,
,
,
,,
,
又,
,
,,
又,,
,
,
.
故选:A.
7.B
【分析】在线段AC上作AF=AB,证明△AEF≌△AEB可得∠AFE=∠B,∠AEF=∠AEB,再证明△CEF≌△CED可得CD=CF,即可求得四边形的周长.
【详解】解:在线段AC上作AF=AB,
∵AE是的平分线,
∴∠CAE=∠BAE,
又∵AE=AE,
∴△AEF≌△AEB(SAS),
∴∠AFE=∠B,∠AEF=∠AEB,
∵AB∥CD,
∴∠D+∠B=180°,
∵∠AFE+∠CFE=180°,
∴∠D=∠CFE,
∵,
∴∠AEF+∠CEF=90°,∠AEB+∠CED=90°,
∴∠CEF=∠CED,
在△CEF和△CED中
∵,
∴△CEF≌△CED(AAS)
∴CD=CF,
∴四边形的周长=AC+AB+BD+CD=AC+AF+CF+BD=2AC+BD=,
故选:B.
8.D
【分析】本题主要考查了三角形的面积、三角形的中线等知识点,能灵活运用三角形的中线以及等分线求面积成为解题的关键.
由、、可以求出的面积和的面积,再结合图形可得即可解答.
【详解】解:∵,
,
∵,
,
∵,
∴,,
,
.
故选:D.
9.A
【分析】本题考查了等腰直角三角形的性质,余角性质,全等三角形的判定和性质等,连接,由等腰三角形的性质可得,,,进而由余角性质得,即得,即可得,得到,利用中线性质求出即可求解,正确作出辅助线是解题的关键.
【详解】解:连接,如图,
∵是等腰直角三角形,点是斜边的中点,
∴,,,
∴,
即,
又∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
故选:.
10.D
【分析】由和等边是正三角形,其性质得三边相等,三个角为,平角的定义和角的和差得,边角边证明,其性质得结论①正确;根据等边三角形的判定得是等边三角形,结论②正确;根据全等三角形的性质和三角形内角和定理即可得结论③正确;角角边证明,其性质和角平分线性质定理的逆定理求出点在的平分线上,结论④正确.
【详解】解:∵和是正三角形,
,
又 ∵,
,
在和中,
,
,
,
∴结论①正确;
,
,
又,
,
在和中,
,
,
,
是等边三角形,故②正确;
,
,
又,,,
,
,结论③正确;
过点分别作于点、两点,如图2所示:
,
,
在和中,
,
,
,
又 ∵在的内部,
∴点在的平分线上,
∴结论④正确;
综合所述,共有 4个结论正确.
故选:D.
二.填空题
11.
【分析】此题考查了三角形中线的性质,利用中线等分三角形的面积进行求解即可,解题的关键是熟练掌握三角形中线的性质及其应用.
【详解】解:∵是的边上的中线,
∴,
∵是的边上的中线,即有是的边上的中线,
∴,,
∴,
∵是的边上的中线,即有是的边上的中线,
∴,
∴,
∴阴影部分的面积是,
故答案为:.
12.
【分析】本题考查全等三角形的判定和性质、等腰直角三角形的性质,解题的关键是添加辅助线构造全等三角形:
如图作于H,由得,再证明得,即可解决问题.
【详解】解:如图作于H,
∵,
∴,
∵,,
∴,
∵和都是等腰三角形,
∴,,
在和中,
,
∴,
∴,,
在和中,
,
∴,
∴,
∴.
故答案为:.
13.或或
【分析】本题考查去啊能三角形的判定和性质,解题的关键是根据题意确定点的位置.
根据运动过程和三角形全等,分类讨论,确定点的位置,从而可得运动路程,除以运动速度,即可得运动时间.
【详解】解:根据题意,进行分类讨论如下:
当点在线段上,时,,
∴,
∵,
∴,
∵,
∴,
∵点的运动速度为个单位/秒,
∴运动时间(秒);
当点在延长线上,时,,
∴,
∵,
∴,
∵,
∴,
∵点的运动速度为个单位/秒,
∴运动时间(秒);
当点在延长线上,时,,
∴,
∵,
∴,
∵点的运动速度为个单位/秒,
∴运动时间(秒)
∴的值为或或,
故答案为:或或.
14.
【分析】(1)根据等腰三角形性质得,,再根据得,然后根据三角形外角性质即可得出的度数;
(2)设,根据三角形外角性质得,由此得,再求出,则,再由三角形外角性质得,证明和中全等得,则,进而得,由此解出继而可得出的度数.
此题主要考查了等腰三角形的性质,全等三角形的判定和性质,理解等腰三角形的性质,熟练掌握全等三角形的判定和性质,灵活运用三角形的内角和定理,三角形的外角性质进行角的计算是解决问题的关键.
【详解】解:(1)当D为中点时,如图1所示:
在中,,,
,
为中点,
,
,
,
,
是的外角,
,
故答案为:90;
(2)当时,如图2所示:
设,
是的外角,
,
又,,
,
,
在中,,,
,
,
,
是的外角,
,
在和中,
,
∴,
,
,
,
解得:,
故答案为:
15.
【分析】本题考查了等腰三角形的性质,等边三角形的判定与性质,直角三角形的性质,解题关键是添加辅助线,能洞察到特殊角在求边长中的用法.
延长交于点,延长交于点,可得是等边三角形,,进而知,然后可得,再利用等腰三角形的性质可得,,从而可得,进而在中,利用含30度角直角三角形的性质可得,据此进行计算即可解答.
【详解】解:如图,延长交于点,延长交于点,
∵,
∴是等边三角形,,
∴,
∵,
∴,
∵,平分,
∴,,
∴,
∴,
∴,
∴.
故答案为:.
16.
【分析】本题考查了等腰三角形的判定与性质,全等三角形的判定与性质,正确掌握相关性质内容是解题的关键.先得出是等腰直角三角形,结合三线合一得,,则都是等腰直角三角形,再通过证明,则,再通过证明,即可作答.
【详解】解:连接,如图所示:
∵,
∴是等腰直角三角形,
∴,
∵点为边的中点,
∴,,
∴都是等腰直角三角形,
∴,,
则,
∴,
∴,,,
∵分别过点作的垂线,垂足分别为,
∴,
∴,是等腰三角形,
∴
∵
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
即,
∴.
∵,
∴四边形的面积
即四边形的面积为
故答案为:
三.解答题
17.(1)证明:在中,,,
∴,
∵是边上的中线,
∴,,,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
(2)解:∵是线段的垂直平分线,
∴,,
∴,
∴,
∵,
∴,
∴,
∴是等边三角形,
∴,
∴,
∴,
∴.
18.(1)解:.
证明:∵三角形纸片沿折叠得到,
∴,,
∴,,
又∵,
∴,
∴;
(2)解:∵三角形纸片沿折叠得到,
∴,,
∴,,
又∵,
∴,
∴.
19.(1)解: 为的中线,
,
,
,
的周长,
,
的周长;
(2)解:如图,即为中边上的高,
(3)解:设点到边的距离为
为的中线, 为的中线,
,
,
,
,
点到边的距离为.
20.(1)解:∵将对折,得到折痕,
∴,
∵将对折,得到折痕,
∴,
∵,
∴,
∴.
(2)解:不变.理由如下:
∵,,,
∴,
即.
∴的大小不随点的运动而变化.
21.(1)①∵,,
∴.
∵,
∴.
②∵平分,
∴.
∵平分,
∴.
∴.
∵,
∴.
∴.
∴.
(2)延长,交于点,如图所示:
∵,
∴.
∴.
∵平分,
∴.
∵平分,
∴.
∵,
∴.
∴.
∴.
∴平分.
22.(1)解:如图1,延长到点,使得,连接.
为边上的中线,
,
在和中,
,
,
,
,
,
即,
;
故答案为:;
(2)证明:如图2,延长交的延长线于点,
,
,
,,
为的中点,
,
,
,,
,
,
即,
平分;
(3)证明:如图3,延长到点,使,连接,
在和中, ,
,
,,
,
,
,
,
,
,
.
23.(1)证明:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
在与中,
∴.
(2)解:,理由如下:
如图,在上截取,连接,
∵是等边三角形,
∴,
又∵,
∴是等边三角形,
∴,,
∵是等边三角形,
∴,,
∴,
∴.
在和中,
∴,
∴,
∴,
即.
24.(1)解:,
,
∵,,
,,
,
,
∵,,,
∴;
,
∵,,
∴;
(2)解:结论:.理由如下:
,
,
,
,
,
,
,
∵,
,
,
,
;
(3)解:延长,过点作于,如图所示:
,,
,
,,
∴,
,,
,
延长,过点作于,如图所示:
,
,
,
,
由平行线间的平行线段相等可得,
.
故答案为:21.
一.选择题(共10小题,满分30分,每小题3分)
1.如图,小深在池塘一侧选取了点,测得,,那么池塘两岸,间的距离可能是( ).
A.9 B.8 C.5 D.2
2.如图,已知,补充下列条件中的一个后,仍不能判定的是( )
A. B. C. D.
3.如图,以△ABC的一边为公共边,向外作与△ABC全等的三角形,可以作( )个
A.3 B.4 C.6 D.9
4.如图,在中,,,平分,点P为线段AD上一点,过点P作交的延长线于点E,则的度数为( )
A. B. C. D.
5.如图,正方形的边长为1,、上各有一点P、Q,如果的周长为2,则的度数为( )
A. B. C. D.
6.如图,是边长为3的等边三角形,点Q是边上一点,于点D,点E为边延长线上一点,且满足,连接交于点F,则的长为( )
A. B. C.1 D.
7.如图,在四边形中,是的平分线,且.若,则四边形的周长为( )
A. B. C. D.
8.如图,D、E分别是边上的点,,,设的面积为,的面积为,若,则( )
A.3 B.2 C. D.4
9.一副三角尺如图放置,为中点,将绕点旋转,边分别与边分别交于点,若,则阴影部分面积为( )
A. B. C. D.
10.如图,点为线段上一动点(不与点、重合),在同侧分别作等边和等边,与交于点,与交于点,与交于点,连接、,以下结论:①;②为等边三角形;③;④平分;正确的有( )个
A.1 B.2 C.3 D.4
二.填空题(共6小题,满分18分,每小题3分)
11.如图,是的边上的中线,是的边上的中线,是的边上的中线,连接,.若的面积是,则阴影部分的面积是 .
12.如图所示,线段,射线于点A,点C是射线上一动点,分别以为直角边作等腰直角三角形,得与中,连接交射线于点M,则的长为 .
13.如图,于点,射线于点B,一动点E从A点出发以2个单位/秒的速度沿射线运动,点D为射线上一动点,随着E点运动而运动,且始终保持,若点E经过t秒与全等,则t的值为 秒.
14.如图,在中,,,D为线段上一动点不与点B,C重合,连接,作,交线段于
(1)当D为中点时, °;
(2)当时, °
15.如图,在等腰三角形中,,点,在等腰三角形的内部,连接,使,且平分.若,则 .
16.如图,在中,,点为边的中点,点分别在边上,且,连接.分别过点作的垂线,垂足分别为,若,则四边形的面积为 .
三.解答题(共8小题,满分72分)
17.(6分)如图,在中,,,是边上的中线,的垂直平分线交于点,交于点,点是上一点,连接,.
(1)求证:;
(2)若,求的长.
18.(6分)把三角形纸片沿折叠.
(1)如图1,点落在四边形内部点A处时,与之间有一种数量关系始终保持不变,写出这种关系并证明;
(2)如图2,点落在四边形外部点A处时,直接写出与之间的数量关系.
19.(8分)如图,为的中线,为的中线.
(1)已知,的周长为,求的周长;
(2)在中作边上的高;
(3)若的面积为40,,则点到边的距离为多少?
20.(8分)如图,等边三角形纸片中,点在边(不包含端点,)上运动,连接,将对折,点落在直线上的点处,得到折痕;将对折,点落在直线上的点处,得到折痕.
(1)若,求的度数;
(2)试问:的大小是否会随着点的运动而变化?若不变,求出的度数;若变化,请说明理由.
21.(10分)如图,四边形中,,平分,,交于点.
(1)如图1,若,
①求证:;
②作平分,如图2,求证:.
(2)如图3,作平分,在锐角内部作射线,交于,若的大小为,试说明:平分.
22.(10分)【特例感知】
如图1,在中,,求边上的中线的取值范围.
(1)中线的取值范围是______.
【类比迁移】
(2)如图2,在四边形中,为的中点,点在上,,,求证:平分.
【拓展应用】
(3)如图3,在中,是边上的中线,E是上一点,连接并延长交于点F,,求证:.
23.(12分)【问题处理】
(1)如图1,为等腰三角形,,为边上的一点,连接,以为边作,.过点作交于,若,求证:.
【拓展提升】
(2)如图2,某家具厂制作等边三角形木质装饰框架,边上有一个预先开槽的固定节点(用于拼接),工人在边安装滑动定位块,并以为边加工等边三角形木片,最后连接加固.为计算木料长度,现需探究(定位块到端点的距离)、(固定节点到端点的距离)、(加固边)的数量关系,请你帮助工匠找出,,之间的数量关系,并说明理由.
24.(12分)(24-25七年级下·河南郑州·期中)【材料阅读】小芳在学习完全等三角形后,她尝试用三种不同方式摆放一副三角板.如图:在中,,;在中,,,并提出了相应的问题.
【发现】如图1,将两个三角板互不重叠地摆放在一起,当顶点摆放在线段上时,过点作,垂足为,过点作,垂足为.
(1)图1中,,,求的长.请补充小芳的过程.
,
,
∵,,
,,
,
,
……
(补充小芳的过程)
(2)【类比】如图2,将两个三角板叠放在一起,当顶点在线段上且顶点在线段上时,过点作,垂足为,猜想,,之间的数量关系,并说明理由.
(3)【拓展】如图3,将两个三角板叠放在一起,当顶点在线段上且顶点在线段上时,若,,连接,请直接写出的面积.
参考答案
一.选择题
1.C
【分析】本题考查了三角形的三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边的知识,掌握以上知识是解答本题的关键;
本题根据三角形的三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边的知识,进行作答,即可求解;
【详解】解:根据三角形的三边关系可得:,
即,
逐一核对选项,只有选项C符合,
故选:C
2.B
【分析】本题考查全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.由全等三角形的判定方法:、、、、,逐一选项分析即可.
【详解】解:A、由能判定,本选项不符合题意;
B、和分别是、的对角,不能判定,本选项符合题意;
C、由能判定,本选项不符合题意;
D、由能判定,本选项不符合题意;
故选B.
3.C
【分析】根据三条边分别对应相等的两个三角形全等,据此进行作图即可得到答案.
【详解】解:根据题意可以作出的三角形如下图所示:
△BAE ≌△ABC △DCB ≌△ABC △CFA ≌△ABC
△ABG ≌△ABC △IBC ≌△ABC △AHC ≌△ABC
故选C.
4.B
【分析】本题主要考查了三角形内角和定理,角平分线的定义,解答的关键是结合图形分析清楚角与角之间的关系.
先根据三角形的内角和定理求得的度数,再根据角平分线的定义求得的度数,从而根据三角形外角的性质即可求出度数,进一步求得的度数.
【详解】解:∵,,
∴,
∵平分,
∴,
∴,
∵,
∴.
故选:B.
5.B
【分析】本题考查了全等三角形的判定与性质,正方形的性质,首先从的周长入手求出,延长至,使,连接,然后利用全等来解.
【详解】解:如图所示,延长至,使,连接,
的周长为2,即,
∵正方形的边长是1,
∴,,,
,
,
在和中,
,
∴,
,,
∴,
,
,
∴,
在与中,,,,
∴,
.
故选:B.
6.A
【分析】本题考查了等边三角形的性质、全等三角形的性质与判定,熟练掌握以上知识点,添加适当的辅助线构造全等三角形是解题的关键.作交的延长线于点,利用全等三角形判定证出,得到,,再证出,得到,再利用线段和差即可求出的长.
【详解】解:作交的延长线于点,
是边长为3的等边三角形,
,,
,
,
,,
,
又,
,
,,
又,,
,
,
.
故选:A.
7.B
【分析】在线段AC上作AF=AB,证明△AEF≌△AEB可得∠AFE=∠B,∠AEF=∠AEB,再证明△CEF≌△CED可得CD=CF,即可求得四边形的周长.
【详解】解:在线段AC上作AF=AB,
∵AE是的平分线,
∴∠CAE=∠BAE,
又∵AE=AE,
∴△AEF≌△AEB(SAS),
∴∠AFE=∠B,∠AEF=∠AEB,
∵AB∥CD,
∴∠D+∠B=180°,
∵∠AFE+∠CFE=180°,
∴∠D=∠CFE,
∵,
∴∠AEF+∠CEF=90°,∠AEB+∠CED=90°,
∴∠CEF=∠CED,
在△CEF和△CED中
∵,
∴△CEF≌△CED(AAS)
∴CD=CF,
∴四边形的周长=AC+AB+BD+CD=AC+AF+CF+BD=2AC+BD=,
故选:B.
8.D
【分析】本题主要考查了三角形的面积、三角形的中线等知识点,能灵活运用三角形的中线以及等分线求面积成为解题的关键.
由、、可以求出的面积和的面积,再结合图形可得即可解答.
【详解】解:∵,
,
∵,
,
∵,
∴,,
,
.
故选:D.
9.A
【分析】本题考查了等腰直角三角形的性质,余角性质,全等三角形的判定和性质等,连接,由等腰三角形的性质可得,,,进而由余角性质得,即得,即可得,得到,利用中线性质求出即可求解,正确作出辅助线是解题的关键.
【详解】解:连接,如图,
∵是等腰直角三角形,点是斜边的中点,
∴,,,
∴,
即,
又∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
故选:.
10.D
【分析】由和等边是正三角形,其性质得三边相等,三个角为,平角的定义和角的和差得,边角边证明,其性质得结论①正确;根据等边三角形的判定得是等边三角形,结论②正确;根据全等三角形的性质和三角形内角和定理即可得结论③正确;角角边证明,其性质和角平分线性质定理的逆定理求出点在的平分线上,结论④正确.
【详解】解:∵和是正三角形,
,
又 ∵,
,
在和中,
,
,
,
∴结论①正确;
,
,
又,
,
在和中,
,
,
,
是等边三角形,故②正确;
,
,
又,,,
,
,结论③正确;
过点分别作于点、两点,如图2所示:
,
,
在和中,
,
,
,
又 ∵在的内部,
∴点在的平分线上,
∴结论④正确;
综合所述,共有 4个结论正确.
故选:D.
二.填空题
11.
【分析】此题考查了三角形中线的性质,利用中线等分三角形的面积进行求解即可,解题的关键是熟练掌握三角形中线的性质及其应用.
【详解】解:∵是的边上的中线,
∴,
∵是的边上的中线,即有是的边上的中线,
∴,,
∴,
∵是的边上的中线,即有是的边上的中线,
∴,
∴,
∴阴影部分的面积是,
故答案为:.
12.
【分析】本题考查全等三角形的判定和性质、等腰直角三角形的性质,解题的关键是添加辅助线构造全等三角形:
如图作于H,由得,再证明得,即可解决问题.
【详解】解:如图作于H,
∵,
∴,
∵,,
∴,
∵和都是等腰三角形,
∴,,
在和中,
,
∴,
∴,,
在和中,
,
∴,
∴,
∴.
故答案为:.
13.或或
【分析】本题考查去啊能三角形的判定和性质,解题的关键是根据题意确定点的位置.
根据运动过程和三角形全等,分类讨论,确定点的位置,从而可得运动路程,除以运动速度,即可得运动时间.
【详解】解:根据题意,进行分类讨论如下:
当点在线段上,时,,
∴,
∵,
∴,
∵,
∴,
∵点的运动速度为个单位/秒,
∴运动时间(秒);
当点在延长线上,时,,
∴,
∵,
∴,
∵,
∴,
∵点的运动速度为个单位/秒,
∴运动时间(秒);
当点在延长线上,时,,
∴,
∵,
∴,
∵点的运动速度为个单位/秒,
∴运动时间(秒)
∴的值为或或,
故答案为:或或.
14.
【分析】(1)根据等腰三角形性质得,,再根据得,然后根据三角形外角性质即可得出的度数;
(2)设,根据三角形外角性质得,由此得,再求出,则,再由三角形外角性质得,证明和中全等得,则,进而得,由此解出继而可得出的度数.
此题主要考查了等腰三角形的性质,全等三角形的判定和性质,理解等腰三角形的性质,熟练掌握全等三角形的判定和性质,灵活运用三角形的内角和定理,三角形的外角性质进行角的计算是解决问题的关键.
【详解】解:(1)当D为中点时,如图1所示:
在中,,,
,
为中点,
,
,
,
,
是的外角,
,
故答案为:90;
(2)当时,如图2所示:
设,
是的外角,
,
又,,
,
,
在中,,,
,
,
,
是的外角,
,
在和中,
,
∴,
,
,
,
解得:,
故答案为:
15.
【分析】本题考查了等腰三角形的性质,等边三角形的判定与性质,直角三角形的性质,解题关键是添加辅助线,能洞察到特殊角在求边长中的用法.
延长交于点,延长交于点,可得是等边三角形,,进而知,然后可得,再利用等腰三角形的性质可得,,从而可得,进而在中,利用含30度角直角三角形的性质可得,据此进行计算即可解答.
【详解】解:如图,延长交于点,延长交于点,
∵,
∴是等边三角形,,
∴,
∵,
∴,
∵,平分,
∴,,
∴,
∴,
∴,
∴.
故答案为:.
16.
【分析】本题考查了等腰三角形的判定与性质,全等三角形的判定与性质,正确掌握相关性质内容是解题的关键.先得出是等腰直角三角形,结合三线合一得,,则都是等腰直角三角形,再通过证明,则,再通过证明,即可作答.
【详解】解:连接,如图所示:
∵,
∴是等腰直角三角形,
∴,
∵点为边的中点,
∴,,
∴都是等腰直角三角形,
∴,,
则,
∴,
∴,,,
∵分别过点作的垂线,垂足分别为,
∴,
∴,是等腰三角形,
∴
∵
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
即,
∴.
∵,
∴四边形的面积
即四边形的面积为
故答案为:
三.解答题
17.(1)证明:在中,,,
∴,
∵是边上的中线,
∴,,,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
(2)解:∵是线段的垂直平分线,
∴,,
∴,
∴,
∵,
∴,
∴,
∴是等边三角形,
∴,
∴,
∴,
∴.
18.(1)解:.
证明:∵三角形纸片沿折叠得到,
∴,,
∴,,
又∵,
∴,
∴;
(2)解:∵三角形纸片沿折叠得到,
∴,,
∴,,
又∵,
∴,
∴.
19.(1)解: 为的中线,
,
,
,
的周长,
,
的周长;
(2)解:如图,即为中边上的高,
(3)解:设点到边的距离为
为的中线, 为的中线,
,
,
,
,
点到边的距离为.
20.(1)解:∵将对折,得到折痕,
∴,
∵将对折,得到折痕,
∴,
∵,
∴,
∴.
(2)解:不变.理由如下:
∵,,,
∴,
即.
∴的大小不随点的运动而变化.
21.(1)①∵,,
∴.
∵,
∴.
②∵平分,
∴.
∵平分,
∴.
∴.
∵,
∴.
∴.
∴.
(2)延长,交于点,如图所示:
∵,
∴.
∴.
∵平分,
∴.
∵平分,
∴.
∵,
∴.
∴.
∴.
∴平分.
22.(1)解:如图1,延长到点,使得,连接.
为边上的中线,
,
在和中,
,
,
,
,
,
即,
;
故答案为:;
(2)证明:如图2,延长交的延长线于点,
,
,
,,
为的中点,
,
,
,,
,
,
即,
平分;
(3)证明:如图3,延长到点,使,连接,
在和中, ,
,
,,
,
,
,
,
,
,
.
23.(1)证明:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
在与中,
∴.
(2)解:,理由如下:
如图,在上截取,连接,
∵是等边三角形,
∴,
又∵,
∴是等边三角形,
∴,,
∵是等边三角形,
∴,,
∴,
∴.
在和中,
∴,
∴,
∴,
即.
24.(1)解:,
,
∵,,
,,
,
,
∵,,,
∴;
,
∵,,
∴;
(2)解:结论:.理由如下:
,
,
,
,
,
,
,
∵,
,
,
,
;
(3)解:延长,过点作于,如图所示:
,,
,
,,
∴,
,,
,
延长,过点作于,如图所示:
,
,
,
,
由平行线间的平行线段相等可得,
.
故答案为:21.
同课章节目录
