第2章《实数的初步认识》章节测试卷(含答案)苏科版八年级数学上册
文档属性
| 名称 | 第2章《实数的初步认识》章节测试卷(含答案)苏科版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 223.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 00:00:10 | ||
图片预览




文档简介
第2章《实数的初步认识》章节测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.有数据显示,长沙海吉星蔬菜批发市场日均蔬菜交易量约为,关于这个近似数,下列说法正确的是( )
A.它精确到 B.它精确到万位
C.它精确到万分位 D.它精确到千位
2.如果自然数a的平方根是±m,那么a+1的平方根用m表示为( )
A.±(m+1) B.(m2+1) C. D.
3.如图,在数轴上,与之间的整数一共有( )
A.7个 B.6个 C.5个 D.4个
4.将,,三个数按图中方式排列,若规定表示第排第列的数,则与表示的两个数的积是( )
A. B. C. D.1
5.下列实数中,满足不等式的是( )
A. B. C. D.
6.若a的算术平方根为17.25,b的立方根为;x的平方根为,y的立方根为86.9,则( )
A. B.
C. D.
7.如图,在做浮力实验时,小华用一根细线将一个正方体铁块拴住,完全浸入盛满水的圆柱形烧杯中,并用一个量筒量得溢出的体积为,由此可估计该正方体铁块的棱长介于( )
A.和之间 B.和之间
C.和之间 D.和之间
8.对于实数a、b,定义的含义为:当时,;当时,.例如:.已知,且和为两个连续正整数,则的立方根为( )
A. B.1 C. D.2
9.根据图中的程序,当输入为时,输出的值是( )
A. B. C. D.
10.观察下列算式:,,,…,它具有一定的规律性,若把第个算式的结果记为,则的值是( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.将5.649精确到百分位所得的近似数是 .
12.若实数,,满足: ,则的值为 .
13.已知的一个平方根是5,的立方根是2,c是的整数部分,则的平方根是 .
14.实数,在数轴上的位置如图所示,化简: .
15.已知,则的值为
16.如果x是一个实数,我们把不超过x的最大整数记为,把x的小数部分记为,即.如:,求: ;满足的整数x的值有 个;已知,则 .
三.解答题(共8小题,满分72分)
17.(6分)计算:
(1); (2).
18.(6分)表达无理数小数部分的方法如下:例如,因为的整数部分是1,所以用这个数减去其整数部分,差就是小数部分.我们可以用来表示的小数部分.
(1)的小数部分是_____;
(2)设的小数部分是,的整数部分是,求的算术平方根.
19.(8分)根据下表回答下列问题:
15 15.1 15.2 15.3 15.4 15.5 15.6 15.7 15.8 15.9
225 228.01 231.04 234.09 237.16 240.25 243.36 246.49 249.64 252.81
(1)______,______,______;
(2)与哪个整数最接近?求的近似值(结果精确到0.01);
(3)若,则满足条件的整数有______个.
20.(8分)【定义】用表示一个数对,其中为任意数,.记,,将数对和称为数对的一对“开方对称数对”.例如:数对的开方对称数对为和.
【知识运用】
(1)直接写出数对的开方对称数对_______;
(2)若数对的一个开方对称数对是,求,的值;
(3)若数对的一个开方对称数对是,求的值.
21.(10分)我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果,其中、为有理数,为无理数;那么必然有,且,据此,解决下列问题.
(1)如果,其中、为有理数,则___________,___________;
(2)如果,其中、为有理数,求的平方根.
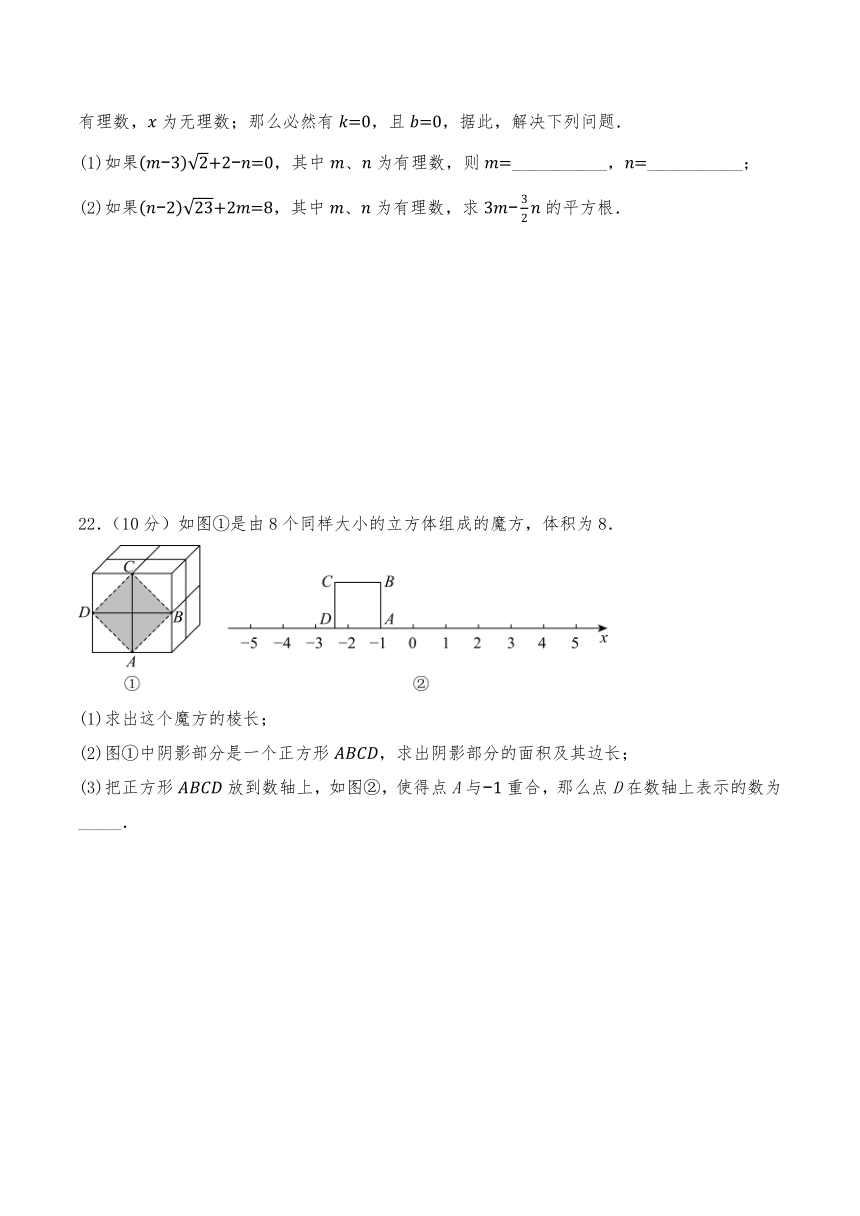
22.(10分)如图①是由8个同样大小的立方体组成的魔方,体积为8.
(1)求出这个魔方的棱长;
(2)图①中阴影部分是一个正方形,求出阴影部分的面积及其边长;
(3)把正方形放到数轴上,如图②,使得点A与重合,那么点D在数轴上表示的数为_____.
23.(12分)本学期学方根和立方根,下表是平方根和立方根的部分内容:
平方根 立方根
定义 一般地,如果一个数的平方等于,即,那么这个数就叫做的平方根(也叫做二次方根) 一般地,如果一个数的立方等于,即,那么这个数就叫做的立方根(也叫做三次方根)
性质 一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根. 正数的立方根是正数;0的立方根是0;负数的立方根是负数.
【类比探索】(1)探索定义:观察;
类比平方根和立方根,给四次方根下定义:__________________________________________________.
(2)探究性质:①81的四次方根是_________;②0的四次方根是_________;③_________(填“有”或“没有”)四次方根.
类比平方根和立方根的性质,归纳四次方根的性质:
①______________________________________________________;
②______________________________________________________;
③______________________________________________________
【拓展应用】(1)_________;
(2)比较大小:_________.
24.(12分)阅读下面的文字,解答问题:
【问题发现】(1)如图1,把两个边长为1的小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就可以得到一个大正方形,所得到的大正方形的面积为________,大正方形的边长为________.
【知识迁移】(2)爱钻研的小思同学受到启发,尝试用两个同样大小的长方形拼出一个正方形.如图2,将两个长和宽分别为3和2的长方形沿对角线剪开,将所得到的4个直角三角形拼出了一个中间有一个镂空小正方形的大正方形,所得到的小正方形的边长为________;大正方形的面积为________,边长为________.
【拓展延伸】(3)小明想用一块面积为的正方形纸片,沿着边的方向裁出一块面积为的长方形纸片,使它的长与宽之比为.请通过计算说明是否可行.
参考答案
一.选择题
1.B
【分析】本题考查了近似数与精确度,熟练掌握精确度的定义是解答本题的关键.近似数的最后一个数字实际在什么位上,即精确到了什么位,要求精确到某一位,应当对下一位的数字进行四舍五入.还原成原数看3所在的数位即可.
【详解】解:∵,
∴该数精确到万位.
故选C.
2.D
【分析】首先根据平方根性质用m表示出该自然数a,由此进一步表示出,从而进一步即可得出答案.
【详解】由题意得:这个自然数a为:,
∴,
故的平方根用m表示为:,
故选:D.
3.B
【分析】此题考查了无理数的估算能力,运用算术平方根的知识进行估算、求解.
【详解】解:∵,
∴,
∵,
∴与之间的整数是,
即与之间的整数一共有6个,
故选:B.
4.B
【分析】本题考查了数字类规律探索,实数的运算,由题意可得,每三个数一循环,即以,,为一个循环节,求出表示的数为,表示的数正好是1,即可得解.
【详解】解:由题意可得,每三个数一循环,即以,,为一个循环节,
在数列中是第个,,故表示的数正好是第10轮的最后一个,为,
在数列中是第个,,故表示的数正好是1,
∴与表示的两个数的积是,
故选:B.
5.C
【分析】本题考查了立方根、平方根、不等式的定义,属于基础题.先根据有理数的乘方、立方根的定义计算选项A、D,然后让每个选项与3比较即可作出判断.
【详解】解:A、,故此选项不符合题意;
B、,故此选项不符合题意;
C、,故此选项符合题意;
D、,故此选项不符合题意;
故选:C.
6.A
【分析】根据平方根、算术平方根和立方根的定义求出a、b、x、y的值,再找出关系即可.
【详解】解:∵a的算术平方根为17.25,b的立方根为-8.69,
∴a=297.5625,b=-656.234909.
∵x的平方根为±1.725,y的立方根为86.9,
∴x=2.975625,y=656234.909,
∴.
故选:A.
7.A
【分析】本题考查正方体的体积,立方根的应用,无理数的估算,掌握夹逼法是解题的关键.根据正方体的体积等于溢出的水的体积建立方程,求出方程的解后用夹逼法估算即可.
【详解】解:设该正方体铁块的棱长为,
由题意得:,
解得,
,
,
即该正方体铁块的棱长介于和之间,
故选A.
8.B
【分析】根据题意求出a、b的值即可得到答案.本题主要考查新定义无理数的估算,立方根的运算,准确理解题意是解题的关键.
【详解】解:∵,,
∴,,
∵a和b为两个连续正整数,,,
∴即,,
∴,
∴,
则的立方根为的1,
故选:B.
9.A
【分析】本题主要考查了与流程图有关的实数计算,立方根,算术平方根,无理数,先把输入,计算出的值,若结果为无理数则输出结果,若结果为有理数,继续把的值输入进行计算,如此反复直至的结果为无理数即可得到答案,掌握知识点的应用是解题的关键.
【详解】解:当输入为时,
,是有理数,
当输入为时,
,是有理数,
当输入为时,
,是无理数,
∴输出的值是,
故选:.
10.D
【分析】本题主要考查了与实数有关的规律探索,通过观察可知,据此可得,再把所求式子裂项相消即可得到答案.
【详解】解:,
,
,
……,
以此类推可知,,
∴,
∴,
∴
,
故选:D.
二.填空题
11.5.65
【分析】本题考查了近似数与精确度,熟练掌握精确度的定义是解答本题的关键.要求精确到某一位,应当对下一位的数字进行四舍五入.
【详解】将5.649精确到百分位所得的近似数是5.65.
故答案为:5.65.
12.4
【分析】本题考查了绝对值,二次根式和完全平方式的非负性,根据几个非负数的和为0,则每个式子的值多位0,求出x、y、z的值,再代入代数式进行计算即可.
【详解】解:∵,,,
且,
,,,
,,,
.
故答案为:4
13.
【分析】本题考查了估算无理数的大小,平方根,立方根,掌握这些知识点是解题的关键.
根据平方根及立方根确定,,再由估算算术平方根的整数部分确定,将其代入代数式,然后计算平方根即可.
【详解】解:的一个平方根是5,
,
解得:.
的立方根是,
,
解得:.
是的整数部分,而,
,
,
的平方根为.
14.2
【分析】本题考查了实数与数轴,利用数轴得出,,进而化简即可.
【详解】解:由数轴,得,,
∴,,,
∴原式
,
故答案为:2.
15.或2或3
【分析】本题考查立方根的性质,根据题意得到,结合立方根等于本身的数有,进行求解即可.
【详解】解:∵,
∴,
∴或,
∴或或;
故答案为:或2或3.
16. 1 3 /
【分析】根据无理数的估算得到,然后根据的定义求解即可求出;
根据得到,然后解不等式组求解即可;首先得到,然后将变形为,然后根据得到,然后由为整数得到,然后代入求出,进而求解即可.
【详解】解:∵,
∴,
∴,
∴;
∵,
∴,
解得,
∴整数x的值有7,8,9,共3个;
∵,
∴,
∵,
∴,
∴,
∴,
∵把x的小数部分记为,
∴,
∴,
∵为整数,
∴为整数,
∴当时,,不符合题意;
当时,,符合题意;
∴,
∴,
∴.
故答案为:1,3,.
三.解答题
17.(1)解:原式.
(2)
.
18.(1)解:(1)∵,
∴,
∴的整数部分为 2,小数部分为;
故答案为:;
(2)∵,,
∴,,
∴的小数部分为,整数部分为 ,
∴,
的算术平方根是.
∴的算术平方根是.
19.(1)解:由表格可知,,
;
,
;
,
.
故答案为:15.6;154;0.152;
(2)解: ,
又 ,,
与158最接近;
,
.
(3)解:对两边同时平方可得,
计算可得,
的取值范围是,
则满足条件的整数的个数为个.
故答案为:306.
20.(1)解:,,
∴数对的开方对称数对,;
(2)解:∵,,将数对和称为数对的一对“开方对称数对”,
∴,
∵数对的一个开方对称数对是,
∴,;
(3)解:若,,
则,,
∴;
若,,
则,,
∴;
的值为或.
21.(1)解:,其中,为有理数,为无理数,
∴,
∴;
(2)解:∵,,为有理数,为无理数,
∴,
解之,得.
则.
∴的平方根是.
22.(1)解:设这个魔方的棱长为,
则,
解得:,
即这个魔方的棱长为2;
(2)解:魔方的棱长为2,则每个小立方体的棱长都为,
每个小正方形的面积都为,
魔方的一面的面积为,
阴影部分的面积,
正方形的面积为,
它的边长为;
(3)解:由(2)可知正方形边长为,
,
点A与重合,
点D在数轴上表示的数为,
故答案为:.
23.类比探索:(1)类比平方根和立方根,给四次方根下定义:一般地,如果一个数x的四次方等于a,即,那么这个数x就叫做a的四次方根;
(2)①81的四次方根是:;②0的四次方根是:0;③没有四次方根;
类比平方根和立方根的性质,归纳四次方根的性质:
①一个正数有两个四次方根,它们互为相反数;
②0的四次方根是0;
③负数没有四次方根;
拓展应用:(1);
(2)∵,
∴.
24.解:(1)由题意得:所得到的大正方形面积为,边长为;
故答案为:2,;
(2)由题意得:所得到的小正方形的边长为:;大正方形的面积为:;边长为;
故答案为:1,13,;
(3)不可行,理由如下:
设截出的长方形纸片的长为,宽为,
则,
∴(负值舍去),
∴截出的长方形纸片的长为,
∴不能用一块面积为的正方形纸片,沿着边的方向裁出一块面积为的长方形纸片,使它的长与宽之比为.
一.选择题(共10小题,满分30分,每小题3分)
1.有数据显示,长沙海吉星蔬菜批发市场日均蔬菜交易量约为,关于这个近似数,下列说法正确的是( )
A.它精确到 B.它精确到万位
C.它精确到万分位 D.它精确到千位
2.如果自然数a的平方根是±m,那么a+1的平方根用m表示为( )
A.±(m+1) B.(m2+1) C. D.
3.如图,在数轴上,与之间的整数一共有( )
A.7个 B.6个 C.5个 D.4个
4.将,,三个数按图中方式排列,若规定表示第排第列的数,则与表示的两个数的积是( )
A. B. C. D.1
5.下列实数中,满足不等式的是( )
A. B. C. D.
6.若a的算术平方根为17.25,b的立方根为;x的平方根为,y的立方根为86.9,则( )
A. B.
C. D.
7.如图,在做浮力实验时,小华用一根细线将一个正方体铁块拴住,完全浸入盛满水的圆柱形烧杯中,并用一个量筒量得溢出的体积为,由此可估计该正方体铁块的棱长介于( )
A.和之间 B.和之间
C.和之间 D.和之间
8.对于实数a、b,定义的含义为:当时,;当时,.例如:.已知,且和为两个连续正整数,则的立方根为( )
A. B.1 C. D.2
9.根据图中的程序,当输入为时,输出的值是( )
A. B. C. D.
10.观察下列算式:,,,…,它具有一定的规律性,若把第个算式的结果记为,则的值是( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.将5.649精确到百分位所得的近似数是 .
12.若实数,,满足: ,则的值为 .
13.已知的一个平方根是5,的立方根是2,c是的整数部分,则的平方根是 .
14.实数,在数轴上的位置如图所示,化简: .
15.已知,则的值为
16.如果x是一个实数,我们把不超过x的最大整数记为,把x的小数部分记为,即.如:,求: ;满足的整数x的值有 个;已知,则 .
三.解答题(共8小题,满分72分)
17.(6分)计算:
(1); (2).
18.(6分)表达无理数小数部分的方法如下:例如,因为的整数部分是1,所以用这个数减去其整数部分,差就是小数部分.我们可以用来表示的小数部分.
(1)的小数部分是_____;
(2)设的小数部分是,的整数部分是,求的算术平方根.
19.(8分)根据下表回答下列问题:
15 15.1 15.2 15.3 15.4 15.5 15.6 15.7 15.8 15.9
225 228.01 231.04 234.09 237.16 240.25 243.36 246.49 249.64 252.81
(1)______,______,______;
(2)与哪个整数最接近?求的近似值(结果精确到0.01);
(3)若,则满足条件的整数有______个.
20.(8分)【定义】用表示一个数对,其中为任意数,.记,,将数对和称为数对的一对“开方对称数对”.例如:数对的开方对称数对为和.
【知识运用】
(1)直接写出数对的开方对称数对_______;
(2)若数对的一个开方对称数对是,求,的值;
(3)若数对的一个开方对称数对是,求的值.
21.(10分)我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果,其中、为有理数,为无理数;那么必然有,且,据此,解决下列问题.
(1)如果,其中、为有理数,则___________,___________;
(2)如果,其中、为有理数,求的平方根.
22.(10分)如图①是由8个同样大小的立方体组成的魔方,体积为8.
(1)求出这个魔方的棱长;
(2)图①中阴影部分是一个正方形,求出阴影部分的面积及其边长;
(3)把正方形放到数轴上,如图②,使得点A与重合,那么点D在数轴上表示的数为_____.
23.(12分)本学期学方根和立方根,下表是平方根和立方根的部分内容:
平方根 立方根
定义 一般地,如果一个数的平方等于,即,那么这个数就叫做的平方根(也叫做二次方根) 一般地,如果一个数的立方等于,即,那么这个数就叫做的立方根(也叫做三次方根)
性质 一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根. 正数的立方根是正数;0的立方根是0;负数的立方根是负数.
【类比探索】(1)探索定义:观察;
类比平方根和立方根,给四次方根下定义:__________________________________________________.
(2)探究性质:①81的四次方根是_________;②0的四次方根是_________;③_________(填“有”或“没有”)四次方根.
类比平方根和立方根的性质,归纳四次方根的性质:
①______________________________________________________;
②______________________________________________________;
③______________________________________________________
【拓展应用】(1)_________;
(2)比较大小:_________.
24.(12分)阅读下面的文字,解答问题:
【问题发现】(1)如图1,把两个边长为1的小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就可以得到一个大正方形,所得到的大正方形的面积为________,大正方形的边长为________.
【知识迁移】(2)爱钻研的小思同学受到启发,尝试用两个同样大小的长方形拼出一个正方形.如图2,将两个长和宽分别为3和2的长方形沿对角线剪开,将所得到的4个直角三角形拼出了一个中间有一个镂空小正方形的大正方形,所得到的小正方形的边长为________;大正方形的面积为________,边长为________.
【拓展延伸】(3)小明想用一块面积为的正方形纸片,沿着边的方向裁出一块面积为的长方形纸片,使它的长与宽之比为.请通过计算说明是否可行.
参考答案
一.选择题
1.B
【分析】本题考查了近似数与精确度,熟练掌握精确度的定义是解答本题的关键.近似数的最后一个数字实际在什么位上,即精确到了什么位,要求精确到某一位,应当对下一位的数字进行四舍五入.还原成原数看3所在的数位即可.
【详解】解:∵,
∴该数精确到万位.
故选C.
2.D
【分析】首先根据平方根性质用m表示出该自然数a,由此进一步表示出,从而进一步即可得出答案.
【详解】由题意得:这个自然数a为:,
∴,
故的平方根用m表示为:,
故选:D.
3.B
【分析】此题考查了无理数的估算能力,运用算术平方根的知识进行估算、求解.
【详解】解:∵,
∴,
∵,
∴与之间的整数是,
即与之间的整数一共有6个,
故选:B.
4.B
【分析】本题考查了数字类规律探索,实数的运算,由题意可得,每三个数一循环,即以,,为一个循环节,求出表示的数为,表示的数正好是1,即可得解.
【详解】解:由题意可得,每三个数一循环,即以,,为一个循环节,
在数列中是第个,,故表示的数正好是第10轮的最后一个,为,
在数列中是第个,,故表示的数正好是1,
∴与表示的两个数的积是,
故选:B.
5.C
【分析】本题考查了立方根、平方根、不等式的定义,属于基础题.先根据有理数的乘方、立方根的定义计算选项A、D,然后让每个选项与3比较即可作出判断.
【详解】解:A、,故此选项不符合题意;
B、,故此选项不符合题意;
C、,故此选项符合题意;
D、,故此选项不符合题意;
故选:C.
6.A
【分析】根据平方根、算术平方根和立方根的定义求出a、b、x、y的值,再找出关系即可.
【详解】解:∵a的算术平方根为17.25,b的立方根为-8.69,
∴a=297.5625,b=-656.234909.
∵x的平方根为±1.725,y的立方根为86.9,
∴x=2.975625,y=656234.909,
∴.
故选:A.
7.A
【分析】本题考查正方体的体积,立方根的应用,无理数的估算,掌握夹逼法是解题的关键.根据正方体的体积等于溢出的水的体积建立方程,求出方程的解后用夹逼法估算即可.
【详解】解:设该正方体铁块的棱长为,
由题意得:,
解得,
,
,
即该正方体铁块的棱长介于和之间,
故选A.
8.B
【分析】根据题意求出a、b的值即可得到答案.本题主要考查新定义无理数的估算,立方根的运算,准确理解题意是解题的关键.
【详解】解:∵,,
∴,,
∵a和b为两个连续正整数,,,
∴即,,
∴,
∴,
则的立方根为的1,
故选:B.
9.A
【分析】本题主要考查了与流程图有关的实数计算,立方根,算术平方根,无理数,先把输入,计算出的值,若结果为无理数则输出结果,若结果为有理数,继续把的值输入进行计算,如此反复直至的结果为无理数即可得到答案,掌握知识点的应用是解题的关键.
【详解】解:当输入为时,
,是有理数,
当输入为时,
,是有理数,
当输入为时,
,是无理数,
∴输出的值是,
故选:.
10.D
【分析】本题主要考查了与实数有关的规律探索,通过观察可知,据此可得,再把所求式子裂项相消即可得到答案.
【详解】解:,
,
,
……,
以此类推可知,,
∴,
∴,
∴
,
故选:D.
二.填空题
11.5.65
【分析】本题考查了近似数与精确度,熟练掌握精确度的定义是解答本题的关键.要求精确到某一位,应当对下一位的数字进行四舍五入.
【详解】将5.649精确到百分位所得的近似数是5.65.
故答案为:5.65.
12.4
【分析】本题考查了绝对值,二次根式和完全平方式的非负性,根据几个非负数的和为0,则每个式子的值多位0,求出x、y、z的值,再代入代数式进行计算即可.
【详解】解:∵,,,
且,
,,,
,,,
.
故答案为:4
13.
【分析】本题考查了估算无理数的大小,平方根,立方根,掌握这些知识点是解题的关键.
根据平方根及立方根确定,,再由估算算术平方根的整数部分确定,将其代入代数式,然后计算平方根即可.
【详解】解:的一个平方根是5,
,
解得:.
的立方根是,
,
解得:.
是的整数部分,而,
,
,
的平方根为.
14.2
【分析】本题考查了实数与数轴,利用数轴得出,,进而化简即可.
【详解】解:由数轴,得,,
∴,,,
∴原式
,
故答案为:2.
15.或2或3
【分析】本题考查立方根的性质,根据题意得到,结合立方根等于本身的数有,进行求解即可.
【详解】解:∵,
∴,
∴或,
∴或或;
故答案为:或2或3.
16. 1 3 /
【分析】根据无理数的估算得到,然后根据的定义求解即可求出;
根据得到,然后解不等式组求解即可;首先得到,然后将变形为,然后根据得到,然后由为整数得到,然后代入求出,进而求解即可.
【详解】解:∵,
∴,
∴,
∴;
∵,
∴,
解得,
∴整数x的值有7,8,9,共3个;
∵,
∴,
∵,
∴,
∴,
∴,
∵把x的小数部分记为,
∴,
∴,
∵为整数,
∴为整数,
∴当时,,不符合题意;
当时,,符合题意;
∴,
∴,
∴.
故答案为:1,3,.
三.解答题
17.(1)解:原式.
(2)
.
18.(1)解:(1)∵,
∴,
∴的整数部分为 2,小数部分为;
故答案为:;
(2)∵,,
∴,,
∴的小数部分为,整数部分为 ,
∴,
的算术平方根是.
∴的算术平方根是.
19.(1)解:由表格可知,,
;
,
;
,
.
故答案为:15.6;154;0.152;
(2)解: ,
又 ,,
与158最接近;
,
.
(3)解:对两边同时平方可得,
计算可得,
的取值范围是,
则满足条件的整数的个数为个.
故答案为:306.
20.(1)解:,,
∴数对的开方对称数对,;
(2)解:∵,,将数对和称为数对的一对“开方对称数对”,
∴,
∵数对的一个开方对称数对是,
∴,;
(3)解:若,,
则,,
∴;
若,,
则,,
∴;
的值为或.
21.(1)解:,其中,为有理数,为无理数,
∴,
∴;
(2)解:∵,,为有理数,为无理数,
∴,
解之,得.
则.
∴的平方根是.
22.(1)解:设这个魔方的棱长为,
则,
解得:,
即这个魔方的棱长为2;
(2)解:魔方的棱长为2,则每个小立方体的棱长都为,
每个小正方形的面积都为,
魔方的一面的面积为,
阴影部分的面积,
正方形的面积为,
它的边长为;
(3)解:由(2)可知正方形边长为,
,
点A与重合,
点D在数轴上表示的数为,
故答案为:.
23.类比探索:(1)类比平方根和立方根,给四次方根下定义:一般地,如果一个数x的四次方等于a,即,那么这个数x就叫做a的四次方根;
(2)①81的四次方根是:;②0的四次方根是:0;③没有四次方根;
类比平方根和立方根的性质,归纳四次方根的性质:
①一个正数有两个四次方根,它们互为相反数;
②0的四次方根是0;
③负数没有四次方根;
拓展应用:(1);
(2)∵,
∴.
24.解:(1)由题意得:所得到的大正方形面积为,边长为;
故答案为:2,;
(2)由题意得:所得到的小正方形的边长为:;大正方形的面积为:;边长为;
故答案为:1,13,;
(3)不可行,理由如下:
设截出的长方形纸片的长为,宽为,
则,
∴(负值舍去),
∴截出的长方形纸片的长为,
∴不能用一块面积为的正方形纸片,沿着边的方向裁出一块面积为的长方形纸片,使它的长与宽之比为.
同课章节目录
