人教A版(2019)必修第二册 8.3.1 球的表面积与体积 课件(共21张PPT)
文档属性
| 名称 | 人教A版(2019)必修第二册 8.3.1 球的表面积与体积 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 68.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-06 09:49:06 | ||
图片预览




文档简介
(共20张PPT)
球的表面积与体积
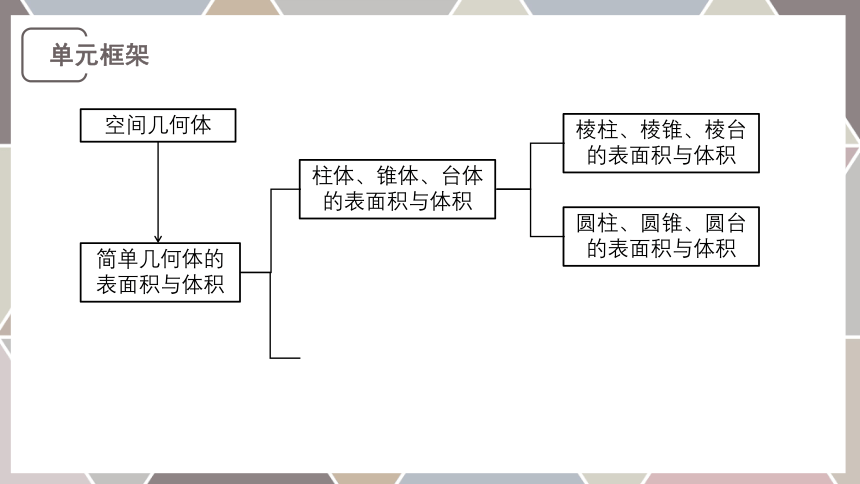
单元框架
简单几何体的表面积与体积
柱体、锥体、台体的表面积与体积
棱柱、棱锥、棱台的表面积与体积
圆柱、圆锥、圆台的表面积与体积
空间几何体
知识回顾
l
O
O'
2πr
r
O'
O
r'
2πr'
r
l
2πr
2πr
O
S
l
r
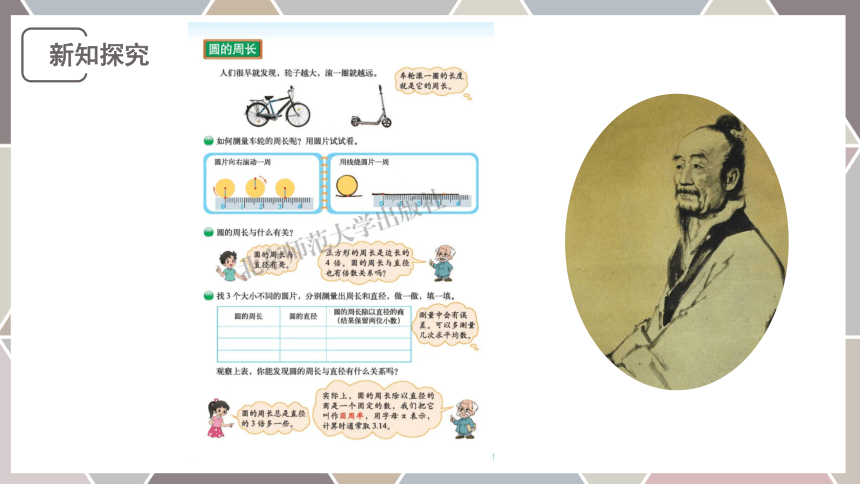
新知探究
新知探究
分割
求和(以直代曲)
取极限
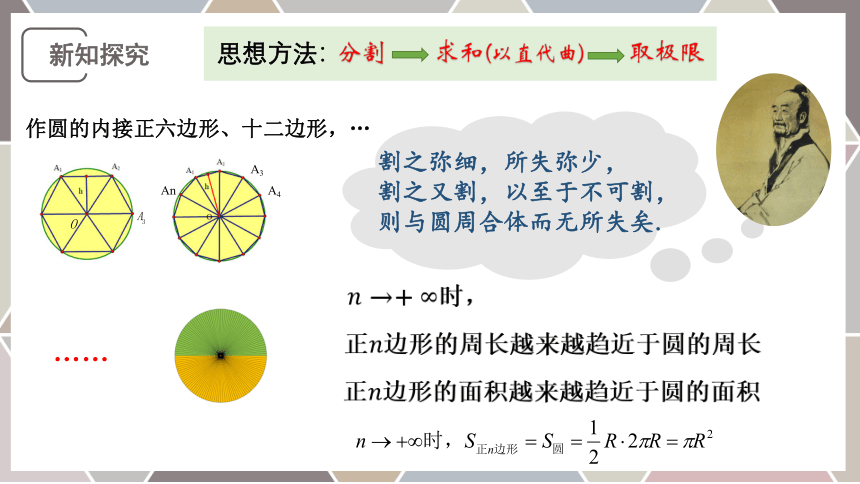
思想方法:
作圆的内接正六边形、十二边形,…
……
A3
An
A4
割之弥细,所失弥少,
割之又割,以至于不可割,
则与圆周合体而无所失矣.
时,
正边形的面积越来越趋近于圆的面积
正边形的周长越来越趋近于圆的周长
新知探究
问题1:类比刘徽的割圆术,如何推导球的表面积公式?
分割
求和(以直代曲)
取极限
思想方法:
将轴截面等弧分割
A
O
A
O
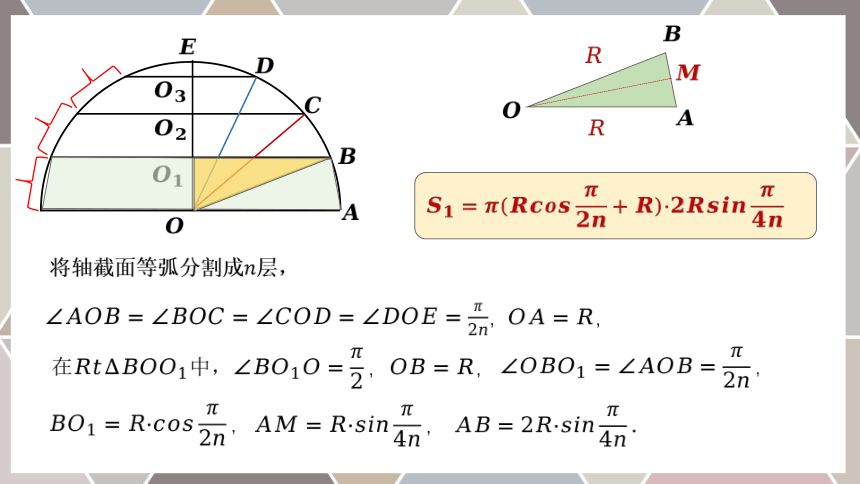
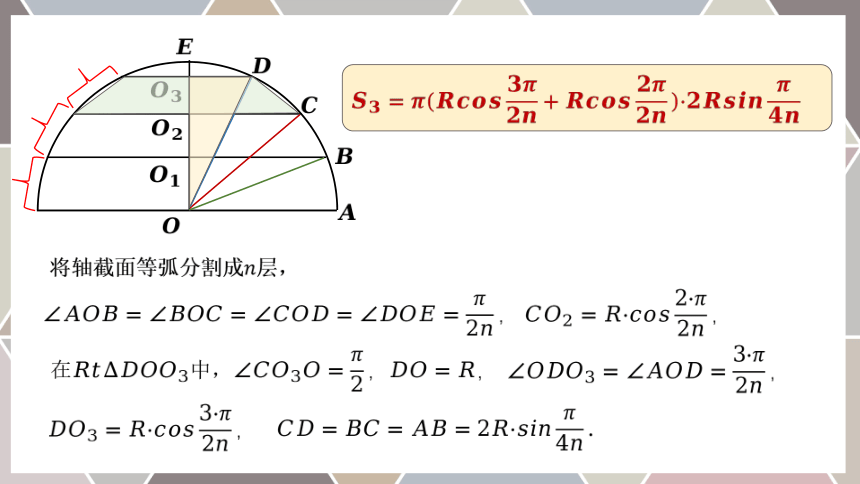
将轴截面等弧分割成层,
,
将轴截面等弧分割成层,
将轴截面等弧分割成层,
从下往上,第i个圆台的上、下底面半径分别为:
母线长为:
侧面积为:
从下往上,第i个圆台的侧面积为:
侧面积之和为:
从下往上,第i个圆台的侧面积为:
侧面积之和为:
1
合作探究
问题2:如何推导球的体积公式?
合作探究
球的体积,等于所有“小锥体”的体积之和.
O
O
球的表面积,等于所有“小锥体”的底面积之和.
分割
求和(以直代曲)
取极限
思想方法:
问题2:如何推导球的体积公式?
典例分析
例3. 如图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m. 如果在浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?(取3.14)
组合体的表面积=圆柱的侧面积+球的表面积
典例分析
例4. 如图,圆柱的底面直径和高都等于球的直径,求球与圆柱的体积之比.
在“圆柱容球”中,
球的体积是圆柱体积的,
球的表面积也是圆柱表面积的.
归纳小结
1.球的表面积公式、体积公式是什么?
2.我们是如何探究球的表面积公式、体积公式的?
探究过程体现了哪些数学思想?
单元框架
简单几何体的表面积与体积
柱体、锥体、台体的表面积与体积
球的表面积与体积
球的表面积
球的体积
棱柱、棱锥、棱台的表面积与体积
圆柱、圆锥、圆台的表面积与体积
空间几何体
空间点、直线、平面之间的位置关系
布置作业
1.基础作业:《固学案》第49页课时3
2.探究作业:阅读课本第121-123页,自学祖暅原理,
探究用祖暅原理推导球的体积公式.
球的表面积与体积
单元框架
简单几何体的表面积与体积
柱体、锥体、台体的表面积与体积
棱柱、棱锥、棱台的表面积与体积
圆柱、圆锥、圆台的表面积与体积
空间几何体
知识回顾
l
O
O'
2πr
r
O'
O
r'
2πr'
r
l
2πr
2πr
O
S
l
r
新知探究
新知探究
分割
求和(以直代曲)
取极限
思想方法:
作圆的内接正六边形、十二边形,…
……
A3
An
A4
割之弥细,所失弥少,
割之又割,以至于不可割,
则与圆周合体而无所失矣.
时,
正边形的面积越来越趋近于圆的面积
正边形的周长越来越趋近于圆的周长
新知探究
问题1:类比刘徽的割圆术,如何推导球的表面积公式?
分割
求和(以直代曲)
取极限
思想方法:
将轴截面等弧分割
A
O
A
O
将轴截面等弧分割成层,
,
将轴截面等弧分割成层,
将轴截面等弧分割成层,
从下往上,第i个圆台的上、下底面半径分别为:
母线长为:
侧面积为:
从下往上,第i个圆台的侧面积为:
侧面积之和为:
从下往上,第i个圆台的侧面积为:
侧面积之和为:
1
合作探究
问题2:如何推导球的体积公式?
合作探究
球的体积,等于所有“小锥体”的体积之和.
O
O
球的表面积,等于所有“小锥体”的底面积之和.
分割
求和(以直代曲)
取极限
思想方法:
问题2:如何推导球的体积公式?
典例分析
例3. 如图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m. 如果在浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?(取3.14)
组合体的表面积=圆柱的侧面积+球的表面积
典例分析
例4. 如图,圆柱的底面直径和高都等于球的直径,求球与圆柱的体积之比.
在“圆柱容球”中,
球的体积是圆柱体积的,
球的表面积也是圆柱表面积的.
归纳小结
1.球的表面积公式、体积公式是什么?
2.我们是如何探究球的表面积公式、体积公式的?
探究过程体现了哪些数学思想?
单元框架
简单几何体的表面积与体积
柱体、锥体、台体的表面积与体积
球的表面积与体积
球的表面积
球的体积
棱柱、棱锥、棱台的表面积与体积
圆柱、圆锥、圆台的表面积与体积
空间几何体
空间点、直线、平面之间的位置关系
布置作业
1.基础作业:《固学案》第49页课时3
2.探究作业:阅读课本第121-123页,自学祖暅原理,
探究用祖暅原理推导球的体积公式.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
