华东师大版九年级上册23.2 相似图形 同步练习(含答案)
文档属性
| 名称 | 华东师大版九年级上册23.2 相似图形 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 134.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 17:27:46 | ||
图片预览



文档简介
23.1 成比例线段 ~23.2 相似图形
一、选择题
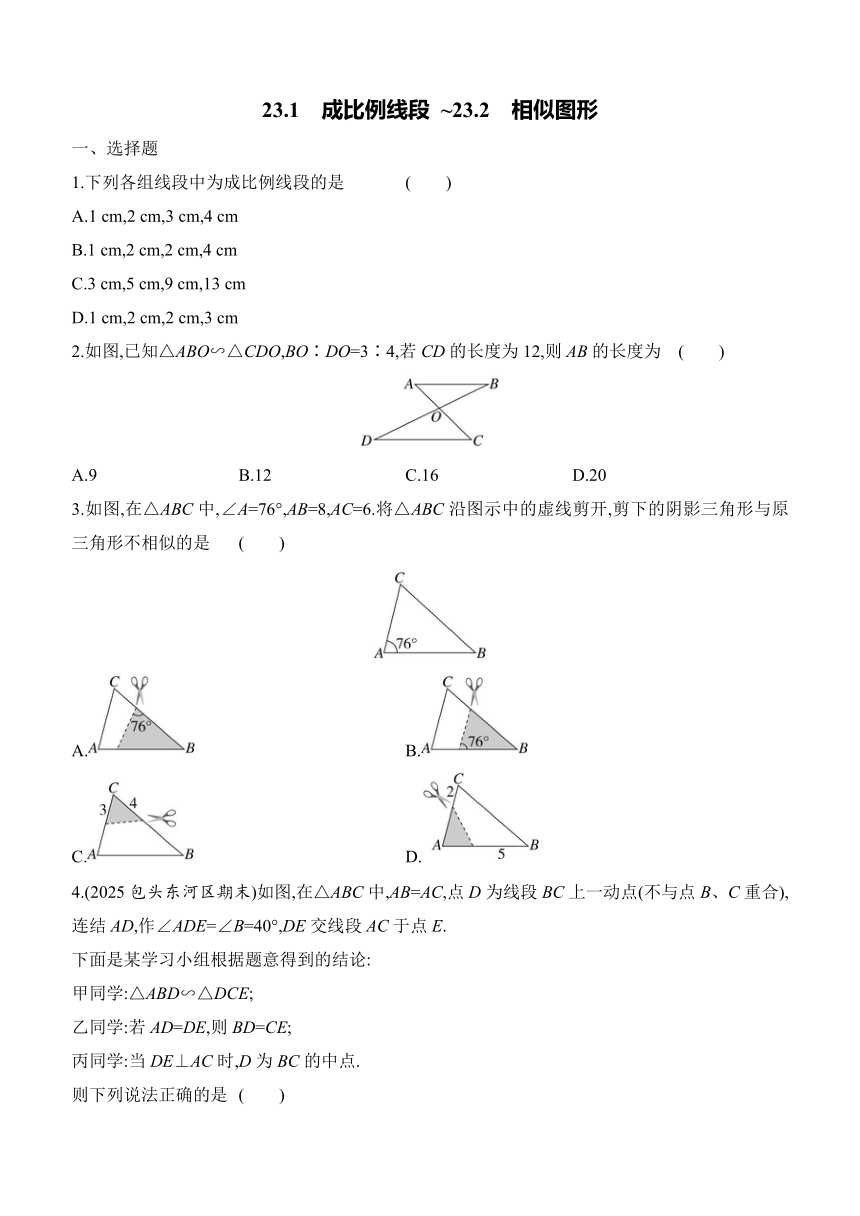
1.下列各组线段中为成比例线段的是 ( )
A.1 cm,2 cm,3 cm,4 cm
B.1 cm,2 cm,2 cm,4 cm
C.3 cm,5 cm,9 cm,13 cm
D.1 cm,2 cm,2 cm,3 cm
2.如图,已知△ABO∽△CDO,BO∶DO=3∶4,若CD的长度为12,则AB的长度为 ( )
A.9 B.12 C.16 D.20
3.如图,在△ABC中,∠A=76°,AB=8,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是 ( )
A. B.
C. D.
4.(2025包头东河区期末)如图,在△ABC中,AB=AC,点D为线段BC上一动点(不与点B、C重合),连结AD,作∠ADE=∠B=40°,DE交线段AC于点E.
下面是某学习小组根据题意得到的结论:
甲同学:△ABD∽△DCE;
乙同学:若AD=DE,则BD=CE;
丙同学:当DE⊥AC时,D为BC的中点.
则下列说法正确的是 ( )
A.只有甲同学得到的结论正确
B.乙和丙同学得到的结论都正确
C.甲和丙同学得到的结论都正确
D.三个同学得到的结论都正确
5.如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;;④AC2=AD·AB,其中不能判定△ABC∽△ACD的条件为 ( )
A.① B.②
C.③ D.④
第5题图 第6题图
6.如图,D为△ABC边AB上任一点,DE∥BC交AC于点E,连结BE、CD,BE、CD相交于点F,则下列等式中不成立的是 ( )
A. B.
C. D.
二、填空题
7.(2024青海中考)如图,AC和BD相交于点O,请你添加一个条件 ,使得△AOB∽△COD.
第7题图 第8题图
8.如图,△ABC∽△AED,∠AED=40°,∠A=60°,则∠C= .
三、解答题
9.(2024常州中考)书画装裱,是指为书画配上衬纸、卷轴以便张贴、欣赏和收藏,是我国具有民族传统的一门特殊艺术.如图,一幅书画在装裱前的大小是1.2 m×0.8 m.装裱后,上、下、左、右边衬的宽度分别是a m、b m、c m、d m.若装裱后AB与AD的比是8∶5,且a=b,c=d,c=2a,求四周边衬的宽度.
10.(2025上海虹口区期中)如图,在平行四边形ABCD中,E、F分别是边BC、CD上的点,且EF∥BD,AE、AF分别交BD于点G和点H,BD=12,EF=8.
(1)求的值.
(2)求线段GH的长.
11.如图,在四边形ABCD中,对角线AC和BD相交于点O,∠BAC=∠BDC.
(1)求证:△AOD∽△BOC.
(2)过点A作AE∥CD,AE交BD于点E,求证:AB·AD=AE·BC.
12.已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是矩形,且DE⊥CF,求证:.
(2)如图2,若四边形ABCD是平行四边形,且∠B+∠EGC=180°,求证:.
图1 图2
【详解答案】
1.B 解析:∵1×4=2×2,∴选项B中线段是成比例线段.故选B.
2.A 解析:∵△ABO∽△CDO,BO∶DO=3∶4,∴AB∶CD=BO∶DO=3∶4,∵CD=12,∴AB∶12=3∶4,
解得AB=9.故选A.
3.C 解析:A.阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;B.阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;C.两三角形的对应边不成比例,故两三角形不相似,故本选项符合题意;D.阴影三角形中,∠A的两边分别为6-2=4,8-5=3,则两三角形的两边成比例且夹角相等,故两三角形相似,故本选项不符合题意.故选C.
4.D 解析:在△ABC中,∵AB=AC,∴∠C=∠B=40°,∵∠B+∠BAD=∠CDE+∠ADE,∠ADE=∠B=40°,
∴∠BAD=∠CDE,∴△ABD∽△DCE,
甲同学得到的结论正确;∵∠C=∠B,∠BAD=∠CDE,AD=DE,∴△ABD≌△DCE,∴BD=CE,乙同学得到的结论正确;当DE⊥AC时,∠DEC=90°,∴∠EDC=90°-∠C=50°,∴∠ADC=∠ADE+∠EDC=90°,∴AD⊥BC,∵AB=AC,∴BD=CD,∴D为BC的中点,丙同学得到的结论正确.综上所述,三个同学得到的结论都正确.故选D.
5.C 解析:∵∠B=∠ACD,∠A=∠A,
∴△ABC∽△ACD,
故①不符合题意;
∵∠ADC=∠ACB,∠A=∠A,
∴△ABC∽△ACD,
故②不符合题意;
∵AC2=AD·AB,∴,
∵∠A=∠A,∴△ABC∽△ACD,
故④不符合题意;
③中∠A不是已知的成比例线段的夹角,故③不能判定△ABC∽△ACD.故选C.
6.C 解析:∵DE∥BC,∴,故A成立.∵DE∥BC,∴△EDF∽△BCF,∴,故B成立.∵DE∥BC,
∴△ADE∽△ABC,∴≠,故C不成立.∵,,∴,故D成立.故选C.
7.∠A=∠C(答案不唯一)
解析:∵∠A=∠C,∠AOB=∠COD,∴△AOB∽△COD.(答案不唯一)
8.80° 解析:∵∠AED=40°,∠A=60°,∠A+∠ADE+∠AED=180°,
∴∠ADE=80°,∵△ABC∽△AED,
∴∠C=∠ADE=80°.
9.解:由题意得,AB=(1.2+c+d)m,AD=(0.8+a+b)m,
∵a=b,c=d,c=2a,
∴AB=(1.2+c+d)m=(1.2+4a)m,AD=(0.8+a+b)m=(0.8+2a)m,
∵AB与AD的比是8∶5,
∴(1.2+4a)∶(0.8+2a)=8∶5,
∴a=0.1,经检验,a=0.1符合题意,
∴b=0.1,c=d=0.2.
答:上、下、左、右边衬的宽度分别是0.1 m、0.1 m、0.2 m、0.2 m.
10.解:(1)∵EF∥BD,∴,
∵BD=12,EF=8,∴,
∴,∵四边形ABCD是平行四边形,∴AB=CD,∴.
(2)∵DF∥AB,∴,
∴,∵EF∥BD,∴,∴,∴GH=6.
11.证明:(1)∵∠BAC=∠BDC,
∠AOB=∠DOC,
∴△AOB∽△DOC,
∴,∴.
又∵∠AOD=∠BOC,
∴△AOD∽△BOC.
(2)∵△AOD∽△BOC,
∴∠ADE=∠BCA.
∵AE∥CD,∴∠AED=∠BDC.
∵∠BAC=∠BDC,
∴∠AED=∠BAC.
∴△AED∽△BAC.
∴,∴AB·AD=AE·BC.
12.证明:(1)∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,AB=CD.
∵DE⊥CF,∴∠FGD=90°.
∴∠ADE+∠CFD=∠DCF+∠CFD=
90°,∴∠ADE=∠DCF,
∴△ADE∽△DCF,∴.
又∵AB=CD,∴.
(2)如图,在AD的延长线上取点M,连结CM,使CM=CF,
∴∠CMF=∠CFM.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD.
∴∠A=∠CDM,∠B+∠A=180°.
∵∠B+∠EGC=180°,
∠EGF+∠EGC=180°,
∴∠EGF+∠A=180°,
∴∠AED+∠AFG=180°.
∵∠CFM+∠AFG=180°,
∴∠AED=∠CFM=∠CMF,
∴△ADE∽△DCM,∴.
又∵AB=CD,CM=CF,∴.
一、选择题
1.下列各组线段中为成比例线段的是 ( )
A.1 cm,2 cm,3 cm,4 cm
B.1 cm,2 cm,2 cm,4 cm
C.3 cm,5 cm,9 cm,13 cm
D.1 cm,2 cm,2 cm,3 cm
2.如图,已知△ABO∽△CDO,BO∶DO=3∶4,若CD的长度为12,则AB的长度为 ( )
A.9 B.12 C.16 D.20
3.如图,在△ABC中,∠A=76°,AB=8,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是 ( )
A. B.
C. D.
4.(2025包头东河区期末)如图,在△ABC中,AB=AC,点D为线段BC上一动点(不与点B、C重合),连结AD,作∠ADE=∠B=40°,DE交线段AC于点E.
下面是某学习小组根据题意得到的结论:
甲同学:△ABD∽△DCE;
乙同学:若AD=DE,则BD=CE;
丙同学:当DE⊥AC时,D为BC的中点.
则下列说法正确的是 ( )
A.只有甲同学得到的结论正确
B.乙和丙同学得到的结论都正确
C.甲和丙同学得到的结论都正确
D.三个同学得到的结论都正确
5.如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;;④AC2=AD·AB,其中不能判定△ABC∽△ACD的条件为 ( )
A.① B.②
C.③ D.④
第5题图 第6题图
6.如图,D为△ABC边AB上任一点,DE∥BC交AC于点E,连结BE、CD,BE、CD相交于点F,则下列等式中不成立的是 ( )
A. B.
C. D.
二、填空题
7.(2024青海中考)如图,AC和BD相交于点O,请你添加一个条件 ,使得△AOB∽△COD.
第7题图 第8题图
8.如图,△ABC∽△AED,∠AED=40°,∠A=60°,则∠C= .
三、解答题
9.(2024常州中考)书画装裱,是指为书画配上衬纸、卷轴以便张贴、欣赏和收藏,是我国具有民族传统的一门特殊艺术.如图,一幅书画在装裱前的大小是1.2 m×0.8 m.装裱后,上、下、左、右边衬的宽度分别是a m、b m、c m、d m.若装裱后AB与AD的比是8∶5,且a=b,c=d,c=2a,求四周边衬的宽度.
10.(2025上海虹口区期中)如图,在平行四边形ABCD中,E、F分别是边BC、CD上的点,且EF∥BD,AE、AF分别交BD于点G和点H,BD=12,EF=8.
(1)求的值.
(2)求线段GH的长.
11.如图,在四边形ABCD中,对角线AC和BD相交于点O,∠BAC=∠BDC.
(1)求证:△AOD∽△BOC.
(2)过点A作AE∥CD,AE交BD于点E,求证:AB·AD=AE·BC.
12.已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是矩形,且DE⊥CF,求证:.
(2)如图2,若四边形ABCD是平行四边形,且∠B+∠EGC=180°,求证:.
图1 图2
【详解答案】
1.B 解析:∵1×4=2×2,∴选项B中线段是成比例线段.故选B.
2.A 解析:∵△ABO∽△CDO,BO∶DO=3∶4,∴AB∶CD=BO∶DO=3∶4,∵CD=12,∴AB∶12=3∶4,
解得AB=9.故选A.
3.C 解析:A.阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;B.阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;C.两三角形的对应边不成比例,故两三角形不相似,故本选项符合题意;D.阴影三角形中,∠A的两边分别为6-2=4,8-5=3,则两三角形的两边成比例且夹角相等,故两三角形相似,故本选项不符合题意.故选C.
4.D 解析:在△ABC中,∵AB=AC,∴∠C=∠B=40°,∵∠B+∠BAD=∠CDE+∠ADE,∠ADE=∠B=40°,
∴∠BAD=∠CDE,∴△ABD∽△DCE,
甲同学得到的结论正确;∵∠C=∠B,∠BAD=∠CDE,AD=DE,∴△ABD≌△DCE,∴BD=CE,乙同学得到的结论正确;当DE⊥AC时,∠DEC=90°,∴∠EDC=90°-∠C=50°,∴∠ADC=∠ADE+∠EDC=90°,∴AD⊥BC,∵AB=AC,∴BD=CD,∴D为BC的中点,丙同学得到的结论正确.综上所述,三个同学得到的结论都正确.故选D.
5.C 解析:∵∠B=∠ACD,∠A=∠A,
∴△ABC∽△ACD,
故①不符合题意;
∵∠ADC=∠ACB,∠A=∠A,
∴△ABC∽△ACD,
故②不符合题意;
∵AC2=AD·AB,∴,
∵∠A=∠A,∴△ABC∽△ACD,
故④不符合题意;
③中∠A不是已知的成比例线段的夹角,故③不能判定△ABC∽△ACD.故选C.
6.C 解析:∵DE∥BC,∴,故A成立.∵DE∥BC,∴△EDF∽△BCF,∴,故B成立.∵DE∥BC,
∴△ADE∽△ABC,∴≠,故C不成立.∵,,∴,故D成立.故选C.
7.∠A=∠C(答案不唯一)
解析:∵∠A=∠C,∠AOB=∠COD,∴△AOB∽△COD.(答案不唯一)
8.80° 解析:∵∠AED=40°,∠A=60°,∠A+∠ADE+∠AED=180°,
∴∠ADE=80°,∵△ABC∽△AED,
∴∠C=∠ADE=80°.
9.解:由题意得,AB=(1.2+c+d)m,AD=(0.8+a+b)m,
∵a=b,c=d,c=2a,
∴AB=(1.2+c+d)m=(1.2+4a)m,AD=(0.8+a+b)m=(0.8+2a)m,
∵AB与AD的比是8∶5,
∴(1.2+4a)∶(0.8+2a)=8∶5,
∴a=0.1,经检验,a=0.1符合题意,
∴b=0.1,c=d=0.2.
答:上、下、左、右边衬的宽度分别是0.1 m、0.1 m、0.2 m、0.2 m.
10.解:(1)∵EF∥BD,∴,
∵BD=12,EF=8,∴,
∴,∵四边形ABCD是平行四边形,∴AB=CD,∴.
(2)∵DF∥AB,∴,
∴,∵EF∥BD,∴,∴,∴GH=6.
11.证明:(1)∵∠BAC=∠BDC,
∠AOB=∠DOC,
∴△AOB∽△DOC,
∴,∴.
又∵∠AOD=∠BOC,
∴△AOD∽△BOC.
(2)∵△AOD∽△BOC,
∴∠ADE=∠BCA.
∵AE∥CD,∴∠AED=∠BDC.
∵∠BAC=∠BDC,
∴∠AED=∠BAC.
∴△AED∽△BAC.
∴,∴AB·AD=AE·BC.
12.证明:(1)∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,AB=CD.
∵DE⊥CF,∴∠FGD=90°.
∴∠ADE+∠CFD=∠DCF+∠CFD=
90°,∴∠ADE=∠DCF,
∴△ADE∽△DCF,∴.
又∵AB=CD,∴.
(2)如图,在AD的延长线上取点M,连结CM,使CM=CF,
∴∠CMF=∠CFM.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD.
∴∠A=∠CDM,∠B+∠A=180°.
∵∠B+∠EGC=180°,
∠EGF+∠EGC=180°,
∴∠EGF+∠A=180°,
∴∠AED+∠AFG=180°.
∵∠CFM+∠AFG=180°,
∴∠AED=∠CFM=∠CMF,
∴△ADE∽△DCM,∴.
又∵AB=CD,CM=CF,∴.
