华东师大版九年级上册23.2 相似图形 同步练习(含答案)
文档属性
| 名称 | 华东师大版九年级上册23.2 相似图形 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 17:38:04 | ||
图片预览


文档简介
23.2相似图形
相似图形(多边形)的定义(判定)
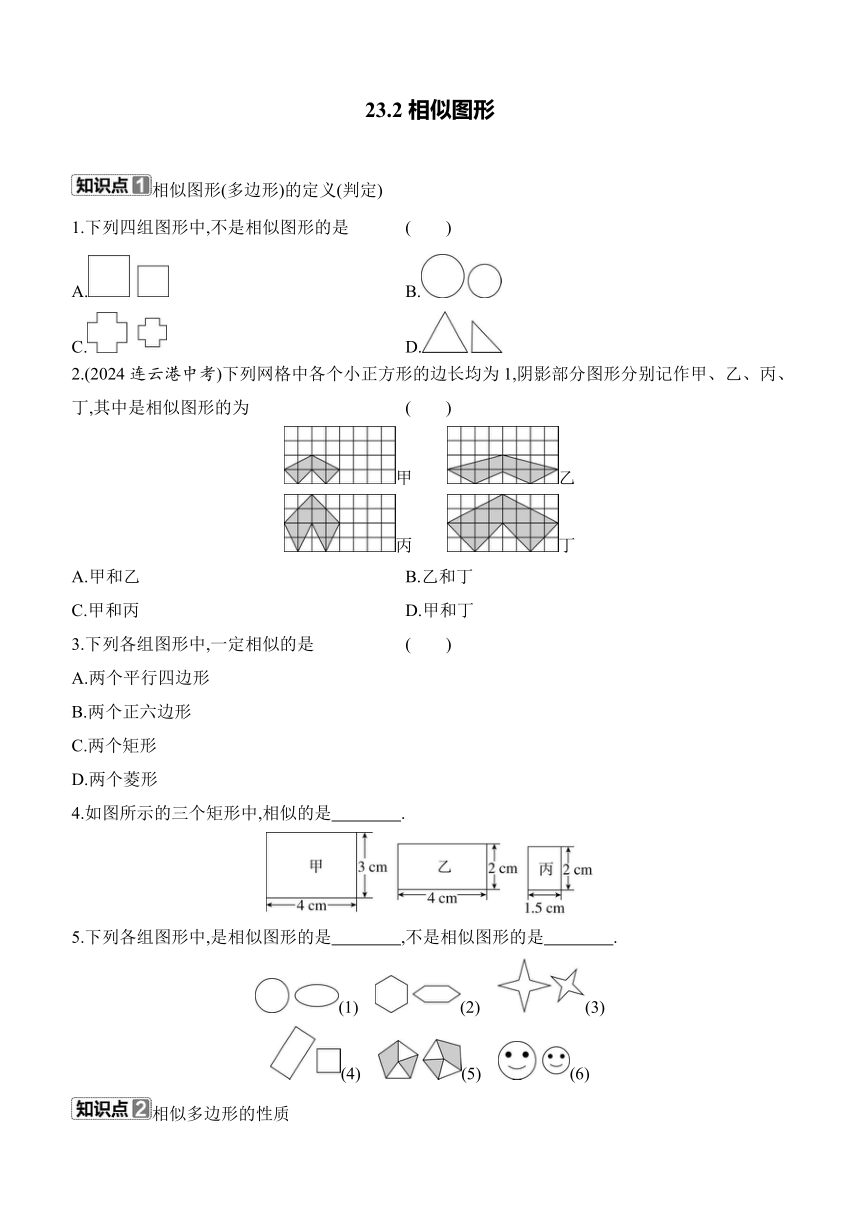
1.下列四组图形中,不是相似图形的是 ( )
A. B.
C. D.
2.(2024连云港中考)下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似图形的为 ( )
甲 乙
丙 丁
A.甲和乙 B.乙和丁
C.甲和丙 D.甲和丁
3.下列各组图形中,一定相似的是 ( )
A.两个平行四边形
B.两个正六边形
C.两个矩形
D.两个菱形
4.如图所示的三个矩形中,相似的是 .
5.下列各组图形中,是相似图形的是 ,不是相似图形的是 .
(1) (2) (3)
(4) (5) (6)
相似多边形的性质
6.(教材P59例变式)如图,四边形ABCD与四边形EFGH相似,点A、B、C、D的对应点分别是点E、F、G、H,则下列角的度数正确的是 ( )
A.∠D=81° B.∠F=83°
C.∠G=78° D.∠H=91°
7.若一个多边形的各边长分别为2、3、4、5、6,另一个和它相似的多边形的最长边长为24,则这个多边形的最短边长为 ( )
A.6 B.8
C.10 D.12
8.如图,四边形ABCD与四边形A1B1C1D1相似,点A、B、C、D的对应点分别为点A1、B1、C1、D1,∠A=116°,∠B=40°,∠C=65°,求∠D1的度数和x的值.
1.下列各项:①两个边长不等的等边三角形;②两个边长不等的正方形;③两个边长不等的菱形;④两个斜边不等的等腰直角三角形,其中的两个图形一定相似的有 ( )
A.①② B.①②③
C.①②④ D.①②③④
2.如图,小康利用复印机将一张长为5 cm,宽为3 cm的长方形图片放大,其中放大后的长方形的和的长为10 cm,则放大后的长方形的面积为 ( )
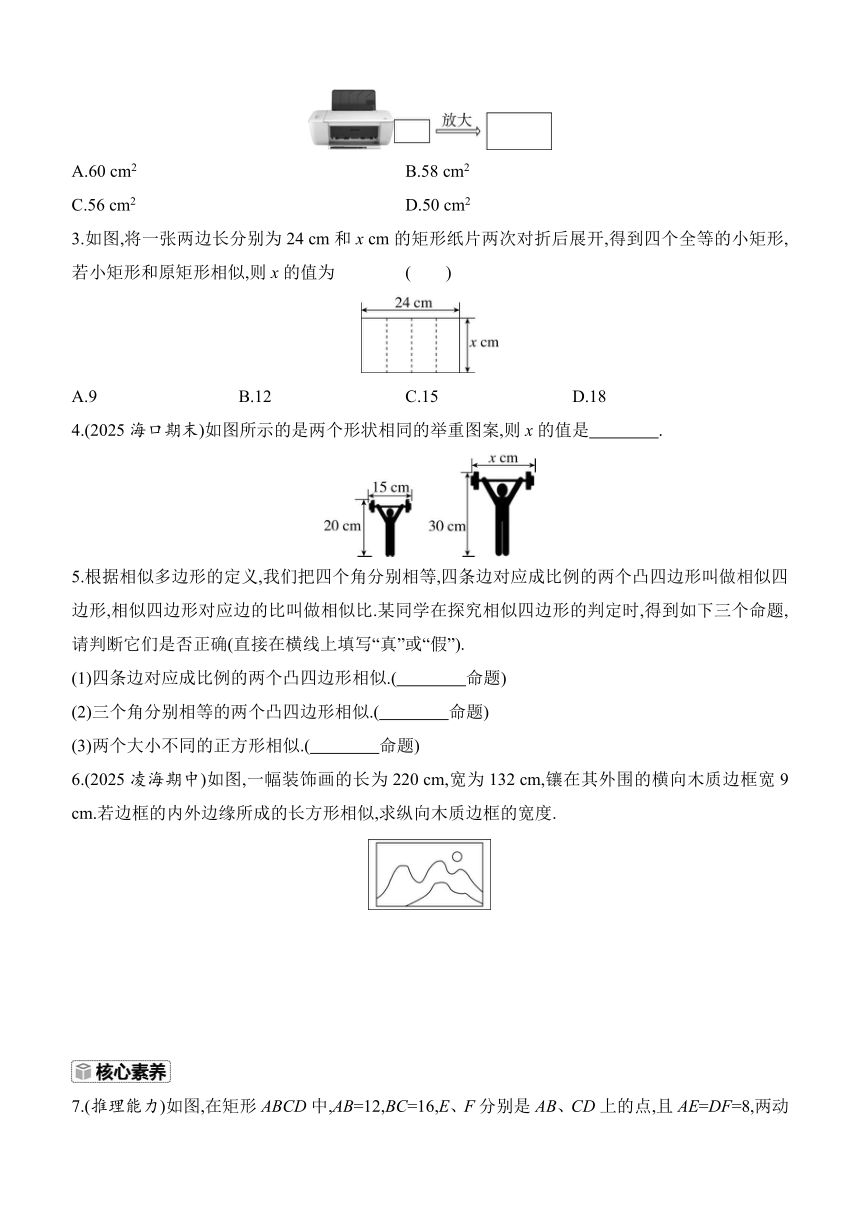
A.60 cm2 B.58 cm2
C.56 cm2 D.50 cm2
3.如图,将一张两边长分别为24 cm和x cm的矩形纸片两次对折后展开,得到四个全等的小矩形,若小矩形和原矩形相似,则x的值为 ( )
A.9 B.12 C.15 D.18
4.(2025海口期末)如图所示的是两个形状相同的举重图案,则x的值是 .
5.根据相似多边形的定义,我们把四个角分别相等,四条边对应成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
(1)四条边对应成比例的两个凸四边形相似.( 命题)
(2)三个角分别相等的两个凸四边形相似.( 命题)
(3)两个大小不同的正方形相似.( 命题)
6.(2025凌海期中)如图,一幅装饰画的长为220 cm,宽为132 cm,镶在其外围的横向木质边框宽9 cm.若边框的内外边缘所成的长方形相似,求纵向木质边框的宽度.
7.(推理能力)如图,在矩形ABCD中,AB=12,BC=16,E、F分别是AB、CD上的点,且AE=DF=8,两动点M、N都以2 cm/s的速度分别从C、F两点沿CB、FE向B、E两点运动,写出当M、N运动多长时间时能使矩形CFNM与矩形AEFD相似,并证明你的结论.
【详解答案】
基础达标
1.D 解析:A.形状相同,但大小不同,符合相似图形的定义,故不符合题意;B.形状相同,但大小不同,符合相似图形的定义,故不符合题意;C.形状相同,但大小不同,符合相似图形的定义,故不符合题意;D.形状不相同,不符合相似图形的定义,故符合题意.故选D.
2.D 解析:观察可得,甲和丁对应角相等,对应边成比例,且形状相同.故选D.
3.B 解析:A.两个平行四边形不一定相似,故本选项错误;B.两个正六边形,形状相同,大小不一定相同,符合相似图形的定义,故本选项正确;C.两个矩形,四个角相等,但是各边不一定对应成比例,所以不一定相似,故本选项错误;D.两个菱形,形状不一定相同,故本选项错误.故选B.
4.甲与丙
5.(3)(5)(6) (1)(2)(4)
6.A 解析:∵四边形ABCD与四边形EFGH相似,点A、B、C、D的对应点分别为点E、F、G、H,∴∠B=∠F=78°,∠A=∠E=118°,∠C=∠G=83°,∴∠D=∠H=360°-78°-118°-83°=81°.故选A.
7.B 解析:设这个多边形的最短边长为x,∵两个多边形相似,∴,解得x=8.故选B.
8.解:∵∠A=116°,∠B=40°,∠C=65°,
∴∠D=360°-116°-40°-65°=139°.
∵四边形ABCD与四边形A1B1C1D1相似,点A、B、C、D的对应点分别为点A1、B1、C1、D1,∴∠D1=∠D=139°,,∴,
∴x=.
能力提升
1.C 解析:①两个边长不等的等边三角形一定相似,符合题意;②两个边长不等的正方形一定相似,符合题意;③两个边长不等的菱形的对应角不一定相等,故不一定相似,不符合题意;④两个斜边不等的等腰直角三角形一定相似,符合题意.故选C.
2.A 解析:设放大后的长方形的宽是x cm,∵放大前后的两个长方形相似,∴5∶10=3∶x,∴x=6,∴放大后的长方形的宽是6 cm,放大后的长方形的面积为10×6=60(cm2).故选A.
3.B 解析:由题意得24∶x=x∶6,解得x=12(负值舍去).故选B.
4.22.5 解析:根据题意得15∶x=20∶30,解得x=22.5.
5.(1)假 (2)假 (3)真 解析:(1)四条边对应成比例的两个凸四边形相似是假命题,角不一定相等.(2)三个角分别相等的两个凸四边形相似是假命题,边不一定成比例.(3)两个大小不同的正方形相似是真命题.
6.解:设纵向木质边框的宽度为x cm,
∵边框的内外边缘所成的长方形相似,
∴,
解得x=15.
答:纵向木质边框的宽度为15 cm.
7.解:当M、N运动1 s或4 s时,能使矩形CFNM与矩形AEFD相似.
证明:设运动t s时能使矩形CFNM与矩形AEFD相似,
由题意知或,
解得t=4或t=1.
当t=4时,NF=8,
∵,四边形CFNM与四边形AEFD都是矩形,∴矩形CFNM与矩形AEFD相似.同理可证当t=1时矩形CFNM与矩形AEFD相似.
相似图形(多边形)的定义(判定)
1.下列四组图形中,不是相似图形的是 ( )
A. B.
C. D.
2.(2024连云港中考)下列网格中各个小正方形的边长均为1,阴影部分图形分别记作甲、乙、丙、丁,其中是相似图形的为 ( )
甲 乙
丙 丁
A.甲和乙 B.乙和丁
C.甲和丙 D.甲和丁
3.下列各组图形中,一定相似的是 ( )
A.两个平行四边形
B.两个正六边形
C.两个矩形
D.两个菱形
4.如图所示的三个矩形中,相似的是 .
5.下列各组图形中,是相似图形的是 ,不是相似图形的是 .
(1) (2) (3)
(4) (5) (6)
相似多边形的性质
6.(教材P59例变式)如图,四边形ABCD与四边形EFGH相似,点A、B、C、D的对应点分别是点E、F、G、H,则下列角的度数正确的是 ( )
A.∠D=81° B.∠F=83°
C.∠G=78° D.∠H=91°
7.若一个多边形的各边长分别为2、3、4、5、6,另一个和它相似的多边形的最长边长为24,则这个多边形的最短边长为 ( )
A.6 B.8
C.10 D.12
8.如图,四边形ABCD与四边形A1B1C1D1相似,点A、B、C、D的对应点分别为点A1、B1、C1、D1,∠A=116°,∠B=40°,∠C=65°,求∠D1的度数和x的值.
1.下列各项:①两个边长不等的等边三角形;②两个边长不等的正方形;③两个边长不等的菱形;④两个斜边不等的等腰直角三角形,其中的两个图形一定相似的有 ( )
A.①② B.①②③
C.①②④ D.①②③④
2.如图,小康利用复印机将一张长为5 cm,宽为3 cm的长方形图片放大,其中放大后的长方形的和的长为10 cm,则放大后的长方形的面积为 ( )
A.60 cm2 B.58 cm2
C.56 cm2 D.50 cm2
3.如图,将一张两边长分别为24 cm和x cm的矩形纸片两次对折后展开,得到四个全等的小矩形,若小矩形和原矩形相似,则x的值为 ( )
A.9 B.12 C.15 D.18
4.(2025海口期末)如图所示的是两个形状相同的举重图案,则x的值是 .
5.根据相似多边形的定义,我们把四个角分别相等,四条边对应成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).
(1)四条边对应成比例的两个凸四边形相似.( 命题)
(2)三个角分别相等的两个凸四边形相似.( 命题)
(3)两个大小不同的正方形相似.( 命题)
6.(2025凌海期中)如图,一幅装饰画的长为220 cm,宽为132 cm,镶在其外围的横向木质边框宽9 cm.若边框的内外边缘所成的长方形相似,求纵向木质边框的宽度.
7.(推理能力)如图,在矩形ABCD中,AB=12,BC=16,E、F分别是AB、CD上的点,且AE=DF=8,两动点M、N都以2 cm/s的速度分别从C、F两点沿CB、FE向B、E两点运动,写出当M、N运动多长时间时能使矩形CFNM与矩形AEFD相似,并证明你的结论.
【详解答案】
基础达标
1.D 解析:A.形状相同,但大小不同,符合相似图形的定义,故不符合题意;B.形状相同,但大小不同,符合相似图形的定义,故不符合题意;C.形状相同,但大小不同,符合相似图形的定义,故不符合题意;D.形状不相同,不符合相似图形的定义,故符合题意.故选D.
2.D 解析:观察可得,甲和丁对应角相等,对应边成比例,且形状相同.故选D.
3.B 解析:A.两个平行四边形不一定相似,故本选项错误;B.两个正六边形,形状相同,大小不一定相同,符合相似图形的定义,故本选项正确;C.两个矩形,四个角相等,但是各边不一定对应成比例,所以不一定相似,故本选项错误;D.两个菱形,形状不一定相同,故本选项错误.故选B.
4.甲与丙
5.(3)(5)(6) (1)(2)(4)
6.A 解析:∵四边形ABCD与四边形EFGH相似,点A、B、C、D的对应点分别为点E、F、G、H,∴∠B=∠F=78°,∠A=∠E=118°,∠C=∠G=83°,∴∠D=∠H=360°-78°-118°-83°=81°.故选A.
7.B 解析:设这个多边形的最短边长为x,∵两个多边形相似,∴,解得x=8.故选B.
8.解:∵∠A=116°,∠B=40°,∠C=65°,
∴∠D=360°-116°-40°-65°=139°.
∵四边形ABCD与四边形A1B1C1D1相似,点A、B、C、D的对应点分别为点A1、B1、C1、D1,∴∠D1=∠D=139°,,∴,
∴x=.
能力提升
1.C 解析:①两个边长不等的等边三角形一定相似,符合题意;②两个边长不等的正方形一定相似,符合题意;③两个边长不等的菱形的对应角不一定相等,故不一定相似,不符合题意;④两个斜边不等的等腰直角三角形一定相似,符合题意.故选C.
2.A 解析:设放大后的长方形的宽是x cm,∵放大前后的两个长方形相似,∴5∶10=3∶x,∴x=6,∴放大后的长方形的宽是6 cm,放大后的长方形的面积为10×6=60(cm2).故选A.
3.B 解析:由题意得24∶x=x∶6,解得x=12(负值舍去).故选B.
4.22.5 解析:根据题意得15∶x=20∶30,解得x=22.5.
5.(1)假 (2)假 (3)真 解析:(1)四条边对应成比例的两个凸四边形相似是假命题,角不一定相等.(2)三个角分别相等的两个凸四边形相似是假命题,边不一定成比例.(3)两个大小不同的正方形相似是真命题.
6.解:设纵向木质边框的宽度为x cm,
∵边框的内外边缘所成的长方形相似,
∴,
解得x=15.
答:纵向木质边框的宽度为15 cm.
7.解:当M、N运动1 s或4 s时,能使矩形CFNM与矩形AEFD相似.
证明:设运动t s时能使矩形CFNM与矩形AEFD相似,
由题意知或,
解得t=4或t=1.
当t=4时,NF=8,
∵,四边形CFNM与四边形AEFD都是矩形,∴矩形CFNM与矩形AEFD相似.同理可证当t=1时矩形CFNM与矩形AEFD相似.
