华东师大版九年级上册23.3.1 相似三角形 同步练习(含答案)
文档属性
| 名称 | 华东师大版九年级上册23.3.1 相似三角形 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 125.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 00:00:00 | ||
图片预览

文档简介
23.3相似三角形
1.相似三角形
相似三角形
1.(2025陇南康县期中)如图,AD、BC相交于点O,且△AOB∽△DOC,点A的对应点为点D,若∠A=30°,∠COD=100°,则∠C的度数为 ( )
A.20° B.30° C.40° D.50°
2.如图,在小正方形网格中,△ABC∽△DEF,则∠BAC的度数为 .
3.如图,已知△AOB∽△DOC,OA=2,OD=7,OB=5,DC=12.求AB、OC的长.
相似比
4.若△ABC∽△DEF,AB=6,DE=4,则△ABC与△DEF的相似比为 ( )
A.2∶3 B.4∶9
C. D.3∶2
由平行判定三角形相似
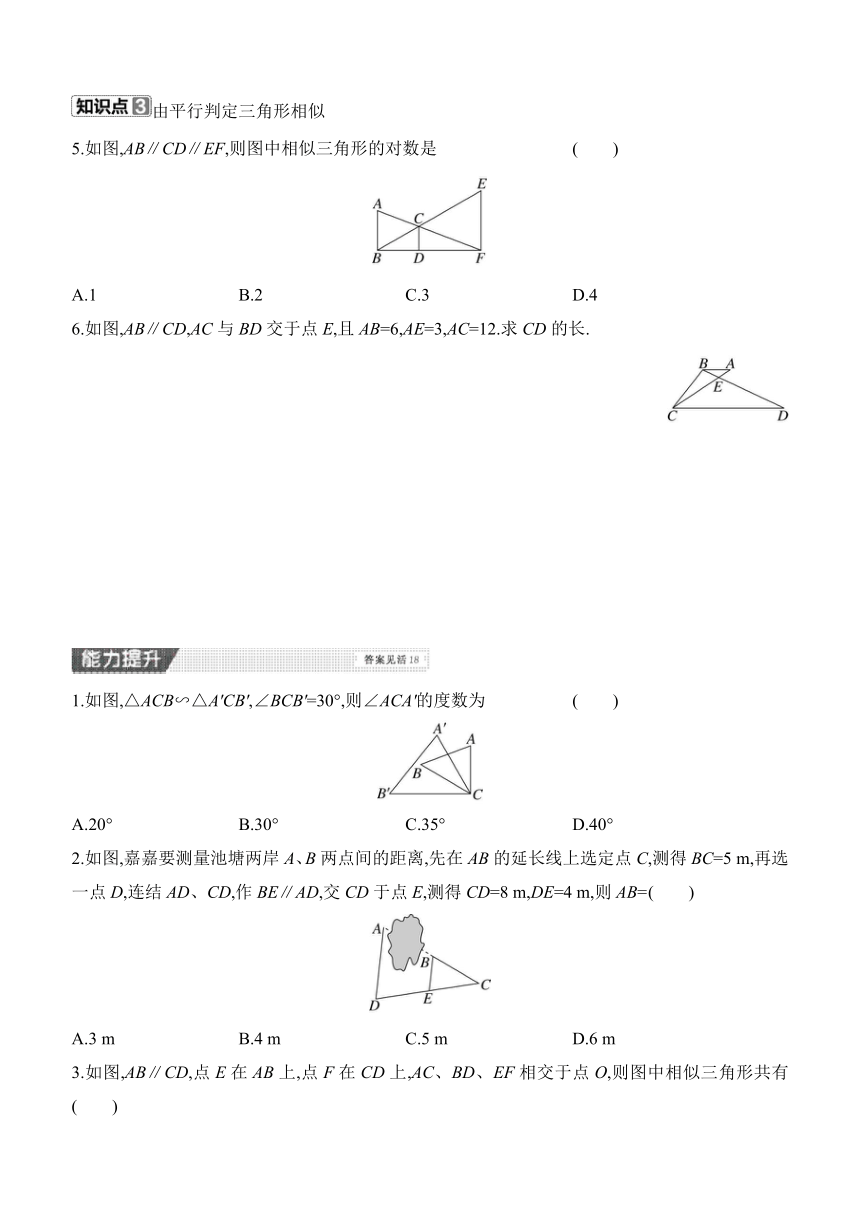
5.如图,AB∥CD∥EF,则图中相似三角形的对数是 ( )
A.1 B.2 C.3 D.4
6.如图,AB∥CD,AC与BD交于点E,且AB=6,AE=3,AC=12.求CD的长.
1.如图,△ACB∽△A'CB',∠BCB'=30°,则∠ACA'的度数为 ( )
A.20° B.30° C.35° D.40°
2.如图,嘉嘉要测量池塘两岸A、B两点间的距离,先在AB的延长线上选定点C,测得BC=5 m,再选一点D,连结AD、CD,作BE∥AD,交CD于点E,测得CD=8 m,DE=4 m,则AB= ( )
A.3 m B.4 m C.5 m D.6 m
3.如图,AB∥CD,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有 ( )
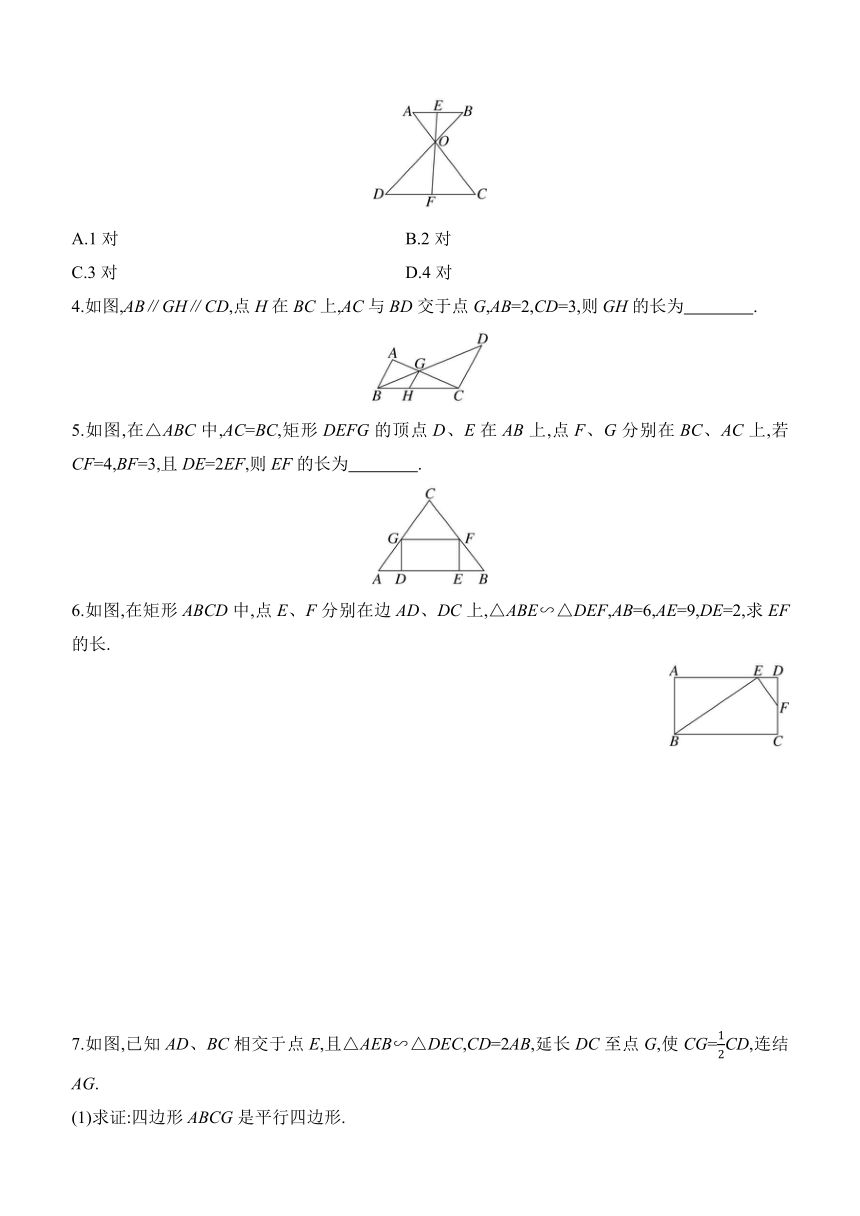
A.1对 B.2对
C.3对 D.4对
4.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH的长为 .
5.如图,在△ABC中,AC=BC,矩形DEFG的顶点D、E在AB上,点F、G分别在BC、AC上,若CF=4,BF=3,且DE=2EF,则EF的长为 .
6.如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
7.如图,已知AD、BC相交于点E,且△AEB∽△DEC,CD=2AB,延长DC至点G,使CG=CD,连结AG.
(1)求证:四边形ABCG是平行四边形.
(2)若∠GAD=90°,AE=2,CG=3,求AG的长.
8.(几何直观)如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于
点G.
(1)求证:△ADE≌△CFE.
(2)若GB=2,BC=4,BD=1,求AB的长.
【详解答案】
基础达标
1.D 解析:∵△AOB∽△DOC,∠A=30°,∴∠D=∠A=30°,∵∠COD=100°,∴∠C=180°-100°-30°=50°.故选D.
2.135° 解析:∵△ABC∽△DEF,
∴∠BAC=∠EDF,又∠EDF=90°+45°=135°,∴∠BAC=135°.
3.解:∵△AOB∽△DOC,∴,∵OA=2,OB=5,DC=12,OD=7,∴,解得OC=,AB=.
4.D 解析:∵△ABC∽△DEF,AB=6,DE=4,∴△ABC与△DEF的相似比为6∶4=3∶2.故选D.
5.C 解析:∵AB∥CD∥EF,∴△BCD∽△BEF,△FCD∽△FAB,△ABC∽△FEC.∴图中共有3对相似三角形.故选C.
6.解:∵AE=3,AC=12,
∴CE=AC-AE=12-3=9.
∵AB∥CD,∴△CDE∽△ABE.
∴.
∴CD==18.
能力提升
1.B 解析:∵△ACB∽△A'CB',
∴∠ACB=∠A'CB',
∴∠ACB-∠A'CB=∠A'CB'-∠A'CB,
∴∠ACA'=∠BCB'.∵∠BCB'=30°,
∴∠ACA'=30°.故选B.
2.C 解析:∵BE∥AD,∴△BCE∽△ACD,∴,∴,即,解得AB=5.故选C.
3.C 解析:∵AB∥CD,∴△AEO∽△CFO,△BEO∽△DFO,△ABO∽△CDO.故选C.
4. 解析:由AB∥GH∥CD可知△CGH∽△CAB,△BGH∽△BDC,
∴,,即①,②.
①+②,得.
∵CH+BH=BC,∴=1,解得GH=.
5. 解析:设EF=x,∵DE=2EF,
∴DE=2x,∵四边形DEFG是矩形,
∴GF∥AB,∴△CGF∽△CAB,
∴,即,
∴AB=,∴AD+BE=AB-DE=-2x=.∵AC=BC,∴∠A=∠B.在△ADG和△BEF中,
∴△ADG≌△BEF.∴AD=BE=,
在Rt△BEF中,BE2+EF2=BF2,
即+x2=32,解得x=(负值舍去).∴EF=.
6.解:∵△ABE∽△DEF,AB=6,AE=9,DE=2,∴,即,解得DF=3.
∵四边形ABCD为矩形,∴∠D=90°,
由勾股定理得
EF=.
7.解:(1)证明:∵△AEB∽△DEC,
∴∠B=∠BCD,∴AB∥CD,
即AB∥CG,∵CD=2AB,CG=CD,
∴AB=CG,
∴四边形ABCG是平行四边形.
(2)∵四边形ABCG是平行四边形,
AE=2,CG=3,
∴AG∥BC,AG=BC,AB=CG=3.
∵∠GAD=90°,∴∠AEB=90°.
在Rt△ABE中,由勾股定理可得
BE=,
即BE=.
∵△AEB∽△DEC,∴,
∴CE=2,∴BC=BE+CE=3,
∴AG=BC=3.
8.解:(1)证明:∵AB∥FC,
∴∠A=∠FCE,
在△ADE和△CFE中,
∴△ADE≌△CFE.
(2)∵AB∥CF,∴△GBD∽△GCF,
∴,∴,
∴CF=3,∵△ADE≌△CFE,
∴AD=CF=3,
∴AB=AD+BD=3+1=4.
1.相似三角形
相似三角形
1.(2025陇南康县期中)如图,AD、BC相交于点O,且△AOB∽△DOC,点A的对应点为点D,若∠A=30°,∠COD=100°,则∠C的度数为 ( )
A.20° B.30° C.40° D.50°
2.如图,在小正方形网格中,△ABC∽△DEF,则∠BAC的度数为 .
3.如图,已知△AOB∽△DOC,OA=2,OD=7,OB=5,DC=12.求AB、OC的长.
相似比
4.若△ABC∽△DEF,AB=6,DE=4,则△ABC与△DEF的相似比为 ( )
A.2∶3 B.4∶9
C. D.3∶2
由平行判定三角形相似
5.如图,AB∥CD∥EF,则图中相似三角形的对数是 ( )
A.1 B.2 C.3 D.4
6.如图,AB∥CD,AC与BD交于点E,且AB=6,AE=3,AC=12.求CD的长.
1.如图,△ACB∽△A'CB',∠BCB'=30°,则∠ACA'的度数为 ( )
A.20° B.30° C.35° D.40°
2.如图,嘉嘉要测量池塘两岸A、B两点间的距离,先在AB的延长线上选定点C,测得BC=5 m,再选一点D,连结AD、CD,作BE∥AD,交CD于点E,测得CD=8 m,DE=4 m,则AB= ( )
A.3 m B.4 m C.5 m D.6 m
3.如图,AB∥CD,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有 ( )
A.1对 B.2对
C.3对 D.4对
4.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH的长为 .
5.如图,在△ABC中,AC=BC,矩形DEFG的顶点D、E在AB上,点F、G分别在BC、AC上,若CF=4,BF=3,且DE=2EF,则EF的长为 .
6.如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
7.如图,已知AD、BC相交于点E,且△AEB∽△DEC,CD=2AB,延长DC至点G,使CG=CD,连结AG.
(1)求证:四边形ABCG是平行四边形.
(2)若∠GAD=90°,AE=2,CG=3,求AG的长.
8.(几何直观)如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于
点G.
(1)求证:△ADE≌△CFE.
(2)若GB=2,BC=4,BD=1,求AB的长.
【详解答案】
基础达标
1.D 解析:∵△AOB∽△DOC,∠A=30°,∴∠D=∠A=30°,∵∠COD=100°,∴∠C=180°-100°-30°=50°.故选D.
2.135° 解析:∵△ABC∽△DEF,
∴∠BAC=∠EDF,又∠EDF=90°+45°=135°,∴∠BAC=135°.
3.解:∵△AOB∽△DOC,∴,∵OA=2,OB=5,DC=12,OD=7,∴,解得OC=,AB=.
4.D 解析:∵△ABC∽△DEF,AB=6,DE=4,∴△ABC与△DEF的相似比为6∶4=3∶2.故选D.
5.C 解析:∵AB∥CD∥EF,∴△BCD∽△BEF,△FCD∽△FAB,△ABC∽△FEC.∴图中共有3对相似三角形.故选C.
6.解:∵AE=3,AC=12,
∴CE=AC-AE=12-3=9.
∵AB∥CD,∴△CDE∽△ABE.
∴.
∴CD==18.
能力提升
1.B 解析:∵△ACB∽△A'CB',
∴∠ACB=∠A'CB',
∴∠ACB-∠A'CB=∠A'CB'-∠A'CB,
∴∠ACA'=∠BCB'.∵∠BCB'=30°,
∴∠ACA'=30°.故选B.
2.C 解析:∵BE∥AD,∴△BCE∽△ACD,∴,∴,即,解得AB=5.故选C.
3.C 解析:∵AB∥CD,∴△AEO∽△CFO,△BEO∽△DFO,△ABO∽△CDO.故选C.
4. 解析:由AB∥GH∥CD可知△CGH∽△CAB,△BGH∽△BDC,
∴,,即①,②.
①+②,得.
∵CH+BH=BC,∴=1,解得GH=.
5. 解析:设EF=x,∵DE=2EF,
∴DE=2x,∵四边形DEFG是矩形,
∴GF∥AB,∴△CGF∽△CAB,
∴,即,
∴AB=,∴AD+BE=AB-DE=-2x=.∵AC=BC,∴∠A=∠B.在△ADG和△BEF中,
∴△ADG≌△BEF.∴AD=BE=,
在Rt△BEF中,BE2+EF2=BF2,
即+x2=32,解得x=(负值舍去).∴EF=.
6.解:∵△ABE∽△DEF,AB=6,AE=9,DE=2,∴,即,解得DF=3.
∵四边形ABCD为矩形,∴∠D=90°,
由勾股定理得
EF=.
7.解:(1)证明:∵△AEB∽△DEC,
∴∠B=∠BCD,∴AB∥CD,
即AB∥CG,∵CD=2AB,CG=CD,
∴AB=CG,
∴四边形ABCG是平行四边形.
(2)∵四边形ABCG是平行四边形,
AE=2,CG=3,
∴AG∥BC,AG=BC,AB=CG=3.
∵∠GAD=90°,∴∠AEB=90°.
在Rt△ABE中,由勾股定理可得
BE=,
即BE=.
∵△AEB∽△DEC,∴,
∴CE=2,∴BC=BE+CE=3,
∴AG=BC=3.
8.解:(1)证明:∵AB∥FC,
∴∠A=∠FCE,
在△ADE和△CFE中,
∴△ADE≌△CFE.
(2)∵AB∥CF,∴△GBD∽△GCF,
∴,∴,
∴CF=3,∵△ADE≌△CFE,
∴AD=CF=3,
∴AB=AD+BD=3+1=4.
