23.3.2.相似三角形的判定第1课时 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 23.3.2.相似三角形的判定第1课时 同步练习(含答案)华东师大版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 127.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 00:00:00 | ||
图片预览


文档简介
2.相似三角形的判定
第1课时 相似三角形的判定定理1
两角分别相等的两个三角形相似
1.已知一个三角形的两个内角分别是40°和60°,另一个三角形的两个内角分别是40°和80°,则这两个三角形 ( )
A.一定不相似 B.不一定相似
C.一定相似 D.一定全等
2.如图,在△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3,则与△ADE相似的三角形的个数为 ( )
A.4 B.3 C.2 D.1
3.张老师在编写下面这个题目的答案时,不小心打乱了解答过程的顺序,证明步骤正确的顺序是 ( )
已知:如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,且DE∥BC,DF∥AC.求证:△ADE∽△DBF.
证明:①又∵DF∥AC,②∵DE∥BC,③∴∠A=∠BDF,④∴∠ADE=∠B,⑤∴△ADE∽△DBF.
A.③②④①⑤ B.②④①③⑤
C.③①④②⑤ D.②③④①⑤
4.如图,△ABC的高AD、BE相交于点O,写出一个与△AOE相似的三角形,这个三角形可以是 .
5.如图,∠B=∠D,∠1=∠2.
求证:△ABC∽△ADE.
6.(2024德阳中考)如图,在菱形ABCD中,∠ABC=60°,对角线AC与BD相交于点O,点F为BC的中点,连结AF与BD相交于点E,连结CE并延长交AB于点G.
(1)求证:△BEF∽△BCO.
(2)求证:△BEG≌△AEG.
1.含60°角的直角三角板ABC(∠A=60°)与含45°角的直角三角板BCD如图放置,它们的斜边AC与斜边BD相交于点E.下列结论正确的是 ( )
A.△ABE∽△CDE
B.△ABE∽△BCE
C.△BCE∽△DCE
D.△ABC∽△DCB
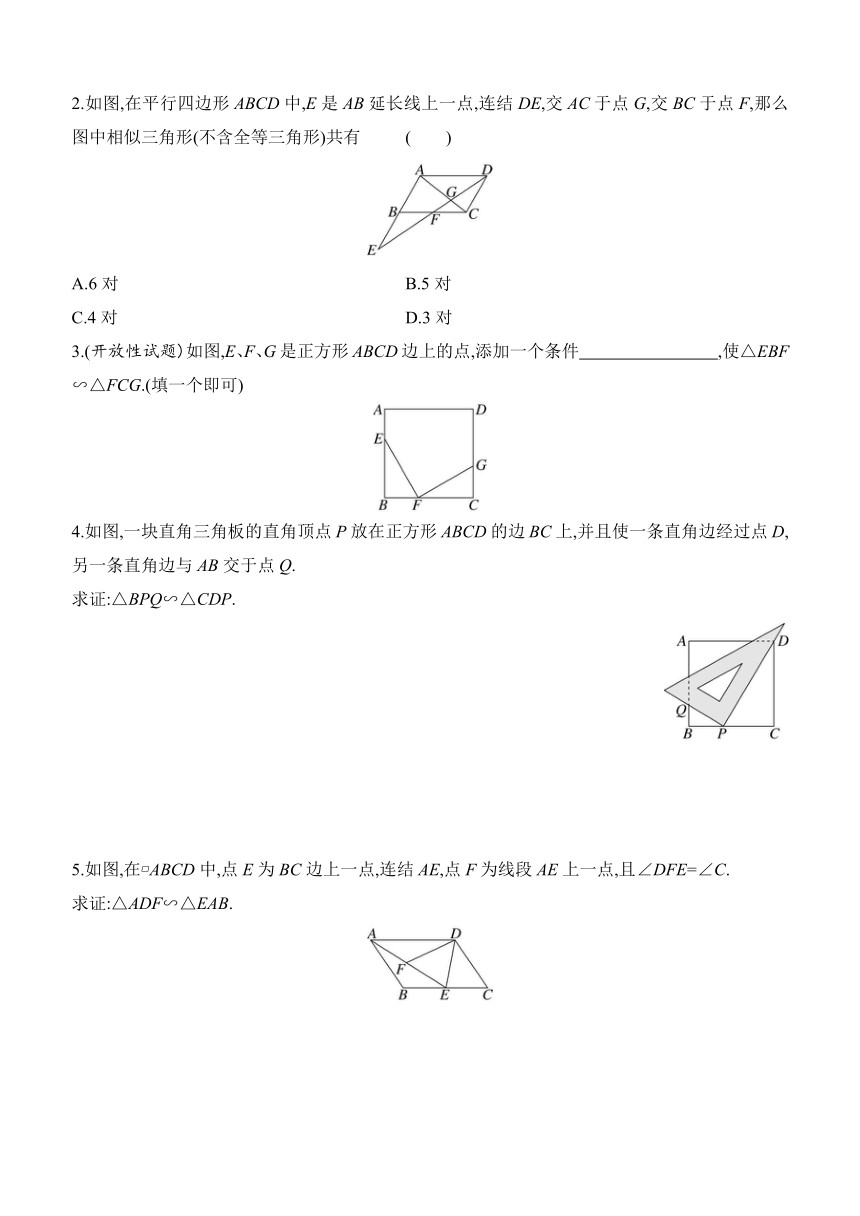
2.如图,在平行四边形ABCD中,E是AB延长线上一点,连结DE,交AC于点G,交BC于点F,那么图中相似三角形(不含全等三角形)共有 ( )
A.6对 B.5对
C.4对 D.3对
3.(开放性试题)如图,E、F、G是正方形ABCD边上的点,添加一个条件 ,使△EBF∽△FCG.(填一个即可)
4.如图,一块直角三角板的直角顶点P放在正方形ABCD的边BC上,并且使一条直角边经过点D,另一条直角边与AB交于点Q.
求证:△BPQ∽△CDP.
5.如图,在 ABCD中,点E为BC边上一点,连结AE,点F为线段AE上一点,且∠DFE=∠C.
求证:△ADF∽△EAB.
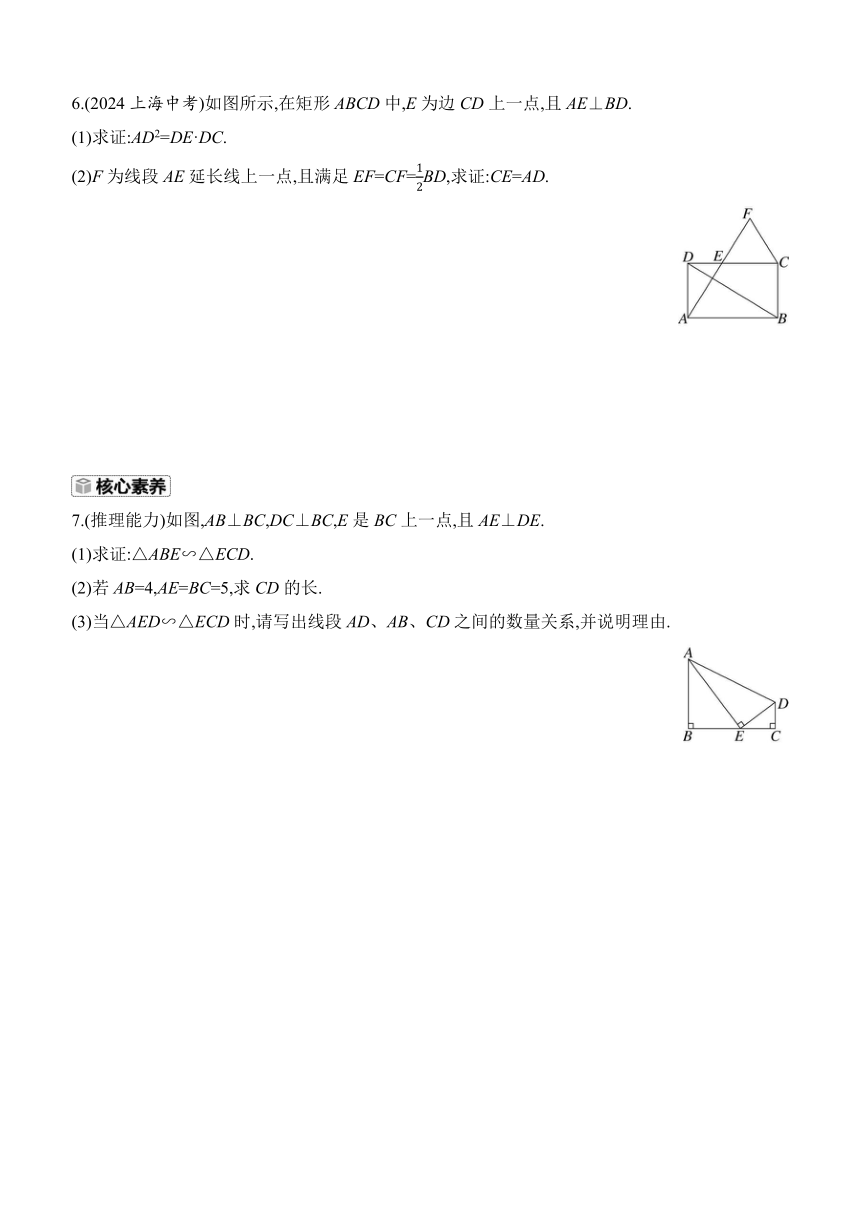
6.(2024上海中考)如图所示,在矩形ABCD中,E为边CD上一点,且AE⊥BD.
(1)求证:AD2=DE·DC.
(2)F为线段AE延长线上一点,且满足EF=CF=BD,求证:CE=AD.
7.(推理能力)如图,AB⊥BC,DC⊥BC,E是BC上一点,且AE⊥DE.
(1)求证:△ABE∽△ECD.
(2)若AB=4,AE=BC=5,求CD的长.
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间的数量关系,并说明理由.
【详解答案】
基础达标
1.C 解析:∵一个三角形的两个内角分别是40°和60°,∴第三个内角是80°.又∵另一个三角形的两个内角分别是40°和80°,∴这两个三角形有两个内角相等.∴这两个三角形相似.故选C.
2.C 解析:∵∠1=∠2,∠A=∠A,
∴△ADE∽△ABC.∵∠1=∠3,∠A=∠A,∴△ADE∽△ACD.∴题图中与△ADE相似的三角形有2个.故选C.
3.B 解析:②∵DE∥BC,④∴∠ADE=∠B,①又∵DF∥AC,③∴∠A=∠BDF,⑤∴△ADE∽△DBF.故选B.
4.△BOD(或△BCE或△ACD)
解析:∵∠AEO=∠BDO=90°,
∠AOE=∠BOD,∴△AOE∽△BOD.
∴∠OAE=∠OBD.又∵∠AEO=∠BEC=90°,∴△AOE∽△BCE.
∵∠AEO=∠ADC=90°,
∠EAO=∠DAC,∴△AOE∽△ACD.
5.证明:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
∴∠BAC=∠DAE,
又∵∠B=∠D,
∴△ABC∽△ADE.
6.证明:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,
又∵∠ABC=60°,
∴△ABC是等边三角形,∴AB=AC,
∵点F为BC的中点,∴AF⊥BC,
∴∠BOC=∠BFE=90°,
又∵∠EBF=∠CBO,
∴△BEF∽△BCO.
(2)∵BO⊥AC,AF⊥BC,
∴CG⊥AB,∴∠BGE=∠AGE.
又∵AC=BC,∴BG=AG.
在△BEG和△AEG中,
∴△BEG≌△AEG.
能力提升
1.A 解析:在Rt△ABC中,∠ABC=90°,∠A=60°,∴∠ACB=30°.
∵∠BCD=90°,∴∠ECD=∠BCD-∠ACB=90°-30°=60°,
∴∠A=∠ECD.∵∠AEB=∠CED,
∴△ABE∽△CDE.故选A.
2.B 解析:∵四边形ABCD是平行四边形,∴∠EBF=∠EAD,∠EFB=∠EDA,
∴△EFB∽△EDA;同理可得,△FGC∽△DGA,△EBF∽△DCF,△GAE∽△GCD,△ADE∽△CFD.故选B.
3.∠BEF=∠CFG(答案不唯一)
解析:可添加∠BEF=∠CFG,
又∵∠B=∠C,∴△EBF∽△FCG.(答案不唯一)
4.证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,∵∠QPD=90°,
∴∠BPQ+∠DPC=90°=∠DPC+∠PDC,∴∠BPQ=∠PDC,
∴△BPQ∽△CDP.
5.证明:在 ABCD中,AD∥BC,
∴∠DAF=∠AEB,∵AB∥CD,
∴∠B+∠C=180°,
∵∠DFE=∠C,∠AFD+∠DFE=180°,∴∠B=∠AFD,
∴△ADF∽△EAB.
6.证明:(1)在矩形ABCD中,
∠BAD=90°,∠ADE=90°,AB=DC,
∴∠ABD+∠ADB=90°,∵AE⊥BD,
∴∠DAE+∠ADB=90°,
∴∠ABD=∠DAE,
∵∠BAD=∠ADE=90°,
∴△ADE∽△BAD,∴,
∴AD2=DE·BA,∵AB=DC,
∴AD2=DE·DC.
(2)如图,连结AC交BD于点O,
在矩形ABCD中,∠ADE=90°,
∴∠DAE+∠AED=90°,∵AE⊥BD,
∴∠DAE+∠ADB=90°,
∴∠ADB=∠AED,∵∠FEC=∠AED,
∴∠ADO=∠FEC.
在矩形ABCD中,OA=OD=BD,
∵EF=CF=BD,
∴OA=OD=EF=CF,
∴∠ADO=∠OAD,∠FEC=∠FCE,
∵∠ADO=∠FEC,
∴∠ADO=∠OAD=∠FEC=∠FCE.
在△ODA和△FEC中,
∴△ODA≌△FEC,∴CE=AD.
7.解:(1)证明:∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,∠BAE+∠AEB=90°.∵AE⊥DE,∴∠AED=90°.
∴∠AEB+∠CED=90°.
∴∠CED=∠BAE.∴△ABE∽△ECD.
(2)在Rt△ABE中,∵AB=4,AE=5,∴BE=3.
∵BC=5,∴EC=5-3=2.
由(1),得△ABE∽△ECD,
∴.∴,∴CD=.
(3)线段AD、AB、CD之间的数量关系:AD=AB+CD.
理由:过点E作EF⊥AD于点F,
∵△AED∽△ECD,
∴∠ADE=∠EDC.
∵DC⊥BC,∴EF=EC.
∵DE=DE,
∴Rt△DFE≌Rt△DCE.
∴DF=DC.
同理可得Rt△ABE≌Rt△AFE,
∴AF=AB.
∴AD=AF+DF=AB+CD.
第1课时 相似三角形的判定定理1
两角分别相等的两个三角形相似
1.已知一个三角形的两个内角分别是40°和60°,另一个三角形的两个内角分别是40°和80°,则这两个三角形 ( )
A.一定不相似 B.不一定相似
C.一定相似 D.一定全等
2.如图,在△ABC中,点D在AB边上,点E在AC边上,且∠1=∠2=∠3,则与△ADE相似的三角形的个数为 ( )
A.4 B.3 C.2 D.1
3.张老师在编写下面这个题目的答案时,不小心打乱了解答过程的顺序,证明步骤正确的顺序是 ( )
已知:如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,且DE∥BC,DF∥AC.求证:△ADE∽△DBF.
证明:①又∵DF∥AC,②∵DE∥BC,③∴∠A=∠BDF,④∴∠ADE=∠B,⑤∴△ADE∽△DBF.
A.③②④①⑤ B.②④①③⑤
C.③①④②⑤ D.②③④①⑤
4.如图,△ABC的高AD、BE相交于点O,写出一个与△AOE相似的三角形,这个三角形可以是 .
5.如图,∠B=∠D,∠1=∠2.
求证:△ABC∽△ADE.
6.(2024德阳中考)如图,在菱形ABCD中,∠ABC=60°,对角线AC与BD相交于点O,点F为BC的中点,连结AF与BD相交于点E,连结CE并延长交AB于点G.
(1)求证:△BEF∽△BCO.
(2)求证:△BEG≌△AEG.
1.含60°角的直角三角板ABC(∠A=60°)与含45°角的直角三角板BCD如图放置,它们的斜边AC与斜边BD相交于点E.下列结论正确的是 ( )
A.△ABE∽△CDE
B.△ABE∽△BCE
C.△BCE∽△DCE
D.△ABC∽△DCB
2.如图,在平行四边形ABCD中,E是AB延长线上一点,连结DE,交AC于点G,交BC于点F,那么图中相似三角形(不含全等三角形)共有 ( )
A.6对 B.5对
C.4对 D.3对
3.(开放性试题)如图,E、F、G是正方形ABCD边上的点,添加一个条件 ,使△EBF∽△FCG.(填一个即可)
4.如图,一块直角三角板的直角顶点P放在正方形ABCD的边BC上,并且使一条直角边经过点D,另一条直角边与AB交于点Q.
求证:△BPQ∽△CDP.
5.如图,在 ABCD中,点E为BC边上一点,连结AE,点F为线段AE上一点,且∠DFE=∠C.
求证:△ADF∽△EAB.
6.(2024上海中考)如图所示,在矩形ABCD中,E为边CD上一点,且AE⊥BD.
(1)求证:AD2=DE·DC.
(2)F为线段AE延长线上一点,且满足EF=CF=BD,求证:CE=AD.
7.(推理能力)如图,AB⊥BC,DC⊥BC,E是BC上一点,且AE⊥DE.
(1)求证:△ABE∽△ECD.
(2)若AB=4,AE=BC=5,求CD的长.
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间的数量关系,并说明理由.
【详解答案】
基础达标
1.C 解析:∵一个三角形的两个内角分别是40°和60°,∴第三个内角是80°.又∵另一个三角形的两个内角分别是40°和80°,∴这两个三角形有两个内角相等.∴这两个三角形相似.故选C.
2.C 解析:∵∠1=∠2,∠A=∠A,
∴△ADE∽△ABC.∵∠1=∠3,∠A=∠A,∴△ADE∽△ACD.∴题图中与△ADE相似的三角形有2个.故选C.
3.B 解析:②∵DE∥BC,④∴∠ADE=∠B,①又∵DF∥AC,③∴∠A=∠BDF,⑤∴△ADE∽△DBF.故选B.
4.△BOD(或△BCE或△ACD)
解析:∵∠AEO=∠BDO=90°,
∠AOE=∠BOD,∴△AOE∽△BOD.
∴∠OAE=∠OBD.又∵∠AEO=∠BEC=90°,∴△AOE∽△BCE.
∵∠AEO=∠ADC=90°,
∠EAO=∠DAC,∴△AOE∽△ACD.
5.证明:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
∴∠BAC=∠DAE,
又∵∠B=∠D,
∴△ABC∽△ADE.
6.证明:(1)∵四边形ABCD是菱形,
∴AB=BC,AC⊥BD,
又∵∠ABC=60°,
∴△ABC是等边三角形,∴AB=AC,
∵点F为BC的中点,∴AF⊥BC,
∴∠BOC=∠BFE=90°,
又∵∠EBF=∠CBO,
∴△BEF∽△BCO.
(2)∵BO⊥AC,AF⊥BC,
∴CG⊥AB,∴∠BGE=∠AGE.
又∵AC=BC,∴BG=AG.
在△BEG和△AEG中,
∴△BEG≌△AEG.
能力提升
1.A 解析:在Rt△ABC中,∠ABC=90°,∠A=60°,∴∠ACB=30°.
∵∠BCD=90°,∴∠ECD=∠BCD-∠ACB=90°-30°=60°,
∴∠A=∠ECD.∵∠AEB=∠CED,
∴△ABE∽△CDE.故选A.
2.B 解析:∵四边形ABCD是平行四边形,∴∠EBF=∠EAD,∠EFB=∠EDA,
∴△EFB∽△EDA;同理可得,△FGC∽△DGA,△EBF∽△DCF,△GAE∽△GCD,△ADE∽△CFD.故选B.
3.∠BEF=∠CFG(答案不唯一)
解析:可添加∠BEF=∠CFG,
又∵∠B=∠C,∴△EBF∽△FCG.(答案不唯一)
4.证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,∵∠QPD=90°,
∴∠BPQ+∠DPC=90°=∠DPC+∠PDC,∴∠BPQ=∠PDC,
∴△BPQ∽△CDP.
5.证明:在 ABCD中,AD∥BC,
∴∠DAF=∠AEB,∵AB∥CD,
∴∠B+∠C=180°,
∵∠DFE=∠C,∠AFD+∠DFE=180°,∴∠B=∠AFD,
∴△ADF∽△EAB.
6.证明:(1)在矩形ABCD中,
∠BAD=90°,∠ADE=90°,AB=DC,
∴∠ABD+∠ADB=90°,∵AE⊥BD,
∴∠DAE+∠ADB=90°,
∴∠ABD=∠DAE,
∵∠BAD=∠ADE=90°,
∴△ADE∽△BAD,∴,
∴AD2=DE·BA,∵AB=DC,
∴AD2=DE·DC.
(2)如图,连结AC交BD于点O,
在矩形ABCD中,∠ADE=90°,
∴∠DAE+∠AED=90°,∵AE⊥BD,
∴∠DAE+∠ADB=90°,
∴∠ADB=∠AED,∵∠FEC=∠AED,
∴∠ADO=∠FEC.
在矩形ABCD中,OA=OD=BD,
∵EF=CF=BD,
∴OA=OD=EF=CF,
∴∠ADO=∠OAD,∠FEC=∠FCE,
∵∠ADO=∠FEC,
∴∠ADO=∠OAD=∠FEC=∠FCE.
在△ODA和△FEC中,
∴△ODA≌△FEC,∴CE=AD.
7.解:(1)证明:∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,∠BAE+∠AEB=90°.∵AE⊥DE,∴∠AED=90°.
∴∠AEB+∠CED=90°.
∴∠CED=∠BAE.∴△ABE∽△ECD.
(2)在Rt△ABE中,∵AB=4,AE=5,∴BE=3.
∵BC=5,∴EC=5-3=2.
由(1),得△ABE∽△ECD,
∴.∴,∴CD=.
(3)线段AD、AB、CD之间的数量关系:AD=AB+CD.
理由:过点E作EF⊥AD于点F,
∵△AED∽△ECD,
∴∠ADE=∠EDC.
∵DC⊥BC,∴EF=EC.
∵DE=DE,
∴Rt△DFE≌Rt△DCE.
∴DF=DC.
同理可得Rt△ABE≌Rt△AFE,
∴AF=AB.
∴AD=AF+DF=AB+CD.
