23.32.相似三角形的判定第2课时 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 23.32.相似三角形的判定第2课时 同步练习(含答案)华东师大版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 123.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 00:00:00 | ||
图片预览


文档简介
2.相似三角形的判定
第2课时 相似三角形的判定定理2
两边成比例且夹角相等的两个三角形相似
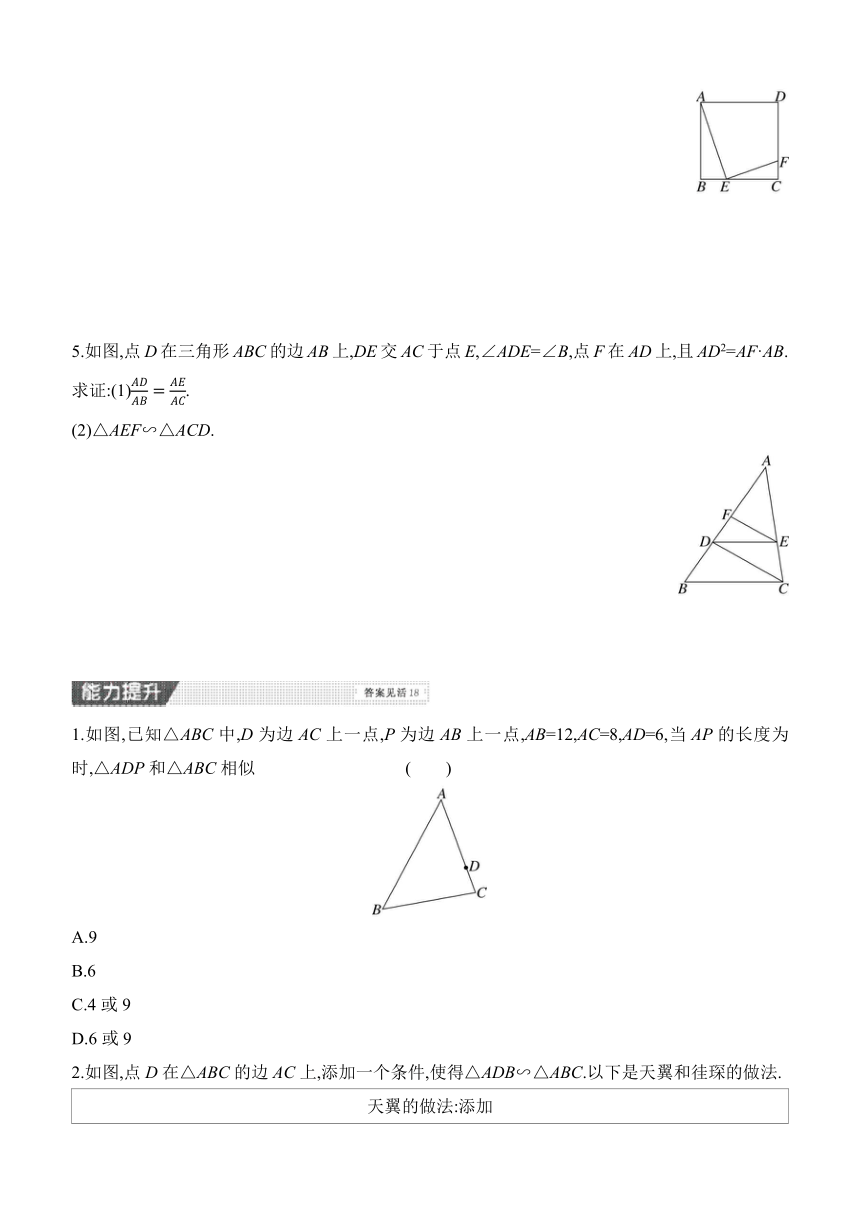
1.下列图形中,与如图所示的△ABC相似的是 ( )
A. B.
C. D.
2.如图,在四边形ABCD中,对角线AC、BD交于点O,若,则下列结论正确的是 ( )
A.△BOA∽△BAD B.△BOA∽△COD
C.△BOC∽△BCD D.△COB∽△CBA
3.如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB,能满足△APC与△ACB相似的条件是 ( )
A.①②④ B.①③④
C.②③④ D.①②③
4.(2024广州中考)如图,点E、F分别在正方形ABCD的边BC、CD上,BE=3,EC=6,CF=2.
求证:△ABE∽△ECF.
5.如图,点D在三角形ABC的边AB上,DE交AC于点E,∠ADE=∠B,点F在AD上,且AD2=AF·AB.
求证:(1).
(2)△AEF∽△ACD.
1.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为 时,△ADP和△ABC相似 ( )
A.9
B.6
C.4或9
D.6或9
2.如图,点D在△ABC的边AC上,添加一个条件,使得△ADB∽△ABC.以下是天翼和徍琛的做法.
天翼的做法:添加 条件∠ABD=∠C. 证明:∵∠ABD= ∠C,∠A=∠A, ∴△ADB∽△ABC. (两角分别相等的 两个三角形相似)徍琛的做法:添 加条件. 证明:∵∠A= ∠A,, ∴△ADB∽△ABC. (两边成比例且夹角相 等的两个三角形相似)
下列说法不正确的是 ( )
A.天翼的做法证明过程没有问题
B.徍琛的做法证明过程没有问题
C.天翼的做法添加的条件没有问题
D.徍琛的做法添加的条件有问题
第2题图 第3题图
3.如图,∠1=∠2,添加一个条件能判定△ABC∽△ADE的是 ( )
①∠C=∠E;②∠B=∠ADE;;④.
A.①②③
B.①②④
C.②③④
D.①②③④
4.如图,在△ABC中,D为BC上一点,BC=AB=3BD,则AD∶AC的值为 .
第4题图 第5题图
5.如图,已知点P是边长为10的正方形ABCD内的一点,且PB=8,BF⊥BP,若在射线BF上有一点M,使以点B、M、C为顶点的三角形与△ABP相似,则BM= .
6.如图,已知四边形ABCD的对角线AC、BD交于点F,点E是BD上一点,且∠BCA=∠ADE,∠CAD=∠BAE.
(1)求证:△ABC∽△AED.
(2)求证:BE·AC=CD·AB.
7.(几何直观)如图,已知AB⊥BD,CD⊥BD,垂足分别为B、D.
(1)若AB=9,CD=4,BD=10,在BD上是否存在点P,使以P、A、B为顶点的三角形与以P、C、D为顶点的三角形相似 若存在,求出PB的长;若不存在,请说明理由.
(2)若AB=9,CD=4,BD=12,在BD上存在多少个符合条件的点P,使以P、A、B为顶点的三角形与以P、C、D为顶点的三角形相似 并求出PB的长.
【详解答案】
基础达标
1.C 解析:∵AB=AC,∠B=75°,
∴∠B=∠C=75°.∴∠A=30°.依据两边成比例且夹角相等的两个三角形相似可知选项C中的图形与△ABC相似.故选C.
2.B 解析:∵,∠AOB=∠DOC,∴△BOA∽△COD.故选B.
3.D 解析:当∠ACP=∠B时,
因为∠A=∠A,所以△APC∽△ACB;
当∠APC=∠ACB时,因为∠A=∠A,
所以△APC∽△ACB;当AC2=AP·AB时,即AC∶AB=AP∶AC,因为∠A=∠A,所以△APC∽△ACB;
当AB·CP=AP·CB时,即PC∶BC=AP∶AB,而∠PAC=∠CAB,
所以不能判断△APC和△ACB相似.故选D.
4.证明:∵BE=3,EC=6,
∴BC=3+6=9,
∵四边形ABCD是正方形,
∴AB=BC=9,∠B=∠C=90°,
∵,,
∴,
∴△ABE∽△ECF.
5.证明:(1)∵∠ADE=∠B,∴DE∥BC,∴.
(2)∵AD2=AF·AB,∴,
由(1)得,∴.
又∵∠A=∠A,∴△AEF∽△ACD.
能力提升
1.C 解析:∠PAD=∠BAC,当AP∶AB=AD∶AC时,△APD∽△ABC,∴AP∶12=6∶8,∴AP=9;当AP∶AC=AD∶AB时,△APD∽△ACB,∴AP∶8=6∶12,∴AP=4,∴AP的长度为4或9时,△ADP和△ABC相似.故选C.
2.B 解析:依题意,∠A=∠A,添加一组对应角相等,可以使得△ADB∽△ABC,故天翼的做法以及过程没有问题,徍琛的做法添加的条件有问题,应为,故B选项符合题意.故选B.
3.B 解析:∵∠1=∠2,∴∠DAE=∠BAC,
①添加∠C=∠E,可判定△ABC∽△ADE,故①符合题意;②添加∠B=∠ADE,可判定△ABC∽△ADE,故②符合题意;③添加,无法判定△ABC∽△ADE,故③不符合题意;④添加,可判定△ABC∽△ADE,故④符合题意.故选B.
4. 解析:∵BC=AB=3BD,
∴.∵∠B=∠B,
∴△ABC∽△DBA.∴.
∴AD∶AC=.
5.8或12.5 解析:∵四边形ABCD是正方形,∴∠ABC=90°,BC=AB=10,
∵BF⊥BP,∴∠ABP+∠CBP=∠CBM+∠CBP=90°,∴∠ABP=∠CBM.当AB∶BM=PB∶BC时,△BAP∽△BMC,
∴10∶BM=8∶10,∴BM=12.5,
当AB∶BC=PB∶BM时,△BAP∽△BCM,∴10∶10=8∶BM,∴BM=8,∴BM的长是8或12.5.
6.证明:(1)∵∠BAE=∠CAD,∠BAC=∠BAE-∠CAE,∠DAE=∠CAD-∠CAE,∴∠BAC=∠DAE,
∵∠BCA=∠ADE,∴△ABC∽△AED.
(2)∵△ABC∽△AED,∴,
又∵∠BAE=∠CAD,∴△ABE∽△ACD,
∴,∴BE·AC=CD·AB.
7.解:(1)存在.
设PB=x,则PD=10-x.
∵∠B=∠D,
∴当时,△ABP∽△PDC,
即,
整理得x2-10x+36=0,此方程没有实数根;
当时,△ABP∽△CDP,
即,解得x=.
综上所述,PB的长为.
(2)存在2个符合条件的点P.
设PB=y,则PD=12-y.
∵∠B=∠D,
∴当时,△ABP∽△PDC,
即,
整理得y2-12y+36=0,
解得y1=y2=6;
当时,△ABP∽△CDP,
即,解得y=.
综上所述,PB的长为6或.
第2课时 相似三角形的判定定理2
两边成比例且夹角相等的两个三角形相似
1.下列图形中,与如图所示的△ABC相似的是 ( )
A. B.
C. D.
2.如图,在四边形ABCD中,对角线AC、BD交于点O,若,则下列结论正确的是 ( )
A.△BOA∽△BAD B.△BOA∽△COD
C.△BOC∽△BCD D.△COB∽△CBA
3.如图,在△ABC中,点P在边AB上,则在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB,能满足△APC与△ACB相似的条件是 ( )
A.①②④ B.①③④
C.②③④ D.①②③
4.(2024广州中考)如图,点E、F分别在正方形ABCD的边BC、CD上,BE=3,EC=6,CF=2.
求证:△ABE∽△ECF.
5.如图,点D在三角形ABC的边AB上,DE交AC于点E,∠ADE=∠B,点F在AD上,且AD2=AF·AB.
求证:(1).
(2)△AEF∽△ACD.
1.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为 时,△ADP和△ABC相似 ( )
A.9
B.6
C.4或9
D.6或9
2.如图,点D在△ABC的边AC上,添加一个条件,使得△ADB∽△ABC.以下是天翼和徍琛的做法.
天翼的做法:添加 条件∠ABD=∠C. 证明:∵∠ABD= ∠C,∠A=∠A, ∴△ADB∽△ABC. (两角分别相等的 两个三角形相似)徍琛的做法:添 加条件. 证明:∵∠A= ∠A,, ∴△ADB∽△ABC. (两边成比例且夹角相 等的两个三角形相似)
下列说法不正确的是 ( )
A.天翼的做法证明过程没有问题
B.徍琛的做法证明过程没有问题
C.天翼的做法添加的条件没有问题
D.徍琛的做法添加的条件有问题
第2题图 第3题图
3.如图,∠1=∠2,添加一个条件能判定△ABC∽△ADE的是 ( )
①∠C=∠E;②∠B=∠ADE;;④.
A.①②③
B.①②④
C.②③④
D.①②③④
4.如图,在△ABC中,D为BC上一点,BC=AB=3BD,则AD∶AC的值为 .
第4题图 第5题图
5.如图,已知点P是边长为10的正方形ABCD内的一点,且PB=8,BF⊥BP,若在射线BF上有一点M,使以点B、M、C为顶点的三角形与△ABP相似,则BM= .
6.如图,已知四边形ABCD的对角线AC、BD交于点F,点E是BD上一点,且∠BCA=∠ADE,∠CAD=∠BAE.
(1)求证:△ABC∽△AED.
(2)求证:BE·AC=CD·AB.
7.(几何直观)如图,已知AB⊥BD,CD⊥BD,垂足分别为B、D.
(1)若AB=9,CD=4,BD=10,在BD上是否存在点P,使以P、A、B为顶点的三角形与以P、C、D为顶点的三角形相似 若存在,求出PB的长;若不存在,请说明理由.
(2)若AB=9,CD=4,BD=12,在BD上存在多少个符合条件的点P,使以P、A、B为顶点的三角形与以P、C、D为顶点的三角形相似 并求出PB的长.
【详解答案】
基础达标
1.C 解析:∵AB=AC,∠B=75°,
∴∠B=∠C=75°.∴∠A=30°.依据两边成比例且夹角相等的两个三角形相似可知选项C中的图形与△ABC相似.故选C.
2.B 解析:∵,∠AOB=∠DOC,∴△BOA∽△COD.故选B.
3.D 解析:当∠ACP=∠B时,
因为∠A=∠A,所以△APC∽△ACB;
当∠APC=∠ACB时,因为∠A=∠A,
所以△APC∽△ACB;当AC2=AP·AB时,即AC∶AB=AP∶AC,因为∠A=∠A,所以△APC∽△ACB;
当AB·CP=AP·CB时,即PC∶BC=AP∶AB,而∠PAC=∠CAB,
所以不能判断△APC和△ACB相似.故选D.
4.证明:∵BE=3,EC=6,
∴BC=3+6=9,
∵四边形ABCD是正方形,
∴AB=BC=9,∠B=∠C=90°,
∵,,
∴,
∴△ABE∽△ECF.
5.证明:(1)∵∠ADE=∠B,∴DE∥BC,∴.
(2)∵AD2=AF·AB,∴,
由(1)得,∴.
又∵∠A=∠A,∴△AEF∽△ACD.
能力提升
1.C 解析:∠PAD=∠BAC,当AP∶AB=AD∶AC时,△APD∽△ABC,∴AP∶12=6∶8,∴AP=9;当AP∶AC=AD∶AB时,△APD∽△ACB,∴AP∶8=6∶12,∴AP=4,∴AP的长度为4或9时,△ADP和△ABC相似.故选C.
2.B 解析:依题意,∠A=∠A,添加一组对应角相等,可以使得△ADB∽△ABC,故天翼的做法以及过程没有问题,徍琛的做法添加的条件有问题,应为,故B选项符合题意.故选B.
3.B 解析:∵∠1=∠2,∴∠DAE=∠BAC,
①添加∠C=∠E,可判定△ABC∽△ADE,故①符合题意;②添加∠B=∠ADE,可判定△ABC∽△ADE,故②符合题意;③添加,无法判定△ABC∽△ADE,故③不符合题意;④添加,可判定△ABC∽△ADE,故④符合题意.故选B.
4. 解析:∵BC=AB=3BD,
∴.∵∠B=∠B,
∴△ABC∽△DBA.∴.
∴AD∶AC=.
5.8或12.5 解析:∵四边形ABCD是正方形,∴∠ABC=90°,BC=AB=10,
∵BF⊥BP,∴∠ABP+∠CBP=∠CBM+∠CBP=90°,∴∠ABP=∠CBM.当AB∶BM=PB∶BC时,△BAP∽△BMC,
∴10∶BM=8∶10,∴BM=12.5,
当AB∶BC=PB∶BM时,△BAP∽△BCM,∴10∶10=8∶BM,∴BM=8,∴BM的长是8或12.5.
6.证明:(1)∵∠BAE=∠CAD,∠BAC=∠BAE-∠CAE,∠DAE=∠CAD-∠CAE,∴∠BAC=∠DAE,
∵∠BCA=∠ADE,∴△ABC∽△AED.
(2)∵△ABC∽△AED,∴,
又∵∠BAE=∠CAD,∴△ABE∽△ACD,
∴,∴BE·AC=CD·AB.
7.解:(1)存在.
设PB=x,则PD=10-x.
∵∠B=∠D,
∴当时,△ABP∽△PDC,
即,
整理得x2-10x+36=0,此方程没有实数根;
当时,△ABP∽△CDP,
即,解得x=.
综上所述,PB的长为.
(2)存在2个符合条件的点P.
设PB=y,则PD=12-y.
∵∠B=∠D,
∴当时,△ABP∽△PDC,
即,
整理得y2-12y+36=0,
解得y1=y2=6;
当时,△ABP∽△CDP,
即,解得y=.
综上所述,PB的长为6或.
