23.3.2相似三角形的判定 第3课时 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 23.3.2相似三角形的判定 第3课时 同步练习(含答案)华东师大版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 167.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 00:00:00 | ||
图片预览


文档简介
2.相似三角形的判定
第3课时 相似三角形的判定定理3
三边成比例的两个三角形相似
1.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是 ( )
A. B.
C. D.
2.将△ABC的各边长作如下变化,得到的新三角形与△ABC相似的是 ( )
A.各边长都加2 B.各边长都减2
C.各边长都乘2 D.各边长都平方
3.(2025邹平期末)如图所示,小正方形网格中相似的两个三角形是 ( )
A.①与③ B.②与③
C.①与④ D.③与④
4.(2025永州蓝山县期中)已知△ABC的三边长分别为12 cm,15 cm,18 cm,△DEF的一边长为4 cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似 ( )
A.2 cm,3 cm
B.4 cm,5 cm
C.5 cm,6 cm
D.6 cm,7 cm
5.在△ABC中,AB=6,AC=8,在△A'B'C'中,A'B'=3,A'C'=4,若BC∶B'C'= ,则△ABC∽ .
6.根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由.
(1)AB=12,BC=15,AC=24,A'B'=25,C'B'=40,C'A'=20.
(2)AB=3,BC=4,AC=5,A'B'=12,B'C'=16,A'C'=20.
7.如图,网格中的小正方形的面积都为1,网格中有△ABC和△DFE(三角形的每个顶点都在格点上).这两个三角形相似吗 请说明理由.
1.如图,在4×1的方格中,每一个小正方形的顶点叫做格点,以其中三个格点为顶点的三角形称为格点三角形,△ABC就是一个格点三角形,现从△ABC的三个顶点中选取两个格点,再从余下的格点中选取一个格点连结成格点三角形,其中与△ABC相似的有 ( )
A.1个 B.2个 C.3个 D.4个
2.如图,A、B、C、D、E、G、H、M、N都是方格纸中的格点(即小正方形的顶点),要使△DEF与△ABC相似,则点F应是G、H、M、N四点中的 ( )
A.点H或点N B.点M或点N
C.点G或点H D.点G或点M
3.下列条件中:①∠A=45°,AB=12,AC=15,∠A'=45°,A'B'=16,A'C'=20;②∠A=47°,AB=1.5,AC=2,∠B'=47°,A'B'=2.8,B'C'=2.1;③AB=BC=2,AC=3,A'B'=B'C'=4,A'C'=6,能判定△ABC与△A'B'C'相似的有 ( )
A.0个 B.1个
C.2个 D.3个
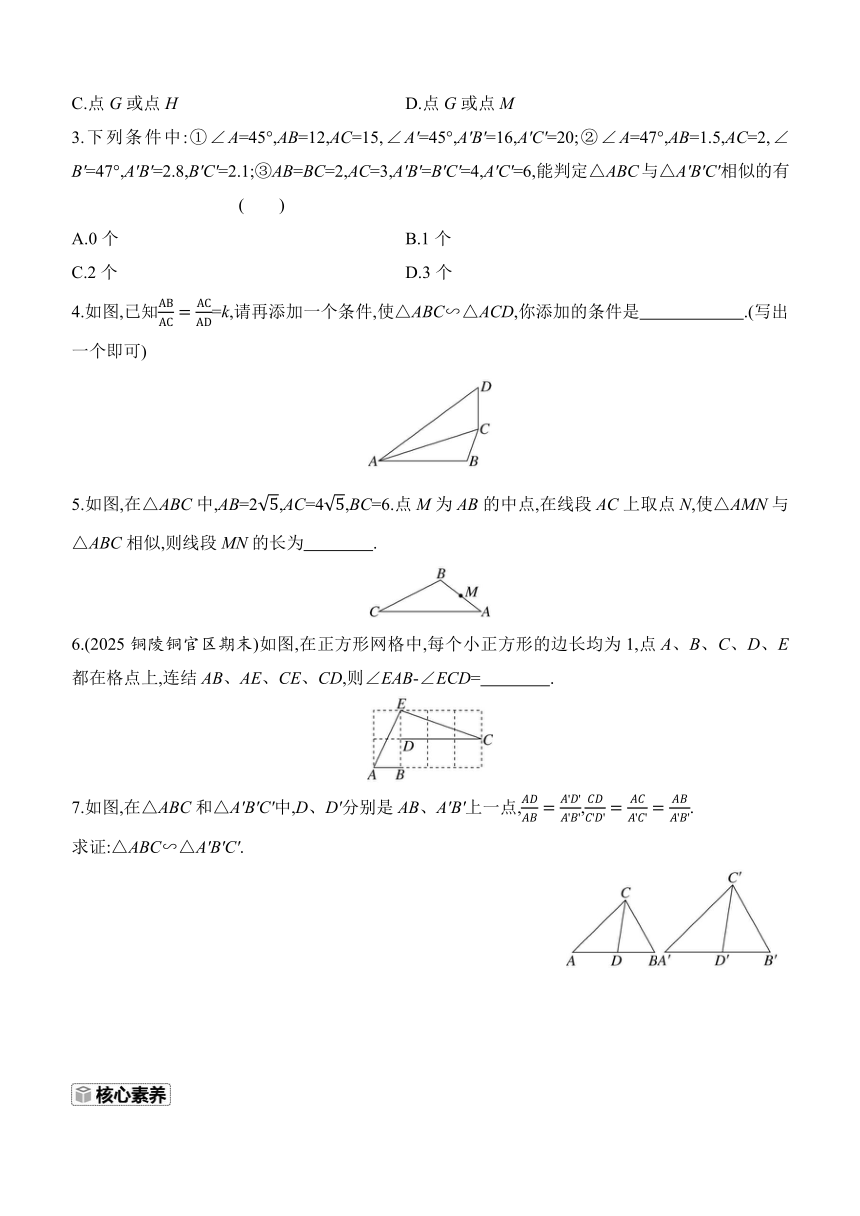
4.如图,已知=k,请再添加一个条件,使△ABC∽△ACD,你添加的条件是 .(写出一个即可)
5.如图,在△ABC中,AB=2,AC=4,BC=6.点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,则线段MN的长为 .
6.(2025铜陵铜官区期末)如图,在正方形网格中,每个小正方形的边长均为1,点A、B、C、D、E都在格点上,连结AB、AE、CE、CD,则∠EAB-∠ECD= .
7.如图,在△ABC和△A'B'C'中,D、D'分别是AB、A'B'上一点,,.
求证:△ABC∽△A'B'C'.
8.(几何直观)如图,在四边形ABCD中,E是对角线AC上一点,且.
(1)若∠DAE=22°,求∠BAD的度数.
(2)判断△ADE与△ACB是否相似,并说明理由.
【详解答案】
基础达标
1.A 解析:根据题意得AB=,AC=2,BC=,
∴BC∶AC∶AB=1∶.A.三边之比为1∶,图中的三角形(阴影部分)与△ABC相似;B.三边之比为∶3,图中的三角形(阴影部分)与△ABC不相似;C.三边之比为1∶∶2,图中的三角形(阴影部分)与△ABC不相似;D.三边之比为2∶,图中的三角形(阴影部分)与△ABC不相似.故选A.
2.C 解析:∵△ABC的边长分别为AB、BC、AC,各边长都乘2,则,,,∴得到的新三角形与△ABC相似,且相似比为2,∴C选项符合题意,A、B、D选项不符合题意.故选C.
3.A 解析:根据网格的特点,设单个网格的边长为1,则①号三角形的三边长分别为、2、,②号三角形的三边长分别为、、3,③号三角形的三边长分别为2、=2、=2,④号三角形的三边长分别为、3、,∵,∴①与③相似.故选A.
4.C 解析:设△DEF的另两边长分别为x cm、y cm,且x5.2∶1 △A'B'C' 解析:∵,∴当时,,∴△ABC∽△A'B'C'.
6.解:(1)相似.理由:∵,
,,
∴,
∴△ABC∽△C'A'B'.
(2)相似.理由:∵,,,
∴,
∴△ABC∽△A'B'C'.
7.解:相似.理由如下:
∵网格中的小正方形的面积都为1,
∴网格中的小正方形的边长都为1,
在△ABC中,AB=,AC=,BC=5.
在△DEF中,DE=,DF=2,EF=.
∵,,,∴.
∴△ABC∽△DEF.
能力提升
1.C 解析:如图,根据勾股定理,得AD=,AC=,BC=,BE=,CF=,又∵AB=2,CD=2,BF=1,CE=1,∴=1,=1,=1,,,,,,
∴,,,∴△ABC∽△CDA,△ABC∽△BCE,△ABC∽△CBF.故选C.
2.B 解析:设小正方形的边长为1,则△ABC的三边长分别为3、、.点F是点M或点N时,△DEF的三边长分别为6、2、2,与△ABC各边对应成比例.故选B.
3.D 解析:①由∠A=∠A',,判定△ABC∽△A'B'C',故①符合题意;②由∠A=∠B',,判定△ABC∽△B'C'A',故②符合题意;③由,判定△ABC∽△A'B'C',故③符合题意.∴能判定△ABC与△A'B'C'相似的有3个.故选D.
4.=k(或∠BAC=∠CAD) 解析:添加=k,∵=k,
∴△ABC∽△ACD.添加∠BAC=∠CAD,
∵=k,∠BAC=∠CAD,
∴△ABC∽△ACD.
5.3或 解析:∵在△ABC中,AB=2,M为AB的中点,∴AM=.当时,△AMN∽△ABC,即,解得MN=3.当时,△AMN∽△ACB,即,解得MN=.∴MN的长为3或.
6.45° 解析:如图,连结AD、EF.
∵AE=,EC=,AD=,DE=1,EF=,CF=2,∴,
∴△EAD∽△ECF,∴∠EAD=∠ECD,
∴∠EAB-∠ECD=∠EAB-∠EAD=∠DAB=45°.
7.证明:∵,∴.
∵,
∴.
∴△ADC∽△A'D'C'.∴∠A=∠A'.
∵,∴△ABC∽△A'B'C'.
8.解:(1)∵,
∴△ABE∽△ACD,
∴∠BAE=∠CAD=22°,
∴∠BAD=∠BAE+∠CAD=44°.
(2)△ADE∽△ACB.理由如下:
∵,∴.
又∵∠DAE=∠CAB,
∴△ADE∽△ACB.
第3课时 相似三角形的判定定理3
三边成比例的两个三角形相似
1.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是 ( )
A. B.
C. D.
2.将△ABC的各边长作如下变化,得到的新三角形与△ABC相似的是 ( )
A.各边长都加2 B.各边长都减2
C.各边长都乘2 D.各边长都平方
3.(2025邹平期末)如图所示,小正方形网格中相似的两个三角形是 ( )
A.①与③ B.②与③
C.①与④ D.③与④
4.(2025永州蓝山县期中)已知△ABC的三边长分别为12 cm,15 cm,18 cm,△DEF的一边长为4 cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似 ( )
A.2 cm,3 cm
B.4 cm,5 cm
C.5 cm,6 cm
D.6 cm,7 cm
5.在△ABC中,AB=6,AC=8,在△A'B'C'中,A'B'=3,A'C'=4,若BC∶B'C'= ,则△ABC∽ .
6.根据下列条件,判断△ABC与△A'B'C'是否相似,并说明理由.
(1)AB=12,BC=15,AC=24,A'B'=25,C'B'=40,C'A'=20.
(2)AB=3,BC=4,AC=5,A'B'=12,B'C'=16,A'C'=20.
7.如图,网格中的小正方形的面积都为1,网格中有△ABC和△DFE(三角形的每个顶点都在格点上).这两个三角形相似吗 请说明理由.
1.如图,在4×1的方格中,每一个小正方形的顶点叫做格点,以其中三个格点为顶点的三角形称为格点三角形,△ABC就是一个格点三角形,现从△ABC的三个顶点中选取两个格点,再从余下的格点中选取一个格点连结成格点三角形,其中与△ABC相似的有 ( )
A.1个 B.2个 C.3个 D.4个
2.如图,A、B、C、D、E、G、H、M、N都是方格纸中的格点(即小正方形的顶点),要使△DEF与△ABC相似,则点F应是G、H、M、N四点中的 ( )
A.点H或点N B.点M或点N
C.点G或点H D.点G或点M
3.下列条件中:①∠A=45°,AB=12,AC=15,∠A'=45°,A'B'=16,A'C'=20;②∠A=47°,AB=1.5,AC=2,∠B'=47°,A'B'=2.8,B'C'=2.1;③AB=BC=2,AC=3,A'B'=B'C'=4,A'C'=6,能判定△ABC与△A'B'C'相似的有 ( )
A.0个 B.1个
C.2个 D.3个
4.如图,已知=k,请再添加一个条件,使△ABC∽△ACD,你添加的条件是 .(写出一个即可)
5.如图,在△ABC中,AB=2,AC=4,BC=6.点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,则线段MN的长为 .
6.(2025铜陵铜官区期末)如图,在正方形网格中,每个小正方形的边长均为1,点A、B、C、D、E都在格点上,连结AB、AE、CE、CD,则∠EAB-∠ECD= .
7.如图,在△ABC和△A'B'C'中,D、D'分别是AB、A'B'上一点,,.
求证:△ABC∽△A'B'C'.
8.(几何直观)如图,在四边形ABCD中,E是对角线AC上一点,且.
(1)若∠DAE=22°,求∠BAD的度数.
(2)判断△ADE与△ACB是否相似,并说明理由.
【详解答案】
基础达标
1.A 解析:根据题意得AB=,AC=2,BC=,
∴BC∶AC∶AB=1∶.A.三边之比为1∶,图中的三角形(阴影部分)与△ABC相似;B.三边之比为∶3,图中的三角形(阴影部分)与△ABC不相似;C.三边之比为1∶∶2,图中的三角形(阴影部分)与△ABC不相似;D.三边之比为2∶,图中的三角形(阴影部分)与△ABC不相似.故选A.
2.C 解析:∵△ABC的边长分别为AB、BC、AC,各边长都乘2,则,,,∴得到的新三角形与△ABC相似,且相似比为2,∴C选项符合题意,A、B、D选项不符合题意.故选C.
3.A 解析:根据网格的特点,设单个网格的边长为1,则①号三角形的三边长分别为、2、,②号三角形的三边长分别为、、3,③号三角形的三边长分别为2、=2、=2,④号三角形的三边长分别为、3、,∵,∴①与③相似.故选A.
4.C 解析:设△DEF的另两边长分别为x cm、y cm,且x
6.解:(1)相似.理由:∵,
,,
∴,
∴△ABC∽△C'A'B'.
(2)相似.理由:∵,,,
∴,
∴△ABC∽△A'B'C'.
7.解:相似.理由如下:
∵网格中的小正方形的面积都为1,
∴网格中的小正方形的边长都为1,
在△ABC中,AB=,AC=,BC=5.
在△DEF中,DE=,DF=2,EF=.
∵,,,∴.
∴△ABC∽△DEF.
能力提升
1.C 解析:如图,根据勾股定理,得AD=,AC=,BC=,BE=,CF=,又∵AB=2,CD=2,BF=1,CE=1,∴=1,=1,=1,,,,,,
∴,,,∴△ABC∽△CDA,△ABC∽△BCE,△ABC∽△CBF.故选C.
2.B 解析:设小正方形的边长为1,则△ABC的三边长分别为3、、.点F是点M或点N时,△DEF的三边长分别为6、2、2,与△ABC各边对应成比例.故选B.
3.D 解析:①由∠A=∠A',,判定△ABC∽△A'B'C',故①符合题意;②由∠A=∠B',,判定△ABC∽△B'C'A',故②符合题意;③由,判定△ABC∽△A'B'C',故③符合题意.∴能判定△ABC与△A'B'C'相似的有3个.故选D.
4.=k(或∠BAC=∠CAD) 解析:添加=k,∵=k,
∴△ABC∽△ACD.添加∠BAC=∠CAD,
∵=k,∠BAC=∠CAD,
∴△ABC∽△ACD.
5.3或 解析:∵在△ABC中,AB=2,M为AB的中点,∴AM=.当时,△AMN∽△ABC,即,解得MN=3.当时,△AMN∽△ACB,即,解得MN=.∴MN的长为3或.
6.45° 解析:如图,连结AD、EF.
∵AE=,EC=,AD=,DE=1,EF=,CF=2,∴,
∴△EAD∽△ECF,∴∠EAD=∠ECD,
∴∠EAB-∠ECD=∠EAB-∠EAD=∠DAB=45°.
7.证明:∵,∴.
∵,
∴.
∴△ADC∽△A'D'C'.∴∠A=∠A'.
∵,∴△ABC∽△A'B'C'.
8.解:(1)∵,
∴△ABE∽△ACD,
∴∠BAE=∠CAD=22°,
∴∠BAD=∠BAE+∠CAD=44°.
(2)△ADE∽△ACB.理由如下:
∵,∴.
又∵∠DAE=∠CAB,
∴△ADE∽△ACB.
