23.3.3.相似三角形的性质 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 23.3.3.相似三角形的性质 同步练习(含答案)华东师大版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 125.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 00:00:00 | ||
图片预览


文档简介
3.相似三角形的性质
相似三角形对应线段的比等于相似比
1.若△ABC∽△DEF,相似比为3∶2,则对应边上的高的比为 ( )
A.3∶2 B.3∶5
C.9∶4 D.4∶9
2.若△ABC∽△A'B'C',AD和A'D'分别是它们的中线,AE和A'E'分别是它们的角平分线,若AD=4 cm,A'D'=6 cm,A'E'-AE=1.5 cm,则AE= cm.
相似三角形周长的比等于相似比
3.(2024内江中考)已知△ABC与△DEF相似,且相似比为1∶3,则△ABC与△DEF的周长之比是 ( )
A.1∶1 B.1∶3
C.1∶6 D.1∶9
4.已知△ABC∽△A'B'C',它们的周长分别为60 cm和72 cm,且AB=15 cm,B'C'=24 cm,求AC和A'C'的长.
相似三角形面积的比等于相似比的平方
5.若两个相似三角形的相似比是1∶,则这两个相似三角形面积的比是 ( )
A.1∶ B.1∶4
C.1∶6 D.1∶3
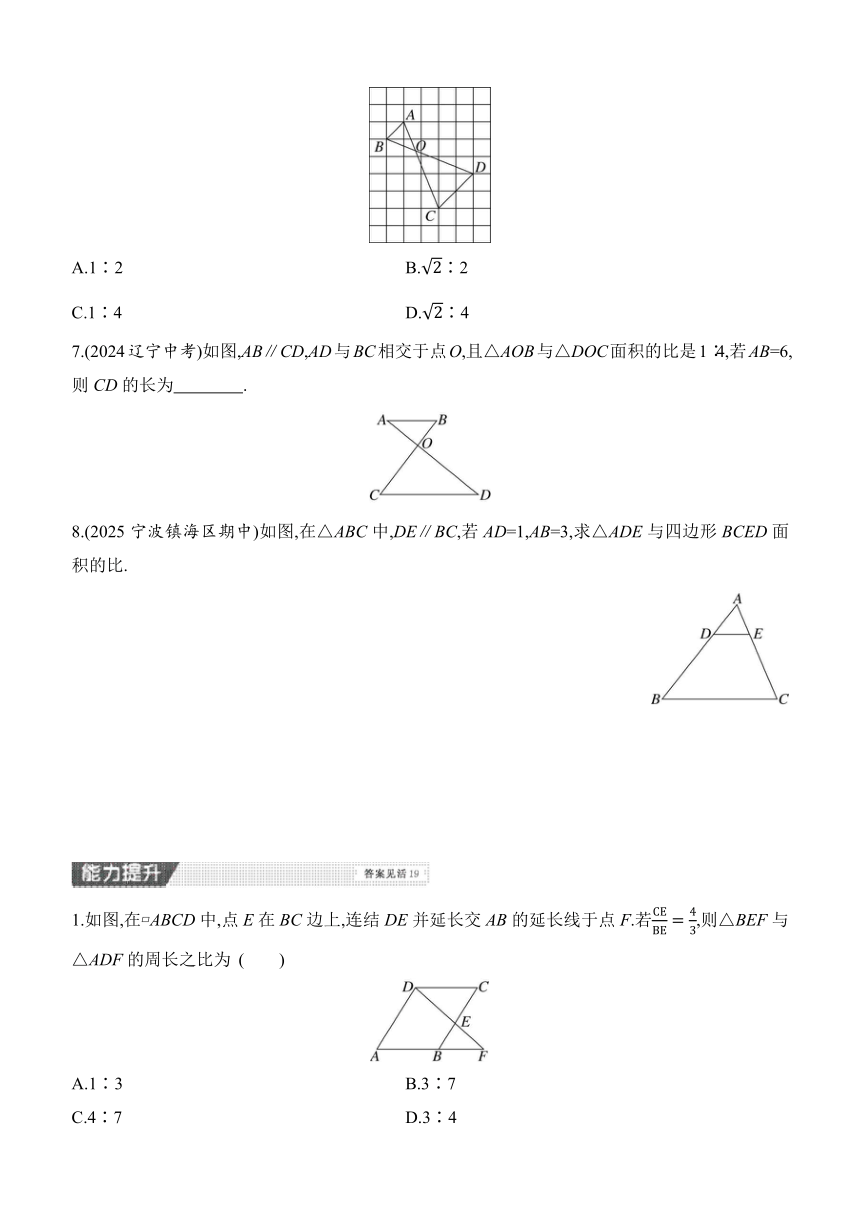
6.如图,在小正方形网格中,A、B、C、D是网格线交点,AC与BD相交于点O,则△ABO的面积与△CDO的面积的比为 ( )
A.1∶2 B.∶2
C.1∶4 D.∶4
7.(2024辽宁中考)如图,AB∥CD,AD与BC相交于点O,且△AOB与△DOC面积的比是1∶4,若AB=6,则CD的长为 .
8.(2025宁波镇海区期中)如图,在△ABC中,DE∥BC,若AD=1,AB=3,求△ADE与四边形BCED面积的比.
1.如图,在 ABCD中,点E在BC边上,连结DE并延长交AB的延长线于点F.若,则△BEF与△ADF的周长之比为 ( )
A.1∶3 B.3∶7
C.4∶7 D.3∶4
2.如图,在平行四边形ABCD中,点E在边AB上,连结DE交对角线AC于点F,如果,CD=6,那么BE的长为( )
A.2 B.3 C.4 D.5
第2题图 第3题图
3.如图,D是△ABC的BC边上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为 ( )
A.5 B. C.10 D.15
4.如图,已知△ABC≌△DCE≌△GEF,点B、C、E、F在同一条直线上,连结BG,分别交AC、DC、DE于点P、Q、K,其中S△DQK=1,则图中三个阴影部分面积的和为 .
5.(2025娄底新化县期末)如图,在△ABC中,AD是边BC上的高,BC=40 cm,AD=30 cm,作矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC、AB上,AD与HG的交点为M,且HG=2HE.
(1)求证:.
(2)试求矩形EFGH的周长.
6.如图,D、E、F分别为△ABC的边BC、CA、AB上的点,DE∥AB,∠A=∠EDF.
(1)求证:∠C=∠BDF.
(2)若,S△ABC=50,求四边形AFDE的面积.
7.(几何直观)如图所示,过△ABC的顶点C作任一直线与边AB及中线AD分别交于点F和E,过点D作DM∥FC交AB于点M.
(1)若S△AEF∶S四边形MDEF=2∶3,求的值.
(2)求证:AE·FB=2AF·ED.
【详解答案】
基础达标
1.A 解析:∵△ABC∽△DEF,相似比为3∶2,∴对应边上的高的比为3∶2.故选A.
2.3 解析:由相似三角形对应角的平分线之比等于相似比、相似三角形对应边上的中线之比等于相似比,得,∴A'E'=AE.
∵A'E'-AE=1.5 cm,∴AE-AE=1.5 cm.∴AE=3 cm.
3.B 解析:∵相似三角形周长的比等于相似比,∴△ABC与△DEF的周长之比为1∶3.故选B.
4.解:因为△ABC∽△A'B'C',
所以.
又因为AB=15 cm,B'C'=24 cm,
所以,
所以A'B'=18 cm,BC=20 cm,
所以AC=60-15-20=25(cm),
A'C'=72-18-24=30(cm).
5.D 解析:∵两个相似三角形的相似比是1∶,∴这两个相似三角形面积的比是12∶()2=1∶3.故选D.
6.C 解析:设小正方形网格的边长为1,由题图可知,AB∥CD,∴△ABO∽△CDO,∵AB=,CD=2,
∴S△ABO∶S△CDO=(AB∶CD)2=(∶2)2=1∶4.故选C.
7.12 解析:∵AB∥CD,∴△AOB∽△DOC,∴,
∴,∵AB=6,∴,
∴CD=12.
8.解:∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴△ADE∽△ABC,
∴,
∴S△ABC=9S△ADE,
∴=
.
能力提升
1.B 解析:∵四边形ABCD是平行四边形,∴CD∥AB,BC∥AD,
∴△CDE∽△BFE,∴,
∴,∵BC∥AD,
∴△BEF∽△ADF,
∴△BEF与△ADF的周长之比为.故选B.
2.A 解析:设△ADC中AC边上的高为h,则S△ADF=×AF×h,S△DFC=×FC×h,∵,∴,在平行四边形ABCD中,AB∥CD,
∴△AEF∽△CDF,∴,
即,解得AE=4,∵AB=CD=6,∴BE=AB-AE=6-4=2.故选A.
3.A 解析:∵∠DAC=∠B,∠C=∠C,∴△ACD∽△BCA.∴.
∵AB=4,AD=2,∴.
∴.∴.∵S△ABD=15,∴S△BCA=S△ABD+S△ACD=15+S△ACD.∴.
∴S△ACD=5.故选A.
4.13 解析:∵△ABC≌△DCE≌△GEF,
∴∠ACB=∠DEC=∠GFE,BC=CE=EF,∴AC∥DE∥GF,∴,,∴KE=2PC,GF=3PC,∵AC∥DE,∴∠D=∠ACD,
又∵DK=DE-KE=3PC-2PC=PC,∠DQK=∠CQP,∴△DQK≌△CQP,设△DQK的边DK的长为x,DK边上的高为h,则xh=1,整理得xh=2,∴S△BPC=·x·2h=xh=2,S四边形CEKQ=×3x·2h-1=3xh-1=3×2-1=5,
S△EFG=×3x·2h=3xh=6,∴三个阴影部分面积的和为2+5+6=13.
5.解:(1)证明:∵四边形HEFG为矩形,
∴HG∥EF,∴△AHG∽△ABC,
∵AD⊥BC,∴AM⊥HG,∴.
(2)由(1)得,设HE=x cm,则HG=2x,则,解得x=12,∴矩形EFGH的周长为2x+4x=6x=72(cm).
6.解:(1)证明:∵DE∥AB,
∴∠A=∠CED.
∵∠A=∠EDF,
∴∠CED=∠EDF,∴DF∥AC,
∴∠C=∠BDF.
(2)由(1)知DF∥AC,
∴△BDF∽△BCA,
∴,∵,
∴,
∴,
∵S△ABC=50,∴S△BDF=8,
∵DE∥AB,∴△CDE∽△CBA,
∴,
∴S△CDE=18,∴四边形AFDE的面积为S△ABC-S△BDF-S△CDE=24.
7.解:(1)∵EF∥DM,
∴△AEF∽△ADM,
∵S△AEF∶S四边形MDEF=2∶3,
∴,
∴.
(2)证明:∵CD=DB,DM∥CF,
∴CD∶DB=FM∶MB=1∶1,
∴FM=MB=FB,∵DM∥CF,
∴AE∶ED=AF∶FM,
即AE∶ED=AF∶FB,
∴AE∶ED=2AF∶FB,
∴AE·FB=2AF·ED.
相似三角形对应线段的比等于相似比
1.若△ABC∽△DEF,相似比为3∶2,则对应边上的高的比为 ( )
A.3∶2 B.3∶5
C.9∶4 D.4∶9
2.若△ABC∽△A'B'C',AD和A'D'分别是它们的中线,AE和A'E'分别是它们的角平分线,若AD=4 cm,A'D'=6 cm,A'E'-AE=1.5 cm,则AE= cm.
相似三角形周长的比等于相似比
3.(2024内江中考)已知△ABC与△DEF相似,且相似比为1∶3,则△ABC与△DEF的周长之比是 ( )
A.1∶1 B.1∶3
C.1∶6 D.1∶9
4.已知△ABC∽△A'B'C',它们的周长分别为60 cm和72 cm,且AB=15 cm,B'C'=24 cm,求AC和A'C'的长.
相似三角形面积的比等于相似比的平方
5.若两个相似三角形的相似比是1∶,则这两个相似三角形面积的比是 ( )
A.1∶ B.1∶4
C.1∶6 D.1∶3
6.如图,在小正方形网格中,A、B、C、D是网格线交点,AC与BD相交于点O,则△ABO的面积与△CDO的面积的比为 ( )
A.1∶2 B.∶2
C.1∶4 D.∶4
7.(2024辽宁中考)如图,AB∥CD,AD与BC相交于点O,且△AOB与△DOC面积的比是1∶4,若AB=6,则CD的长为 .
8.(2025宁波镇海区期中)如图,在△ABC中,DE∥BC,若AD=1,AB=3,求△ADE与四边形BCED面积的比.
1.如图,在 ABCD中,点E在BC边上,连结DE并延长交AB的延长线于点F.若,则△BEF与△ADF的周长之比为 ( )
A.1∶3 B.3∶7
C.4∶7 D.3∶4
2.如图,在平行四边形ABCD中,点E在边AB上,连结DE交对角线AC于点F,如果,CD=6,那么BE的长为( )
A.2 B.3 C.4 D.5
第2题图 第3题图
3.如图,D是△ABC的BC边上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为 ( )
A.5 B. C.10 D.15
4.如图,已知△ABC≌△DCE≌△GEF,点B、C、E、F在同一条直线上,连结BG,分别交AC、DC、DE于点P、Q、K,其中S△DQK=1,则图中三个阴影部分面积的和为 .
5.(2025娄底新化县期末)如图,在△ABC中,AD是边BC上的高,BC=40 cm,AD=30 cm,作矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC、AB上,AD与HG的交点为M,且HG=2HE.
(1)求证:.
(2)试求矩形EFGH的周长.
6.如图,D、E、F分别为△ABC的边BC、CA、AB上的点,DE∥AB,∠A=∠EDF.
(1)求证:∠C=∠BDF.
(2)若,S△ABC=50,求四边形AFDE的面积.
7.(几何直观)如图所示,过△ABC的顶点C作任一直线与边AB及中线AD分别交于点F和E,过点D作DM∥FC交AB于点M.
(1)若S△AEF∶S四边形MDEF=2∶3,求的值.
(2)求证:AE·FB=2AF·ED.
【详解答案】
基础达标
1.A 解析:∵△ABC∽△DEF,相似比为3∶2,∴对应边上的高的比为3∶2.故选A.
2.3 解析:由相似三角形对应角的平分线之比等于相似比、相似三角形对应边上的中线之比等于相似比,得,∴A'E'=AE.
∵A'E'-AE=1.5 cm,∴AE-AE=1.5 cm.∴AE=3 cm.
3.B 解析:∵相似三角形周长的比等于相似比,∴△ABC与△DEF的周长之比为1∶3.故选B.
4.解:因为△ABC∽△A'B'C',
所以.
又因为AB=15 cm,B'C'=24 cm,
所以,
所以A'B'=18 cm,BC=20 cm,
所以AC=60-15-20=25(cm),
A'C'=72-18-24=30(cm).
5.D 解析:∵两个相似三角形的相似比是1∶,∴这两个相似三角形面积的比是12∶()2=1∶3.故选D.
6.C 解析:设小正方形网格的边长为1,由题图可知,AB∥CD,∴△ABO∽△CDO,∵AB=,CD=2,
∴S△ABO∶S△CDO=(AB∶CD)2=(∶2)2=1∶4.故选C.
7.12 解析:∵AB∥CD,∴△AOB∽△DOC,∴,
∴,∵AB=6,∴,
∴CD=12.
8.解:∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴△ADE∽△ABC,
∴,
∴S△ABC=9S△ADE,
∴=
.
能力提升
1.B 解析:∵四边形ABCD是平行四边形,∴CD∥AB,BC∥AD,
∴△CDE∽△BFE,∴,
∴,∵BC∥AD,
∴△BEF∽△ADF,
∴△BEF与△ADF的周长之比为.故选B.
2.A 解析:设△ADC中AC边上的高为h,则S△ADF=×AF×h,S△DFC=×FC×h,∵,∴,在平行四边形ABCD中,AB∥CD,
∴△AEF∽△CDF,∴,
即,解得AE=4,∵AB=CD=6,∴BE=AB-AE=6-4=2.故选A.
3.A 解析:∵∠DAC=∠B,∠C=∠C,∴△ACD∽△BCA.∴.
∵AB=4,AD=2,∴.
∴.∴.∵S△ABD=15,∴S△BCA=S△ABD+S△ACD=15+S△ACD.∴.
∴S△ACD=5.故选A.
4.13 解析:∵△ABC≌△DCE≌△GEF,
∴∠ACB=∠DEC=∠GFE,BC=CE=EF,∴AC∥DE∥GF,∴,,∴KE=2PC,GF=3PC,∵AC∥DE,∴∠D=∠ACD,
又∵DK=DE-KE=3PC-2PC=PC,∠DQK=∠CQP,∴△DQK≌△CQP,设△DQK的边DK的长为x,DK边上的高为h,则xh=1,整理得xh=2,∴S△BPC=·x·2h=xh=2,S四边形CEKQ=×3x·2h-1=3xh-1=3×2-1=5,
S△EFG=×3x·2h=3xh=6,∴三个阴影部分面积的和为2+5+6=13.
5.解:(1)证明:∵四边形HEFG为矩形,
∴HG∥EF,∴△AHG∽△ABC,
∵AD⊥BC,∴AM⊥HG,∴.
(2)由(1)得,设HE=x cm,则HG=2x,则,解得x=12,∴矩形EFGH的周长为2x+4x=6x=72(cm).
6.解:(1)证明:∵DE∥AB,
∴∠A=∠CED.
∵∠A=∠EDF,
∴∠CED=∠EDF,∴DF∥AC,
∴∠C=∠BDF.
(2)由(1)知DF∥AC,
∴△BDF∽△BCA,
∴,∵,
∴,
∴,
∵S△ABC=50,∴S△BDF=8,
∵DE∥AB,∴△CDE∽△CBA,
∴,
∴S△CDE=18,∴四边形AFDE的面积为S△ABC-S△BDF-S△CDE=24.
7.解:(1)∵EF∥DM,
∴△AEF∽△ADM,
∵S△AEF∶S四边形MDEF=2∶3,
∴,
∴.
(2)证明:∵CD=DB,DM∥CF,
∴CD∶DB=FM∶MB=1∶1,
∴FM=MB=FB,∵DM∥CF,
∴AE∶ED=AF∶FM,
即AE∶ED=AF∶FB,
∴AE∶ED=2AF∶FB,
∴AE·FB=2AF·ED.
