23.3.4相似三角形的应用 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 23.3.4相似三角形的应用 同步练习(含答案)华东师大版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 135.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 17:33:07 | ||
图片预览


文档简介
4.相似三角形的应用
利用相似三角形测量物体的高度(宽度)
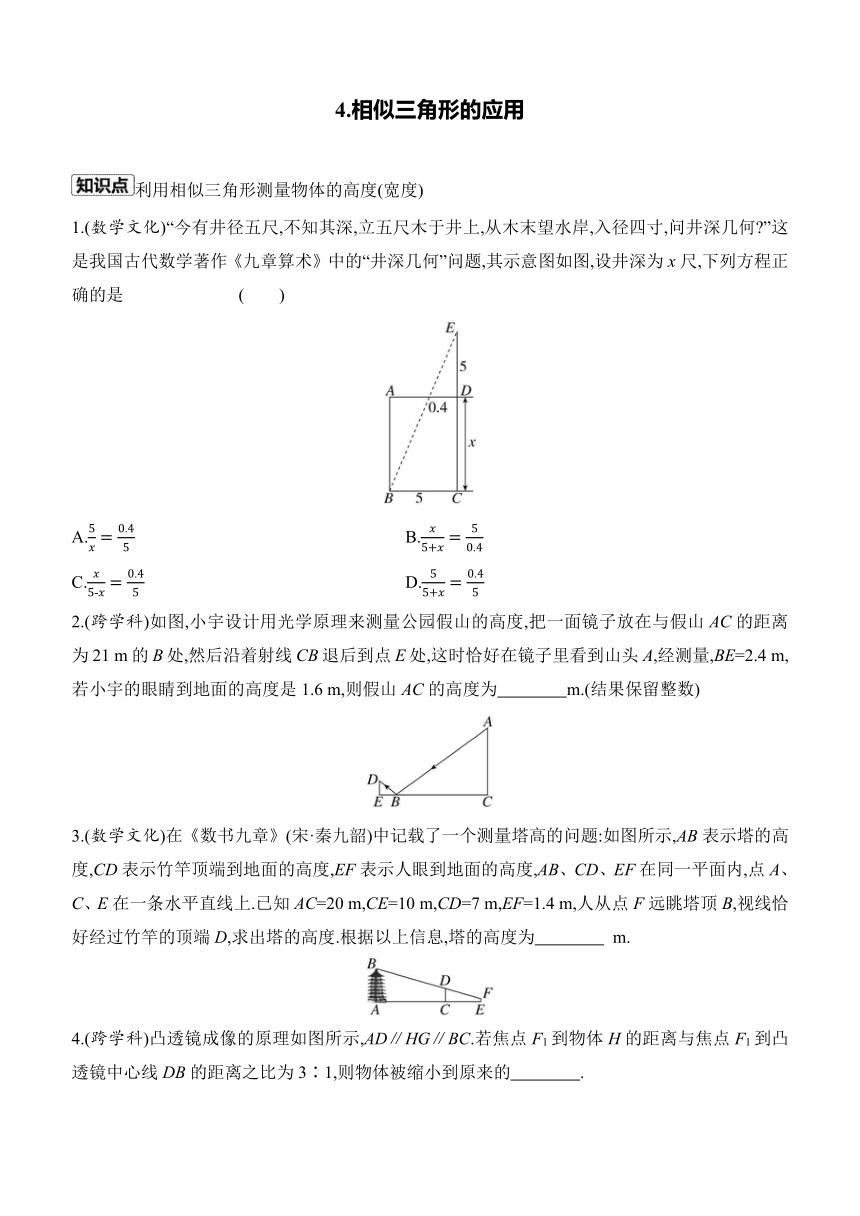
1.(数学文化)“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何 ”这是我国古代数学著作《九章算术》中的“井深几何”问题,其示意图如图,设井深为x尺,下列方程正确的是 ( )
A. B.
C. D.
2.(跨学科)如图,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC的距离为21 m的B处,然后沿着射线CB退后到点E处,这时恰好在镜子里看到山头A,经测量,BE=2.4 m,若小宇的眼睛到地面的高度是1.6 m,则假山AC的高度为 m.(结果保留整数)
3.(数学文化)在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,AB表示塔的高度,CD表示竹竿顶端到地面的高度,EF表示人眼到地面的高度,AB、CD、EF在同一平面内,点A、C、E在一条水平直线上.已知AC=20 m,CE=10 m,CD=7 m,EF=1.4 m,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,求出塔的高度.根据以上信息,塔的高度为 m.
4.(跨学科)凸透镜成像的原理如图所示,AD∥HG∥BC.若焦点F1到物体H的距离与焦点F1到凸透镜中心线DB的距离之比为3∶1,则物体被缩小到原来的 .
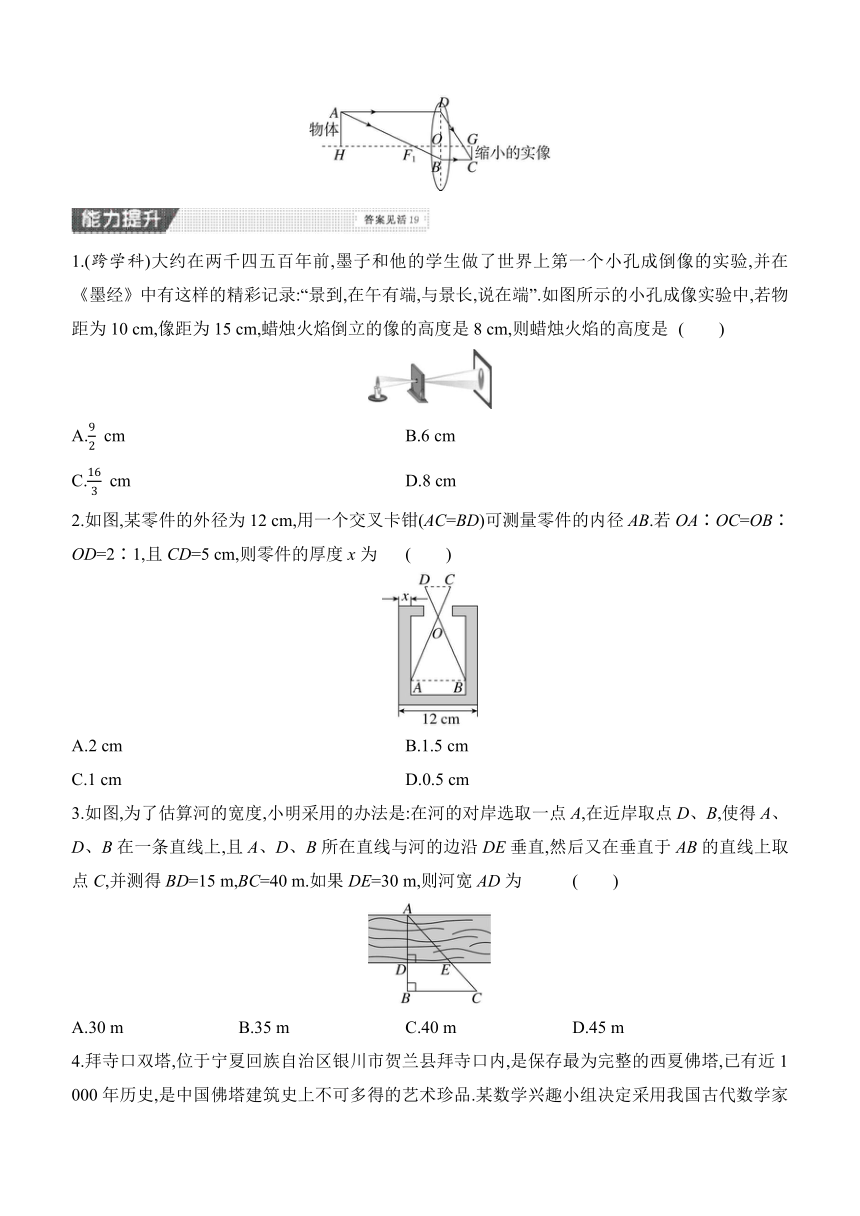
1.(跨学科)大约在两千四五百年前,墨子和他的学生做了世界上第一个小孔成倒像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是8 cm,则蜡烛火焰的高度是 ( )
A. cm B.6 cm
C. cm D.8 cm
2.如图,某零件的外径为12 cm,用一个交叉卡钳(AC=BD)可测量零件的内径AB.若OA∶OC=OB∶OD=2∶1,且CD=5 cm,则零件的厚度x为 ( )
A.2 cm B.1.5 cm
C.1 cm D.0.5 cm
3.如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D、B,使得A、D、B在一条直线上,且A、D、B所在直线与河的边沿DE垂直,然后又在垂直于AB的直线上取点C,并测得BD=15 m,BC=40 m.如果DE=30 m,则河宽AD为 ( )
A.30 m B.35 m C.40 m D.45 m
4.拜寺口双塔,位于宁夏回族自治区银川市贺兰县拜寺口内,是保存最为完整的西夏佛塔,已有近1 000年历史,是中国佛塔建筑史上不可多得的艺术珍品.某数学兴趣小组决定采用我国古代数学家赵爽利用影子对物体进行测量的原理,来测量拜寺口双塔中东塔的高度.如图,东塔的高度为AB,选取与塔底B在同一水平地面上的E、G两点,分别竖立两根垂直地面且高为1.5 m的标杆EF和GH,两标杆间隔EG为46 m,并且东塔AB、标杆EF和GH在同一竖直平面内.从标杆EF后退2 m到D处(即ED=2 m),从D处观察A点,A、F、D在同一直线上;从标杆GH后退4 m到C处(即CG=4 m),从C处观察A点,A、H、C三点也在同一直线上,且B、E、D、G、C在同一直线上,请你根据以上测量数据,帮助兴趣小组求出东塔AB的高度.
微专题4 直角三角形斜边上的高
在直角三角形中,斜边上的高把斜边分成两条线段,高是斜边被分成的两条线段的比例中项,每一条直角边又是斜边与斜边被分成的线段中邻近直角边的线段的比例中项.
几何语言:如图,在Rt△ABC中,∠ACB=90°,CD是斜边上的高,则有
(1)CD2=AD·BD.
(2)AC2=AB·AD.
(3)BC2=AB·BD.
1.如图,在△ABC中,∠BAC=90°,以A为圆心,AC长为半径作弧,交BC于C、D两点,分别以点C和点D为圆心,大于CD长为半径作弧,两弧交于点P,作直线AP,交CD于点E.若CD=6,BE=6,则BC= .
2.在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)求证:AC2=AB·AD.
(2)如果BD=5,AC=6,求CD的长.
【详解答案】
基础达标
1.D 解析:如图,设AD交BE于点F.
∵DF∥BC,∴△EFD∽△EBC,
∴,∵DF=0.4,BC=5,DE=5,CD=x,∴.故选D.
2.14 解析:∵DE⊥CE,AC⊥CE,
∴∠C=∠E=90°,根据反射角等于入射角可得∠DBE=∠ABC,∴△ABC∽△DBE,∴,即,
故AC=14 m.
3.18.2 解析:如图,过点F作FG⊥CD,垂足为G,延长FG交AB于点H,
由题意,得FH⊥AB,AH=CG=EF=1.4 m,AC=GH=20 m,CE=FG=10 m,∴∠DGF=∠BHF=90°.
∵CD=7 m,∴DG=CD-CG=7-1.4=5.6(m).∵∠DFG=∠BFH,
∴△FDG∽△FBH.∴.
∴.∴BH=16.8 m.
∴AB=BH+AH=16.8+1.4=18.2(m).∴塔的高度为18.2 m.
4. 解析:由题意得OB=CG,AH⊥HO,BO⊥HO,∴∠AHO=∠BOH=90°,∵∠AF1H=∠BF1O,
∴△AHF1∽△BOF1,∴,∴BO=AH,∴CG=AH,
∴物体被缩小到原来的.
能力提升
1.C 解析:题中实验的示意图如图,过点O作OE⊥CD,垂足为E,延长EO交AB于点F,
∴OF⊥AB,由题意得OE=15 cm,OF=10 cm,CD=8 cm,AB∥CD,
∵AB∥CD,∴∠A=∠C,∠B=∠D,
∴△ABO∽△CDO,∴,
∴,解得AB=,
∴蜡烛火焰的高度是 cm.故选C.
2.C 解析:∵OA∶OC=OB∶OD=2∶1,∠AOB=∠COD,∴△AOB∽△COD,
∴AB∶CD=OA∶OC=2∶1,∴AB∶5=2∶1,∴AB=10 cm,∵外径为12 cm,∴10+2x=12,∴x=1.故选C.
3.D 解析:∵AB⊥DE,BC⊥AB,
∴DE∥BC,∴△ADE∽△ABC,
∴,即,
∴AD=45 m.故选D.
4.解:设BD=x m,则BC=BD+DG+CG=x+46-2+4=(x+48)m,
∵AB⊥BC,EF⊥BC,
∴AB∥EF.∴△ABD∽△FED.
∴,即.
同理可证△ABC∽△HGC,
∴,即.
∴,解得x=48.
经检验,x=48是原方程的解,
∴.∴AB=36 m.
∴东塔AB的高度为36 m.
微专题4
1.3 解析:由作法得,AP垂直平分CD,∴CE=CD=3,∠AEC=∠AEB=∠BAC=90°,∴∠CAE+∠ACE=∠ABE+∠ACE=90°,∴∠CAE=∠ABE,∴△ACE∽△BAE,∴,即AE2=BE·CE,解得AE==3.
2.解:(1)证明:∵CD⊥AB,
∴∠ADC=90°,又∵∠DAC=∠CAB,
∴Rt△ACD∽Rt△ABC,∴AC∶AB=AD∶AC,∴AC2=AB·AD.
(2)∵AC2=AB·AD,∴62=(AD+5)·AD,整理得AD2+5AD-36=0,解得AD=-9(舍去)或AD=4,
∵CD2=AD·BD,
∴CD==2.
利用相似三角形测量物体的高度(宽度)
1.(数学文化)“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何 ”这是我国古代数学著作《九章算术》中的“井深几何”问题,其示意图如图,设井深为x尺,下列方程正确的是 ( )
A. B.
C. D.
2.(跨学科)如图,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC的距离为21 m的B处,然后沿着射线CB退后到点E处,这时恰好在镜子里看到山头A,经测量,BE=2.4 m,若小宇的眼睛到地面的高度是1.6 m,则假山AC的高度为 m.(结果保留整数)
3.(数学文化)在《数书九章》(宋·秦九韶)中记载了一个测量塔高的问题:如图所示,AB表示塔的高度,CD表示竹竿顶端到地面的高度,EF表示人眼到地面的高度,AB、CD、EF在同一平面内,点A、C、E在一条水平直线上.已知AC=20 m,CE=10 m,CD=7 m,EF=1.4 m,人从点F远眺塔顶B,视线恰好经过竹竿的顶端D,求出塔的高度.根据以上信息,塔的高度为 m.
4.(跨学科)凸透镜成像的原理如图所示,AD∥HG∥BC.若焦点F1到物体H的距离与焦点F1到凸透镜中心线DB的距离之比为3∶1,则物体被缩小到原来的 .
1.(跨学科)大约在两千四五百年前,墨子和他的学生做了世界上第一个小孔成倒像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是8 cm,则蜡烛火焰的高度是 ( )
A. cm B.6 cm
C. cm D.8 cm
2.如图,某零件的外径为12 cm,用一个交叉卡钳(AC=BD)可测量零件的内径AB.若OA∶OC=OB∶OD=2∶1,且CD=5 cm,则零件的厚度x为 ( )
A.2 cm B.1.5 cm
C.1 cm D.0.5 cm
3.如图,为了估算河的宽度,小明采用的办法是:在河的对岸选取一点A,在近岸取点D、B,使得A、D、B在一条直线上,且A、D、B所在直线与河的边沿DE垂直,然后又在垂直于AB的直线上取点C,并测得BD=15 m,BC=40 m.如果DE=30 m,则河宽AD为 ( )
A.30 m B.35 m C.40 m D.45 m
4.拜寺口双塔,位于宁夏回族自治区银川市贺兰县拜寺口内,是保存最为完整的西夏佛塔,已有近1 000年历史,是中国佛塔建筑史上不可多得的艺术珍品.某数学兴趣小组决定采用我国古代数学家赵爽利用影子对物体进行测量的原理,来测量拜寺口双塔中东塔的高度.如图,东塔的高度为AB,选取与塔底B在同一水平地面上的E、G两点,分别竖立两根垂直地面且高为1.5 m的标杆EF和GH,两标杆间隔EG为46 m,并且东塔AB、标杆EF和GH在同一竖直平面内.从标杆EF后退2 m到D处(即ED=2 m),从D处观察A点,A、F、D在同一直线上;从标杆GH后退4 m到C处(即CG=4 m),从C处观察A点,A、H、C三点也在同一直线上,且B、E、D、G、C在同一直线上,请你根据以上测量数据,帮助兴趣小组求出东塔AB的高度.
微专题4 直角三角形斜边上的高
在直角三角形中,斜边上的高把斜边分成两条线段,高是斜边被分成的两条线段的比例中项,每一条直角边又是斜边与斜边被分成的线段中邻近直角边的线段的比例中项.
几何语言:如图,在Rt△ABC中,∠ACB=90°,CD是斜边上的高,则有
(1)CD2=AD·BD.
(2)AC2=AB·AD.
(3)BC2=AB·BD.
1.如图,在△ABC中,∠BAC=90°,以A为圆心,AC长为半径作弧,交BC于C、D两点,分别以点C和点D为圆心,大于CD长为半径作弧,两弧交于点P,作直线AP,交CD于点E.若CD=6,BE=6,则BC= .
2.在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
(1)求证:AC2=AB·AD.
(2)如果BD=5,AC=6,求CD的长.
【详解答案】
基础达标
1.D 解析:如图,设AD交BE于点F.
∵DF∥BC,∴△EFD∽△EBC,
∴,∵DF=0.4,BC=5,DE=5,CD=x,∴.故选D.
2.14 解析:∵DE⊥CE,AC⊥CE,
∴∠C=∠E=90°,根据反射角等于入射角可得∠DBE=∠ABC,∴△ABC∽△DBE,∴,即,
故AC=14 m.
3.18.2 解析:如图,过点F作FG⊥CD,垂足为G,延长FG交AB于点H,
由题意,得FH⊥AB,AH=CG=EF=1.4 m,AC=GH=20 m,CE=FG=10 m,∴∠DGF=∠BHF=90°.
∵CD=7 m,∴DG=CD-CG=7-1.4=5.6(m).∵∠DFG=∠BFH,
∴△FDG∽△FBH.∴.
∴.∴BH=16.8 m.
∴AB=BH+AH=16.8+1.4=18.2(m).∴塔的高度为18.2 m.
4. 解析:由题意得OB=CG,AH⊥HO,BO⊥HO,∴∠AHO=∠BOH=90°,∵∠AF1H=∠BF1O,
∴△AHF1∽△BOF1,∴,∴BO=AH,∴CG=AH,
∴物体被缩小到原来的.
能力提升
1.C 解析:题中实验的示意图如图,过点O作OE⊥CD,垂足为E,延长EO交AB于点F,
∴OF⊥AB,由题意得OE=15 cm,OF=10 cm,CD=8 cm,AB∥CD,
∵AB∥CD,∴∠A=∠C,∠B=∠D,
∴△ABO∽△CDO,∴,
∴,解得AB=,
∴蜡烛火焰的高度是 cm.故选C.
2.C 解析:∵OA∶OC=OB∶OD=2∶1,∠AOB=∠COD,∴△AOB∽△COD,
∴AB∶CD=OA∶OC=2∶1,∴AB∶5=2∶1,∴AB=10 cm,∵外径为12 cm,∴10+2x=12,∴x=1.故选C.
3.D 解析:∵AB⊥DE,BC⊥AB,
∴DE∥BC,∴△ADE∽△ABC,
∴,即,
∴AD=45 m.故选D.
4.解:设BD=x m,则BC=BD+DG+CG=x+46-2+4=(x+48)m,
∵AB⊥BC,EF⊥BC,
∴AB∥EF.∴△ABD∽△FED.
∴,即.
同理可证△ABC∽△HGC,
∴,即.
∴,解得x=48.
经检验,x=48是原方程的解,
∴.∴AB=36 m.
∴东塔AB的高度为36 m.
微专题4
1.3 解析:由作法得,AP垂直平分CD,∴CE=CD=3,∠AEC=∠AEB=∠BAC=90°,∴∠CAE+∠ACE=∠ABE+∠ACE=90°,∴∠CAE=∠ABE,∴△ACE∽△BAE,∴,即AE2=BE·CE,解得AE==3.
2.解:(1)证明:∵CD⊥AB,
∴∠ADC=90°,又∵∠DAC=∠CAB,
∴Rt△ACD∽Rt△ABC,∴AC∶AB=AD∶AC,∴AC2=AB·AD.
(2)∵AC2=AB·AD,∴62=(AD+5)·AD,整理得AD2+5AD-36=0,解得AD=-9(舍去)或AD=4,
∵CD2=AD·BD,
∴CD==2.
