23.4中位线 同步练习(含答案)华东师大版九年级上册
文档属性
| 名称 | 23.4中位线 同步练习(含答案)华东师大版九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 166.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 17:35:06 | ||
图片预览


文档简介
23.4中位线
三角形的中位线
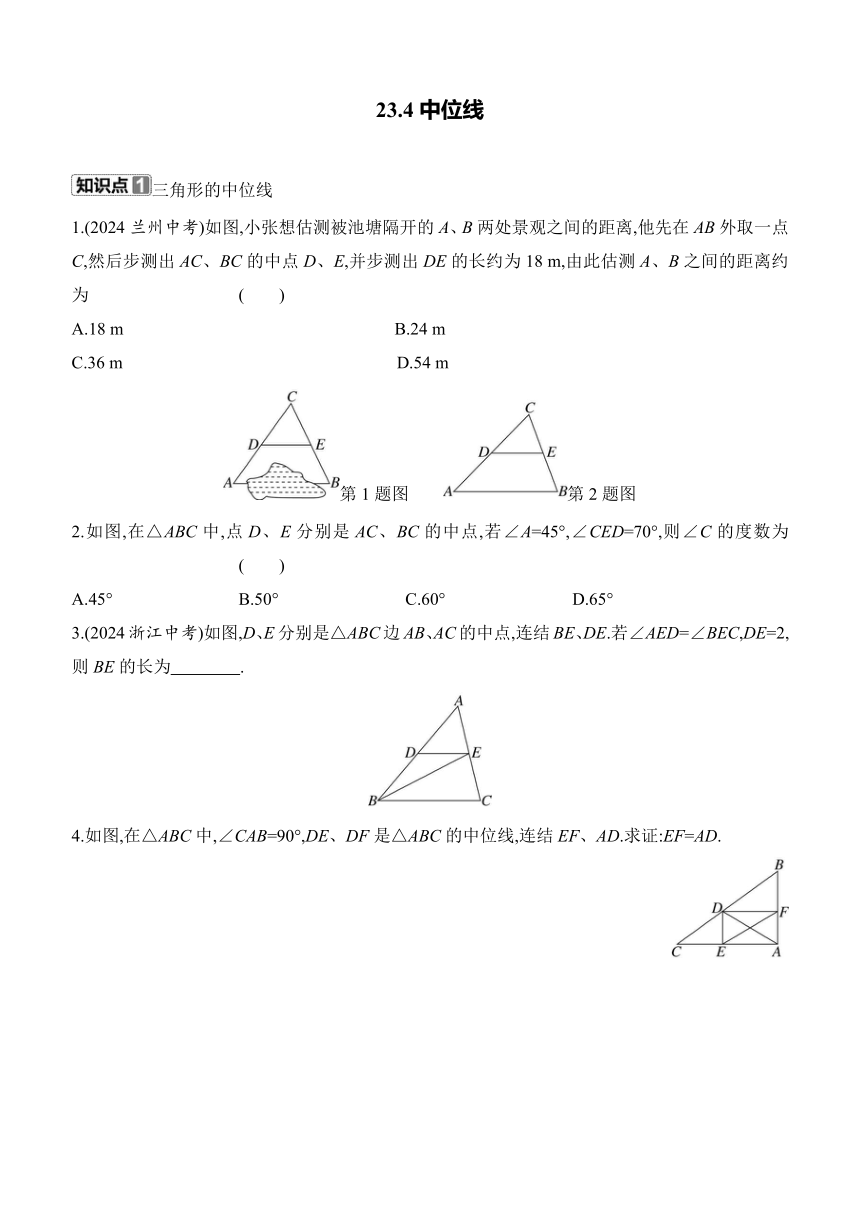
1.(2024兰州中考)如图,小张想估测被池塘隔开的A、B两处景观之间的距离,他先在AB外取一点C,然后步测出AC、BC的中点D、E,并步测出DE的长约为18 m,由此估测A、B之间的距离约为 ( )
A.18 m B.24 m
C.36 m D.54 m
第1题图 第2题图
2.如图,在△ABC中,点D、E分别是AC、BC的中点,若∠A=45°,∠CED=70°,则∠C的度数为 ( )
A.45° B.50° C.60° D.65°
3.(2024浙江中考)如图,D、E分别是△ABC边AB、AC的中点,连结BE、DE.若∠AED=∠BEC,DE=2,则BE的长为 .
4.如图,在△ABC中,∠CAB=90°,DE、DF是△ABC的中位线,连结EF、AD.求证:EF=AD.
三角形的重心
5.如图,△ABC的中线AD、CF相交于点G,连结BG并延长交AC于点E.以下结论一定正确的是 ( )
A.GF=GD
B.AE=CE
C.∠ABE=∠CBE
D.∠AGE=∠CGE
6.已知G是△ABC的重心,GP∥BC,GP交AB边于点P,BC=3,则GP= ( )
A. B. C. D.
1.(教材P80习题23.4 T3变式)如图,在四边形ABCD中,E、F、G分别是AB、CD、AC的中点,若∠DAC=20°,∠ACB=66°,则∠FGE的度数为 ( )
A.112°
B.134°
C.114°
D.132°
2.如图,DE是△ABC的中位线,点F在DB上,DF=2BF.连结EF并延长,与CB的延长线相交于点M.若BC=6,则线段CM的长为 ( )
A. B.7 C. D.8
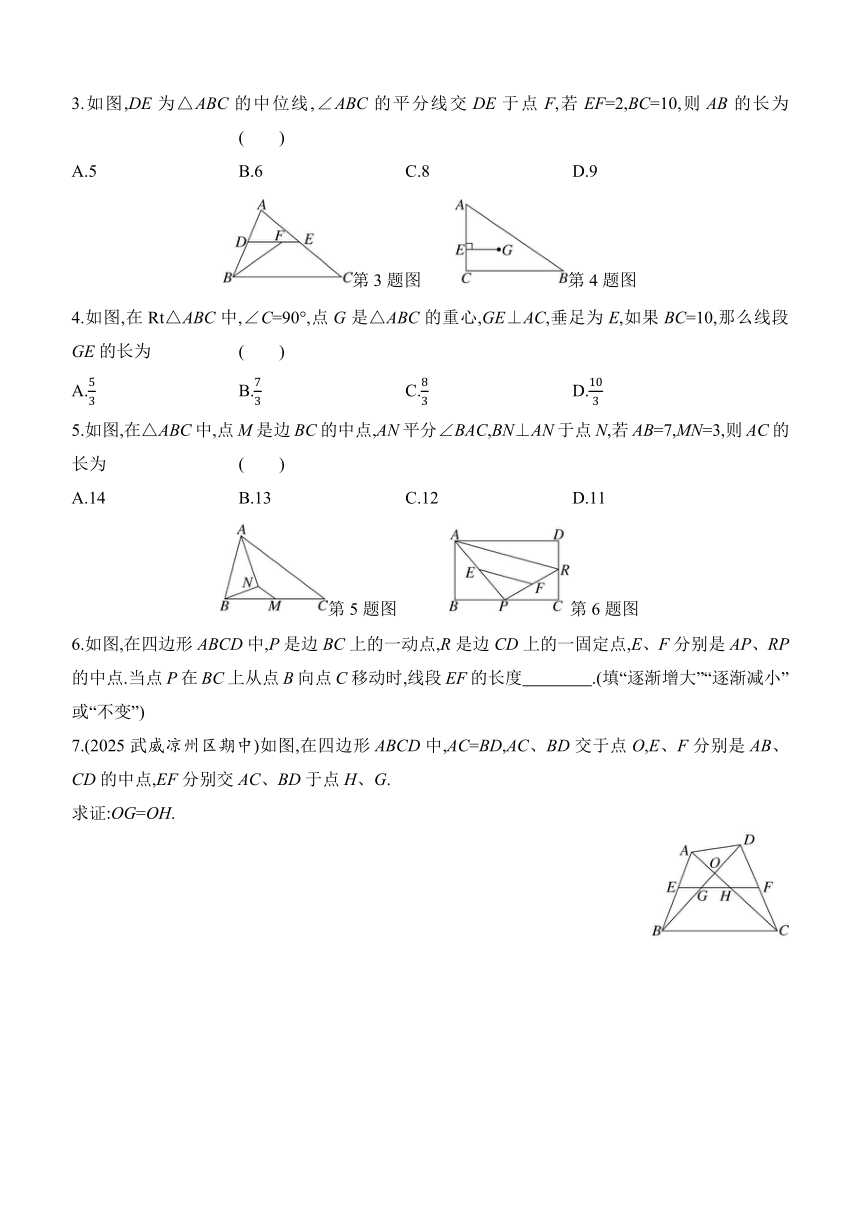
3.如图,DE为△ABC的中位线,∠ABC的平分线交DE于点F,若EF=2,BC=10,则AB的长为 ( )
A.5 B.6 C.8 D.9
第3题图 第4题图
4.如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E,如果BC=10,那么线段GE的长为 ( )
A. B. C. D.
5.如图,在△ABC中,点M是边BC的中点,AN平分∠BAC,BN⊥AN于点N,若AB=7,MN=3,则AC的长为 ( )
A.14 B.13 C.12 D.11
第5题图 第6题图
6.如图,在四边形ABCD中,P是边BC上的一动点,R是边CD上的一固定点,E、F分别是AP、RP的中点.当点P在BC上从点B向点C移动时,线段EF的长度 .(填“逐渐增大”“逐渐减小”或“不变”)
7.(2025武威凉州区期中)如图,在四边形ABCD中,AC=BD,AC、BD交于点O,E、F分别是AB、CD的中点,EF分别交AC、BD于点H、G.
求证:OG=OH.
8.(几何直观)课本再现
已知:如图1,DE是△ABC的中位线.
求证:DE∥BC,且DE=BC.
(1)定理证明
证明:如图2,延长DE至点F,使得EF=DE,连结CF.请你根据所添加的辅助线,写出完整的证明过程.(不再添加新的辅助线)
(2)知识应用
如图3,在四边形ABCD中,AB=6,CD=8,∠BAC=30°,∠ACD=120°,点E、F、M分别是AD、BC、AC的中点,求EF的长.
图1 图2 图3
【详解答案】
基础达标
1.C 解析:∵D、E分别是AC、BC的中点,∴DE是△ABC的中位线,∴AB=2DE=36 m.故选C.
2.D 解析:∵点D、E分别是AC、BC的中点,∴DE是△ABC的中位线,
∴DE∥AB,∴∠B=∠CED=70°,
∴∠C=180°-∠A-∠B=180°-45°-70°=65°.故选D.
3.4 解析:∵D、E分别是△ABC边AB、AC的中点,∴BC=2DE=2×2=4,DE∥BC,∴∠AED=∠C,
∵∠AED=∠BEC,∴∠BEC=∠C,
∴BE=BC=4.
4.证明:∵DE、DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形DEAF是平行四边形,
∵∠CAB=90°,
∴四边形DEAF是矩形,
∴EF=AD.
5.B 解析:∵△ABC的中线AD、CF相交于点G,
∴点G为△ABC的重心.
又∵BG的延长线交AC于点E,
∴BE是△ABC的中线,∴AE=CE,选项B一定成立.
选项A、C、D不一定成立.故选B.
6.B 解析:如图,连结AG,并延长AG交BC于点D.由G为重心可知D为BC的中点,.∴BD=BC=.又∵GP∥BC,
∴△APG∽△ABD.∴.
∴GP=BD=.故选B.
能力提升
1.B 解析:∵E、F、G分别是AB、CD、AC的中点,∴EG、FG分别为△ABC、△ADC的中位线,∴EG∥BC,FG∥AD,∴∠CGE+∠ACB=180°,∠CGF=∠DAC,∵∠DAC=20°,∠ACB=66°,∴∠CGE=114°,∠CGF=20°,
∴∠FGE=114°+20°=134°.故选B.
2.C 解析:∵DE是△ABC的中位线,
∴DE∥BC,DE=BC=×6=3.
∴△DEF∽△BMF.∴=2.∴BM=.∴CM=BC+BM=.故选C.
3.B 解析:∵DE是△ABC的中位线,BC=10,∴DE∥BC,DE=BC=5,∵EF=2,∴DF=3,∵BF平分∠ABC,∴∠ABF=∠FBC,∵DE∥BC,∴∠DFB=∠FBC,∴∠ABF=∠DFB,∴BD=FD=3,∴AB=2BD=6.故选B.
4.D 解析:如图,连结AG并延长交BC于点D.
∵点G是△ABC的重心,∴点D为BC的中点,.
∵BC=10,∴CD=BD=BC=5.
∵GE⊥AC,∴∠AEG=90°.∵∠C=90°,∴∠AEG=∠C=90°.∵∠EAG=∠CAD,∴△AEG∽△ACD,∴.∵,∴.∴,∴GE=.故选D.
5.B 解析:如图,延长BN交AC于点D,在△ANB和△AND中,
∴△ANB≌△AND,
∴AD=AB=7,BN=ND,
又∵M是△ABC的边BC的中点,
∴DC=2MN=6,
∴AC=AD+CD=13.故选B.
6.不变 解析:∵E、F分别是AP、RP的中点,∴EF是△APR的中位线,
∴EF=AR,∵R是边CD上的一固定点,∴AR的长度不变,∴线段EF的长度不变.
7.证明:如图,取BC边的中点M,连结EM、FM,
∵M、F分别是BC、CD的中点,
∴MF∥BD,MF=BD,
同理,ME∥AC,ME=AC,
∵AC=BD,∴ME=MF,
∴∠MEF=∠MFE,∵MF∥BD,
∴∠MFE=∠OGH,
同理,∠MEF=∠OHG,
∴∠OGH=∠OHG,∴OG=OH.
8.解:(1)证明:在△AED和△CEF中,
∴△AED≌△CEF,
∴AD=CF,∠A=∠ECF,
∴AB∥CF.∵AD=BD,∴BD=CF,
∴四边形DBCF为平行四边形.
∴DF∥BC,DF=BC,
∴DE∥BC,DE=BC.
(2)∵点E、M分别是AD、AC的中点,∴EM是△ADC的中位线.
∴EM=CD=4,EM∥CD.
∴∠EMC+∠ACD=180°.
∵∠ACD=120°,∴∠EMC=60°.
易知MF=AB=3,MF∥AB,
∴∠CMF=∠BAC.∵∠BAC=30°,
∴∠CMF=30°,∴∠EMF=90°.
∴EF==5.
三角形的中位线
1.(2024兰州中考)如图,小张想估测被池塘隔开的A、B两处景观之间的距离,他先在AB外取一点C,然后步测出AC、BC的中点D、E,并步测出DE的长约为18 m,由此估测A、B之间的距离约为 ( )
A.18 m B.24 m
C.36 m D.54 m
第1题图 第2题图
2.如图,在△ABC中,点D、E分别是AC、BC的中点,若∠A=45°,∠CED=70°,则∠C的度数为 ( )
A.45° B.50° C.60° D.65°
3.(2024浙江中考)如图,D、E分别是△ABC边AB、AC的中点,连结BE、DE.若∠AED=∠BEC,DE=2,则BE的长为 .
4.如图,在△ABC中,∠CAB=90°,DE、DF是△ABC的中位线,连结EF、AD.求证:EF=AD.
三角形的重心
5.如图,△ABC的中线AD、CF相交于点G,连结BG并延长交AC于点E.以下结论一定正确的是 ( )
A.GF=GD
B.AE=CE
C.∠ABE=∠CBE
D.∠AGE=∠CGE
6.已知G是△ABC的重心,GP∥BC,GP交AB边于点P,BC=3,则GP= ( )
A. B. C. D.
1.(教材P80习题23.4 T3变式)如图,在四边形ABCD中,E、F、G分别是AB、CD、AC的中点,若∠DAC=20°,∠ACB=66°,则∠FGE的度数为 ( )
A.112°
B.134°
C.114°
D.132°
2.如图,DE是△ABC的中位线,点F在DB上,DF=2BF.连结EF并延长,与CB的延长线相交于点M.若BC=6,则线段CM的长为 ( )
A. B.7 C. D.8
3.如图,DE为△ABC的中位线,∠ABC的平分线交DE于点F,若EF=2,BC=10,则AB的长为 ( )
A.5 B.6 C.8 D.9
第3题图 第4题图
4.如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E,如果BC=10,那么线段GE的长为 ( )
A. B. C. D.
5.如图,在△ABC中,点M是边BC的中点,AN平分∠BAC,BN⊥AN于点N,若AB=7,MN=3,则AC的长为 ( )
A.14 B.13 C.12 D.11
第5题图 第6题图
6.如图,在四边形ABCD中,P是边BC上的一动点,R是边CD上的一固定点,E、F分别是AP、RP的中点.当点P在BC上从点B向点C移动时,线段EF的长度 .(填“逐渐增大”“逐渐减小”或“不变”)
7.(2025武威凉州区期中)如图,在四边形ABCD中,AC=BD,AC、BD交于点O,E、F分别是AB、CD的中点,EF分别交AC、BD于点H、G.
求证:OG=OH.
8.(几何直观)课本再现
已知:如图1,DE是△ABC的中位线.
求证:DE∥BC,且DE=BC.
(1)定理证明
证明:如图2,延长DE至点F,使得EF=DE,连结CF.请你根据所添加的辅助线,写出完整的证明过程.(不再添加新的辅助线)
(2)知识应用
如图3,在四边形ABCD中,AB=6,CD=8,∠BAC=30°,∠ACD=120°,点E、F、M分别是AD、BC、AC的中点,求EF的长.
图1 图2 图3
【详解答案】
基础达标
1.C 解析:∵D、E分别是AC、BC的中点,∴DE是△ABC的中位线,∴AB=2DE=36 m.故选C.
2.D 解析:∵点D、E分别是AC、BC的中点,∴DE是△ABC的中位线,
∴DE∥AB,∴∠B=∠CED=70°,
∴∠C=180°-∠A-∠B=180°-45°-70°=65°.故选D.
3.4 解析:∵D、E分别是△ABC边AB、AC的中点,∴BC=2DE=2×2=4,DE∥BC,∴∠AED=∠C,
∵∠AED=∠BEC,∴∠BEC=∠C,
∴BE=BC=4.
4.证明:∵DE、DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形DEAF是平行四边形,
∵∠CAB=90°,
∴四边形DEAF是矩形,
∴EF=AD.
5.B 解析:∵△ABC的中线AD、CF相交于点G,
∴点G为△ABC的重心.
又∵BG的延长线交AC于点E,
∴BE是△ABC的中线,∴AE=CE,选项B一定成立.
选项A、C、D不一定成立.故选B.
6.B 解析:如图,连结AG,并延长AG交BC于点D.由G为重心可知D为BC的中点,.∴BD=BC=.又∵GP∥BC,
∴△APG∽△ABD.∴.
∴GP=BD=.故选B.
能力提升
1.B 解析:∵E、F、G分别是AB、CD、AC的中点,∴EG、FG分别为△ABC、△ADC的中位线,∴EG∥BC,FG∥AD,∴∠CGE+∠ACB=180°,∠CGF=∠DAC,∵∠DAC=20°,∠ACB=66°,∴∠CGE=114°,∠CGF=20°,
∴∠FGE=114°+20°=134°.故选B.
2.C 解析:∵DE是△ABC的中位线,
∴DE∥BC,DE=BC=×6=3.
∴△DEF∽△BMF.∴=2.∴BM=.∴CM=BC+BM=.故选C.
3.B 解析:∵DE是△ABC的中位线,BC=10,∴DE∥BC,DE=BC=5,∵EF=2,∴DF=3,∵BF平分∠ABC,∴∠ABF=∠FBC,∵DE∥BC,∴∠DFB=∠FBC,∴∠ABF=∠DFB,∴BD=FD=3,∴AB=2BD=6.故选B.
4.D 解析:如图,连结AG并延长交BC于点D.
∵点G是△ABC的重心,∴点D为BC的中点,.
∵BC=10,∴CD=BD=BC=5.
∵GE⊥AC,∴∠AEG=90°.∵∠C=90°,∴∠AEG=∠C=90°.∵∠EAG=∠CAD,∴△AEG∽△ACD,∴.∵,∴.∴,∴GE=.故选D.
5.B 解析:如图,延长BN交AC于点D,在△ANB和△AND中,
∴△ANB≌△AND,
∴AD=AB=7,BN=ND,
又∵M是△ABC的边BC的中点,
∴DC=2MN=6,
∴AC=AD+CD=13.故选B.
6.不变 解析:∵E、F分别是AP、RP的中点,∴EF是△APR的中位线,
∴EF=AR,∵R是边CD上的一固定点,∴AR的长度不变,∴线段EF的长度不变.
7.证明:如图,取BC边的中点M,连结EM、FM,
∵M、F分别是BC、CD的中点,
∴MF∥BD,MF=BD,
同理,ME∥AC,ME=AC,
∵AC=BD,∴ME=MF,
∴∠MEF=∠MFE,∵MF∥BD,
∴∠MFE=∠OGH,
同理,∠MEF=∠OHG,
∴∠OGH=∠OHG,∴OG=OH.
8.解:(1)证明:在△AED和△CEF中,
∴△AED≌△CEF,
∴AD=CF,∠A=∠ECF,
∴AB∥CF.∵AD=BD,∴BD=CF,
∴四边形DBCF为平行四边形.
∴DF∥BC,DF=BC,
∴DE∥BC,DE=BC.
(2)∵点E、M分别是AD、AC的中点,∴EM是△ADC的中位线.
∴EM=CD=4,EM∥CD.
∴∠EMC+∠ACD=180°.
∵∠ACD=120°,∴∠EMC=60°.
易知MF=AB=3,MF∥AB,
∴∠CMF=∠BAC.∵∠BAC=30°,
∴∠CMF=30°,∴∠EMF=90°.
∴EF==5.
