第23章 图形的相似 专题训练四 相似三角形的基本模型 (含答案)
文档属性
| 名称 | 第23章 图形的相似 专题训练四 相似三角形的基本模型 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 137.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-07 17:41:51 | ||
图片预览



文档简介
专题训练四 相似三角形的基本模型
“A”字型相似
模型展示
若DE∥BC,则△ADE∽△ABC 若∠1=∠2,则△ADE∽△ABC
1.(2024河南中考)如图,在 ABCD中,对角线AC、BD相交于点O,点E为OC的中点,EF∥AB交BC于点F.若AB=4,则EF的长为 ( )
A. B.1 C. D.2
第1题图 第2题图
2.(2024滨州中考)如图,在△ABC中,点D、E分别在边AB、AC上.添加一个条件使△ADE∽△ACB,则这个条件可以是 .(写出一种情况即可)
3.如图,已知△ADE∽△ABC,DE=3,BC=9.
(1)求的值.
(2)若AE=4,求AC的长.
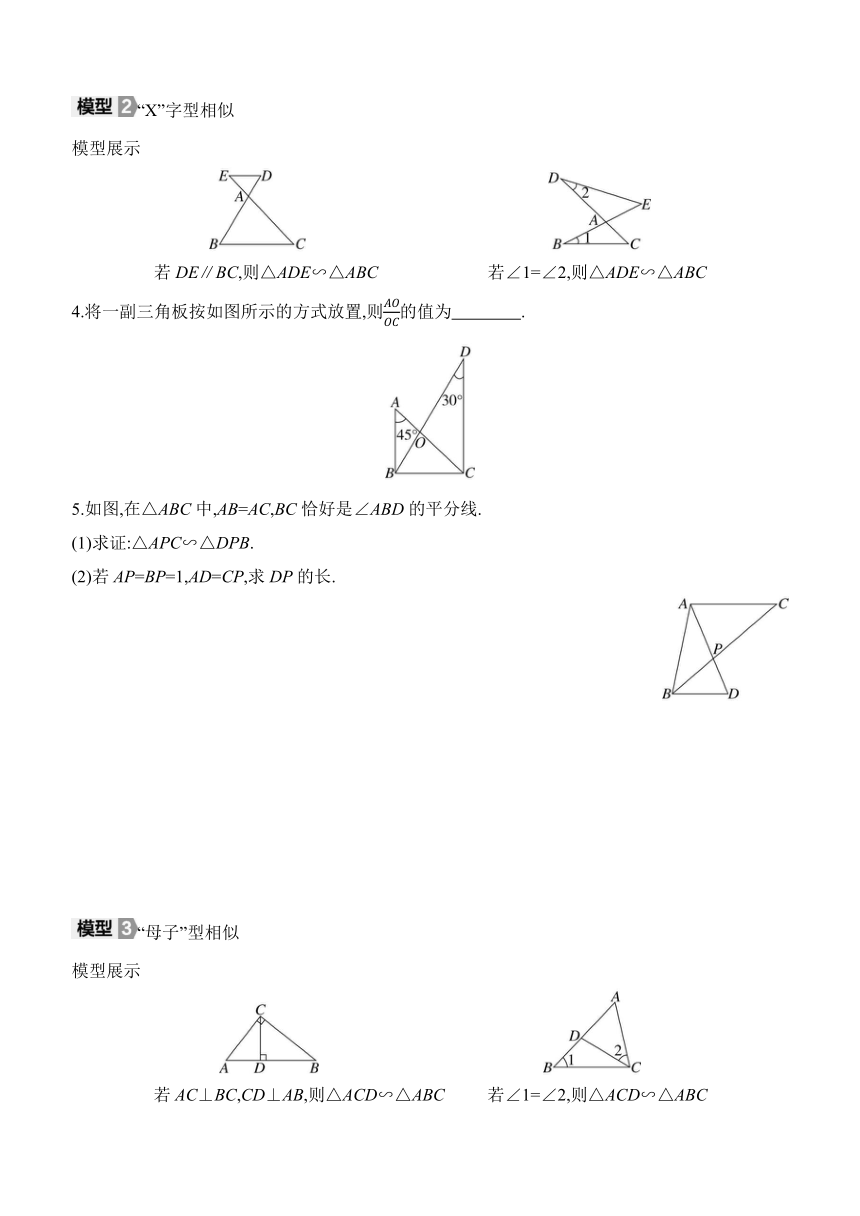
“X”字型相似
模型展示
若DE∥BC,则△ADE∽△ABC 若∠1=∠2,则△ADE∽△ABC
4.将一副三角板按如图所示的方式放置,则的值为 .
5.如图,在△ABC中,AB=AC,BC恰好是∠ABD的平分线.
(1)求证:△APC∽△DPB.
(2)若AP=BP=1,AD=CP,求DP的长.
“母子”型相似
模型展示
若AC⊥BC,CD⊥AB,则△ACD∽△ABC 若∠1=∠2,则△ACD∽△ABC
6.如图,点D是△ABC的边AB上一点,∠ABC=∠ACD.
(1)求证:△ABC∽△ACD.
(2)当AD=2,AB=3时,求AC的长.
7.如图,在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高.
(1)求证:△ABD∽△CBA.
(2)若AB=6,BC=10,求BD的长.
“手拉手”型相似
模型展示
若∠1=∠2,∠B=∠D,则△ADE∽△ABC
8.如图,∠DAB=∠CAE,请你再添加一个条件,使得△ADE∽△ABC.则下列选项不成立的是 ( )
A.∠D=∠B B.∠E=∠C
C. D.
9.如图,D为△ABC内的一点,E为△ABC外的一点,且∠ABC=∠DBE,∠BAD=∠BCE.
(1)求证:△ABD∽△CBE.
(2)若AB∶DB=5∶2,AC=6,直接写出线段DE的长度: .
一线三等角型相似
模型展示
若∠1=∠2=∠3,则△ABC∽△CDE
10.如图,在矩形ABCD中,E、F、G分别在AB、BC、CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是 ( )
A.4 B. C. D.5
11.如图,等边三角形ABC中,D为BC边上一点,E为AC边上一点,∠ADE=60°.
(1)求证:△ABD∽△DCE.
(2)若BD=4,CE=,求△ABC的边长.
【详解答案】
1.B 解析:∵四边形ABCD是平行四边形,∴OC=AC,∵点E为OC的中点,∴CE=OC=AC,∵EF∥AB,∴△CEF∽△CAB,∴,即,∴EF=1.故选B.
2.∠ADE=∠C(答案不唯一)
解析:∵∠DAE=∠BAC,∴添加条件∠ADE=∠C,可以判定△ADE∽△ACB.(答案不唯一)
3.解:(1)∵△ADE∽△ABC,
∴.
(2)∵,AE=4,
∴AC=3AE=12.
4. 解析:由题意得AB∥CD,
∴△ABO∽△CDO,∴,
∵△ABC是等腰直角三角形,设AB=a,则BC=a,∴CD=a,
∴.
5.解:(1)证明:∵AB=AC,∴∠ABC=∠C,∵BC是∠ABD的平分线,
∴∠ABC=∠DBC,∴∠C=∠DBC,
又∵∠APC=∠DPB,
∴△APC∽△DPB.
(2)设DP=x,∵AP=PB=1,
∴AD=AP+DP=1+x,
又∵AD=CP,∴CP=1+x,
由(1)得△APC∽△DPB,
∴AP∶DP=PC∶PB,
即1∶x=(x+1)∶1,∴x2+x=1,
∴x2+x-1=0,
解得x1=,x2=(不合题意,舍去).∴DP=.
6.解:(1)证明:∵∠ABC=∠ACD,
∠CAB=∠DAC,
∴△ABC∽△ACD.
(2)∵△ABC∽△ACD,∴,即,∴AC=.
7.解:(1)证明:∵AD是斜边BC上的高,∴∠BDA=90°.
∵∠BAC=90°,∴∠BDA=∠BAC.
又∵∠B为公共角,
∴△ABD∽△CBA.
(2)由(1)知△ABD∽△CBA,
∴,∴,∴BD=3.6.
8.D 解析:∵∠DAB=∠CAE,
∴∠DAB+∠BAE=∠CAE+∠BAE,
∴∠DAE=∠BAC,∴当添加条件∠D=∠B时,△ADE∽△ABC,故选项A不符合题意;当添加条件∠E=∠C时,△ADE∽△ABC,故选项B不符合题意;当添加条件时,△ADE∽△ABC,故选项C不符合题意;当添加条件时,△ADE和△ABC不一定相似,故选项D符合题意.故选D.
9.解:(1)证明:∵∠ABC=∠DBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,
∴∠ABD=∠CBE,
∵∠BAD=∠BCE,
∴△ABD∽△CBE.
(2)2.4
10.B 解析:∵EF⊥FG,∴∠EFB+∠GFC=90°,∵四边形ABCD为矩形,∴∠A=∠B=∠C=90°,AB=CD,∴∠GFC+∠FGC=90°,
∴∠EFB=∠FGC,∴△EFB∽△FGC,
∴,∵BE=3,BF=2,FC=6,∴,∴CG=4,同理可得△DAE∽△EBF,∴,
∴,∴AE=,∴BA=AE+BE=+3=,∴DG=CD-CG=-4=.故选B.
11.解:(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC,
∴∠BAD+∠ADB=120°.
∵∠ADE=60°,
∴∠ADB+∠EDC=120°,
∴∠DAB=∠EDC,
∴△ABD∽△DCE.
(2)∵△ABD∽△DCE,∴,
∵BD=4,CE=,∴,
解得AB=6.
“A”字型相似
模型展示
若DE∥BC,则△ADE∽△ABC 若∠1=∠2,则△ADE∽△ABC
1.(2024河南中考)如图,在 ABCD中,对角线AC、BD相交于点O,点E为OC的中点,EF∥AB交BC于点F.若AB=4,则EF的长为 ( )
A. B.1 C. D.2
第1题图 第2题图
2.(2024滨州中考)如图,在△ABC中,点D、E分别在边AB、AC上.添加一个条件使△ADE∽△ACB,则这个条件可以是 .(写出一种情况即可)
3.如图,已知△ADE∽△ABC,DE=3,BC=9.
(1)求的值.
(2)若AE=4,求AC的长.
“X”字型相似
模型展示
若DE∥BC,则△ADE∽△ABC 若∠1=∠2,则△ADE∽△ABC
4.将一副三角板按如图所示的方式放置,则的值为 .
5.如图,在△ABC中,AB=AC,BC恰好是∠ABD的平分线.
(1)求证:△APC∽△DPB.
(2)若AP=BP=1,AD=CP,求DP的长.
“母子”型相似
模型展示
若AC⊥BC,CD⊥AB,则△ACD∽△ABC 若∠1=∠2,则△ACD∽△ABC
6.如图,点D是△ABC的边AB上一点,∠ABC=∠ACD.
(1)求证:△ABC∽△ACD.
(2)当AD=2,AB=3时,求AC的长.
7.如图,在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高.
(1)求证:△ABD∽△CBA.
(2)若AB=6,BC=10,求BD的长.
“手拉手”型相似
模型展示
若∠1=∠2,∠B=∠D,则△ADE∽△ABC
8.如图,∠DAB=∠CAE,请你再添加一个条件,使得△ADE∽△ABC.则下列选项不成立的是 ( )
A.∠D=∠B B.∠E=∠C
C. D.
9.如图,D为△ABC内的一点,E为△ABC外的一点,且∠ABC=∠DBE,∠BAD=∠BCE.
(1)求证:△ABD∽△CBE.
(2)若AB∶DB=5∶2,AC=6,直接写出线段DE的长度: .
一线三等角型相似
模型展示
若∠1=∠2=∠3,则△ABC∽△CDE
10.如图,在矩形ABCD中,E、F、G分别在AB、BC、CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是 ( )
A.4 B. C. D.5
11.如图,等边三角形ABC中,D为BC边上一点,E为AC边上一点,∠ADE=60°.
(1)求证:△ABD∽△DCE.
(2)若BD=4,CE=,求△ABC的边长.
【详解答案】
1.B 解析:∵四边形ABCD是平行四边形,∴OC=AC,∵点E为OC的中点,∴CE=OC=AC,∵EF∥AB,∴△CEF∽△CAB,∴,即,∴EF=1.故选B.
2.∠ADE=∠C(答案不唯一)
解析:∵∠DAE=∠BAC,∴添加条件∠ADE=∠C,可以判定△ADE∽△ACB.(答案不唯一)
3.解:(1)∵△ADE∽△ABC,
∴.
(2)∵,AE=4,
∴AC=3AE=12.
4. 解析:由题意得AB∥CD,
∴△ABO∽△CDO,∴,
∵△ABC是等腰直角三角形,设AB=a,则BC=a,∴CD=a,
∴.
5.解:(1)证明:∵AB=AC,∴∠ABC=∠C,∵BC是∠ABD的平分线,
∴∠ABC=∠DBC,∴∠C=∠DBC,
又∵∠APC=∠DPB,
∴△APC∽△DPB.
(2)设DP=x,∵AP=PB=1,
∴AD=AP+DP=1+x,
又∵AD=CP,∴CP=1+x,
由(1)得△APC∽△DPB,
∴AP∶DP=PC∶PB,
即1∶x=(x+1)∶1,∴x2+x=1,
∴x2+x-1=0,
解得x1=,x2=(不合题意,舍去).∴DP=.
6.解:(1)证明:∵∠ABC=∠ACD,
∠CAB=∠DAC,
∴△ABC∽△ACD.
(2)∵△ABC∽△ACD,∴,即,∴AC=.
7.解:(1)证明:∵AD是斜边BC上的高,∴∠BDA=90°.
∵∠BAC=90°,∴∠BDA=∠BAC.
又∵∠B为公共角,
∴△ABD∽△CBA.
(2)由(1)知△ABD∽△CBA,
∴,∴,∴BD=3.6.
8.D 解析:∵∠DAB=∠CAE,
∴∠DAB+∠BAE=∠CAE+∠BAE,
∴∠DAE=∠BAC,∴当添加条件∠D=∠B时,△ADE∽△ABC,故选项A不符合题意;当添加条件∠E=∠C时,△ADE∽△ABC,故选项B不符合题意;当添加条件时,△ADE∽△ABC,故选项C不符合题意;当添加条件时,△ADE和△ABC不一定相似,故选项D符合题意.故选D.
9.解:(1)证明:∵∠ABC=∠DBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,
∴∠ABD=∠CBE,
∵∠BAD=∠BCE,
∴△ABD∽△CBE.
(2)2.4
10.B 解析:∵EF⊥FG,∴∠EFB+∠GFC=90°,∵四边形ABCD为矩形,∴∠A=∠B=∠C=90°,AB=CD,∴∠GFC+∠FGC=90°,
∴∠EFB=∠FGC,∴△EFB∽△FGC,
∴,∵BE=3,BF=2,FC=6,∴,∴CG=4,同理可得△DAE∽△EBF,∴,
∴,∴AE=,∴BA=AE+BE=+3=,∴DG=CD-CG=-4=.故选B.
11.解:(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC,
∴∠BAD+∠ADB=120°.
∵∠ADE=60°,
∴∠ADB+∠EDC=120°,
∴∠DAB=∠EDC,
∴△ABD∽△DCE.
(2)∵△ABD∽△DCE,∴,
∵BD=4,CE=,∴,
解得AB=6.
